Responsiveness of Single versus Composite Measures of Pain in Knee Osteoarthritis

Abstract

Objective

In rheumatoid arthritis, composite outcomes constructed from a combination of outcome measures are widely used to enhance responsiveness (sensitivity to change) and comprehensively summarize response. WOMAC pain is the primary outcome measure in many osteoarthritis (OA) trials. Information from other outcomes, such as rescue medication use, and other WOMAC subscales, could be added to create composite outcomes, but the sensitivity of such a composite has not been tested.

Method

We used data from a completed trial of Tanezumab for knee OA (NCT00733902). The WOMAC questionnaire and rescue medication use were measured at multiple time points, up to 16 weeks. Pain and rescue medication outcomes were standardised and combined into 3 composite outcomes via principal components analysis to produce one score (composite outcome) and their responsiveness was compared to WOMAC pain, the standard. We pooled all treatment doses of Tanezumab into one ‘treatment’ group, for simplicity, and compared this to the control group (placebo).

Results

The composite outcomes showed modestly but not statistically significantly greater responsiveness when compared to WOMAC pain alone. Adding information on rescue medication to the composite improved responsiveness. While improvements in sensitivity were modest, the required sample sizes for trials using composites was 20-40% less than trials using WOMAC pain alone

Conclusion

Combining information from related, but distinct, outcomes considered relevant to a particular treatment improved responsiveness, could reduce sample size requirements in OA trials and might offer a way to better detect treatment efficacy in OA trials.

Introduction

Clinical trialists have a tendency to measure many outcomes in a trial. Several of these outcomes (often deliberately) cover overlapping ‘domains’, in an attempt to ensure that the ‘signal’ of a true change in an outcome following an intervention is captured. Pain is a good example; researchers will often use a variety of similar pain-related outcomes in interventional trials.

Pain is a complex, multidimensional measure(1,2), and generating just one scale or item that adequately captures most, if not all, aspects of pain is challenging. Furthermore, as pain is strongly related to functional limitation(3), the most appropriate pain outcome might cover aspects of both pain and function. The optimal clinical trial pain outcome(s) should additionally be sensitive to change following an intervention, by which we mean the outcome’s ability to detect a change, often also termed an outcome’s “responsiveness”(4), discriminating well between a true signal (treatment effect) and noise (random variation).

Composite outcomes are a way of combining (often related) indices or scores to form one overall outcome. This approach, which has been used in many disease areas, including osteoarthritis(5), rheumatoid arthritis(6–8) and asthma(9), may improve the capture of a domain more completely as it takes account of more information than one outcome alone. Pain measurement appears particularly suited to this approach, given its complexity. Combining information from several different domains may additionally improve a composite’s ability to detect a change when one truly occurs, and therefore the measure’s sensitivity to change (also termed ‘responsiveness’) may also be improved.

Constructing Composites: Available Methods

There are several methods for combining outcomes into composites. Some of these facilitate domain coverage; others increase responsiveness. Ideally, the method used should improve both. The simplest method of combining two or more outcomes is through summing or averaging them(5). This method assumes that the constituent outcomes have equal weighting on the composite, and that units from the constituent outcomes are comparable and exchangeable.

A second method of combining multiple outcomes is via the inclusion of weights, which assign ‘importance’ of constituent outcomes. The composite is produced my multiplying each constituent outcome by its weight, and then summing these scores. An example of this is the DAS28(6,7). Weights can be derived from a variety of sources, including statistical modelling (as in the case of the DAS), but also from group consultation, for example via a Delphi exercise (10–14).

An alternative data-driven approach than those discussed is principal components analysis, a data-reduction method which inherently concentrates as much of the variance from constituent outcomes into as few factors as possible. This method may produce a composite outcome which more completely captures the variance from an underlying multidimensional process, such as pain.

Theoretically, combining several outcomes purporting to measure aspects of pain and its consequences such as function loss and rescue medication use should increase domain coverage (as each outcome contributes some information about the pain signal), and therefore responsiveness. Since all of the contributing outcomes purport to measure that same latent factor, namely pain, the analysis model used should assume a priori a one factor solution, rather than generating multiple outcomes. This way, we can combine all outcomes related to pain into one composite outcome, which will hopefully show maximal responsiveness in pain.

This study sought to combine several pain outcomes using principal components analysis, taken from a large completed clinical trial of a treatment that reduced pain, and compare the relative responsiveness of these composites to the uncombined WOMAC pain subscale score alone, to establish whether the inclusion of additional pain information improves responsiveness following administration of an intervention.

Assessment of responsiveness is optimal in certain trial designs. The ideal trial should contain a treatment arm with an intervention which is known to truly change the construct of interest (pain, for example); a control arm which is known to truly not change the construct of interest, and at least two (ideally more) time points in both arms, over which the change in each outcome is assessed. The trial we selected had these features. If the outcome of interest is not changed during the study, then, it is not possible to assess responsiveness.

In the present study, we sought to assess the responsiveness of several composite outcomes, created using a using the principal components method.

Methods

The data used in this study was taken from a large completed clinical trial of Tanezumab in participants with knee osteoarthritis (NCT00733902). This trial was a 32 week four-arm parallel-group phase III trial, comparing 3 doses of tanezumab (2.5, 5, or 10 mg) against placebo. Participants were observed at baseline, 2, 4, 8, 12, 16, 24, and 32 weeks; we used data from the 2 week visit to the 16 week visit, as data for rescue medication use were collected only at these visits,. For simplicity, we pooled all tanezumab doses (2.5mg, 5mg, and 10mg) together into one ‘treatment’ group and compared this to the placebo group. Further details regarding the trial’s design, as well as data on unstandardised outcome scores in the unpooled treatment groups, have been published previously(15). This study is a reanalysis of completed clinical trial data, and is exempt from ethical review under the NHS Health Research Authority Guidelines.

Variable Definitions

Single Outcomes

We used the following pain and pain-related outcomes featured in NCT00733902: the WOMAC pain, stiffness, and function subscales; and number of rescue medication pills taken per week.

All single outcomes were standardised (converted to z-scores) to allow comparison between outcomes with different scales.

Composite Outcomes

Using four single outcomes to generate composites, and including information from at least two, and up to 4 outcomes in each composite, gives 11 possible combinations available from which composites could be generated. We opted to generate a total of three composite outcomes, which were felt to be the most meaningful combinations of the 11 possible combinations available, as they assess whether including additional components of the WOMAC, or rescue medication, have an impact on the responsiveness observed. Composite 1 consisted of the WOMAC pain subscale plus rescue medication,. Composite 2 consisted of all three WOMAC subscales (pain, stiffness, and function),. Finally, composite 3 consisted of all three WOMAC subscales, plus the rescue medication outcome.. Composite outcomes were derived by including the selected combination of variables in a principal components analysis (PCA), which assumed a one factor solution. We opted for PCA, given its propensity to maximise the amount of variance captured in the first (and in this case, only) derived component. We assumed that all included outcomes measured different aspects of one latent (multidimensional) pain variable, and forcing a one component solution therefore ensured that this variable was derived. This idea is partially supported by previous work by Angst et al. (2005), who found that unrestricted factor analysis of individual WOMAC items established new factors which drew from both the pain and function subscales, and merged them together(16). It also simplified the analysis, as it creates only one composite outcome, rather than allowing many composite factors to be generated in each PCA, as may occur in a factor analysis model. We ran a total of three PCA models, one corresponding to each composite, which in turn generated three composite outcomes. No rotation method was used, as only one component was produced in each model. Rotation of the factor model (of any type, varimax, promax, or other) is not indicated in this method, as a one factor solution effectively has only one possible orientation, which is the one produced in the initial factor solution.

We pooled together data from all study visits in the analysis models (rather than using data from baseline only, for example) assuming that it was best to include the maximum available number of observations and therefore maximise the amount of data used in the PCA models. All composite outcomes produced were also standardised, allowing fair comparison with each other, and to the single outcomes.

Analysis Approach

All composite outcome measures were compared to the standard measure, WOMAC pain.

All of the single outcomes (WOMAC pain subscale score, WOMAC function subscale score, WOMAC stiffness subscale score, and number of rescue medication pills taken) featured had been standardised prior to inclusion in the factor analysis models, and the composites (composite 1, 2, and 3, detailed above) were by default also standardised outcomes. Having all variables standardised (as z-scores) allows direct comparison of outcomes with different units.

We used a random-effects panel linear regression (via SAS software’s PROC MIXED) to assess change in the standardised outcome score over time, with outcome type, study visit, and treatment group (either tanezumab or placebo) and all possible interactions, as predictor variables. Constructing the data in ‘long format’, and using outcome type as a categorical dummy-coded variable allows direct testing for differences in responsiveness between all outcomes in one statistical model (as opposed to generating multiple models, one for each outcome). The full model used was:

y_itj = μ + X_itj1β₁ + X_itj2β_2j + X_itj3β_3t + X_itj4β_4j + X_itj5β_5t + X_itj6β_6j + X_itj7β_7tj + u_i + W_it

where y_itj = standardized score; X_itj1 = treatment group; X_itj2 = outcome type (the categorical data outlined above, which was coded in the form of dummy variables); X_itj3 = study visit (either 2, 4, 8, 12, or 16 weeks, coded as dummy variables) ; X_itj4 = treatment group × outcome interaction; X_itj5 = treatment group × study visit interaction; X_itj6 = outcome type × study visit interaction; X_itj7 = treatment group × outcome type × study visit interaction; μ = model intercept, u_i = subject-level random effect, and W_it = error. This model included a total of 4 types of interaction effects (3 two-way interactions, and one 3-way interaction), which allows the greatest number of degrees of freedom with respect to modelling the different outcomes over time, and therefore makes no prior assumptions about treatment trajectories, at the cost of power to detect differences.

SAS’s PROC MIXED command uses a likelihood-based approach, treating missing observations as missing-at-random.

We used linear combinations of coefficients from the regression model (using SAS PROC ESTIMATE) to produce the difference in standardised change between the WOMAC pain subscale and each composite outcome’s standardised change, at each study time point. This allowed us to formally test whether the outcomes differed from the WOMAC pain subscale in terms of the observed standardised change, at each of the 5 time points in the study.

Statistical analysis used SAS^® software version 9.3; (SAS Institute Inc., Cary, NC, USA). A nominal alpha level of 0.05 was used for all confidence intervals.

Results

Study Sample Demographics

At baseline, the placebo group (N=172) comprised 119 females (69.2%), with a mean age of 62.2 years, Kellgren-Lawrence grades 2, 3 and 4 of 39.5%, 47.7%, and 12.8% respectively, mean WOMAC pain subscale score (0-10) of 7.1, and mean WOMAC function subscale score (0-10) of 6.6. The pooled tanezumab group (N=518) at baseline had 301 females (58.1%), with a mean age of 61.4 years, Kellgren-Lawrence grades 2, 3 and 4 of 38.4%, 46.3%, and 14.5% respectively, mean WOMAC pain subscale score (0-10) of 7.1, and mean WOMAC function subscale score (0-10) of 6.8.

Ten participants had missing observations for all outcomes at the selected time points of interest, giving a total sample size for this analysis of 680, compared with the original trial sample size of 690, with 509 in the pooled tanezumab group, and 171 in the placebo group. Data for the 680 included patients could have been collected on 7 outcomes, at 5 time points, giving a total of 23,800 possible observations. Of these, 20,597 were actual observed data points, meaning that 3,203 observations were missing (13.5%).

Principal Components Analysis Results

The PCA process generated composites with component loadings shown in table 1. WOMAC pain and stiffness subscales consistently had the greatest, and indeed equal, loading, closely followed by the WOMAC function subscale. When all 3 WOMAC subscale variables were included in the PCA model (in composite 3), the rescue medication’s loading dropped considerably.

Table 1. Pain Outcome Combinations Used to Create Composites, with Component Loadings.

		Component Loading
Composite Outcome	Component Eigenvalue	Proportion of Variance Explained by Component	WOMAC Pain	WOMAC Stiffness	WOMAC Function	Number of rescue medication pills/week
Composite 1: WOMAC pain & number of rescue medication pills	1.32	65.86%	0.81			0.81
Composite 2: WOMAC Pain, Stiffness, & Function	2.85	95.03%	0.98	0.98	0.96
Composite 3: WOMAC Pain, Stiffness, & Function, & number of rescue medication pills	2.99	74.77%	0.97	0.97	0.95	0.45

Greyed-out cells indicate that the variable was not used when generating the composite. For example, composite 1 used a principal-components analysis featuring the WOMAC pain subscale score and number of rescue medication pills only. In all principal components models, the first component produced was used as the composite outcome.

Composite Outcome Performance

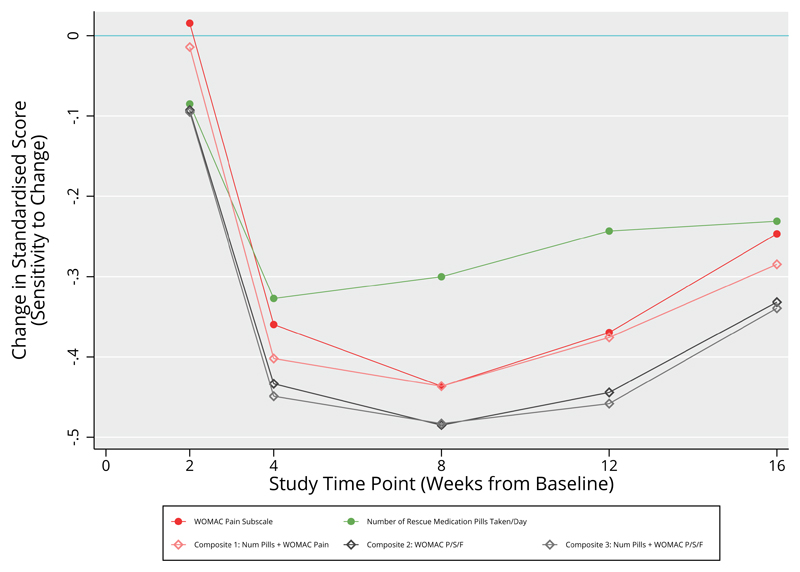
All composites showed responsiveness greater than at least some of their constituent outcomes on their own, and this difference was consistent across multiple time points (figure 1). Composite 1 showed consistently greater responsiveness than the WOMAC pain subscale alone. The remaining two composites displayed responsiveness greater than all other constituent outcomes, except the WOMAC stiffness subscale.

Figure 1.

Sensitivity to Change of Single Pain-Related Outcomes from the Tanezumab Trial. Values plotted are the control-treatment differences in standard score, at different study time points. More negative values indicate increased sensitivity to change

None of the single or composite outcomes showed responsiveness that was consistently statistically significantly better than that observed in the WOMAC pain subscale, at the chosen alpha level (table 2).

Table 2. Required Sample Sizes for a Hypothetical New Trial of the Same Design, Using the Observed Effect Sizes from the Present Trial as the Basis of the Sample Size Calculation.

Primary Outcome of New Trial	Week 2		Week 4		Week 8		Week 12		Week 16
	Expected Between-groups standard-score difference	Required sample size to detect this difference	Expected Between-groups standard-score difference	Required sample size to detect this difference	Expected Between-groups standard-score difference	Required sample size to detect this difference	Expected Between-groups standard-score difference	Required sample size to detect this difference	Expected Between-groups standard-score difference	Required sample size to detect this difference
WOMAC Pain Subscale	0.02	106870	-0.37	236	-0.44	164	-0.38	222	-0.26	476
WOMAC Physical Function Subscale	-0.08	4874	-0.41	188	-0.45	158	-0.42	184	-0.33	298
WOMAC Stiffness Subscale	-0.21	748	-0.52	122	-0.54	108	-0.54	112	-0.43	176
Number of RM Pills Taken/day	-0.08	4362	-0.33	290	-0.31	332	-0.25	496	-0.24	550
Composite 1: WOMAC pain & number of RM pills	-0.01	196818	-0.41	190	-0.45	162	-0.39	214	-0.29	364
Composite 2: WOMAC Pain, Stiffness, & Function	-0.09	3780	-0.44	164	-0.49	134	-0.45	156	-0.34	270
Composite 3: WOMAC P, S, F, & number of RM pills	-0.09	3600	-0.46	154	-0.49	132	-0.47	146	-0.35	260

Sample sizes are calculated for a hypothetical new trial with an expected between-groups standard deviation of 1, power of 0.8, and alpha level of 0.05, in all cases.

We next examined the impact of the observed differences in responsiveness on sample size requirements for a hypothetical new trial featuring the same design (table 3). For example, the WOMAC pain subscale between-groups standardised change at 4 weeks was a difference of -0.37. A hypothetical new trial of identical design observing this between-group difference for the WOMAC pain outcome would require 236 participants (118 per group) to achieve 80% power with a two sided 5% type-I error rate. In contrast, using composite 1 (i.e. including information on rescue medication as well as the WOMAC pain subscale score) as the primary outcome which had an observed difference at 4 weeks of -0.41., the same trial would need 190 participants (95 per group) to achieve 80% power with this difference - a saving of 46 participants. When the observed differences between treatments is smaller, the reduction in sample size was more extreme: the WOMAC pain difference at 16 weeks (-0.26) would require 476 participants for 80% power in a hypothetical new trial, compared to only 364 participants when using composite 1 (using the observed difference of 0.29), a saving of 112 participants.

Table 3. Difference in Between-Group Standard Score Change between Outcomes Considered and WOMAC Pain Subscale.

	Outcome	WOMAC pain subscale between-groups standard score difference (reference)*
		Week 2	Week 4	Week 8	Week 12	Week 16
	WOMAC Pain Subscale (Reference)	0.02 (-0.16 to 0.20), 0.85	-0.37 (-0.55 to -0.18), <0.001	-0.44 (-0.63 to -0.26), <0.001	-0.38 (-0.57 to -0.19), <0.001	-0.26 (-0.45 to -0.07), 0.01
	Outcome	Difference from WOMAC pain subscale, in standard score units**
		Week 2	Week 4	Week 8	Week 12	Week 16
Individual Outcomes	WOMAC Physical Function Subscale	-0.10 (-0.25 to 0.06), 0.22	-0.04 (-0.21 to 0.12), 0.59	-0.01 (-0.18 to 0.16), 0.90	-0.04 (-0.22 to 0.15), 0.70	-0.07 (-0.25 to 0.11), 0.46
	WOMAC Stiffness Subscale	-0.22 (-0.38 to -0.07), 0.01	-0.15 (-0.31 to 0.01), 0.07	-0.10 (-0.27 to 0.06), 0.22	-0.16 (-0.34 to 0.02), 0.09	-0.17 (-0.35 to 0.01), 0.07
	Number of RM Pills Taken/day	-0.10 (-0.26 to 0.05), 0.20	0.04 (-0.13 to 0.20), 0.66	0.13 (-0.03 to 0.30), 0.12	0.13 (-0.05 to 0.31), 0.17	0.02 (-0.17 to 0.20), 0.85
Composite Outcomes	Composite 1: WOMAC pain & number of RM pills	-0.03 (-0.19 to 0.13), 0.71	-0.04 (-0.21 to 0.12), 0.60	0.00 (-0.17 to 0.16), 0.96	-0.01 (-0.19 to 0.18), 0.94	-0.04 (-0.22 to 0.15), 0.69
	Composite 2: WOMAC Pain, Stiffness, & Function	-0.11 (-0.26 to 0.05), 0.17	-0.07 (-0.24 to 0.09), 0.38	-0.05 (-0.21 to 0.12), 0.57	-0.07 (-0.26 to 0.11), 0.42	-0.09 (-0.27 to 0.10), 0.36
	Composite 3: WOMAC P, S, F, & number of RM pills	-0.11 (-0.27 to 0.05), 0.17	-0.09 (-0.25 to 0.07), 0.28	-0.05 (-0.22 to 0.12), 0.56	-0.09 (-0.27 to 0.09), 0.34	-0.09 (-0.28 to 0.09), 0.33

This table outlines the difference in standard score between the control group, and the treatment group, in the variables of interest, at different time points in the study. Values shown are mean (95% CI), p. *This row indicates the difference in standard score between placebo and treatment in the WOMAC pain subscale, at each study time point. Negative values indicate greater pain reduction in the treatment group than the control group, and vice versa. For example, at week 4, the standardised WOMAC pain score in the treatment group reduced by 0.37 points more than the control group at week 4, indicating a greater reduction in pain in the treatment group at week 4. **These rows indicate how the between-groups difference in the other pain outcomes compared to the WOMAC pain subscale. For example, at week 2, the between group difference in the WOMAC physical function standard score was -0.08, indicating that the between group difference differed from the WOMAC pain subscale difference by -0.10 points. This indicates that there was an average greater reduction in pain in the treatment group compared to the control group, in the WOMAC function subscale, as compared to the WOMAC pain subscale, in the same patients at the same time point, and therefore that the WOMAC physical function subscale showed greater sensitivity to a change in pain at this time point than the WOMAC pain subscale. More negative values indicate increased sensitivity to change in the outcome shown, relative to the WOMAC pain subscale. Positive values indicate greater sensitivity to change in the WOMAC pain subscale. RM = rescue medication

Discussion

We found that composite outcomes generally had moderately greater responsiveness in a large OA trial than did the usual standard outcome of these trials, WOMAC pain. That suggests if one of these composite outcomes were used as the primary outcome in an OA trial that fewer subjects would be needed to demonstrate treatment efficacy.

The improvements in responsiveness did not meet the criteria for a statistically significant difference, but perhaps a more salient measure of their import was to determine what effect using these outcomes had on the sample size needed to be likely to show statistically significant effects of treatment vs. placebo. We found that the reduction in sample size was substantial, ranging from roughly 20 to 40%. Thus, composites could substantially diminish the sample sizes needed in an osteoarthritis trial whose main outcome is pain.

Eigenvalues from the three composite models all were much greater than the 1.0 cut-off typically used to select retained factors in a PCA model(17), and a large proportion of the variance in the outcomes was captured by the first component in the PCA model, as anticipated (table 1). The second factor listed in the model output (which was not extracted in this analysis) in all cases had an eigenvalue much less than 1, lending support to the idea that the selected correlated outcomes are well captured as one multidimensional ‘pain’ component.

Rescue medication use, whilst contributing to the ‘pain’ component the least (table 1), appeared to still improve responsiveness: composites including this outcome: composites 1 (WOMAC pain plus rescue medication use) and 3 (WOMAC pain, stiffness, and function, plus rescue medication) showed slight improvements in responsiveness compared with those that did not include rescue medication use.

Aside from the methods used to combine outcomes, the method chosen to assess responsiveness is also important(18,19). Several methods are commonly cited to quantify an outcomes’ responsiveness: the standardised response mean (SRM)(20), the effect size (ES)(18), either Glass' Δ(21) or Cohen’s d(22), depending on the standard deviation used, or Guyatt’s responsiveness index (GRI) (23). All of these methods have two important limitations, however. First, all relate to calculating responsiveness over two time points – these methods cannot easily be generalised to a study which has three or more follow-up visits. This prevents assessment of how responsiveness may fluctuate over time, for example to assess how rapidly a measurement scale changes, and limits the definition of responsiveness only to the magnitude of change relative to its variance, rather than the speed of response. Second, these methods generate coefficients which do not directly assess statistical inference. Any differences in responsiveness coefficients are assessed descriptively. Some methods have been proposed (modified jackknife procedure (5,24,25), bootstrapping (26)) to address this issue, but other methods which directly perform statistical inference as part of the method generating the coefficient would be desirable.

An alternative methodology involves the use of z-scores (standard scores) (27), the method we used. Converting each outcome’s absolute score to a z-score allows direct comparison of change in an outcome at different time points, thereby allowing direct assessment of change over time, and direct comparison between different outcomes. This methodology has been used previously to compare non-composite outcomes(28).

The PCA approach used assumes that an intervention will alter several related aspects of a common construct (i.e. several aspects of pain), and therefore combining all the multidimensional aspects of pain together to form one pain outcome should increase responsiveness. However, if one aspect of pain is changed alone, then the combination of many aspects of pain which do not change may in fact decrease the sensitivity of the composite. The finding that the WOMAC stiffness subscale was the most sensitive outcome may fit this explanation - It may be, at least in this trial, that the WOMAC stiffness subscale was the closest correlate to the actual latent factor altered by the treatment, which would explain why this outcome had the great responsiveness, and the fact that inclusion of other outcomes in the composite eroded the responsiveness. This finding may be limited to this specific intervention (tanezumab) alone – as the agent’s anti-nerve growth factor effect may have a greater impact on the stiffness sensation than other pain subscales(15,29).

Freemantle et al. (2003) provide a comprehensive discussion on the use of composite outcomes in clinical trials(30). They highlight how composite outcomes can obfuscate changes in constituent outcomes. This is particularly problematic when outcomes are unrelated (for example, a composite which combines cardiovascular events and mortality), although they note the statistical advantages (increased power and sensitivity) that arise through the construction of composites(30,31). This discussion highlights how both the outcomes used in the composite, and the method by which they are combined, are important. The present study combined the three WOMAC subscales, pain, stiffness, and function, into one composite outcome. We assumed that these three subscales were all aspects of the same construct (pain). The PCA (table 1) produced extremely high factor loading in all three subscales, suggesting that they are indeed highly correlated, at least in this study. In contrast, if pain and function were discrete constructs, then the PCA should have failed, with one of the components having a much larger factor loading than the other. Both Ryser et al. (1999), and Angst et al. (2005) found close association between pain and function WOMAC subscales, partly supporting this finding(16,32). In addition, a specific analysis of item overlap on the WOMAC pain and function subscales by Stratford et al. (33) found significant item redundancy between the pain and function subscales, and a further factor analysis on the WOMAC items found clustering of items not by subscale, but by activity(34), suggesting that the three subscales are not distinct.

We surmised that responsiveness in the outcomes may differ in time, as well as in magnitude. In this study, all outcomes appeared to have responded at the same time point, and retained their relative positions consistently over time (none of the outcome’s trajectories crossed over each other over time, figure 1),

There are limitations to this analysis. We observed only very few statistically significant differences between outcomes. The trial was designed to observe a difference in the primary outcome between treatment groups (a relatively large difference), and was not designed to compare treatment differences between outcomes (much smaller differences). Therefore even the large sample size in the trial provides relatively low power to detect differences between outcomes. Ideally, in the future, one would design this analysis to take place prior to trial commencement, so that adequate statistical power can be built into the study from the beginning. In addition, to best characterise the model fit to the data, we allowed many interaction effects, which increased model/data fit at the expense of statistical power. We have assumed in this analysis that the covariate structure of the pain outcomes, and the relationship between the outcomes and the latent (unobserved) pain outcome are consistent between studies, and therefore generalisable across other studies. This is a relatively strong assumption, and would require validation in other datasets to allow wider generalisation to other trials with confidence.

While the aim of this approach was to include additional information on pain from rescue medication data, this outcome may not be optimal. Rescue medication is a challenging variable to collect data on accurately, and therefore the likelihood is that measurement error of this variable is high. This may provide an explanation for why the improvement in sensitivity of composites including rescue medication, are small.

Even though the between-outcome differences were not statistically significant, even a small improvement in responsiveness can have an impact upon sample size calculations (table 3). This produces gains in efficiency without collecting any novel data just by reanalysing the data using a method which produces a more sensitive, and therefore efficient, outcome. We could have included further assessment of other composites made from different combinations of the 11 possible from the four single outcomes used, for example one using WOMAC pain plus WOMAC stiffness. We opted to create the three composites which would have the most pragmatic impact on outcome inclusion/exclusion when designing a trial. The alternative, generating all 11 possible combinations and comparing them head to head, would reduce the statistical power of the model to discern differences between all 11 composite outcomes.

The PCA approach to generating a composite outcome by its nature produces a unitless score. While the generated score may have increased responsiveness compared to one of the constituent outcomes, it is more difficult to ascertain the clinical importance of the magnitude of the observed effect, in comparison to another outcome with meaningful units, and an agreed minimally clinical importance difference (MCID). A downside of use of the composite is the absence of known values of MCID but this could be established if a specific composite were widely used.

The choice of primary and secondary outcomes in this trial limited the choice of outcomes available to combine into a composite Ideally, we would have preferred to use a trial featuring a wider range of pain outcomes, particularly the more recent KOOS(35) and ICOAP(36) questionnaires; however a dataset using at least these outcomes among other pain outcomes, and featuring the other requirements was not available to the authors.

The present findings are similar to our previous paper, which used data from two other completed clinical trials of non-drug interventions(28). In both of these trials, the WOMAC stiffness subscale also showed an increased, but non-statistically-significant, degree of responsiveness compared to the other two WOMAC subscales. Angst et al. (2001; 2008), in contrast, found the WOMAC pain subscale to be the most sensitive outcome to change(5,24), however these studies did not examine rescue medication, and used a two-time point approach only. Further, the two studies previously analysed were both prospective cohort studies lacking a control group. Thus, optimizing the detection of treatment effect over placebo was not possible in the two Angst et al. analyses.

In summary, we investigated whether collapsing several measures of a multidimensional construct into one composite outcome through the use of PCA could help improve responsiveness following an intervention. Adding rescue medication alongside other elements of the WOMAC showed improved responsiveness, greater than the constituent outcomes.

Significance & Innovations.

• This study attempts to evaluate meaningful ways of combining single outcomes in a way that improves responsiveness, gaining more power to detect treatment effects without collecting more data.

• This can improve efficiency in future clinical trials, as it helps improve detection of smaller treatment effects with fewer participants.

• Combining outcomes appears to produce composites with greater sensitivity to change than constituent parts.