Significance
Electric field sensing is an important tool in metrology and characterization applications. Here we show that photoluminescent defects in silicon carbide, such as divacancies and silicon vacancies, can provide local information of radio-frequency electric fields. Using all-optical excitation, the charge state of the defect is controlled, measured, and shown to be affected by this electric field. This sensing technique enables spatial 3D mapping as well as spectral resolution of the electric field. By taking advantage of the piezoelectricity in silicon carbide, the technique also provides similar information on local radio-frequency strain waves. This method is expected to be broadly applicable to other materials and of interest for high-power electronics and high-frequency microelectromechanical systems.
Keywords: electrometry, silicon carbide, defects, photoluminescence, charge conversion
Abstract
Optically active point defects in various host materials, such as diamond and silicon carbide (SiC), have shown significant promise as local sensors of magnetic fields, electric fields, strain, and temperature. Modern sensing techniques take advantage of the relaxation and coherence times of the spin state within these defects. Here we show that the defect charge state can also be used to sense the environment, in particular high-frequency (megahertz to gigahertz) electric fields, complementing established spin-based techniques. This is enabled by optical charge conversion of the defects between their photoluminescent and dark charge states, with conversion rate dependent on the electric field (energy density). The technique provides an all-optical high-frequency electrometer which is tested in 4H-SiC for both ensembles of divacancies and silicon vacancies, from cryogenic to room temperature, and with a measured sensitivity of . Finally, due to the piezoelectric character of SiC, we obtain spatial 3D maps of surface acoustic wave modes in a mechanical resonator.
The detection of electric fields and charge is critical to a wide range of applications, including device characterization (1), mapping electrical potential (2), and electrical quantum metrology (3–5). Recently, electrometry was demonstrated using the spin state of optically active point defects, specifically nitrogen-vacancy (NV) centers in diamond, enabling quantum-limited sensitivity with nanoscale spatial resolution (6). Similar experiments were also reproduced in divacancies (VV) in silicon carbide (7). Nevertheless, electric fields (and strain) only weakly interact with the spin state of typical qubit defects by altering the zero-field splitting (7, 8) or hyperfine interaction (9, 10). In contrast, an impurity’s charge state, although not coherently controllable, is directly sensitive to the electric and charge environments which perturb the electronic wavefunction and is drastically modified by defect ionization and recombination (11). The defect charge state provides a naturally occurring analog of quantum point contacts, single electron transistors, or other charge-based electrometry devices (3, 4).
Optical detection of charge states can be adapted, depending on the defect: For the NV center in diamond, a change from the to the provides different emission spectra (12), while in VV or silicon vacancies () in 4H- and 6H-SiC, only one charge state (, ) has a known photoluminescence (PL) spectrum (13, 14). Charge conversion between the various charge states can be efficiently realized by optical pumping at specific wavelengths (11, 15, 16). Here we show that the optical charge conversion (OCC) rate between the bright and dark charge states of both VV and defects is strongly modulated by the presence of an applied radio-frequency (RF) or microwave (megahertz to gigahertz) electric field and therefore can be detected through changes in PL. The frequency range of this electrometry by optical charge conversion (EOCC) would be challenging using conventional spin sensing due to limitations in Rabi drive rates, although a method of circumventing this limit has recently been shown (17). We further demonstrate spectroscopic techniques (frequency and phase resolution) using EOCC as well as its application to 3D microelectromechanical system (MEMS) characterization.
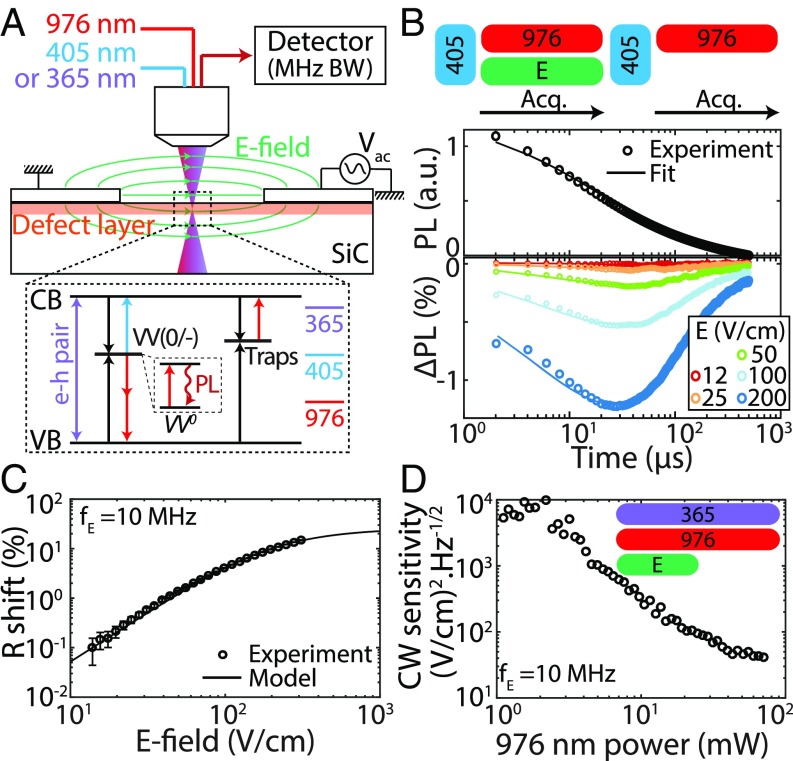
In 4H-SiC, OCC of VV ensembles requires a near- or above-bandgap (3.2 eV) excitation to obtain (bright), while illumination below 1.3 eV pumps the defect toward a dark charge state (likely ) (11, 18). We use either 365 nm (continuous) or 405 nm (pulsed) light as a reset to and 976 nm laser as the dark-state pump, with the 976-nm laser also exciting PL from . Fig. 1A shows all dominant capture and photoionization transitions in the system, as well as electron-hole pair generation by 365 nm illumination as described in ref. 11. The experimental setup consists of two laser beams focused on VVs localized near the surface, in between two metal contacts on top of the SiC substrate (SI Appendix, Fig. S1). Applying a voltage across the contacts generates in-plane electric fields orthogonal to the c axis. We first characterize OCC transient decays by resetting the charge state with 405 nm illumination followed by a 976-nm pump laser. A fast detector is able to capture a complete transient signal from bright to dark in a single experiment (see Materials and Methods for more details), as shown in Fig. 1B (Top). The decay is well fitted by a simple stretched exponential decay , where is the characteristic decay time and the stretch factor, the latter describing the complexity of the charge conversion mechanism ( for simple photoionization and for competition between ionization, carrier capture, and carrier diffusion) (19, 20). We then apply simultaneously an RF electric field along with the 976-nm illumination, resulting in a time-dependent PL variation as plotted in Fig. 1B (Bottom), where is the root-mean-square (rms) amplitude of the electric field with corresponding frequency MHz. The fit function in this case becomes , with and the relative rate and stretch factor shifts under electric field.
Fig. 1.
EOCC. (A) Schematic of the optical setup with one reset color (365 nm or 405 nm) and one pump color (976 nm). Illumination at 365 nm generates electron-hole (e-h) pairs that reset VV to (bright state) in the steady state, at 405 nm directly ionizes (dark state) to , and at 976 nm excitation converts to by direct two-photon ionization or indirectly by one-photon ionization of local traps (11, 18). In addition, photoluminescence is provided through excitation at 976 nm. VV() is the transition energy level between the neutral and negatively charged states. VB and CB are the valence and conduction bands, respectively. An RF electric field (rms amplitude , frequency ) is applied across a coplanar capacitor with a 17-m gap. VVs are created by carbon implantation immediately below the surface. A fast detector with 10-MHz bandwidth (BW) allows for direct detection of a full OCC transient signal in a single measurement. (B) VV is first reset to its bright state () by 405-nm illumination, followed by PL detection (Top) of the charge conversion toward the VV dark state by 976-nm excitation. Bottom shows the difference between conversion with and without applied electric field (10 MHz). Data are fitted to a stretched exponential function with kHz and obtained using a global fit for all electric field values. (C) Fitted decay rate shifts as a function of electric field. Error bars are 95% confidence intervals. (D) EOCC sensitivity with continuous (CW) laser (365 nm and 976 nm) pumping as a function of 976-nm laser power. We estimate a 10% error in electric field estimation, corresponding to 20% error in sensitivity (not shown). Acq, acquisition.
While remains nearly constant ( observed variations), the electric field changes (Fig. 1C) according to a phenomenological quadratic dependence with saturation
| [1] |
where corresponds to a time average over an oscillation of the RF electric field, is the saturation electric field, and is the maximum shift when . We find for VV in this sample and V/cm. It is unclear whether these values are specific to the sample or to the defect itself and additional studies are required. In the first case, EOCC would likely be due to variations in carrier recapture after ionization and would depend on parameters such as mobility or drift velocity. In the second and most likely case, may be directly related to the defect electronic wavefunction and changes in photoionization and capture cross-sections (Fig. 1A). Finally, the EOCC effect was confirmed separately in multiple SiC wafers, in bulk and implanted ensembles, and using different device geometries (Materials and Methods). We also did not observe any magnetic field dependence of EOCC up to 400 G, precluding any spin contribution to the signal.
Due to the quadratic response given by Eq. 1, EOCC effectively measures the electric field energy density. We define the sensitivity of this sensing technique for all values of electric fields below saturation as
| [2] |
where is the signal-to noise ratio (using SD) for a given electric field and is the experiment time (i.e., PL integration time). Fig. 1D shows sensitivity values as a function of 976 nm pump power, optimized by using continuous 976-nm and 365-nm illumination while locking in on the electric field turned periodically on and off. In this sample, we obtain a sensitivity at 10 MHz as high as for an estimated ensemble of VVs within the confocal spot size. Similar sensitivities have been demonstrated with dc and low-frequency (1 MHz) spin sensing (6, 21), although the quadratic dependence in makes it hard to properly compare EOCC and spin-based sensing (linear dependence). Higher sensitivities may be achieved with higher defect densities, e.g., with larger depth profile and higher implantation doses, to the limit of strong pinning of the charge state. Higher laser power may also improve the sensitivity by one to two orders of magnitude by increasing the decay rate R. Resonant optical excitation on the zero-phonon line may also enhance the charge conversion rate due to two-photon ionization (11), and alternative defects with higher ionization cross-section could be investigated. Sensitivities down to 0.1–1 should be achievable with commercially available materials. The measured sample and VV concentrations are similar to those used for typical spin experiments, readily allowing EOCC to be combined with other spin-sensing techniques.
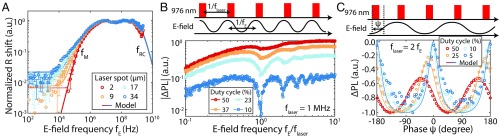
We then characterize in Fig. 2A the frequency response of the EOCC technique by looking at the rate shift as a function of electric field frequency, from quasi-dc (100 Hz) to 2 GHz. Above 1 GHz, diminishes as expected from parasitic capacitances of the device (low-pass filtering). Below 1 MHz, also decreases, possibly owing to the creation of a steady-state space charge defined by the laser spot and the applied electric field. At low frequency, the optical pumping ionizes VV and other defects, resulting in free carriers that redistribute to locally compensate the applied electric field. The decrease in signal is therefore attributed to a lower effective electric field seen by the defects and not a lower EOCC sensitivity. At high enough frequency, the carrier distribution never reaches its steady state and the space charge is not created. The characteristic timescale for space charge formation is the Maxwell relaxation time , where and ( for 4H-SiC) are the vacuum and relative permittivity and is the resistivity (22). Within this description and using the fitting function for described in Materials and Methods, we measure MHz with a corresponding resistivity equal to cm, as expected from typical resistivity values quoted for high-purity semiinsulating 4H-SiC wafers. The space charge creation is also expected to depend on the initial charge distribution which we effectively modify by increasing the laser spot size (Fig. 2A). The fit works well in all cases, and in particular for large spot sizes the low-frequency rate shift is nonzero (above noise level).
Fig. 2.
Frequency and phase domain measurements. (A) Frequency response of the EOCC rate shift (normalized) for different laser spot sizes obtained by changing the microscope focus. At frequencies below , the rate shift decays due to a lower effective electric field, while above , it decays due to the low-pass characteristics of the experimental setup and device impedance. (B) Frequency response of the EOCC contrast under pulsed 976-nm light, corresponding to a filter function for RF electric field spectroscopy. The laser pulse periodicity is . The electric field has a random phase with respect to the laser pulse. The total measurement duration is fixed for all duty cycles. (C) Phase measurement of the RF electric field using the sequence shown at Top. The laser is pulsed at twice the electric field frequency and related by a phase . is defined as the laser pulse coinciding with ; due to finite laser pulse length, this results in asymmetry of the EOCC signal around . For both B and C, a 405-nm reset pulse is used before the sequence.
Having characterized the EOCC frequency response, we now demonstrate the ability to resolve the frequency and phase of the applied RF electric field as shown in Fig. 2 B and C, respectively. These experiments are enabled by pulsing the 976-nm pump light with a given frequency and duty cycle (pulse duration). First, we fix while sweeping with a random initial phase between the two frequencies. This sequence measures the effective filter function of the pulse sequence and shows dips of decreasing intensities for equal to increasingly higher harmonics of (Fig. 2B). The dips arise from the light pulse always overlapping with equal electric field values when matches a harmonic of ; the RF electric field effectively becomes static in this condition and the EOCC signal diminishes as expected from Fig. 2A. The effect is gradually more prominent for decreasing duty cycle as the filter function sharpens. For phase resolution (Fig. 2C), we fix the relative phase between the laser pulse and electric field oscillations and set . Alternating light pulses encounter electric fields with alternating signs but equal amplitude, depending on the phase , and sweeping hence maps the time evolution of the electric field () oscillation. The model in Fig. 2 is calculated without any free parameters using Eq. 1 and the overlap between the electric field wave and the laser pulse.
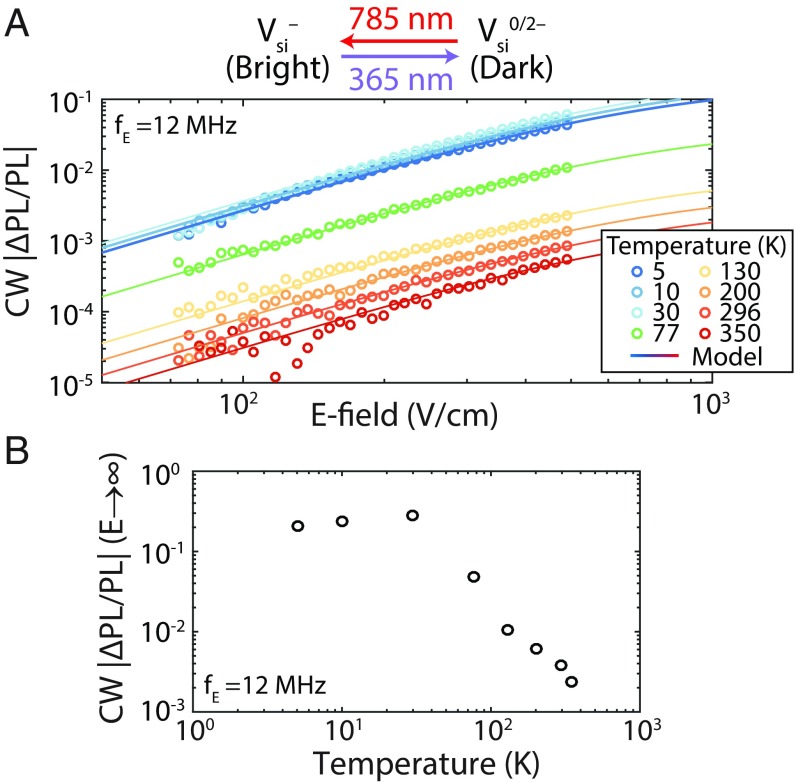
The electrometry technique we have outlined is broadly applicable to other defects with known charge dynamics. For example, can be optically charge converted and, unlike VV, is optically active even at room temperature. The combination of 365-nm (pumping to a dark state) and 785-nm (pumping to a bright state) lasers allows for OCC (11) and therefore the application of EOCC as shown in Fig. 3 A and B. Under continuous illumination at both wavelengths, the electric field modifies the PL for temperatures ranging from 5 K to 350 K. The EOCC contrast is present at all temperatures, although it is strongly reduced above 30–77 K; this behavior could be explained by the thermal activation of shallow impurities or capture barriers. The EOCC frequency dependence was found to be identical between and VV (SI Appendix, Fig. S2). We do not compare here and VV sensitivities as the experimental setup and the sample were optimized only for VV defects.
Fig. 3.
EOCC in silicon vacancies () in 4H-SiC. (A) EOCC contrast as a function of electric field for temperatures ranging from 5 K to 350 K. Lines are fitted to Eq. 1, with fitted to be V/cm independent of temperature. (B) Extrapolated EOCC contrast for as a function of temperature, with 95% confidence intervals (not shown) equal to about 5% of the contrast. CW, continuous wave.
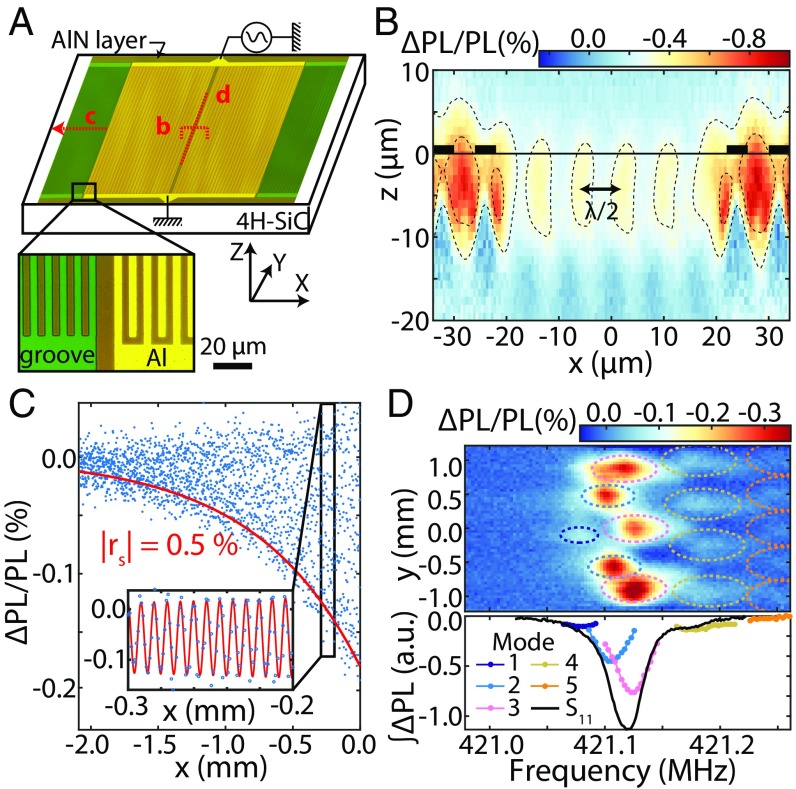
To conclude this work, we demonstrate the application of EOCC to map surface acoustic wave (SAW) modes in an electromechanical resonator in 4H-SiC. As SiC is slightly piezoelectric, any strain or shear wave simultaneously produces a corresponding measurable electric field. The SAW resonator is displayed in Fig. 4A (see Materials and Methods and SI Appendix, Figs. S3 and S4 for further details) with an interdigital transducer (IDT) fabricated on top of a 500-nm AlN layer on top of the SiC substrate. The resonator is composed of Bragg gratings made from grooves in the AlN that act as reflective mirrors, while the IDT couples the electrical drive to the SAW mode. All PL measurements are realized away from the IDT to avoid contribution from the drive electric field. Fig. 4 B–D presents a longitudinal () cross-section in the center of a device where there is a window in the IDT, a cut () across the AlN grooves, and a transverse cut () in the central window, respectively. In the cross-section of the window, we observe wave crests separated by half of the SAW wavelength (m, cavity frequency is 421 MHz), as expected from a quadratic response in the electric field. Numerical simulations confirm the contrast to likely originate from the electric field component of the resonator mode (SI Appendix, Fig. S5). In Fig. 4C, the cut through the grooves shows oscillations from the SAW modulated by an exponential decay. The characteristic decay length is measured to be m and directly related to the reflectivity per grating strip .
Fig. 4.
SAW mapping. (A) Schematic of the SAW device with partial microscope images. The red lines are scans with corresponding panel letters. The AlN grooves extend for 5.4 mm on each side. (B) EOCC contrast of a cross-section () centered at the window of the resonator. The black line indicates the surface and the black boxes the metal from the interdigitated fingers (not to scale). (C) EOCC contrast near the AlN grooves (reflectors) allows for direct measurement of their reflectivity . corresponds here to the position of the first groove. (C, Inset) A zoom-in is shown to emphasize the oscillations from the SAW. (D) SAW drive frequency as a function of transverse () position. Five modes are observed and integrated according to the colored ellipses. The integrated signals for each mode are shown as a function of frequency and compared with the intensity from a Schottky diode. All maps were realized at 0 dBm input power.
A transverse sweep across the central window measured as a function of drive frequency allows for direct observation of various transverse modes of the SAW resonator. Fig. 4D shows modes with one to five peaks (i.e., electric field extrema); their respective signals are separately integrated, plotted (Fig. 4D, Bottom), and compared with a direct reflection () measurement of the cavity. The signal provides only the total contribution from all modes, whereas the EOCC technique fully separates each mode in spatial and in frequency domains. Overall, EOCC offers complementary information to common MEMS characterization methods such as laser Doppler vibrometry (23) and various surface techniques (scanning electron microscopy, atomic force microscopy, etc.) (2). In particular, 3D spatial and high-frequency (gigahertz) sensing available with EOCC is much harder to achieve with these alternative techniques.
In summary, we present an electric field sensing technique for optically active defects in 4H-SiC. This method is purely optical and has a quadratic dependence in the applied electric field, i.e., measures the electric field energy density, whose frequency can be as high as a few gigahertz, likely limited by the experimental setup. Electrometry at such frequencies would be hard to achieve with spin-sensing techniques. We further demonstrate spectroscopy in both the frequency and phase domains. The ability to measure electric field vectors (3 axis) could be realized by taking advantage of the nonlinear (quadratic) response in the electric field. Finally, we demonstrate mapping of a SAW resonator due to the piezoelectricity of SiC, offering a characterization tool for related MEMS. Further improvements in the sensitivity could be achieved by higher defect densities, which should not drastically affect the charge state dynamics contrary to the spin coherence, and higher spatial resolution may be obtained by using single impurities. This technique is likely applicable to defects in other materials, in particular large bandgap crystals such as diamond and other substrates for high-power electronics and high-frequency MEMS.
Materials and Methods
Data associated with the figures in this work have been deposited on figshare (https://figshare.com/s/2b8356b8cd706be82861).
Samples.
The coplanar capacitor device was fabricated on a semiinsulating 4H-SiC commercial wafer from Norstel AB. VV and defects were created by a carbon (12C) implant with a -cm−2 dose at 170 keV with a tilt (300 nm depth), followed by annealing at C in Ar for 2 h. A total of 10/90 nm of Ti/Au was used for the metal gates. The device design is shown in SI Appendix, Fig. S1 and has multiple capacitors in parallel, although the laser spot in all experiments was confined to a single capacitor (with 17.1 m spacing). We confirmed the EOCC effect using other device geometries, including measurements of the electric field produced by a microwave stripline on a printed circuit board a few micrometers away from the sample, as well as devices fabricated on different 4H-SiC wafers (Norstel AB and Cree Inc.). The electric field sensitivity was found to vary between the wafers, mainly due to the OCC efficiency. Indeed, for some samples, the local Fermi level might be pinned by a dominant trap, including VV, preventing charge conversion from occurring, as previously observed in ref. 11. For example, a carbon (12C) implant at cm−2 dose was found to give higher sensitivity than at cm−2 dose in semiinsulating wafers. The total change in PL after charge conversion between the bright and dark states was reduced from a factor of 1,000 in the first sample to a factor of 20 only in the second sample, and consequently the EOCC contrast was similarly reduced. Careful consideration of all impurities present in the substrate is therefore necessary to optimize EOCC.
The SAW resonator (SI Appendix, Figs. S3 and S4) was fabricated on a semiinsulating 4H-SiC commercial wafer from Cree Inc. Defects were created by a carbon (12C) implant with a -cm−2 dose at 170 keV with a tilt (300 nm depth), followed by annealing at C in for 2 h. A total of 500 nm of AlN was sputtered on the Si face of the wafer by OEM Group Inc. The AlN layer has 40 MPa film stress with a rocking curve for AlN (0002) of 1. full width at half maximum (XRD). A total of 150 nm of Al was used for the interdigital contacts (80 finger pairs, with a window in the center equal to 3 of missing fingers). Al and AlN were etched by inductively coupled plasma (ICP) with 10 standard cubic centimeters per minute (sccm) Ar, 30 sccm , 30 sccm , 50 W bias, and 400 W ICP power. The grooves in the AlN were patterned by optical lithography and etched 270 nm deep.
Experimental Setup.
Samples are mounted on a printed circuit board inside a closed-cycle cryostat. All measurements were realized using a single confocal microscopy setup (50× objective, 0.65 numerical aperture) with optics optimized for near-infrared. For VV, OCC was realized using a 365/405-nm and 976-nm laser diode, with 976 nm simultaneously exciting the photoluminescence (1,000 nm). For , OCC was realized using the same 365 nm and a 785-nm laser diode, with 785 nm simultaneously exciting the photoluminescence (875–1,075 nm filtering). For pulsed laser experiments, the 976-nm laser was modulated using an acousto-optic modulator (100 ns rise time) while 405 nm was directly modulated by a current driver (250 kHz). Detection was realized using two separate configurations. For continuous measurements, an InGaAs photodiode with 1-kHz bandwidth was combined with a lock-in amplifier set at the frequency of the electric field amplitude modulation or switching (typically 400 Hz). For direct transient detection, an InGaAs avalanche photodiode (Thorlabs APD410C) in linear regime (M factor = 20) with a 10-MHz bandwidth was used with a fast (125 MHz) acquisition card. Transient signals were acquired with a 50-MHz sampling rate and binned into 2-s samples; differential measurements for PL are numerically processed during acquisition. All maps were taken using a 3-axis linear stage. ac electric fields are generated by two separate sources below and above 40 MHz. Above 40 MHz, the input power is calibrated to be flat across all frequencies by measuring the reflected power from the sample with a Schottky diode.
Low-Frequency Response.
To understand the low-frequency response, we also tested a simpler coplanar capacitor design and a coplanar waveguide design patterned on two different 4H-SiC wafers. We also measured electric fields coming from a coplanar waveguide on a printed circuit board, separated from the sample by a few micrometers. The effect of device impedance at low frequencies is disregarded as we did not observe any change using these various device configurations. The low-frequency behavior can be modeled by an effective electric field with the linear frequency response
| [3] |
where is the electric field value at high frequency; is the imaginary unit; and , , , and are free parameters. Although this equation is purely phenomenological, it is similar to theoretical calculations for the conductivity response from the creation of a space charge (but for different conditions from our experiments) (22). In this case, the parameter is the Maxwell relaxation rate and and are related to the inhomogeneous distribution of free carriers due to photoionization.
Supplementary Material
Acknowledgments
We thank Christopher Anderson, Joseph Heremans, Alexandre Bourassa, Brian Zhou, and Berk Diler for insights, discussions, and reviewing the manuscript. This work was supported by the Army Research Laboratory Office of the Secretary of Defense Quantum Science and Engineering Program and the NSF Grant EFRI 1641099. This work made use of the Materials Research Science & Engineering Center Shared User Facilities (NSF DMR-1420709) and the Pritzker Nanofabrication Facility (Soft and Hybrid Nanotechnology Experimental Resource, NSF ECCS-1542205) at the University of Chicago. G.W. acknowledges support from the University of Chicago/Advanced Institute for Materials Research Joint Research Center. D.D.A. is supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division at Argonne National Laboratory.
Footnotes
The authors declare no conflict of interest.
Data deposition: Data associated with the figures in this work have been deposited on figshare (https://figshare.com/s/2b8356b8cd706be82861).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1806998115/-/DCSupplemental.
References
- 1.Iwasaki T, et al. Direct nanoscale sensing of the internal electric field in operating semiconductor devices using single electron spins. ACS Nano. 2017;11:1238–1245. doi: 10.1021/acsnano.6b04460. [DOI] [PubMed] [Google Scholar]
- 2.Nonnenmacher M, O’Boyle MP, Wickramasinghe HK. Kelvin probe force microscopy. Appl Phys Lett. 1991;58:2921–2923. [Google Scholar]
- 3.Bylander J, Duty T, Delsing P. Current measurement by real-time counting of single electrons. Nature. 2005;434:361–364. doi: 10.1038/nature03375. [DOI] [PubMed] [Google Scholar]
- 4.Schoelkopf RJ. The radio-frequency single-electron transistor (RF-SET): A fast and ultrasensitive electrometer. Science. 1998;280:1238–1242. doi: 10.1126/science.280.5367.1238. [DOI] [PubMed] [Google Scholar]
- 5.Dolde F, et al. Nanoscale detection of a single fundamental charge in ambient conditions using the NV-center in diamond. Phys Rev Lett. 2014;112:097603. doi: 10.1103/PhysRevLett.112.097603. [DOI] [PubMed] [Google Scholar]
- 6.Dolde F, et al. Electric-field sensing using single diamond spins. Nat Phys. 2011;7:459–463. [Google Scholar]
- 7.Falk AL, et al. Electrically and mechanically tunable electron spins in silicon carbide color centers. Phys Rev Lett. 2014;112:187601. doi: 10.1103/PhysRevLett.112.187601. [DOI] [PubMed] [Google Scholar]
- 8.Trusheim ME, Englund D. Wide-field strain imaging with preferentially aligned nitrogen-vacancy centers in polycrystalline diamond. New J Phys. 2016;18:123023. [Google Scholar]
- 9.Bradbury FR, et al. Stark tuning of donor electron spins in silicon. Phys Rev Lett. 2006;97:176404. doi: 10.1103/PhysRevLett.97.176404. [DOI] [PubMed] [Google Scholar]
- 10.Wolfowicz G, et al. Conditional control of donor nuclear spins in silicon using stark shifts. Phys Rev Lett. 2014;113:157601. doi: 10.1103/PhysRevLett.113.157601. [DOI] [PubMed] [Google Scholar]
- 11.Wolfowicz G, et al. Optical charge state control of spin defects in 4H-SiC. Nat Commun. 2017;8:1876. doi: 10.1038/s41467-017-01993-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Aslam N, Waldherr G, Neumann P, Jelezko F, Wrachtrup J. Photo-induced ionization dynamics of the nitrogen vacancy defect in diamond investigated by single-shot charge state detection. New J Phys. 2013;15:013064. [Google Scholar]
- 13.Koehl WF, Buckley BB, Heremans FJ, Calusine G, Awschalom DD. Room temperature coherent control of defect spin qubits in silicon carbide. Nature. 2011;479:84–87. doi: 10.1038/nature10562. [DOI] [PubMed] [Google Scholar]
- 14.Baranov PG, et al. Silicon vacancy in SiC as a promising quantum system for single-defect and single-photon spectroscopy. Phys Rev B. 2011;83:125203. [Google Scholar]
- 15.Golter DA, Lai CW. Optical switching of defect charge states in 4H-SiC. Sci Rep. 2017;7:13406. doi: 10.1038/s41598-017-13813-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.de las Casas CF, et al. Stark tuning and electrical charge state control of single divacancies in silicon carbide. Appl Phys Lett. 2017;111:262403. [Google Scholar]
- 17.Joas T, Waeber AM, Braunbeck G, Reinhard F. Quantum sensing of weak radio-frequency signals by pulsed Mollow absorption spectroscopy. Nat Commun. 2017;8:964. doi: 10.1038/s41467-017-01158-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Magnusson B, et al. 2018. Excitation properties of the divacancy in 4H-SiC. arXiv:1804.01167.
- 19.Van de Walle CG. Stretched-exponential relaxation modeled without invoking statistical distributions. Phys Rev B. 1996;53:11292–11295. doi: 10.1103/physrevb.53.11292. [DOI] [PubMed] [Google Scholar]
- 20.Chen R. Apparent stretched-exponential luminescence decay in crystalline solids. J Lumin. 2003;102-103:510–518. [Google Scholar]
- 21.Chen EH, et al. High-sensitivity spin-based electrometry with an ensemble of nitrogen-vacancy centers in diamond. Phys Rev A. 2017;95:053417. [Google Scholar]
- 22.Chaikovskii IA, Shmelev GM, German AI. AC conductivity of highly inhomogeneous semiconductors. Phys Status Solidi. 1985;129:393–398. [Google Scholar]
- 23.Rothberg S, et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt Lasers Eng. 2017;99:11–22. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.