Significance
To predict how plant growth rate will respond to temperature requires understanding how temperature drives the underlying metabolic rates. Although past studies have considered the temperature dependences of photosynthesis and respiration rates underlying growth, they have largely overlooked the temperature dependence of carbon allocation efficiency. By combining a mathematical model that links exponential growth rate of a population of photosynthetic cells to photosynthesis, respiration, and carbon allocation; to an experiment on a freshwater alga; and to a database covering a wide range of taxa, we show that allocation efficiency is crucial for predicting how growth rates will respond to temperature change across aquatic and terrestrial autotrophs, at both short and long (evolutionary) timescales.
Keywords: growth rate, allocation efficiency, temperature dependence, autotrophs, carbon flux
Abstract
Relating the temperature dependence of photosynthetic biomass production to underlying metabolic rates in autotrophs is crucial for predicting the effects of climatic temperature fluctuations on the carbon balance of ecosystems. We present a mathematical model that links thermal performance curves (TPCs) of photosynthesis, respiration, and carbon allocation efficiency to the exponential growth rate of a population of photosynthetic autotroph cells. Using experiments with the green alga, Chlorella vulgaris, we apply the model to show that the temperature dependence of carbon allocation efficiency is key to understanding responses of growth rates to warming at both ecological and longer-term evolutionary timescales. Finally, we assemble a dataset of multiple terrestrial and aquatic autotroph species to show that the effects of temperature-dependent carbon allocation efficiency on potential growth rate TPCs are expected to be consistent across taxa. In particular, both the thermal sensitivity and the optimal temperature of growth rates are expected to change significantly due to temperature dependence of carbon allocation efficiency alone. Our study provides a foundation for understanding how the temperature dependence of carbon allocation determines how population growth rates respond to temperature.
All autotroph cells show a strong dependence of doubling rate on environmental temperature (1–3). This doubling rate drives exponential population growth rate in unicellular autotrophs and somatic growth in multicellular autotrophs, and is often used as a measure of fitness (4, 5). Global primary productivity depends fundamentally on the growth rates of photosynthetic tissue in aquatic and terrestrial photo-autotrophs—mostly phytoplankton and terrestrial plants, respectively (6, 7). Therefore, understanding the mechanistic, physiological basis of temperature-dependent exponential growth rate in autotroph cell populations is of fundamental importance. In particular, ongoing climate change will not only alter mean temperatures, but also likely exacerbate the thermal variability faced by autotrophs in the future (8, 9), meaning that more populations will be challenged with novel environments in which to compete and persist. In these situations, fitness can be primarily driven by the exponential growth rate of cells, either at low cell densities (e.g., competitive fitness among phytoplankton) or during somatic growth (e.g., germination or phenological change in terrestrial plants) (10, 11).
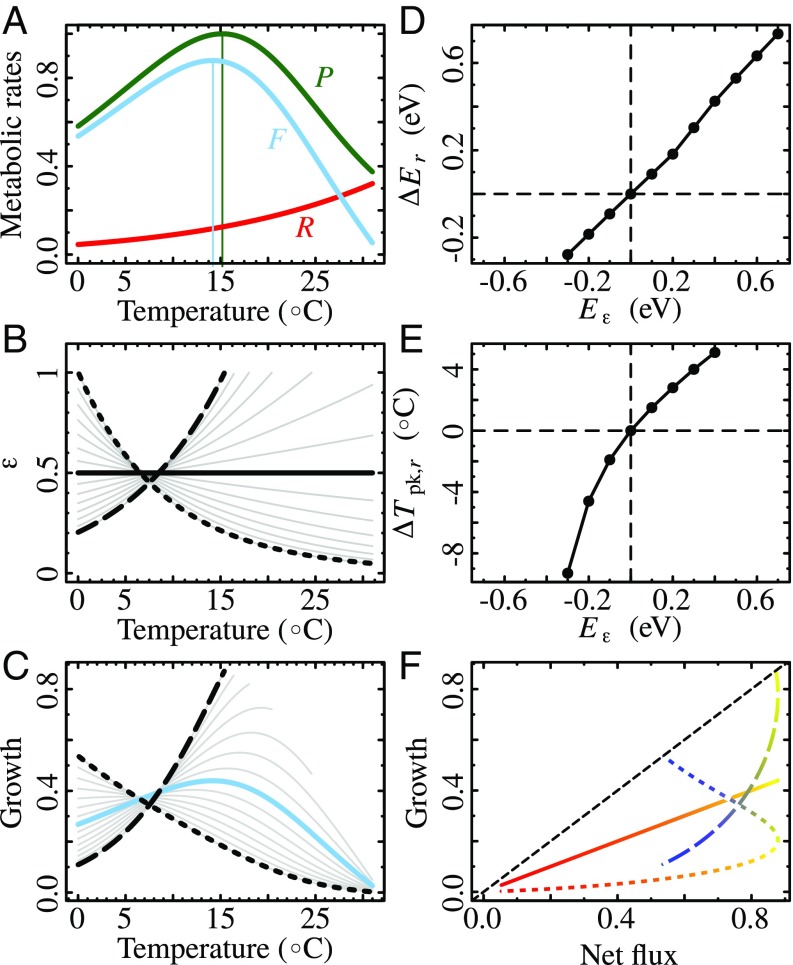
The mechanistic basis for the intraspecific temperature dependence of growth rates in photosynthetic tissue requires an understanding of a number of underlying metabolic processes, especially photosynthesis and respiration. The cell fixes carbon through photosynthesis, and part of that intracellular carbon is used in respiration to generate the carbon skeleton as well as usable forms of energy essential for maintenance and growth (12–15). The temperature dependencies of these metabolic processes take the form of unimodal thermal performance curves (TPCs), with an exponential increase of the rate followed by a sharp decline at higher temperatures (Fig. 1A) (16, 17). Current knowledge suggests that the photosynthesis and respiration TPCs differ, partly because temperature affects their underlying metabolic reactions differently (2, 3, 18, 19). The carbon potentially available for growth is expected to be proportional to the difference between these two metabolic rates (net carbon flux; solid line in Fig. 1F), and therefore differences in the TPCs of these processes should influence the shape of the emergent growth rate TPC (SI Appendix, section S3) (3, 20).
Fig. 1.
The impact of a temperature-dependent allocation efficiency on the TPC of growth rates in a population of photosynthetic cells. (A) Real TPCs for photosynthesis , respiration , and resulting net flux for Cladophora glomerata (a green alga). (B) Allocation efficiency expressed as a Boltzmann–Arrhenius function (Eq. 4 and SI Appendix, section S1.2) with a range of different temperature dependences (set by the activation energy ). (C) The result is a range of different potential growth TPCs. (D and E) (Eq. 5) (D) and (Eq. 6) (E) as functions of the temperature dependence of . (F) Relationships between potential growth and net flux (blues represent colder and reds warmer temperatures). A temperature-dependent affects the shape of the growth TPC and as a result how growth responds to temperature. The growth–net flux relationship can be highly nonlinear in this scenario, with the direction of the nonlinearity (blue-to-red trajectory) depending upon whether increases or decreases with (B). Temperature-independent (solid black line in B) produces growth TPCs that are qualitatively equal to those of net flux (solid blue line in C) and that are unaffected by . In B, C, and F the dotted lines are for and the dashed lines are for . Note that in D and E, larger values of produce curves that do not peak within the experimental temperature range (C).
Not all available carbon in the cell, however, is used in growth (2, 3, 20, 21). This allocation to growth, typically quantified as an efficiency, could be expected to depend on a range of environmental variables, especially temperature, concentration (22), and, in terrestrial plants, water availability or movement of photosynthates out of the cell (23). The temperature dependence of carbon allocation efficiency has received little attention and has rarely been considered in population growth models (14, 19, 24), but may also be a significant factor influencing the growth TPC. Here, we develop a mathematical model for the contribution of the TPCs of photosynthesis, respiration, and carbon allocation efficiency to the temperature dependence of doubling rate of a population of photosynthetic autotroph cells. In particular, we focus on the effect of temperature-dependent carbon allocation efficiency on two key parameters of growth rate TPCs: thermal sensitivity (activation energy, ; Fig. 1) and optimal temperature (). These two parameters strongly determine the temperature dependence of fitness of populations in their operational, ecologically relevant temperature range and have been extensively used in metabolic theories in ecology (SI Appendix, section S4) (25–27). We use laboratory experiments on the freshwater alga Chlorella vulgaris, combined with an analysis of data across a diversity of aquatic and terrestrial plants (38 species in 21 orders covering all major phyla), to quantify how much the temperature dependence of carbon allocation efficiency can affect growth rate TPCs.
Theory
Our model incorporates the TPCs of photosynthesis, respiration, and allocation efficiency into the TPC of doubling rate of a population of photosynthetic autotroph cells (for further details of the model, see SI Appendix, section S1). We begin with a single autotroph population’s biomass density (e.g., g C/ or ) in the exponential phase of growth, integrated over a 24-h period,
| [1] |
where is net carbon flux (1/d) and (dimensionless) is the allocation efficiency and captures the allocation of the fixed intracellular carbon to growth. Growth here accounts for both individual cell growth [e.g., through carbon storage (10, 28)] and population growth. While more complex models that mechanistically include intracellular processes are possible (28–33), the simplicity of our model allows comparisons with the type of experimental data that are typically feasible to collect (e.g., ref. 2). Net carbon flux (henceforth “net flux”) is a measure of mass-specific growth potential, given by
| [2] |
where is net photosynthesis (difference between maximum gross photosynthetic rate in nutrient-saturated and optimal-light conditions and daytime respiration), and is nighttime (dark) respiration. Thus, (blue line in Fig. 1A) represents an upper bound for how much of the carbon fixed in photosynthesis could be available to the cells for growth, after accounting for respiratory and other losses. We fitted the model to laboratory experiments performed in nutrient-saturated conditions—we accordingly assume nutrient saturation. However, the model could be extended to include nutrient limitation (SI Appendix, section S1). We come back to the possible effects of nutrient limitation on growth rate TPCs in Discussion.
An allocation efficiency implies that some of the carbon assimilated is “lost” from the cells. This is to be expected. For example, phytoplankton cells commonly exude photosynthetic assimilates instead of storing them or using them for growth (34, 35), and that carbon then enters the broader carbon cycle (ref. 36 and SI Appendix, section S1.2). In higher plants, carbon may also be allocated away from leaves to nonphotosynthetic tissues; that carbon would no longer be available for growth of the focal population of photosynthetic cells.
We now specify the TPCs of each of the parameters of the growth model (Eq. 1). For photosynthesis and respiration, we use the Schoolfield–Sharpe model without low-temperature inactivation (2, 3, 16):
| [3] |
Here, is a metabolic rate (1/d) at a given temperature (in kelvins), is approximately (37) the rate (1/d) at a reference temperature , and are the activation and deactivation energies (electronvolts) that set the relative rate of increase up to and decrease from the maximum, respectively, is the temperature at which the rate is half inactive due to high temperatures, and eV/K is the Boltzmann constant. Example and TPCs are shown in Fig. 1A. This model has been shown to fit well to photosynthesis and respiration rate data (2, 3, 16, 38, 39).
For the TPC of allocation efficiency, we use the Boltzmann–Arrhenius (BA) equation
| [4] |
where normalization constant is the efficiency at , and sets the relative rate of change of with . There is limited evidence for the temperature dependence of over the operational temperature range of organisms (38, 40, 41); here we make no a priori assumption about the directionality of the temperature dependence and consider both positive and negative values of (Fig. 1B). The BA form for (Eq. 4) allows us to study the effect of putative thermodynamic constraints on the metabolic rates underlying allocation and is also supported by our experimental data (see below). In SI Appendix, section S12 we show that using a more phenomenological quadratic TPC (SI Appendix, sections S1.2 and S6) for does not qualitatively change our results.
To quantify how a temperature-dependent alters the potential growth rate TPC we compare it to the assumption of a constant, temperature-independent [henceforth ], by expressing changes in (activation energy of growth rate) and (temperature of peak growth rate) as a result of the temperature dependence of ; i.e.,
| [5] |
| [6] |
The effect of (Eq. 4) on is straightforward to derive analytically: (Fig. 1D and SI Appendix, section S5). It is not possible to analytically derive the effect of on . However, numerical simulations show that is expected to correlate positively with (Fig. 1E).
Substituting the TPCs of , , and in the population model of Eq. 1 gives the full temperature-dependent model of growth.
The Importance of Temperature-Dependent Allocation in an Experimental System
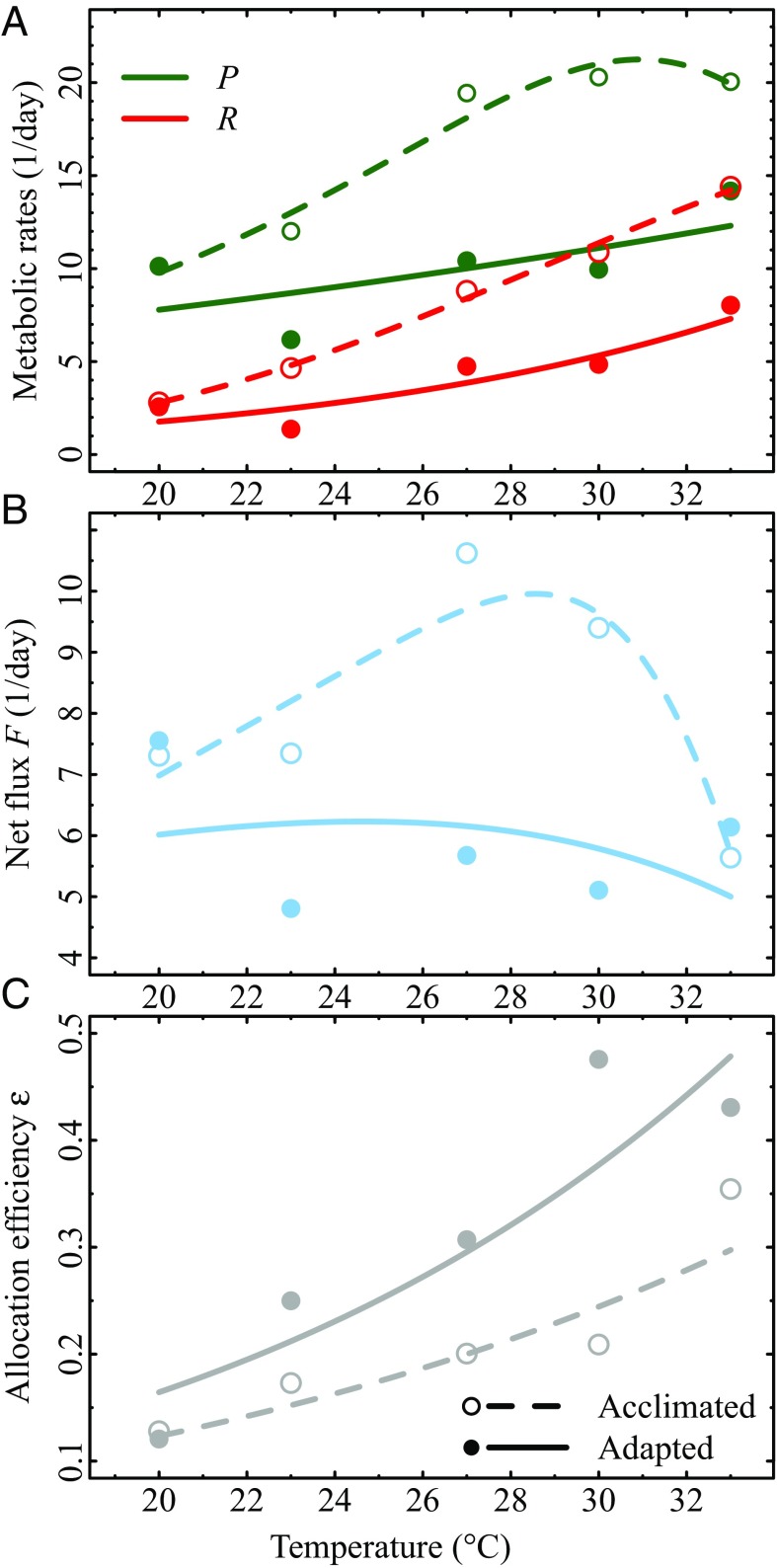
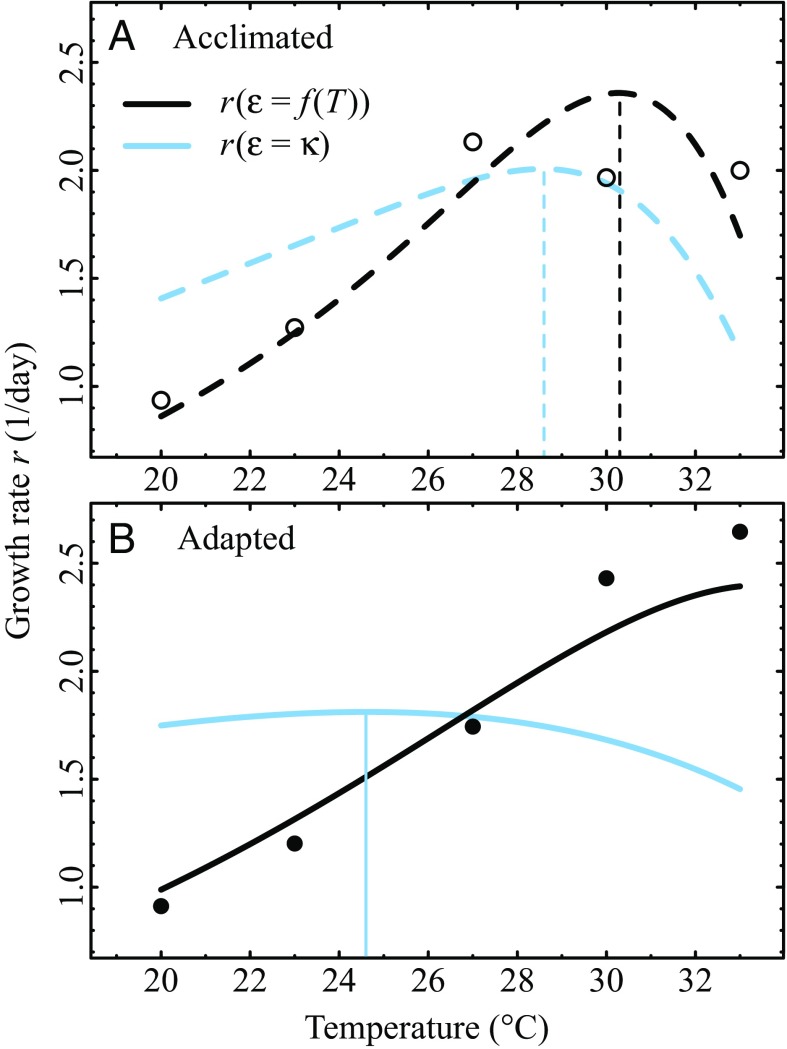
Next, we fitted the model for population growth to data from a laboratory experiment on C. vulgaris (2). In the experiments, net photosynthesis, respiration, and growth rate TPCs were measured for acclimated (10 generations) and adapted (100 generations) populations (Materials and Methods). The temperature-dependent was supported over a temperature-independent (SI Appendix, Table S1). The inferred monotonically increased in both populations (Fig. 2C). We found that has a greater activation energy in adapted (0.64 eV 95% confidence interval) than in acclimated (0.53 eV ) populations. Even though the confidence intervals of both and overlap (Eq. 4 and SI Appendix, Table S2), Fig. 2C shows that adapted populations allocated a greater proportion of the carbon flux to growth and that this proportion increased more rapidly with temperature than that for acclimated populations. Finally, both and (Eqs. 5 and 6) were positive; i.e., both activation energies and increased due to the temperature dependence of allocation efficiency (Fig. 3). As expected from theory (Theory above and SI Appendix, section S5), for both acclimated and adapted populations. The change in due to () was also positive, although the growth rate TPC for adapted populations did not peak within the experimental temperature range.
Fig. 2.
Metabolic rates and allocation efficiencies for experiments on acclimated and adapted C. vulgaris populations. (A) Net photosynthesis and dark respiration rates . (B) Net flux . (C) BA (with of 0.53 eV and 0.64 eV for acclimated and adapted populations, respectively; SI Appendix, Table S2). Dashed lines and open circles are for acclimated responses (10 generations) and solid lines and solid circles are for adapted responses (100 generations). Circles correspond to the means of three replicate experimental values at each growth temperature.
Fig. 3.
Growth rates with temperature-independent and -dependent , for experiments on acclimated and adapted C. vulgaris populations. (A and B) Growth rates for (A) acclimated and (B) adapted populations. Light blue lines are for growth assuming a temperature-independent , while black lines are for growth with the of Fig. 2C. Vertical lines correspond to the respective values. (Eq. 5) was 0.53 eV and 0.64 eV for acclimated and adapted populations, respectively, corresponding to the values of (Fig. 2C) and thus in line with theoretical expectations. (Eq. 6) was C and over C for acclimated and adapted populations, respectively. Circles correspond to the means of three replicate experimental values at each growth temperature.
In addition to the model of Eq. 1, we also fitted an alternative, structurally different, but biologically feasible model (SI Appendix, section S9). In contrast to Eq. 1, in this alternative model, limits how much fixed carbon is available to the cell before respiration occurs. The results show that Eq. 1 is better supported for both acclimated and adapted populations (SI Appendix, Table S1).
The Effect of on Potential Growth Rates Across Species
Finally, we explore how might affect the shape of the growth rate TPC across a wide diversity of species. We calculated the potential growth rate TPCs (Eq. 1) for 38 aquatic and terrestrial autotroph species for which coupled and TPCs were available, assuming different levels of temperature dependence of (e.g., Fig. 1 and Materials and Methods). We parameterized by choosing a value of (Eq. 4) that ensured that between the minimum experimental temperature and , half of the total available carbon was allocated to growth (SI Appendix, section S6). Then, we estimated the impact of temperature dependence of () on both the activation energy () and the optimal temperature () of potential growth. We also compared the resulting distributions of activation energies of potential growth rate TPCs with an empirical distribution estimated from growth TPCs measured in laboratory experiments (Materials and Methods). Because only phytoplankton growth rate data were available for this comparison, here we focus on the potential growth rates calculated for aquatic species only (results including terrestrial species are in SI Appendix, section S12.1).
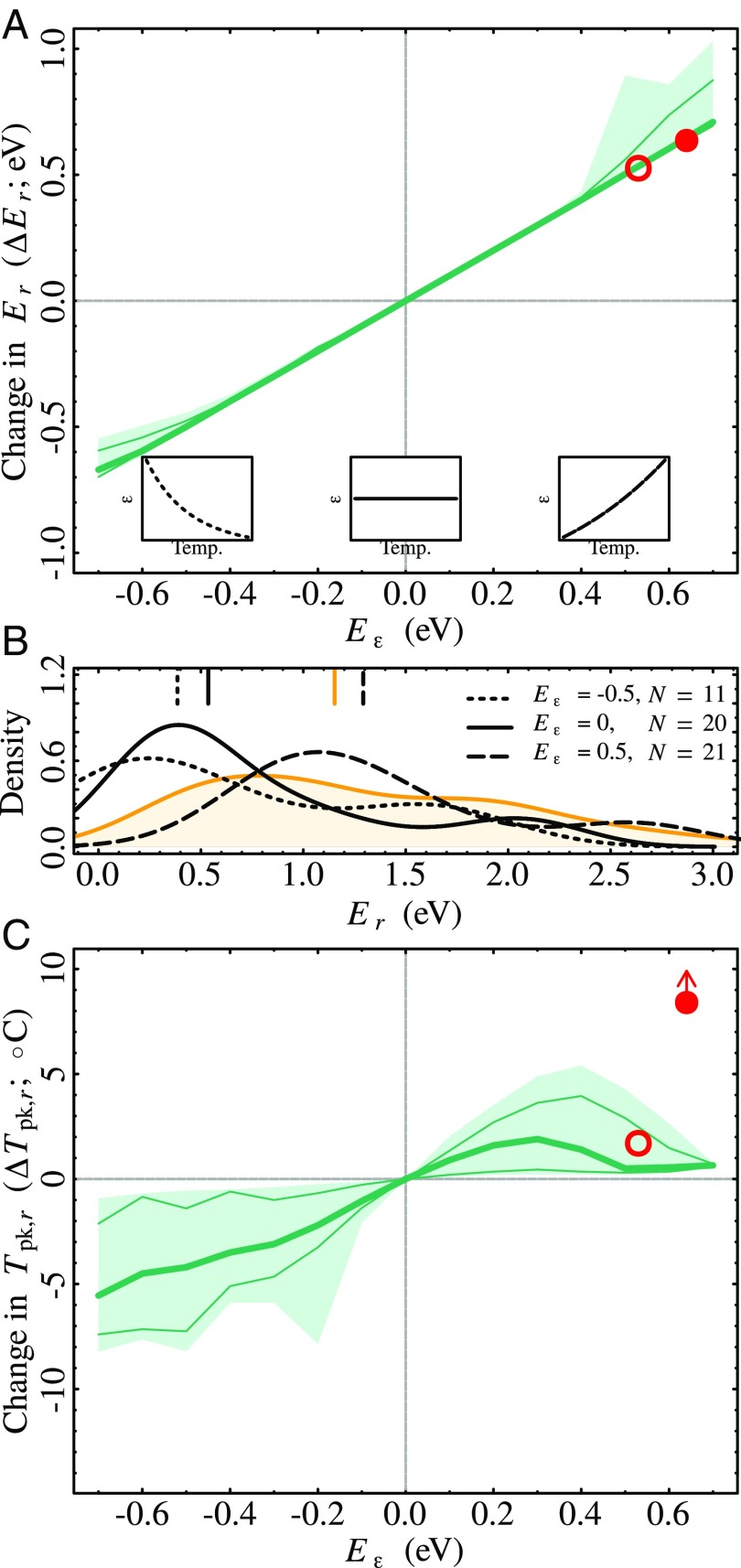
Our results show that can substantially alter the activation energy of growth rate () across species (Fig. 4A). The change in () due to is directly proportional to , as predicted by the theory (SI Appendix, section S5). That is, when increases with (, as found in the laboratory experiments), potential growth curves become more sensitive to temperature. Conversely, when decreases with temperature (), potential growth TPCs become less temperature sensitive. Overall, as seen in Fig. 4B, the distribution of activation energies of potential growth rates depends on the temperature sensitivity of ; the distribution becomes more right skewed as declines (from positive to negative values). Comparing the theoretical activation energy distributions to the empirical one (orange line in Fig. 4B) suggests that a positive temperature dependence of is the most likely scenario in autotrophs (see SI Appendix, section S12.5 for a more detailed discussion), as was also observed in the experimental data (Fig. 2C).
Fig. 4.
Impact of temperature dependence in on and . (A) (Eq. 5) as a function of the activation energy of for the 21 aquatic populations. (B) Theoretical distributions of for different values (black lines) juxtaposed against the empirically observed distribution for phytoplankton (orange line) (see SI Appendix, Fig. S8 for analogous results for combined terrestrial and aquatic species). The vertical lines mark the median activation energies for the respective distributions; note that median activation energy when is closest to that of the empirical distribution. (C) as a function of the activation energy of . For example, in A means that when is estimated with , it is 0.2 eV higher than when is calculated with (Eq. 5). Similarly, in C means that potential growth estimated with a temperature-dependent peaks at a temperature C lower than when growth is calculated with (Eq. 6). The shaded areas in A and C range from 12.5th to 87.5th percentiles across all potential growth rates, thin lines are the 25th and 75th percentiles, and the thick lines are the 50th percentiles. For a specific example with a single pair of and curves, see Fig. 1 D and E. Red circles in A and C show and observed in the laboratory experiments on C. vulgaris: Open and solid circles are for acclimated and adapted populations, respectively (Fig. 3). The growth TPC for the adapted population did not peak within the experimental range, so the arrow on the solid red circle in C indicates that the value is a minimum bound on .
The optimal temperature for potential growth rates, , also varied systematically with the temperature dependence of (Fig. 4C). The response was qualitatively consistent across species: Negative (respectively positive) activation energies of lowered (respectively increased) relative to . However, the degree to which changed varied across taxa, as evidenced by the wide shaded areas in Fig. 4C, meaning that the magnitude of depends on the specific shape of the species’ underlying metabolic rate TPCs. The effect of on can be substantial: For eV, the median is C. The effect is also asymmetrical and nonlinear: For eV, median is C. Note, however, that for the larger values of , many potential growth curves do not peak at all within the experimental temperature range. These were excluded from Fig. 4C and thus likely bias the asymmetry of the pattern. For example, the growth rate TPC for adapted populations of C. vulgaris did not peak within the experimental temperature range (Fig. 3B), perhaps explaining why the corresponding solid red circle in Fig. 4C falls outside the shaded area.
While Fig. 4 shows results for aquatic species only, patterns remain qualitatively similar when also including terrestrial species (SI Appendix, Fig. S8). These results are also largely robust to how is parameterized (SI Appendix, section S12); with an alternative parameterization of Eq. 4, the relationship between and remains the same (SI Appendix, Fig. S9A), while the pattern between and changes quantitatively, but not qualitatively (SI Appendix, Fig. S9C).
Discussion
We have presented a mathematical model for the temperature dependence of exponential growth rates in populations of photosynthetic autotroph cells and used data to both test the theory and understand how the temperature dependence of carbon allocation efficiency contributes to shape growth rate TPCs across a diversity of species. Our results show that temperature dependence in carbon allocation efficiency can be a significant factor in determining the shape of the TPCs of growth rates.
The laboratory experiments on a phytoplankton species (the single-celled green alga C. vulgaris) show that in this species, allocation efficiency is temperature dependent, with exponentially increasing allocation of intracellular carbon to growth with warming. This temperature dependence of in C. vulgaris leads to both a higher activation energy and optimal temperature of the growth rate TPC, compared with if had been assumed to be temperature independent. Padfield et al. (2) previously hypothesized that carbon use efficiency (CUE), a measure of growth “potential” defined as the ratio of net and gross photosynthesis (SI Appendix, section S1.4), plays an important role in the evolution of elevated thermal tolerance in phytoplankton. Here we have shown that it is in fact the marked increase in efficiency of carbon allocation to growth that allowed this evolution of tolerance to high temperature. This increase in carbon allocation efficiency with evolution may result from diversion of metabolic energy away from maintenance and repair [reflected in the high respiration rates of the nonevolved populations at high temperature (Fig. 2)], and toward growth.
Our further investigation of the effect of on potential growth rates across a diverse group of aquatic species showed that despite considerable variation in paired photosynthesis and respiration TPCs, the impact of a temperature-dependent was very consistent across these species. Comparing distributions of activation energies of predicted growth rates with real data suggests that allocation efficiency is likely to increase with temperature across most aquatic autotroph species. This result implies that activation energies of growth rate are expected to be higher than activation energies for net flux. We note that although this analysis focused on aquatic species, the model should also apply to tissue growth in terrestrial plants using locally fixed carbon (e.g., leaves in shoots of young saplings). However, we were unable to find sufficient data on growth rates of such tissues across sufficient multiple temperatures with which to create an empirical distribution of activation energies and perform an analogous comparison for terrestrial plants.
The effect of allocation efficiency on the potential growth rate TPC depends on its temperature dependence in the operational temperature range (the increasing part of the growth TPC, expected to be the ecologically most relevant temperature range). If increases (respectively decreases) with temperature, its effect is likely to increase (respectively decrease) both the activation energy of the potential growth rate TPC () and the optimal temperature for potential growth (). This result qualitatively holds irrespective of the specific shape of (SI Appendix, section S12). The effect of on the activation energy of potential growth rates is very predictable, while the impact on , while qualitatively consistent, is more variable across species and less quantitatively predictable. The reason is simple: When increases with temperature, can only be greater than , but the difference between the two is contingent on the specific shape of the underlying metabolic rate TPCs. When net flux around its peak is relatively insensitive to temperature, it takes only moderate temperature dependence in to substantially change , while when net flux is strongly temperature dependent around its peak, a greater temperature dependence in is necessary to change .
The model can also be extended to explore how uptake of a limiting nutrient (other than carbon, which is typically not limiting in natural environments) may interact with allocation efficiency to affect the shape of potential growth rate TPCs. For instance, let
| [7] |
where is a dimensionless Michaelis–Menten nutrient uptake term which can be theoretically approximated as a monotonically decreasing function of temperature (SI Appendix, section S1.3) (10, 42). In this case, nutrient limitation lowers both and (SI Appendix, Fig. S13). Similar results were obtained by Thomas et al. (43) with a temperature-independent nutrient uptake, although their model was closer to our alternative model structure (SI Appendix, sections S1.5 and S9), where nutrient limitation affects carbon fixation only in photosynthesis. Nutrient limitation could then interact with and, where increases with temperature, counteract its effects on the potential growth rate TPC [by offsetting the increases in both and due to ] or, where decreases with temperature, compound its effects by further reducing and (SI Appendix, Fig. S14). Thus, nutrient limitation would be expected to reduce both the sensitivity of potential growth rates to increases in temperature and the optimal temperature for growth. Despite these predictions from our model, further experiments would be necessary to elucidate whether nutrient availability nonlinearly affects allocation efficiency and its temperature dependence; nutrient limitation could conceivably systematically alter how carbon is allocated.
Our model is intended to apply to unicellular autotrophs (phytoplankton) and other cell populations that use carbon fixed by those cells such as in elongating leaves of terrestrial plants and aquatic macrophytes and shoots of all young multicellular plants (e.g., small saplings). In terrestrial “higher” plants, leaves constitute a single component of a more complex system, and, as a result, could additionally encapsulate carbon that is reallocated to nonphotosynthetic tissue. The findings of our meta-analysis hold even when terrestrial and aquatic species are analyzed together (SI Appendix, section S12.4). However, the model could be expanded to include growth of the whole plant (including nonphotosynthetic tissue). At its simplest, an additional respiration term would be necessary in Eq. 1, to account for nonphotosynthetic tissues. Preferably, nonphotosynthetic biomass could be tracked in an additional, coupled differential equation that would allow for carbon to be transferred between the two components. Such a model would require additional data that are not easily measurable. Understanding how adaptation might be expected to affect TPCs, as a function of long-term changes in temperature and time, also requires further work. The model, currently formulated in rates per day, could be elaborated to explicitly account for adaptation over longer timescales by, for example, letting the parameters that define , , and (e.g., activation energies and normalization constants) be functions of adaptation temperature and time (e.g., ref. 39). Here too, a more substantial volume of data, to include how TPCs vary over time, would be required.
Overall, these findings challenge the common assumption that allocation efficiency is temperature independent (10, 20, 24, 39) and suggest that to understand the link between intraspecific growth rate TPCs and underlying metabolic rates, it is important to include the temperature dependence of the allocation efficiency. In the metabolic theory of ecology (25, 26, 44), growth rate TPCs are often used as a means to infer the temperature dependence of the underlying metabolism or vice versa (39). However, as shown by our meta-analysis, some of the observed variation in the growth rate TPCs (38) may stem from variation in the temperature dependence of allocation efficiency and not be due to that in metabolic rates. Thus, studies that use growth rate TPCs as proxies for the TPCs of metabolism but ignore may reach biased conclusions. More generally, allocation efficiency in heterotrophs (commonly referred to as mass-conversion efficiency in the literature; e.g., ref. 45) has already been shown to broadly increase with temperature (46), and its consequences there also need to be explored more carefully.
Our work also shows that to make further progress toward understanding the temperature dependence of autotroph population growth rates, experimental data where growth rates, , and are measured in the same study are needed. Paucity of data is particularly acute in terrestrial species, where growth rates (in terms of mass) of leaves and shoots are seldom collected across multiple temperatures. Even when all three rates are measured in the same study, usually in aquatic species (e.g., ref. 3), establishing the mechanistic link between a growth rate on the one hand and the underlying metabolic rates on the other hand would require that both are measured at comparable timescales. For example, in phytoplankton, metabolic rates are often measured as acute responses to a change in temperature in short experiments (the order of minutes), while growth rates may take days to estimate. This difference might potentially introduce a confounding effect of acclimation in the processes underlying allocation of carbon to growth [i.e., ]. With appropriate data, can then be estimated by fitting our model directly (as done here) or, alternatively, by fitting different formulations of to .
Finally, further work is required to unpack the metabolic processes involved in allocation efficiency and thus provide a more mechanistic link between population growth and individual metabolism. For example, the role played by respiration is greatly simplified in this model: It simply reduces how much carbon is available to the cells. However, growth can be constrained by respiration (47, 48); its products, such as energy and carbon skeletons, are essential for growth, maintenance, and transport processes (12, 15, 49, 50). However, the efficiency with which these products are generated can depend on which one is in greatest demand (48), which in turn may affect our estimated allocation efficiency. Under certain conditions, alternative (less “efficient”) respiratory pathways may also be activated (47, 51), which would further complicate the link between the measured use of carbon through respiration and growth. To what extent these respiratory processes are reflected in and is unclear, and some elements may in fact be captured in (13). We also exclusively focus on the effect of temperature on allocation efficiency. However, other (potentially covarying) environmental variables could interact with temperature to affect . For instance, external concentration affects metabolic rates (22, 23, 52), and under water stress growth in terrestrial plants is reduced (23) as cells accumulate carbon to maintain osmotic balance. These and other factors such as light availability may well result in systematic differences in the temperature dependence of between terrestrial and aquatic autotrophs, which we are currently unable to detect in the available experimental data.
In conclusion, our model and empirical results link, in the simplest possible way, the temperature dependence of the underlying metabolic rates and allocation, with exponential population or somatic growth in autotrophs. While more detailed models of exponential growth rates have been previously published (28, 31, 32, 53, 54), none of these explicitly consider the temperature dependence of underlying metabolic rates. Our results provide a framework for experimentalists that requires data for only three frequently measured rates (growth rate, net photosynthesis, and dark respiration) across temperatures, to determine the TPC of allocation efficiency , a prerequisite for developing more complex, mechanistic models. The simplicity of our approach means that it has the potential to be used and applied to explore and uncover broader patterns in the metabolic basis for the temperature dependence of growth rates in autotrophs.
Materials and Methods
Experimental Data on C. vulgaris.
Full details on the experimental setup can be found in ref. 2 and more information is provided in SI Appendix, section S10; we here provide a summary. Three replicate populations of C. vulgaris were established per five different growth temperatures (C, C, C, C, and C). Exponential growth rates were estimated for each growth temperature after ∼10 (“acclimated”) and 100 (“adapted”) generations. Padfield et al. (2) also measured the acute short-term responses of metabolic rates (net photosynthesis and dark respiration ) to a range of temperatures for each of the populations grown at the five growth temperatures, after both 10 and 100 generations. Data used from these experiments are available online (55).
Acute responses of metabolic rates to a change in temperature are typically measured in brief (order of minutes) experiments in stressful conditions for the cells. On the other hand, growth rate experiments take longer (order of days), to ensure maximum exponential growth rates are captured. To allow the most direct comparison between metabolic rates and growth rates, we needed acclimated and adapted responses of metabolic rates. We fitted the Schoolfield–Sharpe model (Eq. 3) to each acute response and used the model to estimate the metabolic rates at the culture’s corresponding growth temperature (i.e., we estimated and at C for the cultures acclimated and adapted to C, at C for the cultures grown at C, and so on; SI Appendix, Fig. S6). When fitting the models to the data, we averaged metabolic rates and growth rates across the three replicates. As a result, we had experimental values of , , and growth rates, for both acclimated and adapted responses. For the alternative model structure (SI Appendix, section S9), we assumed that gross photosynthesis (where is daytime respiration) and that (2).
Potential Growth Rate TPCs Across a Range of Autotroph Species.
We compiled a database of intraspecific TPCs of net photosynthesis and respiration extracted from the literature. We digitized data from tables, text, or figures, using DataThief (56) and Plot Digitizer (57), and, when possible, contacted authors to obtain raw data. Most TPCs were measured under saturated light conditions and ambient or saturating concentrations (not all studies reported this information). In all cases, metabolic rates were measured on photosynthetic tissue only; thus, in higher terrestrial plants, rates were measured on leaves only.
Metabolic rates are usually single peaked across their full thermal range; some studies, however, focused on a narrower temperature range such that TPCs can consist of a rise or fall in the trait only. We are specifically interested in the operational temperature range, which typically comprises the rise of a rate up to its maximum value. To be able to accurately characterize this rise in rates with temperature when fitting the Schoolfield–Sharpe model to the data, we kept curves with at least three data points below the rates’ and at least five data points in total. We also removed curves with activation energies greater than three, as higher values are often due to poor fits of the model to the data or the result of performing the experiment over a narrow temperature range (17). Because we were interested in how and interact with to produce a potential intraspecific growth rate TPC, we kept curves for which both and were measured in the same experiment. For experiments in which multiple TPCs were available for the same species and rate, we kept the curve with the highest coefficient of determination . Allocation efficiency can be expected to differ between species and taxonomic groups. However, to be able to parameterize in a way that could allow comparisons across species, we required a fixed reference point common to all curves (SI Appendix, section S6). Because species’ operational temperature ranges are likely to be limited, on the upper range, by the temperature at which photosynthesis peaks (17, 58), we discarded pairs of curves for which net photosynthesis did not peak within the experimental temperature range. We also excluded pairs of curves for which net flux was negative for , because the model implicitly assumes positive net fluxes. The result was a database with 43 pairs of and TPCs (21 aquatic and 22 terrestrial species) for 38 different species, from 27 sources. The rates were integrated over 24 h (giving the total amount of or per unit mass or area per day). Rates were measured in a variety of different units (mol or per unit kg dry weight, fresh weight, chlorophyll, cell, or area per unit time), making comparisons between pairs of curves difficult. We were specifically interested in the impacts of on the qualitative temperature dependence of the potential growth rate. For this reason, for each pair of curves, we normalized both and curves using the peak net photosynthetic rate (), i.e., and . Thus, the maximum net photosynthetic rate was equal to one for all species, while maintaining the relative shapes of the and curves. For this reason, the metabolic rates and resultant growth rates are unitless. Processed data (with unitless normalization constants and integration over 24 h) are provided in Dataset S2.
We describe as a BA function [Eq. 4 and Fig. 1B; although we also use a quadratic in SI Appendix, sections S6 and S12]. The degree of temperature dependence of ( in Eq. 4) was set and varied to assess its effect on the potential growth rate TPC. The maximum was comparable to the value observed in the C. vulgaris laboratory experiments (Fig. 2C). We then introduced each TPC, together with each pair of and curves, into Eq. 1 to produce a potential growth rate TPC for each population and value of . The activation energy of potential growth rates was estimated by fitting a Schoolfield–Sharpe model (Eq. 3) to the growth rate TPC (with adjustments described in SI Appendix, section S7 to ensure acceptable fits; also see SI Appendix, section S8). When estimating the change in due to , potential growth rate TPCs which, due to , declined only with temperature were excluded from this analysis. Similarly, when estimating the change in due to , potential growth rate TPCs that did not peak within the experimental temperature range were excluded.
To test the robustness of our results, we also used an alternative approach to parameterize (Eq. 4 and SI Appendix, section S6); results for this alternative parameterization are given in SI Appendix, section S12.
Real Growth Rate TPCs Across a Range of Phytoplankton Species.
To compare distributions of activation energies for the potential growth rates of aquatic species against activation energies of real, measured growth rates, we compiled a database of phytoplankton growth rate TPCs (taken mainly from refs. 20 and 59–61). Growth rates were estimated under light- and nutrient-saturated conditions. We removed curves that had an activation energy greater than four, and for species with replicate activation energies we kept values corresponding to the fit with the highest . The result was 165 estimates (each for an individual taxon) of activation energy for phytoplankton growth rate TPCs. Activation energies are provided in Dataset S1.
Statistical Methods.
Fitting in all cases was performed using the “nlsLM” function in the “minpack.lm” package in R (62), which uses the Levenberg–Marquardt optimization algorithm for nonlinear least-squares fitting. To ensure the best fit was found, the algorithm was run with 1,000 randomized starting parameters, keeping the fit with the lowest corrected AIC (AICc) score (63). The Sharpe–Schoolfield model was fitted to TPCs of metabolic and growth rates on the scale, and all fits with were excluded.
Model comparisons (between different combinations of model structures and temperature dependences of ; SI Appendix, section S11) were performed on the basis of AIC scores. The population model was fitted on the linear scale.
Supplementary Material
Acknowledgments
We thank Mridul Thomas and Van Savage for valuable discussions and comments on previous versions of the manuscript. We also thank three anonymous reviewers for comments and suggestions that helped substantially improve the manuscript. This study was supported by Natural Environment Research Council Grant NE/M003205/1 (to S.P. and G.Y.-D.), and a Science and Solutions for a Changing Planet Doctoral Training Partnership scholarship (to D.-G.K.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1800222115/-/DCSupplemental.
References
- 1.Way DA, Oren R. Differential responses to changes in growth temperature between trees from different functional groups and biomes: A review and synthesis of data. Tree Physiol. 2010;30:669–688. doi: 10.1093/treephys/tpq015. [DOI] [PubMed] [Google Scholar]
- 2.Padfield D, Yvon-Durocher G, Buckling A, Jennings S, Yvon-Durocher G. Rapid evolution of metabolic traits explains thermal adaptation in phytoplankton. Ecol Lett. 2016;19:133–142. doi: 10.1111/ele.12545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schaum CE, et al. Adaptation of phytoplankton to a decade of experimental warming linked to increased photosynthesis. Nat Ecol E. 2017;1:0094. doi: 10.1038/s41559-017-0094. [DOI] [PubMed] [Google Scholar]
- 4.Angilletta MJ, Steury TD, Sears MW. Temperature, growth rate, and body size in ectotherms: Fitting pieces of a life-history puzzle. Integr Comp Biol. 2004;44:498–509. doi: 10.1093/icb/44.6.498. [DOI] [PubMed] [Google Scholar]
- 5.Knies JL, Kingsolver JG, Burch CL. Hotter is better and broader: Thermal sensitivity of fitness in a population of bacteriophages. Am Nat. 2009;173:419–430. doi: 10.1086/597224. [DOI] [PubMed] [Google Scholar]
- 6.Houghton RA, et al. Annual fluxes of carbon from deforestation and regrowth in the Brazilian Amazon. Nature. 2000;403:301–304. doi: 10.1038/35002062. [DOI] [PubMed] [Google Scholar]
- 7.Clark DA, Piper SC, Keeling CD, Clark DB. Tropical rain forest tree growth and atmospheric carbon dynamics linked to interannual temperature variation during 1984–2000. Proc Natl Acad Sci USA. 2003;100:5852–5857. doi: 10.1073/pnas.0935903100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.García-Carreras B, Reuman DC. Are changes in the mean or variability of climate signals more important for long-term stochastic growth rate? PLoS One. 2013;8:e63974. doi: 10.1371/journal.pone.0063974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.IPCC,Core Writing Team . Climate change 2014: Synthesis report. In: Pachauri RK, Meyer LA, editors. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. IPCC; Geneva: 2014. pp. 35–112. [Google Scholar]
- 10.Reuman DC, Holt RD, Yvon-Durocher G. A metabolic perspective on competition and body size reductions with warming. J Anim Ecol. 2014;83:59–69. doi: 10.1111/1365-2656.12064. [DOI] [PubMed] [Google Scholar]
- 11.Gandhi SR, Yurtsev EA, Korolev KS, Gore J. Range expansions transition from pulled to pushed waves as growth becomes more cooperative in an experimental microbial population. Proc Natl Acad Sci USA. 2016;113:6922–6927. doi: 10.1073/pnas.1521056113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Raven JA. The quantitative role of ‘dark’ respiratory processes in heterotrophic and photolithotropic plant growth. Ann Bot. 1976;40:587–602. [Google Scholar]
- 13.Amthor JS. The role of maintenance respiration in plant growth. Plant Cell Environ. 1984;7:561–569. [Google Scholar]
- 14.Del Giorgio PA, Cole JJ. Bacterial growth efficiency in natural aquatic systems. Annu Rev Ecol Syst. 1998;29:503–541. [Google Scholar]
- 15.Amthor JS, Baldocchi DD. In: Terrestrial Global Productivity: Past, Present and Future. Roy J, Mooney HA, Saugier B, editors. Academic; San Diego: 2001. pp. 33–52. [Google Scholar]
- 16.Schoolfield RM, Sharpe PJH, Magnuson CE. Non-linear regression of biological temperature-dependent rate models based on absolute reaction-rate theory. J Theor Biol. 1981;88:719–731. doi: 10.1016/0022-5193(81)90246-0. [DOI] [PubMed] [Google Scholar]
- 17.Pawar S, Dell AI, Savage VM, Knies JI. Real versus artificial variation in the thermal sensitivity of biological traits. Am Nat. 2016;187:E41–E52. doi: 10.1086/684590. [DOI] [PubMed] [Google Scholar]
- 18.Farquhar GD, von Caemmerer S, Berry JA. A biochemical model of photosynthetic assimilation in leaves of species. Planta. 1980;149:78–90. doi: 10.1007/BF00386231. [DOI] [PubMed] [Google Scholar]
- 19.Raven JA, Geider RJ. Temperature and algal growth. New Phytol. 1988;110:441–461. [Google Scholar]
- 20.López-Urrutia Á, San Martin E, Harris RP, Irigoien X. The metabolic balance of the oceans. Proc Natl Acad Sci USA. 2006;103:8739–8744. doi: 10.1073/pnas.0601137103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Allen AP, Gillooly JF, Brown JH. Linking the global carbon cycle to individual metabolism. Funct Ecol. 2005;19:202–213. [Google Scholar]
- 22.de Kluijver A, et al. Phytoplankton-bacteria coupling under elevated levels: A stable isotope labelling study. Biogeosciences. 2010;7:3783–3797. [Google Scholar]
- 23.Ryan MG. Effects of climate change on plant respiration. Ecol App. 1991;1:157–167. doi: 10.2307/1941808. [DOI] [PubMed] [Google Scholar]
- 24.Baird ME, Emsley SM, McGlade JM. Modelling the interacting effects of nutrient uptake, light capture and temperature on phytoplankton growth. J Plankton Res. 2001;23:829–840. [Google Scholar]
- 25.Brown JH, Gillooly JF, Allen AP, Savage VM, West GB. Toward a metabolic theory of ecology. Ecology. 2004;85:1771–1789. [Google Scholar]
- 26.Savage VM, Gillooly JF, Brown JH, West GB, Charnov EL. Effects of body size and temperature on population growth. Am Nat. 2004;163:429–441. doi: 10.1086/381872. [DOI] [PubMed] [Google Scholar]
- 27.Huey RB, Kingsolver JG. Variation in universal temperature dependence of biological rates. Proc Natl Acad Sci USA. 2011;108:10377–10378. doi: 10.1073/pnas.1107430108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Droop MR. Some thoughts on nutrient limitation in algae. J Phycol. 1973;9:264–272. [Google Scholar]
- 29.Kooijman SALM. Dynamic Energy and Mass Budgets in Biological Systems. Cambridge Univ Press; Cambridge, UK: 2000. [Google Scholar]
- 30.Bonachela JA, Michael R, Levin SA. Dynamic model of flexible phytoplankton nutrient uptake. Proc Natl Acad Sci USA. 2011;108:20633–20638. doi: 10.1073/pnas.1118012108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kempes CP, Dutkiewicz S, Follows MJ. Growth, metabolic partitioning, and the size of microorganisms. Proc Natl Acad Sci USA. 2012;109:495–500. doi: 10.1073/pnas.1115585109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Weiße AY, Oyarzún DA, Danos V, Swain PS. Mechanistic links between cellular trade-offs, gene expression, and growth. Proc Natl Acad Sci USA. 2015;112:E1038–E1047. doi: 10.1073/pnas.1416533112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kempes CP, Wang L, Amend JP, Doyle J, Hoehler T. Evolutionary tradeoffs in cellular composition across diverse bacteria. ISME J. 2016;10:2145–2157. doi: 10.1038/ismej.2016.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Baines SB, Pace ML. The production of dissolved organic matter by phytoplankton and its importance to bacteria: Patterns across marine and freshwater species. Limnol Oceanogr. 1991;36:1078–1090. [Google Scholar]
- 35.Engel A, Thoms S, Riebesell U, Rochelle-Newall E, Zondervan I. Polysaccharide aggregation as a potential sink of marine dissolved organic carbon. Nature. 2004;428:929–932. doi: 10.1038/nature02453. [DOI] [PubMed] [Google Scholar]
- 36.Falkowski PG, Barber RT, Smetacek V. Biogeochemical controls and feedbacks on ocean primary production. Science. 1998;281:200–206. doi: 10.1126/science.281.5374.200. [DOI] [PubMed] [Google Scholar]
- 37.Kontopoulos DG, García-Carreras B, Sal S, Smith TP, Pawar S. Use and misuse of temperature normalisation in meta-analyses of thermal responses of biological traits. PeerJ. 2018;6:e4363. doi: 10.7717/peerj.4363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dell AI, Pawar S, Savage VM. Systematic variation in the temperature dependence of physiological and ecological traits. Proc Natl Acad Sci USA. 2011;108:10591–10596. doi: 10.1073/pnas.1015178108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Luhring T, DeLong JP. Scaling from metabolism to population growth rate to understand how acclimation temperature alters thermal performance. Integr Comp Biol. 2017;57:103–111. doi: 10.1093/icb/icx041. [DOI] [PubMed] [Google Scholar]
- 40.Follows MJ, Dutkiewicz S, Grant S, Chisholm SW. Emergent biogeography of microbial communities in a model ocean. Science. 2007;315:1843–1846. doi: 10.1126/science.1138544. [DOI] [PubMed] [Google Scholar]
- 41.Dell AI, Pawar S, Savage VM. Temperature dependence of trophic interactions are driven by asymmetry of species responses and foraging strategy. J Anim Ecol. 2014;83:70–84. doi: 10.1111/1365-2656.12081. [DOI] [PubMed] [Google Scholar]
- 42.Aksnes DL, Egge JK. A theoretical model for nutrient uptake in phytoplankton. Mar Ecol Prog Ser. 1991;70:65–72. [Google Scholar]
- 43.Thomas MK, et al. Temperature-nutrient interactions exacerbate sensitivity to warming in phytoplankton. Glob Change Biol. 2017;23:3269–3280. doi: 10.1111/gcb.13641. [DOI] [PubMed] [Google Scholar]
- 44.Gillooly JF, Brown JH, West GB, Savage VM, Charnov EL. Effects of size and temperature on metabolic rate. Science. 2001;293:2248–2251. doi: 10.1126/science.1061967. [DOI] [PubMed] [Google Scholar]
- 45.Vucic-Pestic O, Ehnes RB, Rall BC, Brose U. Warming up the system: Higher predator feeding rates but lower energetic efficiencies. Glob Change Biol. 2011;17:1301–1310. [Google Scholar]
- 46.Lang B, Ehnes RB, Ulrich B, Rall BC. Temperature and consumer type dependencies of energy flows in natural communities. Oikos. 2017;126:1717–1725. [Google Scholar]
- 47.Amthor JS. In: Physiology and Determination of Crop Yield. Boote KJ, Bennett JM, Sinclair TR, Paulsen GM, editors. Am Soc Agron; Madison, WI: 1994. pp. 221–250. [Google Scholar]
- 48.Amthor JS. In: Ecophysiology of Photosynthesis. Schulze ED, Caldwell MM, editors. Springer; Berlin: 1994. pp. 71–101. [Google Scholar]
- 49.Atkin OK, Bruhn D, Hurry VM, Tjoelker MG. The hot and the cold: Unravelling the variable response of plant respiration to temperature. Func Plant Biol. 2005;32:87–105. doi: 10.1071/FP03176. [DOI] [PubMed] [Google Scholar]
- 50.Allison SD. Modeling adaptation of carbon use efficiency in microbial communities. Front Microbiol. 2014;5:571. doi: 10.3389/fmicb.2014.00571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Amthor JS. Terrestrial higher-plant response to increasing atmospheric [] in relation to the global carbon cycle. Glob Change Biol. 1995;1:243–274. [Google Scholar]
- 52.Riebesell U. Effects of enrichment on marine phytoplankton. J Oceanogr. 2004;60:719–729. [Google Scholar]
- 53.Shutter B. A model of physiological adaptation in unicellular algae. J Theor Biol. 1979;78:519–552. doi: 10.1016/0022-5193(79)90189-9. [DOI] [PubMed] [Google Scholar]
- 54.Geider RJ, MacIntyre HL, Kana TM. Dynamic model of phytoplankton growth and acclimation: Responses of the balanced growth rate and the chlorophyll a-carbon ratio to light, nutrient-limitation and temperature. Mar Ecol Prog Ser. 1997;148:187–200. [Google Scholar]
- 55.Padfield D. 2018. Data from “Padfield et al. (2016) Rapid evolution of metabolic traits explains thermal adaptation in phytoplankton. Ecology letters.” Zenodo. (Version v1.0) [DOI]
- 56.Tummers B. 2006 Datathief III. Available at https://datathief.org/. Accessed March 1, 2015.
- 57.Huwaldt JA. 2015 Plot digitizer. Available at plotdigitizer.sourceforge.net/. Accessed March 1, 2015.
- 58.Martin TL, Huey RB. Why “suboptimal” is optimal: Jensen’s inequality and ectotherm thermal performance. Am Nat. 2008;171:E102–E118. doi: 10.1086/527502. [DOI] [PubMed] [Google Scholar]
- 59.Rose JM, Caron DA. Does low temperature constrain the growth rates of heterotrophic protists? Evidence and implications for algal blooms in cold waters. Limnol Oceanogr. 2007;52:886–895. [Google Scholar]
- 60.Bissinger JE, Montagnes DJ, Atkinson D. Predicting marine phytoplankton maximum growth rates from temperature: Improving on the Eppley curve using quantile regression. Limnol Oceanogr. 2008;53:487–493. [Google Scholar]
- 61.Thomas MK, Kremer CT, Klausmeier CA, Litchman E. A global pattern of thermal adaptation in marine phytoplankton. Science. 2012;338:1085–1088. doi: 10.1126/science.1224836. [DOI] [PubMed] [Google Scholar]
- 62.Elzhov TV, Mullen KM, Spiess AN, Bolker B. 2015 minpack.lm: R Interface to the Levenberg-Marquardt Nonlinear Least Squares Algorithm Found in MINPACK, Plus Support for Bounds. R package Version 1.2-0. Available at https://cran.r-project.org/web/packages/minpack.lm/index.html. Accessed March 1, 2015.
- 63.Hurvich CM, Tsai CL. Regression and time series model selection in small samples. Biometrika. 1989;76:297–307. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.