Significance
Semantic typology documents and explains how languages vary in their structuring of meaning. Information theory provides a formal model of communication that includes a precise definition of efficient compression. We show that color-naming systems across languages achieve near-optimal compression and that this principle explains much of the variation across languages. These findings suggest a possible process for color category evolution that synthesizes continuous and discrete aspects of previous accounts. The generality of this principle suggests that it may also apply to other semantic domains.
Keywords: information theory, semantic typology, color naming, categories, language evolution
Abstract
We derive a principled information-theoretic account of cross-language semantic variation. Specifically, we argue that languages efficiently compress ideas into words by optimizing the information bottleneck (IB) trade-off between the complexity and accuracy of the lexicon. We test this proposal in the domain of color naming and show that (i) color-naming systems across languages achieve near-optimal compression; (ii) small changes in a single trade-off parameter account to a large extent for observed cross-language variation; (iii) efficient IB color-naming systems exhibit soft rather than hard category boundaries and often leave large regions of color space inconsistently named, both of which phenomena are found empirically; and (iv) these IB systems evolve through a sequence of structural phase transitions, in a single process that captures key ideas associated with different accounts of color category evolution. These results suggest that a drive for information-theoretic efficiency may shape color-naming systems across languages. This principle is not specific to color, and so it may also apply to cross-language variation in other semantic domains.
Languages package ideas into words in different ways. For example, English has separate terms for “hand” and “arm,” “wood” and “tree,” and “air” and “wind,” but other languages have single terms for each pair. At the same time, there are universal tendencies in word meanings, such that similar or identical meanings often appear in unrelated languages. A major question is how to account for such semantic universals and variation of the lexicon in a principled and unified way.
One approach to this question proposes that word meanings may reflect adaptation to pressure for efficient communication—that is, communication that is precise yet requires only minimal cognitive resources. On this view, cross-language variation in semantic categories may reflect different solutions to this problem, while semantic commonalities across unrelated languages may reflect independent routes to the same highly efficient solution. This proposal, focused on linguistic meaning, echoes the invocation of efficient communication to also explain other aspects of language (e.g., refs. 1–4).
Color is a semantic domain that has been approached in this spirit. Recent work has relied on the notion of the “informativeness” of word meaning, has often cast that notion in terms borrowed from information theory, and has accounted for several aspects of color naming across languages on that basis (5–10). Of particular relevance to our present focus, Regier, Kemp, and Kay (ref. 8, henceforth RKK) found that theoretically efficient categorical partitions of color space broadly matched major patterns of color naming seen across languages—suggesting that pressure for efficiency may indeed help to explain why languages categorize color as they do.
However, a fundamental issue has been left largely unaddressed: how a drive for efficiency may relate to accounts of color category evolution. Berlin and Kay (11) proposed an evolutionary sequence by which new terms refine existing partitions of color space in a discrete order: first dark vs. light, then red, then green and yellow, then blue, followed by other basic color categories. RKK’s efficient theoretical color-naming systems correspond roughly to the early stages of the Berlin and Kay sequence, but they leave the transitions between stages unexamined and are based on the false (9, 12, 13) simplifying assumption that color-naming systems are hard partitions of color space. In actuality, color categories are a canonical instance of soft categories with graded membership, and it has been argued (12, 13) that such categories may emerge gradually in parts of color space that were previously inconsistently named. Such soft category boundaries introduce uncertainty and therefore might be expected to impede efficient communication (9). Thus, it remains an open question whether a hypothesized drive for efficiency can explain not just discrete stages of color category evolution, but also how systems evolve continuously from one stage to the next, and why inconsistent naming patterns are sometimes observed.
Here, we argue that a drive for information-theoretic efficiency provides a unified formal explanation of these phenomena. Specifically, we argue that languages efficiently compress ideas into words by optimizing the trade-off between the complexity and accuracy of the lexicon according to the information bottleneck (IB) principle (14), an independently motivated formal principle with broad scope (15–17), which is closely related (ref. 18 and SI Appendix, section 1.3) to rate distortion theory (19). We support this claim by showing that cross-language variation in color naming can be explained in IB terms. Our findings suggest that languages may evolve through a trajectory of efficient solutions in a single process that synthesizes, in formal terms, key ideas from Berlin and Kay’s (11) theory and from more continuous accounts (12, 13) of color category evolution. We also show that soft categories and inconsistent naming can be information-theoretically efficient.
Our work focuses on data compression, in contrast with work that views language in information-theoretic terms but focuses instead on channel capacity (2–4, 7, 20), including work on language evolution (21). Our work also further (e.g., refs. 7 and 22) links information theory to the study of meaning, a connection that has been contested since Shannon’s (23) foundational work. IB has previously been used to find semantically meaningful clusters of words (ref. 15; see also ref. 22), but has not previously been used to account for word meanings as we do here.
Communication Model
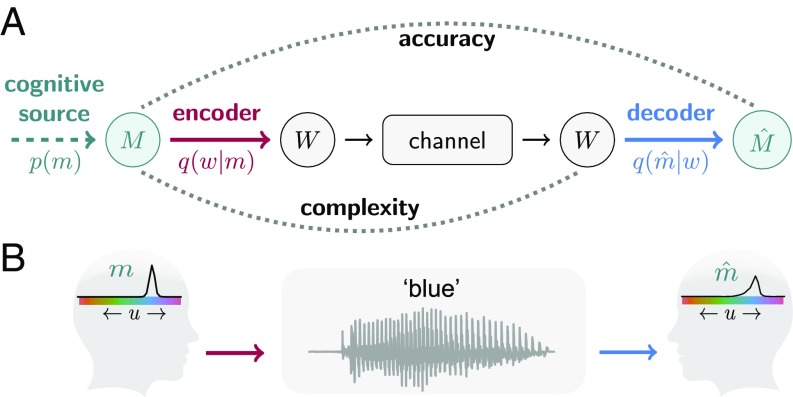
To define our hypothesis precisely, we first formulate a basic communication scenario involving a speaker and a listener. This formulation is based on Shannon’s classical communication model (23), but specifically concerns messages that are represented as distributions over the environment (Fig. 1). We represent the environment, or universe, as a set of objects . The state of the environment can be any object , and we let be a random variable that represents a possible state. We define a meaning to be a distribution over and assume the existence of a cognitive source that generates intended meanings for the speaker. This source is defined by a distribution over a set of meanings, , that the speaker can represent. Each meaning reflects a subjective belief about the state of the environment. If the speaker’s intention is , this indicates that she wishes to communicate her belief that . We consider a color communication model in which is restricted to colors and each is a distribution over colors.
Fig. 1.
(A) Shannon’s (23) communication model. In our instantiation of this model, the source message and its reconstruction are distributions over objects in the universe . We refer to these messages as meanings. is compressed into a code, or word, . We assume that is transmitted over an idealized noiseless channel and that the reconstruction of the source message is based on . The accuracy of communication is determined by comparing and , and the complexity of the lexicon is determined by the mapping from to . (B) Color communication example, where is a set of colors, shown for simplicity along a single dimension. A specific meaning is drawn from . The speaker communicates by uttering the word “blue,” and the listener interprets blue as meaning .
The speaker communicates by producing a word , taken from a shared lexicon of size . The speaker selects words according to a naming policy . This distribution is a stochastic encoder that compresses meanings into words. Because we focus on the uncertainty involved in compressing meanings into words, rather than the uncertainty involved in transmission, we assume an idealized noiseless channel that conveys its input unaltered as its output. This channel may have a limited capacity, which imposes a constraint on the available lexicon size. In this case, the listener receives and interprets it as meaning based on her interpretation policy , which is a decoder. We focus on the efficiency of the encoder and therefore assume an optimal Bayesian listener with respect to the speaker (see SI Appendix, section 1.2 for derivation), who interprets every word deterministically as meaning
| [1] |
where is obtained by applying Bayes’ rule with respect to and .
In this model, different color-naming systems correspond to different encoders, and our goal is to test the hypothesis that encoders corresponding to color-naming systems found in the world’s languages are information-theoretically efficient. We next describe the elements of this model in further detail.
Encoders.
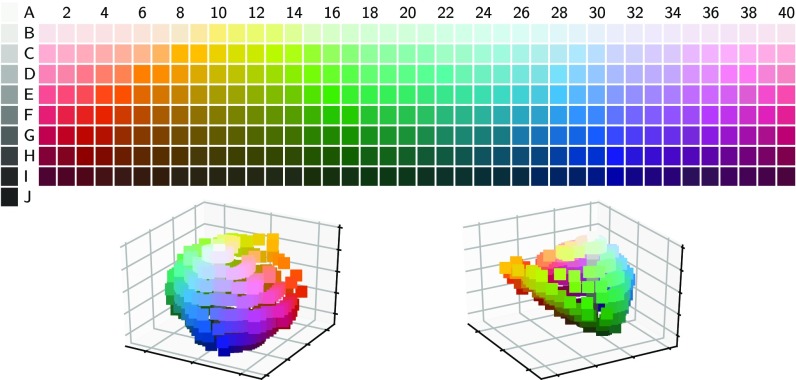
Our primary data source for empirically estimating encoders was the World Color Survey (WCS), which contains color-naming data from 110 languages of nonindustrialized societies (24). Native speakers of each language provided names for the 330 color chips shown in Fig. 2, Upper. We also analyzed color-naming data from English, collected relative to the same stimulus array (25). We assumed that each color chip is associated with a unique meaning and therefore estimated an encoder for each language from the empirical distribution of word given chip (see data rows in Fig. 4 for examples). Each such encoder corresponds to a representative speaker for language , obtained by averaging naming responses over speakers.
Fig. 2.
(Upper) The WCS stimulus palette. Columns correspond to equally spaced Munsell hues. Rows correspond to equally spaced lightness values. Each stimulus is at the maximum available saturation for that hue/lightness combination. (Lower) These colors are irregularly distributed in 3D CIELAB color space.
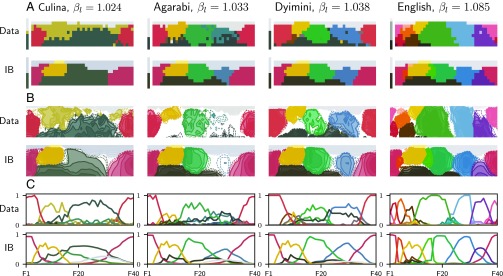
Fig. 4.
Similarity between color-naming distributions of languages (data rows) and the corresponding optimal encoders at (IB rows). Each color category is represented by the centroid color of the category. (A) Mode maps. Each chip is colored according to its modal category. (B) Contours of the naming distribution. Solid lines correspond to level sets between 0.5 and 0.9; dashed lines correspond to level sets of 0.4 and 0.45. (C) Naming probabilities along the hue dimension of row F in the WCS palette.
Meaning Space.
In our formulation, colors are mentally represented as distributions. Following previous work (6, 8), we ground these distributions in an established model of human color perception by representing colors in 3D CIELAB space (Fig. 2, Lower) in which Euclidean distance between nearby colors is correlated with perceptual difference. We define the meaning associated with chip to be an isotropic Gaussian centered at , namely . reflects the speaker’s subjective belief over colors that is invoked by chip , and the scale of these Gaussians reflects her level of perceptual uncertainty. We take , which corresponds to a distance over which two colors can be comfortably distinguished (SI Appendix, section 6.3).
Cognitive Source.
The cognitive source specifies how often different meanings must be communicated by a speaker. In principle, different cultures may have different communicative needs (8); we leave such language-specific analysis for future work and instead consider a universal source for all languages. Previous studies have used the uniform distribution for this purpose (8, 10); however, it seems unlikely that all colors are in fact equally frequent in natural communication. We therefore consider an alternative approach, while retaining the uniform distribution as a baseline. Specifically, we focus on a source that is derived from the notion of least informative (LI) priors (Materials and Methods), a data-driven approach that requires minimal assumptions. This approach also accounts for the data better than another approach based on image statistics (SI Appendix, section 7.2).
Bounds on Semantic Efficiency
From an information-theoretic perspective, an optimal encoder minimizes complexity by compressing the intended message as much as possible, while maximizing the accuracy of its interpretation (Fig. 1A). In general, this principle is formalized by rate distortion theory (RDT) (19). In the special case in which messages are distributions, the IB principle (14) provides a natural formalization. In IB, as in RDT (SI Appendix, section 1.3), the complexity of a lexicon is measured by the number of bits of information that are required for representing the intended meaning. In our formulation the speaker represents her intended meaning by , using an encoder , and thus the complexity is given by the information rate
| [2] |
where . Minimal complexity, i.e., , can be achieved if the speaker uses a single word to describe all her intended meanings. However, in this case the listener will not have any information about the speaker’s intended meaning. To enable useful communication, must contain some information about ; i.e., the complexity must be greater than zero.
The accuracy of a lexicon is inversely related to the cost of a misinterpreted or distorted meaning. While RDT allows an arbitrary distortion measure, IB considers specifically the Kullback–Leibler (KL) divergence,
| [3] |
which is a natural distortion measure between distributions. [For a general justification of the KL divergence see ref. 26, and in the context of IB see ref. 18.] Note that this quantity is 0 if and only if the listener’s interpretation is accurate; namely, . The distortion between the speaker and the ideal listener is the expected KL divergence,
| [4] |
In this case, the accuracy of the lexicon is directly related to Shannon’s mutual information,
| [5] |
Since is independent of , minimizing distortion is equivalent to maximizing the informativeness, or accuracy, of the lexicon, quantified by . This means that mutual information appears in our setting as a natural measure both for complexity and for semantic informativeness.
If the speaker and the listener are unwilling to tolerate any information loss, the speaker must assign a unique word to each meaning, which requires maximal complexity. However, between the two extremes of minimal complexity and maximal accuracy, an optimal trade-off between these two competing needs can be obtained by minimizing the IB objective function,
| [6] |
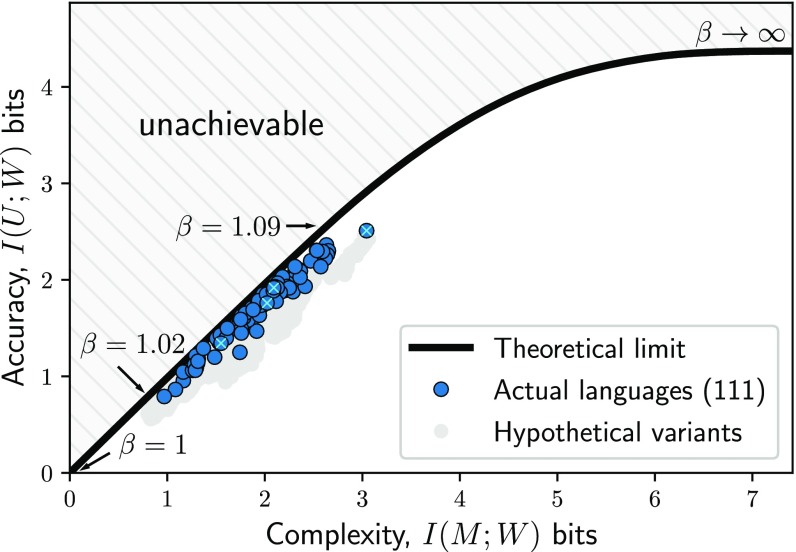
where is the trade-off parameter. Every language , defined by an encoder , attains a certain level of complexity and a certain level of accuracy. These two quantities can be plotted against each other. Fig. 3 shows this information plane for the present color communication model. The maximal accuracy that a language can achieve, given its complexity, is bounded from above. Similarly, the minimal complexity that can achieve given its accuracy is bounded from below. These bounds are given by the complexity and accuracy of the set of hypothetical IB languages that attain the minimum of Eq. 6 for different values of . The IB curve is the theoretical limit defined by these optimal languages, and all trade-offs above this curve are unachievable.
Fig. 3.
Color-naming systems across languages (blue circles) achieve near-optimal compression. The theoretical limit is defined by the IB curve (black). A total of 93% of the languages achieve better trade-offs than any of their hypothetical variants (gray circles). Small light-blue Xs mark the languages in Fig. 4, which are ordered by complexity.
Predictions
Near-Optimal Trade-offs.
Our hypothesis is that languages evolve under pressure for efficient compression, as defined by IB, which implies that they are pressured to minimize for some value of . If our hypothesis is true, then for each language there should be at least one value, , for which that language is close to the optimal . If we are able to find a good candidate for every language, this would support our hypothesis, because such an outcome would be unlikely given systems that evolved independently of . A natural choice for fitting is the value of that minimizes . We measure the efficiency loss, or deviation from optimality, of language by .
Structure of Semantic Categories.
Previous work (e.g., ref. 8) has sometimes summarized color-naming responses across multiple speakers of the same language by recording the modal naming response for each chip, resulting in a hard categorical partition of the stimulus array, called a mode map (e.g., Fig. 4A). However, IB predicts that if some information loss is allowed, i.e., , then an efficient encoder would induce soft rather than hard categories. This follows from the structure of the IB optima (14), given by
| [7] |
which is satisfied self-consistently with Eq. 1 and with the marginal . We therefore evaluate how well our model accounts for mode maps, but more importantly we also evaluate how well it accounts for the full color-naming distribution across speakers of a given language. If languages achieve near-optimal trade-offs, and their category structure is similar to that of the corresponding IB encoders, this would provide converging support for our hypothesis. We evaluate the dissimilarity between the mode maps of and by the normalized information distance (NID) (27) and the dissimilarity between their full probabilistic structures by a generalization of NID to soft partitions (gNID) (Materials and Methods).
Results
We consider the color communication model with the IB objective of efficient compression (IB model) and, as a baseline for comparison, with RKK’s efficiency objective (RKK+ model, see SI Appendix, section 4). We consider each model with the LI source and again with the uniform source. Because the LI source is estimated from the naming data, it is necessary to control for overfitting. Therefore, we performed fivefold cross-validation over the languages used for estimating the LI source. Table 1 shows that IB with the LI source provides the best account of the data. Similar results are obtained when estimating the LI source from all folds, and therefore the results with this source (SI Appendix, Fig. S1) are used for the figures. Table 1 and Fig. 3 show that all languages are near-optimally efficient with that is only slightly greater than 1; this means that for color naming, maximizing accuracy is only slightly more important than minimizing complexity. These trade-offs correspond to the steepest part of the IB curve, in which every additional bit in complexity contributes the most to the accuracy of communication. In this sense, naturally occurring color-naming systems lie along the most active area of the curve, before the point of diminishing returns.
Table 1.
Quantitative evaluation via fivefold cross-validation
| Source | Model | gNID | NID | ||
| LI | IB | 0.18 (±0.07) | 0.18 (±0.10) | 0.31 (±0.07) | 1.03 (±0.01) |
| RKK+ | 0.70 (±0.23) | 0.47 (±0.10) | 0.32 (±0.10) | ||
| U | IB | 0.24 (±0.09) | 0.39 (±0.12) | 0.56 (±0.07) | 1.06 (±0.01) |
| RKK+ | 0.95 (±0.22) | 0.65 (±0.08) | 0.50 (±0.10) |
Shown are averages over left-out languages ± 1 SD for the LI and uniform (U) source distributions. Lower values of ε∕ , gNID, and NID are better. Best scores are in boldface.
IB achieves 74% improvement in and 61% improvement in gNID compared to RKK+ with the LI source; however, the difference in NID is not substantial. Similar behavior appears with the uniform source. This result makes sense: The RKK+ bounds correspond to deterministic limits of suboptimal IB curves in which the lexicon size is restricted (SI Appendix, section 4.6). Because RKK’s objective predicts deterministic color-naming systems, it can account for mode maps but not for full color-naming distributions.
Although Table 1 and Fig. 3 suggest that color-naming systems in the world’s languages are near-optimally efficient, a possible objection is that perhaps most reasonable naming systems are near optimal according to IB, such that there is nothing privileged about the actual naming systems we consider. To rule out the possibility that IB is too permissive, we follow ref. 6 and construct for each language a control set of 39 hypothetical variants of that language’s color-naming system, by rotating that naming system in the hue dimension across the columns of the WCS palette (SI Appendix, section 8). A total of 93% of the languages achieve better trade-offs than any of their hypothetical variants, and the remaining 7% achieve better trade-offs than most of their variants (Fig. 3).
The quantitative results in Table 1 are supported by visual comparison of the naming data with IB-optimal systems. Fig. 4 shows that IB accounts to a large extent for the structure of color naming in four languages with increasing complexity. Similar results for all languages are presented in SI Appendix, section 10. The category colors in Fig. 4 correspond to the color centroids of each category, and it can be seen that the data centroids are similar to the corresponding IB centroids. In addition, the IB encoders exhibit soft category boundaries and sometimes leave parts of color space without a clearly dominant name, as is seen empirically (9, 13). Note that the qualitatively different solutions along the IB rows are caused solely by small changes in . This single parameter controls the complexity and accuracy of the IB solutions.
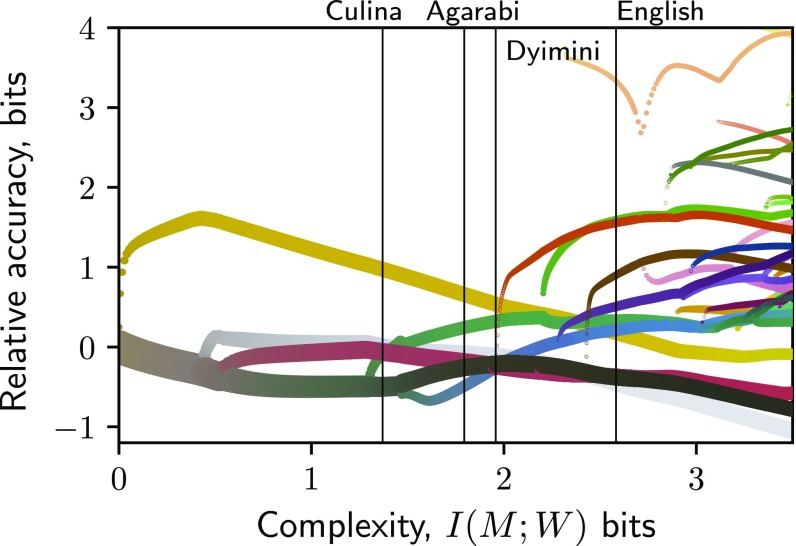
Tracking the IB centroids along the IB curve (Fig. 5) reveals a hierarchy of color categories. These categories evolve through an annealing process (28), by gradually increasing (SI Appendix, Movie S1). During this process, the IB systems undergo a sequence of structural phase transitions, in which the number of distinguishable color categories increases—corresponding to transitions between discrete stages in Berlin and Kay’s (11) proposal. Near these critical points, however, one often finds inconsistent, low-consensus naming—consistent with more continuous views of color category evolution (9, 12, 13). It is in this sense that the IB principle provides a single explanation for aspects of the data that have traditionally been associated with these different positions.
Fig. 5.
Bifurcations of the IB color categories (Movie S1). The axis shows the relative accuracy of each category (defined in Materials and Methods). Colors correspond to centroids and width is proportional to the weight of each category, i.e., . Black vertical lines correspond to the IB systems in Fig. 4.
By assigning to each language we essentially map it to a point on this trajectory of efficient solutions. Consider for example the languages shown in Figs. 4 and 5 (see SI Appendix, Movie S2 for more examples). Culina is mapped to a point right after a phase transition in which a green category emerges. This new green category does not appear in the mode maps of Fig. 4A, Left (data and IB), because it is dominated by other color categories, but it can be detected in Fig. 4C. Such dominated categories could easily be overlooked or dismissed as noise in the data, but IB predicts that they should exist in some cases. In particular, dominated categories tend to appear near criticality, as a new category gains positive probability mass. The color-naming systems of Agarabi and Dyimini are similar to each other and are mapped to two nearby points after the next phase transition, in which a blue category emerges. These two languages each have six major color categories; however, IB assigns higher complexity to Dyimini. The higher complexity for Dyimini is due to the blue category, which has a clear representation in Dyimini but appears at an earlier, lower consensus stage in Agarabi. SI Appendix, Movie S1 shows that low agreement around blue hues is predicted by IB for languages that operate around , and this is consistent with several WCS languages (e.g., Aguacatec and Berik in SI Appendix, section 10; also ref. 29), as well as some other languages (9, 13).
English is mapped to a relatively complex point in the IB hierarchy. The ability of IB to account in large part for English should not be taken for granted, since all IB encoders were evaluated according to a cognitive source that is heavily weighted toward the WCS languages, which have fewer categories than English. There are some differences between English and its corresponding IB system, including the pink category that appears later in the IB hierarchy. Such discrepancies may be explained by inaccuracies in the cognitive source, the perceptual model, or the estimation of .
The main qualitative discrepancy between the IB predictions and the data appears at lower complexities. IB predicts that a yellow category emerges at the earliest stage, followed by black, white, and red. The main categories in low-complexity WCS languages correspond to black, white, and red, but these languages do not have the dominant yellow category predicted by IB. The early emergence of yellow in IB is consistent with the prominence of yellow in the irregular distribution of stimulus colors in CIELAB space (Fig. 2, Lower Right). One possible explanation for the yellow discrepancy is that the low-complexity WCS languages may reflect suboptimal yet reasonably efficient solutions, as they all lie close to the curve.
Discussion
We have shown that color-naming systems across languages achieve near-optimally efficient compression, as predicted by the IB principle. In addition, this principle provides a theoretical explanation for the efficiency of soft categories and inconsistent naming. Our analysis has also revealed that languages tend to exhibit only a slight preference for accuracy over complexity in color naming and that small changes in an efficiency trade-off parameter account to a large extent for the wide variation in color naming observed across languages.
The growth of new categories along the IB curve captures ideas associated with opposing theories of color term evolution (see also refs. 9 and 25). Apart from the yellow discrepancy, the successive refinement of the IB categories at critical points roughly recapitulates Berlin and Kay’s (11) evolutionary sequence. However, the IB categories also evolve between phase transitions and new categories tend to appear gradually, which accounts for low-consensus regions (9, 12, 13). In addition, the IB sequence makes predictions about color-naming systems at complexities much higher than English and may thus account for the continuing evolution of high-complexity languages (25). This suggests a theory for the evolution of color terms in which semantic categories evolve through an annealing process. In this process, a trade-off parameter, analogous to inverse temperature in statistical physics, gradually increases and navigates languages toward more refined representations along the IB curve, capturing both discrete and continuous aspects of color-naming evolution in a single process.
The generality of the principles we invoke suggests that a drive for information-theoretic efficiency may not be unique to color naming. The only domain-specific component in our analysis is the structure of the meaning space. An important direction for future research is exploring the generality of these findings to other semantic domains.
Materials and Methods
Treatment of the Data.
The WCS data are available online at www1.icsi.berkeley.edu/wcs. English data were provided upon request by Lindsey and Brown (25). Fifteen WCS languages were excluded from the LI source and from our quantitative evaluation, to ensure that naming probabilities for each language were estimated from at least five responses per chip (SI Appendix, section 4.1).
LI Source.
A source distribution can be defined from a prior over colors by setting . For each language , we constructed a LI source by maximizing the entropy of while also minimizing the expected surprisal of given a color term in that language (see SI Appendix, section 2 for more details). We obtained a single LI source by averaging the language-specific priors.
IB Curve.
For each value of the IB solution is evaluated using the IB method (14). IB is a nonconvex problem, and therefore only convergence to local optima is guaranteed. To mitigate this problem we fix and use the method of reverse deterministic annealing to evaluate the IB curve (SI Appendix, section 1.4).
Dissimilarity Between Naming Distributions.
Assume two speakers that independently describe by and . We define the dissimilarity between and by
| [8] |
where corresponds to another independent speaker that uses . If and are deterministic, i.e., they induce hard partitions, then gNID reduces to NID (SI Appendix, section 3 for more details).
Relative Accuracy.
We define the informativeness of a word by
| [9] |
where is the prior over before knowing . Note that the accuracy of a language can be written as , and therefore we define the relative accuracy of (y axis in Fig. 5) by .
Supplementary Material
Acknowledgments
We thank Daniel Reichman for facilitating the initial stages of our collaboration, Delwin Lindsey and Angela Brown for kindly sharing their English color-naming data with us, Bevil Conway and Ted Gibson for kindly sharing their color-salience data with us, and Paul Kay for useful discussions. This study was supported by the Gatsby Charitable Foundation (N.T.), IBM PhD Fellowship Award (to N.Z.), and Defense Threat Reduction Agency (DTRA) Award HDTRA11710042 (to T.R.). Part of this work was done while N.Z. and N.T. were visiting the Simons Institute for the Theory of Computing at University of California, Berkeley.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1800521115/-/DCSupplemental.
References
- 1.Ferrer i Cancho R, Solé RV. Least effort and the origins of scaling in human language. Proc Natl Acad Sci USA. 2003;100:788–791. doi: 10.1073/pnas.0335980100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Levy RP, Jaeger TF. Speakers optimize information density through syntactic reduction. In: Schölkopf B, Platt JC, Hoffman T, editors. Advances in Neural Information Processing Systems. Vol 19. MIT Press; Cambridge, MA: 2007. pp. 849–856. [Google Scholar]
- 3.Piantadosi ST, Tily H, Gibson E. Word lengths are optimized for efficient communication. Proc Natl Acad Sci USA. 2011;108:3526–3529. doi: 10.1073/pnas.1012551108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gibson E, et al. A noisy-channel account of crosslinguistic word-order variation. Psychol Sci. 2013;24:1079–1088. doi: 10.1177/0956797612463705. [DOI] [PubMed] [Google Scholar]
- 5.Jameson K, D’Andrade RG. It’s not really red, green, yellow, blue: An inquiry into perceptual color space. In: Hardin CL, Maffi L, editors. Color Categories in Thought and Language. Cambridge Univ Press; Cambridge, UK: 1997. pp. 295–319. [Google Scholar]
- 6.Regier T, Kay P, Khetarpal N. Color naming reflects optimal partitions of color space. Proc Natl Acad Sci USA. 2007;104:1436–1441. doi: 10.1073/pnas.0610341104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baddeley R, Attewell D. The relationship between language and the environment: Information theory shows why we have only three lightness terms. Psychol Sci. 2009;20:1100–1107. doi: 10.1111/j.1467-9280.2009.02412.x. [DOI] [PubMed] [Google Scholar]
- 8.Regier T, Kemp C, Kay P. Word meanings across languages support efficient communication. In: MacWhinney B, O’Grady W, editors. The Handbook of Language Emergence. Wiley-Blackwell; Hoboken, NJ: 2015. pp. 237–263. [Google Scholar]
- 9.Lindsey DT, Brown AM, Brainard DH, Apicella CL. Hunter-gatherer color naming provides new insight into the evolution of color terms. Curr Biol. 2015;25:2441–2446. doi: 10.1016/j.cub.2015.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gibson E, et al. Color naming across languages reflects color use. Proc Natl Acad Sci USA. 2017;114:10785–10790. doi: 10.1073/pnas.1619666114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Berlin B, Kay P. Basic Color Terms: Their Universality and Evolution. Univ of California Press; Berkeley: 1969. [Google Scholar]
- 12.MacLaury RE. Color and Cognition in Mesoamerica: Constructing Categories as Vantages. Univ of Texas Press; Austin, TX: 1997. [Google Scholar]
- 13.Levinson SC. Yélî Dnye and the theory of basic color terms. J Linguistic Anthropol. 2000;10:3–55. [Google Scholar]
- 14.Tishby N, Pereira FC, Bialek W. The information bottleneck method. In: Hajek B, Sreenivas RS, editors. Proceedings of the 37th Annual Allerton Conference on Communication, Control and Computing. Univ of Illinois; Urbana, IL: 1999. pp. 368–377. [Google Scholar]
- 15.Slonim N. 2002. The information bottleneck: Theory and applications. PhD thesis (Hebrew Univ of Jerusalem, Jerusalem)
- 16.Shamir O, Sabato S, Tishby N. Learning and generalization with the information bottleneck. Theor Comput Sci. 2010;411:2696–2711. [Google Scholar]
- 17.Palmer SE, Marre O, Berry MJ, Bialek W. Predictive information in a sensory population. Proc Natl Acad Sci USA. 2015;112:6908–6913. doi: 10.1073/pnas.1506855112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Harremoës P, Tishby N. 2007 The information bottleneck revisited or how to choose a good distortion measure. IEEE International Symposium on Information Theory. Available at https://ieeexplore.ieee.org/document/4557285/. Accessed July 10, 2018.
- 19.Shannon CE. Coding theorems for a discrete source with a fidelity criterion. IRE Nat Conv Rec. 1959;4:142–163. [Google Scholar]
- 20.Jaeger TF. Redundancy and reduction: Speakers manage syntactic information density. Cogn Psychol. 2010;61:23–62. doi: 10.1016/j.cogpsych.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Plotkin JB, Nowak MA. Language evolution and information theory. J Theor Biol. 2000;205:147–159. doi: 10.1006/jtbi.2000.2053. [DOI] [PubMed] [Google Scholar]
- 22.Pereira F, Tishby N, Lee L. Distributional clustering of English words. In: Schubert LK, editor. Proceedings of the 31st Annual Meeting of the Association for Computational Linguistics. Association for Computational Linguistics; Stroudsburg, PA: 1993. pp. 183–190. [Google Scholar]
- 23.Shannon C. A mathematical theory of communication. Bell Syst Tech J. 1948;27:623–656. [Google Scholar]
- 24.Cook RS, Kay P, Regier T. The World Color Survey database: History and use. In: Cohen H, Lefebvre C, editors. Handbook of Categorization in Cognitive Science. Elsevier; Amsterdam: 2005. pp. 223–242. [Google Scholar]
- 25.Lindsey DT, Brown AM. The color lexicon of American English. J Vis. 2014;14:17. doi: 10.1167/14.2.17. [DOI] [PubMed] [Google Scholar]
- 26.Csiszár I, Shields P. Information theory and statistics: A tutorial. Found Trends Commun Inf Theor. 2004;1:417–528. [Google Scholar]
- 27.Vinh NX, Epps J, Bailey J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. JMLR. 2010;11:2837–2854. [Google Scholar]
- 28.Rose K. Deterministic annealing for clustering, compression, classification, regression, and related optimization problems. Proceedings of the IEEE. 1998;86:2210–2239. [Google Scholar]
- 29.Lindsey DT, Brown AM. Color naming and color consensus: “Blue” is special. J Vis. 2004;4:55. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.