Significance
Vector-borne diseases represent complex infection transmission systems; previous epidemiological models have been unable to formally capture the relationship between the ecological limits of vector species and the dynamics of pathogen transmission. By making this advance for the key disease, Rift Valley fever, we are able to show how seasonally varying availability of water bodies and ambient temperatures dictate when the mosquito vector populations will persist and importantly, those sets of conditions resulting in stable oscillations of disease transmission. Importantly, under the latter scenario, short-term health control measures will likely fail, as the system quickly returns to the original configuration after the intervention stops. Our model, therefore, offers an important tool to better understand vector-borne diseases and design effective eradication programs.
Keywords: vector-borne diseases, zoonosis, cross-species transmission, stability analysis, Floquet analysis
Abstract
Vector-borne diseases (VBDs) of humans and domestic animals are a significant component of the global burden of disease and a key driver of poverty. The transmission cycles of VBDs are often strongly mediated by the ecological requirements of the vectors, resulting in complex transmission dynamics, including intermittent epidemics and an unclear link between environmental conditions and disease persistence. An important broader concern is the extent to which theoretical models are reliable at forecasting VBDs; infection dynamics can be complex, and the resulting systems are highly unstable. Here, we examine these problems in detail using a case study of Rift Valley fever (RVF), a high-burden disease endemic to Africa. We develop an ecoepidemiological, compartmental, mathematical model coupled to the dynamics of ambient temperature and water availability and apply it to a realistic setting using empirical environmental data from Kenya. Importantly, we identify the range of seasonally varying ambient temperatures and water-body availability that leads to either the extinction of mosquito populations and/or RVF (nonpersistent regimens) or the establishment of long-term mosquito populations and consequently, the endemicity of the RVF infection (persistent regimens). Instabilities arise when the range of the environmental variables overlaps with the threshold of persistence. The model captures the intermittent nature of RVF occurrence, which is explained as low-level circulation under the threshold of detection, with intermittent emergence sometimes after long periods. Using the approach developed here opens up the ability to improve predictions of the emergence and behaviors of epidemics of many other important VBDs.
Vector-borne diseases (VBDs) form an important class of infectious diseases, with over 1 billion human cases and 1 million human deaths per year (1), and they are a significant contributor to global poverty. Current patterns of VBD occurrence are likely to change in the future due to the accelerating rate of global climate and other environmental change that is predicted over the next century (2). Climate and land use change as well as globalization are expected to affect the geographic distribution of arthropod species (3) through a variety of mechanisms, such as changes to the variability in weather conditions that alter survival; reproduction and biting rates of the vectors; changes to the availability of water bodies via, for instance, new irrigation patterns and dam constructions, creating new habitats for disease-competent vectors; and human mobility and animal trade increasing the opportunity for vectors to reach and establish in new areas. Pathogen ecology is influenced by climate and weather as well; for instance, temperature affects both the susceptibility of vectors to infection and pathogen extrinsic incubation periods, which usually require pathogen replication at ambient temperatures (4, 5). From here on, we refer to “ambient temperature” as “temperature.”
These issues provide the basis of the work reported here. We focus on Rift Valley fever (RVF), an important mosquito-borne viral zoonosis. The causative virus is responsible for major epidemics in Africa, and its range seems to be expanding as shown by phylogeographic analysis (6) and recent epidemic occurrence in Saudi Arabia and Yemen (7–10). Furthermore, concern has been raised about the potential for environmental/climatic changes causing increased impact of RVF in endemic areas or facilitating its spread to new regions of the world (10–12). Rift Valley fever virus (RVFV) has a significant economic impact on the livestock industry in Africa and can cause fatal disease in humans (13).
RVFV has a complex, multispecies epidemiology, and it is transmitted by biting mosquitos and occasionally, directly by animal body fluids. Infected mosquitos transmit RVFV when taking a blood meal, potentially infecting a wide range of species. The disease is most significant in domestic ruminants, although wild animals [e.g., buffalos (14) and rodents (15)] might play an important role as reservoir hosts. Although more than 40 mosquito and midge species are known to be capable of transmitting RVFV (16), Aedes sp., Mansoni sp., and Culex sp. are thought to be the most important for virus transmission to livestock and people.
Climatic drivers, such as temperature and rainfall, have a strong impact on the complex ecology of both RVFV and its vectors (17–20). Thus, the epidemiology of RVFV is likely to be strongly impacted by climate change (21). Other environmental, cultural, and socioeconomic factors, such as gathering of large numbers of people and domestic animals during religious festivities, have relevant implications for the infection dynamics of RVFV, including driving epidemics (22–25).
The complex features of RVFV infection dynamics have led to many studies. Empirical statistical approaches have identified key environmental variables (e.g., temperature and rainfall) that are associated with disease epidemics, enabling disease risk to be mapped (11, 18, 19, 22, 23, 25–35). Mechanistic models have added crucial insights for understanding links between disease transmission and the environment by exploring the impact of seasonality and studying the processes leading to epidemic transmission (24, 36–52). Despite progress, these approaches are still subject to important limitations: the earlier mechanistic models do not incorporate seasonality; most models tend to include either only rainfall or only temperature as a contributing factor; and if included, seasonality is usually incorporated only as an ad hoc periodic variation in the response (e.g., oviposition rate) rather than in the causative variable, undermining the realism of the approaches.
A further critical limitation of these studies is that they rely on rainfall data. In empirical statistical approaches, rainfall is often considered a “predictor variable” [with the commonly associated problem of collinearity (53)]. In mechanistic models, rainfall is usually a proxy for breeding sites. In complex hydrogeological models, rainfall is merely an input to represent water bodies; the major problem with this approach is that the dependence of RVFV on rainfall varies widely across countries and ecoregions due to, for example, different types of terrain, evaporation rates, delay between rainfall occurrence and establishment of water bodies, etc.
To overcome these limitations, we developed a unified, process-based model built on a realistic representation of how the dynamics of water bodies obtained from satellite images (rather than rainfall) and temperature influence the ecology of the primary mosquito vectors and the epidemiology of RVFV. A critical feature of using this approach is our ability to investigate the combined impact of seasonality on both water availability and temperature, allowing us to (i) capture the influence of seasonal patterns of temperature and water bodies on the quantitative transmission dynamics of RVFV, (ii) quantify the environmental drivers that lead to regional endemicity of RVFV, (iii) assess if transovarial transmission in Aedes sp. (the only species of mosquitos for which ovarian transmission is known) is necessary for RVFV persistence, (iv) isolate the mechanisms allowing virus reemergence after long periods of inactivity in endemic regions (43, 54), and (v) identify if and under which conditions the complex patterns of RVFV epidemics resemble chaotic behavior [i.e., the system being highly sensitive to initial conditions (55), rendering disease predictions difficult].
Analysis
Our analyses were conducted within two main contexts: a theoretical case, represented by a simple sinusoidal variation of the surface area of water bodies and of temperature (represented by Eqs. 5 and 6), and a realistic situation, where we used empirical data for Kenya [viz., spatially averaged temperature (56) and the total surface area of water bodies over the entire territory divided by the surface of Kenya] (SI Appendix, SI Text). Here and throughout, we refer to these two situations as “theoretical model” and “realistic model,” respectively. We first ran the theoretical model by systematically changing the mean annual temperature and mean annual surface area of water bodies (i.e., parameters and in Eqs. 5 and 6); for each simulation, we ascertained whether the predictions result in sustained fluctuations in populations of Culex sp. or Aedes sp. [the dominant vectors in Kenya (57)] or in the prevalence of RVFV in livestock. All other parameters were kept the same, and the surface area of water bodies and temperature were allowed to fluctuate in phase with annual periodicity (e.g., the parameters in Eqs. 5 and 6) (SI Appendix, SI Text discusses a situation where this constraint was relaxed). We conducted analyses in both the theoretical and realistic models using different initial conditions and numbers of livestock. How frequently the surface areas of water bodies change is likely to have an impact on mosquito populations. Thus, for the theoretical model, we varied the frequency of water bodies’ body surface area fluctuation (i.e., in Eqs. 5 and 6) while ensuring the same overall annual surface area of water bodies. To investigate the intermittent nature of observed RVF epidemics, we assumed that, when the mean number of infected livestock is below a certain threshold, the epidemic is not detected. This is a reasonable assumption considering the frequency of subclinical infections and the limited diagnostic facilities available in endemic areas. Cases detected within 30 d are assumed to be part of the same epidemic. We then ran the realistic model 100 times with the initial number of livestock and with infection prevalence in the livestock randomly drawn from uniform distributions (100–5,000 for the number of livestock and 5–20% for the infection prevalence, respectively). All other parameters were kept the same. The simulation was also run in the absence of transovarial transmission. In each case, we then estimated the periods of time during which RVFV was not detected. Predictions of the duration of interepidemic periods for the realistic model were compared with historical data of RVF epidemics that had occurred in Kenya from 2004 to 2013 obtained from the Global Animal Disease Information System, EMPRES-i (58).
Results
Influence of the Seasonal Patterns of Temperature and Water Bodies on the Quantitative Dynamics of RVFV.
The theoretical model shows (Fig. 1; more details are in SI Appendix, Fig. S19) that different amplitudes and frequencies of fluctuations in temperature and water availability within the system result in different disease patterns. It is possible, for example, that one or both mosquito species might go extinct, that there could be stable oscillations with one or more annual peaks in the mosquito population but in an RVFV-free situation, that there could be stable mosquito populations with sporadic RVFV epidemics, or that RVFV might become endemic.
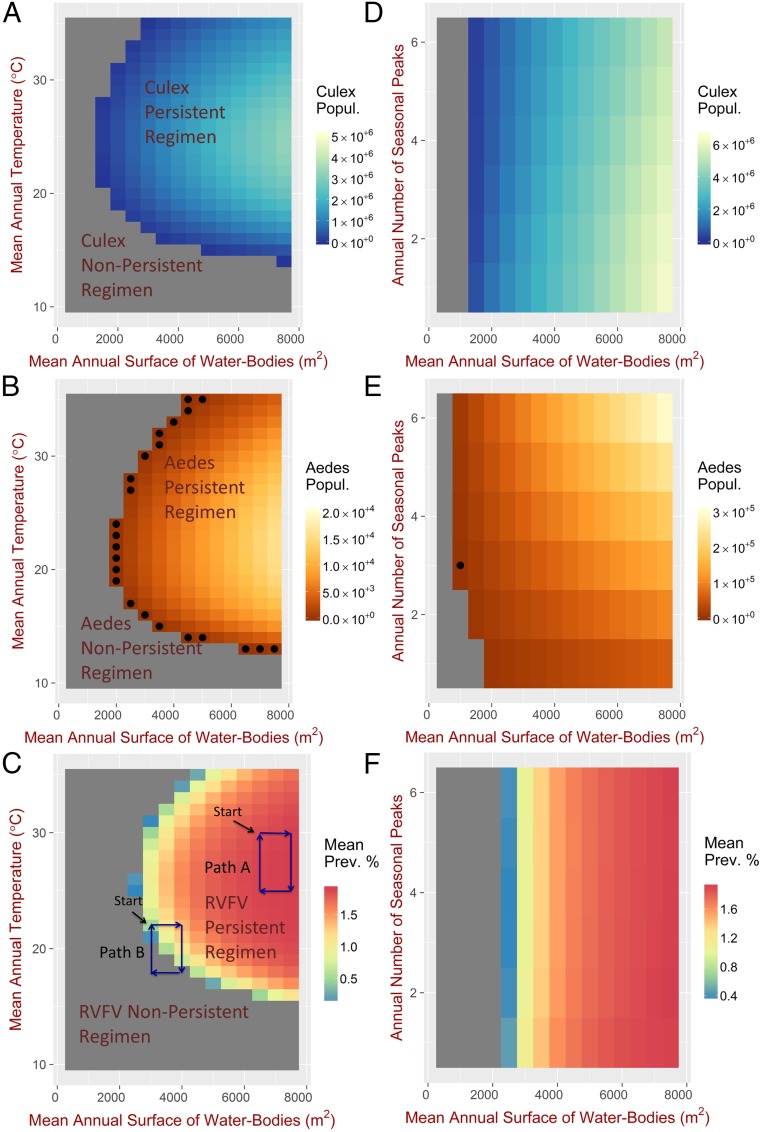
Fig. 1.
Environmental constraints leading to persistent and nonpersistent regimens mosquitos and RVFV. (A–C) Impact of mean water bodies’ surface area and mean temperature on the population of mosquitos and RVFV prevalence. Water bodies’ surface area and temperature are described by sinusoidal functions according to Eqs. 5 and 6. The x axis shows the mean water bodies’ surface area , while the y axis shows the mean temperature ; these are the only parameters that are changed in the simulations while the frequency () and phase () are kept constant. (D–F) Impact of frequency of oscillations in water bodies’ surface area on the population of mosquitos. Water bodies’ surface area is described by sinusoidal functions according to Eq. 5 with , while the temperature is kept constant (C). The x axis shows the mean water bodies’ surface area , while the y axis shows the annual number of seasonal peaks in water bodies’ surface area; these are the only parameters that are changed in the simulations. The gray areas correspond to a region in the space of parameters where the mosquitos population (A, B, D, and E) or the yearly averaged infection prevalence in livestock (C and F) drops to zero after a transient phase (negative largest Floquet exponents of the linearized system around the null solution). The colored regions with no black dots correspond to a region in the space of parameters where the mosquitos population or the yearly averaged infection prevalence in livestock will always establish sustained oscillations after a transient phase (negative largest Floquet exponents of the linearized system around a periodic limit cycle solution). The intensity of the color corresponds to the yearly average number of mosquitos or infection prevalence in livestock. The black dots in B and E identify a region in the space of parameters where the solution is unstable (positive largest Floquet exponents; this is because the time considered is too short for the solution to stabilize).
Quantifying the Environmental Drivers Leading to Regional Endemicity of RVFV.
The theoretical model predicts the existence of a temperature-dependent threshold in mean surface area of water bodies below which mosquito populations and RVFV always fade out (gray areas in Fig. 1, which are referred to as the “nonpersistent regimen”). The model also showed the parameter space (i.e., the set of all possible combinations of values for the different parameters) resulting in a “persistent regimen” (i.e., sustained oscillations in the vectors and RVFV) (colored areas in Fig. 1). The intensity of the color reflects the yearly averaged population of the mosquitos or the yearly averaged prevalence of RVFV in livestock. The optimal conditions for mosquito occur when the mean body surface area is at its greatest and when the mean temperature is C for Culex and C for Aedes (Fig. 1). The prevalence of RVFV in livestock is predicted to be highest when temperature is C. The ranges of mean annual temperature and mean annual water-body surface area resulting in sustained fluctuations in mosquito abundance, in particular for Aedes sp., differ from those causing sustained oscillations of RVFV in livestock. There are some regions where RVFV endemicity is possible in the absence of Aedes sp., and there are a few situations where a persistent mosquito population does not support RVFV endemicity (SI Appendix, Fig. S19). Under a constant temperature of C, the average abundance of Culex sp. decreases with increasing frequency of oscillation in water availability (Fig. 1D). This is due to nontrivial interactions arising from particular mosquito population sizes at times when the surface of water bodies starts decreasing. In contrast, Aedes sp. abundance increases with the frequency of oscillations in water-body surface area (Fig. 1E). This is not surprising, as in contrast to Culex sp., the hatching of Aedes sp. eggs is driven by flooding and desiccation cycles. In the extreme case of no water-body fluctuation, Aedes sp. is expected to go extinct, although this does not always occur, as a small proportion of Aedes eggs hatches spontaneously without desiccation/flooding (59) (SI Appendix, Fig. S20). The domain of the RVFV persistent conditions is dependent on the abundance of livestock, , in particular when this impacts on the biting and oviposition rate (SI Appendix, Figs. S21–S23). The intensity of the fluctuations in temperature and in the surface area of water bodies seems to have little impact on mosquito abundance and on whether RVFV becomes endemic (SI Appendix, Fig. S24).
When Does the Complexity of RVFV Dynamics Resemble Chaotic Behavior?
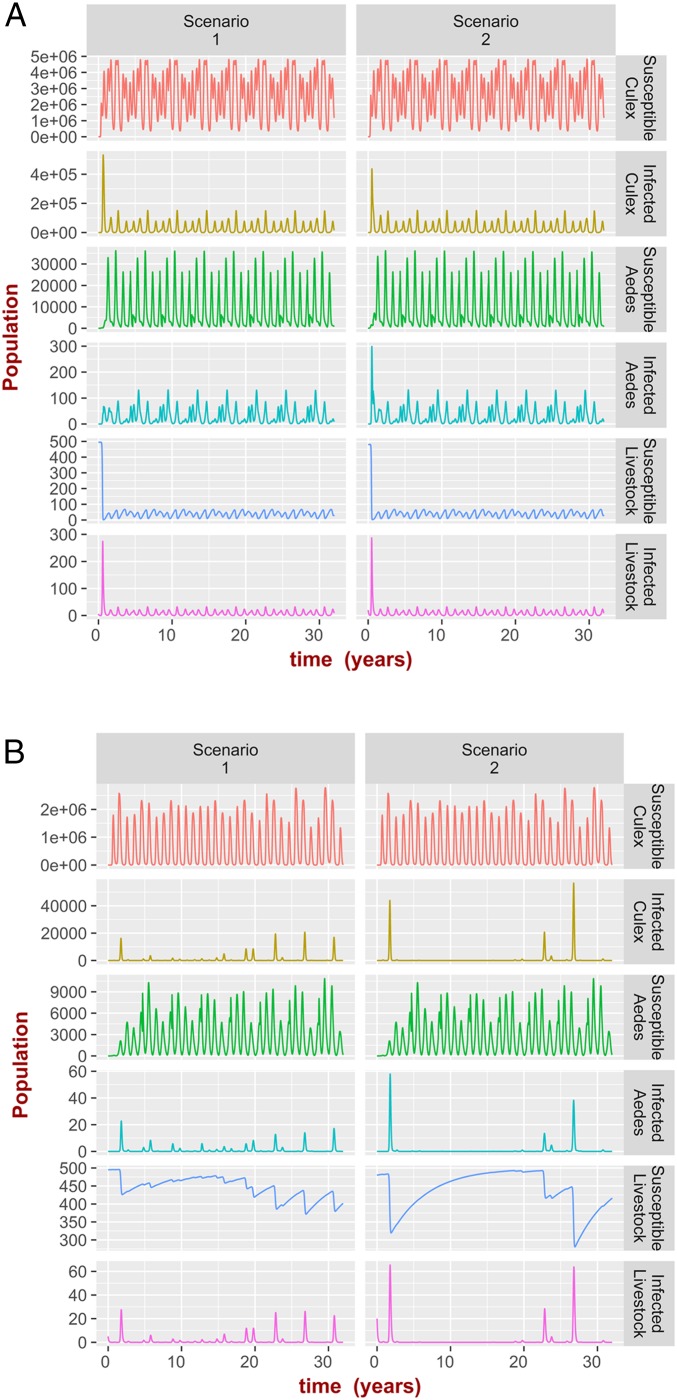
Stability refers to the property of an ecosystem to return to equilibrium if perturbed (55) or equivalently, that the system will always reach the equilibrium state regardless of the initial conditions. In the theoretical model, the equilibria are represented by extinction of mosquito species and/or RVFV infection (nonpersistent regimen) or more or less complex periodic oscillations (persistent regimen). For the mosquito populations, Floquet analysis (Materials and Methods and SI Appendix, SI Text) shows that the long-term mathematical solutions are stable. For RVFV infection, numerical computations show that the solutions are stable after the initial conditions (i.e., the initial number of livestock) are fixed (SI Appendix, Fig. S25). Changing the initial number of livestock has no practical effect on the overall population of mosquitos when the impact of livestock on mosquito oviposition and biting rate is assumed to be negligible (i.e., for very large values of the parameter as in this case, but other scenarios are shown in SI Appendix, Fig. S23). The number of livestock, however, predictably impacts the temporal patterns of infected mosquitos and infected livestock (SI Appendix, Fig. S25), and the system can no longer be considered stable if the number of livestock is externally perturbed. Accordingly, animal movements, including the immigration of infected animals, might have a significant impact on the pattern of RVFV infection. Similar behavior is observed for the realistic model, where simulations show that, regardless of the initial conditions, the system approaches the same asymptotic limit, with only the initial number of livestock having a direct impact on the patterns of infections (SI Appendix, Fig. S25). The property that the system always reverts to the same asymptotic solution (after fixing the initial number of livestock) is not general. An important counterexample is shown in Fig. 2 (SI Appendix, Fig. S26). In this simulation experiment, we consider the two scenarios illustrated by path A and path B in Fig. 1C: first, when the mean temperature and mean surface area of water bodies are always within the RVFV persistent regimen, and second, when these values transit from RVFV persistence to RVFV nonpersistence and then back again. To do so, we divided the entire time (32 y) into eight cycles; each 4-y cycle (described either by path A or by path B in Fig. 1C) consists of four intervals of 1 y each (represented by the segments in the paths). For each interval, we let the mean values or in Eqs. 5 and 6 change year by year (SI Appendix, Fig. S27). For each situation, represented by paths A and B (Figure 2A and 2B respectively), we then considered two scenarios (scenario 1 and scenario 2 in Figure 2 A and B) by imposing different initial conditions in the infection prevalence but the same total number of livestock, i.e., we kept the total number of livestock 500, but the infection prevalence for scenario 1 was set to 1% (5 infected livestock out of 495) and the infection prevalence for scenario 2 was set to 4% (20 infected livestock out of 480). When the mean temperature and mean surface area of water bodies vary within the RVFV persistent regimen (path A), the system reaches the same limit irrespective of the different initial conditions (Fig. 2A). In contrast, for the situation described by path B, different values of the initial infection prevalence lead to qualitatively different solutions (Fig. 2B), a phenomenon resembling chaotic systems observed in meteorology. This phenomenon can be stronger for different parameter values, leading to situations where the overall mosquito populations as well as their infection prevalence are asymptotically different (SI Appendix, Fig. S26).
Fig. 2.
During the simulation (32 y), the mean surface area of water bodies and mean temperature are cyclic changing according to paths A and B illustrated in Fig. 1C. For path A, during the first year, the mean surface area of water bodies increases according to a stepwise function in a 4-mo interval (SI Appendix, Fig. S27) from 6,500 to 7,500 m2, and the mean temperature is constant at C; this is followed by a second year with constant mean surface area of water bodies at 7,500 m2, while the mean temperature is decreasing according to a stepwise function in a 2-mo interval from C to C. During the third year, the mean surface area of water bodies decreases according to a stepwise function in a 4-mo interval from 7,500 to 6,500 m2, and the mean temperature is constant at C; this is followed by a fourth year, when the mean temperature is increasing according to a stepwise function in a 2-mo interval from C to C and the mean surface area of water bodies is constant at 6,500 m2. For path B, the dynamics is the same as for path A, but the range of the mean surface area of water bodies is between 3,000 and 4,000 m2 and the range for mean temperature is between C and C. (A) Dynamics of mosquitos population and RVFV infection in livestock when mean temperature and mean surface area of water bodies change according to path A for two different initial conditions. In scenario 1, exposed and removed livestock and all mosquitos stages are set to zero, except for the susceptible and infected livestock and , respectively, and mosquitos eggs , . Scenario 2 is like scenario 1 but with and , respectively, and mosquitos eggs , . The asymptotic behavior is the same in both scenarios. B is the same as A, but the mean temperature and mean surface area of water bodies change according to path B. The asymptotic behavior is different for the different scenarios.
Is Transovarial Transmission in Aedes Necessary for RVFV Persistence?
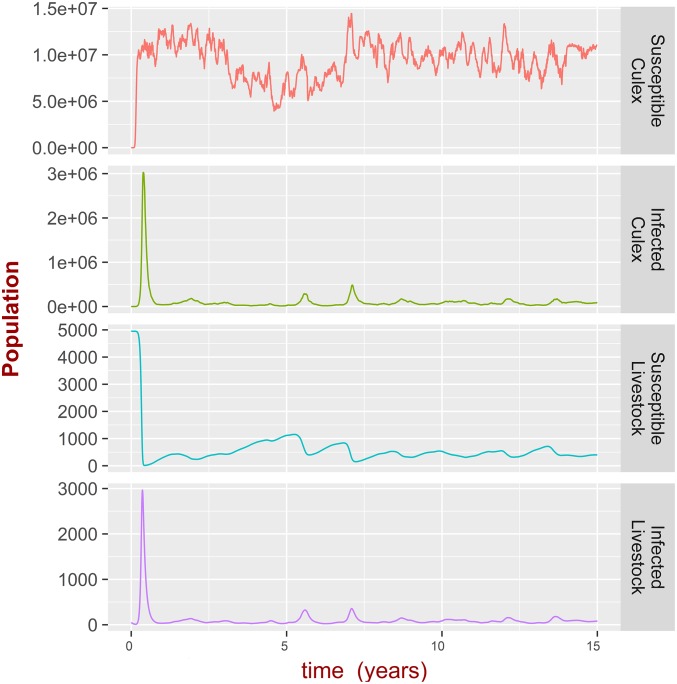
The simulations of RVFV dynamics showed persistence in Culex sp. in the absence of Aedes mosquitos (Fig. 3) over 15 y in the realistic model. The numerical simulation shows that persistent patterns of RVFV occur in the absence of Aedes sp. In the theoretical model, the use of Floquet theory should prevent the problem of infection persistence at unrealistic low levels [“atto-fox problem” (60)], as the theory focuses on the stability of the precise zero or periodic solution (although here, the stability of RVFV was studied only numerically). In general, random extinctions of RVFV preclude persistence of infection, although one could argue that deterministic models mimic the fact that random extinctions are compensated by random immigration of infected mosquitos or livestock. Incorporating demographic stochasticity and spatial immigration would address this concern. Taking all of this into account, we cautiously conclude that the transovarial transmission of RVFV in Aedes sp. is not a prerequisite for RVFV persistence over time, although the models provide no evidence to discount this as an important (49) transmission route in reality.
Fig. 3.
Assessing the impact of transovarial transmission. Dynamics of Culex sp. population and RVFV infection in livestock in the absence of Aedes sp. population for the realistic model. The theoretical case is exemplified in SI Appendix, Fig. S19B.
Isolate the Drivers Enabling the Virus to Reemerge After Long Periods of Inactivity in Endemic Regions.
Here, we assumed that, when the mean number of infected livestock is below a certain threshold (chosen to be 50) (SI Appendix, SI Text discusses 5 infected animals and infection prevalence), the epidemic is not detected by routine surveillance. The patterns of the distribution of these disease-undetected times (Fig. 4) are similar for the situations where both mosquitos species are present and where Aedes sp. and thus, transovarial transmission are absent. The empirical interepidemic periods observed in Kenya from 2004 to 2013 (58) are shown for comparison. The similarity of the patterns suggests a strong impact of external drivers and variation in immunity in livestock populations compared with the impact of the mosquito species. Both distributions are multimodal (Fig. 4), with several peaks occurring; interestingly, several small peaks occur over long time periods ( y). This shows that RVFV can circulate in the system at very low, undetectable levels, emerging unexpectedly after very long time periods. For a lower level of threshold (SI Appendix, Fig. S29), the probability of observing long interepidemic periods is smaller. This further highlights the importance of including stochasticity in the diagnostic (the detection threshold). As discussed above, demographic stochasticity allows for the extinction of the infection, and other factors, such as spatial immigration, would allow reemergence. Incorporating this mechanism would likely have a detectable impact on patterns of the interepidemic periods.
Fig. 4.
Assessing the intermittent nature of RVFV. The histograms represent the distribution of duration of interepidemic periods for empirical data, for the model where Aedes spp. is absent (origin due only to undetected cases) and where both mosquitos species are present (origin due to undetected cases and transovarial transmission).
Discussion
We identified the range of seasonally varying temperatures and water-body extent leading either to extinction of mosquito populations and/or RVFV or to established mosquito populations and endemicity of the infection. These results allow prediction of future geographic distribution of RVFV due to changes in environmental and climatic conditions across the globe.
To achieve this, we developed a process-based mathematical model, which unifies environmental factors, the ecology of mosquitos, and the epidemiology of RVFV.
A Unified Framework for the Dynamics of VBDs.
A key advantage of this model is its conceptual simplicity, with the undeniable complexity of the system reduced to a few fundamental factors: surface area of water bodies governing mosquito oviposition rates, temperature affecting mosquito developmental rates, and their survival and biting rates as well as the extrinsic incubation period of RVFV. The impact of these parameters cascades on the dynamics of the mosquito population and thus, RVFV. The seasonality of mosquito abundance and infection prevalence is largely governed by the seasonality in water-body surface area and temperature. The resulting patterns, however, are not trivial due to the nonlinearity of the system; even in a theoretical system represented by simple sinusoidal variation of water-body surface area and temperature, the different combinations of these result in qualitatively different regimens, including one or both mosquitos becoming extinct, an RVFV-free scenario but with established mosquito populations, or sustained oscillations of mosquito abundance and RVFV prevalence (in mosquitos and livestock) with one or more annual peaks. The modular nature of the model facilitates its calibration and validation. For example, the mosquito model can be tested in an RVFV-free situation, only subsequently including the effects of the disease.
Environmental Conditions Allowing Established Mosquito Populations and Viral Persistence.
The abundance of mosquito eggs is ultimately constrained by the maximum density of eggs (i.e., number of eggs per unit surface area) and the surface area of water bodies, resulting in a carrying capacity that results in a stable mosquito population irrespective of initial conditions. In the realistic scenarios, this was shown numerically; in the theoretical systems, we proved the stability of the system by using Floquet analysis. This showed a lower threshold in mean water-body surface areas, below which the mosquito populations will go extinct; otherwise, it will result in sustained oscillation. The value of this threshold depends nonmonotonically on the mean temperature, and it is confined between lower and upper values, reflecting the fact that mosquitos do not survive in very cold or very dry hot temperatures. The analysis also showed the importance of the frequency of fluctuations in water-body dynamics, especially for Aedes sp. Similar thresholds in temperature and water bodies occur for the persistence of RVFV in livestock, reflecting the geographic distribution of the disease. Here, livestock numbers were also critical. The biophysical interpretation of stability analysis is extremely important. For example, stable oscillations in the mosquito population imply that, unless there is a permanent change in the drivers (e.g., average surface area of water bodies), any temporary measure aiming to reduce the mosquito population (e.g., chemical control) will not result in a permanent solution, as mosquito abundance is expected to return to the original values after application of control measures stops. Similarly, if mosquitos are imported into a region with temperature and water-body parameters that are in the persistent regimen, then they will become established in this new environment.
Intermittent Nature of RVFV and the Problem of Predictability.
Epidemics of RVFV are intermittent and typically are not very predictable (43, 54). Severe epidemics are provoked by flooding after protracted periods of drought. Transovarial transmission in Aedes mosquitos is a mechanism of RVFV persistence (61) and a possible explanation for the intermittent nature of RVFV epidemics, as presumably infected Aedes sp. eggs can survive for several years. Another explanation is that RVFV is always circulating in the population, perhaps in a cryptic reservoir (14, 15, 62), at very low level and is not detected. This is supported by evidence of interepidemic RVFV seropositivity among humans and animals (63, 64) and the indication of subclinical infection in livestock (65). Our model suggests that transovarial transmission is not necessary for interepidemic persistence of RVFV and that the infection may continuously circulate at low and largely undetectable levels in between irregular epidemics; change in immunity in livestock populations is playing an important role in the irregularity of the infection patterns. This result is strictly valid, however, when all animals and mosquitos are well-connected (e.g., through animal movement), as our deterministic model is based on the assumption of uniform mixing. Our theoretical model shows that, after the initial number of livestock is fixed, the solution is stable, and long-term behavior can be accurately predicted even if the initial conditions, such as the exact number of infected animals or the abundance of mosquitos at a given time, are not known. If the number of livestock, however, is perturbed, the solutions are qualitatively and quantitatively different even if all other conditions are kept identical. Thus, for reliable predictions, accurate information on the demography of livestock is necessary (the impact of the livestock size on infection is discussed in SI Appendix, SI Text). In some situations, however, this is not sufficient. The mean surface areas of water bodies and temperatures can change (as in Kenya, where mean surface area of water bodies decreased during ) (SI Appendix, Fig. S4) and transit from the persistent to nonpersistent regimen and vice versa. In such situations, the system becomes highly sensitive to the initial values of infection prevalence, a situation that resembles chaotic behavior. Thus, the irregularity of the system can arise even from small variations in the infection prevalence due to, for example, immigration of a few infected livestock. Variations in the demography of livestock [such as occurs in festivals (24)] and transitions across persistent and nonpersistent regimens are additional causes of the intermittent patterns in the epidemics of RVFV.
A Program for Future Work.
This work identified important challenges that could be addressed by further theoretical work and model-guided fieldwork. Fieldwork can be designed to test well-defined hypotheses that emerge from the model, such as the predicted larger abundance of Aedes sp. in regions where water bodies are fluctuating more frequently and the existence of thresholds in surface area of water bodies and temperature confining the domain of the persistent regimens for mosquito species and RVFV infection. Further experiments to gauge the impact of livestock density on mosquito oviposition and biting rates (66) are crucial, as this will have an important effect on the mosquito population and on patterns of RVFV infection (SI Appendix, SI Text). In most cases, we focus on one host only. Copresence of multiple hosts can dilute or amplify the disease. Further investigations on host feeding preference (67) and the relationship between mosquito abundance and host population size are critical to estimate this effect (68). A challenging point is the large uncertainty associated with many parameter values; in particular, the life history parameters of mosquitos stage are often based on laboratory conditions and inferred for different species of mosquitos. Theoretical works like this can steer future fieldwork and experimentation to reduce the knowledge gaps that emerged from the model.
The potential impacts of multiple hosts, including wildlife hosts (e.g., buffalo), also need to be investigated. We assumed uniform mixing between mosquitos and livestock. As a result, the predicted patterns of infection in Aedes sp., Culex sp., and livestock are qualitatively similar. The model should be generalized to incorporate heterogeneity occurring in nature. Furthermore, the model needs to be refined to incorporate the impact of vegetation and natural predators on the ecology of mosquitos. This could be done, for example, by allowing the birth and mortality rates to depend on such factors and calibrating the model accordingly. The presence of livestock and other animals might attract mosquitos from neighbor areas via CO2 emission, resulting in a density-dependent vector-to-host ratio relationships (68). In general, climate change is expected to cause an increase in not only the average temperature but also, rainfall intensity and frequency. Climate projections can be readily incorporated into the model for a more accurate analysis of the impact of climate change on the ecology of mosquitos and the epidemiology of RVFV. The impact of animal movement is another crucial driver of RVFV (ref. 34 and discussion in ref. 69). Future research should address, for instance, how the epidemiology of RVFV changes in the presence of livestock immigration and how this is affected by the size of these imports and the number of infected animals in each batch.
Our analysis was done using a deterministic model, but environmental stochasticity and external periodic drivers (e.g., seasonality in temperature and surface area of water bodies) can resonate with the natural frequencies of the ecosystem (70), with large effects on the ecology of mosquitos and the epidemiology of RVFV. Furthermore, patterns of the interepidemic periods should be assessed by taking into account stochastic variability in demography and diagnostics at different spatial settings. These are crucial questions to consider in future research. Extension of the model to include spatial variability is the natural progression of this work. By using high spatiotemporal resolution of water bodies (71), temperature (56), type of vegetation data, and animal census, the model could be carefully calibrated to assess whether the environmental variables are within the persistent regimens. Then, the approach could be used to generate a map of potentially endemic regions for RVFV or other VBDs to plan interventions more effectively (e.g., aiming at long-term control of environmental conditions, such as reducing the size of water bodies, in endemic areas and short-term measures, such as limiting animal movement, in nonendemic areas). If the environmental variables are at the interface between persistent and nonpersistent regimens, then more robust uncertainty and sensitivity analysis are required, exploring not only the space of parameters but also, the plausible distribution of the initial conditions, such as livestock population and its infection prevalence. This also raises important practical and theoretical questions on the reliability of statistical models based on presence/absence of cases when the epidemiology is subject to chaotic behavior.
Materials and Methods
The model combines an ecological, stage-structured population dynamics model for the Aedes sp. and Culex sp. with an epidemiological susceptible–exposed–infectious–recovered compartmental model for the livestock and a susceptible–exposed–infectious model for the two mosquito populations. For simplicity, we assume only one host, although the model can be readily extended to include multiple heterogeneous hosts (e.g., goats, cattle, sheep). The stage-structured population dynamics of the mosquitos is largely based on the model of Otero et al. (72), which includes the effect of temperature on the development rate of the mosquitos. Important additions to the model of Otero et al. (72) are (i) the dependence of the oviposition process on the water bodies’ surface, (ii) the separation of Aedes sp. eggs into mature and immature eggs, and (iii) the dependency of the number of eggs per batch on the density of livestock. Below, we emphasize aspects of the model, while a detailed formulation of the framework is presented in SI Appendix, SI Text.
Ecoepidemiological Model.
The Culex sp. populations consist of eggs (), larvae (), pupae (), nulliparous females [i.e., female adults not having laid eggs ()], flyers (), and female adults having laid eggs (); the Aedes sp. consists of immature and mature eggs ( and , respectively), larvae (), pupae (), nulliparous females (), flyers (), and female adults having laid eggs (). Adult male mosquitos are not explicitly included, and only one-half of the emerging adults are females. After the first gonotrophic cycle (i.e., feeding on blood meal and laying of eggs) ends, the nulliparous female becomes a flyer ( and ) in search of breeding sites followed by a series of cyclic transitions regulated by the second gonotrophic cycle to the adult stage ( and ) and back to the flyer status ( and ).
Temperature-dependent development rates for the gonotrophic cycles, in the limit of infinitely available blood meal, were based on parametrization presented in the literature (42); the other stages were modeled according to the simplification by Schoolfield et al. (73) of the model by Sharpe and DeMichele for poikilotherm development based on data from ref. 74 (SI Appendix, SI Text and Table S6). Life stage-specific mortality rates for Culex quinquefasciatus and Aedes aegypti were extracted from data collected under standard laboratory conditions from ref. 74. Ordinary least squares regression models were fitted with mortality rate as the response variable and temperature (15 °C to 34 °C) as the explanatory variable (SI Appendix, SI Text and Figs. S17 and S18). Other than the daily mortality in the pupal stage, there is an additional mortality associated with the emergence of the adult (72).
The population dynamics of eggs is regulated by the availability and dynamics of suitable breeding sites [i.e., temporary water bodies (dambos) (SI Appendix, Figs. S13 and S14) typically formed by heavy rainfall]. In contrast with Culex sp., Aedes sp. lay their eggs in the moist soils above mean high water surrounding the water body (SI Appendix, Fig. S14). According to ref. 75, the average time for egg deposition is d in laboratory conditions, which are assumed to be ideal conditions; at field scale, the mosquitos need to search for a suitable breeding site, reducing the oviposition rate (i.e., the number of times that a flyer lays a batch of eggs per time unit). Thus, the oviposition rate is modeled as , where (assumed to be the same for both species of mosquito) corresponds to the typical size of the terrain scanned by a flyer to detect suitable breeding sites and is the overall surface at time of the breeding sites dispersed in a region of area . This region is estimated as based on some indication that the spatial range of the activity of mosquitos would be up to 1,500 m to the nearest suitable water body (76); the time-varying surface was obtained by satellite images (71). For simplicity, the contribution of small artificial containers with water, such as tires, flower pots, tin cans, clogged rain gutters, etc., is not included. This is justified by the fact that common species of the genus Aedes involved in the transmission of RVFV, such as Aedes mcintoshi, Aedes circumluteolus, and Aedes ochraceus, breed in temporary grassland depressions (dambos) (17). Breeding sites already occupied by eggs prevent further ovipositions; we, therefore, introduced a carrying capacity in the egg load rates (i.e., the number of eggs laid by all flyers per time unit) as and , where and are the total numbers of Culex sp. and Aedes sp. eggs already laid. In the first case, , and in the second case, it is the sum of mature and immature eggs irrespective of their infected status. and are the numbers of eggs per batch, and the carrying capacities and take into account that the maximum number of eggs that can be laid over a water body is limited by its surface , namely and , where and are the densities of eggs per surface unit (either water for Culex sp. or soil for Aedes sp.). and represent the fractions of the breeding site suitable for eggs deposition and survival; for Culex sp., this corresponds to an inner area around the edge of the water body, and for Aedes sp., it is the outer moist soil around the water body (here, we assumed that both surface areas are proportional to the total surface area of the water bodies). In addition, mosquitos cannot produce eggs without ingesting blood meals; thus, following the same argument presented in ref. 66 for triatomines, the numbers of Culex sp. and Aedes sp. eggs per batch, and , respectively, are rescaled by factors and , where and are the maximum numbers of Culex sp. and Aedes sp. eggs produced per batch in the limit of infinite resources, respectively. and are the calculated vector-to-host ratios (here assumed to be of the total number of mosquitos divided the number of livestock) (SI Appendix, SI Text), and is the particular vector-to-host ratio for which vector fecundity is divided by two (but if both mosquitos species are present, then we consider the total vector-to-host ratio to be ). Based on the same argument (66), the rates of gonotrophic cycles, which are assumed to be the same as the biting rates, were rescaled in the same manner. Accordingly, in the absence of host (i.e., no blood meal), the number of eggs per batch and the biting rate drop to zero.
Aedes sp. eggs require a minimum desiccation period ; after this period, they are ready to hatch provided that they are submerged in water, although of newly embryonated Aedes sp. eggs hatch spontaneously without flooding (59); Aedes sp. eggs can survive desiccation for several years. Therefore, we distinguish two egg stages and , with development time of newly laid eggs conditioned to
| [1] |
where is the temperature dependency of development rate of the eggs (72) (SI Appendix, Eqs. S14 and S21 and Table S6).
Aedes sp. eggs will hatch at the time of the first flood [e.g., at time when ], Thus, during a small time , the variation in the number of mature eggs due to hatching can be modeled as
| [2] |
(i.e., if the water body is shrinking, no eggs will be submerged, and thus, no eggs will hatch). This leads to
| [3] |
where the superficial density of eggs at time was estimated as . The continuous counterpart of the above equation leads to
| [4] |
where the term represents the rate of change of the surface area of a water body.
Combined Mosquito and Livestock Population Model in the Presence of Infection.
RVFV transmission in Aedes mosquitos can be transovarial or horizontal, while only horizontal transmission, mediated by biting infectious hosts, is possible for Culex sp. Both adult Culex sp. and Aedes sp. can become infected after feeding on infectious livestock . More precisely, for Culex sp., the movements out from the susceptible categories, and , are and , respectively; of these, and mosquitos move to the exposed flyer category, . The remaining and move to the susceptible flyer category, . Similar arguments apply to Aedes sp., but in this case, there is an additional infectious category for nulliparous mosquitos, , emerging out of infectious eggs due to transovarial transmission. The exposed categories then transit to the adult infectious categories ( and for Culex and and for Aedes) with rates and , respectively. The exposed and infectious populations will lead to the exposed and infectious flyer populations ( and for Culex sp. and and for Aedes sp.) followed by cyclic transitions to the corresponding exposed and infectious adult stages and back to the exposed and infectious flyer stages. Furthermore, infected Aedes sp. flyers [i.e., either exposed () or infectious ()] will deposit infectious eggs , which will turn into infectious larvae , infectious pupae , infectious nulliparous adults , etc. The explicit set of differential equations is presented in SI Appendix, SI Text. Parameters are based on data presented in the literature (refs. 40, 42, and 72 and references therein) (SI Appendix, Tables S3–S5) and adapted to the Kenya situation [e.g., temperature (56) and water bodies (71)].
Stability Analysis for Seasonal Systems: Floquet Theory.
Floquet analysis is a well-established tool suitable to study the stability of seasonal systems (77, 78). In the simplest scenarios, temperature and water bodies can be approximated by the periodic functions
| [5] |
| [6] |
where and are the frequencies of oscillations in surface areas of water bodies and temperature; the terms and represent the mean surface area of water bodies and mean temperature during periods and , respectively; and are the maximum amplitudes in the oscillations; and and are the respective phases. Then, we ran the model and calculated the corresponding Floquet multipliers for a range of frequencies, mean surface areas of water bodies, and mean temperatures to explore which of these parameters lead to stable solutions. More details are in SI Appendix, SI Text.
Supplementary Material
Acknowledgments
We thank Dr. Erasmus Zu Ermgassen for his help during the preliminary stages of the work. This work was mainly conducted within the Dynamic Drivers of Disease in Africa Consortium, Natural Environment Research Council (NERC) Project NE-J001570-1, which was funded with support from the Ecosystem Services for Poverty Alleviation (ESPA) program. The ESPA program is funded by the Department for International Development, the Economic and Social Research Council, and the NERC. The work was partially supported by the National Institute for Health Research (NIHR) Health Protection Research Unit in Environmental Change and Health at the London School of Hygiene and Tropical Medicine in partnership with Public Health England (PHE) and in collaboration with the University of Exeter, University College London, and the Met Office. A.A.C. and J.L.N.W. are also supported by European Union FP7 Project ANTIGONE (Contract 278976). A.A.C. was supported by a Royal Society Wolfson Research Merit Award. J.L.N.W. is supported by the Alborada Trust. D.W.R. is supported by a Medical Research Council UK Research and Innovation/Rutherford Fellowship (MR/R02491X/1). The views expressed are those of the author(s) and not necessarily those of the National Health Service, the NIHR, the Department of Health, or PHE.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1803264115/-/DCSupplemental.
References
- 1.WHO 2016 Vector-borne diseases. Available at www.who.int/en/news-room/fact-sheets/detail/vector-borne-diseases. Accessed June 13, 2018.
- 2.IPCC . In: Summary for Policymakers. Pachauri R, Meyer L, editors. IPCC; Geneva: 2014. pp. 2–26. [Google Scholar]
- 3.Semenza JC, Menne B. Climate change and infectious diseases in Europe. Lancet Infect Dis. 2009;9:365–375. doi: 10.1016/S1473-3099(09)70104-5. [DOI] [PubMed] [Google Scholar]
- 4.Brubaker JF, Turell MJ. Effect of environmental temperature on the susceptibility of Culex pipiens (Diptera: Culicidae) to Rift Valley fever virus. J Med Entomol. 1998;35:918–921. doi: 10.1093/jmedent/35.6.918. [DOI] [PubMed] [Google Scholar]
- 5.Turell MJ. Effect of environmental temperature on the vector competence of Aedes taeniorhynchus for Rift Valley fever and Venezuelan equine encephalitis viruses. Am J Trop Med Hyg. 1993;49:672–676. doi: 10.4269/ajtmh.1993.49.672. [DOI] [PubMed] [Google Scholar]
- 6.Soumaré POL, et al. Phylogeography of Rift Valley fever virus in Africa reveals multiple introductions in Senegal and Mauritania. PLoS One. 2012;7:23–26. doi: 10.1371/journal.pone.0035216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Balkhy HH, Memish ZA. Rift Valley fever: An uninvited zoonosis in the Arabian peninsula. Int J Antimicrob Agents. 2003;21:153–157. doi: 10.1016/s0924-8579(02)00295-9. [DOI] [PubMed] [Google Scholar]
- 8.Abdo-Salem S, et al. Descriptive and spatial epidemiology of Rift Valley fever outbreak in Yemen 2000-2001. Ann New York Acad Sci. 2006;1081:240–242. doi: 10.1196/annals.1373.028. [DOI] [PubMed] [Google Scholar]
- 9.Chevalier V, Pépin M, Plée L, Lancelot R. Rift Valley fever–a threat Europe? Euro Surveill Bull Européen sur les maladies transmissibles. Eur Commun Dis Bull. 2010;15:19506. [PubMed] [Google Scholar]
- 10.Rolin AI, Berrang-Ford L, Kulkarni Ma. The risk of Rift Valley fever virus introduction and establishment in the United States and European Union. Emerg Microbes Infect. 2013;2:e81. doi: 10.1038/emi.2013.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Taylor D, et al. Environmental change and Rift Valley fever in eastern Africa: Projecting beyond health futures. Geospat Health. 2016;11:115–128. doi: 10.4081/gh.2016.387. [DOI] [PubMed] [Google Scholar]
- 12.Golnar AJ, Kading RC, Hamer GL. Quantifying the potential pathways and locations of Rift Valley fever virus entry into the United States. Transbound Emerg Dis. 2018;65:85–95. doi: 10.1111/tbed.12608. [DOI] [PubMed] [Google Scholar]
- 13.Gerdes GH. Rift Valley fever the importance of Rift Valley fever for animal and public. Rev Sci Tech. 2004;23:613–623. doi: 10.20506/rst.23.2.1500. [DOI] [PubMed] [Google Scholar]
- 14.Beechler BR, et al. Rift Valley fever in Kruger National Park: Do buffalo play a role in the inter-epidemic circulation of virus? Transbound Emerg Dis. 2015;62:24–32. doi: 10.1111/tbed.12197. [DOI] [PubMed] [Google Scholar]
- 15.Gora D, et al. The potential role of rodents in the enzootic cycle of Rift Valley fever virus in Senegal. Microbes Infect. 2000;2:343–346. doi: 10.1016/s1286-4579(00)00334-8. [DOI] [PubMed] [Google Scholar]
- 16.Meegan J, Bailey C, editors. Rift Valley Fever. The Arboviruses: Epidemiology and Ecology. CRC; Boca Raton, FL: 1989. [Google Scholar]
- 17.Davies FG, Linthicum KJ, James AD. Rainfall and epizootic Rift Valley fever. Bull World Health Organ. 1985;63:941–943. [PMC free article] [PubMed] [Google Scholar]
- 18.Linthicum KJ. Climate and satellite indicators to forecast Rift Valley fever epidemics in Kenya. Science. 1999;285:397–400. doi: 10.1126/science.285.5426.397. [DOI] [PubMed] [Google Scholar]
- 19.Anyamba A, et al. Prediction of a Rift Valley fever outbreak. Proc Natl Acad Sci USA. 2009;106:955–959. doi: 10.1073/pnas.0806490106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Anyamba A, et al. Climate teleconnections and recent patterns of human and animal disease outbreaks. PLoS Negl Trop Dis. 2012;6:e1465. doi: 10.1371/journal.pntd.0001465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Martin V, Chevalier V, Ceccato P, Anyamba A, Simone LD. The impact of climate change on the epidemiology and control of Rift Valley fever vector-borne diseases Rift Valley fever and climate change. Rev Sci Tech. 2008;27:413–426. [PubMed] [Google Scholar]
- 22.Abdo-Salem S, et al. Can environmental and socioeconomic factors explain the recent emergence of Rift Valley fever in Yemen, 2000-2001? Vector Borne Zoonotic Dis. 2011;11:773–779. doi: 10.1089/vbz.2010.0084. [DOI] [PubMed] [Google Scholar]
- 23.Métras R, et al. Risk factors associated with Rift Valley fever epidemics in South Africa in 2008-11. Sci Rep. 2015;5:9492. doi: 10.1038/srep09492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Xiao Y, et al. Modelling the effects of seasonality and socioeconomic impact on the transmission of Rift Valley fever virus. PLoS Negl Trop Dis. 2015;9:e3388. doi: 10.1371/journal.pntd.0003388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Redding DW, Tiedt S, Lo Iacono G, Bett B, Jones KE. Spatial, seasonal and climatic predictive models of Rift Valley fever disease across Africa. Philos Trans R Soc B. Biol Sci. 2017;372:20160165. doi: 10.1098/rstb.2016.0165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Clements AC, Pfeiffer DU, Martin V, Otte MJ. A Rift Valley fever atlas for Africa. Prev Vet Med. 2007;82:72–82. doi: 10.1016/j.prevetmed.2007.05.006. [DOI] [PubMed] [Google Scholar]
- 27.Vignolles C, et al. Rift Valley fever in a zone potentially occupied by Aedes vexans in Senegal: Dynamics and risk mapping. Geospat Health. 2009;3:211–220. doi: 10.4081/gh.2009.221. [DOI] [PubMed] [Google Scholar]
- 28.Soti V, et al. Identifying landscape features associated with Rift Valley fever virus transmission, Ferlo region, Senegal, using very high spatial resolution satellite imagery. Int J Health Geogr. 2013;12:10. doi: 10.1186/1476-072X-12-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Caminade C, et al. Rift valley fever outbreaks in Mauritania and related environmental conditions. Int J Environ Res Public Health. 2014;11:903–918. doi: 10.3390/ijerph110100903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sindato C, et al. Spatial heterogeneity of habitat suitability for Rift Valley fever occurrence in Tanzania: An ecological Niche modelling approach. PLoS Negl Trop Dis. 2016;10:e0005002. doi: 10.1371/journal.pntd.0005002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gikungu D, et al. Dynamic risk model for Rift Valley fever outbreaks in Kenya based on climate and disease outbreak data. Geospat Health. 2016;11:377. doi: 10.4081/gh.2016.377. [DOI] [PubMed] [Google Scholar]
- 32.Tran A, et al. Development and assessment of a geographic knowledge-based model for mapping suitable areas for Rift Valley fever transmission in Eastern Africa. PLoS Negl Trop Dis. 2016;10:e0004999. doi: 10.1371/journal.pntd.0004999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Munyua PM, et al. Predictive factors and risk mapping for Rift Valley fever epidemics in Kenya. PLoS One. 2016;11:e0144570. doi: 10.1371/journal.pone.0144570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lancelot R, et al. Drivers of Rift Valley Fever epidemics in Madagascar. Proc Natl Acad Sci USA. 2017;114:938–943. doi: 10.1073/pnas.1607948114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Olive MM, et al. Reconstruction of Rift Valley fever transmission dynamics in Madagascar: Estimation of force of infection from seroprevalence surveys using Bayesian modelling. Sci Rep. 2017;7:39870. doi: 10.1038/srep39870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mpeshe SC, Haario H, Tchuenche JM. A mathematical model of Rift Valley fever with human host. Acta Biotheor. 2011;59:231–250. doi: 10.1007/s10441-011-9132-2. [DOI] [PubMed] [Google Scholar]
- 37.Xue L, Scott HM, Cohnstaedt LW, Scoglio C. A network-based meta-population approach to model Rift Valley fever epidemics. J Theor Bio. 2012;306:129–144. doi: 10.1016/j.jtbi.2012.04.029. [DOI] [PubMed] [Google Scholar]
- 38.Niu T, Gaff HD, Papelis YE, Hartley DM. An epidemiological model of Rift Valley fever with spatial dynamics. Comput Math Methods Med. 2012;2012:138757. doi: 10.1155/2012/138757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Soti V, et al. Combining hydrology and mosquito population models to identify the drivers of Rift Valley fever emergence in semi-arid regions of West Africa. PLoS Negl Trop Dis. 2012;6:e1795. doi: 10.1371/journal.pntd.0001795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Barker CM, Niu T, Reisen WK, Hartley DM. Data-driven modeling to assess receptivity for Rift Valley fever virus. PLoS Negl Trop Dis. 2013;7:e2515. doi: 10.1371/journal.pntd.0002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gao D, Cosner C, Cantrell RS, Beier JC, Ruan S. Modeling the spatial spread of Rift Valley fever in Egypt. Bull Math Biol. 2013;75:523–542. doi: 10.1007/s11538-013-9818-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fischer EA, Boender GJ, Nodelijk G, de Koeijer AA, van Roermund HJ. The transmission potential of Rift Valley fever virus among livestock in The Netherlands: A modelling study. Vet Res. 2013;44:58. doi: 10.1186/1297-9716-44-58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Manore CA, Beechler BR. Inter-epidemic and between-season persistence of Rift Valley fever: Vertical transmission or cryptic cycling? Transbound Emerg Dis. 2015;62:13–23. doi: 10.1111/tbed.12082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chitnis N, Hyman JM, Manore CA. Modelling vertical transmission in vector-borne diseases with applications to Rift Valley fever. J Biol Dyn. 2013;7:11–40. doi: 10.1080/17513758.2012.733427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mweya CN, Holst N, Mboera LEG, Kimera SI. Simulation modelling of population dynamics of mosquito vectors for Rift Valley fever virus in a disease epidemic setting. PLoS One. 2014;9:e108430. doi: 10.1371/journal.pone.0108430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chamchod F, et al. A modeling approach to investigate epizootic outbreaks and enzootic maintenance of Rift Valley fever virus. Bull Math Biol. 2014;76:2052–2072. doi: 10.1007/s11538-014-9998-7. [DOI] [PubMed] [Google Scholar]
- 47.Pedro SA, Abelman S, Ndjomatchoua FT, Sang R, Tonnang HEZ. Stability, Bifurcation and Chaos analysis of vector-borne disease model with application to Rift Valley fever. PLoS One. 2014;9:e108172. doi: 10.1371/journal.pone.0108172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mpeshe SC, Luboobi LS, Nkansah-gyekye YAW. Stability analysis of the Rift Valley fever dynamical model. J Math Comput Sci. 2014;4:740–762. doi: 10.1155/2014/627586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pedro SA, Abelman S, Tonnang HEZ. Predicting Rift Valley fever inter-epidemic activities and outbreak patterns: Insights from a stochastic host-vector model. PLoS Negl Trop Dis. 2016;10:e0005167. doi: 10.1371/journal.pntd.0005167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gachohi J, Njenga MK, Kitala P, Bett B. Modelling vaccination strategies against Rift Valley fever in livestock in Kenya. PLoS Negl Trop Dis. 2016;10:e0005049. doi: 10.1371/journal.pntd.0005049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Miron RE, Giordano GA, Kealey AD, Smith RJ. Multiseason transmission for Rift Valley fever in North America multiseason transmission for Rift Valley fever in North America. Math Popul Stud. 2016;23:71–94. [Google Scholar]
- 52.Scoglio CM, et al. Biologically informed Individual-based network model for Rift Valley fever in the US and evaluation of mitigation strategies. PLoS One. 2016;11:e0162759. doi: 10.1371/journal.pone.0162759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lo Iacono G, et al. Challenges in developing methods for quantifying the effects of weather and climate on water-associated diseases: A systematic review. PLoS Negl Trop Dis. 2017;11:e0005659. doi: 10.1371/journal.pntd.0005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Paweska JT, Jansen van Vuren P. Rift Valley Fever Virus in the Role of Animals in Emerging Viral Diseases. Academic; Boston: 2014. pp. 169–200. [Google Scholar]
- 55.May RMRM. Stability and Complexity in Model Ecosystems. 2nd Ed Princeton Univ Press; Princeton: 2001. [Google Scholar]
- 56.Menne MJ, Durre I, Vose RS, Gleason BE, Houston TG. An overview of the global historical climatology network-daily database. J Atmos Oceanic Technol. 2012;29:897–910. [Google Scholar]
- 57.Sang R, et al. Distribution and abundance of key vectors of Rift Valley fever and other arboviruses in two ecologically distinct counties in Kenya. PLoS Negl Trop Dis. 2017;11:e0005341. doi: 10.1371/journal.pntd.0005341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sang R, et al. 2017 Global animal disease information system. Available at empres-i.fao.org/eipws3g/. Accessed June 28, 2017.
- 59.Focks DA, Haile DG, Daniels E, Mount GA. Dynamic life table model for Aedes aegypti (Diptera: Culicidae): Analysis of the literature and model development. J Med Entomol. 1993;30:1003–1017. doi: 10.1093/jmedent/30.6.1003. [DOI] [PubMed] [Google Scholar]
- 60.Mollison D. Dependence of epidemic and population velocities on basic parameters. Math Biosci. 1991;107:255–287. doi: 10.1016/0025-5564(91)90009-8. [DOI] [PubMed] [Google Scholar]
- 61.LaBeaud AD, Kazura JW, King CH. Advances in Rift Valley fever research: Insights for disease prevention. Curr Opin Infect Dis. 2010;23:403–408. doi: 10.1097/QCO.0b013e32833c3da6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pretorius A, Oelofsen MJ, Smith MS, van der Ryst E. Rift Valley fever virus: A seroepidemiologic study of small terrestrial vertebrates in South Africa. Am J Trop Med Hyg. 1997;57:693–698. doi: 10.4269/ajtmh.1997.57.693. [DOI] [PubMed] [Google Scholar]
- 63.LaBeaud AD, et al. Interepidemic Rift Valley fever virus seropositivity, northeastern Kenya. Emerg Infect Dis. 2008;14:1240–1246. doi: 10.3201/eid1408.080082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Mroz C, et al. Seroprevalence of Rift Valley fever virus in livestock during inter-epidemic period in Egypt, 2014/15. BMC Vet Res. 2017;13:87. doi: 10.1186/s12917-017-0993-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Nanyingi M, et al. Seroepidemiological survey of Rift Valley Fever virus in ruminants in Garissa, Kenya. Vector-Borne Zoonotic Dis. 2016;17:141–146. doi: 10.1089/vbz.2016.1988. [DOI] [PubMed] [Google Scholar]
- 66.Pelosse P, et al. Influence of vectors’ risk-spreading strategies and environmental stochasticity on the epidemiology and evolution of vector-borne diseases: The example of Chagas’ disease. PLoS One. 2013;8:e70830. doi: 10.1371/journal.pone.0070830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tchouassi DP, et al. Mosquito host choices on livestock amplifiers of Rift Valley fever virus in Kenya. Parasit Vectors. 2016;9:184. doi: 10.1186/s13071-016-1473-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lo Iacono G, Robin CA, Newton JR, Gubbins S, Wood JLN. Where are the horses? With the sheep or cows? Uncertain host location, vector-feeding preferences and the risk of African horse sickness transmission in Great Britain. J R Soc Interf. 2013;10:20130194. doi: 10.1098/rsif.2013.0194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lo Iacono G, et al. A unified framework for the infection dynamics of zoonotic spillover and spread. PLoS Negl Trop Dis. 2016;10:e0004957. doi: 10.1371/journal.pntd.0004957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lo Iacono G, van den Bosch F, Gilligan CA. Durable resistance to crop pathogens: An epidemiological framework to predict risk under uncertainty. PLoS Comput Biol. 2013;9:e1002870. doi: 10.1371/journal.pcbi.1002870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Anonymous 2016 Copernicus global land service. Available at land.copernicus.eu/global/. Accessed June 2, 2016.
- 72.Otero M, Schweigmann N, Solari HG. A stochastic spatial dynamical model for Aedes aegypti. Bull Math Biol. 2008;70:1297–1325. doi: 10.1007/s11538-008-9300-y. [DOI] [PubMed] [Google Scholar]
- 73.Schoolfield RM, Sharpe PJ, Magnuson CE. Non-linear regression of biological temperature-dependent rate models based on absolute reaction-rate theory. J Theor Biol. 1981;88:719–731. doi: 10.1016/0022-5193(81)90246-0. [DOI] [PubMed] [Google Scholar]
- 74.Rueda LM, Patel KJ, Axtell RC, Stinner RE. Temperature-dependent development and survival rates of Culex quinquefasciatus and Aedes aegypti (Diptera: Culicidae) J Med Entomol. 1990;27:892–898. doi: 10.1093/jmedent/27.5.892. [DOI] [PubMed] [Google Scholar]
- 75.Christophers R. Aedes aegypti (L.), The Yellow Fever Mosquito. Cambridge Univ Press; Cambridge, UK: 1960. [Google Scholar]
- 76.Diallo D, et al. Temporal distribution and spatial pattern of abundance of the Rift Valley fever and West Nile fever vectors in Barkedji, Senegal. J Vector Ecol. 2011;36:426–436. doi: 10.1111/j.1948-7134.2011.00184.x. [DOI] [PubMed] [Google Scholar]
- 77.Grimshaw R. Nonlinear Ordinary Differential Equations. Blackwell Scientific; Oxford: 1990. [Google Scholar]
- 78.Klausmeier CA. Floquet theory: A useful tool for understanding nonequilibrium dynamics. Theor Ecol. 2008;1:153–161. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.