Linear response of east Greenland’s tidewater glaciers to ocean/atmosphere warming

Significance

Mass loss from the Greenland Ice Sheet is expected to be a major contributor to 21st Century sea-level rise, but projections retain substantial uncertainty due to the challenges of modeling the retreat of the tidewater outlet glaciers that drain from the ice sheet into the ocean. Despite the complexity of these glacier–fjord systems, we find that over a 20-y period much of the observed tidewater glacier retreat can be explained as a predictable response to combined atmospheric and oceanic warming, bringing us closer to incorporating these effects into the ice sheet models used to predict sea-level rise.

Abstract

Predicting the retreat of tidewater outlet glaciers forms a major obstacle to forecasting the rate of mass loss from the Greenland Ice Sheet. This reflects the challenges of modeling the highly dynamic, topographically complex, and data-poor environment of the glacier–fjord systems that link the ice sheet to the ocean. To avoid these difficulties, we investigate the extent to which tidewater glacier retreat can be explained by simple variables: air temperature, meltwater runoff, ocean temperature, and two simple parameterizations of “ocean/atmosphere” forcing based on the combined influence of runoff and ocean temperature. Over a 20-y period at 10 large tidewater outlet glaciers along the east coast of Greenland, we find that ocean/atmosphere forcing can explain up to 76% of the variability in terminus position at individual glaciers and 54% of variation in terminus position across all 10 glaciers. Our findings indicate that (i) the retreat of east Greenland’s tidewater glaciers is best explained as a product of both oceanic and atmospheric warming and (ii) despite the complexity of tidewater glacier behavior, over multiyear timescales a significant proportion of terminus position change can be explained as a simple function of this forcing. These findings thus demonstrate that simple parameterizations can play an important role in predicting the response of the ice sheet to future climate warming.

Loss of mass from tidewater glaciers to the ocean through iceberg calving and submarine melting is a major component of the mass budget of the Greenland Ice Sheet (GrIS). The contribution of this frontal ablation to ice-sheet mass balance can vary dramatically on short timescales: Increased frontal ablation was responsible for 39% of GrIS mass loss from 1991 to 2015 (1), and accounted for as much as two-thirds of GrIS mass loss during a phase of rapid retreat, acceleration, and thinning of outlet glaciers between 2000 and 2005 (2). Understanding the controls on frontal ablation is thus crucial if its contribution to the mass budget of the GrIS is to be predicted by models (e.g., ref. 3).

Frontal ablation and tidewater glacier retreat are closely interlinked––if ice loss at the terminus is more rapid than the delivery of ice from up-glacier, the terminus will retreat. A leading hypothesis attributes the recent rapid retreat of many of Greenland’s tidewater glaciers to an increase in submarine melting, and consequently calving, in response to oceanic warming (e.g., ref. 4). Alternatively, retreat may have been driven by increasing surface melt, with meltwater runoff draining through glaciers and entering fjords at depth to form buoyant plumes which enhance submarine melting at glacier termini (e.g., refs. 5 and 6). It has also been suggested that increased surface melt and runoff may accelerate calving through hydrofracturing of near-terminus crevasses (e.g., ref. 3), or by increasing basal water pressure and hence basal motion (e.g., ref. 7). A third hypothesis links retreat to increased calving rates following a reduction in terminus buttressing by ice mélange and land-fast sea ice (e.g., refs. 8 and 9). In most cases, however, it has not proven possible to attribute observed variability in terminus position to a particular cause, especially when multiple glaciers are considered (e.g., refs. 9–13).

The lack of a clear relationship between observed tidewater glacier retreat and changing environmental conditions presents a significant issue for modeling studies which seek to predict mass loss from the GrIS under a warming climate (e.g., refs. 14 and 15). One challenge in establishing a causal relationship between environmental forcings and tidewater glacier retreat is that at the scale of individual glaciers these relationships often appear highly nonlinear, with feedbacks triggered as the terminus retreats across uneven bed topography obscuring the forcing driving the initial retreat (e.g., ref. 16). This difficulty is compounded by a poor understanding of the oceanic forcing of these glaciers, due both to the scarcity of observations and the complexities of calving and submarine melt processes at glacier termini (17). A further issue is that accurately representing these processes in ice sheet and ocean models would require model resolution and a knowledge of boundary conditions that lies beyond current capabilities (18).

In this paper, we seek to address these challenges to improve our understanding of the retreat of Greenland’s tidewater glaciers on timescales relevant to predictions of mass loss over coming decades. We focus our study on 10 tidewater glaciers along Greenland’s east coast of varying size and spanning >10° of latitude (Fig. 1 and SI Appendix, Table S1). Over a 20-y period (1993–2012) we compare the observed pattern and rate of retreat with variability in five environmental forcings, assessing the ability of these forcings to explain variability in the terminus position (P) of the study glaciers, both individually and collectively. These forcings comprise near-terminus air temperature (T_A), glacier meltwater runoff (Q), ocean temperature (T_O), and two parameterizations of combined ocean/atmosphere forcing (M₁ and M₂). These ocean/atmosphere forcing parameterizations reflect the theory that frontal ablation will depend not only on ocean temperature but also runoff due to its role in stimulating buoyant upwelling adjacent to the terminus (e.g., refs. 5 and 19) and driving the renewal of warm water in the fjord (e.g., refs. 20 and 21), thereby increasing the transfer of heat between the ocean and ice. To represent this combined ocean/atmosphere forcing we define M₁ = Q(T_O − T_f) and M₂ = Q^1/3(T_O − T_f). In these parameterizations, ocean temperature is expressed relative to the in situ freezing point at the calving front, approximated as T_f = −2.13 °C based on a depth of 300 m and salinity of 34.5 psu (e.g., ref. 22). M₁ is thus a simple product of runoff and the oceanic heat available for melting, while the addition of the exponent to the formulation for M₂ is based on the expectation that submarine melt rate will scale linearly with temperature and with runoff raised to the power of 1/3 (5).

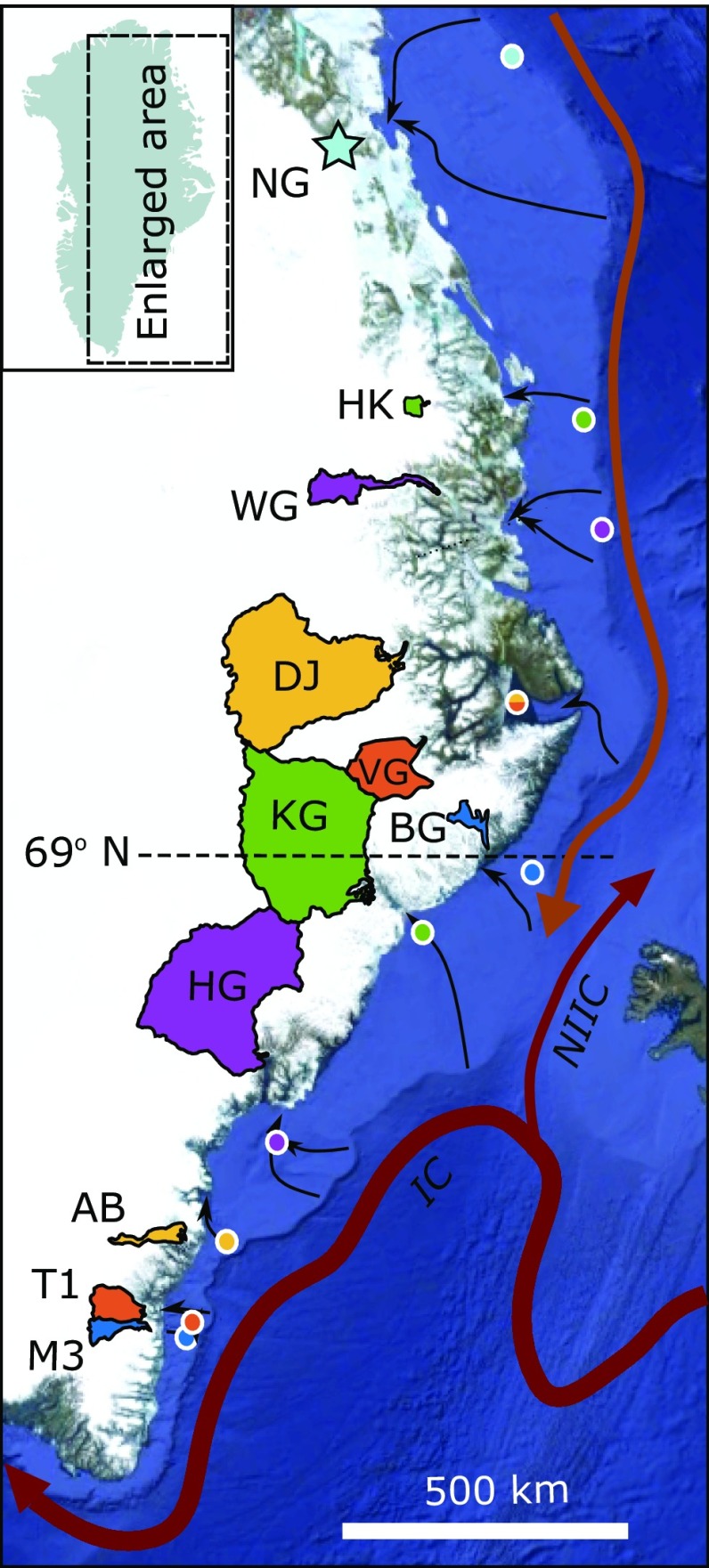
Fig. 1.

Map showing the location of the 10 study glaciers (SI Appendix, Table S1) in east Greenland: AB; BG, Borggraven; DJ; HG; HK, Heinkel Glacier; KG, Kangerdlugssuaq Glacier; M3; T1, Tingmjarmiut 1; VG, Vestfjord Glacier; WG. The location of Nioghalvfjerdsbræ (NG), which is referenced but does not constitute one of the study glaciers, is marked with a star. Hydrological catchments are shaded, and the divide between the northern and southern study glaciers at ∼69° N is marked with the dashed line. The sample locations for ocean reanalysis temperature for the glaciers are shown as colored circles. Also shown are the approximate locations of warm ocean currents (22), with IC, Irminger Current and NIIC, North Iceland Irminger Current, and cross-shelf troughs that may allow warm subsurface waters to access the study glaciers (black arrows; ref. 44). The background image shows a satellite mosaic of Greenland with shaded sea-floor bathymetry [Google Earth; Data: Scripps Institution of Oceanography (SIO), National Oceanic and Atmospheric Administration (NOAA), US Navy, National Geospatial-Intelligence Agency (NGA), General Bathymetric Chart of the Oceans (GEBCO); Image: Landsat/Copernicus, International Bathymetric Chart of the Arctic Ocean (IBCAO), US Geological Survey].

Results

Time series of variability in T_A, Q, T_O, and P for each of the study glaciers are plotted in Fig. 2 (see also Methods). These time series, along with the two ocean/atmosphere forcings M₁ and M₂, are displayed as normalized values for each glacier in Fig. 3. Glaciers are grouped into “northern” and “southern” subsets based on their location with respect to a steep latitudinal gradient in ocean temperature at ∼69° N, which reflects the influence of the Irminger Current (23) (Fig. 1). Features specific to the individual glaciers (in particular, fjord and subglacial topography) may modify their response to environmental forcings (e.g., ref. 12), and so the normalized values are also averaged for the five southern and five northern glaciers to show the regional trends, thereby emphasizing the climatic signal (Fig. 3 F and L).

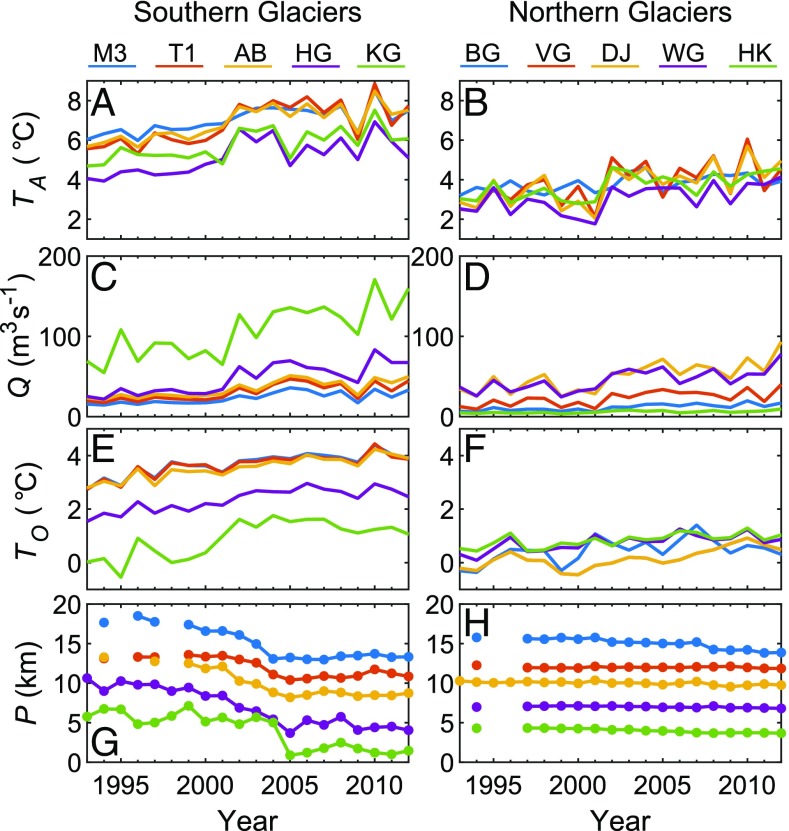
Fig. 2.

Annual average values of (A and B) air temperature (T_A), (C and D) runoff (Q), (E and F) depth-averaged subsurface ocean temperature (T_O), and (G and H) glacier terminus position (P), relative to an arbitrary up-glacier location, for the 10 study glaciers (Methods and SI Appendix, Table S1). Left and right columns show glaciers south and north of ∼69N, respectively, and colors are as for Fig. 1.

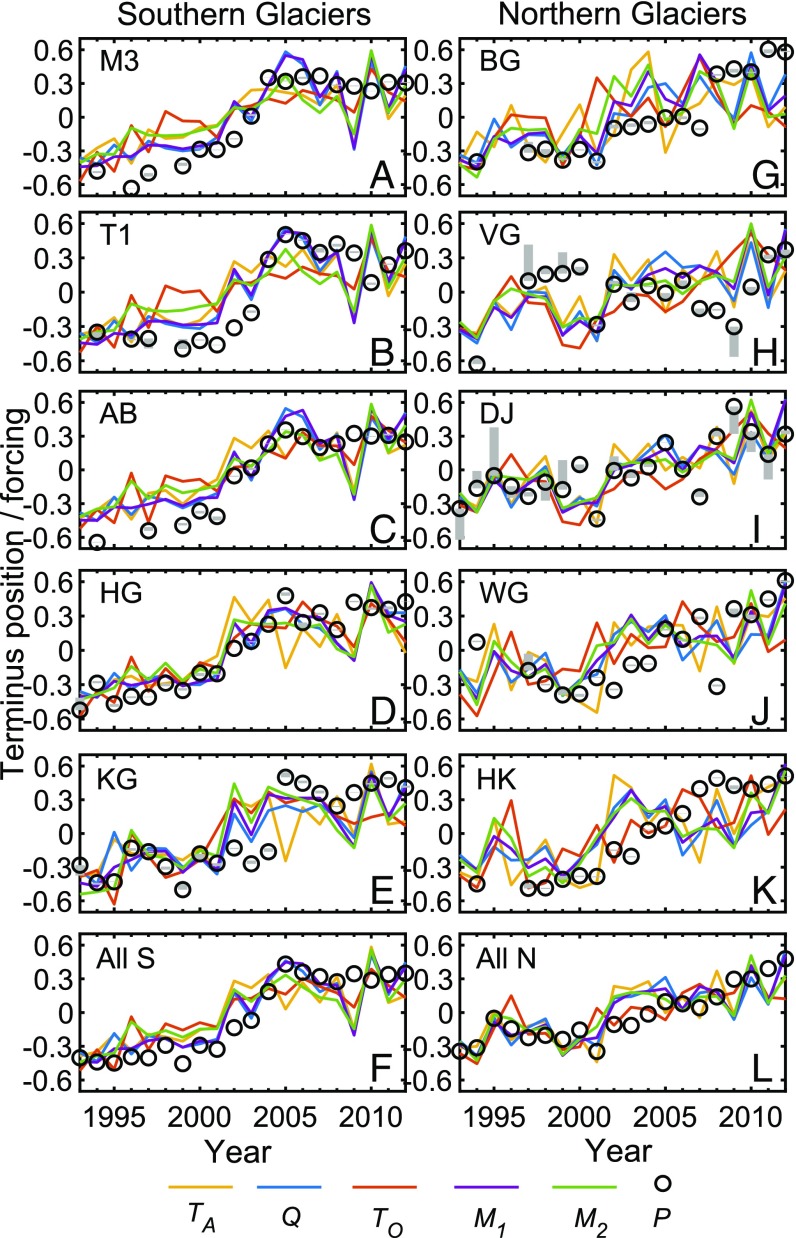
Fig. 3.

Time series of normalized anomalies in air temperature (${\stackrel{\sim }{T}}_A$, orange), runoff ($\stackrel{\sim }{Q}$, blue), ocean temperature (${\stackrel{\sim }{T}}_O$, red), ${\stackrel{\sim }{M}}_1$ (purple), and ${\stackrel{\sim }{M}}_2$ (green), and terminus position ($\stackrel{\sim }{P}$, black circles) for (A–E) southern glaciers, and (G–K) northern glaciers. F and L show the combined southern and northern glaciers, respectively. Anomalies are expressed relative to the 20-y mean, and all values are normalized with respect to the observed range at that glacier. For ease of comparison, $\stackrel{\sim }{P}$ is shown inverted (i.e., positive change means retreat) and is in some cases discontinuous due to lack of observations. Vertical gray bars indicate the adjustment of P relative to P_mean (SI Appendix).

We begin by examining the relationship between terminus position and the environmental forcings at the scale of individual glaciers. At the southern glaciers, there is a marked increase in the values of the forcings and retreat of the glaciers between 2000 and 2005, with periods of relative stability either side (Figs. 2 and 3 A–F). There are strong correlations between P and the forcings (R² = 0.24–0.76, depending on the glacier and forcing; Fig. 4 and SI Appendix, Table S3) for both the individual glaciers and regional trends. Because the time series involved are nonstationary, there is however an increased risk of spurious correlations resulting from similar long-term trends in the forcing and response variables existing over the study period (24). We therefore run an Engle–Granger test for cointegration (25), which facilitates statistical comparison between two (or more) nonstationary time series showing stochastic trends (SI Appendix). We find that P is significantly cointegrated (P < 0.05) with Q and M₁ at all of the southern study glaciers, with T_A and T_O at Mogens 3 (M3), AP Bernstorffs Glacier (AB), and Helheim Glacier (HG), and with M₂ at AB and HG (Fig. 4 and SI Appendix, Table S3). Cointegration indicates a temporally constant functional relationship, meaning that these results support the existence of causal relationships between P and the environmental forcings. However, because the forcings demonstrate similar temporal variability to each other, determining which (if any) is the key control on terminus position from this analysis alone remains difficult.

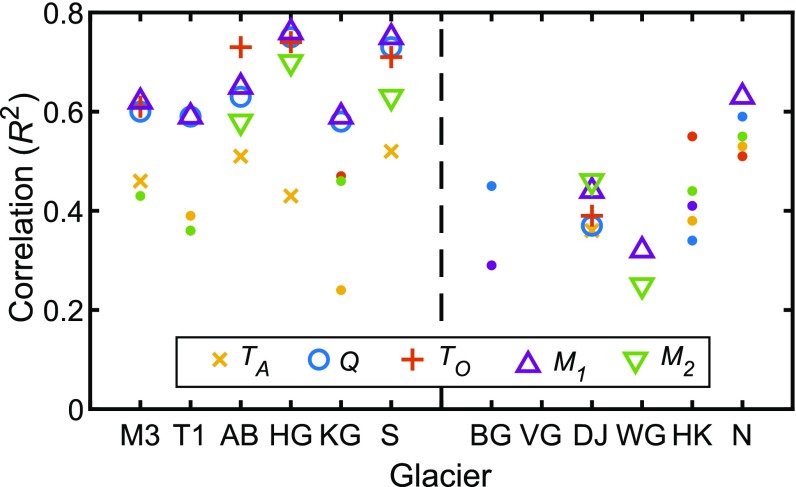
Fig. 4.

R² values for the relationship of terminus position (P) with air temperature (T_A), runoff (Q), ocean temperature (T_O), and M₁ and M₂ at each glacier and for the averaged regional southern ("S") and northern ("N") trends (Fig. 3). Large markers show time series that are significantly cointegrated at P < 0.05. Solid dots show instances which are correlated at P < 0.05, but are not cointegrated at this confidence level. No marker is shown where the time series are not significantly correlated or cointegrated. The dashed line separates the southern (Left) and northern (Right) glacier subsets. Statistical values are given in SI Appendix, Table S3.

The results are qualitatively similar at the northern glaciers, which show a brief retreat during a phase of higher T_A, Q, and T_O (and thus also M₁ and M₂) between ∼1994 and 1995, then a slight readvance, before embarking on a more sustained retreat in keeping with the increase in the forcings after ∼2001 (Fig. 3 G–L). The statistical significance of these trends is however weaker at the northern glaciers (Fig. 4 and SI Appendix, Table S3), with significant cointegration of P with all forcings at Daugaard–Jensen Glacier (DJ) and with M₁ and M₂ at Waltershausen Glacier (WG). This may be due in part to the smaller absolute variability in the time series at the northern glaciers, increasing the magnitude of short-term noise relative to the long-term trends (Figs. 2 and 3). Nevertheless, clear similarities appear between the variability in the forcings in P when the normalized data from the northern glaciers are combined to show the regional trends (Fig. 3L). Correlation of the individual forcings and P for the combined northern glaciers data sets give R² values of 0.51–0.63 (significant at P < 0.01, Fig. 4 and SI Appendix, Table S3); however, only M₁ is significantly cointegrated with P at P < 0.05.

This analysis indicates that, despite the complexities introduced by bed topography and ice dynamics, over timescales of a few years or more many individual glaciers display a largely linear response to environmental forcings. This is particularly apparent at the southern glaciers, where both the increase in forcings and glacier retreat have been more pronounced (Figs. 2 and 3). However, because at this level P demonstrates strong correlations with multiple forcings, it remains unclear whether this retreat has been driven primarily by warming of the atmosphere, ocean, or both. To gain further insight, we therefore examine variation in glacier retreat across all 10 study glaciers.

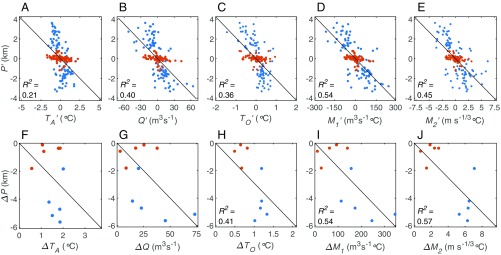
Any environmental control on P should also be able to explain variation in retreat rate between glaciers. In particular, the absolute magnitude of retreat is consistently lower at the northern compared with the southern glaciers (with the SD in P at the northern glaciers just 17% of that exhibited at the southern glaciers), a trend which remains true for an expanded sample of 32 of east Greenland’s tidewater glaciers (23). When the absolute variability at all glaciers is considered together, there is a significant (P < 0.01) correlation of P with T_A (Fig. 5A; R² = 0.21), Q (Fig. 5B; R² = 0.40), and T_O (Fig. 5C; R² = 0.36) (SI Appendix, Table S4). However, while T_A, Q, and T_O are all typically higher at the southern than the northern glaciers, the latitudinal difference in the magnitude of the variability is less marked compared with that in P: the SD in T_A, Q, and T_O at the northern glaciers is 93%, 60%, and 74%, respectively, of the SD at the southern glaciers. The implication is that for a given change in these forcings, the southern glaciers have responded more sensitively than the northern glaciers. Combining Q and T to create M₁ and M₂ increases the latitudinal gradient in the forcings to give better agreement with that observed in P, with the SD in both M₁ and M₂ at the northern glaciers 36% of that exhibited at the southern glaciers. Combined with a good correlation at the glacier level (Fig. 4), this helps to strengthen the correlation of P with M₁ (Fig. 5D; R² = 0.54), and to a lesser extent the slightly more complex ocean/atmosphere forcing parameter M₂ (Fig. 5E; R² = 0.45) (SI Appendix, Table S4).

Fig. 5.

(A–D) Relationship between anomalies in terminus position (P′) and (A) air temperature (T_A′), (B) runoff (Q′), (C) ocean temperature (T_O′), and ocean/atmosphere forcing (D) M₁′ and (E) M₂′. Anomalies are shown relative to the 20-y mean at each glacier. (F–J) Relationship between overall change in terminus position (ΔP) and (F) air temperature (ΔT_A), (G) runoff (ΔQ), (H) ocean temperature (ΔT_O), and ocean/atmosphere forcing (I) ΔM₁ and (J) ΔM₂. In each case, the overall change is calculated by subtracting the mean 1993–1995 value from the mean 2010–2012 value. On all plots, blue and red markers denote data from the southern and northern glaciers subsets, respectively, and black lines show the best fit to all data. R² values (all significant at P < 0.05) are shown on all plots except F and G, which are not significant at this level. Statistical values are given in SI Appendix, Table S4.

We additionally test the ability of the environmental forcings to explain only the interglacier variability in long-term retreat rate, a property of arguably greater importance than the year-to-year variability from the perspective of predicting future ice-sheet mass loss. To examine this, we compare the overall retreat of each glacier (defined as the difference between the mean values from 1993 to 1995 and 2010 to 2012) against the equivalent change in the five forcings. Again, M₁ and M₂ provide the strongest correlation, giving R² values of 0.54 and 0.57 (P < 0.01), respectively, compared with 0.41 (P < 0.01) for T_O (Fig. 5 E–H and SI Appendix, Table S4). There is no significant correlation between the magnitude of the overall change in P and T_A and Q at P < 0.05, with the northern glaciers again showing a much smaller retreat for a given increase in the atmospheric forcing.

Discussion

Our findings demonstrate that the timing and magnitude of tidewater glacier retreat along Greenland’s east coast can be effectively explained as a combined linear response to atmospheric and oceanic conditions. While variation in runoff alone can explain a large proportion of glacier retreat at individual glaciers (Fig. 4), the sensitivity of this relationship is much stronger in southeast Greenland where ocean waters are warmer (and continued to warm more rapidly over the study period) compared with northeast Greenland (Fig. 5 A, B, F, and G). It may thus be that contact with warm ocean waters preconditions the southern glaciers to greater sensitivity to changes in atmospheric temperature and hence runoff––if the ocean temperature is close to the in situ freezing point, this will limit the potential for submarine melting, irrespective of the vigor of runoff-driven circulation. While previous studies have hypothesized that regional differences in glacier stability in east Greenland may be linked to the strong latitudinal ocean temperature gradient (23, 26) and that a combined warming of ocean and atmosphere may provide the key trigger for rapid glacier retreat (8, 11), we are able to demonstrate quantitatively that the combined influence of ocean and atmospheric temperature provides the strongest predictor of both spatial and temporal variation in glacier terminus position (Fig. 5). In this way, our results agree with recent observations from the Antarctic Peninsula which show that, while there has been a strong atmospheric warming trend in this region, the magnitude of glacier retreat is much greater in areas where glaciers are in contact with warm Circumpolar Deep Water (27). While the existence of a correlation cannot alone provide conclusive evidence of a causal link, our results thus join a growing body of evidence indicating a role for both oceanic and atmospheric warming in driving the retreat of marine-terminating outlet glaciers.

Our results suggest that variability in terminus position across the 10 study glaciers can be parameterized as

$$\frac{dP}{dt}=a\frac{d{M}_1}{dt},$$ [1]

where t is time and a = −0.014 ± 0.002 or −0.018 ± 0.006 km/(m³ s⁻¹ °C) depending on whether the parameterization is fitted to maximize agreement with the year-to-year variability (Fig. 5D) or overall retreat (Fig. 5I), respectively (SI Appendix, Table S4). This simple formulation effectively captures both the temporal variability in the rate of change of glacier front position and the widely differing magnitude of response at the different outlet glaciers (Fig. 6). Across 10 glaciers, Eq. 1 can explain 54% of year-to-year variability in terminus position (Fig. 5D) and 54% of variation in the overall retreat rate (Fig. 5I). As such, while the prediction of individual tidewater glacier behavior on timescales of a few years or less may require detailed glacier-specific knowledge of bedrock topography (e.g., refs. 12 and 28) and high-resolution modeling of ice dynamics (e.g., ref. 29), our results show that on longer timescales variation in the glaciers’ terminus positions can be captured with much simpler parameterizations. These parameterizations translate the complex interaction of ice sheets with the atmosphere and ocean into simple yet statistically strong relationships that provide a pathway for the inclusion of tidewater glacier retreat in the large-scale ice-sheet models needed to predict global sea-level rise (e.g., refs. 15 and 30).

Fig. 6.

Change in terminus position P at the (A) southern glaciers and (B) northern glaciers, as observed (solid lines) and parameterized based on Eq. 1 (dashed lines). P is shown relative to an arbitrary up-glacier location, as in Fig. 2 E and F.

This quasi-linear behavior likely reflects the complex topography and thus relatively frequent occurrence of pinning points (such as lateral constrictions and submarine sills) within Greenlandic glacier–fjord systems. This means that, unlike regions of West Antarctica where bed topography may precondition the ice sheet to centennial-scale unstable retreat (e.g., ref. 31), change at many of Greenland’s tidewater glaciers may occur as series of rapid short-lived retreats which collectively do not deviate far from the linear response to climate warming. Capturing the exact timing and magnitude of these steps is difficult and may not be necessary if the aim is to predict ice-sheet mass loss on timescales of decades or longer. A good example of this can be seen when comparing Kangerdlugssuaq Glacier (KG) and HG: As the forcings increased between 2000 and 2005, HG retreated steadily while KG remained comparatively stable before undergoing a rapid ∼5-km retreat between topographic pinning points in 2004–2005 (Fig. 3 D and E and SI Appendix, Fig. S2). If viewed over the period 2000–2005, the retreat of KG appears sudden while the retreat of HG appears prolonged; however, when considered over the full 20-y time series, both glaciers exhibited a broadly similar retreat between 2000 and 2005 with periods of comparative stability before and after.

This topographic influence accounts for some of the largest outliers in the relationship between P and M₁ (Fig. 5D), with an ∼3–4-km discrepancy between the observed and parameterized modeled terminus position briefly existing at KG due to the delayed response of this glacier to ocean/atmosphere warming during 2000–2005 (Figs. 3E and 6A). At KG, this discrepancy is short-lived, but this observation illustrates how Eq. 1 is likely to be least effective at glaciers at which current behavior is particularly strongly influenced by topography: For example, looking to west Greenland, Jakobshavn Isbræ may have been undergoing an unstable retreat into deeper water due to the loss of its floating tongue in the late 1990s (32), while the stability of Store Glacier to the north is attributed to the presence of an exceptionally prominent topographic pinning point (29). While such glaciers will ultimately adjust to a new climatically stable position, their terminus position may differ more strongly from the linear trend in the short term. Nevertheless, our findings suggest that simple formulations such as Eq. 1 can play an important role in parameterizing the response to climate warming of many tidewater glaciers, including major outlets such as KG, HG, and DJ.

The efficacy of this approach is likely to be dependent on the timeframe in question. The influence of topographic pinning points will be magnified on short timescales (∼5 y or less), with this effect reduced when retreat rates are averaged over longer timescales. Furthermore, the slow response time of glaciers will modulate climatic signals by filtering out higher-frequency variation––for example, this may explain the muted response of the southern glaciers to the short-lived cooling/warming over 2009–2010 (Figs. 2 and 3). At much longer timescales, glaciers will become less sensitive to the ocean as they retreat into shallower water and onto dry land, while evolving ice-sheet mass balance and geometry will also likely impact upon the relationship between forcings and terminus position. We therefore suggest that the relationship described in Eq. 1 is most appropriate when considering processes on timescales of ∼5–100 y, with uncertainty increasing either side of this window.

The dependency of retreat rate on both runoff and ocean temperature points to a key role for calving front processes in driving the retreat of Greenland’s tidewater glaciers. The obvious link lies in submarine melting: Theory and modeling suggest that submarine melt rate is dependent on both ocean temperature and runoff, with the latter driving buoyant plumes that increase the turbulent transfer of oceanic heat to glacier calving fronts (e.g., refs. 5 and 33). The role of submarine melting as a control on terminus position appears straightforward where glaciers are relatively slow flowing and warm ocean waters are capable of inducing submarine melt rates on par with ice velocity; in such circumstances undercutting by submarine melting may be the primary source of frontal ablation (34, 35), such that changes in terminus position are determined by the difference between ice velocity and submarine melt rate (36). The applicability of this mechanism at faster-flowing glaciers is less clear, however, as predictions of ice-front-averaged submarine melt rates fall far below terminus velocities (37, 38). Indeed, observations indicate a mechanistic difference between the small-scale calving in submarine-melt-dominated systems (35) and the massive buoyant calving of icebergs from Greenland’s largest and fastest-flowing glaciers (39). Nevertheless, our findings indicate that terminus position at these large and fast-flowing glaciers also responds rapidly and predictably to variability in ocean/atmosphere forcing.

We also note that the lack of improvement in the correlation between P and M₂ [= Q^1/3(T_O − T_f)] compared with M₁ [= Q(T_O − T_f)] is at odds with the dependency expected if retreat rate was a direct function of submarine melt rate (5). It may be that this theoretical relationship (which is yet to be validated by field data) does not reflect the reality of the relationship between T_O, Q, and submarine melting––for example, Slater et al. (40) report that the correct value for the exponent may be as high as 3/4 under certain circumstances. Alternatively, the apparently simple relationship between P and M₁ may be the integrated result of not only submarine melting but also additional factors including ice mélange/sea ice coverage (e.g., refs. 8 and 9) and hydrologically forced acceleration of ice motion (e.g., ref. 7). The stronger correlations between P and Q rather than T_A (Figs. 4 and 5) indicate that catchment-wide melt, and hence runoff, is of greater importance than local air temperatures at the terminus as a control on retreat rate. While this suggests that processes driven by local surface melting (e.g., through hydrofracture-driven calving) are of secondary importance, we cannot discount the possibility that our results reflect a more complex mix of processes related to basal hydrology, glacier dynamics, submarine melting, and calving. Thus, while our findings indicate that a combined ocean/atmosphere forcing is a key control on the stability of even large, fast-flowing tidewater glaciers, further research is needed to identify and constrain the processes that link this forcing with frontal ablation and glacier retreat.

Over a 20-y period, we have observed a significant correlation between variability in glacier terminus position and a simple parameterization that combines oceanic and atmospheric forcings at 10 tidewater glaciers along Greenland’s east coast. Our results demonstrate that while increased melting and runoff in response to atmospheric warming can explain much of the temporal variability in glacier terminus position, the temperature of the adjacent ocean waters is also a strong determinant of the absolute magnitude of retreat. We find that even at very large and fast-flowing glaciers like KG and HG, where the nonlinear response to climate forcing has previously been emphasized, over timescales of a few years or longer, this forcing dominates over site-specific effects relating to the complexities of local topography. While topography remains an important factor in modulating the response of tidewater glaciers to climate, our findings nevertheless suggest that simple parameterizations linking terminus retreat to runoff and ocean temperature, suitable for inclusion in large-scale ice-sheet models, have an important role to play in modeling the response of the Greenland ice sheet to atmospheric and oceanic warming.

Methods

Details of the 10 study glaciers are given in SI Appendix, Table S1. These glaciers represent a subset of the 32 glaciers documented by Seale et al. (23), chosen to span a range of conditions along the east coast of Greenland. For each glacier, we obtain 20-y (1993–2012) time series of air temperature T_A, runoff Q, ocean temperature T_o, and terminus position P. T_A is based on the May–September mean of monthly temperatures from European Reanalysis (ERA)-Interim global atmospheric reanalysis (41), while Q is obtained from a 1-km surface melting, retention, and runoff model forced using ERA-Interim reanalysis (42). T_O is based on the mean 200–400-m temperature from GLORYS2V3 1/4° ocean reanalysis (43), adjusted to better agree with available in situ observations. P is obtained from automated classification of Moderate Resolution Imaging Spectroradiometer (MODIS) scenes (23) and manual classification of Envisat (11) and Landsat scenes. For a more complete description of these methods, please see SI Appendix.