Distributed deep learning networks among institutions for medical imaging

Abstract

Objective

Deep learning has become a promising approach for automated support for clinical diagnosis. When medical data samples are limited, collaboration among multiple institutions is necessary to achieve high algorithm performance. However, sharing patient data often has limitations due to technical, legal, or ethical concerns. In this study, we propose methods of distributing deep learning models as an attractive alternative to sharing patient data.

Methods

We simulate the distribution of deep learning models across 4 institutions using various training heuristics and compare the results with a deep learning model trained on centrally hosted patient data. The training heuristics investigated include ensembling single institution models, single weight transfer, and cyclical weight transfer. We evaluated these approaches for image classification in 3 independent image collections (retinal fundus photos, mammography, and ImageNet).

Results

We find that cyclical weight transfer resulted in a performance that was comparable to that of centrally hosted patient data. We also found that there is an improvement in the performance of cyclical weight transfer heuristic with a high frequency of weight transfer.

Conclusions

We show that distributing deep learning models is an effective alternative to sharing patient data. This finding has implications for any collaborative deep learning study.

Introduction

With the advent of powerful graphics processing units, deep learning has brought about major breakthroughs in tasks such as image classification, speech recognition, and natural language processing.^1–3 Due to the proficiency of neural networks at pattern recognition tasks, deep learning has created practical solutions to the challenging problem of automated support for clinical diagnosis. Recent studies have shown the potential of deep learning in detecting diabetic retinopathy, classifying dermatological lesions, predicting mutations in glioma, and assessing medical records.^4–7 Deep learning models take raw data as input and apply many layers of transformations to calculate a classification label of interest. The high dimensionality of these transformations allows these algorithms to learn complex patterns with a high level of abstraction.⁸

A requirement for the application of deep learning within the medical domain is a large quantity of training data, especially when the difference between imaging phenotypes is subtle or if there is large heterogeneity within the population. However, patient sample sizes are often small, especially for rarer diseases.⁹ Small sample sizes may result in a neural network model with low generalizability.

A possible solution to the foregoing challenges is to perform a multicenter study, which can significantly increase the sample size as well as sample diversity. Ideally, patient data is shared to a central location where the algorithm can then be trained on all the patient data. However, there are challenges to this approach. First, if the patient data takes up a large amount of storage space (such as very high-resolution images), it may be cumbersome to share these data. Second, there are often legal or ethical barriers to sharing patient data, making dispersal of some or all of the data not possible.⁹ Third, patient data is valuable, so institutions might simply prefer not to share data.¹⁰

In such cases, instead of sharing patient data directly, distributing the trained deep learning model may be a more appealing alternative. The model itself has much lower storage requirements than the patient data and does not contain any individually-identifiable patient information. Thus, distribution of deep learning models across institutions can overcome the weaknesses of distributing the patient data. However, the optimal method of performing such a task has not yet, to our knowledge, been studied.

There are several existing approaches to distributed training. In model averaging, separate models are trained for each split of the data and the weights of the model are averaged every few mini-batches.¹¹ In asynchronous stochastic gradient descent, separate models are trained for each split of the data and the gradients of each separate model are transferred to a central model.¹² However, these methods were developed with the intention of optimizing training speed. Although applying such data parallel training methods in a multi-institution study in which data is not exchanged between institutions is possible, they also represent a significant logistical challenge. Specifically, training would have to take place in parallel across all institutions. This would be especially challenging if institutions have drastically different network connection speeds or deep learning hardware. While nonparallel methods of distributed training may be slower than parallel methods, they would avoid the logistical challenges.

In this study, we simulate the distribution of deep learning models across institutions using various nonparallel training heuristics. We compare the results with a deep learning model trained on centrally hosted patient data. We demonstrate these simulations on 3 datasets: retinal fundus photos, mammography, and ImageNet. We aim to assess (1) the performance of distributing deep learning models compared to sharing patient data, (2) whether the performance distributing deep learning models is compromised when variability is introduced to an institution, and (3) if distributing deep learning models can achieve high performance on a large scale (i.e., when there are many institutions).

Methods

Initial Image Collection

Preprocessing

We obtained 35 126 color digital retinal fundus (interior surface of the eye) photos from the Kaggle Diabetic Retinopathy competition.¹³ Each image was rated for disease severity by a licensed clinician on a scale of 0–4 (absent, mild, moderate, severe, and proliferative retinopathy, respectively). The images came from 17 563 patients of multiple primary care sites throughout California and elsewhere. The acquisition conditions were varied, with a range of camera models, levels of focus, and exposures. In addition, the resolutions ranged from 433 × 289 pixels to 5184 × 3456 pixels.¹⁴ The images were preprocessed via the method detailed in the competition report by the winner, Ben Graham.¹⁵ To summarize his method, the OpenCV Python package was used to rescale images to a radius of 300, followed by local color averaging and image clipping. The images were then resized to 256 × 256 to reduce the memory requirements for training the neural network. To simplify training of the network, the labels were binarized to Healthy (scale 0) and Diseased (scale 2, 3, or 4). Furthermore, mild diabetic retinopathy images (scale 1, n = 2443 images), which represent a middle ground between Healthy and Diseased, were not used for our experiments. It is also known that there is a correlation between the disease status of the left eye and the status of the right eye. To remove this as a confounding factor in our study, only images from left eye were utilized.

Convolutional neural network

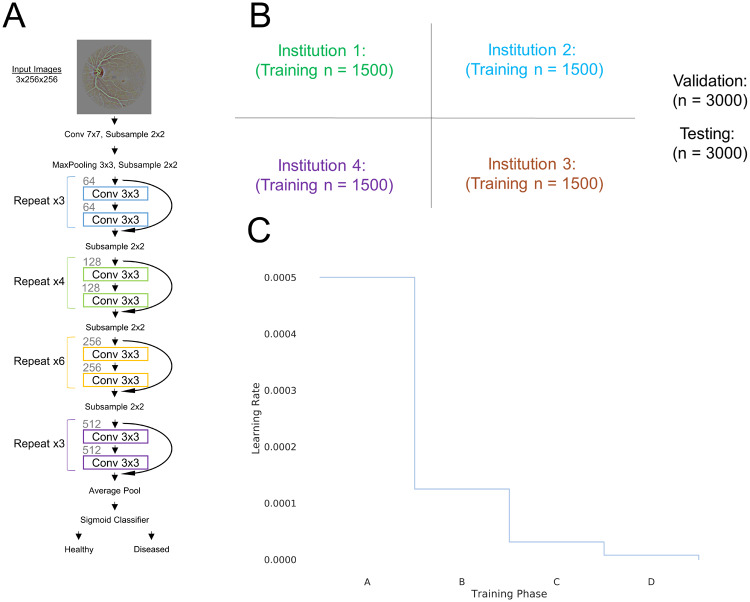
We utilized the 34-layer residual network (ResNet34) architecture (Figure 1A).¹⁶ Our implementation was based on the Keras package with Theano backend.^17,18 The convolutional neural networks were run on a NVIDIA Tesla P100 Graphics Processing Unit. During training, the probability of samples belonging to Healthy or Diseased class was computed with a sigmoid classifier. The weights of the network were optimized via a stochastic gradient descent algorithm with a mini-batch size of 32. The objective function used was binary cross-entropy. The learning rate was set to 0.0005 and momentum coefficient of 0.9. The learning rate was multiplied by 0.25 when the same training images were used to train the neural network 20 times with no improvement of the validation loss. The learning rate was decayed a total of 3 times (Training Phases A–D, Figure 1C). Biases were initialized using the Glorot uniform initializer.¹⁹ To prevent overfitting and to improve learning, we augmented the data in real-time by introducing random rotations (0–360 degrees) and flips (50% change of horizontal or vertical) of the images at every epoch. The final model was evaluated by calculating the accuracy on the unseen testing cohort.

Figure 1.

(A) ResNet-34 architecture was utilized for the Diabetic Retinopathy dataset. (B) The dataset was randomly divided into 4 institutions along with a validation and testing set. (C) The learning rate decayed to 0.25 of its value when the same input samples were inputted into the network 20 times at a given learning rate without an improvement of the validation loss.

Model training heuristics with 4 institutions

The dataset was randomly sampled, with equal class distributions, into 4 “institutions,” each institution having n = 1500 patients. In addition, the dataset was sampled to create a single validation cohort (n = 3000 patients) and a single testing (n = 3000 patients) cohort, again with equal class probabilities (Figure 1B). Sampling was without replacement such that there are no overlapping patients in any of the cohorts. The image intensity was normalized within each channel across all patients within each cohort. Because model performance plateaus as the number of training patient samples increases, the number of patients per institution was limited to 1500 to prevent saturation of learning for models trained in single institutions.

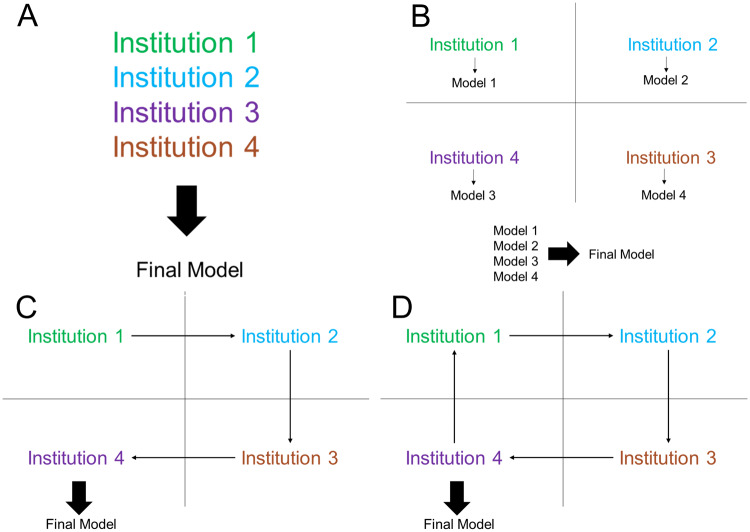
We tested several different training heuristics (Figure 2) and compared the results. The first heuristic is training a neural network for each institution individually, assuming there is no collaboration between the institutions. The second heuristic is collaboration through pooling of all patient data into a shared dataset (centrally hosted data, Figure 2A). The third heuristic was averaging the output of the 4 models trained on the institutions individually (ensemble single institution models, Figure 2B). The fourth heuristic was training a model at a single institution until reaching a plateau of validation loss and then transferring the model to the next institution (single weight transfer, Figure 2C). Under the single weight transfer training heuristic, the model is transferred to each institution exactly once. The last heuristic was training a model at each institution for a predetermined number of epochs (weight transfer frequency) before transferring the model to the next institution (cyclical weight transfer, Figure 2D). Under the cyclical weight transfer training heuristic, the model is transferred to each institution more than once. The frequencies of weight transfer we studied were every 20 epochs, 10 epochs, 5 epochs, 4 epochs, 2 epochs, and every epoch.

Figure 2.

Model training heuristics investigated include (A) centrally hosted, (B) ensemble single institution models, (C) single weight transfer, and (D) cyclical weight transfer.

Introduction of an institution with variability

In our initial division of the different institutions, we assumed that each institution had the same number of patients, ratio of healthy to diseased patients, and image quality. However, in a real scenario, there will likely be variability within institutions that may compromise the predictive performance of the model. To simulate this possibility, we introduced variability into one of the 4 institutions and assessed the performance of the different training heuristics. We simulated two scenarios: In the first, we decreased the resolution of the images by a factor of 16. In the second, we significantly decreased the number of patients (from n = 1500 to n = 150) and introduced class imbalance (ratio of healthy to diseased was 9:1). We assessed the performance of centrally hosted data, ensembling single institution models, single weight transfer, and cyclical weight transfer with weight transfer at every epoch. For single weight transfer, we experimented with ordering of the institutions, specifically whether the variable institution was Institution 1, 2, 3, or 4. For cyclical weight transfer, we assessed the performance of not skipping vs skipping the variable institution entirely.

Cyclical weight transfer with 20 institutions

We next addressed whether cyclical weight transfer can improve model performance when the performance of any individual institution is no better than random classification. To do this, we divided 6000 patient samples from the Kaggle Diabetic Retinopathy dataset into 20 institutions (n = 300 per institution) with equal class distributions. As with our previous experiments, we also sampled a single validation cohort (n = 3000 patient samples) and a single testing cohort (n = 3000 patient samples) with equal class probabilities. We then performed experiments with different numbers of collaborating institutions, starting with 1 and increasing to all 20 institutions. We utilized the cyclical weight transfer training heuristic with a weight transfer frequency of 1 epoch. We evaluated model performance via testing cohort accuracy. We compared testing accuracies with that of random classification and with the testing accuracy of a model trained with all 6000 patient samples centrally hosted. A summary of all experiments performed with the Kaggle Retinopathy Dataset is summarized in Table 1.

Table 1.

A Summary of all Experiments Performed with the Kaggle Retinopathy Dataset

Experiment	Summary
Model training heuristics with 4 institutions	In this experiment, there are 4 equivalent institutions. We evaluate the performance of model ensembling, single weight transfer, and cyclical weight transfer compared to centrally hosted patient data
Introduction of an institution with variability	In this experiment, there are 4 institutions but one of the institutions has a mode of variability introduced (either low-resolution images or a low number of patients with class imbalance). We evaluate the effectiveness of model ensembling, single weight transfer, and cyclical weight transfer compared to centrally hosted patient data
Cyclical weight transfer with 20 institutions	In this experiment, there are 20 institutions. The number of patients at each institution is such that a model trained on patients from a single institution is no better than random classification. We evaluate the performance of cyclical weight transfer as the number of collaborating institutions increase from 1 to all 20

Repetition of Experiment in a Second Image Collection

To demonstrate the reproducibility of our results, we repeated our experiment on model training heuristics with 4 institutions on the Curated Breast Imaging Subset of the Digital Database for Screening Mammography (DDSM) dataset, an open source labeled dataset of mammograms.²⁰ Details of the dataset and neural network training can be found in the Supplementary Materials section.

Repetition of Experiment in a Nonmedical Image Collection

We further demonstrate the reproducibility of our results by repeating our experiment on model training heuristics with 4 institutions on the ImageNet dataset.²¹ Details of the dataset and neural network training can be found in the Supplementary Materials section. We evaluated our models by assessing both the top-1 and top-5 accuracies. Top-1 accuracy is calculated by comparing the ground truth label with the top predicted class. Top-5 accuracy is calculated by comparing the ground truth label with the top 5 predicted classes.

Results

Retinal Fundus Dataset

Single institution training

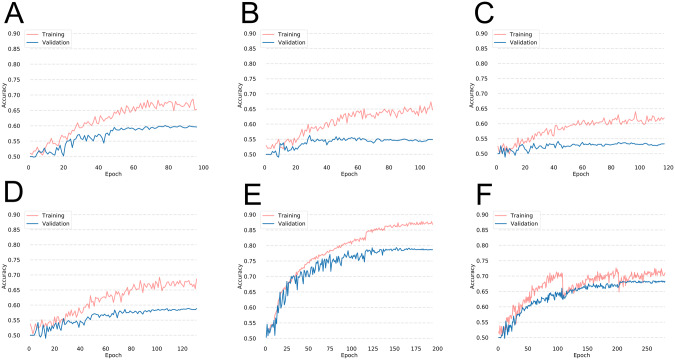
The models trained on single institutions had poor performance (Figure 3A–D). The average testing accuracies for the single institution models was 56.3% (Table 2). The highest testing accuracy for a network trained on a single institution was 59.0%.

Figure 3.

Performance of a neural network when trained on (A) Institution 1, (B) Institution 2, (C) Institution 3, and (D) Institution 4 for the Diabetic Retinopathy dataset. The training and validation accuracies for a model trained with the centrally hosted training and single weight transfer training heuristics are shown in (E) and (F), respectively.

Table 2.

Training, Validation, and Testing Accuracy of the Neural Network When Trained on Single Institutions for the Diabetic Retinopathy, DDSM, and ImageNet Datasets

Diabetic retinopathy	Training accuracy	Validation accuracy	Testing accuracy
	(n = 1500, %)	(n = 3000, %)	(n = 3000, %)
Institution 1	68.1	59.6	59.0
Institution 2	66.8	54.9	53.8
Institution 3	64.3	53.3	54.3
Institution 4	69.5	58.8	58.2

DDSM	Training accuracy	Validation accuracy	Testing accuracy
	(n = 257–270, %)	(n = 229, %)	(n = 229, %)
Institution 1	59.1	55.5	55.0
Institution 2	56.1	57.2	52.8
Institution 3	59.0	52.8	60.3
Institution 4	61.6	56.3	54.6

ImageNet	Training accuracy		Validation accuracy		Testing accuracy
	(n = 1500, %)		(n = 3000, %)		(n = 3000, %)
	Top-1	Top-5	Top-1	Top-5	Top-1	Top-5
Institution 1	62.1	93.5	30.4	71.4	31.0	71.2
Institution 2	66.1	95.0	31.1	70.0	32.4	71.5
Institution 3	64.5	94.3	31.5	71.3	32.4	71.1
Institution 4	66.8	94.5	31.6	70.8	32.1	71.6

Abbreviation: DDSM: Digital Database for Screening Mammography.

Centrally hosted training

When patient data from all institutions were pooled together, the collective size of the dataset was 6000. A network trained on the combined dataset had a high performance with a testing accuracy of 78.7% (Figure 3E and Table 3).

Table 3.

Training, Validation, and Testing Accuracy of Centrally Hosted Training, Ensembling Single Institution Model Outputs, and Single Weight Transfer for Diabetic Retinopathy, Digital Database for Screening Mammography, and ImageNet Datasets

Diabetic retinopathy	Training accuracy	Validation accuracy	Testing accuracy
	(n = 6000, %)	(n = 3000, %)	(n = 3000, %)
Centrally hosted	89.4	78.6	78.7
Ensemble models	63.2	60.9	60.0
Single weight transfer	70.4	68.3	68.1

Digital Database for Screening Mammography	Training accuracy	Validation accuracy	Testing accuracy
	(n = 1050, %)	(n = 229, %)	(n = 229, %)
Centrally hosted	77.0	71.6	70.7
Ensemble models	63.7	56.3	61.1
Single weight transfer	61.3 ± 0.9	61.2 ± 0.8	61.1 ± 1.8

ImageNet	Training accuracy		Validation accuracy		Testing accuracy
	(n = 6000, %)		(n = 3000, %)		(n = 3000, %)
	Top-1	Top-5	Top-1	Top-5	Top-1	Top-5
Centrally hosted	82.9	98.4	49.5	83.4	48.9	83.8
Ensemble models	50.2	88.6	37.0	76.5	38.6	77.0
Single weight transfer	45.5	84.5	36.0	76.2	37.9	75.5

Ensembling single institution models

Averaging the sigmoid probability of the single institution models resulted in a testing accuracy of 60.0% (Table 3). Notably, the ensembled model outperformed any network trained on a single institution in terms of validation and testing accuracy.

Single weight transfer

Using the single weight transfer heuristic, the model was trained at each institution until the plateau of validation loss was reached, followed by transferring of the model to the next institution. The resulting model had a testing accuracy of 68.1% (Figure 3F and Table 3).

Cyclical weight transfer

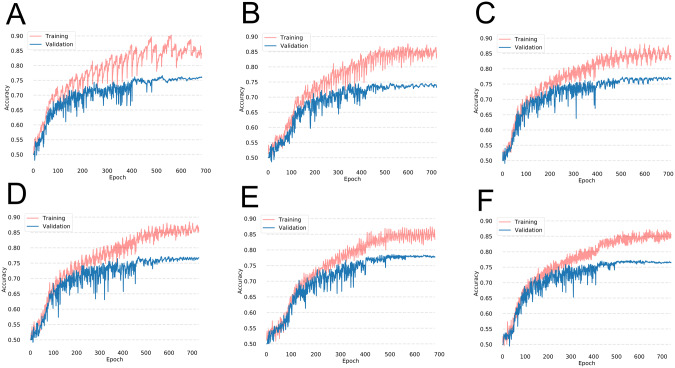
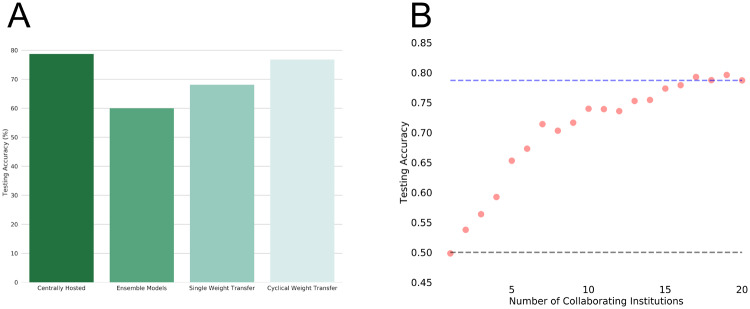
In our initial experiment, we trained the network for 20 epochs at each institution before transferring the weights to the next institution. The average testing accuracy after repeating this experiment 3 times was 76.1% (Figure 4A and Table 4).

Figure 4.

Training and validation accuracies during training on the Diabetic Retinopathy dataset with cyclical weight transfer with weight transfer frequencies of every (A) 20 epochs, (B) 10 epochs, (C) 5 epochs, (D) 4 epochs, (E) 2 epochs, or (F) every epoch.

Table 4.

Training, Validation, and Testing Accuracy for Cyclical Weight Transfer for Diabetic Retinopathy, Digital Database for Screening Mammography, and ImageNet Datasets.

Diabetic retinopathy	Training accuracy	Validation accuracy	Testing accuracy
	(n = 6000, %)	(n = 3000, %)	(n = 3000, %)
Cyclical weight transfer, every:
20 Epochs	85.8 ± 0.9	76.0 ± 0.6	76.1 ± 1.0
10 Epochs	87.9 ± 1.6	75.6 ± 2.0	75.9 ± 1.2
5 Epochs	86.8 ± 0.9	76.1 ± 0.6	76.1 ± 0.8
4 Epochs	88.9 ± 1.1	76.6 ± 0.1	77.4 ± 0.2
2 Epochs	89.1 ± 1.7	77.3 ± 0.5	77.8 ± 0.3
Epoch	89.4 ± 2.3	77.3 ± 1.3	77.3 ± 0.9

Digital Database for Screening Mammography	Training accuracy	Validation accuracy	Testing accuracy
	(n = 1050, %)	(n = 229, %)	(n = 229, %)
Cyclical weight transfer, every:
20 Epochs	72.7 ± 1.3	66.5 ± 3.5	65.4 ± 1.1
10 Epochs	70.5 ± 4.7	68.9 ± 0.9	68.1 ± 3.6
5 Epochs	71.5 ± 3.0	69.1 ± 0.2	68.1 ± 1.2
4 Epochs	71.7 ± 1.9	65.9 ± 1.8	68.7 ± 2.4
2 Epochs	71.9 ± 1.5	69.3 ± 2.4	69.9 ± 2.7
Epoch	74.8 ± 2.0	68.9 ± 1.3	69.1 ± 2.9

ImageNet	Training accuracy		Validation accuracy		Testing accuracy
	(n = 6000, %)		(n = 3000, %)		(n = 3000, %)
	Top-1	Top-5	Top-1	Top-5	Top-1	Top-5
Cyclical weight transfer, every:
20 Epochs	77.2 ± 3.2	97.7 ± 0.8	46.9 ± 0.8	82.8 ± 0.7	46.6 ± 0.9	83.2 ± 0.9
10 Epochs	78.5 ± 1.2	98.0 ± 0.4	47.8 ± 0.9	82.9 ± 0.4	47.3 ± 0.6	83.8 ± 0.1
5 Epochs	77.7 ± 2.6	97.7 ± 0.4	47.7 ± 0.7	83.0 ± 0.1	47.5 ± 1.4	83.3 ± 0.5
4 Epochs	78.5 ± 3.5	97.9 ± 0.6	47.2 ± 0.9	83.2 ± 0.5	48.1 ± 0.6	83.6 ± 0.2
2 Epochs	79.0 ± 3.2	97.8 ± 0.9	47.9 ± 0.0	82.8 ± 0.4	47.6 ± 1.1	84.1 ± 0.4
Epoch	83.2 ± 3.5	98.6 ± 0.6	49.2 ± 0.3	83.9 ± 0.7	49.3 ± 1.0	84.7 ± 0.1

Weight transfer frequencies investigated include every 20 epochs, 10 epochs, 5 epochs, 4 epochs, 2 epochs, and 1 epoch. The accuracies for cyclical weight transfer are shown as mean ± standard deviation for 3 repetitions.

We also investigated whether having a higher frequency of weight transfer can improve the testing accuracy. We experimented with weight transfer frequencies of 10, 5, 4, 2, and every epoch, repeating each experiment 3 times (Figure 4 and Table 4). The average testing accuracy of lower frequency weight transfer (every 20, 10, or 5 epochs) was 76.1% while the average testing accuracy of higher frequency weight transfer (every 4, 2, or 1 epoch) was 77.5% (2-sample t-test P < .001). Thus, a higher frequency weight transfer had a statistically significant increase in testing accuracy. The average training testing accuracy for all cyclical weight transfer experiments was 76.8% (Figure 5A).

Figure 5.

(A) Testing accuracies of centrally hosted training, ensembling models, single weight transfer, and cyclical weight transfer for our 4 “institution” experiment on the Diabetic Retinopathy dataset. Cyclical weight transfer had the performance that was on par with centrally hosted training. (B) To show distributed computation on a larger scale, we performed a 20 “institution” experiment with n = 300 patients per institution. The plot shown is the testing accuracy as a function of the number of collaborating institutions. All models were trained using the cyclical weight transfer training heuristic with a weight exchange frequency of 1. For reference, testing accuracy expected from random classification (bottom dotted line) and centrally hosted data (n = 6000 patients, top dotted line) are shown.

Introduction of an institution with variability

We next addressed what would happen if variability was introduced into one of the institutions. The modes of variability were either an institution with low-resolution images or an institution with few patients and class-imbalance. Among the various model-sharing training heuristics that was trained on all 4 institutions, cyclical weight transfer had the highest testing performance (Table 5), with a testing accuracy of 72.7% in experiments with an institution with low-resolution images and 73.3% in experiments with an institution with a small number of patients with class-imbalance. This is of comparable performance to that of centrally hosted data, which had testing accuracies of 72.2% and 75.4%, respectively. It is interesting to note that the performance of single weight transfer was dependent on the ordering of the institutions (i.e., whether the variable institution was institution 1, 2, 3, or 4). We also assessed performance of cyclical weight transfer when the variable institution was skipped. The resulting testing accuracy was 74.4%, which is comparable to cyclical weight transfer that included the variable institution.

Table 5.

The Testing Accuracy of the Various Training Heuristics With the Various Training Heuristics when Variability (Low-resolution Images or Few Patients with Class-imbalance) was Introduced into One of the Institutions

Training Heuristic	Variable institution:	Variable institution:
	low-resolution	small and imbalanced
	Testing accuracy	Testing accuracy
	(n = 3000, %)	(n = 3000, %)
Centrally hosted	72.2	75.4
Ensembling models	57.8	58.9
Single weight transfer (variable institution as Institution 1)	55.2	54.7
Single weight transfer (variable institution as Institution 2)	64.6	67.6
Single weight transfer (variable institution as Institution 3)	57.4	67.2
Single weight transfer (variable institution as Institution 4)	50.4	64.3
Cyclical weight transfer, every epoch	72.7	73.3
Cyclical weight transfer, every epoch (skipping variable institution)	74.4

Cyclical weight transfer with 20 institutions

We next addressed whether cyclical weight transfer can improve model performance when the performance of any individual institution is no better than random classification. To do this, we divided 6000 patient samples into 20 institutions, each with n = 300 patients. We trained models with increasing numbers of collaborating institutions, from 1 to 20. We utilized the cyclical weight transfer training heuristic with the weight transfer frequency of 1. As we increased the number of collaborating institutions, the testing accuracy increased (Figure 5B). The testing accuracy for a single institution was 49.8%, which is equivalent to random classification as there are equal numbers of healthy and diseased patients. The testing accuracy for 20 collaborating institutions was 78.7%, which is on par with the performance of centrally hosted data with all 6000 patient samples.

Mammography Dataset

When we repeated the experiments on the DDSM dataset, the average testing accuracy was 55.7% for single institution models (Table 2 and Supplementary Figure S1A–D), only slightly better than a majority classifier. A model trained on centrally hosted data had a testing accuracy of 70.7% (Table 3 and Supplementary Figure S1E). Ensembling single institution models resulted in a testing accuracy of 61.1% and the single weight transfer training heuristic also resulted in an average testing accuracy of 61.1% (Table 3 and Supplementary Figure 1F). Cyclical weight transfer resulted in an average testing accuracy of 67.2% for low frequencies of weight transfer (every 20, 10, or 5 epochs), which was lower than the average testing accuracy of 69.2% for high frequency of weight transfer (every 4, 2, or 1 epoch, P < .05) (Supplementary Figure S2 and Table 4).

ImageNet Dataset

When these experiments were repeated for the ImageNet dataset, the average testing top-1 accuracy was 32.0% (top-5 accuracy = 71.4%) for single institution models (Table 2 and Supplementary Figure S3A–D). In comparison, a model trained on centrally hosted data had a testing top-1 accuracy of 48.9% (top-5 accuracy = 83.8%) (Table 3 and Supplementary Figure S3E). Ensembling single institution models resulted in a testing top-1 accuracy of 38.6% (top-5 accuracy = 77.0%), while the single weight transfer training heuristic resulted in a testing top-1 accuracy of 37.9% (top-5 accuracy = 75.5%) (Table 3 and Supplementary Figure S3F). Cyclical weight transfer resulted in an average testing top-1 accuracy of 47.1% (top-5 accuracy = 83.4%) for low frequencies of weight transfer (every 20, 10, or 5 epochs), which was lower than the average testing top-1 accuracy (48.3%, top-5 accuracy = 84.1%) for high frequency of weight transfer (every 4, 2, or 1 epoch, P < .01) (Table 4 and Supplementary Figure S4).

Discussion

All training heuristics, either data sharing or model distribution, outperformed models trained only on one institution in terms of testing accuracy. This shows the benefits of collaboration among multiple institutions in the context of deep learning. Unsurprisingly, a model trained on centrally hosted data had the highest testing accuracy, serving as a benchmark for the performance of our various model sharing heuristics. In this study, we investigate if a model sharing heuristic can replace having the data be centrally hosted.

To overcome limitations in data-sharing, we tried several approaches—ensembling of single institution models, single weight transfer, and cyclical weight transfer. Ensembling of neural networks trained to perform the same task is a common approach to significantly improve the generalization performance.²² In comparison, the concept of single weight transfer is very similar to that of transfer learning, which is derived from that idea that a model can solve new problems faster by using knowledge learned from solving previous problems in other domains.^23,24 In practice, this involves training a model on one institution’s dataset and fine-tuning the model on a different dataset. If we consider each institution as a separate dataset, the model is trained on institution 1 and fine-tuned on institutions 2, 3, and 4. Both ensembling single institution models and single weight transfer resulted in higher testing accuracies than any single institution model for Kaggle Diabetic Retinopathy, DDSM, and ImageNet datasets. Single weight transfer outperformed ensembling models for the Kaggle Diabetic Retinopathy dataset while ensembling models and single weight transfer had the same testing performance for the DDSM dataset. For the ImageNet dataset, ensembling models outperformed single weight transfer.

The highest testing accuracies among training heuristics involved cyclical weight transfer. On average, the testing accuracy of models trained with cyclical weight transfer was 1.9%, 2.5%, and 1.2% less than that of a model trained on centrally hosted data for the Kaggle Diabetic Retinopathy, DDSM, and ImageNet datasets, respectively. This means nonparallel distributed training produced model performance comparable to centrally hosted model performance, and parallel distributed training was not required to achieve this performance. Additionally, it important to note that even though the model is transferred to each institution more than once in cyclical weight transfer, overfitting did not occur, as evidenced by the high testing accuracy. Furthermore, we find that a higher frequency of weight transfer had a higher testing accuracy than a lower frequency of weight transfer. For the Kaggle Diabetic Retinopathy dataset, the higher frequency of weight transfer had, on average, a 1.4% increase in testing accuracy compared to lower frequency of weight transfer. Similarly, for the DDSM dataset, a higher frequency of weight transfer had, on average, a 2.0% increase in testing accuracy compared to lower frequency of weight transfer. Finally, for the ImageNet dataset, a higher frequency of weight transfer had, on average, a 1.1% increase in testing accuracy compared to lower frequency of weight transfer. The disadvantage of having a higher frequency of weight transfer, however, is that it may be more logistically challenging and may add to the total model training time. In these cases, a lower frequency of weight transfer would still produce results that are comparable to that of a model trained on centrally hosted data. Lastly, we show that cyclical weight transfer is robust even when there was an institution with variability (either low-resolution images or few patients with class-imbalance), simulating a real-world scenario. We show that cyclical weight transfer performs similarly when the variable institution was introduced compared to when the variable institution is skipped entirely in terms of testing accuracy. In other words, variability did not significantly compromise the performance of the model with the cyclical weight transfer training heuristic.

In our experiments with 4 institutions, we show that we are able to achieve high model performance without having the data centrally hosted. We next investigated whether high model performance can be achieved when the performance of any single institution is no better than random classification. We divided 6000 patient samples from the Diabetic Retinopathy dataset into 20 institutions, each with 300 patient samples. Indeed, when we trained a model using data from one institution, the performance was no better than random classification. As we increased the number of collaborating institutions (using cyclical weight transfer), we observed an increase in testing accuracy. With all 20 institutions, cyclical weight transfer achieved a testing accuracy on par with centrally hosted data with all 6000 patient samples. This simulates a scenario where patient data are dispersed sparsely across many different institutions, and it is impossible to build a predictive model with data from any single institution. There are many situations (especially with rarer patient conditions) where no single institution has much patient data. In such cases, model distribution can effectively utilize data from many institutions as long as the institutions are willing to distribute the model. In other words, if all institutions participate, they can, in essence, build a model capable of performing as if they had open access to all the data.

One limitation is that our “institutions” were sampled from a single dataset (such as Kaggle Diabetic Retinopathy dataset) and thus, do not display much variability from one institution to the next. To address the possibility of variability, we performed experiments in which we altered one institution to either have low-resolution images or low numbers of patients with class imbalance. Future studies can explore the scenario where there is variability in multiple institutions such as the case where there is class imbalance in multiple institutions or the case where each institution is derived from a unique patient population. Furthermore, for the Diabetic Retinopathy and DDSM datasets, the neural networks were trained to perform a binary classification problem. In practice, multi-label problems are commonplace, but our work does not address how the added complexity would impact the various training heuristics. Future work can investigate the performance of distributed training heuristics in scenarios with multiple labels and more narrow decision boundaries. Also, we only investigated distributed learning in the context of a convolutional neural network. Distribution of models across institutions for other forms of deep learning, such as autoencoders, generative adversarial networks, and recurrent neural networks, warrant further study. Lastly, parallel distributed training methods could be explored as an option for cases when faster training is required. Future work will be on developing an open-source platform for distributed training. One key feature that is needed within this platform for cyclical weight transfer is that training at a given institute only begins after the training at the previous institute is completed.

Conclusion

In this study, we address the question of how to train a deep learning model without sharing patient data. We found that cyclical weight transfer performed comparably to centrally hosted data, suggesting that sharing patient data may not always be necessary to build these models. This finding has applications for any collaborative deep learning study.

Funding

This project was supported by a training grant from the National Institutes of Health Blueprint for Neuroscience Research (T90DA022759/R90DA023427). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.

This research was carried out in whole or in part at the Athinoula A. Martinos Center for Biomedical Imaging at the Massachusetts General Hospital, using resources provided by the Center for Functional Neuroimaging Technologies, P41EB015896, a P41 Biotechnology Resource Grant supported by the National Institute of Biomedical Imaging and Bioengineering, National Institutes of Health.

This study was also supported by National Institutes of Health grants U01CA154601, U24CA180927, U24CA180918, U01CA190214, and U01CA187947.

Competing interests

None.

Contributors

KC, NB, CKL, DY, and JMB performed the experiments. KC and NB prepared the figures. KC, NB, JMB, and AB. wrote the main body of the manuscript. KC, NB, CKL, DY, JMB, and AB interpreted the results. BRR, DLR, and JK conceived the study, designed the experiments, and supervised the work. All authors reviewed the manuscript.