Travelling breathers and solitary waves in strongly nonlinear lattices

Abstract

We study the existence of travelling breathers and solitary waves in the discrete p-Schrödinger (DpS) equation. This model consists of a one-dimensional discrete nonlinear Schrödinger (NLS) equation with strongly nonlinear inter-site coupling (a discrete p-Laplacian). The DpS equation describes the slow modulation in time of small amplitude oscillations in different types of nonlinear lattices, where linear oscillators are coupled to nearest-neighbours by strong nonlinearities. Such systems include granular chains made of discrete elements interacting through a Hertzian potential (p = 5/2 for contacting spheres), with additional local potentials or resonators inducing local oscillations. We formally derive three amplitude PDEs from the DpS equation when the exponent of nonlinearity is close to (and above) unity, i.e. for p lying slightly above 2. Each model admits localized solutions approximating travelling breather solutions of the DpS equation. One model is the logarithmic NLS equation which admits Gaussian solutions, and the other is fully nonlinear degenerate NLS equations with compacton solutions. We compare these analytical approximations to travelling breather solutions computed numerically by an iterative method, and check the convergence of the approximations when . An extensive numerical exploration of travelling breather profiles for p = 5/2 suggests that these solutions are generally superposed on small amplitude non-vanishing oscillatory tails, except for particular parameter values where they become close to strictly localized solitary waves. In a vibro-impact limit where the parameter p becomes large, we compute an analytical approximation of solitary wave solutions of the DpS equation.

This article is part of the theme issue ‘Nonlinear energy transfer in dynamical and acoustical systems’.

1. Introduction

Energy localization in discrete media occurs in many contexts, such as the propagation of stress waves in granular media [1,2] (or voltage pulses in nonlinear transmission lines [3]), the excitation of nonlinear oscillations in crystals by atom bombardment [4,5] and the nonlinear localization of vibrations in macromolecules [6]. In this framework, nonlinear Hamiltonian lattices consisting of one-dimensional chains of coupled oscillators (spatially homogeneous or periodic) have been widely analysed. Relevant phenomena include the propagation of solitary waves [7] (spatially localized travelling waves), as well as the trapping of vibrational energy in the form of discrete breathers, i.e. spatially localized oscillations [8] (see [9–12] for more references). In addition, the analysis of travelling breathers constitutes a notoriously difficult problem (see e.g. [9,10,13] for reviews). Modulation theory based on the Korteweg–de Vries (KdV) equation [14–16] and the nonlinear Schrödinger (NLS) equation [17,18] constitutes a classical approach to approximate small amplitude solitary waves and static or travelling breathers over long time scales.

In this paper, we consider more specifically strongly nonlinear lattices for which all oscillators become uncoupled in the linearized equations, so that energy cannot propagate through purely linear effects. Another direct consequence of strong nonlinearity is that the usual KdV and NLS asymptotics describing the balance between linear dispersion and nonlinearity do not apply. One application of strongly nonlinear lattices comes from the design of granular crystals [1,19–21] (or other kinds of highly nonlinear acoustic metamaterials) for the passive control of acoustic waves, including impact mitigation and redirection, acoustic lensing and filtering. In granular crystals, contact interactions between discrete elements are governed by the (generalized) Hertzian potential

1.1

where p > 2, and nonlinear stiffness has been normalized to unity. This potential describes the contact force ∝( − x) + ^α (with α = p − 1) between two initially tangent elastic bodies (in the absence of precompression) after a small relative displacement x. The most classical case is obtained for p = 5/2 (α = 3/2) and corresponds to contact between spheres, or more generally two smooth non-conforming surfaces.

An example of granular metamaterial is given by the so-called locally resonant granular chain. Such metamaterials have been experimentally tested in the form of chains of spherical beads with internal linear resonators (mass-in-mass chain) [22], granular chains with external ring resonators attached to the beads (mass-with-mass chain) [23] (see also [24]) and woodpile phononic crystals consisting of vertically stacked slender cylindrical rods [25,26]. Under certain conditions, each of these systems can be described by a chain of particles coupled to nearest-neighbours by a Hertzian potential, with a secondary mass attached to each element by a linear spring. The dynamical equations take the form

1.2

where u_n(t) and v_n(t) denote the (dimensionless) displacements of the nth primary and secondary masses, respectively. The frequency ω corresponds to the (rescaled) natural frequency of the internal or external resonators [22,23] or the primary bending vibration mode of the cylindrical rods in the woodpile set-up [25]. Alternatively, ρ = 1/ω² can be interpreted as the rescaled mass of the local resonators.

In the limit , one obtains u_n = v_n and the model (1.2) reduces to the one for a regular (non-resonant) homogeneous granular chain, which is known to support compression solitary waves [1,7,27–30]. The width of these solitary waves is independent of their amplitude and their spatial decay is doubly exponential [29,31]. In the opposite limit with and zero initial conditions for v_n(t), the system approaches a model of Newton's cradle (figure 1a), a granular chain with quadratic onsite potential, which is governed by

1.3

Both static and travelling breather solutions have been found numerically in system (1.3) [32–34]. It is, therefore, not surprising that for finite values of ω, the model (1.2) admits a rich variety of localized solutions, namely solitary waves [35], weakly non-local solitary waves or nanoptera [26,35–37], long-lived static breathers [38] and travelling breathers (figure 1b).

Figure 1.

(a) Schematic of a Newton's cradle. (b) Space–time evolution of the contact forces V^′(u_n+1 − u_n) (grey levels) for system (1.1) and (1.2) with p = 2.5 and ρ = 3. We simulate a chain of 52 particles with fixed-end boundary conditions, i.e. u₀ = u₅₁ = 0. A unit initial velocity is given to first the primary mass (i.e. ), while all the other elements are initially at rest. This excitation generates a localized propagating wave taking the form of a travelling breather (its internal oscillations are clearly visible through an alternance of black and grey strips).

The analytical study of static and travelling breathers in systems (1.2) and (1.3) is quite delicate. Owing to the lack of smoothness (for p = 5/2) and strongly nonlinear character of the Hertzian interaction potential, classical approaches based on spatial centre manifold reduction [39] or NLS reduction [17,18] do not apply. In addition, it has been proved it [38] that exact time-periodic breathers do not exist in system (1.2) (i.e. without precompression of the chain), despite the fact that similar excitations can persist over long (but finite) times.

An interesting insight into the dynamics of systems (1.2) and (1.3) can be obtained through the analysis of a spatially discrete modulation equation, namely the discrete p-Schrödinger (DpS) equation introduced in [32]. This model reads

1.4

where 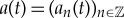denotes a time-dependent complex sequence and

the discrete p-Laplacian with p > 2. This model is reminiscent of the discrete nonlinear Schrödinger (DNLS) equation studied in detail in a number of different contexts, including nonlinear optics and atomic physics [40]. However, the DpS equation is fundamentally different in that it contains a fully nonlinear inter-site coupling term and shares some structural similarities with the Fermi–Pasta–Ulam (FPU) model with homogeneous potential [41–44].

The DpS equation describes how small amplitude oscillations of Newton's cradle (1.3) are slowly modulated in time [32–34,45], and it achieves the same (for well-prepared initial data) for the locally resonant granular chain (1.2) when ω is small (or equivalently when the attached mass ρ is large) [38]. To be more precise, let ϵ denote a small parameter and in (1.1) and (1.2) (α > 1). Consider a solution a of (1.4) and the ansatz u^a,ϵ_n(t) = ϵa_n(ω₀ϵ^α−1t) e^it + c.c., where ω₀ is an appropriate renormalization constant depending solely of α [38] and c.c. stands for complex conjugate. 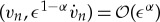In that case (see theorem 3.1 in [38]), for all ϵ small enough, if is -close to at t = 0 and at t = 0, then the same bounds hold true over long times . In particular, all localized solutions of the DpS equation provide localized solutions of (1.1) and (1.2) persisting over long times.

The existence of time-periodic breather solutions with super-exponential localization has been proved in [46] for the DpS equation (1.4), thereby implying the existence of long-lived static breathers in systems (1.3) [45] and (1.2) [38]. The existence of solitary waves and travelling breathers is still an open question for the DpS equation, despite travelling breathers having been found in dynamical simulations [32–34,46]. Such solutions correspond to long-lived travelling breather solutions of Newton's cradle (1.3) and the locally resonant granular chain (1.2).

In the present paper, we extend to the setting of travelling breathers an idea used in [46] to approximate time-periodic breathers in the DpS equation. In this work, it was shown numerically that a breather envelope converges towards a Gaussian when the nonlinearity exponent is close to unity, i.e. . This asymptotic behaviour was explained by relating the stationary DpS equation to a stationary logarithmic Schrödinger equation [47], the latter having explicit Gaussian solutions. It is interesting to note that the case when p is relatively close to 2 is not merely a mathematical game. Indeed granular chains involving different orders of nonlinearity have recently attracted much attention (see [48,49] and references therein). In particular, experimental and numerical studies on solitary wave propagation have been performed with chains of hollow spherical particles of different width [50] and chains of cylinders [51], leading to different values α in the range 1.15 ≤ α ≤ 1.5 (see also [52] for other systems with α close to unity).

The travelling breathers considered in the DpS equation (1.4) take the specific form a_n(t) = y(n − vt) e^−iθn, where y is spatially localized, v denotes the breather velocity and −θ corresponds to the breather phase shift after it propagates from one site to the next (hence θ = 0 corresponds to a solitary wave). Using a multiple-scale analysis, we formally derive in §2 three different PDEs describing the slow modulation of periodic travelling waves for p ≈ 2⁺. In §3, we use these modulation equations to derive approximate travelling breather solutions and analyse their qualitative properties. The first amplitude equation is a (time-dependent) logarithmic Schrödinger equation having Gaussian localized solutions [47] (see [12,53,54] for related works on the logarithmic KdV equation). The two additional models correspond to fully nonlinear degenerate NLS equations with compacton solutions (an equation of the same type was derived in [34] in the stationary case and for p = 5/2). In §4b, we compare the above analytical approximations to travelling breather solutions computed numerically by the Gauss–Newton method. We observe convergence when and a rather good accuracy for p = 5/2.

Further properties of travelling breathers are discussed, in particular the occurrence of small amplitude non-vanishing oscillatory tails consisting of resonant travelling waves, for generic parameter values (§§3d and 4). In addition, we observe a vanishing of the tail for particular parameter values (e.g. specific velocities of a travelling breather having unit energy) where numerical solutions become close to strictly localized solitary waves (§4c). We also obtain in §3c an analytical approximation of solitary waves of system (1.4) when p is large, which corresponds to a ‘vibro-impact’ limit in the Hertz potential (1.1) (see [55] for related models). Lastly, some open analytical problems are discussed in §5.

2. Multiscale analysis for

Before examining the limit of (1.4), let us consider the case p = 2

2.1

where Δ = Δ₂ is the usual discrete linear Laplacian. Equation (2.1) sustains linear waves a_n(t) = A e^i(Ωt−qn), where q denotes the wavenumber, the wave amplitude, and the frequency Ω is given by the dispersion relation Ω(q) = 4sin²(q/2). In addition, there exist solutions of (2.1) consisting of modulated waves

2.2

where ϵ > 0 is a small scaling parameter, τ = ϵ²t, ξ = ϵ(n − c_qt) and c_q = Ω^′(q) = 2sinq denotes the group velocity [56]. Such solutions can be approximated using solutions of the continuum linear Schrödinger equation [57]. Let us briefly sketch the procedure. Setting

2.3

we look for approximate solutions of (2.1) in the form

2.4

where the envelope function A is assumed sufficiently smooth. After lengthy but straightforward computations, one obtains the residual error

2.5

To minimize the residual error when ϵ ≈ 0, A has to satisfy the linear Schrödinger equation

2.6

which yields . If A(ξ, 0) displays sufficient smoothness and fast decay at infinity, there exists a modulated wave (2.2) solution of (2.1) which satisfies (2.3) uniformly in (this property can be readily seen on the representation of a_n(t) as a Fourier integral [57]). Consequently, the solution (2.2) remains -close to the linear Schrödinger approximation (2.4) over long times .

Extensions of this idea to the weakly nonlinear setting lead to the NLS equation (e.g. [17] and references therein). In that case one derives a suitable (small amplitude) ansatz minimizing the residual error, with a leading-order term modulated by the NLS equation, and Gronwall estimates allow us to control the resulting approximation over long time scales.

In what follows, we generalize to the nonlinear case the computations performed above for p = 2 by considering equation (1.4) in the limit . In this setting, we do not make any assumption of small amplitude waves. Instead, we consider a family of finite-amplitude periodic travelling waves which are slowly modulated in time (over time scales ) and space (spatial scale ). Owing to the invariance of (2.1), one can restrict the discussion to wavenumbers q∈[0, π] without loss of generality. The results presented below do not apply to solutions of (1.4) varying slowly in space, so we further assume q≠0. We investigate solely the different types of amplitude equations resulting from the above limit and do not attempt to provide error bounds.

To determine a suitable scaling relating the small parameters (p − 2) and ϵ, we rewrite (1.4) in the form

2.7

where the forward and backward differences δ^± are defined by

and the nonlinear term of (2.7) reads

2.8

Let us denote by the Banach space of bounded and continuous functions , endowed with the supremum norm. When , we have in

2.9

As we consider solutions of (1.4) which are not slowly varying in space, the nonlinear term of (2.7) is . This leads us to fix ϵ² = p − 2, so that dispersive and nonlinear effects act on a similar time scale. Moreover, we replace ansatz (2.4) by

2.10

with ϕ_n(t) = e^{i(Ω|R|p−2t − qn)} , τ = (p − 2)|R|^p−2t, . This ansatz respects the scaling invariance of (1.4).

For A = 1, (2.10) defines exact solutions of (1.4) corresponding to periodic travelling waves [32]. This is due to the fact that 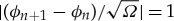, so

We now estimate the residual error obtained from (1.4) and (2.10) in the case of a general envelope function A (assumed sufficiently smooth). For this purpose, we first evaluate Δ_pa^app. The expansions performed below are valid when A(ξ, τ)≠0 is fixed and .

From the expansions

2.11

we obtain

2.12

Moreover, expanding (2.11) at higher order, we get

2.13

As Δ_pa^app = (δ⁺a^app)|δ⁺a^app|^p−2 − (δ⁻a^app)|δ⁻a^app|^p−2, combining (2.12) and (2.13) yields

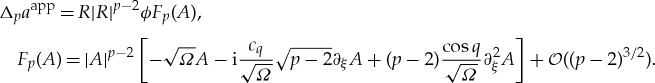2.14

Consequently, ansatz (2.10) yields the residual error

2.15

2.16

From this expansion, we deduce different amplitude equations which minimize the residual error when p ≈ 2⁺ and lead to . Note that, due to the phase invariance of the nonlinear term N_p of (2.7), no higher harmonics ϕ^k are generated in (2.16). As a consequence, it is not necessary to add higher order terms to the ansatz (2.10) in order to achieve .

The first amplitude equation deduced from (2.16) is the logarithmic Schrödinger equation (log-NLS)

2.17

Indeed, if A denotes a non-vanishing solution of (2.17) then ansatz (2.10) provides a residual error (substitute expansion (2.9) and in (2.16)).

As an alternative to (2.17), one can consider the following p-dependent fully nonlinear NLS equations:

2.18

and

2.19

(the log-NLS equation corresponds to leading-order terms in (2.18) and (2.19) when ). If A denotes a non-vanishing solution of (2.18) or (2.19) bounded independently of p, then ansatz (2.10) yields when .

Remark 2.1. —

Equation (2.19) could be derived more straightforwardly using the relative variables b_n = a_n − a_n−1 (see [27] for a similar discussion in the case of Hertzian solitary waves).

As we shall see in §3b, equations (2.17)–(2.19) possess some explicit stationary solutions which are strongly localized in space in the focusing case q∈(π/2, π]. These solutions consist of a Gaussian for equation (2.17) and compactons for equations (2.18) and (2.19), and provide approximate travelling (or static) breather solutions of (1.4). Their strong spatial localization (faster than exponential) is due to the singular logarithmic nonlinearity in (2.17), and to a vanishing dispersion in the limit of zero amplitude in the case of systems (2.18) and (2.19). The superexponential localization of approximate solutions is in good agreement with results established in [46] for exact static breathers solutions of (1.4).

Remark 2.2. —

The more classical (and p-dependent) NLS equation

2.20

yields also . However, its localized stationary solutions decay only exponentially at infinity, albeit at a fast rate . Owing to this loss of superexponential localization, we shall not resort to equation (2.20) in this study.

Remark 2.3. —

Given a sufficiently smooth solution of (2.17), (2.18) or (2.19), we have shown that whenever A(ξ, τ)≠0 is fixed and . If A(ξ, τ) ≈ 0, the residue (2.15) is also small, roughly .

One can note that is a conserved quantity for equations (2.17)–(2.19) (originating from phase invariance), similar to the conserved quantity of (1.4)

Another interesting observation relates to Hamiltonian structure. The original system (1.4) is Hamiltonian, with energy

Preservation of this Hamiltonian structure is not automatic, except if one uses specific derivation procedures [58,59]. The log-NLS equation is Hamiltonian, since it can be formally written with

Remark 2.4. —

There exists a Hamiltonian amplitude equation taking the form of a fully nonlinear NLS equation similar to (2.18) and (2.19) and leading to . The Hamiltonian reads

leading to the dynamical equation

3. Analytical approximations of travelling breathers and solitary waves

(a). Equivalent characterizations

Exact travelling breathers are spatially localized solutions of (1.4) satisfying

3.1

for some parameters v≠0 (the breather velocity) and (−θ corresponds to the breather phase shift after it propagates from one site to the next). If θ = 0(2π), the solution corresponds to a solitary wave.

Equation (3.1) is equivalent to

3.2

Indeed, if (3.2) holds true, then both sides of (3.1) define solutions of (1.4) which coincide at t = 0, and thus are equal for all . Characterization (3.2) will be used in §4 to compute travelling breathers numerically.

Rewriting (3.1) as a_n(t) = e^−iθa_n−1(t − 1/v) and proceeding by induction, we find that (3.1) is equivalent to

3.3

and a_n(t) defines a travelling breather solution provided a₀ decays to 0 at infinity. It can be convenient to rewrite (3.3) in the form

3.4

with A₀(t) = a₀(t) e^−iωt and q, ω linked by the identity

3.5

In §3b, we shall compute approximate travelling breather solutions taking the form (3.4) using the amplitude equations derived in §2 in the case p ≈ 2⁺. Section 3c will address the approximation of solitary waves in the opposite limit when p is large. In both cases, we will compare the analytical approximations with numerical simulations of localized propagating waves excited by a localized perturbation. In §3d, additional qualitative properties of travelling breathers and solitary waves will be discussed in connection with the above findings.

(b). Approximate travelling breather solutions for p ≈ 2⁺

From now on, we consider the case when q∈(π/2, π]. In that case, all the amplitude equations derived in §2 admit stationary localized solutions described below. These solutions generate two-parameter families of approximate travelling breathers through ansatz (2.10) when p ≈ 2⁺.

(i). Gaussian approximation

The logarithmic NLS equation (2.17) admits Gaussian stationary solutions [47]

3.6

With ansatz (2.10), we obtain consequently approximate travelling breather solutions of (1.4) for p ≈ 2

3.7

These travelling breathers are parametrized by their amplitude R and the wavenumber q∈(π/2, π] of the microscopic pattern. In particular, for q = π, the group velocity c_q = 2sinq vanishes and the breathers become stationary.

(ii). Compacton approximation from equation (2.19)

A stationary solution of (2.19) with compact support has been computed in [27] (this type of solution is called ‘compacton’). It can be obtained by setting A(ξ) = B^1/(p−1)((Ω/(p − 2)|cosq|)^1/2ξ) in (2.19) (assuming A, B≥0), which yields

3.8

with r = p/(p − 1)∈(1, 2). Integrating (3.8) leads to the equation (B^′)² + B² = (2/r)B^r, which admits the solution

3.9

defined for |ξ|(1 − r/2) ≤ π/2. This yields the compacton solution of (2.19)

3.10

with

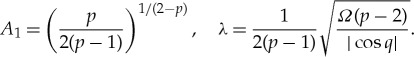With ansatz (2.10), we obtain approximate travelling breather solutions of (1.4) with compact support

3.11

We note that , and one has for all fixed

It follows that for all fixed . Consequently, the compacton approximation (3.11) and the Gaussian approximation (3.7) become close when .

(iii). Compacton approximation from equation (2.18)

In the stationary case (and for A≥0), equation (2.18) can be recast in the form (3.8) with r = 4 − p, setting A(ξ) = B((Ω/(p − 2)|cosq|)^1/2ξ). We further assume p∈(2, 4), so that r∈(0, 2). From the solution (3.9) of equation (3.8) (defined for |ξ|(1 − r/2) < π/2), we obtain the solution of (2.18)

3.12

where

Note that equation (2.18) must be interpreted with caution when p∈[3, 4), because Ã′′_c is singular at (piecewise continuous for p = 3 and unbounded for 3 < p < 4) but Ã′′_cÃ^p−2_c is C¹.

As previously one can check that 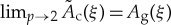for all fixed . Ansatz (2.10) yields approximate travelling breather solutions of (1.4) with compact support

3.13

(iv). Comparison with a dynamical simulation

In this section, we illustrate the excitation of a travelling breather from a localized perturbation in system (1.4). Numerical computations are performed for a long chain (1 ≤ n ≤ 1500) and free-end boundary conditions. We set p = 2.1 and consider the initial condition a_n(0) = 0 for n≥2 and a₁(0) = − i. This perturbation generates a travelling breather whose profile will be compared to the analytical approximations derived above for p ≈ 2⁺. Throughout this paper, time-integrations of (1.4) are performed using the standard ODE solver of the software package Scilab.

Figure 2 illustrates the evolution of a_n(t) under the DpS equation (1.4). One can note a robust propagating localized mode (travelling breather) followed by a weak and fairly extended ‘wake’. The travelling breather propagates almost steadily, with the amplitude of the main pulse (i.e. supremum of |a_n(t)| over time) decaying by only 0.12% after it travels over 100 sites from n = 1280. Its velocity is v ≈ 1.51 and its phase θ ≈ 0.31. The wake consists of dispersive wave trains having a rather complex structure, clearly separated from the breather by a (weakly modulated) sinusoidal tail of very small amplitude. This tail is close to a periodic travelling wave solution of (1.4), as we will see in more detail in §3d(ii).

Figure 2.

(a) Space–time evolution of |a_n(t)| for system (1.4) with p = 2.1, free-end boundary conditions and an initial condition localized on the first particle (a₁(0) = − i, a_n(0) = 0 for n≥2). (b) Spatial profile of Re a_n(t) at t = t₀ = 900 (black line). The travelling breather is followed by a tail close to a sinusoid which extends over 257 sites. Within this region behind the breather, one has Re a_n(t) ≈ ρcos(k(n − n₀)), with ρ ≈ 0.0024, k ≈ 0.36, n₀ = 1351. This sinusoidal approximation is represented by the dashed blue line. (c) Time-evolution of Re a_n(t) at n = 1175 after the passage of the moving breather (black line), and comparison with the sinusoidal approximation Re a_n(t) ≈ ρcos(ω_tw(t − t₀) − k(n − n₀)) with ω_tw = ρ^p−2(2sin(k/2))^p ≈ 0.065 (dashed blue line).

Let us now compare the travelling breather profile with the approximate travelling breather solutions (3.7), (3.11) and (3.13). These approximations take the form (3.4) with

3.14

and ω = 4sin²(q/2)|R|^p−2. Using (3.5), their phase θ satisfies consequently

3.15

Using the values of θ and v computed from the numerical simulation, we get q ≈ 2.142 from (3.15) and R ≈ 0.34 from (3.14). Figure 3 compares the three resulting analytical approximations to the outcome of the numerical simulation. The relative error between numerical solution and analytical approximations (supremum norm for t∈[862, 882], normalized by the breather amplitude) is 11.6% for the Gaussian approximation (3.7) (blue curve), 11.8% for the compacton (3.13) (green curve) and 13% for the compacton (3.11) (black curve). The error on the travelling breather amplitude is much smaller, 0.024% for the Gaussian approximation (3.7), 1.3% for the compacton (3.13) and 3.4% for the compacton (3.11). The comparison is thus quite satisfactory given the additional errors induced by the determination of parameters θ and v and the fact that the moving breather has not yet reached a fully steady regime. A more precise comparison will be made in §4, where exact travelling breathers will be computed more precisely using an iterative method, and values of p closer to 2 will be considered as well.

Figure 3.

Time-evolution of |a_n(t)| (a) and Re (a_n(t)) (b) during the passage of the moving breather at n₁ = 1340. The red dashed lines correspond to the numerical simulation of figure 2. In (b), we have applied an appropriate phase shift, i.e. we plot Re (a_n(t) e^iφ) with φ =  − 0.3. These profiles are compared with the analytical approximations a^app_n−n1(t − t₁) obtained for p ≈ 2⁺, where we set n = n₁, t₁ = 872.35, q ≈ 2.142, R ≈ 0.34 and p = 2.1. The blue line corresponds to the Gaussian approximation (3.7), the black line to the compacton approximation (3.11), and the green line to the compacton approximation (3.13).

(c). Solitary waves for p large

In order to investigate the ‘vibro-impact’ limit corresponding to large values of p, we start by simulating the evolution of a localized perturbation in a chain of 330 particles with free-end boundary conditions. We set a_n(0) = 0 for n≥2 and |a₁(0)| = 1. When p is large, one observes after a short transient the formation of a solitary wave with velocity v close to 2/π (figure 4). The solitary wave is strongly localized (mainly on two lattice sites) and is followed by a small and quasi-stationary tail (see the lower plot of figure 4). The tail amplitude decays relatively slowly with increasing n (it is O(1/n)). We observe a convergence of the propagating pulse towards a limiting profile a_n(t) = y(n − v t) when (the limiting profile is described in figure 5). Owing to the phase invariance of (1.4), this profile is unique up to a factor e^iφ determined by the phase of the initial localized perturbation.

Figure 4.

(a) Space–time evolution of |a_n(t)| for system (1.4) with p large, free-end boundary conditions and an initial condition localized on the first particle (a₁(0) = − i, a_n(0) = 0 for n≥2). We have fixed p = 201 in the numerical simulation. One observes a solitary wave with velocity v ≈ 0.63 ≈ 2/π. (b) Spatial profile of |a_n(t)| at t = 479.84 (semi-logarithmic scale).

Figure 5.

Real part (a) and imaginary part (b) of the travelling pulse when p is large. The dashed blue line corresponds to e^iφa_n0(t), where a_n(t) denotes numerical solution obtained in figure 4 for p = 201, n₀ = 230 and φ ≈ 2. Dots correspond to e^iφa_n1(t + Δt) with n₁ = 270 and Δt = 63. The graphs obtained with n = n₀ and n = n₁ coincide almost perfectly, illustrating the steady wave propagation at velocity v ≈ 2/π ≈ (n₁ − n₀)/Δt. The full black line corresponds to analytical approximation (3.25) appropriately shifted in time and space (we plot 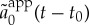with t₀ = 359.39). One observes that this approximation is extremely close to the numerical solution. (Online version in colour.)

Remark 3.1. —

Owing to the scaling invariance of (1.4), choosing |a₁(0)| = R results in v∼2R^p−2/π when p is large, hence one generates slow or fast solitary waves depending whether R < 1 or R > 1.

We describe below a heuristic method which allows to approximate the limiting solitary wave profile and velocity v. We consider an infinite chain () and look for solitary waves a_n(t) = y(ξ) with ξ = n − vt (v≠0) and . Equation (1.4) reduces to

3.16

where

3.17

Remark 3.2. —

Front solutions satisfying for some constants c + ≠c − do not exist for the DpS equation. Indeed, integrating (3.16) yields for some constant c. If y admits two finite limits c_± at ± ∞, which implies vanishing of f at infinity, we have then , i.e. c +  = c −  = c. This property of the (translation-invariant, first-order) DpS equation contrasts with the case of the (translation-invariant, second-order) FPU model. In the case of FPU solitary waves [30] (in particular with Hertzian potentials [27]), it is known that particle displacements correspond to fronts connecting constant displacement fields at infinity, and relative displacements decay to 0 at infinity.

Upon rescaling v, one can restrict (3.16) and (3.17) to solutions satisfying ∥B∥_∞ = 1. In that case, letting yields formally the following limit problem:

3.18

where 1_|z|=1 denotes the characteristic function of the unit circle in , y is assumed absolutely continuous and (3.18) holds true almost everywhere.

We shall not attempt to justify approximation (3.18) rigorously. Instead, we explicitly compute a family of localized solutions of (3.18), and we check numerically that one of them correctly approximates the propagating pulse.

We look for solutions of (3.18) having the following structure:

3.19

In conjunction with (3.18), this assumption leads to y^′ = 0 a.e. in ( − ∞,  − 1)∪(1, + ∞), and thus y(ξ) = 0 for |ξ|≥1 for a solitary wave decaying to 0 at infinity. This property is consistent with the observed localization of the travelling pulse on two lattice sites when .

Assumption (3.19) and equation (3.18) lead to (d/dξ)(y(ξ) + y(ξ − 1)) = 0 a.e. in (0, 1); hence there exists 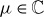such that

3.20

It follows that B = 2y − μ on [0, 1], which implies |μ| = 1 (since |B(1)| = 1 and y(1) = 0). Owing to the invariance of (3.18), one can fix μ = 1 without loss of generality. Then we infer from (3.18)

3.21

Recalling that y( ± 1) = 0 and using (3.20), equation (3.21) is supplemented by the boundary conditions

3.22

Solving (3.21) and (3.22) leads to v = 2/((2k + 1)π) () and

3.23

where we have used (3.20) to compute y_|[−1,0] from y_|[0,1]. One can check that assumption (3.19) is consistently satisfied by (3.23), hence (3.23) defines a solution of (3.18) for all . Returning to the original variable a_n(t) and fixing k = 0 in (3.23), one obtains the following approximate solution of (1.4) when p is large:

3.24

Taking into account symmetries of (1.4), this provides a more general family of approximate solitary wave solutions

3.25

where , , 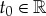and are arbitrary constants. As illustrated by figure 5, this approximation is very close to the travelling pulse computed numerically for large p, for appropriate choice of parameters φ, n₀, t₀ and c = 0.

(d). Additional qualitative properties of travelling breathers

(i). A constraint on exact travelling breather solutions

Let us consider the evolution problem (1.4) in (the Banach space of summable sequences). Equation (1.4) admits the conserved quantity which originates from translational invariance (an analogous result holds true with periodic boundary conditions). This conserved quantity induces a constraint on travelling breather solutions satisfying . Indeed, the conservation of and property (3.1) lead to

3.26

therefore, we have for θ≠0 (2π)

3.27

In what follows we evaluate the constraint (3.27) for the approximate travelling breather solutions a^app_n obtained in §3b when . We fix q∈(π/2, π) and consider the Gaussian approximation (3.7) for simplicity. Using Poisson's summation formula and identity (3.5), one obtains after some algebraic manipulations

where Â_g denotes the Fourier transform of (3.6). This yields after lengthy but straightforward computations

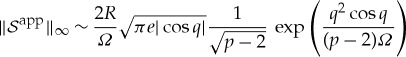3.28

when . Consequently, the constraint (3.27) is almost satisfied by ansatz (3.7) when , up to an exponentially small error given by (3.28).

Remark 3.3. —

Solitary waves need not satisfy (3.27) (case θ = 0(2π)). For example, with the approximate solitary wave solution (3.24) obtained when p is large, one finds

after some simplifications (the sum contains only two non-vanishing terms).

(ii). Travelling breathers with oscillatory tails

In standard periodic nonlinear lattices (i.e. excluding ‘sonic vacua’ where the linearized equations do not support phonon waves), exact travelling breathers are generally superposed on non-decaying oscillatory tails lying at both sides of the main pulse. This phenomenon has been mathematically analysed in a number of works (e.g. [13,60–62] and references therein) and the corresponding solutions are often referred to as ‘generalized’ travelling breathers or solitary waves, or ‘nanopterons’ (thereafter we shall use the denomination ‘travelling breather’ independently of the presence or the absence of a non-decaying oscillatory tail). The tails are close to a linear phonon (or a superposition thereof) whose wavenumber q and frequency ω satisfy a resonance condition reminiscent of (3.5) [13,63]. Typically, the tail amplitude can vary freely in some interval, with a lower bound exponentially small compared with the main pulse at small amplitude, a limit in which the wave becomes loosely localized (e.g. [13] and references therein). In generic models, the tail may exactly vanish only under special choices of the speed of the travelling breather (or the system parameters) [64,65]. In connection with the above phenomena, travelling breathers excited from localized initial perturbations are often followed by a small oscillatory tail, see e.g. [34,37] in the context of granular crystals.

Part of the above phenomenology can be transposed to the present setting despite the fact that equation (1.4) is fully nonlinear. Indeed, instead of weakly modulated phonons, the tails can involve nonlinear periodic travelling waves of (1.4) taking the form [32]

3.29

where Ω(k) = 4sin²(k/2). These solutions are parametrized by the wavenumber k, amplitude ρ > 0 and phase φ (expression (3.29) can be obtained by setting A = 1 and in (2.10)). These periodic waves (or slow modulations thereof) are good candidates to approximate oscillatory tails of exact travelling breathers when , or to describe the small oscillations emitted at the rear of (non-stationary) moving breathers generated from localized perturbations.

In order for a ‘resonant’ travelling wave to match (3.1), the wavenumber k and amplitude ρ must satisfy the compatibility condition

3.30

From the above equation, ρ can be expressed as a function of k (except for the trivial branch a_n(t) = ρ e^iφ if θ = 0(2π)); therefore, resonant periodic travelling waves form a one-parameter family parametrized by k. In particular, ρ is close to 0 when θ≠0(2π) and k lies slightly above θ.

In connection with the above observation, let us now examine more closely the numerical simulation of §3b(iv) performed for p = 2.1. We recall that the travelling breather excited by a localized perturbation satisfies v ≈ 1.51, θ ≈ 0.31 and is followed by a small oscillatory tail of amplitude close to ρ ≈ 0.0024. In the tail region, one observes that a_n(t) is close to the periodic wave (3.29) with k ≈ 0.36 and an appropriate phase φ (figure 2). This leads to k − (1/v)Ω^p/2(k)ρ^p−2 ≈ 0.32 which is close to θ, hence the compatibility condition (3.30) is almost satisfied. Note that a perfect match cannot be expected because the tail is actually weakly modulated and the travelling breather slightly non-stationary.

Another manifestation of the above phenomenology will be illustrated in §4, where we compute travelling breathers iteratively for a wide range of parameter values. These computations reveal oscillatory tails with a rather wide range of amplitudes and wavenumbers. In particular, we find travelling breathers with very small tails (compared with the amplitude of the main pulse) and k close to θ, which is consistent with the case ρ ≈ 0 of equation (3.30). Preliminary computations also indicate that the tail amplitude can become exponentially small when p is close to 2 (see §4b), a limit leading to travelling breathers with a large spatial extent. However, we will not attempt to compute the minimal tail size for given parameter values, and in particular to determine if the tail may exactly vanish or not (these problems are quite delicate and out of the scope of this study).

4. Newton-type computations

In this section, we compute exact travelling breather solutions of (1.4) iteratively and compare the numerical solutions to the approximations of §3b.

(a). Numerical method

Any initial condition determines a unique solution of (1.4) denoted by a_n(t) = Φ_n(t;a⁰). Our aim is to compute initial conditions a⁰ corresponding to travelling breather solutions. We fix two parameters , v > 0 and look for solutions satisfying (3.2). One can fix v > 0 without loss of generality due to the invariance of (1.4). From equation (3.2), searching for exact travelling breather solutions reduces to finding zeros of the nonlinear map defined by

Note also that Φ_n(t;Ra⁰) = RΦ_n(|R|^p−2t;a⁰) due to the scale invariance of (1.4). We have thus

4.1

i.e. varying breather velocity is equivalent to rescaling its amplitude.

In our numerical computations, the infinite chain is replaced by a periodic chain with N particles and F_θ,v translates to a map in , whose zeros can be computed iteratively. The zeros of F_θ,v are not isolated due to the invariance of (1.4) under time shift and the phase invariance . Moreover, in the particular case θ = 0(2π) corresponding to travelling waves, the translational invariance () yields additional degeneracy. To remove degeneracies due to invariances under time and phase shifts, we exploit the existence of a reversibility symmetry and reflectional symmetry for (1.4). More precisely, we restrict our attention to reversible travelling breather solutions satisfying 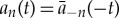, which is equivalent to fixing 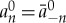. In addition, we impose in order to match the constraint (3.27) for localized travelling breathers and to remove degeneracy due to translational invariance when 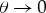. Fixing N odd, the set of symmetric zero-mean initial conditions a⁰ is isomorphic to .

We use the Gauss–Newton method [66] to minimize ∥F_θ,v∥₂ on (time integrations are performed using Scilab). The relative residual error for the last (kth) Newton iteration satisfies in all cases

and the incremental error (relative variation of the last two iterates) always satisfies

4.2

The number of particles must be fixed relatively large due to the broadening of the breathers when 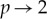(see §3b). More generally, it is interesting to consider a large number of particles in order to be closer to the case of an infinite lattice. Indeed, the numerical iteration tends to converge towards travelling breathers with oscillatory tails, and one is able to capture a wider set of tail sizes when N is large.

A two-parameters family of travelling breather solutions of (1.4) can be computed by varying the breather velocity v and the phase θ in (3.2). We use the Gaussian approximation (3.7) to initiate the Gauss–Newton method with a^app_n(0) when p is close to 2. To select an approximate breather solution with given velocity v and phase , one has to determine ansatz parameters q, R through system (3.14) and (3.15) which admits an infinity of solutions. Consequently, one can anticipate that the Gauss–Newton iteration may converge towards different travelling breather solutions depending on the choice of initial guess a^app_n(0) for a⁰ (i.e. on the choice of q). From a practical point of view, we shall treat q∈(π/2, π) as a parameter and determine θ using (3.15). Once q is fixed, equation (3.14) determines the amplitude parameter R of ansatz (3.7). In addition, the ansatz (3.7) is appropriately translated in order to fulfil the constraint of zero mean.

Remark 4.1. —

A classical approach to compute travelling wave or travelling breather solutions in lattices consists in solving a corresponding advance-delay differential equation (or an integral form thereof), using pseudospectral methods or high-order quadrature formula for discretization and suitable iterative methods to handle the discretized nonlinear problem [27,30,40]. For equation (1.4), setting a_n(t) = y(n − vt) e^−iθn leads to

4.3

where f = B|B|^p−2 and B(ξ) = y(ξ) − e^iθy(ξ − 1). We do not use this approach because the right side of (4.3) is not C² everywhere when p∈(2, 3), which may lower the precision of the above numerical discretizations.

(b). Continuation in p

In this section, we compare travelling breather solutions computed numerically and analytical approximations of §3b when θ, v are fixed in (3.2) and p varies. In particular, we check that the relative errors between exact and approximate solutions decay to 0 (uniformly in time and space) when . We fix N = 499 in our numerical computations.

Firstly, let us show that the breather velocity v can be normalized without loss of generality, which leaves only one free parameter θ in (3.2). Consider a travelling breather solution a_n satisfying (3.2) and an analytical approximation a^app_n of the form (2.10) (defined either by (3.7), (3.11) or (3.13)), with parameters q, R satisfying (3.14) and (3.15). One can write , where 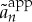corresponds to the case R = 1 of (2.10). Similarly, setting , we obtain a travelling breather solution of (1.4) satisfying (3.2) for v = 2sinq (due to property (4.1) and identity (3.14)). The relative error between numerical solution and analytical approximation satisfies

4.4

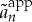where we have used property (3.3) satisfied by the travelling breather solution and the ansatz . Consequently, one can restrict the error analysis to the case v = 2sinq of (3.2), where q and θ are linked by identity (3.15). We shall therefore fix R = 1 in the choice of the analytical approximation.

In what follows we fix q = 3π/4, which corresponds to and . Using the numerical procedure described in §4a, we study the evolution of the breather profile when p is varied in the interval (2, 4]. The Gaussian approximation (3.7) is used to initiate the Newton iteration when p < 3.1 (since breather width varies strongly with p, path-following would require very small steps) and path following is used for larger values of p.

When p converges towards 2, the breather envelope becomes nearly Gaussian and breather solutions converge towards approximation (3.7) (figures 6 and 7). As indicated in §3b, the Gaussian and the two compacton approximations become essentially equivalent in this regime (figure 6). Discrepancies between the numerical and analytical profiles appear for larger values of p. For p = 5/2 (relevant case for Hertzian interactions), Gaussian approximation (3.7) and compacton approximation (3.11) yield a relative error around 14% in supremum norm, and compacton (3.13) yields a slightly larger error around 16%. Above p = 2.9, compacton approximation (3.13) becomes much less accurate than the Gaussian approximation (3.7) and compacton approximation (3.11). These two approximations are roughly of the same accuracy (figures 6 and 8).

Figure 6.

Relative error (4.4) between the numerical solution a (obtained for , θ ≈  − 0.058) and the Gaussian approximation (3.7) (blue line), the compacton approximations (3.11) (black line) and (3.13) (green line) with q = 3π/4, R = 1. The error is plotted as a function of p. Note that ∥a₀∥_∞ has negligible variations when p varies in (2, 4] (∥a₀∥_∞ increases from 0.89 to 0.95).

Figure 7.

Spatial profile (at t = 0) of the travelling breather solution computed numerically in figure 6 in the case p = 2.02 (dots). This solution is compared with the Gaussian approximation (3.7) (blue line). The real part (a) and modulus (b) of the numerical solution and Gaussian approximation almost perfectly coincide. (Online version in colour.)

Figure 8.

Comparison of |a₀(t)| for the numerical solution (red line), the compacton approximation (3.11) (black line) and the Gaussian approximation (3.7) (blue line) of figure 6, when p = 2.5 (a) and p = 4 (b). Note that Gaussian approximation works better at the time of maximal amplitude while compacton approximation is more accurate (with respect to the uniform norm) in the steepest region.

Spatial profiles of travelling breather solutions at t = 0 are represented in figures 9 and 10 for different values of p. A zoom at both sides of the breather centre reveals the existence of small non-decaying oscillatory tails which are very close to sinusoids of the form a_n =  ± iρ e^−iθn at t = 0. This is consistent with the analysis of §3d(ii), as the case ρ ≈ 0 of (3.30) corresponds to k ≈ θ. Figure 11 describes the dependency in p of the tail amplitude ρ. For p∈[2.1, 2.35] we find ρ∝e^−c/(p−2) with c ≈ 1.55 (for smaller values of p − 2, the tail amplitude becomes comparable to the numerical error (4.2) so that tail computations are not reliable). By extrapolation this suggests that the minimal tail amplitude should lie beyond all orders when in an infinite chain. Another interesting question concerns the limit of the above numerical solution when lattice size goes to infinity and p is fixed. Tail size may vanish, leading to fully localized travelling breather solutions (this situation is non-generic in usual lattice models, as discussed in §3d(ii)). Another possibility is the convergence of the numerical solution towards an heteroclinic solution connecting periodic travelling waves (3.29) satisfying the compatibility condition (3.30).

Figure 9.

Spatial profiles of the travelling breather solution computed numerically in figure 6 in the case p = 2.5. The curves correspond to the real part (a,c) and imaginary part (b,d) of the numerical solution. Panels (c,d) display more lattice sites and provide a zoom at small amplitude, which reveals the existence of small non-decaying oscillatory tails at both sides of the moving breather. These tails are very close to sinusoids (dots) of the form a_n = iσρ e^{−iθ(n−n₀)} with ρ = 0.00337, n₀ = 250, σ =  ± 1 = sign(n − n₀). (Online version in colour.)

Figure 10.

Same as in figure 9 for p = 4. In that case, the oscillatory tail is bigger (ρ ≈ 0.02) and visible at the scale of the moving breather. (Online version in colour.)

Figure 11.

Amplitude of the tails of the travelling breather solutions computed numerically in figure 6, expressed as a function of 1/(p − 2). The amplitude is computed within the index set S corresponding to |n − 250|≥125 (i.e. sufficiently far from the breather centre). The vertical axis corresponds to . One has for p∈[2.1, 4].

We have numerically tested for different values of p the robustness of the propagation of the travelling breathers computed by the Gauss–Newton method (data not shown). For this purpose, one starts from the initial condition computed with the Newton method and one integrates (1.4) over long times (keeping the same periodic boundary conditions). For p ≤ 2.4, we have obtained an almost perfect steady motion of the breather, travelling e.g. over 7500 lattice sites (the end of the simulation) for p = 2.4. As already noted in [46], breather mobility decreases when p increases, but in our worst case (p = 4) the solution propagates steadily over 190 lattice sites before getting trapped.

(c). Continuation in (v, θ) at fixed energy

In this section, we fix p = 5/2 and numerically compute travelling breather solutions when θ and v vary in (3.2). Their values are determined by systems (3.14) and (3.15), where q∈(π/2, π) and R are free parameters. We use a shorter periodic chain of N = 99 particles to reduce computation time. Owing to the scaling invariance of (1.4), we further restrict the numerical study to solutions with unit energy.

As previously, we use the Gaussian approximation of §3b to initiate the Gauss–Newton method and proceed by path following. Numerical computations are performed by fixing R = 1 and varying q (then v = 2sinq). Note that when , and hence the integration time in the shooting method diverges in this limit. For each value of q, a solution with unit energy is obtained by multiplying a numerical solution with energy by . The velocity v of this new solution is then given by (3.14).

Figure 12 shows typical travelling breather profiles obtained with the above procedure. They correspond to a localized excitation superposed in most cases to an oscillatory tail. Tail size exhibits important variations with respect to v (or equivalently q) during numerical continuation. This is due to the fact that in the limit of an infinite chain, a continuum of solutions can be expected in the neighbourhood of a travelling breather for the same value of (v, θ). Indeed, as discussed in §3d(ii), we expect that travelling breathers can be superposed on an oscillatory tail with amplitude and wavenumber linked by equation (3.30), and the tail amplitude provides an additional free parameter.

Figure 12.

Real part of travelling breather solutions with unit energy , for the following parameter values (from top to bottom and left to right) : v ≈ 0.08 (q ≈ 3.08, θ ≈  − 0.92), v ≈ 0.16 (q ≈ 3.02, θ ≈  − 1.42), v ≈ 1.02 (q ≈ 2.36, θ ≈  − 0.06), v ≈ 1.05 (q ≈ 2.33, θ ≈ 3.4 · 10⁻⁴), v ≈ 1.08 (q ≈ 2.30, θ ≈ 0.06), v ≈ 1.17 (q ≈ 2.21, θ ≈ 0.21), v ≈ 1.22 (q ≈ 1.86, θ ≈ 0.52), v ≈ 1.39 (q ≈ 1.63, θ ≈ 0.57). Computations are performed for p = 5/2.

We have performed an extensive numerical exploration of the profiles of travelling breathers when q varies in the interval (π/2, π). We have observed a local drop in the tail size close to v = 1.05, where tail size over breather amplitude is close to 1.6 × 10⁻³. At this local minimum, the energy density |a_n+1(0) − a_n(0)|^p in the tail is extremely small (of the order of 10⁻¹⁶, i.e. machine precision). This value of v corresponds to θ close to 0, i.e. the solution is close to a solitary wave (θ ≈ 3.4 × 10⁻⁴ and q ≈ 2.33). This result suggest that strictly localized solitary waves exist in the DpS equation (1.4) with p = 2.5. Another local drop in tail size occurs close to v = 0.3, but the phenomenon is less clear. Indeed, in this region where breather velocity v is relatively small, tail size tends to be small for all values of v. This is consistent with the fact that static breathers (case v = 0) are strictly localized [46].

5. Discussion

We have derived several amplitude equations to approximate slowly modulated periodic waves in the DpS equation with nonlinearity exponent close to unity. These models provide analytical approximations of travelling breather solutions with superexponential spatial decay (either Gaussian or with compact support). From a numerical point of view, we have computed exact travelling breather solutions for p∈(2, 4] and compared them to the approximate solutions, observing convergence when . Travelling breathers computed numerically are generally superposed on a small non-vanishing oscillatory tail, except in special cases when they are close to strictly localized solitary waves. In the vibro-impact limit when p becomes large, we have obtained an analytical approximation of the solitary wave excited by an initial perturbation applied to the first particle in the chain. Thanks to the available error bounds relating the Dps dynamics to Newton's cradle (1.3) [45] and the resonant granular chain (1.2) for ω ≈ 0 [38], our numerical results (supplemented by analytical approximations) imply the existence of long-lived travelling breather solutions in the above models.

A first problem left open in this study concerns the theoretical validation of the multiscale analysis performed for p ≈ 2⁺. In the spirit of classical modulation theory leading to the NLS equation [17], it would be interesting to prove that sufficiently smooth solutions of the logarithmic NLS equation approximate true solutions of DpS on long time intervals when p ≈ 2. In this context, the log-NLS equation seems more suitable than the fully nonlinear NLS equations (2.18) or (2.19), as its well-posedness has been established in [67], and consistency estimates in appear more tractable. However, some non-trivial features can be expected due to the non-Lipschitzian character of the leading logarithmic nonlinearity in (2.9).

Another open problem concerns an existence proof for exact travelling breather solutions of the DpS equation. According to our numerical results, we conjecture the existence of solutions of (1.4)–(3.2) (close to the Gaussian or compacton approximations for p ≈ 2), consisting of strictly localized solitary waves for θ = 0 (2π), and superposed on non-vanishing oscillatory tails for θ≠0 (2π). These problems might be addressed using critical point theory in the spirit of the works [68,69] concerning periodic and quasi-periodic travelling waves in generalized DNLS equations. Indeed equation (4.3) corresponds (for localized solutions) to the Euler equation for the Lagrangian

It is also important to note that our numerical procedure does not penalize the tail size during minimization; therefore, we may have missed strictly localized travelling breathers existing away from θ = 0 (2π). This problem constitutes an interesting possible extension of the numerical part of this work. Travelling breathers with minimal tail are expected to display negligible dispersion when their tail is truncated in the direction of propagation, whereas dispersion should be much stronger for larger tails. Consequently, solitary waves or travelling breather with minimal tail are good candidates to approximate (dispersive) ‘attractors’ forming after excitation of a single lattice site, which display a small oscillatory tail at the rear of the pulse and decay to 0 at the front.

Another interesting theoretical problem concerns the analysis of localized waves in the limit . When p is large but finite in (1.4), it would be interesting to prove the existence of exact solitary waves close to the approximate solutions obtained in the present study, and to approximate the time-evolution of general classes of initial conditions. Results in this direction have been obtained for some classes of nonlinear wave equations [70] and nonlinear diffusion equations (see [71] and references therein), but to the best of our knowledge there is currently no rigorous theory available for discrete NLS-type systems.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

The author thanks the PAZI Fund (Israel Atomic Energy Commission) (grant no. 263/15) for financial support.