Nonlinear couplings and energy transfers in micro- and nano-mechanical resonators: intermodal coupling, internal resonance and synchronization

Abstract

Extensive development of micro/nano-electromechanical systems (MEMS/NEMS) has resulted in technologies that exhibit excellent performance over a wide range of applications in both applied (e.g. sensing, imaging, timing and signal processing) and fundamental sciences (e.g. quantum-level problems). Many of these outstanding applications benefit from resonance phenomena by employing micro/nanoscale mechanical resonators often fabricated into a beam-, membrane- or plate-type structure. During the early development stage, one of the vibrational modes (typically the fundamental mode) of a resonator is considered in the design and application. In the past decade, however, there has been a growing interest in using more than one vibrational mode for the enhanced functionality of MEMS/NEMS. In this paper, we review recent research efforts to investigate the nonlinear coupling and energy transfers between multiple modes in micro/nano-mechanical resonators, focusing especially on intermodal coupling, internal resonance and synchronization.

This article is part of the theme issue ‘Nonlinear energy transfer in dynamical and acoustical systems’.

1. Introduction

Advances in micro-scale fabrication techniques have led to the extensive development of micro/nano-electromechanical systems (MEMS/NEMS) by enabling the integration of sophisticated mechanical and electrical elements into miniaturized devices. Their compact dimensions, immense flexibility in materials and designs, and inherent multiphysical nature allow these devices to exhibit remarkable attributes for various applications with ultralow power consumption. Their performance largely depends on the functionality of the mechanical components, which are often designed to exhibit mechanical motion at or near their resonant frequencies. The high structural quality combined with the reduced effective mass allows such mechanical resonators to operate at very high resonant frequencies and with extremely high Q factors (i.e. low damping). These beneficial characteristics provide a basis for exceptional performance in resonator-based MEMS/NEMS applications. Examples include extremely sensitive sensors, mechanical energy harvesters [1], high-frequency radio-frequency (RF) electronic components [2,3], micro/nano-relays [4,5] and field effect transistors [6,7].

For most micro/nano-mechanical resonators, one of the vibrational modes is used to fulfil their design purpose in their applications. For instance, MEMS/NEMS resonant sensors monitor the changes in frequency or amplitude of one of the resonant modes caused by an external mass/force perturbation to the resonator. In this case, the actuated resonant mode is modelled as a single degree of freedom (SDOF) harmonic oscillator either by considering a lumped model or by applying model reduction to a continuous system equation (e.g. Euler–Bernoulli beam). In the past decades, however, there has been a growing interest in exploiting rich dynamic features for use in practical MEMS/NEMS applications because the matured fabrication technology and transduction schemes allow considerable opportunities to realize, tailor and exploit their rich dynamic behaviour. One of the main areas of interest is exploiting the nonlinear features originating from various sources in MEMS/NEMS devices. These include geometric nonlinearity, nonlinear external potential, nonlinear damping and inertial nonlinearity, all of which are well explained in previous reviews [8–12].

More recently, there has been an increasing interest in exploring multiple modes via modal coupling. Multimodal functionality of MEMS/NEMS can be achieved either by coupling two or more mechanical resonators via electrostatic, optical and mechanical forces or by nonlinearly coupling two or more vibrational modes within a unitary resonator. In a linear context, coupling two mechanical resonators via an elastic spring has been common in the designs of MEMS filters [13–16] and inertial sensors [17–19] from the early development stage. For mass sensing, multimode measurements of a resonator or coupled resonators have become a new paradigm to improve sensitivity and accuracy [20–23]. As a turning point, in the early 2000s, complex nonlinear dynamics characterized in an electrostatically coupled microbeam array [24] and intrinsic mode localization observed in a microcantilever array mechanically coupled via a common overhang [25,26] have drawn attention and motivated theoretical and experimental works in the field. To achieve a coherent response from these micro/nano-array systems, investigation of the synchronization of mechanical oscillators has also been initiated. Hence, modal coupling has become an important issue in the design and analysis of MEMS/NEMS, where appropriate engineering of the modal coupling mechanisms leads to unprecedented rich nonlinear features that open up new windows to deal with fundamental quantum, transduction and design problems. At the same time, internal resonance, achieved by enforcing an integral frequency ratio between the coupled modes, has also attracted significant interest as a mechanism to promote stronger coupling and energy transfer.

Hence, we aim to provide a review of previous and ongoing research efforts related to nonlinear interactions between resonance modes in micro- and nano-mechanical resonators. The nonlinear nature of mode coupling induces various interesting phenomena, and this review mainly focuses on (i) nonlinear intermodal coupling within a mechanical resonator, (ii) internal resonance and its applications and (iii) phase synchronization in mechanical oscillators.

2. Nonlinear intermodal coupling

While a micro/nano-mechanical resonator is often modelled as a SDOF oscillator when one of the modes is driven, there theoretically exist an infinite number of vibrational modes in a continuous system. When two or more of these modes are excited simultaneously in a nonlinear resonator, the single resonator system should be modelled as multi-DOF (MDOF) oscillators coupled with each other while the engaged modes are internally coupled; this is called (nonlinear) intermodal coupling. The most common type of micro/nanostructures that have been used to study nonlinear intermodal interactions are beams, tubes, membranes and discs with all boundaries fixed to an anchor. These devices are suitable to trigger nonlinear intermodal interactions between two or more vibrational modes via the displacement-induced tension in the structure. This mechanism is similar to the tension-induced hardening behaviours commonly modelled by a Duffing equation for a SDOF system. Even in an inextensional structure such as a cantilever with one free end, the nonlinear modal interaction can still originate from curvature and inertia nonlinearities [27,28]. Dissipative coupling is another mechanism that has been suggested to couple vibrational modes in a fixed–fixed beam incorporating a nanoscale beam attachment [29,30]. In all these cases, the intermodal interaction modifies the damping and/or stiffness of the modal response. The coupled equations of motion to describe a mechanical resonator eliciting two modal responses can be generalized as follows:

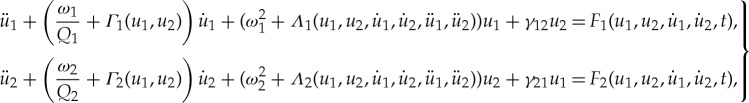2.1

where 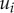is modal coordinate; ω_i and Q_i are linear resonant frequency and quality factor, describing the linear dynamic aspects of each mode; 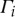and 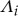are the terms manifesting nonlinearity in the global dynamic response by modulating the modal damping, stiffness and inertia with respect to the dynamic motions of elicited modes, whereas γ₁₂ and γ₂₁ are the linear coupling coefficients. Note that the functions of 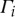and 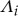can induce nonlinearity by the amplitude and velocity of both their own mode and another mode when coupled. For example, 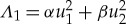brings about cubic nonlinear stiffness and coupling terms (i.e. 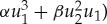in the first modal equation in (2.1). The geometry, material, boundary conditions and transduction schemes should determine the types of these functions and coupling coefficients to alter the global nonlinear dynamics of the resonator with nonlinear intermodal interactions. Generally, when two vibrational modes are actuated simultaneously, the nonlinear modal interaction should affect the modal resonant behaviour by altering the resonance frequency and/or Q factor.

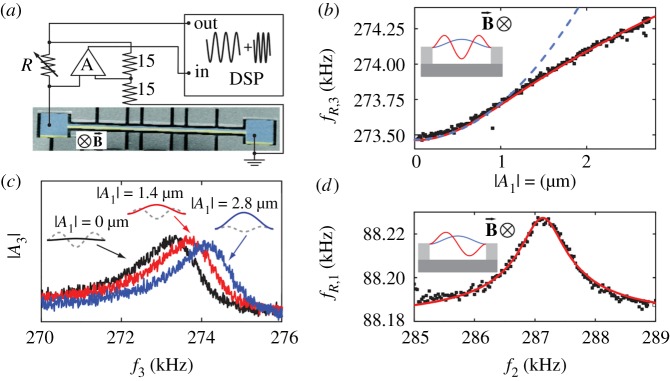
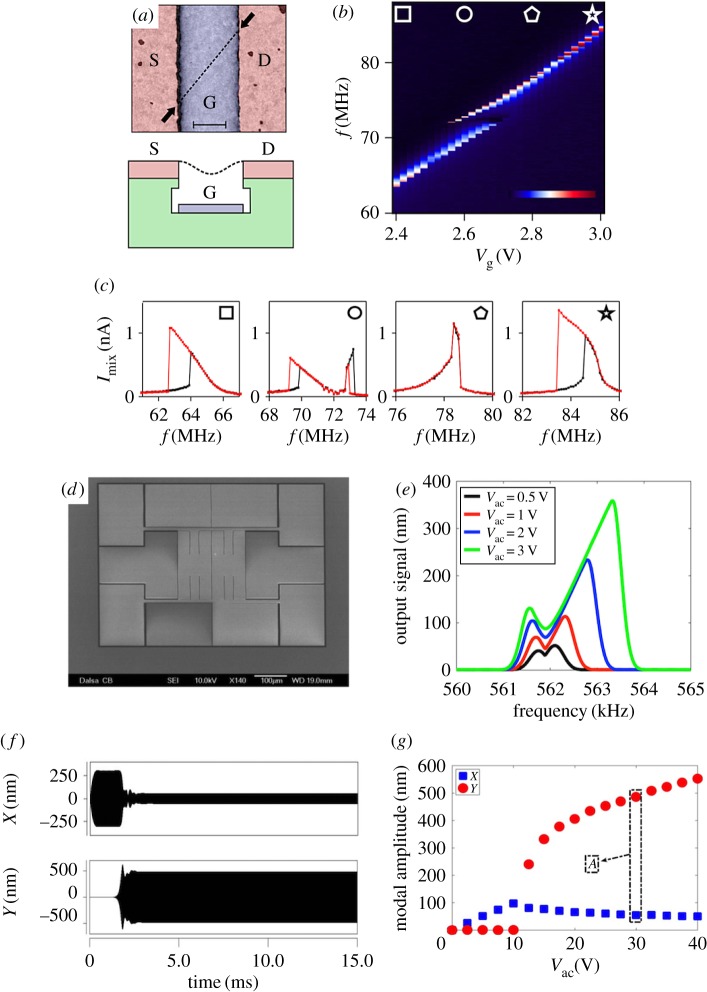
Baskaran et al. [31] reported one of the earliest works experimentally observing modal coupling in a torsional oscillator in 2003. The device showed non-degenerate parametric coupling between the torsional modes as it was electrostatically excited at the sum of the first and second modes. For the directly excited intermodal coupling, Westra et al. [32] reported the detailed experimental characterization of intermodal coupling in a microresonator in 2010. A single-crystalline silicon beam with both ends fixed, shown in figure 1a, was driven at two frequencies near the first and third flexural mode, and its dynamics were monitored at each mode. Figure 1b,c show that the resonance frequency of the third mode increases with respect to the amplitude of the first modes. By using the modal interaction, the second mode resonance can be detected by monitoring the frequency shift in the first resonance frequency as shown in figure 1d. Such a resonance detection scheme exploiting the intermodal interaction has also been used in later works [33–35]. In these works, the intermodal coupling was used as a tool to obtain the spectrum of a mechanical structure by monitoring the first mode frequency shift using a phase-locked loop, while an auxiliary drive signal scanned for other (higher) modes. This mechanism was also suggested to fulfil a quantum nondemolition measurement of the excitation level by measuring the phase shift of the ancilla oscillation that is internally coupled to the excitation mode [36].

Figure 1.

Modal interaction in a doubly clamped microbeam [32]. (a) Experimental set-up, with a coloured SEM image of the resonator beam. (b) Larger amplitude oscillations in the first mode (A₁) increase the resonant frequency of mode 3. (c) The resonance frequency of mode 3 is increased by an increase in the first mode amplitude (A₁). (d) The resonance of the second mode can be detected by monitoring the shift in the first resonance frequency. (Online version in colour.)

The simplest modelling approach has been proposed in [37], with a solely linear coupling term where DC bias voltage is used to couple two orthogonal in-plane and out-of-plane modes of a silicon nitride string. The authors further studied diabatic to adiabatic transitions between the two modes in the region of strong coupling. In Truitt et al. [38], the mechanism of linear and nonlinear coupling was investigated in a clamped–clamped nanobeam driven electrostatically. Here, the nonlinear coupling was again induced by the displacement-dependent tension to result in a frequency shift. The authors also found that the electrostatic tuning enabled the degenerate modes elicited with linear coupling, which led to natural frequency veering (i.e. an avoided crossing of the resonant frequencies). Quadratic coupling can also arise in circular membrane resonators [39,40] or when there is a static deflection in the system [41]. To characterize the accurate intermodal coupling experimentally, Matheny et al. [42] proposed an experimental protocol enforcing a highly linear transduction scheme.

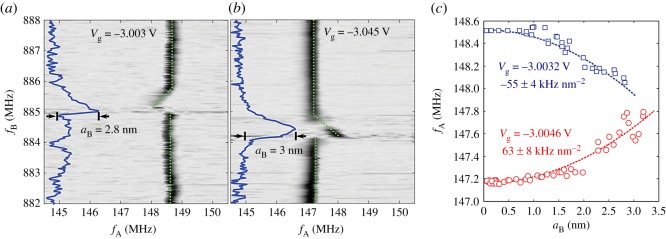
In later works by Castellanos-Gomez et al. [28], it was shown that the mechanism of the intermodal interaction can be different in a carbon nanotube (CNT) resonator. Compared to the silicon systems in which modal coupling is dominated by displacement-induced tension and results in stiffness-hardening effects only, the single-electron tunnelling in a CNT provides a coupling between the modes six orders of magnitude stronger. Hence, by controlling an external gate voltage, the coupling can be tailored to be stiffness softening or stiffness hardening, as shown in figure 2. Moreover, the high-frequency tunability and capacity to sustain the large strains achievable in CNT and graphene resonators make them ideal for investigating the nonlinear phenomena related to tunable intermodal coupling [40,41,43]. Modal coupling has also been reported to exist between planar and whirling modes in a fixed–fixed CNT [44] and between flexural modes in a fixed–free CNT [45]. The coupled mode can confine the amplitude of the self-resonating oscillator via the mechanism of modal energy transfer.

Figure 2.

Modal interaction in a carbon nanotube resonator [28]. (a) The resonant frequency of mode A shifts to lower frequencies when the RF signal of the second generator hits the resonance frequency of mode B. (b) At slightly higher gate voltage, the trend changes and modal interaction increases the resonant frequency of mode A. (c) Depending on the gate voltage, the intermodal coupling can induce either stiffness-softening or stiffness-hardening effect. (Online version in colour.)

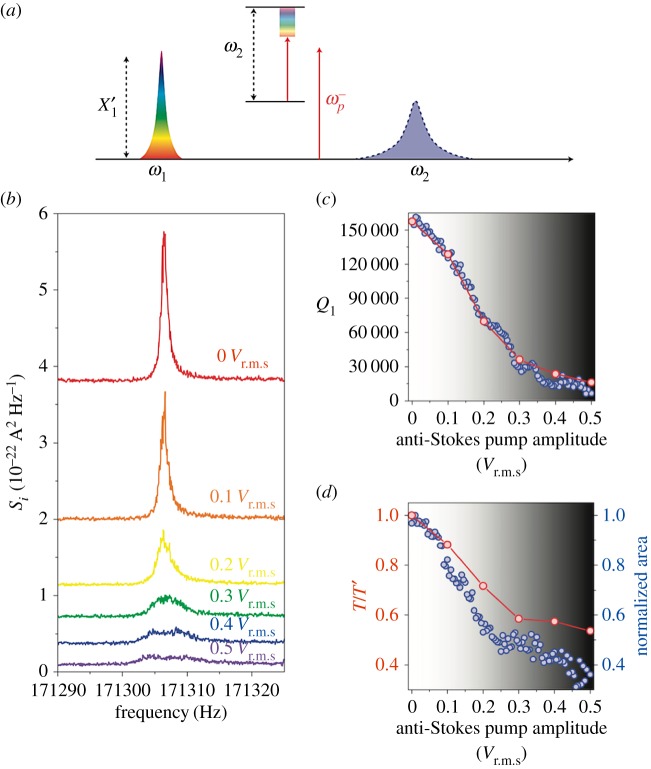
Intermodal coupling is also exploited as a mechanism to tune the dissipation of mechanical modes [27,40,43,46–48]. In these works, the internally coupled secondary mode is considered to be a mechanical (phonon) cavity as a counterpart of a photon cavity in cavity optomechanics [49]. Just as is achieved in cavity optomechanical systems, the mechanical sideband excitation enables control of the Q factor and the achievement of a mechanically induced transparency, as illustrated in figure 3.

Figure 3.

Cooling the fundamental mode through a phonon cavity [46]. (a) Energy in the first mode can be transferred to the phonon cavity by pumping energy in the anti-Stokes sideband frequency. (b) Higher level of pumping drains more energy from the first mode. (c=d) At higher anti-Stokes pumping levels, almost all the displacement energy is transferred to the phonon cavity, resulting in the quality fraction Q₁ and temperature T of the first mode reducing. (Online version in colour.)

3. Internal resonance

The nonlinear coupling and associated nonlinear energy transfer become stronger when the engaged modes are commensurate or nearly commensurate with an integer frequency ratio [50], which is called internal resonance or autoparametric resonance. When internally coupled modes operate at well-separated and non-commensurate frequencies, the effect of coupling is rather modest compared with the case of internal resonance, in which the global dynamics and resonance curve can be completely altered. One of the interesting features enabled by internal resonance is the amplitude saturation phenomenon: above a threshold force triggering strong nonlinear modal coupling, the energy pumped in the driven mode is transferred into the undriven, internally resonated mode, and then the amplitude of the driven mode is saturated to be constant.

To implement internal resonance in a device, a careful structural design is typically required to enforce an integral ratio between mode frequencies. In micro/nano-systems, however, the attributes of frequency tunability, highly nonlinear coupling and low damping make achievement of internal resonance relatively feasible. For example, Younis & Nayfeh analytically investigated the possibility of activating a 3 : 1 internal resonance in an electrostatically driven microbeam resonator as the mode frequencies are varied by the applied DC voltage [51]. In a recent study by Li et al. [52], the internal resonance in a similar system was more thoroughly investigated based on the method of multiple scales to describe the resonance curves, nonlinear energy transfer and vibration profile curves. The authors also performed Hopf bifurcation analysis to determine the effect of frequency detuning and electrostatic force level on the strength of the modal coupling. Motivated by the experimental study of the aforementioned microarrays, nonlinear internal resonance of a microbeam array was also studied analytically [53–55]. Another analytical study was conducted by Vyas et al. [56–59], and the authors suggested a unique T-beam structure to explore the characteristic features of internal resonance for MEMS applications. This approach was extended to a hyperelastic plate with material nonlinearity [60]. More recent analytical investigations of internal resonance are found in [61–64].

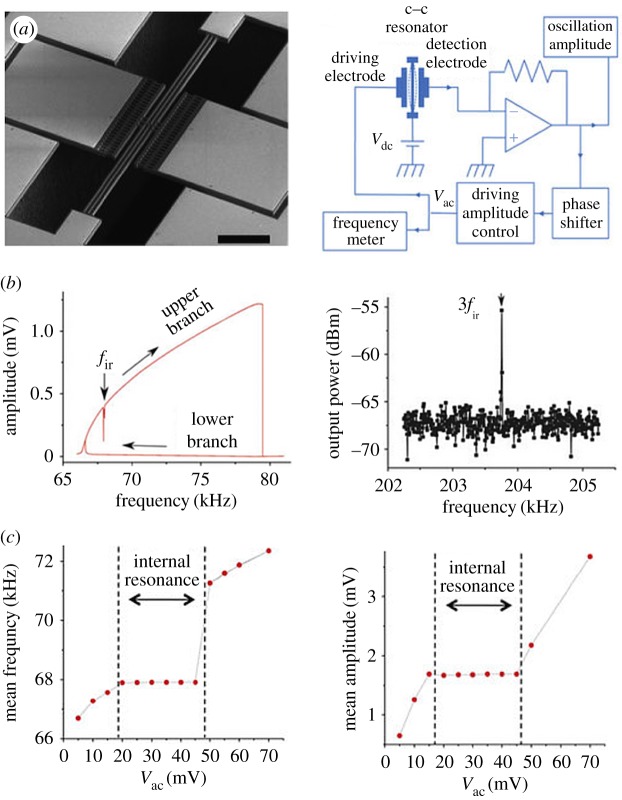
While many theoretical investigations about internal resonance thrived in the 2000s, experimental realization and applications matured starting in the early 2010s. To the best of the authors’ knowledge, Antonio et al. [65] first reported on the internal resonance encountered in a beam resonator, in which the third mode frequency happened to be near three times the first mode frequency. Given the nonlinear energy transfer via internal coupling between these two modes, the authors exploited internal resonance as a mechanism to stabilize the frequency in a MEMS oscillator, as illustrated in figure 4. The hardening nonlinear resonance curve of the first mode in figure 4b shows a sharp dip at the frequency of f_ir, where the internal resonance occurs. At this internal resonance condition, the higher-frequency mode drains mechanical energy from the first mode to drop its modal amplitude while generating a higher-frequency peak at 3f_ir. By using the nonlinear energy mechanism, the output frequency of a MEMS oscillator based on this resonator was stabilized within the range over which the internal resonance condition was satisfied (cf figure 4c). In another work by Kirkendall et al. in 2013 [66], a similar sharp dip in the resonance response of a quartz crystal was observed due to 1 : 1 modal coupling. In a more recent work from the same group [63], rich multistability and dynamic bifurcations were observed in experimentally measured reflection parameters in an electroelastic crystal plate due to a 1 : 3 internal resonance. The authors investigated the effect of frequency sweep rate on the resulting nonlinear dynamics, and interestingly, their experiments were able to capture drastic changes of response with respect to the sweep rate.

Figure 4.

Frequency stabilization via the mechanism of internal resonance [65]. (a) A microbeam resonator and circuit schematic to fulfil a MEMS oscillator. (b) Resonance curve of the first mode with a sharp dip in the upper branch of the amplitude curve at f_ir, because part of the mechanical energy of the first mode is transferred to a higher-frequency mode via the mechanism of internal resonance. Accordingly, the resonance of the higher-frequency mode at 3f_ir produces a peak in the output power spectrum. (c) Mean frequency and amplitude of the MEMS oscillatior. The frequency (amplitude) versus driving amplitude curve flattens when the internal resonance condition is reached. (Online version in colour.)

At about the same time and thereafter, internal resonance was also observed in nano-mechanical systems based on novel nanomaterials such as CNT [41], graphene [40] and MoS₂ [67]. Because the mode frequency of nanomaterials is highly tunable, the internal resonance condition of an integer frequency ratio between modes is more possibly satisfied within the tunable frequency range, as seen in figure 5a–c. While the resonance frequency was tuned from 62 to 84 MHz by varying the gate voltage, the M-shape of frequency response, which is characteristic for internal resonance, was observed around 70 MHz. In micro-scale devices, a careful optimization to satisfy the commensurate condition was applied to design an H-shape resonator incorporating 1 : 2 internal resonance [68,69]. The experimental characterization of these systems has clearly shown the characteristic dynamic features due to internal resonance, exotic M-shaped resonance curve, nonlinear energy transfer and amplitude saturation, as illustrated in figure 5d–f. Autoparametric amplification was also reported in a micromechanical disc resonator due to internal resonance between the degenerate vibrational modes, when the frequencies of these modes are electrostatically tuned to match perfectly [70].

Figure 5.

(a–c) Internal resonance in a carbon nanotube (CNT) resonator [41]. (a) The coloured SEM image of the suspended CNT with the schematic side view of the system on the bottom. (b) Contour map of the resonant frequency as a function of gate voltage reaveals high-frequency tunability of CNT. (c) Frequency response plots at increasing gate voltages from left to right while AC voltages in gate and source electrodes are kept constant. The characteristic M-shaped resonance is observed when internal resonance is activated (symbol ○). (d–g) 2 : 1 internal resonance in an H-shaped resonator [68]. (d) SEM image of the H-shaped resonator with actuation and detection electrodes. (e) Experimental internal resonance curve at increasing forcing level. (f) Simulation results show the energy transfer between the two coordinate displacements, X and Y, due to internal resonance. (g) Amplitude saturation in the driven mode when internal resonance is triggered. (Online version in colour.)

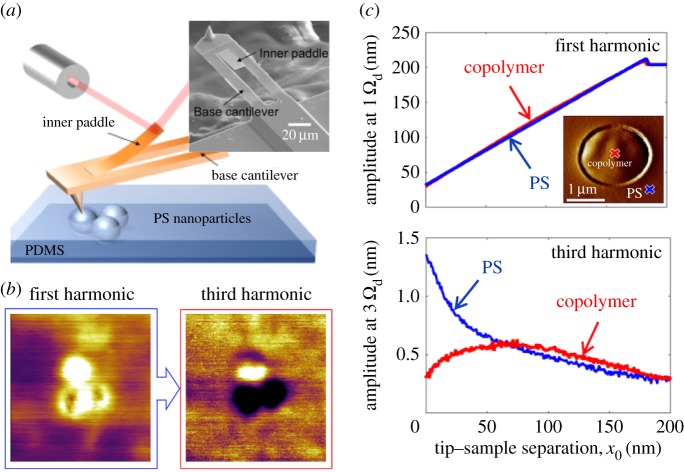
Internal resonance has also been exploited in a microcantilever design to achieve multifrequency atomic force microscopy (AFM) [71–76]. Various schemes of multifrequency AFM have been developed to characterize a sample beyond topography [22]. For bimodal AFM, one of the representative multifrequency techniques, two modes of a microcantilever are excited and detected to measure the topography and material compositional map simultaneously [77,78]. Recent works, however, have shown that a microcantilever specifically designed to realize internal resonance can trigger two modes even with single-frequency excitation. Specifically, in [73–76], a microcantilever was designed with an inner paddle, as shown in figure 6, so that the linearized frequencies of the leading bending modes of the base cantilever and the inner paddle are in a 1 : n rational relationship. When nonlinearity is included in the dynamics through the strong non-smooth nonlinear tip–sample interactions generated during the AFM tapping operation, a strong nth harmonic component is passively triggered in the response of the paddle via the internal resonance mechanism. Through detailed experimental and theoretical study, the efficacy of the cantilever design was demonstrated to show that the nth harmonic signal amplified through internal resonance provides stronger sensitivity to material composition compared with the first harmonic signal.

Figure 6.

Multi-frequency atomic force microscopy realized by a new micro-cantilever design using internal resonance. (a) The inner paddle attached to the base cantilever is designed to exhibit 1 : 3 internal resonance with nonlinear tip–sample interaction. (b)The third harmonic signal amplified by internal resonance is sensitive to material stiffness. (c) Experimental sensitivity curves of first and third harmonics show that the third harmonic is sensitive to the material composition compared with the first harmonic [73,75]. (Online version in colour.)

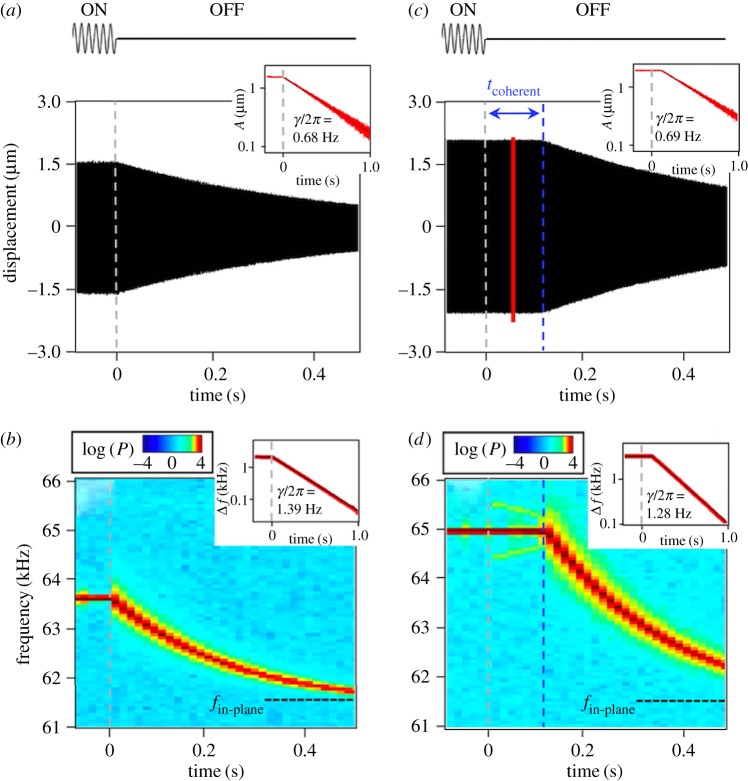
Even more interestingly, the mechanism of internal resonance provides a unique pathway to transfer the energy internally between the modes, which potentially suggests novel dissipation engineering strategies. In the work of Chen et al. [79], the coherent energy transfer was demonstrated in a clamped–clamped beam with 1 : 3 mode coupling as illustrated in figure 7. When the input energy to the lower mode of the system is switched off, the higher mode coherently transfers the energy back to the lower mode, instead of dissipating it to the environment, so that the amplitude of the lower mode remains constant for a period of time until the energy of the higher mode is exhausted. This occurs because the rate of energy exchange between the nonlinearly coupled modes is orders of magnitude faster than the energy exchange from extrinsic sources. In the same context, it was theoretically shown in [80] that the decay of vibrational modes becomes strongly non-exponential and depends on the vibration amplitude, whereas the higher mode acts as a thermal reservoir to the lower mode.

Figure 7.

Coherent energy transfer between coupled mechanical modes by internal resonance [79]: the ring down response is shown when the external drive is turned off at time equals 0, when the internal resonance condition is unsatisfied in (a,b) and satisfied (c,d). The oscillation amplitude of the in-plane mode and its temporal frequency response are plotted in (a,c) and (b,d), respectively. Through the mechanism of internal resonance in (c,d), the coherent energy transfer happens for approximately 108 ms after the ring down starts to maintain the envelope of the oscillation constant. (Online version in colour.)

4. Synchronization

Synchronization is defined as self-tuning rhythms of oscillation patterns in the wake of weak coupling between oscillators, and it is sometimes used interchangeably with frequency locking or phase locking. Exploitation of this behaviour is suggested for a number of applications, such as signal processing, timing, computing and networking, because a coherent response can be enforced in multiple oscillators. One of the early research interests in synchronization in MEMS/NEMS is Hoppensteadt [81], in which the possibility of using networks of coupled oscillators as data storage systems was theoretically investigated. Later works by Cross et al. [82,83] also analytically modelled synchronization induced by nonlinear frequency pulling in a system with reactive coupling to study the onset of synchronization and regions where full synchronization occurs. Other works subsequently investigated enhanced frequency precision achieved by synchronization [84]. Sahai et al. [85] employed dome-shaped oscillators as a specific example to study the design parameters in which synchronization is implemented in two slightly detuned oscillators. Most of the research conducted in the 2000s explored the analytical aspects of the synchronization phenomena.

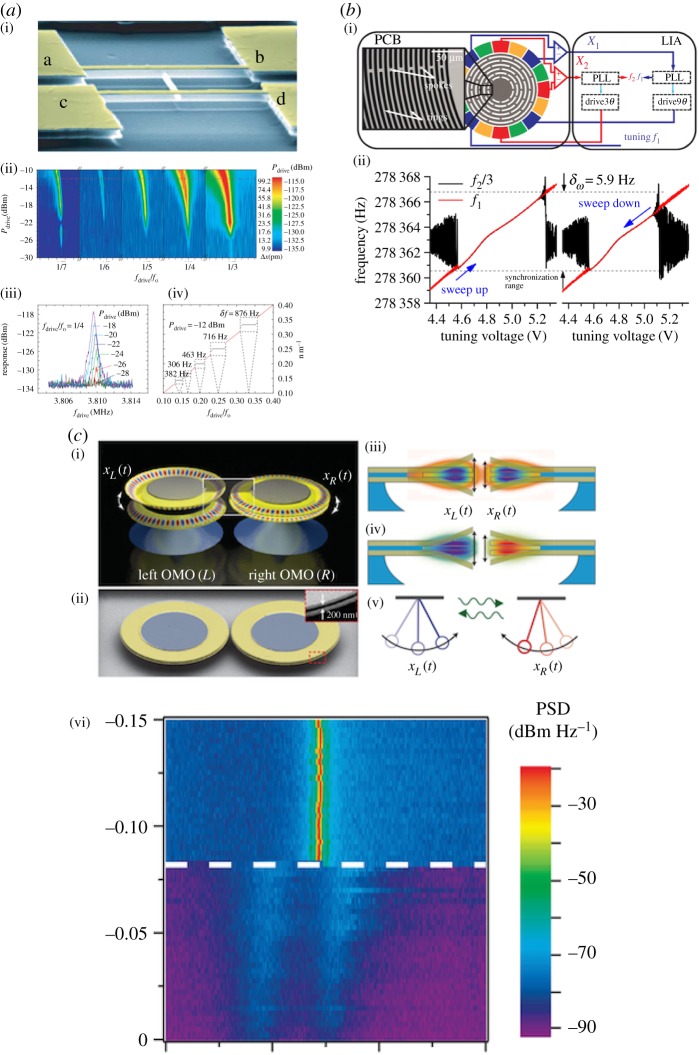
In an experimental context, Shim et al. [86] reported one of the earliest experimental works in the MEMS/NEMS field, achieving synchronization in a system of two microbeams mechanically coupled by an elastic spring (cf. figure 8a). They excited one of two beams at different subharmonic and superharmonic frequencies of the resonant mode and monitored the frequency content of the second beam. The multiple regions of frequency entrainment were represented graphically by characteristic Arnold's tongues and devil's staircase at different subharmonics of the fundamental frequency. Agrawal et al. [90,91] investigated the mutual synchronization in electrically coupled oscillators based on the double-end tuning forks resonator and discussed the dependence of the locking range on system parameters such as amplitude, cubic nonlinearity and coupling strength. Their experimental results showed a clear enhancement of synchronization range with an increase in feedback voltage, which was related to amplitude–frequency dependence with cubic nonlinearity. Such enhancement of synchronization by nonlinearity was also confirmed in other works [87,92,93]. One of the obvious beneficial features of the synchronized state is the improvement of frequency stability and reduction of phase noise, commonly reported in most of these synchronized systems. More examples are found in [94–96].

Figure 8.

Experimental realization of synchronization. (a) Phase synchronization in a mechanically coupled pair of doubly clamped beams [87]. One beam is excited at different orders of subharmonics of fundamental resonance and the second beam response content around the first mode is recorded which gives Arnold's tongues. Different ranges of entrainment are shown in devil's staircase plot. (b) Phase synchronization in a micro disc having a 3 : 1 subharmonic frequency relationship [88]. Synchronization range measured for upwards and downwards frequency sweeps. (c) Phase synchronization using light [89]. Optically coupled optomechanical systems can synchronize their mechanical oscillations when the input optical power is sufficient. The bottom contour map (the frequency spectrum with respect to the relative laser frequency on y-axis and the oscillator frequency on x-axis) shows that the two self-sustained oscillators with a mismatched frequency (below the white line) get synchronized (above the white line). (Online version in colour.)

Synchronization has also been suggested to improve the performance of gyroscopes [70,88]. Experiments were performed on a silicon disc oscillator and its phase synchronization was demonstrated. The lower mode frequency was controlled by the internally resonated higher mode as illustrated in figure 8b. The measurements showed that synchronization range increases as the first mode amplitude increases, but the reverse occurs when the second mode amplitude goes up. The authors also characterized three different operational schemes of synchronization to investigate its impact on the performance of gyroscopes and concluded that frequency stability is enhanced at the expense of amplitude fluctuations. The authors also studied a silicon quad-mass resonator excited and characterized using capacitive forcing and sensing [97]. They measured the frequency responses at different bias voltages and observed hardening (with third-order nonlinearity), hardening-to-softening transition (combined third- and fifth-order nonlinearity) and softening (with fifth-order nonlinearity) as bias voltage increased. Accordingly, monolithic increase in synchronization range was observed when the response was purely hardening or softening, but in the transition response, the synchronization range first decreased and then started to increase.

Optomechanical oscillators are a broad research area where coupling through the concept of optomechanics offers advantages such as achieving strong, controllable coupling with less optical loss, and the possibility of implementing to different complex geometries and physical sizes. While this area itself is not highly correlated to the subject of this review, mainly considering mechanical oscillators, it is worth noting that the optical coupling between mechanical oscillators is another mechanism to induce synchronization. Optically coupled optomechanical oscillators (cf figure 8c) in which coupling is achieved through an optical cavity radiation field have been shown to be a unique platform to study synchronization of mechanical oscillators [89,98]. The onset of synchronization between two mechanical oscillators or oscillator arrays was experimentally realized by varying the laser pump power. Furthermore, it was shown that the phase noise in synchronized signals can drop below the thermomechanical noise limit of a single oscillator. Synchronization enabled by optical cavity coupling has been also applied in other geometries, such as a pair of microbeams [99] and nano-membranes [100].

5. Conclusion

Exploring the rich dynamics and energy transfers uniquely enabled by nonlinearity has been a long-time research and engineering topic over a broad spectrum of scientific and technological areas. MEMS/NEMS have realized various types of nonlinear behaviours, either intentionally or inadvertently. Given the liberal flexibility in the fabrication and materials, micro/nano-mechanical resonators have also presented an ideal testbed to study the fundamental aspect of nonlinear resonance and quantum-level problems. At the same time, the explored nonlinear dynamic features can be widely implemented in resonator-based MEMS/NEMS applications to expand functionality and improve performance.

While the understanding and exploitation of the primary hardening/softening resonance and parametric resonance in micro/nano-systems has matured over the last three decades, the nonlinear energy transfers in micro/nano-mechanical resonators with modal coupling are in the early stage of exploration for potential MEMS/NEMS applications. This is largely because primary nonlinear and parametric resonance has been routinely observed in MEMS/NEMS due to geometric nonlinearity and time-varying electrostatic forces, whereas the multimodal operation requires a careful design of systems and experiments. Regardless of nonlinear resonance types, the constructive utilization of nonlinear phenomena and energy transfers can provide diverse pathways to develop new applications and technologies related to MEMS/NEMS, as reviewed in this paper. With the ability to tailor and optimize targeted nonlinear behaviour based on a firm fundamental understanding of nonlinear systems, MEMS/NEMS will continue to revolutionize science and technology.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This work was financially supported in part by Defense Advanced Research Projects Agency (Young Faculty Award D16AP00110).