Tunable, synchronized frequency down-conversion in magnetic lattices with defects

Abstract

We study frequency conversion in nonlinear mechanical lattices, focusing on a chain of magnets as a model system. We show that, by inserting mass defects at suitable locations, we can introduce localized vibrational modes that nonlinearly couple to extended lattice modes. The nonlinear interaction introduces an energy transfer from the high-frequency localized modes to a low-frequency extended mode. This system is capable of autonomously converting energy between highly tunable input and output frequencies, which need not be related by integer harmonic or subharmonic ratios. It is also capable of obtaining energy from multiple sources at different frequencies with a tunable output phase, due to the defect synchronization provided by the extended mode. Our lattice is a purely mechanical analogue of an opto-mechanical system, where the localized modes play the role of the electromagnetic field and the extended mode plays the role of the mechanical degree of freedom.

This article is part of the theme issue ‘Nonlinear energy transfer in dynamical and acoustical systems’.

1. Introduction

Frequency converting processes have applications in a variety of problems, for example in obtaining different wavelengths from a fixed-frequency laser [1], harvesting energy from vibration sources [2] and generating entangled photons [3]. Typically, frequency conversion is accomplished through wave mixing [4] (which requires at least two input signals with a prescribed frequency difference), harmonic generation [1] (which produces an output that is a multiple of the input signal) and subharmonic bifurcations [5] (which produce an output that is an integer fraction of the original signal). In addition, these frequency conversion mechanisms prescribe the output's signal phase, which hinders the process of harvesting energy from multiple sources. Combination resonances [6]—processes that arise in the presence of multiple nonlinearly interacting modes—can achieve frequency down-conversion between arbitrary input and output signals not related by harmonic or subharmonic ratios. The resulting input and output frequencies can be tuned by adjusting the modes' frequencies. Combinational resonances can be found, for example, in vibrating beams [7], membranes and plates [8].

In this paper, we show that nonlinear lattices have the potential to act as frequency-converting devices, due to the combination resonances arising from the nonlinear interaction between the lattice's normal modes. Chains of nonlinearly interacting elements have been studied for decades, beginning in the Fermi–Pasta–Ulam problem [9,10]. They present a wide variety of phenomena, including solitons [11,12], band gaps [13], energy trapping [14], breathers [15,16], unidirectional wave propagation [17], negative or extreme stiffness [18], localized modes with tunable profile [19], shocks and rarefaction waves [20]. These phenomena can be used to realize acoustic rectifiers [17], logic gates [21], lenses [22], filters [23], vibration attenuation [24] and energy-harvesting systems [16]. Nonlinear lattices can be implemented using a broad range of materials [25], geometries [26] and interactions [27], allowing the masses, coupling strengths and damping values of the particles to be tuned to optimize the performance under the required operating conditions. Because of this tunability, nonlinear metamaterials are promising candidates for energy-converting devices.

2. Experimental system

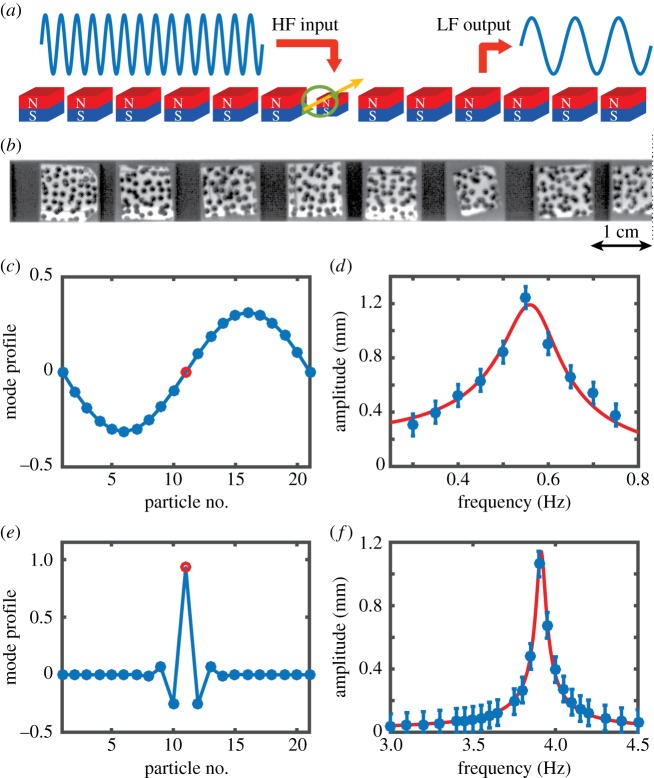
Our experimental set-up consists of a chain of magnets [27] floating on an air table (figure 1a,b). Each magnet is embedded in a three-dimensional (3D) printed case that adds an additional mass, with different case designs resulting in different particle masses (m = 0.45 g for the non-defect particles, m_D1 = 0.197 g for the first defect and m_D2 = 0.244 g for the second defect). Owing to its periodic nature, the lattice presents extended mechanical resonances (figure 1c,d). The presence of defects introduces localized modes around each defect particle (figure 1e,f). When these modes are excited, the resulting motion is exponentially localized around the defect. In our experimental set-up, the defects act as inputs for the frequency conversion system. We excite them by passing current through a small conductive wire normal to the length of the chain (figure 1a). The wire is driven harmonically with a signal generator (Agilent 33220A) amplified by an audio amplifier (Topping TP22, class D). An extended mode of vibration (figure 1c,d) interacts with the localized mode to introduce frequency conversion. We monitor the motion of the magnets using a computer vision camera (Point Grey GS3-U3-41C6C-C), with a frame rate between 40 and 200 fps that allows us to resolve all particles' motion. We use the software VIC-2D from correlated solutions to track the particles and determine their trajectory.

Figure 1.

Frequency-converting metamaterial concept. (a) Metamaterial design, consisting of a chain of nonlinearly interacting magnets. The central particle of the chain is a defect, which has a lower mass. This magnet acts as the high-frequency (HF) input to the system. The down-converted energy can be extracted far away from the defect. In our experiments, the defect is driven by a wire carrying an electrical current (yellow arrow). LF, low frequency. (b) Cropped image of the experimental magnet chain, obtained using the same computer vision camera that is also used to track the magnet positions. Each magnet is enclosed in a three-dimensional printed case, and has a random speckle pattern to facilitate its tracking by digital image correlation. (c) Extended mode of vibration. The red hollow circle is the defect particle, while the blue solid dots represent the other particles. (d) Experimental frequency response of the extended mode (blue dots) and Lorentzian fit (red solid line). (e) Localized mode of vibration. (f) Experimental frequency response of the localized mode (blue dots) and Lorentzian fit (red solid line). (Online version in colour.)

3. Experimental results for the system with a single defect

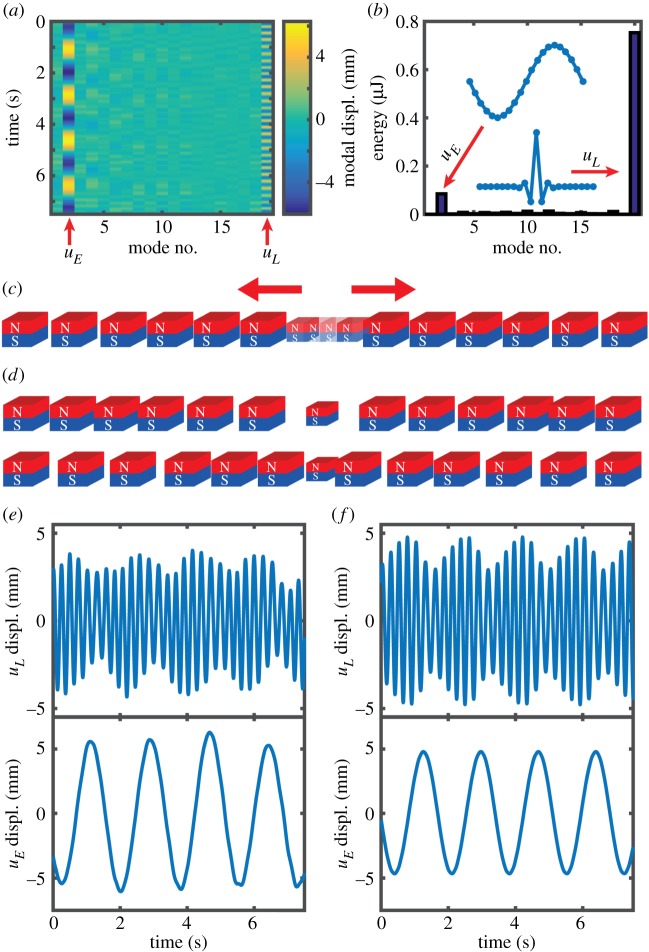
We start by studying a lattice of 21 magnets containing a single defect (m_D1 = 0.197 g) in the middle position (i = 11). The first and last magnets are fixed. We set the excitation frequency to approximately the sum of the defect's frequency (figure 1f) and the extended mode's frequency (figure 1d), with the goal of exciting a combinational resonance (ω_E + ω_L) between the extended and localized modes [6]. We slowly increase the excitation amplitude until a threshold is reached and self-sustaining oscillations develop far away from the defect, indicating the transfer of energy between the localized mode and an extended mode (figure 2a). In this regime, the defect motion is modulated by the extended mode (figure 2b). Owing to the exponential localization of the defect's motion, the Fourier transform far from the defect particle's displacement (figure 2c) does not reveal significant motion at the input frequency, and consists almost exclusively of down-converted energy. The frequency conversion efficiency, defined as the energy transferred to the extended mode in comparison with the energy input into the system 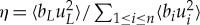, equals 10.8 ± 0.9%. (Here b_i and u_i are modal masses and displacements, respectively, which will be determined from the magnetic particle's equations of motion in the Theoretical model section.) This efficiency arises from our particular system parameters and is not an absolute limit.

Figure 2.

Experimental response of the system under harmonic excitation. (a) Position of the magnets as a function of time. The red dotted line corresponds to the defect magnet, which acts as the input to the frequency-converting system. The green dashed line is taken as the output of the system. (b) Fourier transform of the defect magnet's position, which is modulated at the extended mode's frequency. The vertical dotted line represents the excitation frequency. (c) Fourier transform of the output magnet's position. This magnet's motion happens primarily at the second extended mode's frequency. (Online version in colour.)

4. Theoretical model

Our theoretical model describes the magnets as point masses. We model the interaction between particles using an empirical power-law model, F(d) = Ad^B, with A = 3.378 × 10⁻¹² N m^4.316 and B = −4.316 determined experimentally (see electronic supplementary material, Information, for the fitted force–displacement curves). This model does not have a straightforward physical justification in terms of the material properties and the geometry of the magnets, but it is chosen because it reproduces the experimental force law with very high precision and low complexity. Using this force–displacement law, we can write the equation of motion for the system (the indices in parentheses indicate that no summation is performed over them),

4.1

where m_(i) and b_(i) are the mass and damping coefficient of the ith particle, respectively, A and B are the magnetic force law parameters, F_i(t) is the external driving force acting on the ith particle (which may be zero if the particle is not externally driven), and d₀ is the distance between magnets at rest. When performing the reduced-order analysis, we will assume that d₀ is the same for all magnets. This is an approximation, because magnets that are not in the centre of the lattice are subject to asymmetric long-range forces. However, we have found this approximation to yield acceptable results. We emphasize that our theoretical model is not limited to nearest-neighbour interactions and takes into account the magnetic force between all pairs of magnets. All numerical integration in this paper is done using a fourth-order Runge–Kutta algorithm with a time step of 1 ms.

5. Reduced modal description and frequency conversion mechanism

The mechanism responsible for the frequency conversion in our lattice becomes much clearer when we look at the evolution of the system in terms of the normal modes of the linearized system. We start building the reduced-order description by approximating the force–displacement relation by a second-order Taylor series. When we do this approximation, the system becomes

5.1

Here, the indices j and k are summed over all degrees of freedom, and M, B denote the mass and damping matrices defined conventionally. The driving force F_i is zero for all particles except at the defects, where a harmonic excitation of the form Fcos(2πft) is considered. The terms K and Γ in equation (5.1) are obtained by Taylor expansion of the force law,

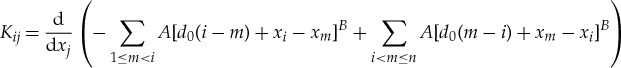5.2

and

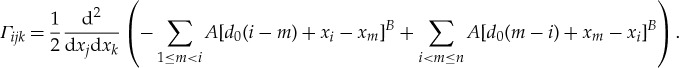5.3

Since M is symmetric and positive definite and K is symmetric, we can find an invertible matrix P such that P^TMP and P^TKP are both diagonal, by choosing the matrix P, so its columns are the normalized eigenvectors of M⁻¹K. For simplicity, we assume that the damping matrix B can be expressed as a linear combination of the mass and stiffness matrices and, therefore, is also diagonalized by the matrix P. This diagonalization process is equivalent to expressing the particle displacements x_j in equation (5.1) in terms of modal displacements u_n, using the relation x_j = P_jnu_n, and then left-multiplying both sides by P^T, resulting in

5.4

The diagonalized system in equation (5.4) does not provide any significant numerical advantage, because Γ_ijk is highly non-local in the modal basis (i.e. modes far apart in frequency interact as strongly as nearby modes). However, we can see the motivation for this approach if we look at the experimental results in the modal basis (figure 3a). In this basis, most of the motion occurs in the second extended mode and in the localized mode. In fact, these modes hold around 90% of the system's energy (figure 3b). Therefore, we can restrict our description to these two modes without incurring a significant error. To construct this reduced description, we consider equation (5.5) for the indices m = E and m = L, where E and L are the mode numbers corresponding to the localized and second extended modes, respectively. We also prescribe the values of u_n and u_l to be zero for all values of n and l different from E and L. With these restrictions in place, equation (5.4) can be rewritten as

5.5

and

5.6

Figure 3.

Reduced-order description of the frequency conversion process. (a) Projection of the experimental time evolution (figure 2a) on the linear modal basis. (b) Average energy as a function of the mode number. The system's energy is highly concentrated in the second extended mode and the localized defect mode. (c) Dynamic expansion of the defect mode. When the defect vibrates, the nonlinear magnetic interaction results in a non-zero average force acting on the defect's neighbours. (d) The motion of the second extended mode modulates the distance between the defect particle and its neighbours, dynamically tuning the defect mode frequency. (e) Detail of the extended mode and localized mode evolution, measured experimentally. (f) Theoretical prediction for the extended and localized mode evolution, obtained from a reduced-order model considering only two modes (equations (5.6) and (5.7)). The numerical simulation in (f) corresponds to a system with m_E = 0.45 g, m_L = 0.232 g, f_E = 0.5664 Hz, f_L = 3.913 Hz, f_I = 4.38 Hz, F_I = 45 µN, Q_E = 4.518, Q_L = 66.62 and γ = 1.801 N m⁻², where k_X = m_X(2πf_X)² and b_X = m_X2πf_X/Q_X. (Online version in colour.)

In this reduced description, u_L and u_E are the displacements of the localized and extended modes, respectively; F_I is the input force; f_I is the input frequency; m_L = P_iLM_ijP_jL, b_L = P_iLB_ijP_jL and k_L = P_iLK_ijP_jL are the effective mass, damping and stiffness of the localized defect mode, respectively; and m_E = P_iEM_ijP_jE, b_E = P_iEB_ijP_jE and k_E = P_iEK_ijP_jE are the effective mass, damping and stiffness of the extended mode, respectively. The term γ = Γ_ijkP_iEP_jLP_kL = Γ_ijkP_iLP_jEP_kL = Γ_ijkP_iLP_jLP_kE denotes the quadratic nonlinear interaction between modes. Both the nonlinear term γ and the linear stiffness k_L and k_E can be determined theoretically by performing a Taylor expansion of the interaction force, or experimentally by analysing the frequency response of the local and extended modes (see electronic supplementary material, Information), with good agreement between the two approaches. The damping terms b_E and b_L are determined experimentally by fitting the modal resonances (figure 1d,f). There is no driving force acting on the extended mode. This is because the extended mode has a node at the defect site, where the excitation takes place (figure 1c), and, as a consequence, the projection P_imF_i(t) is zero for this mode. We note that the reduced equations of motion present an asymmetry: there is no term proportional to 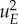in equation (5.5) and there is no term proportional to u_Eu_L in equation (5.6). These terms are generally not zero, but they do not appear in our lattice due to the symmetric location of the defect: the lattice has reflection symmetry around the defect (mapping 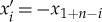), and, therefore, the equations of motion must be invariant under such transformation. This symmetry changes the sign of the localized mode, but leaves the extended mode invariant, and, therefore, forbids the missing nonlinear terms. In the electronic supplementary material, Information, we investigate the nonlinear coupling terms in the case where the defect is not centred. The interaction between modes can be understood in the following way: owing to nonlinearity, the vibration of the defect mode is rectified into a static force pushing against its neighbours, in a way that is analogous to thermal expansion of a crystal [18] or the optical pressure in an opto-mechanical system (figure 3c). For small amplitudes, this expansion is proportional to the square of the vibration amplitude, resulting in the term 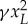in the extended mode equation. In addition, the motion of the extended mode modulates the distance between the defect particle and its neighbours (figure 3d). This affects the localized mode's effective stiffness and introduces the parametric term Δk_L = γu_E, analogous to the modulation of the optical cavity wavelength in an opto-mechanical system. This type of interaction appears in a variety of systems, such as phonon modes in superconductors [28], and can be used to build stochastic heat engines [29]. This reduced-order model can reproduce the experimentally observed behaviour (figure 3e,f) with remarkable accuracy. We highlight that the only fitting parameter used is the excitation amplitude. The particle mass, mode quality factor and inter-particle force law have all been measured experimentally.

The two-mode system, described in equations (5.5) and (5.6), is a purely mechanical analogue of an opto-mechanical system [30–32]. The extended mode plays the role of the low-frequency mechanical motion, while the localized mode plays the role of the high-frequency electromagnetic field. The term 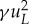acting on the extended mode plays the role of the optical pressure, while the term 2γu_Eu_L acting on the localized mode reproduces the modulation of the Fabry–Perot resonance by the mechanical degree of freedom in the opto-mechanical system. This analogy can be made explicit by expressing the motion of the defect mode as u_L(t) = (1/2)[a(t)e^iωt + a*(t)e^−iωt] and assuming that a(t) changes slowly and that 1/Q_L ≪ 1. With these assumptions, we arrive at the following equation (a detailed derivation and comparison with the full model are provided in the electronic supplementary material, Information):

5.7

and

5.8

Here, ω₀ is the natural frequency of the localized mode and the detuning Δ(u_E) is the difference between the localized mode's natural frequency and the defect's excitation frequency, as a function of the extended mode's position. All other parameters have the same meaning as they did in equations (5.5) and (5.6). While being an approximation, this form has numerical advantages by not containing rapidly changing components at the frequency of the localized mode, and not requiring the evaluation of trigonometric functions for the excitation. Besides numerical reasons, the description provided in equations (5.7) and (5.8) is identical to the model of an opto-mechanical system [30,32,33], for which there is extensive analytical literature [32,34]. This analogy provides a lucid interpretation of the frequency-converting mechanism, whereby the self-sustaining oscillations of the extended mode are the result of a feedback mechanism between the extended mode's motion and the localized mode amplitude. In this picture, the localized mode amplitude a depends on the extended mode displacement through the term Δ(u_E). Equation (5.8) imposes a retardation between a and u_E and, as a consequence, the term γ| a|² has a quadrature component (shifted 90° from u_E(t)) that results in negative damping [31]. When this negative damping exceeds the value of b_E, the system develops self-sustaining oscillations, which saturate at a finite value due to nonlinearity [31].

6. Multiple-defect synchronized frequency conversion

Systems containing multiple defects can present synchronized frequency conversion, where the motion of multiple defects is affected by the same extended mode, thereby synchronizing the defect's modulation envelopes and resulting in the conversion of energy from multiple input frequencies to a single output frequency. The use of an extended mode to synchronize multiple resonant elements appears in the context of Josephson junction arrays [35], and, here, we use it to extract energy from multiple sources of mechanical vibrations. Our experimental system consists of 20 magnets, with defect particles in positions 7 (0.244 g) and 14 (0.197 g). The initial and final particles are fixed. As in the case with a single defect, we set an excitation frequency for each defect equal to the defect's frequency plus an extended mode's frequency. This time we use the third extended mode instead of the second, because it presents two regions of maximum strain at the two defects' positions. As we did in the single defect case, we increase both defects' excitation amplitudes simultaneously, until we observe self-sustaining oscillations far from the defect. Figure 4a shows the trajectories of the magnets in the self-sustaining regime. We calculate the energy transfer between both defects and the extended mode, by using the empirical force–displacement relation and the defect's trajectories, and we observe that both defects are contributing energy to the extended mode with a power (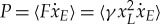) of 16.9 ± 1.5 and 25.8 ± 4.0 nW, respectively, indicating successful extraction of energy from multiple sources. The frequency conversion efficiency is 20.5 ± 10.4%. As in the previous case, the motion of the defects presents sidebands indicating a modulation by the extended mode (figure 4b). Far from the defect, the motion takes place exclusively at the extended mode's frequency, as required for successful frequency conversion operation.

Figure 4.

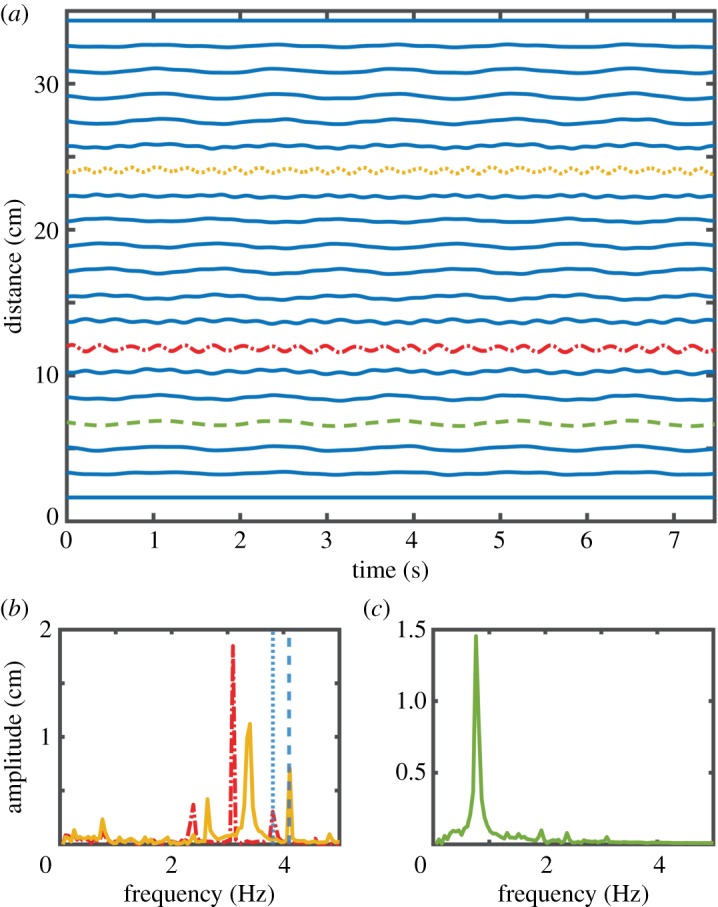
Synchronized frequency conversion. (a) Position of the magnets as a function of time. The yellow dotted line (particle 7) and the red dotted-dashed line (particle 14) are defect magnets that act as the high-frequency inputs of the system. The green dashed line is the low-frequency output. (b) Fourier transform of the defects' positions, which are modulated at the extended mode's frequency. The vertical dotted line represents the excitation frequency. (c) Fourier transform of the output magnet's position. This magnet's motion happens primarily at the third extended mode's frequency. (Online version in colour.)

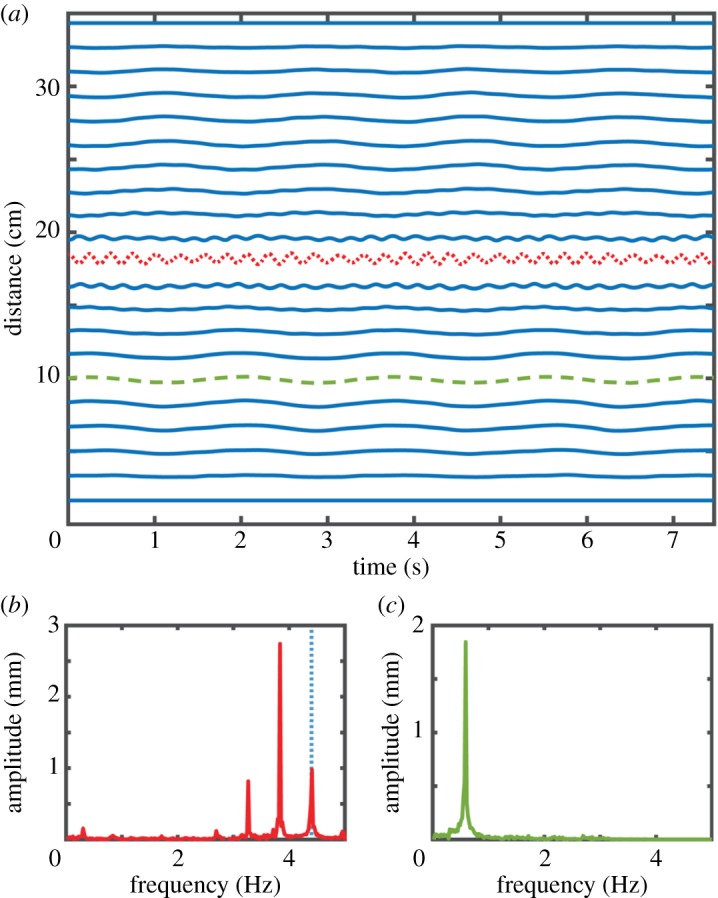
As in the case with a single defect, expressing the magnet's trajectories in terms of the lattice's linear normal modes reveals that the motion (figure 5a) and the energy (figure 5b) are primarily concentrated in an extended mode (figure 5c(i)) and in the two localized modes, the profiles of which are depicted in figure 5c. This energy concentration allows us to formulate a reduced-order description following the same procedure as in the system with a single defect. The resulting system of equations has the form

6.1

6.2

6.3

The model in equations (6.1)–(6.3) is capable of qualitatively predicting the evolution of the modes (figure 5d,e), but underestimates the output amplitude relative to the experiments. We attribute this difference to uncertainty in the system's resonance frequencies and quality factors. This is suggested by the difference between theory and experiment in the extended mode's frequencies (see electronic supplementary material, Information) and in the phase of the localized mode's modulation.

Figure 5.

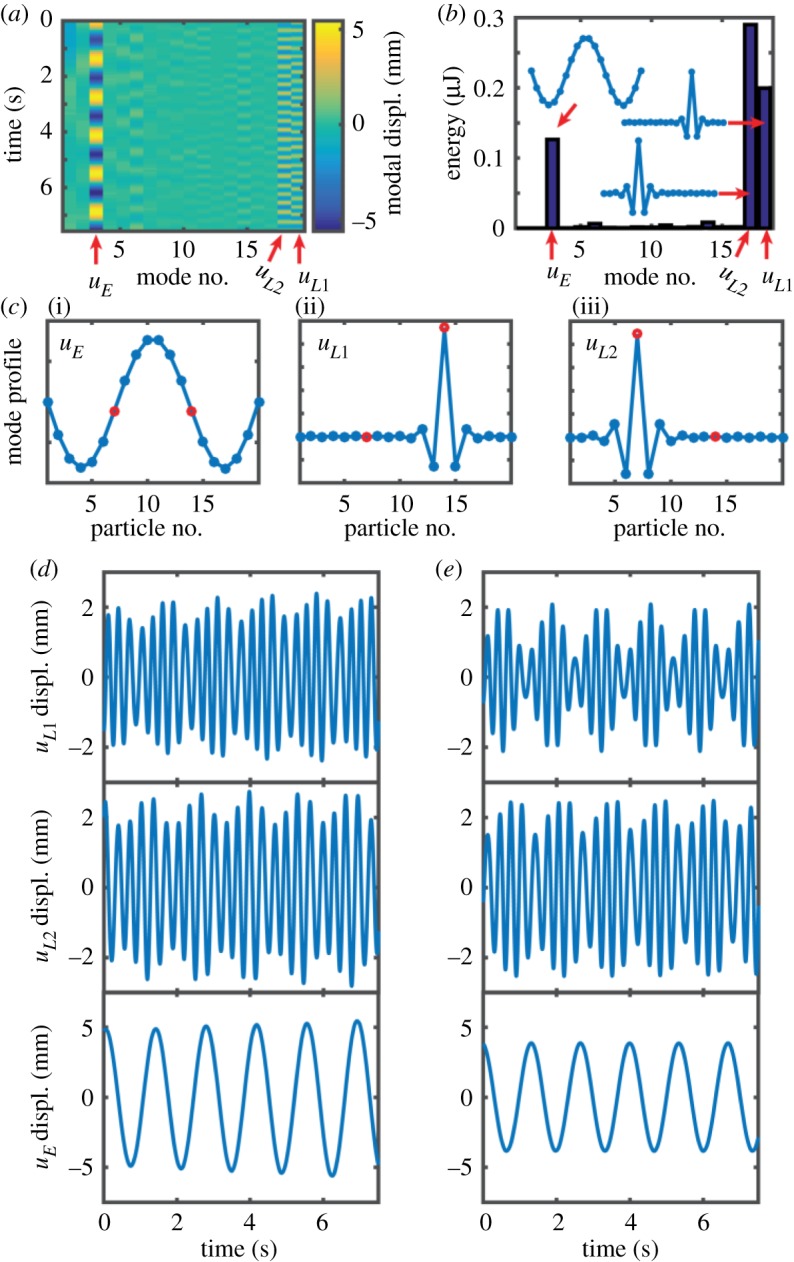
Reduced-order description of the synchronized frequency conversion. (a) Time evolution of the magnets in terms of the linear eigenmode basis. (b) Energy distribution in each normal mode. The energy is concentrated in the third extended mode and in the two localized defect modes. (c) Mode profiles of the three most relevant eigenmodes. (d) Experimental time evolution of the third extended mode u_E and the two localized modes u_L1 and u_L2 as a function of time. (e) Theoretical prediction for the time evolution of the eigenmodes. The theoretical predictions have been obtained using a 3 degrees of freedom reduced-order model. The numerical parameters used in (e) are: m_E = 0.45 g, m_L1 = 0.2318 g, m_L2 = 0.2915 , f_E = 0.7494 Hz, f_L1 = 3.404 Hz, f_L2 = 3.063 Hz, f_I1 = 4.1 Hz, f_I2 = 3.81 Hz, F_I1 = F_I2 = 42 µN, Q_E = 12.27, Q_L1 = 39.3, Q_L2 = 60.27, γ₁ = −2.4293 N m⁻², γ₂ = 2.5761 N m⁻²_. (Online version in colour.)

7. Output phase tunability

In our lattice, the output signal's phase is not prescribed by the inputs and can be dynamically tuned while the system is operating. This offers an opportunity to synchronize multiple devices, create passive and tunable phased arrays or transfer information by modulating the output signal's phase. In this section, we will theoretically investigate this tunability. For simplicity, we will focus our study in the single-magnet configuration of figures 2 and 3. The set-up, concept and main results are presented in figure 6a–c. The phase modulation is accomplished by perturbing the last particle following a Gaussian profile given by 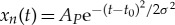(figure 6a), where A_P denotes the maximum perturbation amplitude, t₀ is the moment when the perturbation is applied and σ represents the width of the perturbation. We choose a Gaussian profile because it is highly localized in both the time and frequency domains. The effect of this perturbation is to change the frequency of the extended mode, causing it to oscillate faster or slower due to the well-known dependence between modal frequencies and strain in nonlinear lattices [19,23]. As a consequence of the temporary shift in oscillation frequency during the perturbation, the extended mode becomes advanced or delayed with respect to an unperturbed system. This effect introduces a shift in the output signal phase that persists long after the perturbation has vanished. Figure 6b shows the extended mode's displacement 1790 s after a perturbation, for different perturbation amplitudes. In this calculation, the perturbation width σ = 30 s is much smaller than the wait time, ensuring that any transient has decayed by the time the results are obtained. Two remarkable observations shall be made regarding the phase tunability shown in figure 6c. Firstly, this tunability covers the whole range (0°–360°). Secondly, the perturbation-induced phase shift persists for a period of time that is much longer than any of the system's time constants. This can be observed from the fact that the phase difference between perturbed and unperturbed systems does not change significantly if we wait an additional 1000 s until t = 1790 s (figure 6c). In the experimental system, this phase stability would be limited by the presence of external noise sources and Brownian motion.

Figure 6.

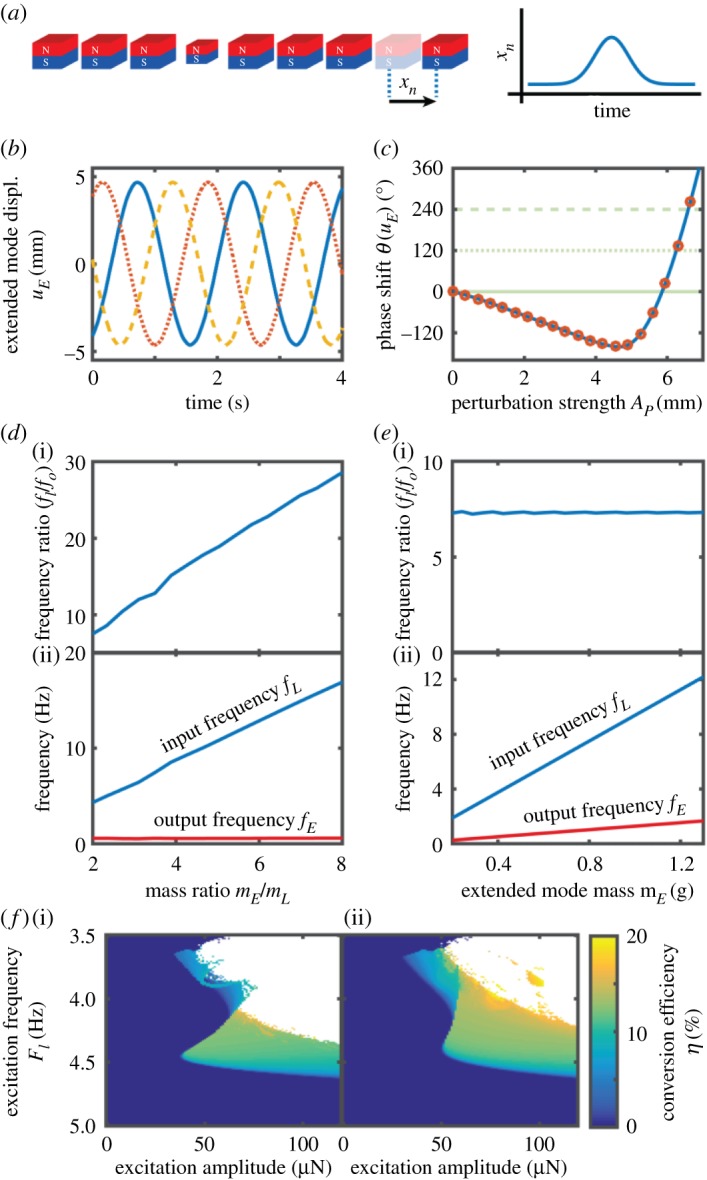
Theoretical investigation of phase and frequency tunability. (a) Phase tuning scheme. The output signal's phase is tuned by moving the last particle (x_n) following a Gaussian profile. (b) Extended mode signal 1790 s after the phase-shifting perturbation has been effected. The lines correspond to perturbations with A₀ equal to 0 mm (blue, solid), 6.2562 mm (red, dotted) and 6.5917 mm (yellow, dashed). (c) Output phase as a function of the maximum displacement of the phase-adjusting perturbation. The blue solid line is measured 1790 s after the perturbation, while the circles are measured 1000 s after the first measurement, 2790 s after the perturbation's peak. (b) and (c) have been obtained by integrating the full equation of motion (equation (4.1)) with d₀ = 16.3 mm, m_i,i≠11 = 0.45 g, m₁₁ = 0.197 g, b_i,i≠11 = 306.83 µNs m⁻¹, b₁₁ = 42.62 µNs m⁻¹, F_i,i≠11 = 0 N, F₁₁ = F_I sin 2πf_it, F_I = 48.45 µN and f_I = 4.38 Hz. The force-law parameters are as described in the Theoretical model section. (d) Frequency down-conversion ratio (i) and input and output frequencies (ii) as a function of the mass ratio between the defect and extended modes. These plots have been obtained by keeping the extended mode's mass constant and modifying the defect's mass. (e) Frequency down-conversion ratio (i) and input and output frequencies (ii) as a function of the extended mode mass, while keeping the modal mass ratio m_E/m_L constant. (f) Conversion efficiency as a function of the excitation frequency and amplitude, calculated with the experimentally determined extended mode damping (i) and with twice the damping (ii). Points that are not coloured correspond to combinations of excitation frequency and amplitude for which the system does not have a steady-state solution. In this figure, all parameters are identical to those in figure 3f unless otherwise indicated. (Online version in colour.)

8. Frequency tunability

A remarkable feature of our frequency-converting system is the possibility of tuning the input and output frequencies over a broad range, both during the design phase and dynamically once the system has been built. Figure 6d,e theoretically explores the relationship between the input and output frequencies and the modal masses. We first explore the effect of the mass ratio by altering the mass of the defect mode without altering that of the extended mode (figure 6d). This results in a change in the optimal input frequency without a significant effect on the output frequency. We then proceed to alter the masses of the localized and extended mode simultaneously (figure 6e). This affects both input and output frequencies, while maintaining the down-conversion ratio constant. In the conversion ratio calculation, we identify the optimal input frequency by sweeping the input between the resonance frequency of the localized mode and the resonance frequency of the localized mode plus twice the resonance frequency of the extended mode, and finding the input frequency that results in the highest energy transfer. In addition to the particle's mass, there are many unexplored avenues for tuning the frequency conversion ratio. Examples include the static compression applied on the chain, the magnets' strength and geometry and the application of an external magnetic field [36]. In addition, modern 3D printed materials allow us to engineer nonlinear inter-particle interactions [37] beyond these offered by magnetic systems.

9. Conversion robustness

We finally investigate the robustness of the proposed frequency-converting system to changes in the excitation frequency and amplitude. Figure 6f illustrates the conversion efficiency as the excitation of the system is varied. We observe that the system presents a well-defined region of efficient operation. In this region, the amount of energy per period dissipated in the extended mode equals the amount of energy transferred by the nonlinear inter-modal coupling. Outside of this region, two different phenomena may occur: when the excitation force is insufficient, there is not enough energy transfer for the oscillation of the extended mode to self-sustain, and frequency conversion will not occur, while, for high enough excitation forces, the system presents oscillations that grow without bounds (although in experiments, this growth will be limited by factors such as mechanical collisions between the particles). Remarkably, in the region of operation, the conversion efficiency is considerably robust. For example, for an excitation frequency of 4.43 Hz, when the excitation frequency is varied between 40 and 120 µN, the conversion efficiency stays between 10.7% and 11.4%. Figure 6f also shows that the system is robust to changes in quality factor: duplicating the damping acting on the extended mode results in a slightly increased conversion efficiency and broader region of operation, but the behaviour remains qualitatively the same. Additionally, in our experiments, we did not observe any significant disturbances due to the presence of environmental noise, and previous results [29] indicate that modified versions of the system described in equations (5.5) and (5.6) may be able to generate a low-frequency output even when driven by a pure noise signal with no deterministic component, which is interesting from a thermodynamic point of view.

10. Conclusion and outlook

We have demonstrated that lattices composed of magnetically interacting particles with defects are capable of converting energy from high frequencies to lower frequencies, which need not be linked by harmonic/subharmonic relations. This is possible through the nonlinear coupling between extended and localized normal modes. Such a frequency-converting lattice, analogous to opto-mechanical systems, is highly tunable in both frequency and phase, and can extract energy from multiple signals at different frequencies to generate a single-component output. This work may motivate the design of innovative nonlinear metamaterials and devices with tunable energy conversion capabilities.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

C.D. acknowledges support from the National Science Foundation under EFRI grant no. 1741565.