Tensor factorization toward precision medicine

Abstract

Precision medicine initiatives come amid the rapid growth in quantity and variety of biomedical data, which exceeds the capacity of matrix-oriented data representations and many current analysis algorithms. Tensor factorizations extend the matrix view to multiple modalities and support dimensionality reduction methods that identify latent groups of data for meaningful summarization of both features and instances. In this opinion article, we analyze the modest literature on applying tensor factorization to various biomedical fields including genotyping and phenotyping. Based on the cited work including work of our own, we suggest that tensor applications could serve as an effective tool to enable frequent updating of medical knowledge based on the continually growing scientific and clinical evidence. We encourage extensive experimental studies to tackle challenges including design choice of factorizations, integrating temporality and algorithm scalability.

Introduction

The collection of electronic medical data, while growing rapidly, poses technical challenges owing to large volume, uncertainty from noise and missing data and the fact that it draws from multiple modalities including clinical and genomic profiles, medication prescriptions and environmental exposures. Precision medicine aims to harness information from all modalities, develop a comprehensive view of a patient’s pathophysiologic progression and administer personalized therapies. Existing efforts are often based on only a few biomarkers, and their generalization demands new computational solutions, particularly to address the growing volume, uncertainty and number of modalities of data.

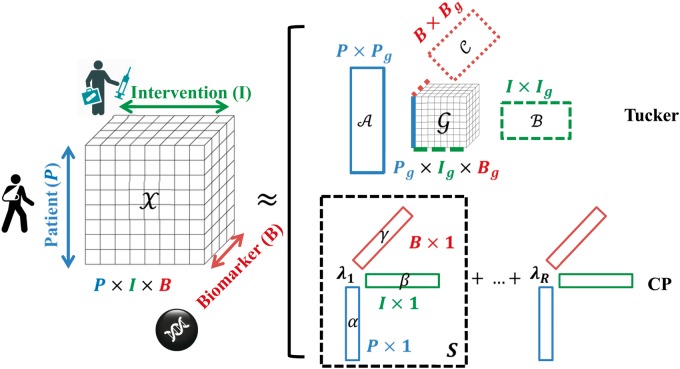
Tensor factorization has emerged as a promising solution for the computational challenges of precision medicine. A tensor is a multidimensional array where each modality spans one dimension (mode of a tensor). Figure 1 shows the tensor for modeling interactions among patients, biomarkers and interventions. Various factorization schemes have been proposed to decompose a tensor into factor matrices, which not only reduces dimensionality but also helps discover latent groups in each modality and identify group-wise interactions (see [1] for a general review). Typical matrix factorization approaches concatenate multiple data modalities into a single second dimension of the matrix, thus disallowing explicit representation of interactions among these modalities. In contrast to matrix factorization [2], different tensor factorizations can also integrate additional domain-specific prior knowledge to constrain the tensor structure. Figure 1 shows a visualization of two types of factorization: Tucker [3] and CANDECOMP/PARAFAC (CP) [4].

Figure 1.

Tensor modeling and factorization schemes. The data tensor x models the interactions among modes including patient, biomarker and medical intervention. The Tucker factorization (above, [3]) decomposes x into three factor matrices specifying groups in each mode and a core tensor 𝒢 specifying levels of interaction between the groups from different modes. In general, number of groups in each mode is less than the dimensionality of that mode and the core tensor 𝒢 can be thought of as a compression of x. The CP factorization (below, [4]) decomposes x as a weighted sum of rank-1 sub-tensors, each of which is the outer-product ($S,S_{ijk}={\alpha }_i{\beta }_j{\gamma }_k$) of a patient factor vector (α), an intervention factor vector (β) and a biomarker factor vector (γ). The weights ${\lambda }_r,r=1\dots R$ indicate relative importance of sub-tensors. Compared with Tucker, the structural hypothesis of CP requires the same number of groups for each mode.

Tensor factorization in biomedical informatics

Applying tensor factorization to biomedical informatics has gained traction over the past decade. Earlier applications focused on DNA microarray or sequencing data. Tucker and/or CP factorizations have been frequently applied to subjects including functionally related gene sets regarding protein/gene locus links and responses to stimulants [5], bacteria sub-lineage structure characterized by multiple types (modalities) of biomarkers [6], mouse brain genetic organizations across three-dimensional anatomical voxel positions [7] and relations between genes and transcription factors extracted from scientific literature [8]. To account for uncertainty, multiple authors proposed probabilistic Tucker and/or CP factorizations to incorporate priors on tensor structural parameters. Those priors can specify dependence between exposure to environmental chemicals and single nucleotide polymorphism level differences [9], or probability of gene sequence conditioned on the composing nucleotides and chromosomal positions [10, 11].

As an alternative to Tucker or CP factorizations, another vein of work viewed tensor factorization as a series of matrix factorizations with shared structural constraints, and termed their models Generalized Singular Value Decomposition (GSVD) or Higher-Order Singular Value Decomposition (SVD) (HOSVD). Some authors performed comparative analysis using ‘organism × gene × experimental condition’ tensors [12–14], or ‘nucleotide × sequence position × organism’ tensors [15]; others studied the effect and regulation of targeted pathways [16, 17] and further predicted treatment responses [18, 19]. When two of the tensor modalities are symmetric, eigenvalue decomposition replaces SVD, as seen in gene network functional grouping using binary/weighted ‘network × gene × gene’ tensors [20, 21]. However, it is difficult to extend GSVD/HOSVD to probabilistic versions to account for uncertainty.

In other biomedical fields, CP and Tucker factorizations have been used to localize and extract artifacts from Electroencephalogram (EEG) data to analyze epileptic seizures [22–24], where tensor modes include time points, electrodes of the multi-channel EEG and subjects (see [25] for a brief review). Probabilistic CP was shown to improve EEG classification accuracy when missing data are present [26]. In image analysis, HOSVD was applied to factorize a ‘patient × voxel × fMRI (functional Magnetic Resonance Imaging) mode’ tensor and to classify cognitive normal or declining status [27]. Wang et al. [28] demonstrated the potential of using tensor modeling to generalize sparse logistic regression to multiple modalities on fMRI data. In Electronic Health Record (EHR) phenotyping, CP has been adapted to enforce sparsity constraints [29], to explicitly account for interactions among groups of the same modality [30] and to incorporate medical knowledge via customized regularization terms [31], all with the goal of extracting clinically meaningful groups of patients. Both Tucker and CP seem to have broader adoptions than GSVD/HOSVD in non-genomic biomedical fields, perhaps owing to the relative ease of imposing probabilistic and other regularizations. Although CP produces summation of rank-1 sub-tensors (Figure 1) and leads to simplified interpretation, Tucker provides a more flexible and sometimes more realistic factorization by allowing varying number of groups in different modalities. Selecting a type of factorization is largely a design choice dependent on both data and outcome, and deserves extensive experimental studies and characterizations.

Toward precision medicine—discussion and future work

The advent of precision medicine initiatives, coupled with the welcome growth of new modes of data, suggests that medical knowledge needs continuous update. The current revision process, often involving meta-analysis of multiple studies and agreement of consensus groups, has difficulty in keeping up with the pace of change. An interesting alternative is to allow data-driven processes to suggest nimble and timely updates. Toward this goal, Luo et al. [32, 33] aimed to automatically identify from pathology reports a panel of test results that are diagnostic of lymphoma subtypes. Compared with a conventional ‘patient × word’ matrix, they composed a ‘patient × test result × word’ tensor and used non-negative Tucker factorization to identify diagnostic panels of test results. One can use such panels to suggest amendment to diagnostic guidelines in a format understandable to clinicians. However, extending tensor factorization to enable frequent updating in other fields such as genomics and biomedical signal processing remains an open question.

Another big challenge concerns how to properly model temporality within tensor factorization. Most existing work treats time points as independent, thus losing significant information [16, 17, 22–24]. Although we can add temporal locality constraints as an additional regularizer, this imposes new computational complexity and still lacks constraints on temporal ordering. Integrating stochastic processes into tensor factorization represents a theoretically appealing approach toward modeling temporality, but related work with biomedical applications is still in its infancy [26]. Specifically, it remains a major challenge to select appropriate stochastic processes based on consistency with biologic knowledge instead of mathematical convenience, yet maintain efficient inference procedures. Tensor factorization also needs to address data sparsity and algorithm scalability, which are more broadly recognized challenges in general domains. Only successfully answering all these challenges can lead to breakthroughs in supporting personalized medicine by properly drawing evidence with uncertainty from multi-modal, longitudinal and constantly evolving medical big data and the medical knowledge base.

Key Points

• Precision medicine demands new computational solutions generalizing from limited number of biomarkers to address the growing volume, uncertainty and number of modalities of electronic medical data.

• Tensor factorizations can easily integrate multiple data modalities, reduce dimensionality and identify latent groups in each mode for meaningful summarization of both features and instances in medical data.

• Tensor factorizations demonstrated successes in genotyping and phenotyping applications, and showed promises in enabling frequent updating of medical knowledge out of continuously growing scientific and clinical evidence.

• Challenges including design choices of factorization schemes, integrating temporality, addressing data sparsity and algorithm scalability pose exciting research opportunities to bioinformatics community, toward fully harnessing tensor factorization in the emerging horizon of precision medicine.

Biographies

Yuan Luo is an assistant professor at Northwestern University, Department of Preventive Medicine. He works in the area of natural language processing, time series analysis and computational genomics, with a focus on medical and clinical applications.

Fei Wang is an associate professor at University of Connecticut, Department of Computer Science and Engineering. His research interests include data mining, machine learning algorithms and their applications in health informatics.

Peter Szolovits is a professor at Massachusetts Institute of Technology, Department of Electrical Engineering and Computer Science. His research centers on the application of Artificial Intelligence methods to problems of medical decision making, natural language processing to extract meaningful data from clinical narratives to support translational medicine and the design of information systems for health care institutions and patients.