Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Apr 24;140(19):6164–6168. doi: 10.1021/jacs.8b02905

A Two-Dimensional ‘Zigzag’ Silica Polymorph on a Metal Support

David Kuhness †, Hyun Jin Yang †, Hagen W Klemm †, Mauricio Prieto †, Gina Peschel †, Alexander Fuhrich †, Dietrich Menzel †,‡, Thomas Schmidt †, Xin Yu †, Shamil Shaikhutdinov †, Adrian Lewandowski †, Markus Heyde †,*, Anna Kelemen §, Radosław Włodarczyk §, Denis Usvyat §,*, Martin Schütz §, Joachim Sauer §, Hans-Joachim Freund †
PMCID: PMC6078382  PMID: 29688718

Abstract

graphic file with name ja-2018-029056_0005.jpg

We present a new polymorph of the two-dimensional (2D) silica film with a characteristic ‘zigzag’ line structure and a rectangular unit cell which forms on a Ru(0001) metal substrate. This new silica polymorph may allow for important insights into growth modes and transformations of 2D silica films as a model system for the study of glass transitions. Based on scanning tunneling microscopy, low energy electron diffraction, infrared reflection absorption spectroscopy, and X-ray photoelectron spectroscopy measurements on the one hand, and density functional theory calculations on the other, a structural model for the ‘zigzag’ polymorph is proposed. In comparison to established monolayer and bilayer silica, this ‘zigzag’ structure system has intermediate characteristics in terms of coupling to the substrate and stoichiometry. The silica ‘zigzag’ phase is transformed upon reoxidation at higher annealing temperature into a SiO2 silica bilayer film which is chemically decoupled from the substrate.

Introduction

Ultrathin silica films have been grown on a number of metal single crystals and have become a research topic of their own.1−8 Depending on the oxygen affinity of the metal substrate, either single layers directly bound to the metal substrate or bilayer films only van der Waals bound to the substrate, or both on the same substrate, have been prepared. Especially bilayer films were thoroughly studied with a particular emphasis on the analysis of crystalline and amorphous structures. It is of fundamental interest to understand how different silica structures are formed in terms of the structural elements and transformed into each other. This knowledge will allow us the possibility to identify general principles of dynamic processes and structural transformations in silica. As it is the most abundant material in our earth’s crust, it is relevant in various branches of modern technologies.

Ru(0001) is the metal substrate where both monolayer and bilayer films have been prepared.9 We have therefore concentrated on this metal substrate to investigate the above-mentioned transformational aspects. Here we present a new 2D crystalline silica polymorph which forms on Ru(0001). It is experimentally studied and characterized with scanning tunneling microscopy (STM), low energy electron diffraction (LEED), infrared reflection absorption spectroscopy (IRAS), and X-ray photoelectron spectroscopy (XPS) measurements. A structural model is proposed on the basis of density functional theory (DFT) calculations suggesting a silica structure comprising three- and four-membered Si rings within a rectangular unit cell with glide mirror plane symmetry.

Results and Discussion

Preparation and experiments on ultrathin silica films grown on Ru(0001) were performed under ultrahigh vacuum (UHV) conditions. 2D silica mono- and bilayers on Ru(0001) have been prepared according to the procedures described in ref (5). Here we define a monolayer (ML) of silica as half the amount of silicon which is needed to form a homogeneous SiO2 silica bilayer covering the entire Ru(0001) metal surface.

In Figure 1a, a LEED pattern from a new silica phase formed after deposition of 2.0 ML Si onto an oxygen precovered Ru(0001) surface in ambient oxygen (typically 2 × 10–7 mbar) and subsequent oxidation at 1130 K in 2 × 10–6 mbar O2 is shown.11 This pattern is clearly distinguishable from the typical LEED patterns of the silica monolayer (Figure 1b), the crystalline bilayer with its sharp hexagonal 2 × 2 spots (Figure 1c), and the typical ring pattern from amorphous bilayer phase (Figure 1d). In the LEED pattern of the new silica phase, the reciprocal unit cells of three unique domains of the overlayer structure, each rotated by 120° toward each other, are indicated in blue, green, and yellow. From the LEED measurements a rectangular real space unit cell can be deduced with its unit cell vector lengths being as = 9.4 Å and bs = 7.6 Å, where the shorter vector bs follows the high symmetry directions of the hexagonal atomic structure of the underlying Ru(0001) surface. An incommensurate overlayer matrix can be defined as MS = 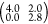Inline graphic. The spots belonging to the overlayer structure are slightly elongated along the shorter reciprocal unit cell vector direction, their length being independent of the order of diffraction of the spots. This points to a limited size of the domains with the new structure. According to the length of the LEED spots, the domain sizes are found to be in the range of 5 nm × 15 nm, where the smaller value limits the size of the domains in the direction of the longer real space unit cell vector as. Interestingly, independent of the energy of the incoming electrons, one spot at the corner of the reciprocal unit cells is missing. The position of the missing spot for one of the reciprocal unit cells is indicated with a white circle in Figure 1a. This phenomenon points to the presence of a glide mirror plane symmetry within the structure.12

Figure 1.

Figure 1

Open in a new tab

Comparison of LEED patterns and STM images of the ‘zigzag’ phase (a, e), the monolayer (b, f), the crystalline bilayer (c, g), and the amorphous bilayer of 2D silica (d, h), respectively. All LEED measurements taken at 42 eV and at room temperature. The reciprocal unit cell of the Ru(0001) substrate is indicated with a black line, the unit cells of the overlayers are indicated in blue, green, and yellow (a) and in orange (b, c). All STM images have been obtained at 4 K with a size of 3.8 nm × 3.8 nm. The following tunneling parameters have been used: (e) IT = 20 pA, VS = 0.7 V. (f) IT = 100 pA, VS = 50 mV. (g) IT = 100 pA, VS = 2.0 V (image reproduced from ref (10)). (h) IT = 60 pA, VS = 2.0 V.

In Figure 1e, a high-resolution STM image of the new phase is shown with a rectangular unit cell marked in blue. This contrast is clearly distinguishable from monolayer (Figure 1f), crystalline (Figure 1g), and amorphous (Figure 1h) bilayer STM images. Typical parallel zigzag lines can be distinguished which are oriented perpendicular to the three high symmetry orientations of the Ru(0001) substrate surface. At low bias the STM contrast reveals that the parallel zigzag lines seem to be interconnected by regularly appearing bridges, highlighted with white ellipses in Figure 1e. Large scale STM measurements can be found in the Supporting Information for further information. Over the sample, domains with three orientations have been found, consistent with results obtained from the LEED pattern. The rotational domains are typically divided by translation domain boundaries into smaller domain sizes with dimensions between 10 and 20 nm in width. Due to its characteristic structure the phase is further on called silica ‘zigzag’ phase in this manuscript.

Based on these experimental findings several structural models have been constructed by performing DFT geometry optimizations. These optimizations were carried out by using both, the atomic orbital and plane wave based codes CRYSTAL and VASP, respectively.13,14 A unit cell size of 9.4 Å × 7.6 Å has been assumed. Starting from crystalline silica bilayer configurations with rectangular unit cells according to Malashevich et al. also other configurations with bonds to the metal substrate have been considered.15 The most stable resulting model is shown in Figure 2. This model consists of a complex arrangement of interconnected tetrahedral SiO4 building units comprising parallel wavy bilayer rows which are responsible for the zigzag line appearance of the structure. These parallel zigzag lines form chains of slightly distorted vertically arranged four-membered rings of Si atoms, interconnected via shared O atoms. The zigzag lines comprising vertical four-membered Si rings are bound together with bridging SiO4 units in the top layer of the system, thereby forming distorted nonplanar eight-membered Si rings in the top view and vertically arranged three-membered Si rings in the side view (see top and side views of the model with marked Si rings in Figures 2 and 3). In the silica monolayer all Si atoms bind with a single O atom to the metal substrate, while in the ‘zigzag’ phase only two Si atoms are connected over two separate O atoms each to the Ru substrate per unit cell. The stoichiometry for the silica monolayer is SiO2.5 and for the silica bilayer it is SiO2.0, whereas, for the silica ‘zigzag’ phase, according to the model, it is found to be SiO2.17.

Figure 2.

Figure 2

Open in a new tab

Ball and stick model of the silica ‘zigzag’ phase: (a) Top and (b) side view (side view along the Ru[11 2̅0] direction). The topmost Si atoms are dark green, all other Si atoms are light green, O atoms are orange, and Ru atoms are gray. (c) The structure of the topmost Si atoms superimposed on an STM image of the ‘zigzag’ phase. The overlayer unit cell is marked in blue. Eight-membered Si rings are marked with light blue hatched areas. STM image: 3.8 nm × 3.8 nm, IT = 20 pA, VS = 0.7 V.

Figure 3.

Figure 3

Open in a new tab

Binding of the 2D silica phases to the Ru(0001) substrate surface. XPS measurements of (a) the O 1s and (b) Ru 3d5/2 core level region for the ‘zigzag’ silica (black line), bilayer silica (red dashed line), Ru(0001)-(2 × 2)-3O (blue dashed line), and the Ru(0001)-(2 × 2)-1O (green dashed line). (c–e) Model side views of the 2D silica phases on Ru(0001): for (c) the monolayer, (d) the ‘zigzag’ (side view along the Ru[1̅100] direction), and (e) the bilayer phase. Topmost Si atoms are dark green, all other Si atoms are light green, O atoms are orange, and Ru atoms are gray. Three- and four-membered rings are marked with orange and green hatched areas, respectively.

For demonstration of the match between the DFT-model and the experimentally found STM contrast of the ‘zigzag’ structure, a superposition of the topmost Si atoms, together with its coordinated O atoms, onto a STM image is shown in Figure 2c. The whole structure fulfills the requirement posed by the LEED measurements for a glide mirror plane symmetry. Additional visualizations of the two most stable calculated DFT structures and a STM simulation for the most stable model are shown in the Supporting Information.

To probe the chemical nature of the oxide phases, corresponding XPS measurements have been taken in the O 1s, Ru 3d5/2, and Si 2p core level region.11 O 1s and Ru 3d5/2 spectra are shown in Figure 3a and b, the Si 2p spectrum is shown in the Supporting Information. The shape of the O 1s spectrum of the silica ‘zigzag’ phase can be fitted with a main peak at 531.7 eV and a smaller peak at 529.9 eV binding energy, indicating that two different O species at least must be present in the structure. Comparison of this spectrum with the O 1s peak positions of the strongly bound silica monolayer system on Ru(0001) reveals that O species assigned to the peak position around 529.8 eV are likely to be part of Ru–O–Si bonding.5 This observation hints toward a bonding of the 2D silica ‘zigzag’ layer to the underlying Ru(0001) substrate surface. The Ru 3d5/2 spectrum has a significantly lower intensity at the higher binding energy side compared to the spectra belonging to the silica bilayer, where a Ru(0001)-(2 × 2)-3O coverage is supposed to be still present at the metal–oxide interface.5 This may indicate that the Ru(0001)-(2 × 2)-3O coverage is missing for the silica ‘zigzag’ phase. The Si 2p spectrum can be fitted with one peak at 102.8 eV binding energy which is found to be shifted to higher binding energy by 0.3 eV as compared to the peak position corresponding to the silica bilayer phase. This fact points to a higher oxidation state of the Si atoms within the silica ‘zigzag’ phase compared to the ones in the 2D SiO2 bilayer system. The findings of the XPS measurements, namely the fingerprints for the bonding of the 2D silica layer to the underlying Ru substrate and its higher oxidized stoichiometry, in comparison to the one of the 2D silica bilayer, are fully in line with the suggested structural model for the silica ‘zigzag’ phase presented above.

In Figure 3c–e model side views of the three observed 2D silica phases on Ru(0001), the monolayer, the ‘zigzag’, and the bilayer phase, are shown, respectively. The comparison allows for insights into the differences in thickness and oxide–substrate coupling via oxygen bonds of the three different 2D silica phases on Ru(0001). Compared to the silica ‘zigzag’ phase, the distance between the Ru metal surface and the topmost Si atoms appears to be larger for the chemically decoupled silica bilayer phase, although both phases comprise a bilayer system.

Additionally, IRAS measurements have been performed to investigate the absorption properties of the silica ‘zigzag’ phase. A typical IRAS measurement over the range 600 to 1400 wavenumbers is shown in Figure 4. The most prominent absorption frequency is at 1230 cm–1. The smaller absorption peaks marked with red and blue background bars are at similar positions as the most prominent IR absorption frequencies for the silica mono- and bilayer phase, respectively, which may to some extent coexist at the surface (see Supporting Information for IRAS spectra of the silica mono- and bilayer phase and ref (5)). In Figure 4 also the calculated infrared reflection (IR) intensities for the model are presented. Virtually all of the observed absorption peaks are nicely reproduced, within the expected accuracy of the calculations. Only the intensity of the 867 cm–1 peak of the calculation appears as too weak in comparison with the corresponding experimental peak, yet the positions deviate by only 17 cm–1. In general the complex silica ‘zigzag’ phase structure, comprising three- and four-membered vertically arranged rings, may essentially generate modes of mixed character. Still, some trends can be identified. The most prominent peak at 1230 cm–1 can be assigned to antisymmetric stretching of the vertical Si–O–Si linkage that goes in-phase along the ‘zigzag’ bilayer rows. The mode at 1060 cm–1 is similar apart from going antiphase along the ‘zigzag’ lines. Besides, for this mode the vertical Si–O–Si vibrations in the three-membered rings are more pronounced than those in the four-membered rings. The mode at 1000 cm–1 can be assigned to vertical antisymmetric Si–O–Si stretches of three-membered rings, horizontal antisymmetric Si–O–Si of four-membered rings, and also the antisymmetric stretch of the bridging Si–O–Si, that goes further in the direction of O–Ru. Other modes correspond to symmetric Si–O–Si stretching, which, in addition of the inter-ring coupling, are also coupled to the O–Ru stretches.

Figure 4.

Figure 4

Open in a new tab

Comparison of IRAS measurements for the silica ‘zigzag’ phase (black curve) and IR calculations (red curve). The absorption peaks marked with a red and blue background bar are associated with the silica mono- and bilayer phase, respectively.5

Additionally, a comparison of calculated IR intensities for the here presented model and another DFT-optimized structural model, consistent with the glide-plane symmetry, can be found in the Supporting Information. The agreement between experimental and calculated IRAS spectra support strongly the here presented model.

The silica ‘zigzag’ phase is always formed following the above-mentioned preparation conditions and has been reproduced several times on different Ru(0001) single crystal substrates. The silica polymorph can easily be transformed into a single phase silica bilayer upon annealing in 2 × 10–6 mbar O2 at 1260 K for 10 min. The silica bilayer system has not been observed to transform back to the silica ‘zigzag’ phase at varying preparation conditions so far. Therefore, the here presented silica phase with zigzag structure can be understood as a metastable silica phase, intermediate between mono- and bilayer in terms of substrate coupling which demonstrates the richness of the ultrathin silica phases. Insight into growth modes and transformations of 2D silica films may thereby support understanding of glass transitions.

In this manuscript we address the successful preparation of a new ultrathin 2D silica polymorph on Ru(0001) and its structural and chemical characterization using the surface science techniques LEED, STM, IRAS, and XPS. Furthermore, a DFT based structural model is presented which is consistent with the experimental findings.

Experimental Section

The results of experiments presented here have been conducted in three different UHV chambers, all with base pressures below 2 × 10–10 mbar, and equipped with low energy electron diffraction (LEED) optics, electron beam evaporators, and the typical facilities for sample manipulation and cleaning. Scanning tunneling microscopy (STM) experiments have been performed in a custom-designed UHV system, equipped with a low temperature STM which was operated in constant current mode using a PtIr tip. X-ray photoelectron spectroscopy (XPS) and LEED were carried out at the Low Energy and Photoemission Electron microscope (LEEM/PEEM) SMART operating at the synchrotron radiation source BESSY II of the Helmholtz-Zentrum Berlin (HZB).16

Ru(0001) single crystals were cleaned by several cycles of Ar+ sputtering and annealing in UHV at 1370 K. A Ru(0001)(2 × 2)3O reconstruction was established prior to deposition of Si by heating the sample to 1200 K in 2 × 10–6 mbar O2. 1.8 to 2.2 MLs of Si were evaporated at room temperature from a pure Si rod via an e-beam evaporator in 2 × 10–7 mbar O2. The sample was subsequently annealed in 2 × 10–6 mbar O2 at 1130 to 1180 K for 15 min.

Acknowledgments

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 669179). We thank HZB for the allocation of synchrotron radiation beam time and CRC 1109 for financial support of the theoretical calculations.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b02905.

  • Experimental setup; additional STM, XPS, and IRAS data; description of calculation method, including additional DFT models and visualization, additional calculated IR peaks, and model coordinates; references (PDF)

The authors declare no competing financial interest.

Author Status

∥ Deceased on 25-Feb-2018.

Supplementary Material

ja8b02905_si_001.pdf (904.2KB, pdf)

References

  1. Schröder T.; Hammoudeh A.; Pykavy M.; Magg N.; Adelt M.; Bäumer M.; Freund H. J. Single crystalline silicon dioxide films on Mo(112). Solid-State Electron. 2001, 45, 1471–1478. 10.1016/S0038-1101(01)00250-7. [DOI] [Google Scholar]
  2. Kaya S.; Baron M.; Stacchiola D.; Weissenieder J.; Shaikhudinov S.; Todorova T. K.; Sierka M.; Sauer J.; Freund H.-J. On the geometrical and electronic structure of an ultra-thin crystalline silica film grown on Mo(112). Surf. Sci. 2007, 601, 4849. 10.1016/j.susc.2007.07.030. [DOI] [Google Scholar]
  3. Löffler D.; Uhlrich J. J.; Baron M.; Yang B.; Yu X.; Lichtenstein L.; Heinke L.; Büchner C.; Heyde M.; Shaikhutdinov S.; Freund H.-J.; Włodarczyk R.; Sierka M.; Sauer J. Growth and Structure of Crystalline Silica Sheet on Ru(0001). Phys. Rev. Lett. 2010, 105, 146104. 10.1103/PhysRevLett.105.146104. [DOI] [PubMed] [Google Scholar]
  4. Lichtenstein L.; Büchner C.; Yang B.; Shaikhutdinov S.; Heyde M.; Sierka M.; Włodarczyk R.; Sauer J.; Freund H.-J. The Atomic Structure of a Metal-Supported Vitreous Thin Silica Film. Angew. Chem., Int. Ed. 2012, 51, 404–407. 10.1002/anie.201107097. [DOI] [PubMed] [Google Scholar]
  5. Yang B.; Kaden W. E.; Yu X.; Boscoboinik J. A.; Martynova Y.; Lichtenstein L.; Heyde M.; Sterrer M.; Włodarczyk R.; Sierka M.; Sauer J.; Shaikhutdinov S.; Freund H.-J. Thin silica films on Ru(0001): monolayer, bilayer and three-dimensional networks of [SiO4] tetrahedra. Phys. Chem. Chem. Phys. 2012, 14, 11344–11351. 10.1039/c2cp41355h. [DOI] [PubMed] [Google Scholar]
  6. Altman E. I.; Götzen J.; Samudrala N.; Schwarz U. D. Growth and Characterization of Crystalline Silica Films on Pd(100). J. Phys. Chem. C 2013, 117, 26144–26155. 10.1021/jp4101152. [DOI] [Google Scholar]
  7. Crampton A. S.; Ridge C. J.; Rötzer M. D.; Zwaschka G.; Braun T.; D’Elia V.; Basset J.-M.; Schweinberger F. F.; Günther S.; Heiz U. Atomic Structure Control of Silica Thin Films on Pt(111). J. Phys. Chem. C 2015, 119, 13665–13669. 10.1021/acs.jpcc.5b02667. [DOI] [Google Scholar]
  8. Jhang J.-H.; Zhou C.; Dagdeviren O. E.; Hutchings G. S.; Schwarz U. D.; Altman E. I. Growth of two dimensional silica and aluminosilicate bilayers on Pd(111): from incommensurate to commensurate crystalline. Phys. Chem. Chem. Phys. 2017, 19, 14001–14011. 10.1039/C7CP02382K. [DOI] [PubMed] [Google Scholar]
  9. Heyde M.; Shaikhutdinov S.; Freund H.-J. Two-dimensional silica: Crystalline and vitreous. Chem. Phys. Lett. 2012, 550, 1–7. 10.1016/j.cplett.2012.08.063. [DOI] [PubMed] [Google Scholar]
  10. Lichtenstein L.; Heyde M.; Freund H.-J. Atomic Arrangement in Two-Dimensional Silica: From Crystalline to Vitreous Structures. J. Phys. Chem. C 2012, 116, 20426–20432. 10.1021/jp3062866. [DOI] [Google Scholar]
  11. Klemm H. W. Ph.D. Thesis, TU Berlin, 2018. [Google Scholar]
  12. Van Hove M. A.; Weinberg W. H.; Chan C.-M.. Low-Energy Electron Diffraction: Experiment, Theory and Surface Structure Determination; Springer-Verlag: Berlin Heidelberg, 1986. [Google Scholar]
  13. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  14. Dovesi R.; Orlando R.; Erba A.; Zicovich-Wilson C. M.; Civalleri B.; Casassa S.; Maschio L.; Ferrabone M.; De La Pierre M.; D’Arco P.; Noël Y.; Causà M.; Rérat M.; Kirtman B. CRYSTAL14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. 10.1002/qua.24658. [DOI] [Google Scholar]
  15. Malashevich A.; Ismail-Beigi S.; Altman E. I. Directing the Structure of Two-Dimensional Silica and Silicates. J. Phys. Chem. C 2016, 120, 26770–26781. 10.1021/acs.jpcc.6b07008. [DOI] [Google Scholar]
  16. Fink R.; et al. SMART: a planned ultrahigh-resolution spectromicroscope for BESSY II. J. Electron Spectrosc. Relat. Phenom. 1997, 84, 231–250. 10.1016/S0368-2048(97)00016-9. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja8b02905_si_001.pdf (904.2KB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES