Joint Solution for PET Image Segmentation, Denoising, and Partial Volume Correction

Abstract

Segmentation, denoising, and partial volume correction (PVC) are three major processes in the quantification of uptake regions in post-reconstruction PET images. These problems are conventionally addressed by independent steps. In this study, we hypothesize that these three processes are dependent; therefore, jointly solving them can provide optimal support for quantification of the PET images. To achieve this, we utilize interactions among these processes when designing solutions for each challenge. We also demonstrate that segmentation can help in denoising and PVC by locally constraining the smoothness and correction criteria. For denoising, we adapt generalized Anscombe transformation to Gaussianize the multiplicative noise followed by a new adaptive smoothing algorithm called regional mean denoising. For PVC, we propose a volume consistency-based iterative voxel-based correction algorithm in which denoised and delineated PET images guide the correction process during each iteration precisely. For PET image segmentation, we use affinity propagation (AP)-based iterative clustering method that helps the integration of PVC and denoising algorithms into the delineation process. Qualitative and quantitative results, obtained from phantoms, clinical, and pre-clinical data, show that the proposed framework provides an improved and joint solution for segmentation, denoising, and partial volume correction.

Graphical abstract

1. Introduction

Positron emission tomography (PET) has been extensively used in oncology applications. It provides diagnostic and therapeutic interpretations by measuring tracer activity, which could be related to various physiological and pathological functionalities. It has been used for other diseases, including neurological disorders, infection, and inflammation. In radiation oncology applications, for instance, PET helps localization and staging of the tumors. PET images have high contrast, but low spatial resolution compared to magnetic resonance imaging (MRI) and computed tomography (CT). While low spatial resolution leads to inevitable partial volume effect, the reconstruction process of the PET images includes inherent multiplicative noise (i.e., image dependent) (Kirov et al. (2008); Chatziioannou and Dahlbom (1994)). Partial volume effect (PVE) is one of the major sources of information loss in PET images due to relatively poor spatial resolution. Therefore, there is a strong need for correcting partial volume before quantification of lesion metabolism and physiology. Similarly, noise removal methods (i.e., denoising) are vital because they enhance both quantitative metrics and visual quality for better diagnostic decisions. For image-based quantitative metrics, boundary delineation of the PET lesions is of utmost importance. For instance, disease severity and therapy response assessment require metabolic tumor volume (MTV) to be calculated on the delineated regions. Moreover, signal strength-based metrics such as the maximum and mean standardized uptake value (SUV_max and SUV_mean, respectively) are routinely used for cancer staging, tumor characterization, and therapy response assessment.

Many effective solutions have been proposed in the literature to address these three problems. These methods mainly fall under two categories depending on their input: reconstruction-based and post-reconstruction methods. Reconstruction methods correct the PET signal during image generation, usually with maximum a posteriori estimation, and incorporation of anatomical information from CT imaging (Cheng-Liao and Qi (2011); Comtat et al. (2002); Kazantsev et al. (2011); Baete et al. (2004b,a); Somayajula et al. (2011); Chan et al. (2009)). Under most circumstances, images are more accessible than original scanner signal, therefore in this paper, we focus on the post-reconstruction techniques in addressing these three challenges. Most post-reconstruction based methods either treat these three problems independently, or by solving two of them at simultaneously (such as PVC and denoising (Boussion et al. (2009))). Some works have also exploited the relationship between voxel clusters and imaging markers for specific applications such as kinetics parameters for dynamic myocardial perfusion PET (Mohy ud Din et al. (2015b)). However, to the best of our knowledge, no previous post-reconstruction methods have been applied for general purpose PET image processing to address all these three tasks jointly by using their interdependent associations. We hypothesize that solving these three tasks jointly will improve each task’s individual performance as well as final quantitative evaluations of the PET images. Our hypothesis stems from the following facts:

• Fact 1: Noise degrades the performance of image segmentation (Foster et al. (2014a)),

• Fact 2: Incorporation of object information (through delineation) into the denoising process improves denoising performance (Xu et al. (2014)),

• Fact 3: Post-reconstruction PVC approaches amplifies noise (Rousset et al. (1998)),

• Fact 4: Incorporation of segmented lesions into PVC improves accuracy of quantification as boundary information helps in determining the amount of spillover in PET images (Zaidi et al. (2006)),

• Fact 5: PVC in noisy images could lead to erroneous inferences about uptake in certain regions (Soret et al. (2007)).

Background and Related Work

1.1. Noise

Noise in PET images follows non-Gaussian distribution (Bagci and Mollura (2013)). Noise reduces the sensitivity of image-based quantitative metrics due to distortion in PET image appearance. Hence, denoising is a necessary step for improving quantitative evaluations of PET images. There are reconstruction and post-reconstruction based denoising methods in the literature. In this paper, we confine ourselves into post-reconstruction approaches only. The existing post-reconstruction methods for denoising PET images can be categorized into three classes: filter-based, patch-based, and statistics-based. Details of these categories are the following.

Most popular filter-based approaches are Gaussian smoothing, adaptive diffusion filtering (Tauber et al. (2011); Xia et al. (2015)), and filtering in image transform domain with support by anatomical information (Turkheimer et al. (2008)). None of these methods provide optimal denoising of PET images because Gaussian filtering often leads to information loss due to excessive blurring. Although adaptive diffusion filtering is considered capable of partially solving heavy blurring problem in anatomical images, it is not highly effective for PET images since the necessary structural information about diffusion process is limited by PET’s low resolution. Incorporation of anatomical information (through corresponding CT or MRI tissue segmentation) can help in defining regional homogeneities for the purpose of denoising, but it may also create artifacts. It is because anatomical-functional correspondence does not always hold for all voxel locations (Bagci et al. (2013a); Kramer-Marek et al. (2012); Bagci et al. (2013b)). Note that this issue is different from the voxel correspondence problem, which can be solved by image registration algorithms (Bagci et al. (2013a); Bagci and Bai (2007)).

Statistics-based methods, on the other hand, build a deterministic relationship between noise and statistical measurements. Yet, strong image structures such as ridges, edges, and textures can have negative effects on the statistical estimations. Among statistics-based denoising approaches, the-state-of-the-art method is the soft-thresholding approach (Bagci and Mollura (2013)). Although noise distribution modeling in (Bagci and Mollura (2013)) is more realistic than other methods, considering PET noise as sole Poisson or Gaussian distribution is still sub-optimal, and some recent reconstruction-based approaches assume more realistic assumption of Poisson Noise. Lastly, patch-based methods have gathered a lot of interests due to their effectiveness in simultaneously estimating noise level and denoising. For instance, non-local means based denoising strategy (Buades et al. (2005)) is shown to preserve structures, even for images with low signal-to-noise-ratio (SNR) by considering global similarity measurement. Some works used non-local means method for PET image denoising, such as including temporal neighbor patches from dynamic PET images (Dutta et al. (2013)), patch-based denoising on the reconstruction process (Wang and Qi (2012)), and making use of CT anatomical priors (Chan et al. (2014)). Our method is significantly different from (Dutta et al. (2013)) because here in this study we aim to denoise static PET images and without the need for corresponding CT images as prior. Further, we modify the original non-local means method by considering the characteristics of PET images. Wang’s method (Wang and Qi (2012)), on the other hand, belongs to reconstruction-based denoising methods.

In the nuclear medicine imaging field, detailed noise characteristics of PET images are still open to debate and need to be carefully considered when choosing/designing an appropriate denoising approach. It is important to note that in the Sinogram domain (i.e. projection space), noise statistics are well-modeled by a Poisson distribution. With tractable optimization of Poisson likelihoods, reconstruction-based approaches have been proposed in the literature. It is also well-known that in a high count PET image, the noise distribution can be well approximated by a Gaussian based on the Central Limit Theorem. However, the opposite is not true for low count PET image. Several studies (Boulanger et al. (2010); Zhang et al. (2008); Salmon et al. (2014)), including our earlier technical paper in (Bagci and Mollura (2013); Mansoor et al. (2014)), propose to use variance stabilizing transform (VST) (Anscombe (1948)) to Gaussianize the non-Gaussian noise (purely Poisson was assumed) in PET images before noise minimization procedure. The motivation in such methods is to model noise with a more realistic noise models. In this work, we improve our earlier assumption of purely Poisson noise model by proposing a more realistic and advanced mixed Poisson-Gaussian model. This is mainly due to the observations and the facts of the nature of PET imaging where both Poisson and enhancing additive noise by PVC have been observed. Next, we develop a new patch-based denoising algorithm called “regional means denoising”, pertaining to the family of non-local means denoising methods.

1.2. Segmentation

PET image segmentation aims at separating and delineating the PET image into different uptake regions. Several methods have been proposed for PET image segmentation. Among thresholding-based methods (fixed, adaptive, and iterative), iterative-based thresholding approaches are most intuitive ones (van Dalen et al. (2007)). These methods are easy to implement but difficult to generalize due to lack of information on local intensity distribution and sub-optimal thresholding levels. Alternatively, more sophisticated approaches have been proposed such as machine learning techniques that exploit local appearance: Gaussian mixture model and supervised/unsupervised clustering methods (Foster et al. (2014b); Kerhet et al. (2009)) belong to this category. For defining a specific region of interest, region growing (Li et al. (2008)), level-set (Hsu et al. (2008)), and graph-cut (Bagci et al. (2011)) are some of the most popular region and boundary-based methods. Lately, co-segmentation (joint segmentation) methods that incorporate anatomical information from CT and/or MR have been introduced to further promote region definition accuracy (Bagci et al. (2013b); Song et al. (2013); Xu et al. (2015)). Readers can refer to a recent review paper (Foster et al. (2014a)) for a comprehensive comparison of the PET image segmentation methods. Recent development of deep learning has enabled more robust, efficient, and accurate segmentation for many modalities, and most state-of-the-art techniques in segmentation are now based on deep convolutional neural networks. For example, the best performing methods for retinal vessel segmentation from fundus image (Liskowski and Krawiec (2016)), lung segmentation from CT image (Harrison et al. (2017)), and brain MR image segmentation (Akkus et al. (2017)) are mostly based on deep learning. However, PET image features unique characteristics of low resolution, relatively high contrast, and limited contextual information. Therefore, so far, only few studies used deep learning for PET image segmentation (Ibragimov et al. (2016)), and deep learning based approach has not been shown to be a significantly superior choice. In the current work, we target at delineating the boundaries between uptake regions across the entire image so that not only the high uptake regions, but other regions can also be used as prior information for both PVC and denoising processes.

1.3. Partial volume effect (PVE)

PVE is the change in apparent activity when an object partially occupies the volume of the imaging instrument both in space and time(Erlandsson et al. (2012)). It is a major hurdle particularly for clinical assessment of PET images where MTV is often needed to be derived from the images. The challenges for correcting PVE are posed by noise and unknown uptake region definition. Typical PVC methods rely on one or more assumptions for the point spread function (PSF) of the imaging device as well as PET noise characteristics (Erlandsson et al. (2012)). Note that the reconstructed PET image can be described as a convolution of the true activity distribution with the PSF because the PSF corresponds to the image of a point source and characterizes the spatial resolution. Thus, the ultimate goal in PVC is to reverse the effects of the system PSF in a PET image, leading to the restoration of true activity distributions. This inverse operation is called deconvolution, which can be employed either in image or frequency space. It is also important to note that the majority of PET images are reconstructed using an iterative method based on a Poisson likelihood model such as the frequently used OSEM algorithm. These methods produce images that are non-linear functions of the high-dimensional data. Conventionally, EM (expectation maximization) based iterative algorithms have been used to characterize the mean and covariance of PET images. Due to non-linearity, these iterative methods do not have a point spread function and they map the Poisson data into images where noise distribution is no longer truly Poisson (Barrett et al. (1994); Xu and Tsui (2009); Ding et al. (2016)). This information, in fact, also supports our observation and claim about the mixed nature of the Poisson and Gaussian.

Deconvolution-based PVC methods are vastly common in the literature (Erlandsson et al. (2012); Yang et al. (1996)). Although these methods depend solely on PET data and promising results are obtained, noise amplification is inevitable, and ringing artifacts can appear in the vicinity of sharp boundaries. In order to address noise amplification problems, there have been many improved deconvolution-based methods presented. For instance, deconvolution methods such as Van Cittert, Richardson-Lucy, and MLEM (Kirov et al. (2008); Tohka and Reilhac (2008)), iteratively solve the restoration problem by better controlling the effects of noise. Noise can also be controlled for some special tasks with iterative deconvolution scheme (Mohy-ud Din et al. (2014); Mohy ud Din et al. (2015a); Naqa et al. (2006)). Nevertheless, post-processing smoothing via a proper denoising method remains a necessity in these methods due to unknown levels of PET noise. More recently, joint use of PET image with its high resolution anatomical correspondence (CT or MRI) is considered as an effective way for solving PVC problem (Thomas et al. (2011); Chan et al. (2013)). The general aim in such methods is to infer structural information from anatomical images as a prior information for stabilizing the problem. These approaches require anatomical images to be segmented accurately, which is in itself a difficult and ill-posed problem to solve. Moreover, segmented regions are often considered to be functionally homogeneous; however, this assumption does not always hold, either.

Regarding the mostly used PVC methods, it is worth noting the seminal contribution of Hoffman et al (Hoffman et al. (1979)), one of the first works in PVC, where authors define a parameter called Recovery Coefficient to reflect the apparent activity concentration of an object divided by its true concentration (Gallivanone et al. (2011)). Basically, for objects of different sizes and shapes scanned in a PET system, different recovery coefficient parameters are recorded similar to most look-up table approaches. The recovery coefficient method is then further improved for handling multiple regions so that not only spill-out, but also spill-in effects can be considered in recovery coefficient definition. This improved method is called Geometric Transfer Matrix (GTM) (Rousset et al. (1998)). Main shortcomings of the recovery coefficient and GTM methods stem from the ineffective use of local structural information, which eventually causes sub-optimal recovery of true activity distribution. Interested readers can find a review article on PVC methods, including both reconstruction and post-reconstruction approaches, and their detailed comparisons in (Erlandsson et al. (2012)).

As can be inferred from relevant works, denoising, segmentation, and PVC are closely related to each other such that the improvement of one could simplify and/or improve the solution of the other. However, to the best of our knowledge, there is no study solving these three important problems jointly, and in the same setting by utilizing their complementary strengths. Herein, we design an iterative approach for solving PET image segmentation, denoising, and PVC with the following steps:

• Step 1: Stabilize mixed Poisson-Gaussian noise by generalized Anscombe transformation (GAT),

• Step 2: Estimate boundary of local uptake regions using affinity propagation (AP) clustering,

• Step 3: Denoise transformed PET images using “regional means denoising”,

• Step 4: Employ PVC by utilizing the region definition from segmentation solutions, and

• Step 5: Conduct optimal inverse GAT (IGAT) to transform the enhanced PET images into original intensity domain (SUV).

Steps (2-4) are performed in an iterative manner so that they can mutually benefit from each other. A flowchart of the proposed steps 1-5 is shown in Fig. 1. Preliminary idea and the initial results of the proposed method were presented at MICCAI 2014 (Xu et al. (2014)). In the next sections, we present our novel joint solution framework with validation and evaluation on large data sets including phantom, clinical, and pre-clinical PET imaging data.

Figure 1.

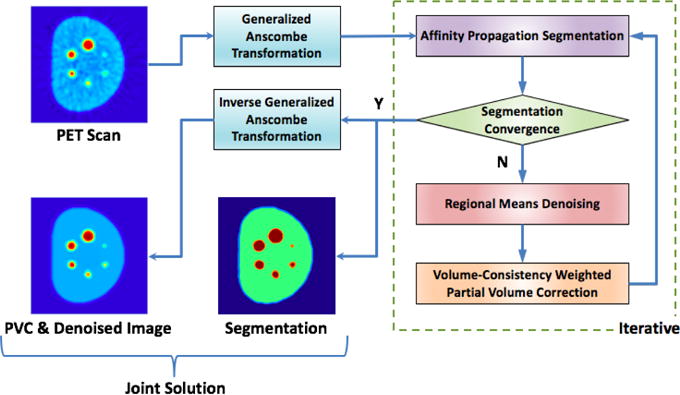
Flowchart of the joint solution platform for denoising, segmentation, and PVC of PET images. After PET images are transformed into a Gaussian space via Generalized Anscombe Transformation, affinity propagation based clustering algorithm is used iteratively to delineate regions of interest. Denoising is performed through a new regional means denoising algorithm that helps precise definition of segmented regions and PVC itself. The algorithm stops when segmentation converges. The output of the image is transformed back into the original image domain through the optimal inverse transformation of Anscombe’s method.

Summary of our contributions

Our proposed system is novel as a whole. To our best of knowledge, our attempt is the first that jointly conducts segmentation, denoising, and partial volume correction (PVC) in an iterative manner. For each component (segmentation, denoising, and PVC) of the unified algorithm, we also have either incremental novelties or totally new approaches: for denoising, we have improved the current state of the denoising algorithms with a new noise model, which is more realistic and advance model consisting of Gaussian and Poisson. Nonlocal means based algorithm was modified and adapted to general PET image processing framework and the proposed regional means denoising method has been shown to be very effective with the cost of increased computational complexity. For PVC, we propose a totally new algorithm inspired by RBV algorithm (i.e., region based voxel-wise) which has been further improved through appropriate region definitions from segmentation and denoising steps. For segmentation component, we do not propose any new algorithm but show the necessary algorithmic background how PET image segmentation method can be integrated into the joint solution platform seamlessly. In the current setting, we use our recently published method of adapted affinity propagation algorithm (Foster et al. (2014b)), which allows iterative update of denoising and PVC algorithms. One another purpose of this study is to assess the extent to which these factors are affecting quantification process from PET images. Surprisingly, there has been no detailed investigation of the joint solution for PET image post-processing in the literature. We have conducted several different experiments consisting of phantoms, pre-clinical, and clinical PET scans. For clinical scans, we have used both PET/CT and PET/MRI. Our extensive evaluations prove the usefulness of joint solution for PET post-processing both in visual evaluation and quantification.

2. Methods

Methods pertaining to the proposed framework (see Fig. 1) are described below in details.

Step 1 and 5: Generalized Anscombe Transformation and its Optimal Inverse

Additive white noise (Gaussian) is the basic hypothesis for most denoising methods regardless of the image modality. Gaussian noise is usually suppressed by averaging operation due to the assumption that the noise at different spatial locations are considered independent and identically distributed (i.e., Gaussian assumption). For non-Gaussian noise distributions, either new methods need to be developed, or non-Gaussian noise should be transformed into a more tractable Gaussian model.

In PET images, noise is more complex with multiple sources: while true signal, random and scatter coincidences during photon counting follows Poisson distribution (Chatziioannou and Dahlbom (1994); Bagci and Mollura (2013); Zaidi et al. (2006)), partial volume correction and other image reconstruction methods introduce additive white noise (Zaidi et al. (2006); Turkheimer et al. (2008)). Therefore, a mixed Poisson-Gaussian noise assumption is more realistic than either model alone. In practice, it will be tractable to transform the non-Gaussian noise into a Gaussian space in spite of explicitly modeling the unknown distribution of mixed Poisson-Gaussian noise (Anscombe (1948)). For this purpose, we adopt GAT and it’s optimal inverse, which have been shown to be optimal when transforming multiplicative noise into approximately Gaussian (Makitalo and Foi (2013)), as also indicated in our earlier study (Mansoor et al. (2014)).

GAT (Makitalo and Foi (2013)) is used for balancing the noise variation under the non-Gaussian noise assumption as follows. Signals are modeled as Poisson variables corrupted by additive white (i.e., Gaussian) noise. Assuming that p denotes a Poisson distribution (i.e., $\mathrm{p}\sim \mathrm{P}(\lambda )$) with underlying expected value (and variance) λ, and n denotes the Gaussian noise with mean μ and standard deviation σ (i.e., $n\sim \mathcal{N}(\mu ,{\sigma }^2)$), then the observed PET image intensities are defined as:

$$x=\alpha \mathrm{p}+n,$$ (1)

where α denotes the scale term accounting for the relationship between observed pixel data and the presumed Poisson model. Note that here we assume a continuous approximation of Poisson model when applying to images. For an observed intensity x, stabilization of the noise can then be achieved by GAT as follows:

$$\mathit{GAT}(x)=\{\begin{array}{ll}\frac{2}{\alpha }\sqrt{\alpha x+\frac{3}{8}{\alpha }^2+{\alpha }^2-\alpha \mu ,}\hfill & x>-\frac{3}{8}\alpha -\frac{{\sigma }^2}{\alpha }+\mu \hfill \\ 0,\hfill & \text{otherwise,}\hfill \end{array}$$ (2)

where y = GAT (x) has approximately unit variance. These parameters are set a priori according to resolution and homogeneity properties of the candidate images. For instance, clinical and pre-clinical PET images show different resolution characteristics; therefore, it is recommended to learn/tune the parameters in a training step. Similarly, homogeneity of the images can be used to fine-tune these parameters. In our study, we inferred the parameter selection method by following (Makitalo and Foi (2013); Foi et al. (2008)) where authors estimated the parameters from a single noisy image by fitting a global parametric model into locally estimated expectation and standard deviation pair. We have done this process for each experiments separately: phantom, pre-clinical, and clinical studies. Once PET image intensities are transformed by GAT, Gaussianized noise can be removed with the proposed joint solution framework. Final step (after employing denoising) is the inverse GAT operation in which the denoised PET images are transformed back into the original image space (called SUV domain). For inverse GAT (IGAT, step 5), we use the exact unbiased inverse of the GAT (Makitalo and Foi (2013)) to restore intensity information in SUV domain optimally without loss of information. Given y = GAT (x), λ, and α; IGAT is formulated as IGAT (y) = E(y|λ, α), where

$$E(y|\lambda ,\alpha )={\displaystyle \int \mathit{GAT}(x)p(x|\lambda ,\alpha )dx,}$$ (3)

and p(x|λ, α) is simply the probability density function for a variable x pertaining to Poisson distribution family.

Step 2: Affinity Propagation for PET Image Segmentation

As recently shown, the AP-based clustering algorithm can optimally delineate PET images without the need for prior information such as the number of clusters and shape/size of lesions (Foster et al. (2014b)). In this study, we integrate both newly designed PVC and denoising approaches into the iterations of this segmentation algorithm for generating a joint solution. In each iteration, solutions of the PVC, denoising, and delineation are updated and fed into the next iteration. This process is repeated until no more change is observed in the delineated regions.

To make the manuscript self-contained, we briefly summarize the AP-based PET image segmentation as follows: AP (Frey and Dueck (2007)) is a general clustering method for partitioning the data into clusters, using a pre-defined similarity criterion between data points. In our previous study (Foster et al. (2014b)), we have adapted AP to find optimal thresholding levels that cluster PET images into multiple distinct regions in an unsupervised manner. The adapted version of the AP is useful for PET image segmentation since AP is efficient, insensitive to clustering initialization, and produces clusters at a low(er) error rate than its alternatives. In Frey and Dueck’s paper (Frey and Dueck (2007)), clustering of the data samples is conducted through a message passing algorithm consisting of two messages between every data point (i.e., voxels in our case) using a similarity criterion: responsibility and availability. Initially, all voxels are considered as exemplars, and responsibility and availability messages are refined iteratively to choose fewer exemplars for the best representation of the clusters. Both responsibility and availability utilize similarity between data points as a driving force for the message passing algorithm.

The similarity function, responsibility & availability messages, and their iterative optimization are summarized in Fig. 2. Note that we use AP clustering to find optimal boundary information with respect to the similarity function, which is a novel and considering intensity level as well as their spatial arrangements together. Further details of the AP-based PET image segmentation method can be found in (Foster et al. (2014b)).

Figure 2.

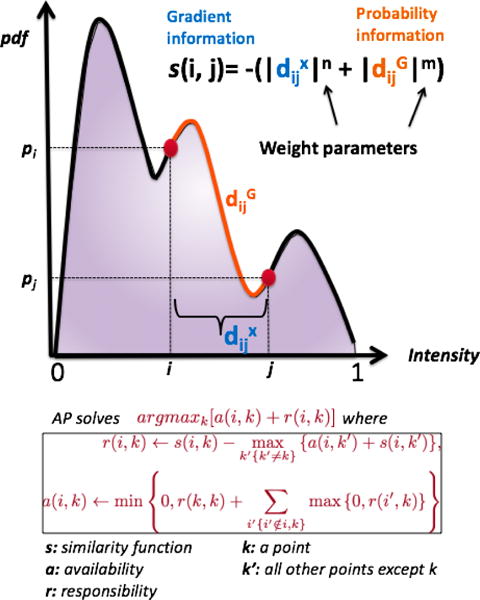
AP uses max-product belief propagation to define representative exemplars through maximizing the objective function of argmax_k[a(i, k) + r(i, k)]. The similarity (s(i, j)) between data point i and point j is obtained from the probability density function (pdf) estimate of the PET image histogram. Note that the larger the probability difference between points i and j is, the smaller the probability of having the same label for data points i and j. Furthermore, $d_{ij}^G$ is the computed geodesic distance between point i and j along the pdf of the histogram, and $d_{ij}^x$ is the Euclidean distance between point i and j along the x-axis. In summary, AP applies the data clustering operation on the pdf of the PET histogram, and separation of the clusters are provided by the optimal threshold(s) obtained from the maximization of the AP function.

Step 3: Regional Means (RM) Denoising

We present a new denoising method called “regional means denoising”, which can be considered as a non-local means based denoising with a new restricted search strategy different from conventional local search. Ultimately, the enhanced image can help AP generate improved delineation that in turn is beneficial to the denoising in the next iteration.

Theoretically, non-local means denoising is performed as follows: For a selected voxel in an image (Buades et al. (2005)), the weighted average of all voxels in the image is computed rather than using solely its neighbors. The non-local means algorithm uses the information of structural patterns within the image by considering the similarity between local patches with a size of N × N × N. However, this process is computational expensive and contains information redundancy due to the fact that the majority of patches can be irrelevant. Therefore in practice, the search of similar patches is generally restricted in a larger “search window” of M × M × M (M > N). This significantly reduced the actual computation, but in the mean time restricted the information utilization. To avoid this restriction, we have applied AP-based clustering algorithm to use object information gauging local patch similarity, thereby waiving the search restriction as follows.

Let J = GAT (I) be GAT transformed correspondence of 3-D PET image I. An observed intensity of a voxel u ∈ Z³ in image J is defined as J(u), and let L denotes the label (i.e., 0,1,2,…) of a voxel u obtained as an outcome of AP-based segmentation. For efficiency and simplicity in algorithmic implementation, class labels are ordered consecutively, such that L (u) > L(v) if J(u) > J(v). Assume also that G denotes a size operation; hence, G (L (u)) simply indicates the number of voxels having the same label as that of voxel u. In the proposed pre-screening approach, regions Ω are searched as follows:

1. Locally search the image with a window size of M × M × M in 3D,

2. Randomly sample min{M³, G(L(u))} voxels in the regions with class label L(u) (candidate region),

3. Randomly sample min{M³, G(L(u) 1)} voxels in the regions with class label L(u) −1 (neighboring region I) if L (u) > 1,

4. Randomly sample min {M³, G (L(u) + 1)} voxels in the regions with class label L(u) + 1 (neighboring region II) if L(u) < max_u L(u).

Here, we introduce additional samples from neighboring regions I and II to avoid potential “artificial boundaries” generated by confined smoothing. For example in Fig. 3, a theoretically homogeneous region could be classified into two groups due to imperfect thresholding under significant noise. Without adding more search regions, these two groups will be denoised separately, which eventually creates an artificial boundary between the two during iterations, leading to false segmentation. By introducing neighboring regions, this “self-reinforcement” effect can be eliminated. This may further be true for even more separations (homogeneous region gets classified into 3 or 4 intensity groups) under severe noise/artifacts, but according to our experiments and from a realistic perspective, we chose the two immediate neighbors.

Figure 3.

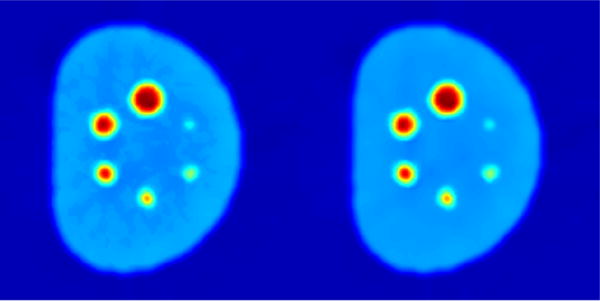
PET denoising results: without (left) and with (right) neighboring regions I and II.

The resulting search region Ω is not restricted to local regions because we use only samples from segmentation. Then, we apply regional means (RM) averaging for recovering the actual value of the voxel u as:

$$RM(u)={\displaystyle \sum _{v\in \Omega }w(u,v)J(v).}$$ (4)

By convention, the weights w(u, v) can be defined based on the similarity between two patches, and, centered at voxels u and v such that

$$w(u,v)=\frac{1}{\mathcal{Z}(u)}{e}^{-\Vert {\mathcal{A}}_u-{\mathcal{A}}_v\Vert {}_2^2/{\mathcal{F}}^2},$$ (5)

where ${\Vert {\mathcal{A}}_u-{\mathcal{A}}_v\Vert }_2$ represents the l₂ distance between two intensity vectors from the two patches, and $\mathcal{Z}(u)$ is a normalizing constant $\mathcal{Z}(u)={\displaystyle {\sum }_v{e}^{-\Vert {\mathcal{A}}_u-{\mathcal{A}}_v\Vert {}^2/{\mathcal{F}}^2}}$. The weighting parameters satisfy the conditions: 0 ≤ w(u, v) ≤ 1 and ${\displaystyle {\sum }_{v}w(u,v)=1}$, and parameter $\mathcal{F}$ determines the degree of filtering. With the information inferred from AP-based segmentation, our technique is capable of covering a sufficient number of voxels that can contribute to the denoising at voxel u. Indeed, as compared with conventional local-search NLM, the proposed method can increase the patch number up to four times. In return, the limited search space is significantly extended, leading to better performance. Histogram smoothing from AP is performed by utilizing a diffusion-based kernel-density estimation that uses the image local information effectively. Performing regional means denoising prior to delineation operation produces more reliable segmentation because smoothly estimated histogram of PET images can lead to better threshold levels maximizing the distance between clusters. More details and rationale are discussed in our previous work (Xu et al. (2014)).

Step 4: Partial Volume Correction (PVC)

A simplified model for true uptake value t and observed image f can be represented by f = t * h + n, where h is PSF of an imaging system, * denotes convolution operation, and n is Gaussian noise, which will be handled with regional means denoising algorithm in step 3. Here for partial volume correction, we followed the method of RBV (region-based voxel-wise) (Thomas et al. (2011)) by incorporating reliable object information from AP-based segmentation. The incorporation of object information into the PVC helps recover true uptake distribution with low error and high efficiency. Specifically, to benefit from object information in step 2, a region definition from AP-based delineation is used to estimate the spill-over followed by the GTM method (Rousset et al. (1998)). GTM is used to obtain estimates of the true mean values within all regions. Since AP-based delineation algorithm is known to be optimal in multi-region segmentation in PET images, inclusion of an effective object definition in PVC is guaranteed. At the end of this process, an intermediate image is created as s (p) = g_i, ∀p ∈ b_i where g_i is the GTM corrected value of voxels within ith region of the segmented image b, obtained from the delineation step. Note that it is assumed that b includes non-overlapping regions z > 1 (i.e., segmented clusters) such that $b={\cup }_{i=1:z}{b}_i$, and g_i is a single scalar value determined from the region i through GTM correction. Then following RBV (Thomas et al. (2011)) method, the final voxel-wise correction is perform by multiplying with by a correction term calculated from the GTM corrected image and the point-spread function (Thomas et al. (2011)).

We incorporate object information into the PVC with a parameter called the volume consistency weighting parameter, which is calculated based on Dice Similarity Coefficient (DSC) between current and previous iteration of the segmentation process resulted from step 2: c_i = DSC(b_i, b_i+1). Note that DSC indicates the accuracy of volume overlap between two segmentations (b_i, b_i+1). By setting t₀ = f, PVC for a given voxel p is then performed as

$$t_{i+1}(p)=t_i(p)+c_i\cdot f(p)\cdot \left(\frac{s_i(p)}{s_i(p)\ast h}-1\right).$$ (6)

It is worth mentioning that a global control factor is applied to prevent PVC for a given pixel to be larger than 1 (i.e., boundary condition). At each step, a maximum fraction of the correction is allowed, which is further factored by DSC. The accumulative correction is monitored and stopped at 1 or before. If segmentation convergence has not been reached at 1, further steps will no longer have PVC, and a message will be generated suggesting users to adjust the parameter (although it is rare, this may happen with quick convergence only). If early stop happens, then additional PVC will be applied at the end. The proposed algorithm has been designed to reflect all these scenarios in a practical manner. In this way, higher degree of PVC is applied to later iterations when segmentation becomes stable (i.e., higher c_i value), implying a more precise estimation of the uptake region.

3. Experiments and Results

3.1. Data

To evaluate denoising, PVC, and segmentation performances, we used three data sets: (i) phantom, (ii) clinical, and (iii) pre-clinical PET scans. Phantom images were used for precise evaluations of the proposed framework since ground truths were available. We have also included clinical PET scans in our experiments to test our system’s performance in routine practice. Furthermore, due to a wide range of applications of PET imaging in pre-clinical studies, we extended our experiments to include small animal PET/CT scans and showed robustness and generalizability of our system.

Phantom data

In our experiments consisted of 20 PET-CT images obtained from two different NEMA phantoms with different reconstruction parameters. The first phantom is from the RIDER PET-CT phantom collection (Clark et al. (2013)), containing six spheres with diameters of 10, 13, 17, 22, 28, and 37 mm; background activity concentration was 0.44 uCi/ml, and hot sphere concentration is 1.75 uCi/ml. Images were reconstructed using 3D-OSEM algorithm. The spatial resolution was 128×128×47 with a voxel spacing of 2.73 × 2.73 × 3.27 mm, and the image intensities were in units of Bq/ml. The second phantom had five spheres with diameters of 4, 5, 6, 8, and 10 mm. The true activities were 32.2 mCi/ml in the spheres and 6.2 mCi/ml in the background. The spatial resolution was 256×256×95 with a voxel spacing of 0.95 ×0.95 ×1.90 mm, and the image intensities were in units of mCi/ml. These ground truth activity concentrations and CT correspondence allowed us to evaluate our proposed method’s performances reliably.

Clinical data

20 human PET/CT and 20 PET/MR images pertaining to patients diagnosed with different cancer types (i.e., lung, colon, and hereditary leiomyomatosis renal cell cancer) were collected after the IRB approval. For PET/MR, dixon sequence for attenuation correction and T2-weighted sequences for anatomic allocation were used for reconstruction (mMR, Siemens). The spatial resolution of the PET images was 172×172 in-plane with varying number of slices (i.e., 189 to 211), and had a voxel spacing of 4.17×4.17×2.00 mm. There was no need to re-register images as they were already in registration, due to the nature of hybrid imaging modalities. A subset of PET/CT and PET/MRI were obtained from the same patients who underwent both scanning in one week interval. Patients were injected with 8.82-10.79 mCi of ¹⁸F-FDG radiotracer and imaged 58-150 min(s) post-injection. A fully 3D ordered subset expectation maximization (3D-OSEM) algorithm was used for PET image reconstruction.

Pre-clinical data

20 PET scans obtained from 5 rabbits (4 longitudinal scans from each animal) were tested. The rabbits were aerosol infected with Mycobacterium Tuberculosis (Kbler et al. (2015)). Such pulmonary infection cases feature distributed metabolic activities with diffuse or multi-focal radiotracer uptake, leading to more challenging problems of partial volume, noise, and segmentation to be handled. The rabbits were injected via the marginal ear vein, with 1-2 mCi of 18F-FDG radiotracer and imaged 45-min post-injection with 30 min static PET acquisition. The spatial resolution was 128×128×120 with a voxel spacing of 1×1×1 mm. PET images were reconstructed using 3D OSEM (nanoScan, Mediso).

3.2. Evaluation on Method Convergence

The stopping criteria of the overall system is based on the DSC greater than a pre-defined threshold between two iterations. We defined the value of threshold to be 95%. The AP algorithm (Foster et al. (2014b)) accepts 200 maximum iterations for convergence, and it takes less than a second to segment one slice. Overall, implemented in pseudo-3D manner (slice-by-slice), the proposed algorithm mostly stops before 10th iteration for all experimental data, and the average processing time is 5 seconds per slice.

3.3. Evaluation of Denoising

We compared the proposed denoising strategy’s performance with commonly used PET image denoising methods including Gaussian filtering, anisotropic diffusion, and more advanced approaches such as non-local means and block matching (Dabov et al. (2007)). All methods were performed after GAT stabilization for a fair comparison because as we showed in our earlier publication (Mansoor et al. (2014)) that denoising without GAT is inferior to results with GAT in all instances. We also removed the PVC block from the proposed method for showing the effect of denoising method itself without the contribution of PVC (i.e., PVC enhances the noise). In addition, note that although non-local means has been adopted for dynamic PET image denoising (Dutta et al. (2013)) and denoising with anatomical prior (Chan et al. (2014)), a proper way to apply it for static PET image without external anatomical information has not been well investigated. In this work, we included non-local means with anatomical prior (Chan et al. (2014)) for comparison. Several parameters had been experimented for each of the methods in comparison, and a set of parameters resulting in a similar quantitative gradient value at ROI boundaries and visually-comparable structural preserving results have been selected.

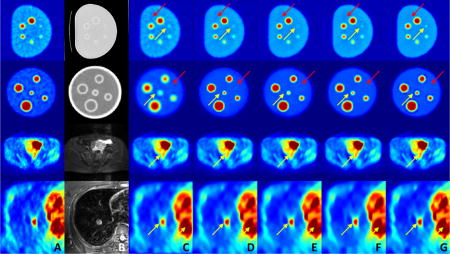
Quantitative parameters for noise reduction, including SNR and max/mean uptake value, were computed for all uptake regions from several regions of interests (ROIs). The ROIs were identical for both original and filtered images. ROIs were drawn by experts, mainly over anatomical structures with uniformity assumption. For phantom analysis, all spheres and nearby background regions were selected for the evaluation. For human images, to ensure structure definition, a subset of human data with all three PET/CT/MRI modalities has been used. For qualitative evaluations, results at sample slices from both phantom and human images are shown in Fig. 4. As shown, the proposed method achieves greater noise reduction while preserving fine details from over-smoothing/blurring. Also note that non-local means with anatomical prior relies heavily on the quality of anatomical guidance. It performs similar to conventional non-local means with relatively weak anatomical prior (top two rows), while generating crisper edges with stronger anatomical information (bottom two rows). However, it can also lead to artificial discontinuities due to the anatomical boundaries (last row).

Figure 4.

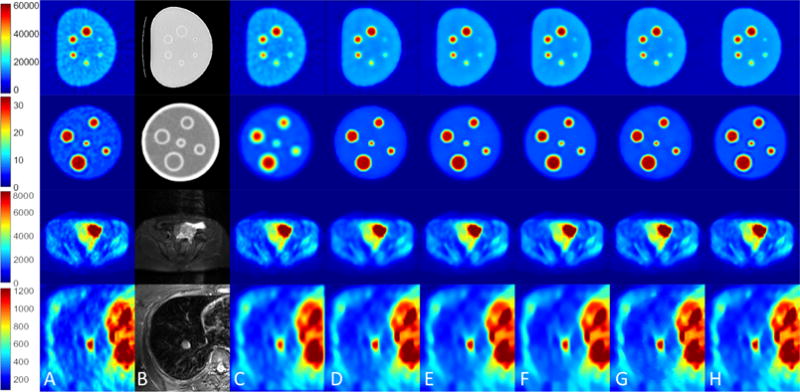
Qualitative evaluations for denoising: (A) PET images, (B) the corresponding anatomical images (CT and MR), (C) Gaussian filtering, (D) anisotropic diffusion, (E) non-local means, (F) block matching, (G) non-local means with anatomical prior, and (H) the proposed method. Colorbar corresponds to raw data numbers (counts).

Furthermore, relative contrast (RC) was calculated from measuring object-to-background contrast, which is not revealed by SNR. SNR and RC are conventionally defined as:

$$\begin{gathered} \mathit{SNR}={\mu }_{\mathcal{L}}/{\sigma }_{\mathcal{L}}, \\ RC=\left|{\mu }_{\mathcal{H}}-{\mu }_{\mathcal{L}}\right|/\sqrt{{\sigma }_{\mathcal{H}}{\sigma }_{\mathcal{L}}}, \end{gathered}$$ (7)

where ${\mu }_{\mathcal{H}}$, ${\mu }_{\mathcal{L}}$, ${\sigma }_{\mathcal{H}}$, and ${\sigma }_{\mathcal{L}}$ denote the mean and standard deviation of high/low uptake regions. For denoising methods to be effective, two most commonly used imaging markers for PET images, SUV_max and SUV_mean, are expected to be not degraded after denoising.

Table 1 presents the quantitative results with the following parameters: SNR, RC, max/mean intensity value reduction rate (RR) and the ratio of uptake values in comparison with ground truths (phantom). In RR, we used both for object ratio (OR) and background ratio (BR) for relative comparison. Since the ground truth uptake value is known for the phantom image, these two evaluations provide us the information regarding how much suppression is resulted from denoising. In experimental results, the proposed method outperformed other methods in all quantitative metrics. Note that for clinical data (i.e. human subjects (H)), OR and BR were not available because the true local uptake value was unknown unlike in the phantom case (i.e., P).

Table 1.

Quantitative evaluations for the proposed denoising strategy in comparison with other methods are presented. P: phantom; H: human. Higher SNR, RC, OR, BR, and lower max RR, mean RR indicate better performance. We have chosen only a subset of PET images from PET/CT and PET/MRI because half of the imaging data were obtained from the same patients who have underwent both scanning in one-week interval.

	SNR		RC		Max RR		Mean RR		OR	BR
	P	H	P	H	P	H	P	H	P	P
Original	11.73	7.08	11.32	34.14	0%	0%	0%	0%	59.28%	85.02%
Gaussian	15.62	7.01	12.88	27.76	11.08%	9.27%	9.55%	5.51%	53.99%	85.21%
Diffusion	21.05	7.25	16.38	33.98	13.20%	7.20%	7.37%	3.37%	55.99%	85.72%
Non-Local Means	21.88	7.69	13.70	37.67	13.27%	7.04%	11.03%	3.61%	54.41%	85.89%
Block Matching	20.36	9.92	14.02	39.97	7.32%	6.96%	6.87%	3.59%	56.27%	85.41%
Anatomical Prior	21.73	8.41	14.62	40.33	9.68%	6.92%	6.31%	2.14%	56.73%	85.85%
Proposed Method	35.55	11.82	19.15	52.40	2.97%	3.55%	2.61%	1.29%	58.24%	86.26%

3.4. Evaluation of PET Image Segmentation

Segmentation analysis was applied only to phantom data with ground truth, since it does not require multiple annotators to evaluate surrogate of the truth as in real cases. DSC and Hausdorff distance (HD) were calculated for quantitative evaluation of segmentation results. High DSC and low HD values were obtained as follows: 92.75% for DSC and 3.14 mm for HD (pixel size of 2.73 × 2.73 mm), indicating highly satisfying delineation performance. Without denoising and PVC steps, the resulting average DSC and HD values were found to be 74.7% and 6.59 mm, respectively. The main reason for improving segmentation results with denoising is the improvement in the similarity function definition, where removing noise increases the similarity of the voxel intensities. Similarly, the PVC method improves true values of the voxel intensities; hence, similarity function of the AP.

3.5. Evaluation of PVC method

To quantitatively evaluate the performance of the proposed method, we used PET/CT images of the NEMA phantom. With phantom images, the ground truth regarding the precise boundaries of multiple spheres (representing the lesions with different sizes), as well as the true uptake values, which the partial volume correction attempted to recover, were known. Fig. 5 shows the intensity profiles along three example lines (marked as 1, 2, 3 in Fig. 5) before (Fig. 5(A), red) and after (Fig. 5(B), blue) applying the proposed PVC algorithm. Final segmentation is shown in Fig. 5(C). Finally, Fig. 5(D1-D3) depicts the results obtained from the proposed volume-consistency based PVC. In comparison, Fig. 5(E1-E3) denotes the result with evenly distributed weights instead of volume-consistency weights, and Fig. 5(F1-F3) shows the result obtained from the conventional deconvolution approach (Gallivanone et al. (2011)). As can be seen, the proposed algorithm successfully corrects PVE for different-sized objects successfully while minimizing the noise and segmenting the image. Note that for the evenly distributed weights (E1-E2), the signal was preserved, but not well-recovered to its theoretical value (almost unchanged). It could be due to false correction at earlier stages (region boundaries falsely identified), leading to ineffective recovery, which is further suppressed by denoising.

Figure 5.

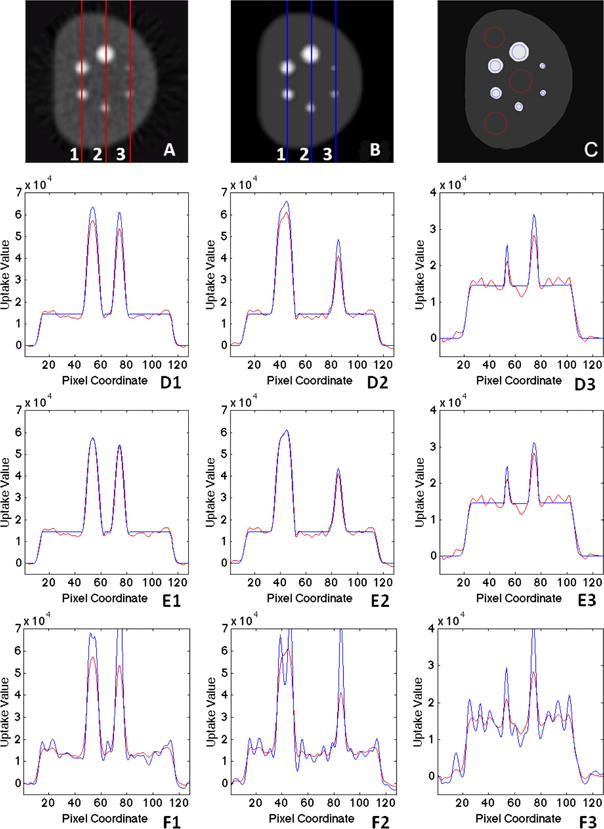
Intensity profile along three (1, 2, 3) sample lines in PET image (A) before and (B) after PVC with (C) showing the grouped final AP segmentation result with object (blue) and background (red) ROI definition: (D1-D3) the proposed method with volume consistency weights. (E1-E3) the proposed iterative method with evenly distributed weights, and (F1-F3) deconvolution method.

Fig. 6 presents the quantitative results of the proposed PVC, compared with true object and background regions for the phantom images (i.e., ground truth). Phantoms were used as baselines for PVC, and the ratio was calculated to test the performance of the PVC methods; the perfect correction was indicated by a ratio of 1. As illustrated in Fig. 6, the proposed method promoted the signal strength while keeping it around 1. Gibbs effect and overshooting were observed in deconvolution-based method (as much as 40%). We compared our method with two widely used PVC methods from the literature (RBV (Thomas et al. (2011)) and Iterative-Yang (Erlandsson et al. (2012))). We used publicly available implementation from (Thomas et al. (2016)). As can be depicted from Fig. 6, the proposed iterative method with evenly distributed weights has almost the same PVC performance with the state-of-the-art methods. While RBV method utilized the GTM approach voxel-by-voxel, GTM provided the regional values for the segmented regions. On the other hand, Iterative-Yang algorithm estimated the region mean values within the 5 iteration loop and very similar to RBV algorithm. Note that these state-of-the-art methods rely heavily on the pre-defined segmentation map, which is often obtained from CT or MRI. For PET-only cases, it is very important that the mask is as accurate as possible, and a carefully selected manual threshold plays a critical role in generating the mask as an input to PVC algorithm. Last, but not least, overall uptake ratio may be good in those methods, but for small lesions, an artificial appearance (discontinuity in local uptake distribution) is inevitable. In our case, the proposed method did not impose any of these limitations.

Figure 6.

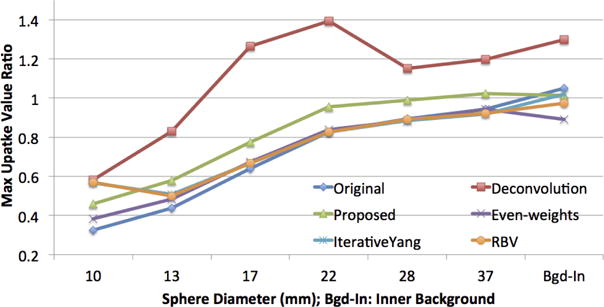
Quantitative evaluations for the PVC: max uptake value ratio within ROIs as compared with phantom truth and two state of the art methods (RBV (Thomas et al. (2011)) and IterativeYang (Erlandsson et al. (2012)).)

3.6. Evaluation on Human PET/CT and MRI/PET Scans

We used human PET/CT and PET/MRI scans, for which there was no “ground truth” available. Hence, we measured relative SNR and RC values for all ROIs defined by expert interpreters. Also, the percentage change in SUV_max and SUV_mean were computed for which, a small change is desirable for the precise denoising approach. Fig. 7 and Fig. 8 illustrate the results for the proposed joint solution for PET/CT and PET/MR images, respectively. Blue and red circles show the regions used to compute RC (high and low contrast regions) percentage change in SUV_max and SUV_mean. We also included a measure of kurtosis for evaluation of denoising algorithms, since noise variation is linked to kurtosis of the local regions and studied extensively in the literature for estimating unknown noise level (Zoran and Weiss (2009)). With kurtosis-based evaluation, lower kurtosis value (obtained from a local region) indicates a lower standard deviation of the noise pertaining to that region. Therefore, instead of measuring noise variation, which is rather difficult or impossible to measure, without prior assumptions, kurtosis can be used to estimate the underlying noise level of the images.

Figure 7.

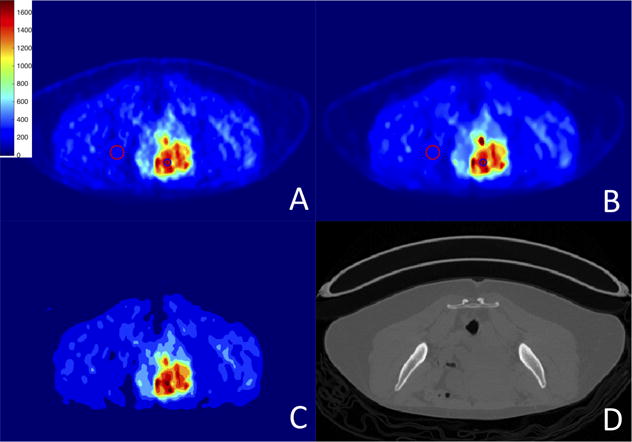
PET/CT scans: (A) original image; (B) after PVC and denoising; (C) final segmentation result; (D) corresponding CT image. Colorbar corresponds to raw data numbers (counts).

Figure 8.

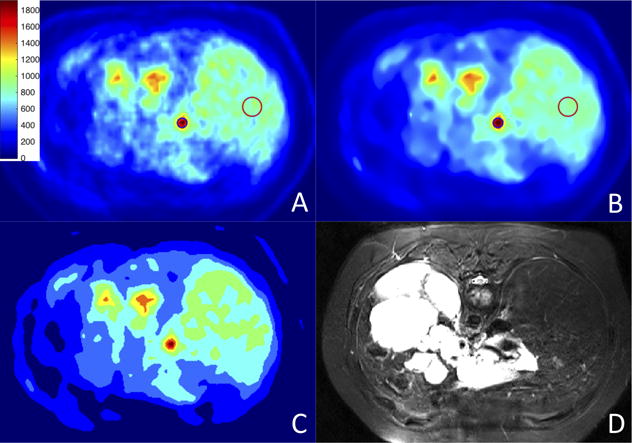
PET/MRI scans: (A) original image; (B) after PVC and denoising; (C) final segmentation result; (D) corresponding MR image. Colorbar corresponds to raw data numbers (counts).

Kurtosis (κ) can be defined as $\kappa \left(X\right)=C_4\left(X\right)/C_2^2\left(X\right)$ where C_k(.) is the k-th cumulant function. Table 2 presents the quantitative metrics of SNR, RC, kurtosis, rate of change in SUV_max & SUV_mean, and R_max and R_mean of the ROIs. Since PVC promotes the signal, both SUV_max and SUV_mean were greater than the corresponding values in unprocessed images. RC were higher in denoised images due to improved contrast. Similarly, kurtosis was found to be lower in denoised images owing to less variation in noise level.

Table 2.

Denoising performance of the proposed method on clinical and pre-clinical images. High SNR, RC; low kurtosis and low uptake change rate indicate superior performance.

		PET/CT	MRI/PET	Preclinical
SNR	Original	8.67	16.02	3.37
	Proposed	23.79	39.70	7.54
RC	Original	26.17	8.38	29.26
	Proposed	49.70	14.13	41.08
Kurtosis	Original	2.51	3.80	4.48
	Proposed	2.21	2.72	2.33
Uptake Change Rate	SUVmean	1.8%	5.11%	3.14%
	SUVmax	3.47%	6.28%	3.09%

3.7. Evaluation on Small Animal PET Scans

Fig. 9 shows original, denoised and corrected, and segmented images pertaining to small animal PET images. These images served as small animal models for infectious disease: unlike cancer cases, uptake patterns often appear as multi-focal and diffuse. Therefore, it is quite challenging to correct partial volume for high uptake regions. AP is well suited to delineate such uptake regions as shown previously in our study (Foster et al. (2014b)). Then, object information can be used to simplify PVC strategy. Table 2 (last column) presents the quantitative results of SNR, RC, SUV_max and SUV_mean change rate of the ROIs pertaining to the pre-clinical PET scans.

Figure 9.

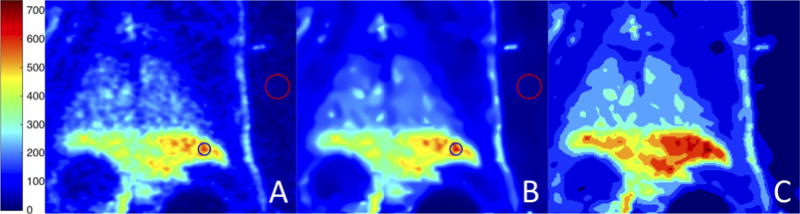
Pre-clinical PET scans: (A) original image; (B) after PVC and denoising; (C) final segmentation result.

3.8. Quantitative Evaluations With Respect to Image Quality

SNR, RC, and kurtosis can be considered as the image quality factors in PET imaging. While we use SNR to reflect the quality factor of noise, we use RC (relative contrast) to obtain contrast and sharpness information from the images, and kurtosis to estimate the standard deviation of the noise locally. In our experiments, we noticed that our algorithm works best when both SNR and RC are high, and kurtosis is low. Furthermore, we did not observe any cases where the algorithm fails to improve image quality (SNR, RC, kurtosis). Relatively less improvements were obtained when image SNR or RC was too low. While the average of lowest SNRs in all experiments was 3.37 (from preclinical studies), more than 100% improvements were obtained. This was the same for RC and kurtosis-based evaluations. It is also noteworthy to mention for images even with low SNR, RC, and kurtosis (indicating lower image quality, high noise, and artifacts) were improved with the presented framework.

3.9. Visual Assessment by Expert Interpreters

For qualitative assessment of denoised and partial volume corrected PET images, two expert interpreters (double-boarded by radiology and nuclear medicine, and having more than 15 and 10 years of experiences, respectively) ranked the output of five different methods based on the overall quality for diagnostic purposes on all clinical PET/CT and PET/MR images: Gaussian, anisotropic diffusion, non-local means, block matching, and the proposed. Sample images were labeled as “Method 1” to “Method 5” without revealing the specific algorithm, and the experts rated the sample images from 1-to-5, 1 being the best and 5 being the worst in terms of visual/diagnostic quality. Note that this evaluation accounts for human perception, rather than for computerized analysis, and the visual judgment from experts can be quite subjective based on one’s individual preferences.

In total 50 samples were included in this study. Images for a single subject were randomized and presented simultaneously to viewers. Viewers were asked to evaluate the overall quality of each image based on the clarity of large and small regions, noise level, strength of the edges by assessing continuity of the borders, smoothness level, and visible (expected) texture. Table 3 listed the summary of this qualitative evaluation. As shown from the result, all filtered images were significantly better than the original images, and the proposed method consistently performed better than all other methods. For the methods of anisotropic diffusion, non-local means, and block matching, the two human experts have different opinions on the performance of anisotropic diffusion v.s. block matching, and non-local means denoising was rated slightly higher than those two (i.e., lower the rate, better the method). We have also compared these five methods’s results with paired t-test. The results were found to be statistically significantly different from each other (P< 0.05).

Table 3.

Qualitative evaluation result for different methods.

	Expert 1 Score		Expert 2 Score
	Mean	Stdev	Mean	Stdev
Original Images	5	0	4.76	0.66
Anisotropic Diffusion	2.34	0.66	3.08	1.07
Non-local Means	3.86	0.35	3.52	0.65
Block Matching	2.8	0.49	2.5	0.93
Proposed Method	1	0	1.14	0.35

4. Discussion

We proposed a generalized framework for jointly solving three major problems pertaining to PET image interpretation and analysis: PVC, segmentation, and denoising. Individual effects of these major problems on diagnostic decisions have been largely studied in the literature (Foster et al. (2014a); Bagci and Mollura (2013); Erlandsson et al. (2012)). In this study, we confine ourselves to image quality assessment and correctness of the image quantification parameters from a system point of view; therefore, detailed exploration of each effect in purely clinical cases is kept outside the scope of this paper.

As it was mentioned in the beginning, the detailed characteristics of the PET image noise is not entirely known. Positron emission itself is well characterized by a Poisson distribution, but Gaussian noise assumption is often being considered in the literature due to other noise characteristics coming from scanner’s detection system as well as other electronic components in the scanner. Resulting noise is further altered during image reconstruction and correction steps. However, noise realizations are shown to be conflicting with this assumptions as shown in different studies (Vardi et al. (1985); Rzeszotarski (1999)). In Teymurazyan et al. (2013), authors have evaluated statistical properties of the PET data and compared five noise models (Poisson, normal, negative binomial, and Gamma). Authors have showed that different reconstruction techniques could affect the type of noise. For instance, RAMLA-reconstructed PET images are well characterized by Gamma distribution while filtered back projection based reconstructed PET images produce comparable conformity with both normal and Gamma statistics. It was also indicated in the study that the noise was neither Gaussian nor Poisson. Although this study showed evidence of noise statistics as a combination of Gaussian and Poisson, authors have chosen to model the combined model as a Gamma distribution instead of mixed Poisson-Gaussian. In our current effort, instead of relying on a single Gamma distribution, we model the noise without restricting its distribution either into Gamma noise either, because Gamma model is not as flexible as a mixture model of Poisson-Gaussian. Note that the Gamma distribution is deeply intertwined with more Poisson distribution than Gaussian. It is because converging Gamma into Gaussian requires a large shape parameterization, which may not be desirable for a flexible noise distribution modeling (Kotlarski (1967)).

GAT has a significant role in the proposed framework but it is also desirable to identify when GAT has the most and least roles. We observed the following facts, which are overlapping with the findings from the literature: (1) when noise variation across different patches is small, GAT has a minimal role. This is expected because the underlying noise distribution in the image is almost Gaussian. (2) Conversely, GAT is the most effective when variation of noise is large, implying that the underlying noise distribution is almost Poisson. It is worth noting that mixture of Gaussian and Poisson with an analytic formulation depicted in Eq. 1 allows us to switch the noise model either into fully Gaussian nature or the opposite (i.e., fully Poisson). With a proper parameter tuning, weight of each model can be arranged accordingly. Since GAT will not distort images that are already with Gaussian noise, it will be more effective when the noise is mixed. In order to ensure that GAT behaves properly, we used a non-classical SVT (i.e., generalized Anscombe’s transform: GAT) where GAT encompasses the suffers that Anscombe’s original formulation may have when there are too high variation in the PET images.

It should be noted that PVC is comparatively more challenging in pre-clinical imaging where sizes of structures are very small relative to the achievable resolution on pre-clinical PET scanners. PVC studies in this aspect are limited, and available methods are often tuned for clinical studies. In our work, the proposed joint solution is general enough that both clinical and pre-clinical images were partial volume corrected, denoised, and segmented successfully. One of the limitations of our work is that the correction of motion effects is not considered within the scope of this paper. Motion, due to cardiac, respiratory, or patient movement, is another factor that can introduce additional distortions. Herein, we confine ourselves to PVC without specifically characterizing the source of PVE.

There are numerous parameters in our proposed framework due to the integration of three major frameworks. One may wonder if those parameters are set during the iterations of the system or a priori. In our current implementation, most parameters were learned from representative image samples prior to the experiments, and they were kept the same during iterations of the proposed system. One also may wonder if there is a substantial theoretical proof about the mixed noise model where two important parameters are being used to weight Poisson and Gaussian portion. To our best of knowledge, there is no theoretical proof yet confirming the theoretical optimality of the inversion and noise minimization except the work in (Mansoor et al. (2014)) where we experimentally showed how GAT de-correlate non-Gaussian noise. Since GAT is known to perform well when noise is Poisson, this information partially proves the mix nature of the Poisson and Gaussian.

Although this study is focused on a post-reconstruction algorithm for PVC and noise removal, it should be noted that there are strong aspects of reconstruction driven PVC and noise reduction methods that make them attractive (Barrett et al. (1994); Xu and Tsui (2009); Ding et al. (2016)). Since post-reconstruction based PVC algorithms can increase both respiratory-gated and non-gated values significantly, a significant source of error may appear when quantifying lesions particularly at lung regions. Instead, reconstruction driven PVC methods with distance dependent PSF and motion incorporation can easily alleviate this problem. However, both motion and variable PSF integration into the reconstruction algorithm is not straightforward and requires experimental validations.

Our proposed joint solution requires a delineation method to be accurate, and provides feedback on multiple tissue types (with respect to the level of uptake). Therefore, any segmentation method providing this information can be replaced by AP-based segmentation algorithm. In this sense, our joint solution platform is flexible, and open to further improvements. Depending on the application, the strength and weakness of the proposed framework can both lay on the integrated system. On one hand, the three tasks can be mutually beneficial to each other and improve the performance; on the other, the proposed method makes it difficult to decouple one from each other, and thus the computational cost is naturally higher if only one function is needed. We have further qualitatively experimented some variations of the proposed method by replacing certain components. Specifically, we have done the following three: replacing RBV correction with conventional deconvolution; replacing regional means denoising with anisotropic diffusion; and replacing affinity propagation segmentation with k-means clustering. The results are shown in Fig. 10, as shown, with regular deconvolution, there will be a smoothed ringing artifact, while with anisotropic diffusion, there will be residual noise. As for k-means clustering, we find that the result are almost identical with reasonable choice of clusters, indicating that for PVC and denoising, our method is not sensitive to clustering method.

Figure 10.

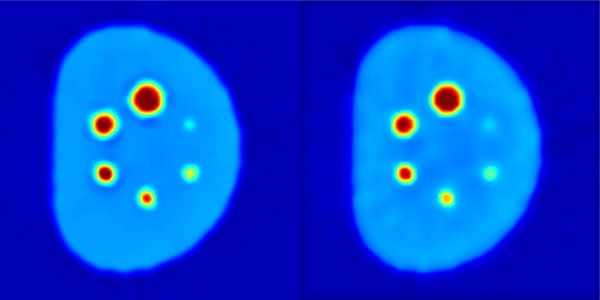
Replacing RBV correction component with deconvolution(left) and replacing regional means denoising with anisotropic diffusion (right).

There are studies in the literature showing joint segmentation of PET/CT and PET/MRI (Bagci et al. (2013b); Song et al. (2013); Xu et al. (2015)), and even denoising approach utilizing both PET and MRI was proposed based on wavelet coefficient exchange between structural and functional images (Turkheimer et al. (2008)). In the present research, we did not explore joint denoising, PVC, and segmentation of anatomical structures (from CT or MRI). These studies summarize the benefit of using effective anatomical information in PET image analysis tasks. As an extension to the current study, a similar system can be built for CT/MR images where both anatomical and functional images can be utilized. It should also be noted that for MR images, there will be additional steps such as intensity inhomogeneity correction and standardization prior to denoising (Bagci et al. (2012, 2010)).

In radiology and nuclear imaging sciences, visual assessment is often accepted as ground truth evaluation or complementary qualification. However, human visual judgment can be quite subjective, especially for tasks without definite answer. Even experts can have significant variations. During qualitative evaluation, some experts may give preference to low noise level and clearly-defined structure boundaries for its clarity in diagnosis; while others may view similar patterns as “artificial” and consider moderate amount of noise as more “realistic”. Despite potential biases, qualitative judgment is still desirable to be used in real clinical settings, and it is more powerful when combined with quantitative results. In our experiments, potential uncertainties due to these variations are explained.

5. Conclusion

We presented an effective framework for generating a joint solution for PET image denoising, partial volume correction, and segmentation. We incorporated uptake region delineations into the novel regional means denoising technique to enhance the SNR, which in turn helps improve the segmentation and PVC accuracies. We utilized generalized Anscombe transformation, and its optimal inverse before and after the denoising-segmentation procedure, which essentially Gaus-sianize the noise in PET images under the mixed Poisson-Gaussian model. For PVC, we used a new volume-consistent voxel-wise correction method where effective use of the object information was inferred from the segmentation iterations. Experimental results demonstrated that the proposed joint solution framework successfully removes the noise, corrects the partial volume effect, and delineates uptake regions with high efficacy.

Highlights.

• Interactions among segmentation, denoising, and partial volume corrections have been utilized to improve solution of each of these problems for PET images.

• Noise in PET imaging is modeled as mixed Poisson-Gaussian, as it is more realistic than the current standards.

• Partial volume correction is shown to improve when segmentation and noise information are incorporated into the proposed joint solution model.

• Segmentation process gets benefit from denoising and partial volume correction step, leading to improved boundary definitions of lesions in PET images.

• Extensive set of experiments (phantom, pre-clinical, and clinical) with PET, PET/CT, and PET/MRI validate the proposed algorithm?s performance.