Abstract
Objective: Quality assurance of large ontological systems such as SNOMED CT is an indispensable part of the terminology management lifecycle. We introduce a hybrid structural-lexical method for scalable and systematic discovery of missing hierarchical relations and concepts in SNOMED CT.
Material and Methods: All non-lattice subgraphs (the structural part) in SNOMED CT are exhaustively extracted using a scalable MapReduce algorithm. Four lexical patterns (the lexical part) are identified among the extracted non-lattice subgraphs. Non-lattice subgraphs exhibiting such lexical patterns are often indicative of missing hierarchical relations or concepts. Each lexical pattern is associated with a potential specific type of error.
Results: Applying the structural-lexical method to SNOMED CT (September 2015 US edition), we found 6801 non-lattice subgraphs that matched these lexical patterns, of which 2046 were amenable to visual inspection. We evaluated a random sample of 100 small subgraphs, of which 59 were reviewed in detail by domain experts. All the subgraphs reviewed contained errors confirmed by the experts. The most frequent type of error was missing is-a relations due to incomplete or inconsistent modeling of the concepts.
Conclusions: Our hybrid structural-lexical method is innovative and proved effective not only in detecting errors in SNOMED CT, but also in suggesting remediation for these errors.
Keywords: SNOMED CT, ontology, quality assurance, non-lattice subgraph
OBJECTIVES
SNOMED CT is the most comprehensive clinical health care terminology worldwide, and its use is mandated in the United States as a part of the Meaningful Use incentive program. Quality assurance is an indispensable part of the lifecycle management of biomedical terminologies, including SNOMED CT.1 However, quality assurance of such a large terminology system is difficult due to its sheer size and complex structure. Effective, automated approaches for improving the quality of SNOMED CT are needed to overcome the limitations of manual work.
In this paper, we introduce a novel approach to systematically identify inconsistencies, which may manifest missing hierarchical relations and concepts in SNOMED CT, based on the structural properties of non-lattice subgraphs and the lexical properties of concepts involved in these subgraphs. A random subset of subgraphs automatically generated using this approach was reviewed by domain experts to confirm the uncovered inconsistencies.
BACKGROUND AND SIGNIFICANCE
SNOMED CT
Biomedical ontologies play an important role in health care information management, biomedical information extraction, and data integration.2 SNOMED CT, managed by the International Health Terminology Standards Development Organisation (IHTSDO), is the largest clinical terminology worldwide. SNOMED CT supports the development of high-quality electronic health records (EHRs) and facilitates information retrieval, semantic interoperability, and clinical decision support and quality measures.3,4 Under the Health Information Technology for Economic and Clinical Health Act,5 SNOMED CT has been required in the United States for encoding relevant clinical information in certified EHR systems.6
SNOMED CT contains over 300 000 concepts organized in 19 top-level hierarchies including Clinical finding, Procedure, Body structure, and Substance. Each concept in SNOMED CT represents a unique clinical meaning and is assigned a unique identifier, as well as a unique fully specified name. There are over 1 360 000 relations among these concepts, relating concepts using subtype relationships (aka is-a) and attribute relationships (eg, associated morphology, causative agent, finding site).7
Quality assurance of SNOMED CT
Given the size and complexity, it is unavoidable that errors are introduced in SNOMED CT as part of its development, update, and maintenance lifecycle. It is impractical for domain experts to systematically detect errors and inconsistencies purely based on manual review. Automatic and effective approaches to quality assurance are highly desirable, moving the role of domain experts into reviewing and confirming automatically uncovered error candidates and, ideally, correcting these errors in subsequent versions.
Researchers have proposed lexical, structural, and semantic methods for auditing and quality improvement of biomedical terminologies.8–10 Bodenreider et al.11 evaluated the consistency of SNOMED using lexical methods. Agrawal and Elhanan12 proposed a lexical method to detect inconsistencies in the formal definitions in SNOMED CT. Jiang and Chute13 audited the semantic completeness of SNOMED CT using formal concept analysis, a structural method, and identified missing concepts. Rector and Iannone14 audited the use of common qualifiers in SNOMED CT definitions by combining lexical and semantic techniques. Wang et al.15–17 proposed structural methodologies based on abstraction networks to detect erroneous concepts in SNOMED CT. Ochs et al.18,19 presented subject-based and “tribal-based” abstraction network methods to audit SNOMED CT. Zhang and Bodenreider20,21 proposed a lattice-based approach to structurally and exhaustively audit SNOMED CT.
Lattice-based structural auditing of SNOMED CT
A lattice is a specific type of directed acyclic graph such that any 2 nodes have a unique maximal common descendant, as well as a unique minimal common ancestor. A lattice is a desirable structural property for a well-formed ontology.20–22 The philosophical and mathematical reason for this can be elucidated using formal concept analysis, a theory for formalizing concepts and concept hierarchies (or ontologies) from a collection of objects and their attributes. Each concept represents the set of objects (called extension) that share the same attributes (called intension) of the concept. The concept hierarchy derived always forms a complete lattice.23,24
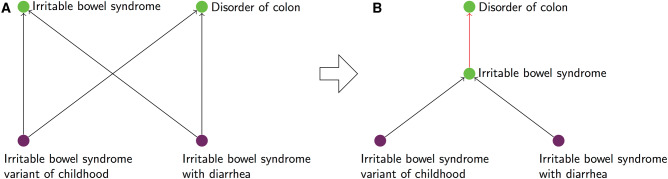
Concepts in SNOMED CT can have multiple parents and are structured as a rooted directed acyclic graph with respect to the is-a taxonomic relationship. However, the SNOMED CT concept hierarchy does not form a lattice.20 This suggests that investigating concept pairs that violate the lattice property (or non-lattice pairs) provides a mechanism for identifying potentially problematic fragments in SNOMED CT, regardless of the type of error involved (eg, missing intermediary concept, missing hierarchical relation). For example, in Figure 1A the concept pair Irritable bowel syndrome variant of childhood and Irritable bowel syndrome with diarrhea have both Irritable bowel syndrome and Disorder of colon as shared parents. A hierarchical structure in which 2 concepts have multiple shared parents is a special case of non-lattice fragment. Moreover, Irritable bowel syndrome is not classified as a Disorder of colon, as it should be. This is a typical example of a missing is-a relation causing a non-lattice fragment. If Irritable bowel syndrome was placed as a child of Disorder of colon, Irritable bowel syndrome variant of childhood and Irritable bowel syndrome with diarrhea would only have Irritable bowel syndrome as a single shared parent and the hierarchical structure would become a lattice (see Figure 1B). This example illustrates our approach to lattice-based ontology quality improvement. A non-lattice fragment represents a possible error, typically a missing hierarchical relation or missing intermediary concept. After correcting the error, the hierarchical structure acquires the properties of a lattice. In this example, the shared ancestors were direct parents. More generally, however, non-lattice fragments may involve shared ancestors beyond direct parents, making their identification a nontrivial, computationally intensive task.
Figure 1.
(A) An example of a non-lattice pair, Irritable bowel syndrome variant of childhood and Irritable bowel syndrome with diarrhea (lower two nodes), sharing two minimal common ancestors, Irritable bowel syndrome and Disorder of colon (upper two nodes). (B) A suggested correction for (A). By making Irritable bowel syndrome a child of Disorder of colon, the subgraph is transformed into a lattice.
The lattice-based approach20 to auditing SNOMED CT aims to systematically detect all non-lattice pairs for further analysis. In early experiments using an Resource Description Framework (RDF) triple store and SPARQL query language for RDF, it took nearly 3 months to compute all the non-lattice pairs in the July 2009 version of SNOMED CT using a high-end desktop machine.21 In more recent work,25,26 it took less than 3 hours using MapReduce parallel processing framework in a 30-node Hadoop cloud.
Specific contribution
The specific contribution of this work is to combine structural and lexical information to identify missing hierarchical relations or missing intermediary concepts in SNOMED CT. We extend our earlier work on non-lattice subgraphs by incorporating lexical patterns to precisely identify error types in SNOMED CT, along with suggestions for remediation. Compared to other methods developed for quality assurance in SNOMED CT, the main difference in our approach is that other methods only identify potential errors, while we also provide remediation for the errors identified.
MATERIALS AND METHODS
Our approach to identifying potential errors in SNOMED CT based on structural and lexical information can be summarized as follows. We identify non-lattice pairs in SNOMED CT and generate the corresponding non-lattice subgraphs. We identify lexical patterns indicative of missing concepts or hierarchical relations, which we apply to the non-lattice subgraphs. Finally, experts evaluate a sample of the potential errors detected, as well as the proposed remediation. We used the distribution files of the September 2015 version of SNOMED CT (US edition).
Identifying non-lattice pairs
A non-lattice pair is a concept pair having more than one maximal shared common descendant. A non-lattice pair determines a graph fragment consisting of the concepts between any member of the non-lattice pair and any member of the maximal shared common descendants (Alternatively, one can consider minimal shared ancestors due to duality20,21).
It is possible that multiple non-lattice pairs have identical maximal common descendants. For example, in Figure 2, three non-lattice pairs, Neoplasm of pancreas and Mass of pancreas (p1), Neoplasm of pancreas and Neoplasm of digestive organ (p2), and Mass of pancreas and Neoplasm of digestive organ (p3), share the same maximal common descendants, Benign neoplasm of pancreas and Tumor of exocrine pancreas. It would not be economical to analyze each of the three non-lattice pairs separately. Moreover, simple aggregation of all non-lattice pairs with the same maximal common descendants may include concepts with ancestor-descendant relationships, which may again result in redundant analysis.
Figure 2.
An example of a non-lattice graph. Three pairs of concepts (among the three upper nodes) share the same maximal common descendants (the two lower nodes).
Identifying non-lattice subgraphs
To avoid such redundant subgraphs, we introduce the notion of non-lattice subgraphs to only include the minimal concepts sharing the same maximal common descendants. Here a non-lattice subgraph is determined by a given non-lattice pair p = (c1, c2) and its maximal common descendants mcd(p), and can be obtained by
reversely computing the minimal common ancestors of the maximal common descendants, denoted by mca(mcd(p)), and
aggregating all the concepts and edges between (including) any concept in mca(mcd(p)) and any of the maximal common descendants mcd(p).
We call mca(mcd(p)) and mcd(p) the upper bounds and lower bounds of the non-lattice subgraph, respectively. For the three non-lattice pairs p1, p2, and p3 in Figure 2, they derive the same non-lattice subgraph shown in Figure 2. The size of a non-lattice subgraph is the number of concepts it contains. Thus the subgraph in Figure 2 is of size 6.
In previous work, we computed the maximal common descendants for each candidate pair of concepts using a MapReduce pipeline in order to generate an exhaustive list of non-lattice pairs.25,26 Concept pairs with more than one maximal shared common descendant were identified as non-lattice pairs. To determine the non-lattice subgraphs suitable for error pattern mining, we used all non-lattice pairs as seeds and generated non-lattice subgraphs by modifying the MapReduce pipeline to compute mca(mcd(p)) for each candidate pair p = (c1, c2).
Identifying lexical patterns indicative of missing concepts and relations
Because it is impractical to manually review large numbers of non-lattice subgraphs, we introduce an automatic approach that leverages additional lexical information (concept names) to identify lexical patterns in non-lattice subgraphs indicative of certain types of errors. We consider the fully specified name of a concept c as a set (bag) of words in lower case {c}. For instance, the fully specified name of the concept ID 235838003, (c), is Irritable bowel syndrome variant of childhood (see Figure 1), and its set of words, {c}, is {irritable, bowel, syndrome, variant, of, childhood}. Utilizing the information of sets of words for concepts in the upper and lower bounds, we define four lexical patterns indicative of a situation where hierarchical relations or intermediary concepts may be missing: Containment, Intersection, Union, and Union-Intersection.
Containment
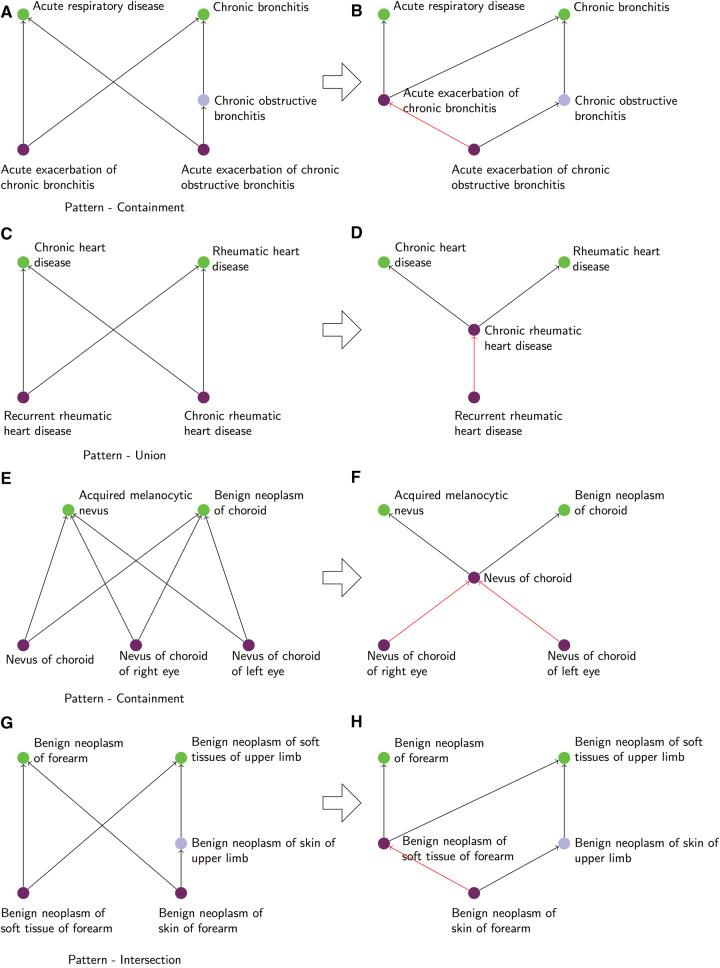
The set of words for one concept in the upper bounds is contained in the set of words for another concept in the upper bounds; or the set of words for one concept in the lower bounds is contained in the set of words for another concept in the lower bounds. This situation generally suggests a missing hierarchical relation between concepts in the upper bounds (or in the lower bounds). For instance, the lower bounds of the non-lattice subgraph in Figure 3A {duodenal, ulcer, with, perforation, and, obstruction} is contained in {chronic, duodenal, ulcer, with, perforation, and, obstruction}. Here, there is a missing hierarchical relation between concepts in the lower bounds, because Chronic duodenal ulcer with perforation AND obstruction is more specific than Duodenal ulcer with perforation AND obstruction. Of note, for this pattern, we specifically excluded non-lattice subgraphs with concepts that contain negation words such as not, no, without, absence, and except, because a missing hierarchical relation would be wrongly suggested between the concept with the negation and the same concept without negation. For example, the set of words for the concept Anemia during pregnancy – baby not yet delivered contains the concept Anemia during pregnancy – baby delivered as a subset, but the two concepts are obviously not hierarchically related.
Figure 3.
Examples of non-lattice subgraphs exhibiting the patterns Containment (A), Intersection (C), Union (E), and Union-Intersection (G) (left side), along with their corresponding suggested remediations (B), (D), (F), and (H), respectively (right side).
Intersection
The intersection of sets of words for concepts in the lower bounds is equal to the set of words for some concept in the upper bounds. This situation generally suggests a missing hierarchical relation between concepts in the upper bounds. For example, in Figure 3C, the intersection of {irritable, bowel, syndrome, variant, of, childhood} and {irritable, bowel, syndrome, with, diarrhea} is {irritable, bowel, syndrome}, which is equal to the set of words for the concept Irritable bowel syndrome in the upper bounds. Here, there is a missing hierarchical relation between concepts in the upper bounds, because Irritable bowel syndrome is more specific than Disorder of colon.
Union
The union of the sets of words for concepts in the upper bounds is equal to the set of words for some concept in the lower bounds. This situation generally suggests a missing hierarchical relation between concepts in the lower bounds. For instance, in Figure 3E, the union of {epithelial, neoplasm, of, skin} and {malignant, neoplasm, of, skin} is {malignant, epithelial, neoplasm, of, skin}, which is equal to the set of words for the concept Malignant epithelial neoplasm of skin in the lower bounds. Here, there is a missing hierarchical relation between concepts in the lower bounds, because Squamous cell carcinoma of skin is more specific than Malignant epithelial neoplasm of skin.
Union-Intersection
The union of the sets of words for concepts in the upper bounds is equal to the intersection of sets of words for concepts in the lower bounds. This situation generally suggests a missing intermediary concept between the upper bounds and the lower bounds. For instance, in Figure 3G, the union of {neoplasm, right, upper, lobe, of, lung} and {malignant, neoplasm, upper, lobe, of, lung} is {malignant, neoplasm, right, upper, lobe, of, lung}, which is equal to the intersection of {secondary, malignant, neoplasm, right, upper, lobe, of, lung} and {primary, malignant, neoplasm, right, upper, lobe, of, lung}. Here, there is a missing concept, Malignant neoplasm of right upper lobe of lung, representing the features common to the two concepts in the lower bounds (Primary malignant neoplasm of right upper lobe of lung and Secondary malignant neoplasm of right upper lobe of lung), inherited from both concepts in the upper bounds (Malignant neoplasm of upper lobe of lung and Neoplasm of right upper lobe of lung).
Analyzing non-lattice subgraphs with lexical patterns
As shown above, these patterns may suggest remediation strategies for transforming a non-lattice subgraph into a lattice subgraph. For example, for the non-lattice subgraph in Figure 3A exhibiting a Containment pattern (indicative of a missing hierarchical relation between concepts in the upper bounds or lower bounds), there is indeed a missing hierarchical relation between the two lower bound concepts Duodenal ulcer with perforation AND obstruction and Chronic duodenal ulcer with perforation AND obstruction, because the added notion of chronicity makes the latter more specific. The suggested correction is to add the relation Chronic duodenal ulcer with perforation AND obstructionis-a Duodenal ulcer with perforation AND obstruction (see Figure 3B).
For the non-lattice subgraph in Figure 3C exhibiting an Intersection pattern (indicative of a missing hierarchical relation between concepts in the upper bounds), there is indeed a missing hierarchical relation between the two upper bound concepts Irritable bowel syndrome and Disorder of colon, because the colon is the anatomical location of this syndrome. The suggested correction is to add the relation Irritable bowel syndromeis-aDisorder of colon (see Figure 3D).
For the non-lattice subgraph in Figure 3E exhibiting a Union pattern (indicative of a missing hierarchical relation between concepts in the lower bounds), there is indeed a missing hierarchical relation between the two lower bound concepts Malignant epithelial neoplasm of skin and Squamous cell carcinoma of skin, because squamous cell carcinoma is a type of malignant epithelial neoplasm. The suggested correction is to add the relation Squamous cell carcinoma of skinis-aMalignant epithelial neoplasm of skin (see Figure 3F).
For the non-lattice subgraph in Figure 3G exhibiting a Union-Intersection pattern (indicative of a missing intermediary concept between the upper bounds and lower bounds), the concept Malignant neoplasm of right upper lobe of lung is indeed missing between the concepts in the lower bounds and the concepts in the upper bounds (see Figure 3H), because the characteristics malignant (neoplasm) and right (upper lobe), each represented by one concept in the upper bounds, are both shared by the two concepts in the lower bounds.
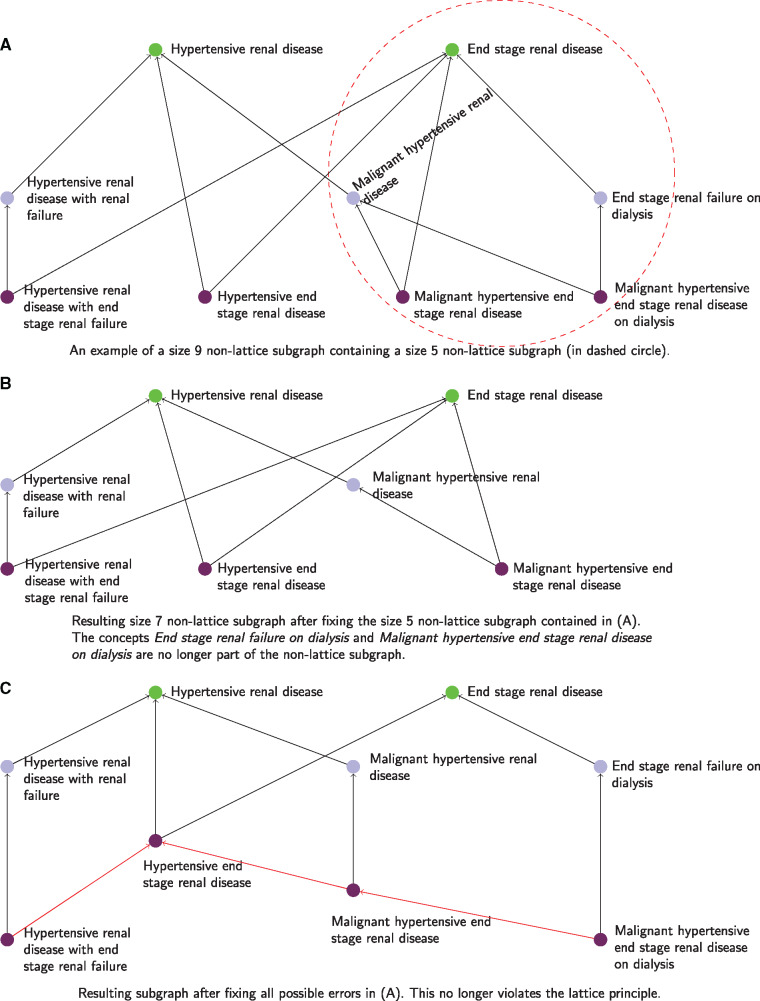
It is worth noting that smaller non-lattice subgraphs may be contained in larger subgraphs. As a consequence, correcting errors in smaller non-lattice subgraphs will mechanically result in the correction of the same errors in larger subgraphs that contain these smaller subgraphs. For instance, Figure 4A shows an example of a size 9 non-lattice subgraph that contains a size 5 non-lattice subgraph (in dashed circle). A possible correction for this size 5 non-lattice subgraph (exhibiting a Containment pattern) is to add the relation Malignant hypertensive end stage renal disease on dialysisis-aMalignant hypertensive end stage renal disease. Applying this correction in the size 5 non-lattice subgraph will also eliminate the same error (dashed circle) in the larger non-lattice subgraph in Figure 4A. Moreover, the larger subgraph may become a smaller non-lattice subgraph after correction (which may contain additional errors). For example, Figure 4B shows the resulting size 7 non-lattice subgraph obtained after applying the above-mentioned correction, which exhibits a Union pattern. A possible further correction for this size 7 non-lattice subgraph is to add two relations, Hypertensive renal disease with end stage renal failureis-aHypertensive end stage renal disease, and Malignant hypertensive end stage renal diseaseis-a Hypertensive end stage renal disease.Figure 4C presents the resulting graph after fixing all possible errors in the size 9 non-lattice subgraph in Figure 4A. Note that this subgraph, shown in Figure 4C, is no longer a non-lattice subgraph, ie, it does not violate the lattice property.
Figure 4.
(A) An example of a size 9 non-lattice subgraph containing a size 5 non-lattice subgraph (in dashed circle). (B) The resulting size 7 non-lattice subgraph obtained by fixing the size 5 non-lattice subgraph contained in (A). (C) The resulting graph after fixing all possible errors in (A).
In this paper, we focused our investigation on small non-lattice subgraphs of size 4, 5, or 6. These small subgraphs are easier to inspect visually, and they are embedded in nearly 50% of all non-lattice subgraphs (see the Results section for details).
Evaluation
To assess the effectiveness of our method in identifying real errors in SNOMED CT, we focused on small non-lattice subgraphs following any of the four lexical patterns. A random sample of 100 such subgraphs was selected from the two largest subhierarchies, Clinical finding and Procedure. The sample non-lattice subgraphs were rendered in scalable vector graphics to facilitate visualization and evaluation by experts.
To minimize the time and effort needed by the experts to review the subgraphs, author GQZ first triaged the 100 non-lattice subgraphs, eliminating the most complex cases (eg, those with multiple problems) as well as cases for which IHTSDO would be unlikely to integrate the suggested correction. For example, the triaged subgraphs include those with terms containing “AND/OR,” which are progressively being eliminated by IHTSDO. Other examples include cases requiring systematic pre-coordination, which IHTSDO tends to avoid (eg, “missing” intermediary concept Tobramycin measurement in blood between the lower bounds Serum tobramycin measurement and Plasma tobramycin measurement and upper bounds Measurement of level of drug in blood and Tobramycin measurement).
Authors JTC and OB, clinical experts familiar with SNOMED CT, independently reviewed the erroneous subgraphs selected by GQZ and the suggested remediation. Differences between the two experts were resolved by discussion.
RESULTS
Identifying non-lattice pairs and subgraphs
In total, 631 006 non-lattice pairs were found in the September 2015 version of SNOMED CT (US edition). From these pairs, 171 011 non-lattice subgraphs were generated, with sizes ranging from 4 to 5137. About 90% of the non-lattice subgraphs had sizes 4–100 (see Supplementary Appendix I online for the distribution of non-lattice subgraphs by size), with size 6 being the most frequent (6541).
Small non-lattice subgraphs
A total of 3339 non-lattice subgraphs of size 4 were contained in 28 292 larger subgraphs, 3773 subgraphs of size 5 were contained in 34 808 larger subgraphs, and 5342 subgraphs of size 6 were contained in 40 404 larger subgraphs. In total, 70 250 distinct larger non-lattice subgraphs contained smaller subgraphs of size 4, 5, or 6. Moreover, none of the size 4 non-lattice subgraphs were contained in any size 5 subgraphs, and none of the size 5 subgraphs were contained in any size 6 subgraphs. Only 197 size 4 non-lattice subgraphs were contained in size 6 subgraphs. Overall, nearly half of the non-lattice subgraphs were related to subgraphs of size 4, 5, or 6 (ie, either they were size 4, size 5, or size 6 non-lattice subgraphs themselves, or they were larger non-lattice subgraphs containing these smaller subgraphs).
Analyzing non-lattice subgraphs with lexical patterns
In total, 6801 non-lattice subgraphs were found exhibiting any of the four lexical patterns, among which 2046 were small non-lattice subgraphs (of size 4, 5, and 6). These small subgraphs exhibiting any of the four lexical patterns were contained in 15 776 larger non-lattice subgraphs. Table 1 shows the distribution of small non-lattice subgraphs exhibiting each pattern by size. The Intersection pattern accounted for the largest proportion (1085). Table 2 presents the distribution of small non-lattice subgraphs exhibiting any of the four lexical patterns by SNOMED CT subhierarchy. Clinical finding, the largest subhierarchy in SNOMED CT, accounted for the largest number. Of the 2046 smaller subgraphs, 1300 were in two classes, namely Clinical Finding (728) and Procedure (572).
Table 1.
Numbers of small non-lattice subgraphs exhibiting any of the 4 lexical patterns (Containment, Intersection, Union, and Union-Intersection) according to size
| Size | Number of non-lattice subgraphs |
||||
|---|---|---|---|---|---|
| Containment | Intersection | Union | Union-Intersection | Total | |
| Size 4 | 160 | 336 | 31 | 17 | 544 |
| Size 5 | 229 | 291 | 75 | 13 | 608 |
| Size 6 | 347 | 458 | 58 | 31 | 894 |
| Total | 736 | 1085 | 164 | 61 | 2046 |
Table 2.
Numbers of small non-lattice subgraphs (of size 4, 5, and 6) exhibiting any of the four lexical patterns according to the SNOMED CT subhierarchy
| Subhierarchy | Total |
|---|---|
| Clinical finding | 728 |
| Procedure | 572 |
| Body structure | 267 |
| Pharmaceutical/biologic product | 202 |
| Substance | 115 |
| Physical object | 71 |
| Qualifier value | 20 |
| Specimen | 19 |
| Organism | 17 |
| Social context | 15 |
| Observable entity | 9 |
| Situation with explicit context | 7 |
| Environment or geographical location | 2 |
| Event | 1 |
| Physical force | 1 |
| Total | 2046 |
Evaluation
Of the 100 subgraphs randomly selected from the 1300 small-size subgraphs from the two main hierarchies on SNOMED CT, 65 were in the Clinical finding subhierarchy and 35 in the Procedure subhierarchy. Of these subgraphs, 37 exhibited the Containment pattern, 46 the Intersection pattern, 13 the Union pattern, and 4 the Union-Intersection pattern.
Of the 100 non-lattice subgraphs, 59 were triaged for review by the medical experts. In each case, the experts confirmed the existence of an error. Therefore, the error rate among the 100 subgraphs is at least 59%, since some erroneous subgraphs may not have been selected for review during the triage process.
Among the 59 erroneous subgraphs examined, 34 exhibited a Containment pattern, 14 an Intersection pattern, 8 a Union pattern, and 3 a Union-Intersection pattern. These 59 erroneous subgraphs were contained in 656 larger non-lattice subgraphs, indicating that fixing errors in these 59 subgraphs would automatically eliminate similar errors in 656 larger subgraphs (although additional errors may remain in the larger subgraphs).
For 6 of the erroneous non-lattice subgraphs, although the experts acknowledged the existence of an error, they rejected the suggested remediation, because manual examination revealed deeper modeling issues in SNOMED CT that needed further investigation. Analysis of the 53 other erroneous subgraphs resulted in a total of 61 verified errors (see Supplementary Appendix II online for the visualized non-lattice subgraphs and corrections). Figure 5 shows four examples of the non-lattice subgraphs that were evaluated, as well as their verified corrections. Note that an erroneous non-lattice subgraph may reveal multiple errors and suggested changes. For example, Figure 5E is a non-lattice subgraph of size 5, and its analysis revealed two missing is-a relations: Nevus of choroid of left eyeis-aNevus of choroid, and Nevus of choroid of right eyeis-aNevus of choroid (see Figure 5F).
Figure 5.
Examples of evaluated non-lattice subgraphs (left side) and their remediation (right side).
Among the 61 suggested corrections, 59 were missing is-a relations and 2 were missing concepts. Table 3 lists 10 examples of the verified missing is-a relations (see Supplementary Appendix III online for a complete list of corrections). We will submit these suggested corrections to IHTSDO through the regular content request submission process for inclusion in its ongoing internal quality improvement activities.
Table 3.
Ten examples of missing is-a relations in SNOMED CT, along with the lexical patterns of their corresponding non-lattice subgraphs and the location of the missing relation (LB: lower bound; UB: upper bound)
| Child | Parent | Pattern | Location of the missing relation |
|---|---|---|---|
| Acute exacerbation of chronic obstructive bronchitis | Acute exacerbation of chronic bronchitis | Containment | LB→LB |
| (Figures 5A and B) | |||
| Compartment syndrome of abdomen due to trauma | Abdominal compartment syndrome | Intersection | LB→LB |
| Recurrent rheumatic heart disease | Chronic rheumatic heart disease | Union | LB→LB |
| (Figures 5C and D) | |||
| Removal of foreign body of cornea by incision | Incision of cornea | Intersection | LB→LB |
| Acute endometritis | Acute uterine in inflammatory disease | Intersection | UB→UB |
| Nevus of choroid of left eye | Nevus of choroid | Containment | LB→LB |
| (Figures 5E and F) | |||
| Nevus of choroid of right eye | Nevus of choroid | Containment | LB→LB |
| (Figures 5E and F) | |||
| Acromioclavicular joint pain | Shoulder joint pain | Union | LB→LB |
| Benign neoplasm of skin of forearm | Benign neoplasm of soft tissue of forearm | Intersection | LB→LB |
| (Figures 5G and H) | |||
| Cervical spondylosis with myelopathy | Cervical spondylosis | Containment | LB→LB |
DISCUSSION
Significance
In this paper, we mined non-lattice subgraphs exhibiting four lexical patterns to uncover missing hierarchical relations or missing concepts in SNOMED CT. Our approach not only uncovered novel (ie, unreported) SNOMED CT errors, but also suggested appropriate remediation in many cases. While most approaches to quality assurance in SNOMED CT merely indicate the presence of a possible error, our hybrid approach overlays lexical information onto structural information to facilitate the analysis of the precise nature of the error and propose a correction. The ability to suggest remediation for the errors we identify sets us apart from other methods and will likely drive adoption. Focusing on non-lattice subgraphs of smaller size is an effective way to audit hierarchical relations in SNOMED CT. Not only is it easier for experts to review and examine these graphs, but the errors found in small graphs are mechanically propagated to larger graphs. Since virtually all biomedical ontologies are organized into subsumption hierarchies and have concept names, our non-lattice–based approach can be generalized and applied to other biomedical terminologies for quality assurance purposes.
Practical quality impact of suggested SNOMED CT remediation
Addressing quality issues in SNOMED CT can improve the quality of downstream information systems and tools relying on its hierarchies.3 Practical areas of impact include value set definition for EHR decision support, quality reporting, and cohort selection.4 Value sets are increasingly defined in intension, ie, as the list of concepts sharing some common feature, eg, all descendants of Malignant epithelial neoplasm of skin.Squamous cell carcinoma of skin is currently not listed as one of its descendants, and would thus be missing from the corresponding intensional value set. As a consequence, patients with Squamous cell carcinoma of skin would not be selected for a cohort of patients with Malignant epithelial neoplasm of skin. Of note, some of the errors we identified involve concepts from the widely used Clinical Observations Recordings and Encoding Problem List Subset of SNOMED CT,27 which contains concepts widely used across many health care institutions. For example, Shoulder joint pain and Acromioclavicular joint pain are two concepts from the Clinical Observations Recordings and Encoding subset, but a missing is-a relation between the two concepts was identified in this work (see the 43rd non-lattice subgraph in the Supplementary Appendix II online).
Generalization
Most existing approaches to quality assurance of SNOMED CT typically take advantage of specific knowledge in the terminology, such as lexical information11,12,14 or structural information on specific subhierarchies,15–19 but have limitations in scalability and applicability. This work not only leverages both structural and lexical information and is not limited to a specific subhierarchy, but is also scalable and widely applicable to other terminologies. The scalability of exhaustive computation of non-lattice subgraphs has been demonstrated in our previous work,25,26 where 8 versions of SNOMED CT based on all subhierarchies have been used for experiments.
Abstraction networks (AbNs) have been systematically explored for quality assurance of biomedical ontologies from a structural point of view.15–18 The AbN approach utilizes “hypergraphs,” where each node contains a collection of concepts sharing some common attributes, used for summarizing structural information. Distinct from AbNs, the non-lattice subgraphs in this work are directly based on the same concrete level of the underlying graph structure rather than on an abstraction thereof. Moreover, our non-lattice subgraphs are generated from the hierarchical is-a relationships, while AbNs rely on outgoing attribute relationships for grouping concepts into areas or partial areas. Since concept names and the is-a taxonomy, ie, a hierarchical backbone, are present in virtually all biomedical terminologies, our hybrid approach combining non-lattice subgraph and lexical information is widely applicable for quality assurance purposes.
Another key distinction of this work from other terminology quality assurance work requiring manual review by domain experts to uncover potential errors is the potential to automatically suggest remediation for potential errors uncovered, saving domain experts’ manual review and correction effort.
Failure analysis of complex cases
It is worth noting that the remediation suggested by the presence of a lexical pattern is not always accurate. For example, for the non-lattice subgraph with an Intersection pattern in Figure 5G, the correction associated with the pattern is a missing hierarchical relation between concepts in the upper bounds. In this case, however, the missing hierarchical relation is between concepts in the lower bounds instead. In this example, a related fact is that Benign neoplasm of skin of forearmis-a Benign neoplasm of soft tissues of upper limb, which indicates that skin is a kind of soft tissue, and therefore the correction is to add the relation Benign neoplasm of skin of forearmis-aBenign neoplasm of soft tissue of forearm.
Also note that even though non-lattice subgraphs might reveal modeling problems in SNOMED CT, they might not be easily fixed by adding a missing is-a relation or a missing concept. For instance, Figure 6A presents an erroneous non-lattice subgraph. Here again, the Intersection pattern suggests a missing hierarchical relation between concepts in the upper bounds, ie, between Evoked magnetic fields and Procedure on central nervous system. However, Evoked magnetic fields is a primitive concept. While adding a hierarchical relation would make this subgraph a lattice, a more sensible solution would be to create a complete logical definition for Evoked magnetic fields, from which a description logic classifier would simply infer a hierarchical relation to Procedure on central nervous system.
Figure 6.
(A) An example of problematic non-lattice subgraph revealing modeling problems. (B) Non-lattice subgraph pattern for which new lexical patterns would be required (eg, leveraging synonymy between neoplasm and tumor).
Limitations and future work
A limitation of this work is that our suggested remediation (eg, to add missing hierarchical relations) is based on the inferred concept hierarchy of SNOMED CT. Since this hierarchy is produced by a description logic classifier based on the logical definitions for the concepts, a more meaningful remediation would be to modify the logical definitions so that the appropriate hierarchy can be inferred. When we submit the missing hierarchical relations we identified to the IHTSDO, we expect that the editors will address the root cause (ie, incomplete logical definitions) rather than simply add the relations.
As mentioned earlier, due to the strategy of the evaluation, we can only report the lower bound of the rate of identified errors, because there may be errors in the subgraphs that were not selected for review. While this may seem suboptimal, our choice was justified by the need to minimize the workload of domain experts in this labor-intensive review process, and the purpose of the evaluation was to show the promise of combining non-lattice subgraphs and lexical patterns to not only detect potential errors in SNOMED CT, but also facilitate remediation (as a proof of principle). A larger, more thorough evaluation is planned.
Leveraging lexical patterns proved an effective way to identify potential errors in non-lattice subgraphs. However, the four patterns we consider in this investigation only cover some of the subgraphs. It would be interesting to investigate additional patterns or new lexical approaches. For example, the non-lattice subgraph shown in Figure 6B does not follow any of the four patterns. However, if we considered neoplasm and tumor as synonyms, it would exhibit the Intersection pattern. Figure 2 illustrates another such example. Finally, we also plan to use all the synonyms in SNOMED CT, as well as additional synonyms from the Unified Medical Language System Metathesaurus, to complement the fully specified terms used in this investigation.
CONCLUSIONS
In this paper, we introduced a novel hybrid approach leveraging non-lattice subgraphs and lexical information in concept names for detecting missing hierarchical relations or missing concepts in SNOMED CT. Our approach differs from other quality assurance methods in that we also suggest remediation for the errors identified. We showed that identifying and analyzing small non-lattice subgraphs in SNOMED CT with lexical patterns is a simple and effective quality assurance technique.
Funding
This work was supported by the National Institutes of Health (NIH) National Center for Advancing Translational Sciences through grant UL1TR001998 and National Science Foundation through grant ACI-1626364. This work was also supported by the Intramural Research Program of the NIH, National Library of Medicine. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Competing Interests
The authors have no competing interests to declare.
Contributors
LC, GQZ, and OB conceptualized and designed this study. LC implemented the idea, generated the auditing results, and prepared the sample non-lattice subgraphs for evaluation. WZ and ST assisted with implementation of the idea with respect to the rendering of scalable vector graphics graphs for the evaluation and for the figures in the manuscript. GQZ reviewed the random collection of non-lattice subgraphs and proposed initial corrections for evaluation. JTC and OB reviewed and verified the proposed corrections and suggested additional corrections. LC, GQZ, and OB wrote and revised the manuscript. JTC provided feedback on writing and revising the manuscript.
SUPPLEMENTARY MATERIAL
Supplementary material is available at Journal of the American Medical Informatics Association online.
Supplementary Material
References
- 1. Geller J, Perl Y, Halper M, Cornet R. Special issue on auditing of terminologies. J Biomed Inform. 2009;42:407–11. [DOI] [PubMed] [Google Scholar]
- 2. Bodenreider O. Biomedical ontologies in action: role in knowledge management, data integration and decision support. Yearb Med Inform. 2008:67–79. [PMC free article] [PubMed] [Google Scholar]
- 3. Lee D, de Keizer N, Lau F et al. Literature review of SNOMED CT use. J Am Med Inform Assoc. 2014;21:e11–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Winnenburg R, Bodenreider O. Metrics for assessing the quality of value sets in clinical quality measures. AMIA Annu Symp Proc. 2013:1497–1505. [PMC free article] [PubMed] [Google Scholar]
- 5. Health Information Technology for Economic and Clinical Health (HITECH) Act. 2009. http://www.healthit.gov/sites/default/files/hitech_act_excerpt_from_arra_with_index.pdf. Accessed April 6, 2015.
- 6. ONC Stage 2 Meaningful Use Final Rule. 2012. http://www.gpo.gov/fdsys/pkg/FR-2012‐09‐04/pdf/2012‐20982.pdf. Accessed April 6, 2015.
- 7. SNOMED CT Starter Guide. 2014 http://ihtsdo.org/fileadmin/user_upload/doc/download/doc_StarterGuide_Current-en-US_INT_20141202.pdf. Accessed April 6, 2015.
- 8. Cimino JJ, Hripcsak G, Johnson S et al. Designing an introspective, controlled medical vocabulary. In: Proceedings of the Thirteenth Annual SCAMC. 1989:513–18. [Google Scholar]
- 9. Cimino JJ. Auditing the unified medical language system with semantic methods. J Am Med Inform Assoc. 1998;5:41–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zhu X, Fan JW, Baorto DM et al. A review of auditing methods applied to the content of controlled biomedical terminologies. J Biomed Inform. 2009;42:413–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Bodenreider O, Burgun A, Rindflesch TC. Assessing the consistency of a biomedical terminology through lexical knowledge. Int J Med Inform. 2002;67:85–95. [DOI] [PubMed] [Google Scholar]
- 12. Agrawal A, Elhanan G. Contrasting lexical similarity and formal definitions in SNOMED CT: Consistency and implications. J Biomed Inform. 2014;47:192–98. [DOI] [PubMed] [Google Scholar]
- 13. Jiang G, Chute CG. Auditing the semantic completeness of SNOMED CT using formal concept analysis. J Am Med Inform Assoc. 2009;16:89–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Rector A, Iannone L. Lexically suggest, logically define: quality assurance of the use of qualifiers and expected results of post-coordination in SNOMED CT. J Biomed Inform. 2012;45:199–209. [DOI] [PubMed] [Google Scholar]
- 15. Wang Y, Halper M, Min H et al. Structural methodologies for auditing SNOMED. J Biomed Inform. 2007;40:561–81. [DOI] [PubMed] [Google Scholar]
- 16. Wang Y, Halper M, Wei D et al. Abstraction of complex concepts with a refined partial-area taxonomy of SNOMED. J Biomed Inform. 2012;45:15–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wang Y, Halper M, Wei D et al. Auditing complex concepts of SNOMED using a refined hierarchical abstraction network. J Biomed Inform. 2012;45:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ochs C, Geller J, Perl Y et al. Scalable quality assurance for large SNOMED CT hierarchies using subject-based subtaxonomies. J Am Med Inform Assoc. 2015;22:507–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Ochs C, Geller J, Perl Y et al. A tribal abstraction network for SNOMED CT target hierarchies without attribute relationships. J Am Med Inform Assoc. 2015;22:628–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Zhang GQ, Bodenreider O. Using SPARQL to Test for Lattices: application to quality assurance in biomedical ontologies. The Semantic Web-ISWC. 2010;273–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Zhang GQ, Bodenreider O. Large-scale, exhaustive lattice-based structural auditing of SNOMED CT. AMIA Annu Symp Proc. 2010:922–26. [PMC free article] [PubMed] [Google Scholar]
- 22. Zweigenbaum P, Bachimont B, Bouaud J et al. Issues in the structuring and acquisition of an ontology for medical language understanding. Methods Inform Med. 1995;34:15–24. [PubMed] [Google Scholar]
- 23. Ganter B, Wille R. Formal Concept Analysis. Berlin: Springer; 1999. [Google Scholar]
- 24. Troy AD, Zhang GQ, Tian Y. Faster concept analysis. In: Conceptual Structures: Knowledge Architectures for Smart Applications. 2007:206–19. [Google Scholar]
- 25. Zhang GQ, Zhu W, Sun M et al. MaPLE: A MapReduce Pipeline for Lattice-based Evaluation and Its Application to SNOMED CT. IEEE BigData. 2014;754–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Cui L, Tao S, Zhang GQ. Biomedical ontology quality assurance using a big data approach. ACM Transact Knowledge Discov Data. 2016;10:41. [Google Scholar]
- 27. The CORE Problem List Subset of SNOMED CT. 2016. https://www.nlm.nih.gov/research/umls/Snomed/core_subset.html. Accessed October 3, 2016.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.