Subcellular topography modulates actin dynamics and signaling in B-cells

Abstract

B-cell signaling activation is most effectively triggered by the binding of B-cell receptors (BCRs) to membrane-bound antigens. In vivo, B-cells encounter antigen on antigen-presenting cells (APC), which possess complex surfaces with convoluted topographies, a fluid membrane and deformable cell bodies. However, whether and how the physical properties of antigen presentation affect B-cell activation is not well understood. Here we use nanotopographic surfaces that allow systematic variation of geometric parameters to show that surface features on a subcellular scale influence B-cell signaling and actin dynamics. Parallel nanoridges with spacings of 3 microns or greater induce actin intensity oscillations on the ventral cell surface. Nanotopography-induced actin dynamics requires BCR signaling, actin polymerization, and myosin contractility. The topography of the stimulatory surface also modulates the distribution of BCR clusters in activated B-cells. Finally, B-cells stimulated on nanopatterned surfaces exhibit intracellular calcium oscillations with frequencies that depend on topography. Our results point to the importance of physical aspects of ligand presentation, in particular, nanotopography for B-cell activation and antigen gathering.

INTRODUCTION

B-lymphocytes mediate humoral immunity by recognizing foreign antigens through surface B-cell receptors (BCRs) and producing antibodies specific to these antigens (Ags). B-cells typically encounter cognate antigens within the secondary lymphoid organs, such as the spleen and lymph nodes (Harwood and Batista, 2009). The antigens can be soluble (Unanue et al., 1972) or can be membrane bound on the surfaces of antigen-presenting cells (APCs) such as marginal-zone macrophages and follicular dendritic cells (Batista et al., 2001). Although soluble antigens can activate B-cells, recent studies indicate that activation by surface-anchored antigens is significantly more effective (Batista et al., 2001; Tolar et al., 2005). Consequently, the physical nature of the antigen-presenting surface is likely to be important in modulating B-cell activation. For instance, it has previously been shown that substrate stiffness (Hui et al., 2015; Zeng et al., 2015) and ligand mobility (Ketchum et al., 2014) affect B- and T-cell signaling.

In vitro studies on planar substrates have greatly enhanced our understanding of the mechanisms underlying B-cell activation and signaling initiation. However, cells do not encounter planar topographies in vivo. B-cells mainly encounter Ags presented on APCs, such as marginal zone macrophages (Junt et al., 2007) and follicular dendritic cells (FDCs) (Szakal et al., 1988; Bajenoff and Germain, 2009; Suzuki et al., 2009). In vivo, B-cells migrate in the secondary lymphoid organs and encounter topographically complex architectures. One of the main APCs for B-cells are FDCs, which capture and retain immune complexes (Qi et al., 2006) for presentation to B-cells. The surfaces of dendritic cells are highly convoluted, with folds that have radii of curvature on the order of 200–300 nm (Felts et al., 2010). The dendrites of FDCs found in B-cell follicles form intricate three-dimensional networks that are several microns in length and 100–300 nm in diameter (Szakal et al., 1985). In some cases, FDC dendrites exhibit characteristic varicosities (150–300 nm radius). In vivo imaging shows that B-cells move on FDCs while scanning for Ags (Bajenoff et al., 2006, 2007). Thus, during Ag scanning, B-cells encounter topographies with radii of curvature in the range of 100–300 nm and length scales that range over several micrometers. The impact of such topography on B-cell signaling is not well understood.

B-cell activation is marked by a dramatic reorganization of the actin cytoskeleton, leading to B-cell spreading on the antigen-­presenting surface and to the formation of signaling microclusters (Fleire et al. 2006). This process is followed by cell contraction, which is required for signaling down-regulation (Liu et al., 2013). Actin dynamics are modulated by a host of actin regulatory proteins and are closely connected to the spatiotemporal distribution of BCRs (Liu et al., 2011, 2012a,b, 2013; Song et al., 2013; Seeley-Fallen et al., 2014). These results suggest that the presence of topographical features may geometrically constrain spreading, thus disrupting lamellipodia and the organization of the actin cytoskeleton that drives them. It has also been shown that novel actin structures can arise as an active response to the topography of the substrate (Vogel and Sheetz, 2006). Modulation of the actin network can regulate the diffusion and oligomerization of BCRs on the nanoscale (Batista et al., 2010; Treanor and Batista, 2010; Treanor et al., 2011) and BCR translocation and cluster formation on the mesoscale (Ketchum et al., 2014). These phenomena may down- or up-regulate BCR signaling. BCR signaling in turn enhances actin remodeling through regulatory proteins such as Btk, WASp, and N-WASp. Thus, we hypothesize that feedback between BCR activation and the organization and dynamics of the actin cytoskeleton are sensitive to topographic features of the substrate and that the modulation of actin reorganization in response to surface topography influences BCR distribution and B-cell signaling.

Here we use nanotopographic surfaces with a systematic variation of geometric parameters to study the effect of topography on B-cell signaling and actin dynamics. We find that cell morphology, actin dynamics, BCR distribution, and B-cell signaling are modulated by the topography of the activating surfaces. Parallel nanoridges with spacings of 3 μm or greater induce actin intensity oscillations on the ventral cell surface that are consistent with actin polymerization waves. Nanotopographically induced actin dynamics requires BCR signaling, actin polymerization, and myosin contractility. The topography of the stimulatory surface also modulates the distribution of BCR clusters in activated B-cells. Furthermore, B-cells stimulated on nanopatterned surfaces exhibit intracellular calcium (Ca²⁺) oscillations with frequencies that depend on topography. These data suggest that topography-induced changes in the distributions of BCRs and the actin cytoskeleton initiate a feedback loop between Ca²⁺ signaling and actin dynamics. Our results demonstrate that surface topography regulates B-cell actin dynamics and signaling.

RESULTS

Surfaces with ridges alter actin distribution in B-cells

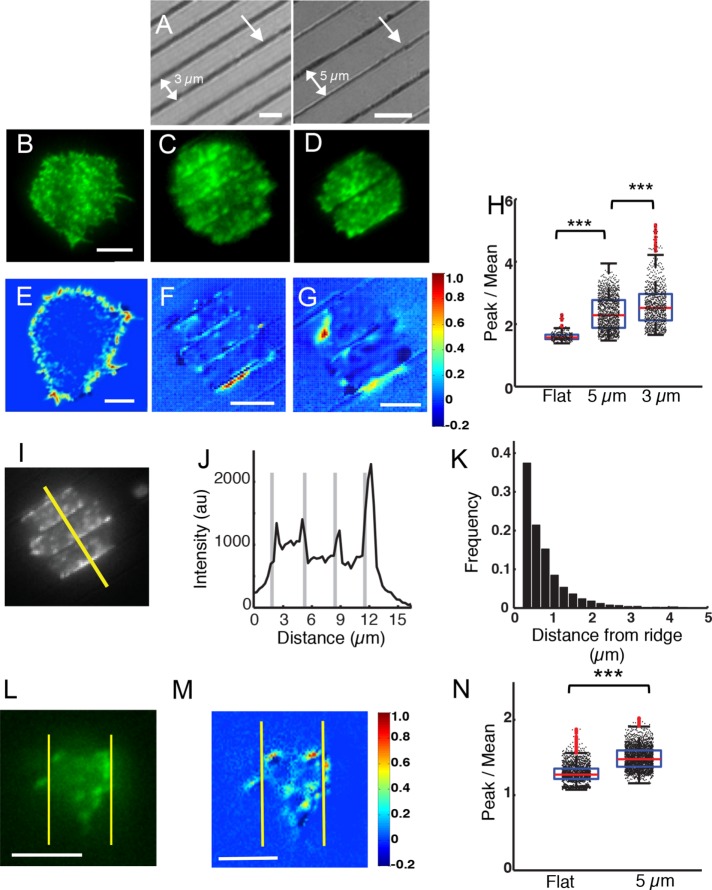
To examine how B-cells respond to topographic features of the substrate, we used multiphoton absorption polymerization (MAP) to create parallel nanoridges with specified spacing (LaFratta et al., 2007; Driscoll et al., 2014). Master patterns created using MAP were molded in an acrylic resin (see Materials and Methods), with a similar refractive index to that of glass, to allow live-cell imaging using total internal reflection fluorescence (TIRF) and fluorescence confocal microscopy. The ridges were ∼200 nm wide and ∼600 nm high, with a spacing of either 3.0 or 5.0 µm. Figure 1A shows representative substrates with 3-µm (left) and 5-µm (right) ridge spacings. The dark lines in the interference reflection microscopy (IRM) images correspond to ridges, and the lighter portions correspond to the spaces between ridges. Enhanced green fluorescent protein (EGFP) actin–expressing A20 B-cells were allowed to spread on surfaces coated with F(ab)₂ antimouse immunoglobulin M+G (IgM+G) antibody, which activates BCRs. We verified that the coating densities of Fab on the patterned and flat surfaces were similar (Supplemental Figure S1). The cell behavior on flat surfaces (Figure 1B) was compared with that on ridges (Figure 1, C and D). TIRF microscopy was used to image cells as they made contact with the antibody-coated surface. The fluorescence from labeled actin was visualized in the spaces between the ridges. As is the case for flat activating surfaces, cells readily spread on the nanoridges, increasing their contact area while exhibiting robust actin dynamics (Figure 1, C and D). The maximum B-cell spread area was normally achieved within ∼6 min after contact with either flat or ridged activating substrates. We therefore examined various cellular parameters after 6 min of contact initiation with the substrates.

FIGURE 1:

B-cells on nanotopographic surfaces exhibit enhanced actin polymerization. (A) Interference reflection micrographs of surfaces with parallel nanoridges. The single arrow indicates a ridge and the double arrow represents the spacing between ridges. Left panel: 3-µm ridge spacing; right panel: 5-µm ridge spacing. Scale bars are 3 and 5 µm, respectively. (B) Representative EGFP-actin–expressing A20 cell spread on an activating, flat glass surface. Scale bar: 5 μm. (C) Representative EGFP-actin A20 cell spread on a surface with a 3-µm ridge spacing. (D) Representative EGFP-actin A20 cell spread on a surface with 5.0-µm ridge spacing. Heat maps showing the MNA of actin fluorescence from representative EGFP-actin–expressing A20 cells on (E) a flat substrate, (F) a surface with a 3-μm ridge spacing, and (G) a surface with a 5-µm ridge spacing. Scale bars: 5 μm. (H) Peak-to-mean ratio of actin fluorescence intensity for all time points over entire cells (N = 9 cells for flat, N = 16 cells for 5 µm, and N = 15 cells for 3 µm) (p < 0.001 KS test). (I) A representative EGFP-actin–expressing A20 B-cell on a surface with a 3-µm ridge spacing. Scale bar: 3 µm. (J) Actin fluorescence intensity profile along a line perpendicular to the ridges (see representative white line in I). Note the enrichment of actin adjacent to ridges (thick gray lines). (K) Histogram of the widths of actin-enriched regions as a function of distance from the center of the nearest ridge (N = 14 cells). (L) A representative Lifeact-GFP–expressing primary B-cell on a surface with a 5-µm ridge spacing. Scale bar: 5 µm. (M) Heat map showing the MNA of actin fluorescence from a representative Lifeact-GFP–expressing primary B-cell on 5-µm spaced ridges. Scale bar: 5 µm. (N) Peak-to-mean ratio of actin fluorescence intensity for all time points in primary cells (N = 9 cells both on flat and 5-μm ridges, p < 0.001 KS test). All box-whisker plots are as follows: central marks in the box denote median values, boxes denote the 25th and 75th percentile values, and whiskers denote extreme values of the distributions. Outliers are shown in red.

For cells spread on patterned substrates, we observed an enhancement in the actin fluorescence intensity adjacent to the ridges. For a detailed analysis of actin enrichment along the ridges, we calculated the pixelwise, mean-normalized autocovariances (MNAs) of the fluorescence intensity (see Materials and Methods). High MNA values indicate cellular regions in which enhanced intensity accumulations persist over time. For cells activated on flat substrates, the MNA values were highest at the cell edges, which is consistent with enhanced actin dynamics associated with lamellipodial movements during cell spreading (Figure 1E). For cells activated on patterned substrates, the MNA values were highest along the ridges, indicating enhanced actin accumulation in the regions adjacent to ridges (Figure 1, F and G).

We further quantified the actin enhancement on ridged surfaces using the ratio of peak actin fluorescence intensity to the mean actin fluorescence intensity over the entire cell/surface contact zone. This ratio increased significantly from a median value of 1.57 ± 0.14 (mean ± SD) on flat surfaces to 2.29 ± 0.54 and 2.52 ± 0.65 on ridges with 5- and 3-μm spacing, respectively (p < 0.001, Kolmogorov–Smirnov [KS] test) (Figure 1H). These results are indicative of enhanced accumulation of actin proximal to the cell-surface contact on ridged surfaces.

We quantified the spatial extent of actin enrichment along ridges by measuring fluorescence intensity profiles along lines perpendicular to the direction of the ridges across the cell spread area (Figure 1, I and J). EGFP-actin intensity maxima in the vicinity of ridges were identified as peaks when the maximum intensity was greater than a threshold value (the mean intensity plus two-thirds of the difference between the mean and minimum intensities of the line profile). The widths of these peaks were measured at half height. The distribution of two times the measured width, which approximates the width at the base of the fluorescence peak, indicates the presence of strongly enriched actin regions extending for ∼1.0 µm from the ridges (Figure 1K). This distance is significantly greater than our imaging resolution, so we can rule out optical waveguiding effects and the additional surface area of the ridges as causes for the enhanced fluorescence.

To test whether primary B-cells exhibit similar actin patterns, we allowed murine B-cells from mice expressing Lifeact-GFP (which binds to F-actin) to spread on antibody-coated substrates and imaged them as described above (Figure 1L). The pixelwise MNA values were highest adjacent to the ridges, which is indicative of enhanced actin accumulation over time in these regions (Figure 1M). We also found that the peak-to-mean fluorescence intensity ratios of actin on the ridged surfaces were significantly greater than those for cells on flat surfaces (Figure 1N). These observations suggest that nanoridges promote the polymerization of actin in B-cells.

Surface topography modulates actin dynamics

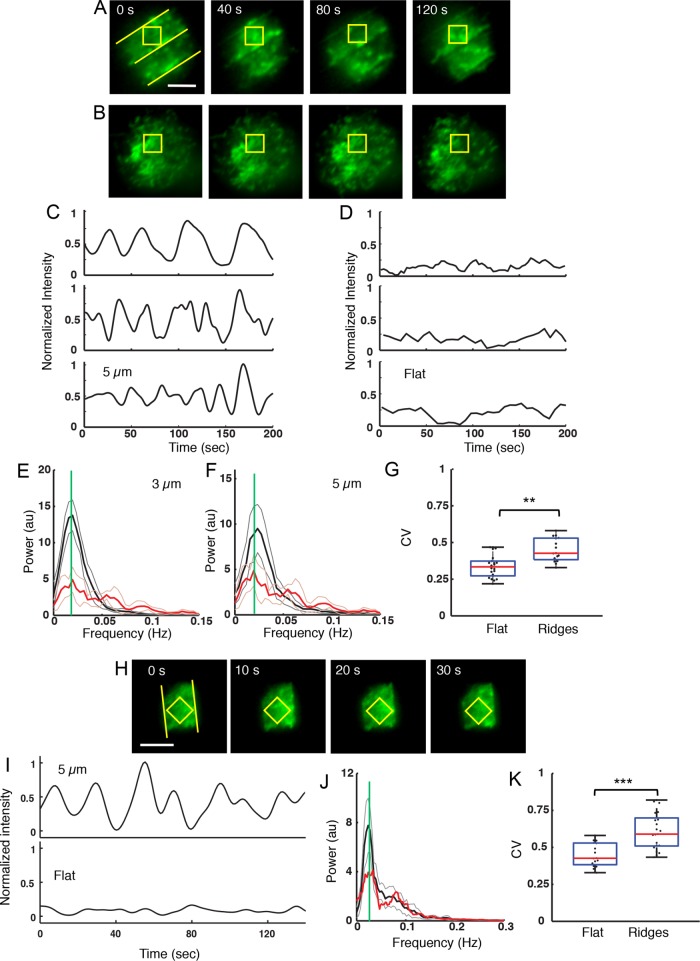
To investigate the influence of surface topography on the dynamics of the actin cytoskeleton, we allowed EGFP-actin–­expressing A20 B-cells to spread on antibody-coated surfaces and imaged the cells every 1–3 s. The temporal dynamics of the actin fluorescence intensity was measured after 6 min of cell spreading. On ridged surfaces we observed oscillations of the actin fluorescence intensity over large portions of the cell contact area, which is indicative of repeated cycles of actin polymerization and depolymerization. Representative images for a cell on 5-μm-spaced ridges are shown in Figure 2A. These waves tend to propagate radially, both inward and outward. In contrast, for cells on flat surfaces the actin is distributed in patches and appears to fluctuate stochastically (Figure 2B).

FIGURE 2:

Surfaces with ridges induce actin fluorescence intensity oscillations. (A) A representative EGFP-actin A20 B-cell on a surface with a 5-µm ridge spacing exhibiting repeated actin fluorescence intensity oscillations. The yellow ROI is centered between two ridges. Scale bar: 5 µm. (B) A representative EGFP-actin A20 B-cell on a flat surface does not exhibit actin fluorescence intensity oscillations. (C) Representative examples of actin fluorescence intensity dynamics, within a square ROI of 5-µm diagonal length, on surfaces with a 5-μm ridge spacing. All traces in C, D, and J were mean-subtracted and normalized by the maximum peak-to-peak intensity of the trace in the top panel in C. (D) Representative examples of actin fluorescence intensity dynamics, within a square ROI of 5-µm diagonal length, on flat substrates. (E) Composite power spectrum of actin fluorescence intensity oscillations for nine cells on substrates with a 3-µm ridge spacing (solid black trace) and nine cells on flat substrates (red trace). The green line denotes the peak at 0.020 Hz. The light gray and light red traces indicate the 99% confidence interval for the cell on the patterned surface and the flat surface, respectively. (F) Same as in E but for a 5-μm ridge spacing. (G) Coefficient of variation (CV) of actin dynamics on flat substrates and on ridged substrates with 5- and 3-µm spacings (p < 0.001 KS test N = 21 cells on ridged, N = 16 cells on flat). (H) EGFP-Lifeact primary B-cell exhibiting actin oscillations on a surface with a 5-µm ridge spacing. Scale bar: 5 µm. (I) Representative example of integrated actin fluorescence intensity levels for a primary B-cell on a substrate with a 5-µm ridge spacing. (J) Composite power spectrum of actin fluorescence intensity oscillations for primary cells (N = 9) on substrates with 5-µm ridge spacing. (K) CV for EGFP-Lifeact primary B-cells on flat substrates and on substrates with 5- and 3-µm ridge spacings (p = 0.0012 KS test, N = 16 cells ridged, N = 22 cells flat).

We quantified actin enrichment on ridged surfaces using a square region of interest (ROI). The ROI was centered over the actin enrichment area and sized to fit between two ridges, such that the length of the ROI diagonal was equal to the ridge spacing (Figure 2A). The integrated fluorescence intensity inside such an ROI was roughly periodic (Figure 2C). For comparison, the actin fluorescence intensity dynamics on flat substrates was studied using similarly sized ROIs that were placed at arbitrary locations within the contact area. On flat substrates, the actin fluorescence intensity fluctuated over time but did not undergo the large-scale oscillations observed for cells on ridged surfaces (Figure 2D). We chose the ROI in this manner to not overemphasize the effect of the regions proximal to the ridges, but rather to sample the area between adjacent ridges. Additional tests verified that the choice of ROI did not affect the qualitative results. Supplemental Figure S2 shows two examples in which the intensity variation in the chosen ROI is compared with the intensity variation in an alternate ROI in which the sides of the square were parallel to the ridges. The intensity time series show the same oscillations in both cases, albeit with somewhat different intensities.

We performed Fourier analysis to identify the major frequency components in the fluorescence intensity time traces obtained from the ROIs. The composite spectral density obtained from the Fourier transform of the intensity traces on the patterned surfaces shows peaks at 0.02 Hz (corresponding to a 50-s period) for B-cells on ridges with both spacings (Figure 2, E and F). Intensity traces on flat surfaces (red curve) exhibited a weak peak at 0.02 Hz. This result suggests that BCR stimulation may drive weak oscillations of actin concentration, which is greatly enhanced by the presence of nanoridges on stimulatory surfaces.

We further analyzed the temporal variability in the actin fluorescence intensity using the coefficient of variation (CV), which is defined as σ/µ, where σ and μ are the SD and mean of the intensity value, respectively. We calculated the CV for the integrated intensity time traces obtained from the ROIs. The CV values were similar for cells on ridges with 3- and 5-µm spacings, with a combined mean value of 0.61 ± 0.12 (Figure 2G). The results were the same to within the uncertainty using the alternate ROI tested in Supplemental Figure S2. In contrast, cells on flat surfaces exhibited a mean CV of 0.45 ± 0.08. These results suggest that the presence of ridges on the activating surface leads to a greater degree of variability in actin dynamics, as reflected in the enhanced intensity oscillations on ridged substrates.

To examine whether similar behavior of actin dynamics is recapitulated in primary B-cells, we imaged Lifeact-GFP–expressing murine B-cells spreading on antibody-coated surfaces (Figure 2H). We again observed actin fluorescence intensity oscillations after the primary B-cells were allowed to spread for 6 min on ridged surfaces with 3- or 5-µm spacings but not on flat surfaces (Figure 2I) and spectral analysis showed a clear peak at ∼0.025 Hz (Figure 2J). The median value of the CV in specified ROIs for primary B-cells on ridged surfaces was 0.43 ± 0.08, as compared with 0.33 ± 0.08 on flat surfaces (Figure 2K).

BCR signaling and nonmuscle myosin II activity are required for nanotopographically induced actin dynamics

To determine whether the B-cell actin dynamics induced by ridged surfaces require BCR stimulation, we coated the substrates with transferrin instead of antibodies. This coating allows B-cells to bind to the surface via the transferrin receptor but does not induce BCR activation, thus acting as a no-antigen control. EGFP-actin–expressing A20 B-cells spread on the transferrin-coated surfaces but did not exhibit actin fluorescence intensity oscillations or enrichment of actin along 5-μm-spaced ridges (Supplemental Figure S3A). Peak-to-mean analysis of actin fluorescence intensities on transferrin-coated ridged substrates yielded a median ratio of 1.59 ± 0.13 (Supplemental Figure S3B), as compared with (2.47 ± 0.37) on antibody-coated ridged substrates. Thus, BCR stimulation is essential for the accumulation of actin in proximity to the ridges on activating surfaces.

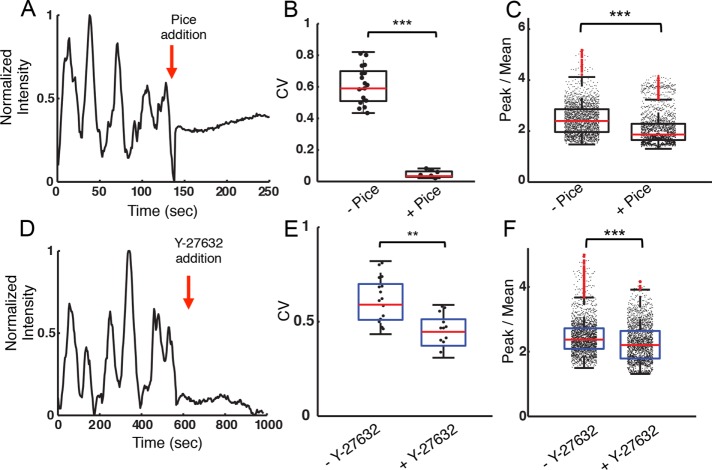
We next examined whether a signaling molecule proximal to BCRs is required for nanotopographically mediated modulation of actin dynamics. The tyrosine kinase Syk enables actin reorganization downstream of receptors that contain immunoreceptor tyrosine-based activation motifs (ITAM) (DeFranco et al., 1995). We inhibited the tyrosine kinase activity of Syk using piceatannol, a phenolic stilbenoid that competes for the tyrosine-containing substrate binding site (Geahlen and McLaughlin, 1989; Oliver et al., 1994). B-cells that were spread on ridges with 3- or 5-µm spacing initiated the characteristic oscillatory actin dynamics described above. Piceatannol (50 µM) was added to the imaging medium 12 min after the initiation of spreading. Within seconds of inhibitor addition, actin intensity oscillations ceased (Figure 3A). The CV also decreased dramatically following the addition of piceatannol (Figure 3B). Furthermore, actin accumulation along the ridge bases was significantly reduced, as shown by the peak-to-mean values of actin fluorescence intensity (Figure 3C). These results indicate that both dynamic actin enrichment and semistatic actin accumulation are dependent on competent signaling by the BCRs, as well as on the geometry of the activating surface.

FIGURE 3:

Actin fluorescence intensity oscillations are dependent on BCR signaling and are driven by myosin. (A) Actin fluorescence intensity within a representative ROI in an EGFP-actin A20 cell activated on a ridged surface with 3-μm spacing before and after the addition of piceatannol. The red arrow indicates the time of inhibitor addition. (B) CV for fluorescence intensity traces before and after piceatannol addition (N = 21, N = 12 cells, respectively, p < 0.001 KS test). The CV was measured in a 6-min interval both before and after inhibitor addition. (C) Peak-to-mean ratio of actin fluorescence intensity for cells on ridges with 3- and 5-µm spacing before and after piceatannol addition (p << 0.001 KS test, N = 10 cells). (D) Integrated actin fluorescence intensity of an ROI in a representative EGFP-actin A20 cell activated on a ridged surface with 3-μm spacing before and after Y-27632 addition. (E) Coefficient of variation for fluorescence intensity traces before and after Y-27632 addition (N = 21, N = 17, respectively, p < 0.01 KS test). The CV was measured in 6-min intervals both before and after inhibitor addition. (F) Peak-to-mean ratio of actin fluorescence intensity for cells on ridges with 3- and 5-µm spacings before and after Y-27632 addition (p < 0.001 KS test, N = 13 cells)

We next probed the role of myosin in the actin fluorescence intensity oscillations induced by activating ridged surfaces, as myosin-based contractility often leads to oscillations of the actin network in cells (Martin et al., 2009; Gorfinkiel, 2013). The contractile activity of nonmuscle myosin IIA, a major isoform of myosin proteins that is expressed in B-cells, is mediated through the phosphorylation of myosin light chain by the Rho-associated protein kinase (ROCK). We utilized the ROCK inhibitor Y-27632 to block the activation of nonmuscle myosin IIA (Ishizaki et al., 2000; Narumiya et al., 2000). Cells were allowed to spread on substrates with 3- or 5-µm ridge spacings for 12 min before the addition of 10 µM Y-27632. As shown in the time series of integrated actin intensity within an ROI constructed as described before, the ROCK inhibitor immediately abolished actin oscillations (Figure 3D). The CV of the intensity time series was reduced significantly in the presence of Y-27632 (Figure 3E). Actin accumulation as quantified using the peak-to-mean values of actin fluorescence intensity was also significantly smaller on ROCK inhibition (Figure 3F). These results show that myosin activity is essential to the oscillatory behavior of actin levels in B-cells on ridged substrates.

BCR clustering is modulated by nanotopography

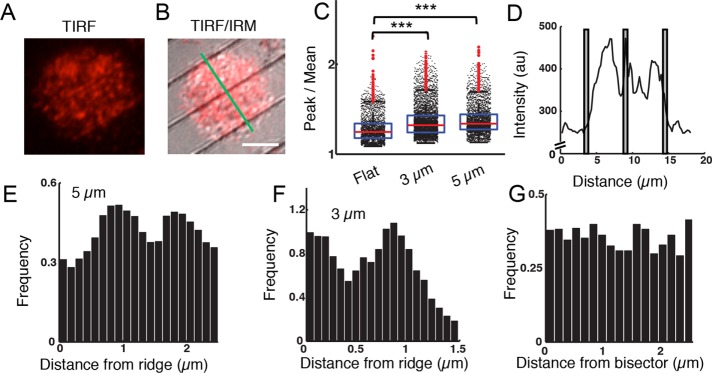
Previous studies have shown that actin dynamics and surface BCR reorganization are likely to be linked through a feedback loop during signaling activation, suggesting that nanotopography could influence BCR clustering and signaling. We therefore investigated the spatiotemporal organization of surface BCRs in B-cells spread on substrates with 3- and 5-µm ridge spacings. Surface BCRs of EGFP-actin A20 B-cells were labeled with monobiotinylated Fab′ fragment of the anti-mouse IgM+G antibody that was tagged with Alexa Fluor 546 and activated by streptavidin-coated ridged surfaces. We used TIRF microscopy to visualize BCR clusters (Figure 4A) and IRM to visualize the ridges (Figure 4B), and we analyzed BCR clustering in relation to the position of the ridges. The fluorescence intensity of individual BCR clusters is significantly higher on ridged surfaces than on flat surfaces, as indicated by the peak-to-mean ratio (Figure 4C), demonstrating that BCRs cluster more efficiently to obtain higher receptor density on ridged substrates.

FIGURE 4:

Nanotopography modulates the distribution of BCR clusters. (A) TIRF image of an A20 B-cells with AF546-labeled BCR on ridges with a 5-µm spacing. (B) A merged TIRF/IRM image of the same cell. The green line was used to calculate the intensity profile in D. Scale bar: 5 µm. (C) Peak-to-mean ratio of BCR fluorescence intensity over the entire cell/surface contact zone and observation time for cells spread on flat surfaces and on widely spaced ridged surfaces. (p < 0.001 KS test; N = 13 for flat, N = 24 for 3-µm and N = 19 for 5-µm surfaces). (D) Fluorescence intensity profile of AF546-labeled BCR along the line shown in (B). The gray bars indicate the locations of the ridges. (E) Normalized histogram of BCR cluster locations with respect to the nearest ridge for 5-μm spaced ridges (N = 19). (F) Normalized histogram of BCR cluster locations with respect to the nearest ridge for 3-μm-spaced ridges (N = 7). (G) Normalized histogram of BCR cluster locations for a flat surface with respect to a line bisecting the cell in a chosen direction (N = 10).

Although the maximum actin fluorescence intensity was observed directly adjacent to ridges, fluorescence intensity line profiles of AF546-labeled BCRs perpendicular to ridges show distinct BCR peaks between ridges as well (Figure 4D). We identified BCR clusters, determined the distance of each from the closest ridge, and thereby obtained the spatial distribution of cluster distances relative to ridges. In contrast with the uniform BCR cluster distribution on flat surfaces (Figure 4G), on ridges with 3- and 5-µm spacings the distribution of clusters peaked at a distance of ∼1.0 µm from the nearest ridge, indicating enhanced clustering (Figure 4, E and F). The distributions of BCR cluster distances on the ridged surfaces differed significantly from those on flat surfaces. Our previous observations have shown that BCR clusters are localized proximal to, rather than colocalized with, F-actin-rich zones (Ketchum et al., 2014). This observation suggests that the accumulation of actin within ∼1 μm of ridges may be responsible for the preferential accumulation of BCR clusters at a location somewhat farther from each ridge, implying a close coupling between the spatial organization of actin and BCR clusters on nanotopographic substrates.

Calcium signaling in B-cells is modulated by nanotopography

The earliest events of B-cell activation are characterized by the release of Ca²⁺ from intracellular stores to the cytoplasm, which then activates Ca²⁺ influx. Under some conditions this initial Ca²⁺ flux can result in intracellular Ca²⁺ oscillations. Ca²⁺ oscillations regulate frequency-sensitive transcription factors in B-cells (Smedler and Uhlen, 2014). To investigate the effects of surface topography on B-cell signaling, we examined the intracellular concentration of Ca²⁺. A20 B-cells loaded with the calcium-sensitive dye Oregon Green 488 BAPTA-1 (OGB1) were allowed to spread fully on antibody-coated flat or ridged substrates for 6 min and imaged. Ca²⁺ oscillations were observed in all cases. The OGB fluorescence intensity time series were smoothed over a 10-s window and measured the time intervals between adjacent peaks of OGB1 fluorescence intensity. As seen in Figure 5A, the period of calcium oscillations was dependent on ridge spacing. B-cells spread on flat substrates had the shortest Ca²⁺ oscillation periods, with a median value of 13.9 ± 0.6 s. On ridged surfaces the oscillation period increased to a median of 55.6 ± 4.0 s (Figure 5B). This observation indicates that nanotopography has a substantial effect on the calcium response of B-cells.

FIGURE 5:

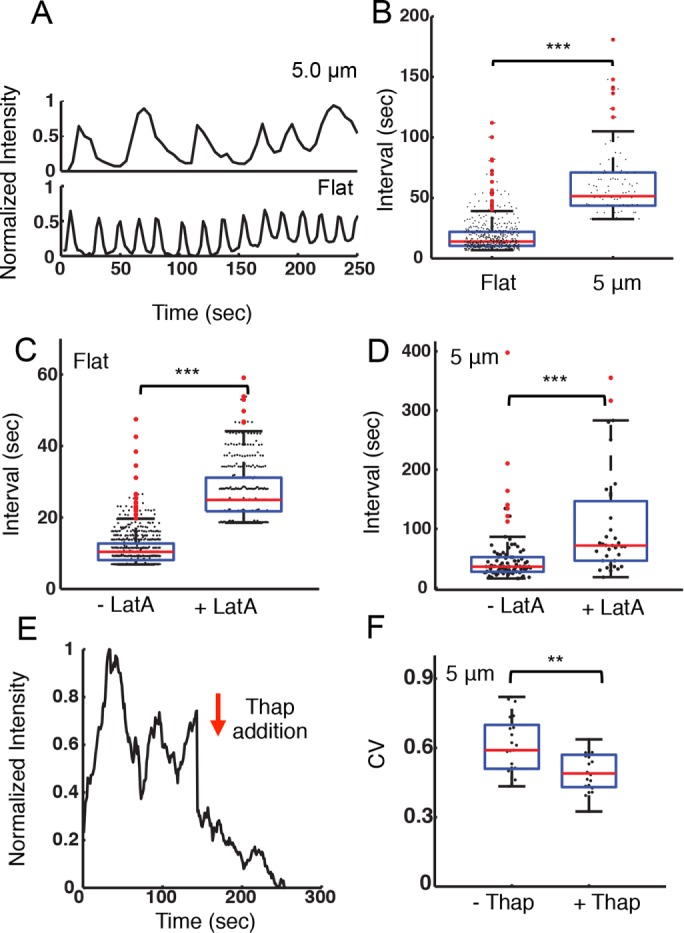
Nanotopography influences intracellular calcium signaling. (A) Integrated, whole-cell fluorescence intensity of the calcium-sensitive dye OGB-1 for representative A20 cells on flat surfaces and on ridges with a 5-μm spacing. (B) Distribution of peak-to-peak intervals between adjacent oscillations in OGB-1 fluorescence intensity for A20 cells on flat substrates (N = 27) and on ridges with a 5-μm spacing (N = 17). The average interval is significantly different for the two substrates (p << 0.001 KS test). (C) Distribution of peak-to-peak intervals between adjacent oscillations in OGB-1 fluorescence intensity for cells on a flat substrate before (–LatA, N = 27) and after (+LatA, N = 20) addition of 100 nM latrunculin-A (p << 0.001 KS test). (D) Distribution of peak-to-peak intervals between adjacent oscillations in OGB-1 fluorescence intensity for cells on ridges with a 5-μm spacing before (–LatA, N = 14) and after (+LatA, N = 12) addition of 100 nM latrunculin-A (p << 0.001 KS test). (E) Representative time dependence of the integrated actin fluorescence intensity within an ROI of an EGFP-actin A20 cell before and after 1 µM thapsigargin addition on ridges with a 5-μm spacing. The arrow indicates the time of the addition. (F) Coefficient of variation for integrated EGFP-actin intensity in ROIs as described previously, before (–Thap) and after (+Thap) the addition of 1 µM thapsigargin (N = 21, N = 20, respectively, p < 0.01 KS test).

To test whether the actin cytoskeleton plays a role in the modulation of the calcium oscillation frequency in B-cells, we inhibit actin polymerization using latrunculin-A (LatA, 100 nM) after the establishment of calcium oscillations (∼6 min). Peak-to-peak analysis showed that LatA treatment significantly increased the period of the calcium pulses for B-cells on flat surfaces (Figure 5C). For cells on ridges with 5-μm spacing, LatA treatment similarly increased the average period of calcium pulses (Figure 5D). Qualitatively similar results were obtained on substrates with 3-μm spacing. Addition of 1 µM thapsigargin, a noncompetitive inhibitor of the sarco/endoplasmic reticulum Ca^²+ ATPase, immediately suppressed the oscillations in actin fluorescence intensity and caused the overall actin fluorescence intensity to decay slowly (Figure 5E). The CV of the actin intensity traces decreased significantly in the presence of thapsigargin (Figure 5F), further verifying the dependence of actin oscillations on Ca²⁺. Our results suggest that actin and calcium dynamics are involved in a feedback loop.

DISCUSSION

Our results demonstrate that nanotopography has a substantial influence on the actin dynamics, BCR distribution, and Ca²⁺ signaling in B-cells. APCs have complex surfaces with convoluted topographies, including long extensions, dendrites, membrane ruffles, and invaginations (Saino et al., 2011; Kwon et al., 2012) characteristic of follicular dendritic cells. These features have radii of curvature ranging from 100 to 300 nm (Szakal et al., 1985; Felts et al., 2010), thereby providing a topographically complex contact surface. Thus, our ridged substrates mimic feature dimensions encountered by B-cells in vivo. We found that antigen-coated nanoscale ridges enhance actin dynamics in B-cells, promoting actin fluorescence intensity oscillations that may arise from actin polymerization waves. The actin dynamics are dependent on BCR signaling, Ca²⁺ signaling, and nonmuscle myosin II activity. Furthermore, BCR clusters are preferentially enriched between ridges, adjacent to, but not overlapping, the actin-rich zones along the ridges. Although all of the activating surfaces studied here induced Ca²⁺ flux, which is a characteristic of B-cells during activation, the frequency of calcium oscillations is modulated by substrate topography, indicating that B-cell signaling also responds to the nanotopography of the antigen-presenting surface.

Our current understanding of B-cell activation has been greatly advanced by in vitro studies on planar substrates. These studies underscore the importance of actin dynamics and the actin cytoskeleton in BCR diffusion, clustering, and movement at the B-cell surface (Fleire et al., 2006; Liu et al., 2011, 2012a, 2013; Treanor et al., 2011; Ketchum et al., 2014). The work presented here indicates that local patterning of actin cytoskeleton by substrate topography may play a critical role in B-cell activation in vivo. It has been observed previously in Dictyostelium discoideum and neutrophils that nanotopography can nucleate and guide actin polymerization in a process called esotaxis (Driscoll et al., 2014; Sun et al., 2015). The enrichment of actin near ridges in the present study suggests that B-cells also exhibit esotaxis.

Nanotopography has been shown to affect many aspects of cell behavior, such as morphology, movement, and gene expression, for cell types including keratinocytes and fibroblasts (Pot et al., 2010; Fu et al., 2014). Topography also modulates immune cell behavior, as seen in increased levels of cytokine secretion by macrophages and guidance of immune cell migration (Pot et al., 2010; Kwon et al., 2012; Lomakina et al., 2014; Rostam et al., 2015; Sun et al., 2015). The migration of Dictyostelium discoideum and human neutrophils is also guided by patterned substrates through the topographic modulation of the actin network dynamics (Sun et al., 2015).

Actin dynamics generates forces that are essential for lateral movement, microcluster formation, and the merger of surface BCRs. Nanotopographically triggered actin remodeling can therefore regulate the mobility of BCRs and their assembly into microclusters (Batista et al., 2010; Treanor et al., 2011; Ketchum et al., 2014). Here, we demonstrated that the modulation of B-cell actin dynamics by nanotopography is driven by BCR signaling, suggesting that this signaling may trigger and/or amplify intrinsic actin responses to the environment. Finally, differential actin responses to topography may permit B-cells to spread adaptively on encountering variable membrane features, allowing the cells to engage as much antigen as possible, thereby to maximize activation.

The modulation of Ca²⁺ oscillations is another pathway through which nanotopography can influence B-cell activation. Ca²⁺ oscillations have been observed in numerous cell types (Tsien and Tsien, 1990), including lymphocytes (Wilson et al., 1987; Lewis and Cahalan, 1989). The frequency and amplitude of Ca²⁺ oscillations encode cell-specific information (Healy et al., 1997; Dolmetsch et al., 1998). For instance, Ca²⁺ oscillations have been shown to regulate the activation of frequency-sensitive transcription factors, which play critical roles in the activation of B-lymphocytes (Smedler and Uhlen, 2014). Ca²⁺ also modulates the contractile behavior of actin networks through phosphorylation of myosin light chain and the accumulation of actin nucleators such as N-WASP (Wollman and Meyer, 2012). Thus, substrate nanotopography could enhance the coupling between actin and Ca²⁺ dynamics in B-cells, thereby affording an added level of control for adapting to external stimuli. An important distinction between our studies and previous observations of Ca²⁺ oscillations induced by antigens is that the latter is a global stimulus, whereas topography is localized. The ridges occupy less than 5% of the contact area but are able to induce global changes in Ca²⁺ dynamics. Although our studies implicate an intricate feedback loop involving BCRs, kinases such as Syk and Ca²⁺, and the actomyosin cytoskeleton in mediating B-cell responses to nanotopography, fundamental questions about the mechanistic basis of the sensing of nanotopography remain.

Based on our results shown here and prior work on esotaxis in other systems (Driscoll et al., 2014; Sun et al., 2015), we propose the following qualitative model. The engagement of surface BCRs with ligands triggers early signaling, including Syk. This process in turn initiates actin remodeling through signaling cascades, such as actin depolymerization and subsequent repolymerization (Rolli et al., 2002). This initial actin remodeling enables B-cells to adapt to nanoridges. Nanoridges promote the accumulation of curvature-sensitive proteins that can activate actin nucleators (Galic et al., 2012), catalyzing actin polymerization. The nucleation of actin polymerization near ridges, and the resulting higher levels of F-actin, promote network connectivity. When polymerized actin levels increase beyond a threshold, enhanced myosin motor activity leads to large-scale waves in the actin network, thus increasing the local actin density even further. In support of this picture, in vitro studies have shown that higher actin concentrations lead to macroscopic contraction of the acto-myosin network (Kohler and Bausch, 2012). High concentrations of actomyosin, and possibly the build-up of calcium, can lead to transient depolymerization of the actin network (Wilson et al., 2010). The cycle then begins anew, leading to the oscillatory dynamics of actin observed here. This conceptual model suggests how nanotopography might modulate actin dynamics.

In the context of B-cells, actin dynamics induced by the topography of the antigen-presenting surface may impact where and how surface BCRs move and form clusters. These topographical features may alter receptor mobility by directly acting as diffusion barriers as well as inducing dense actin networks that impede BCR diffusion (Treanor et al., 2011), consequently altering B-cell signaling, such as the Ca²⁺ flux that we have measured. Further, we find that activation of BCR stimulation induces Ca²⁺ oscillations in a nanotopography-dependent manner. The increase in the Ca²⁺ oscillation period by topography or actin depolymerization is indicative of the direct interaction between actin dynamics and Ca²⁺ influx. A similar feedback interaction between Ca²⁺ and actin has been shown in mast cells on FcεRI receptor stimulation and is mediated by phosphatidylinositol 4,5-bisphosphate (PIP₂) signaling and cdc42 activation (Wollman and Meyer, 2012). One potential mechanism linking nanotopography, actin polymerization and Ca²⁺ dynamics is the spatial organization and accumulation of curvature-sensing (Bin-Amphiphysin-Rvs [BAR] domain containing) proteins in regions of high substrate curvature (Takano et al., 2008). A number of these proteins have been shown to promote actin nucleation via the activation of upstream regulators such as Missing-in-Metastasis (Mattila et al., 2007), the N-BAR domain protein, Bridging integrator 3 (Bin3), and Arf-GAP family proteins (Myers and Casanova, 2008), which are also expressed in B-cells. Local-curvature-mediated accumulation of these BAR-domain proteins may lead to activation of cdc42 and Rac1, resulting in enhanced actin polymerization and clustering of BCRs as well as Ca²⁺ activation. A number of other proximal signaling molecules, including CD19, PLCγ2, Vav, Btk, and Rap, as well as Src family kinases such as Lyn (Takata et al., 1994) have been shown to be involved in actin-mediated B-cell spreading and BCR clustering (Fujimoto et al., 2002; Arana et al., 2008; Depoil et al., 2008; Weber et al., 2008), and it would be interesting to study how these contribute to actin dynamics in response to topographic cues.

Our results suggest that the topographically complex surfaces encountered by B-cells in vivo are likely to affect both morphology and cytoskeletal dynamics, with consequent effects on BCR organization and signaling. More complex features such as nanoposts, nanopits, and fibers, which can be fabricated by the optical techniques used here, may further shed light on how specific topographic features modulate B-cell signaling. Taken together with our previous work (Ketchum et al., 2014), these studies point to the importance of physical aspects of ligand presentation, including ligand mobility, substrate stiffness, antigen density, and nanotopography in B-cell activation and antigen gathering. This work could aid further advances in the development of bioengineering strategies for immunogen-presenting substrates for the development of effective immunological therapies and vaccines.

MATERIALS AND METHODS

Cell culture and materials

A20 cells or EGFP-actin–expressing A20 cells were cultured as described previously (Liu et al., 2012a; Ketchum et al., 2014). A density 7 × 10⁵ cells/ml was used for imaging. For surface BCR visualization experiments, we used an Alexa Fluor 546 labeled monobiotinylated Fab′ fragment of anti-mouse IgM+G antibody (AF546-mB-Fab′-anti-Ig, 2.5 μg/ml; Jackson ImmunoResearch, West Grove, PA), which was generated as described previously (Liu et al., 2012a; Ketchum et al., 2014) at 4°C. The labeled cells were incubated on streptavidin-coated surfaces. Piceatannol (5 mg stock) was procured from Cayman Chemical. Y-27632 was procured from SelleckChem. CK666 was procured from Sigma Aldrich. LatrunculinA (100-µg stock) was procured from Sigma Aldrich. OGB1 was obtained from Molecular Probes. Primary splenic B-cells were obtained from EGFP-Lifeact–expressing mice and were imaged in the same manner as A20 cells.

Calcium imaging was performed by resuspending A20 B-cells in Hank’s balanced salt solution (with calcium, magnesium, no phenol red; ThermoFisher) containing 1% fetal bovine serum (FBS; Life Technologies), 2 μM Oregon Green 488 BAPTA-1, AM (OGB1) cell permeant dye (ThermoFisher), and 0.02% Pluronic F-127 (Sigma-Aldrich). Cells were incubated for 30 min at room temperature (RT). Cells were then washed and maintained in fresh L-15 medium for 15 min at RT to permit intracellular enzymatic hydrolysis of the AM ester to proceed to completion. The calcium-loaded A20 B-cells were then seeded into the chamber and imaged via TIRF with a 60×, 1.49 NA objective and a 491-nm laser (100 mW; Cobolt Calypso).

Substrate preparation and imaging

The preparation of the nanotopographic surfaces has been previously described (Driscoll et al., 2014; Sun et al., 2015). Briefly, a master surface composed of nanoridges was fabricated with multiphoton absorption polymerization on an acrylate-functionalized glass slide using acrylic resin. The resin was composed of 49 wt% Tris (2-hydroxyethyl) isocyanurate triacrylate (SR368; Sartomer), 49 wt% dipentaerythritol pentaacrylate (SR399; Sartomer), and 2 wt% Lucirin TPO-L (Ciba). The master surface was treated with ethylenediamine and then with perfluorooctadecanoic acid to reduce the surface energy. A composite polydimethylsiloxane (PDMS) mold was created to replicate the nanoridges. To prepare the mold, 1.7 g of vinyl PDMS prepolymer (VDT-731; Gelest), 9 μl of Pt catalyst (SIP6831.2; Gelest), 0.05 g of modulator (87927; Sigma-Aldrich), 0.5 g of hydrosilane (HMS-301; Gelest), and 1 g of hexane was mixed and spin coated on the master surface at 1000 rpm for 40 s. The sample was allowed to sit at room temperature for 2 h and prebaked at 60°C for 1 h. Next, the base and the curing agent of Sylgard 184 (Dow Corning) were mixed at a 10:1 mass ratio. After degassing, the mixture was poured onto the precured sample to form a 5-mm-thick layer and cured at 60°C for 1 h. The mold was then peeled off of the master surface along the direction of nanoridges. To replicate the nanoridges, a drop of acrylic resin composed of 49 wt% Tris (2-­hydroxyethyl) isocyanurate triacrylate (SR368; Sartomer), 49 wt% ethoxylated trimethylolpropane triacrylate (SR499; Sartomer), and 2 wt% Lucirin TPO-L (Ciba) was sandwiched between the mold and an acrylate-functionalized cover glass and UV cured for 5 min. The surfaces were then soaked in ethanol overnight and dried at 90°C for 30 min. Surfaces were then coated with 0.01% poly-l-lysine for 10 min and dried for 1 h and coated with 1.3 μg/ml Fab2-anti-IgG+IgM overnight, and then rinsed three times with phosphate-buffered saline. Before use substrates were blocked with BSA for 10 min at 37°C. As a nonactivating control, substrates were coated with transferrin (1.3 μg/ml) instead of activating antibody. We used AlexaFluor-546 labeled Fab2 to verify that both the flat and ridged surfaces were uniformly coated.

Cells were seeded onto chambers for imaging and maintained at 37°C using an airstream incubator (ASI400 Nevtek, Williamsville, VA). Images were collected using an inverted microscope (TE2000 PFS; Nikon, Melville, NY) with a cooled charge-coupled device camera (Coolsnap HQ2; Photometrics, Tucson, AZ) at a frame interval of 3 s. EGFP-actin and fluorescent receptors were imaged with TIRF using the 60×, 1.49 NA objective lens, the 491-nm laser for EGFP excitation, and a 561-nm laser (75 mW; Cobolt Jive) for AF546 excitation. Identical imaging conditions were used for all types of substrates.

Image analysis

Mean-normalized autocovariances of the actin intensity were performed using a pixelwise algorithm (Smoligovets et al., 2012). The fluctuations of intensity away from the time-average value was computed using

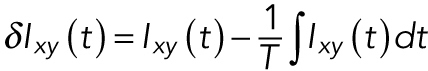(1)

where xy denotes the location of the pixel, t is time, and T is the total length of the time trajectory. The pixelwise MNA was then computed using

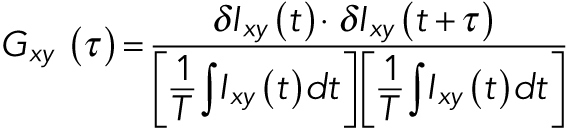(2)

where τ is the delay time between measurements and <> denotes an average over time. MNA-sum heat maps were calculated by integrating the G_xy(τ) values for each pixel over τ and then normalizing by the maximum time-lag. Spectral analysis of the fluorescence intensity data was performed using multitaper analysis with a taper width of three times (N_tapers = 4) the sampling frequency. The 99% confidence interval of the estimated power spectrum was computed as two times the SD of the ensemble of N_cells × N_tapers spectra (Mitra and Pesaran, 1999).

Optical flow measurements were performed using frame-by-frame analysis (Sun et al., 2010) obtained from http://cs.brown.edu/∼black/code.html and implemented in MATLAB. Results were masked to include only the area under the cell footprint. After correction for stage drift, the image stack was smoothed with a local regression using weighted linear least squares and a first-degree polynomial model over seven consecutive frames. Statistical comparisons were done using the KS test for nonparametric comparisons of distributions or Student’s t test for comparisons of mean values.

Abbreviations used:

APC

antigen-presenting cell

BAPTA

1,2-bis(o-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid

BAR

Bin-Amphiphysin-Rvs

BCR

B-cell receptor

Btk

Bruton’s tyrosine kinase

CD19

cluster of differentiation 19

CV

coefficient of variation

EGFP

enhanced green fluorescence protein

F(ab)

fragment antigen binding

FDC

follicular dendritic cell

GFP

green fluorescence protein

Ig

immunoglobulin

IRM

interference reflection microscopy

ITAM

immunoreceptor tyrosine-based activation motifs

KS

Kolmogorov–Smirnov

MAP

multiphoton absorption polymerization

MLC

myosin light chain

MNA

mean-normalized autocovariance

N-WASp

Neural Wiskott–Aldrich syndrome protein

PLCγ2

phospho-lipase C γ2

ROCK

Rho-associated protein kinase

ROI

region of interest

TIRF

total internal reflection fluorescence

WASp

Wiskott–Aldrich syndrome protein