HCN channels generate rhythmic firing patterns in the brain and heart. Alvarez-Baron et al. identify key amino acids responsible for functional differences between cAMP-sensitive and insensitive HCN isoforms, revealing their role in communication between the nucleotide-binding domain and the pore.
Abstract
Hyperpolarization-activated, cyclic nucleotide–gated (HCN) channels generate rhythmic activity in the heart and brain. Isoform-specific functional differences reflect the specializations required for the various roles that they play. Despite a high sequence and structural similarity, HCN isoforms differ greatly in their response to cyclic nucleotides. Cyclic AMP (cAMP) enhances the activity of HCN2 and HCN4 isoforms by shifting the voltage dependence of activation to more depolarized potentials, whereas HCN1 and HCN3 isoforms are practically insensitive to this ligand. Here, to determine the molecular basis for increased cAMP efficacy in HCN2 channels, we progressively mutate residues in the C-linker and cyclic nucleotide–binding domain (CNBD) of the mouse HCN2 to their equivalents in HCN1. We identify two clusters of mutations that determine the differences in voltage-dependent activation between these two isoforms. One maps to the C-linker region, whereas the other is in proximity to the cAMP-binding site in the CNBD. A mutant channel containing just five mutations (M485I, G497D, S514T, V562A, and S563G) switches cAMP sensitivity of full-length HCN2 to that of HCN1 channels. These findings, combined with a detailed analysis of various allosteric models for voltage- and ligand-dependent gating, indicate that these residues alter the ability of the C-linker to transduce signals from the CNBD to the pore gates of the HCN channel.
Introduction
Hyperpolarization-activated, cyclic nucleotide–gated (HCN) channels are nonselective cation channels that, unlike other members of the voltage-gated ion channel (VGIC) family, open upon hyperpolarization. In pacemaker centers of the heart and brain, inward sodium currents through HCN channels depolarize the membrane, bringing it close to the threshold for action potentials and, therefore, set the frequency of spontaneous firing (Biel et al., 2009; DiFrancesco, 2010). During a “fight or flight” response, the frequency of pacemaking in the sinoatrial node of the heart increases partially because cAMP, produced in response to β-adrenergic stimulation, binds to the HCN4 isoform and makes these channels open at more depolarized potentials (Brown et al., 1979; DiFrancesco and Tortora, 1991). In contrast, the predominant HCN isoform (HCN1) expressed in neurons involved in frequency detection in the cochlear nucleus is impervious to cAMP modulation (Bal and Oertel, 2000). In these neurons, HCN channel conductances are tightly correlated with those of the voltage-gated delayed potassium channel KCNA, which results in low input resistances and short time constants for excitatory postsynaptic potentials (Cao and Oertel, 2011). This allows the principal cells of the cochlear nucleus to assess coincidence in the timing of signals with submillisecond resolution (Golding and Oertel, 2012). Any modulation of the HCN channel conductances in these neurons has to be matched with potassium channel conductances to maintain this timing circuit, which ultimately determines the precision with which mammals are able to localize sound in their surrounding environment.
Although they are part of the VGIC superfamily, HCN channels belong to an ancient clade of voltage-gated ion channels with C-terminal cyclic nucleotide–binding domain (CNBD; Yu et al., 2005). Their transmembrane architecture is similar to the other members of the VGIC superfamily. The last transmembrane segment in these channels is linked to the CNBD via the C-linker regions (Lee and MacKinnon, 2017), a conserved structure among HCN and CNG channels (Zagotta et al., 2003; Lolicato et al., 2011; Lee and MacKinnon, 2017; Li et al., 2017) that is present in some prokaryotic members of this family (Kesters et al., 2015; James et al., 2017), but not in others (Clayton et al., 2004; Nimigean et al., 2004; Chiu et al., 2007). This region contains six α-helices (A′–F′), which assemble into a ring-like structure below the pore. The CNBD, which follows the C-linker, is formed by an eight-stranded antiparallel β-roll flanked by one α-helix in the N terminus (A) and two α-helices in the C terminus (B and C; Zagotta et al., 2003; Xu et al., 2010; Lolicato et al., 2011; Lee and MacKinnon, 2017).
Of the four different isoforms of HCN channels found in vertebrates (HCN1–4), HCN2 (Ludwig et al., 1998) and HCN4 (Ludwig et al., 1999) are strongly stimulated by cAMP, in contrast to HCN1 (Santoro et al., 1998) and HCN3 (Mistrík et al., 2005; Stieber et al., 2005). The shifts in the voltage dependence of activation in the HCN1 isoform is minimal even at saturating concentrations of ligand, which indicates that cAMP is less efficacious in activating this isoform (Chen et al., 2001; Wang et al., 2001). By making chimeras between HCN1 and HCN2, Siegelbaum and colleagues (Wang et al., 2001) have shown that the isoform-specific differences in cAMP efficacy are entirely caused by the C-linker and CNBD region.
Surprisingly, comparison of the available apo and holo structures of HCN1 and HCN2 (Zagotta et al., 2003; Lolicato et al., 2011; Goldschen-Ohm et al., 2016; Lee and MacKinnon, 2017) provides limited insights into why these functional differences exist. Structures of the bound C-terminal regions of HCN1 and HCN2 and the apo and holo structures of HCN1 superimpose closely (Lolicato et al., 2011; Lee and MacKinnon, 2017). In contrast, the apo and holo structures of the HCN2 C-terminal regions display major differences (Goldschen-Ohm et al., 2016), suggesting that the conformation of the unbound form of this isoform is a key determinant of its responsiveness to cAMP, as suggested by biochemical studies (Zagotta et al., 2003; Zhou et al., 2004; Lolicato et al., 2011).
The goal of the present study is to identify the minimal molecular determinants that contribute to differences in cAMP efficacy between HCN1 and HCN2. This information will allow us to focus on the key allosteric pathways that transduce ligand binding by regulating the dynamics of the C-terminal region. Here, we find that out of the isoform-specific 18 residues in this region, only 5 are needed to account for the differences in cAMP efficacy between the two isoforms. Quantitative modeling of the channel as an allosteric system regulated by voltage and ligand shows that these mutations determine the strength of the coupling of the CNBD to the pore gates and the state of the C-linker.
Materials and methods
Molecular biology
Mouse HCN2 gene in the oocyte expression plasmid pSP64 was provided by Dr. Michael Sanguinetti (University of Utah, Salt Lake City, UT; Chen et al., 2000). Mutagenesis was performed using PfuUltra II Fusion polymerase (Agilent) according to the conventional Quikchange protocol. Mutagenic oligonucleotides or synthetic gene fragments were obtained from Integrated DNA Technologies. All mutations were confirmed by sequencing of both strands of the complete open reading frame. mRNA was prepared by linearization of the template with XbaI and in vitro transcription using AmpliCap SP6 kit from Cellscript. Before the start of the mutagenesis, we noticed the presence of three inadvertent mutations in the mHCN2 backbone (E55G, R237H, and R283K). Because the cAMP- and voltage-dependent properties of the channel were nearly identical to the data previously published by others (Wang et al., 2001), this backbone was used to generate all mutants in the current study and will henceforth be referred to as WT throughout all experiments.
Oocyte treatment and injection
Xenopus laevis oocytes harvested in house were treated by mechanical dissociation and collagenase A (catalog number 11088793001; Sigma) to obtain individual oocytes. When still present, the follicular layer was removed mechanically after treatment. Oocytes were stored at 16–18°C in ND96 solution containing (in mM) NaCl 96, KCl 2, MgCl2 1, CaCl2 1.8, Hepes 5, pH 7.4, with NaOH, 201 mOsm, supplemented with 0.5 mg/ml BSA and a cocktail of antibiotics (50 µg/ml gentamicin, 100 U/ml penicillin, 100 µg/ml streptomycin, 50 µg/ml tetracycline, 100 µg/ml amikacin, and 50 µg/ml ciprofloxacin). Oocytes were injected with 10–50 ng RNA and recorded 2–4 d after injection. The injector used was Nanoject II (Drummond Scientific Company).
Electrophysiology and data analysis
HCN currents were recorded in macropatches in the inside-out configuration. The vitelline layer of injected oocytes was removed with forceps. Glass pipettes were fabricated with patch glass (Warner Instruments) using a Sutter Instrument micropipette puller P-97. Pipettes were subsequently broken and repolished using a microforge (MF-830; Narishige) to obtain the desired shape. Bath and pipette recording solutions were symmetric containing (in mM) KCl 107, NaCl 5, Hepes 10, MgCl2 1, EGTA 1, pH 7.3, with KOH, 216 mOsm. Electrode resistance in this solution was ∼500 KΩ. Inside-out patches were perfused for ∼9 min before recordings to minimize the effects of current rundown. Patches were recorded at room temperature first in control solution followed by an identical solution containing 10 µM cAMP. Recordings were performed using an Axopatch 1D amplifier (Molecular Devices), digitized with a Digidata 1440A data acquisition system (Molecular Devices), and acquired using Clampex 10.0 at 20 KHz with a low-pass filter of 5 KHz.
HCN channel currents were measured using protocols described previously (Wang et al., 2001). Briefly, from a holding potential of −40 mV, patches were stimulated with 3-s voltage pulses in 5- or 10-mV increments followed by return to the holding potential. No leak subtraction was used. The mean amplitude of the tail currents during a short plateau region was plotted against the activation potential.
Curves were fitted to a Boltzmann function, , where A2 is the maximum tail current amplitude, A1 is the current offset, V1/2 is the midpoint of activation, and z is the slope, using Origin 9.0 (OriginLab Corporation). Tail currents from individual patches were normalized to the maximal fitted tail current (A2) determined in each individual recording or to the maximal fitted tail current (A2) for the patch recorded with cAMP. V1/2 from the individual fits were used for most analysis. For all mutants, the cAMP-dependent shift (ΔV1/2) was calculated as V1/2 +cAMP − V1/2 −cAMP for individual patches. Data presented are mean ± SEM. Statistical significance was estimated by Student’s t test or one-way ANOVA using Excel or Origin. A P value < 0.05 was regarded as significant.
Modeling
All modeling was performed using the program KineticModelBuilder 2.0 (Goldschen-Ohm et al., 2014). Models were built using binary elements for pore (P), voltage sensors (VS), and ligand-binding domain (CNBD) with or without an element for the linker (L). The initial rate constants for the transitions of the pore and voltage sensor in Scheme 1 were obtained from the eight-state allosteric model described previously (Chen et al., 2007). Because in our experiments we only used zero or saturating concentration of cAMP (10 µM), the rate constants of the ligand-binding domain were fixed to give a bound probability of ∼1 in the cAMP condition. The charges (q) of the transitions of the voltage sensor in units of e were calculated using the voltage-dependent slope factors (s) in mV in Chen et al. (2007) according to Eqs. 1 and 2:
| (1) |
| (2) |
where kB is the Boltzmann constant (8.6173324 × 10−5 eV/K), T is temperature, and sα and sβ are the slope factors for voltage sensor activation (α) and deactivation (β).
The initial values for the interaction energies (ΔG and ΔG‡) between the binary elements of Scheme 1 were computed using the rate constants in Chen et al. (2007) according to Eqs. 3 and 4 (Goldschen-Ohm et al., 2014). For example, to calculate the interaction energies between pore and voltage sensors (Fig. S1), we first determined the effect of voltage sensor activation on the rate constants for pore opening:
where ΛP-VS is an interaction factor between the pore (P) and the voltage sensor (VS; Fig. S1), kB is the Boltzmann constant [0.0019872041 kcal/(mol⋅K)], and T is temperature. Rearranging,
| (3) |
is the difference in the energy barrier for pore opening when the voltage sensor is activated as compared with nonactivated (Goldschen-Ohm et al., 2014).
To calculate ,
where ΘP-VS is a second interaction factor between the pore (P) and the voltage sensor (VS; Fig. S1).
Rearranging,
| (4) |
is the energy difference between the pore and the voltage sensor both being in the activated configuration compared with the sum of the energies of activation for either the pore or the voltage, but not both (Goldschen-Ohm et al., 2014).
Models were optimized simultaneously to fit families of current responses both with and without cAMP from the same patch, by minimizing the weighted sum of squared errors between simulated and experimental data.
The time-dependent probabilities of state occupancies were solved numerically from the transition rates matrix as described previously (Colquhoun and Hawkes, 1995; Goldschen-Ohm et al., 2014). The overall evaluation of the model fits was done by visual inspection based on the quality of the fits to (a) the currents at steady state, (b) the conductance to voltage curves, (c) the sigmoidicity in the activation, and (d) the kinetics of the tail currents.
All parameters were fitted to experimental data for WT HCN2 in Schemes 2–5. To fit experimental data from the HCN2/1 chimera and HCN1minimal mutant for each scheme, only some of the parameters were allowed to vary. Schemes 1–3 were fitted by simultaneously changing the interaction energies between the binding domain and the pore (ΔG‡pore–CNBD and ΔGpore–CNBD) and the binding domain and voltage sensors (ΔG‡VS–CNBD and ΔGCNBD–VS), depending on the scheme (see Results). Schemes containing a linker (4 and 5) were fitted by simultaneously changing the rate constants for the linker (kI-A and kA-I), the interaction energies between the pore and linker (ΔG‡pore–linker and ΔGpore–linker), the voltage sensors and the linker (ΔG‡VS–linker and ΔGlinker–VS), and the linker and the binding domain (ΔG‡linker–CNBD and ΔGlinker–CNBD).
Online supplemental material
Fig. S1 shows a kinetic scheme representing interacting binary elements for pore and voltage sensor. Fig. S2 shows that the maximal conductance at saturating voltages in HCN channels is smaller in the absence than in the presence of cAMP. Fig. S3 shows that mutations L565I and S575T do not affect cAMP-dependent ΔV1/2 in the HCN1minimal background. Fig. S4 shows fits of allosteric models of voltage- and ligand-dependent gating in WT HCN2 without a linker module. Fig. S5 shows that models lacking a linker domain do not describe the behavior of the HCN2/1 chimera. Fig. S6 shows fits of allosteric models of voltage- and ligand-dependent gating with a linker module. Fig. S7 shows that kinetic Scheme 4 described the behavior of the HCN2/1 chimera as well as that of WT HCN2. Fig. S8 shows that kinetic Scheme 5 is not a significant improvement over Scheme 4. Table S1 summarizes the voltage-dependent activation parameters with and without cAMP for mHCN2 mutants with HCN1 substitutions. Table S2 summarizes the allosteric model parameters for WT HCN2. Table S3 summarizes the allosteric model parameters for the HCN2/1 chimera. Table S4 summarizes the allosteric model parameters for Schemes 4 and 5 for the HCN1minimal mutant.
Results
C-terminal residues largely account for the differential efficacy of cAMP between HCN2 and HCN1
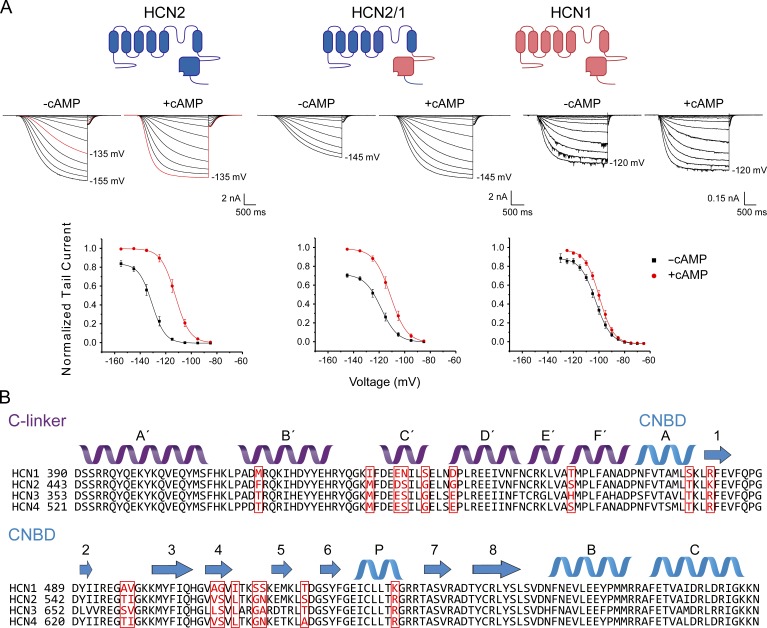
Macropatch recordings in oocytes derived from X. laevis injected with mHCN1 or mHCN2 show that these isoforms display a substantial difference in the efficacy of cAMP to induce channel activation (Fig. 1 B; Chen et al., 2001; Wang et al., 2001). As reported previously (Wang et al., 2001), HCN1 channels are activated at potentials more negative than −80 mV with a midpoint of activation (V1/2) of −103 ± 1 mV. Application of 10 µM cAMP to the intracellular side induces a right shift of 3.4 ± 0.4 mV (Fig. 1 A and Table S1).
Figure 1.
Voltage dependence and sequence comparison of HCN1, HCN2 and chimeric HCN2 with C-linker and CNBD of HCN1. (A) Representative current traces in the inside-out configuration and conductance–voltage curves obtained in the presence and absence of 10 µM cAMP. The same patch was recorded in both conditions. Tail currents from HCN2 (n = 19 patches), HCN2/1 (n = 19), and HCN1 (n = 21) were normalized to the maximum fitted tail current recorded in the presence of cAMP for each patch. Data presented are mean ± SEM. (B) Sequence alignment and secondary structures of mouse HCN1–4. The 18 residues that differ between HCN1 and HCN2 are highlighted in red.
The maximal conductance at saturating voltages, as evaluated by tail currents or the steady-state conductances at the end of the activation pulses, is only slightly increased by cAMP (less than 10% increase; Figs. 1 A and S2).
In contrast, HCN2 channels open at more hyperpolarized potentials with a V1/2 of −133 ± 2 mV in the absence of cAMP, whereas cAMP induces a shift of 18.8 ± 0.6 mV (Fig. 1 A and Table S1). The cAMP-dependent increase in maximal tail current or conductance at saturating voltages for HCN2 was comparable to that of HCN1 (Fig. S2).
To identify the specific regions accounting for these differences between isoforms, we substituted the 18 residues that are different between the isoforms within the C-linker and CNBD (Fig. 1 B), thus creating a chimeric channel containing the N terminus, transmembrane domains, and extreme C terminus of HCN2 and the CNBD and C-linker of HCN1 (HCN2/1). In contrast to a previous study (Wang et al., 2001), in our experiments, the substitution of the C-linker and CNBD residues accounted only partially for the difference between isoforms. V1/2 without cAMP was −118.2 ± 1.8 mV in the chimera, and cAMP induced a shift of 7.2 ± 0.6 mV (Fig. 1 A and Table S1). As evaluated by one-way ANOVA, there was a significant difference in ΔV1/2 between HCN1, HCN2, and the chimera (F(1279.4, 5.4) = 236.7, P = 0). Surprisingly, the effect of cAMP on the maximal tail current amplitude or steady-state conductance at saturating voltages is significantly higher in the chimera, with a ∼30% increase versus ∼15% in HCN2 (Fig. S2). Despite these differences, these results indicate that residues within the C-linker and CNBD account for a large fraction of the differences in voltage- and ligand-dependent gating between HCN1 and HCN2.
M485, G497, and S514 in the C-linker are primary determinants of isoform-specific differences
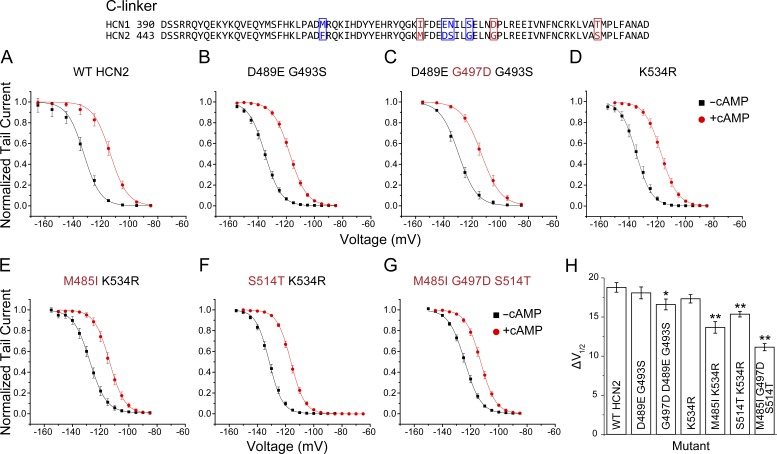
The bound structures (Zagotta et al., 2003; Lolicato et al., 2011; Lee and MacKinnon, 2017) and protein sequence of the C-linker and CNBD of HCN1 and HCN2 are highly conserved (Fig. 1 B). The majority of the 18 mutations between the isoforms are conservative, and in principle, any combination of these 18 sites can define the unique properties of these isoforms, meaning that there are in total 262,143 possibilities. However, if the majority of the sites are neutral and the contributions of other sites are approximately additive, then the problem of the identification of nonneutral sites may be tractable through a combinatorial approach. In this section, we focus on the C-linker region (mutants 1–12 in Table S1).
The initial round of mutations (mutants 1–5) prioritized the sites where mutations were expected to have relatively strong effects (e.g., G497D) or are seen interacting in the crystal structures (e.g., D489E and K534R). Surprisingly, a combination mutant containing most of such residues (mutant 5) showed only a small difference in the ΔV1/2 induced by cAMP compared with WT HCN2 (Table S1). By comparing different sets of combinations (mutants 1–5), it can be deduced that substitution G497D alone explains the effect of mutant 5 on the cAMP-dependent ΔV1/2 (Fig. 2, A–C; and Table S1). Subsequent rounds of mutagenesis aimed to test the additivity of the remaining sites by pooling mutations together based on spatial proximity (mutants 6–11). Analysis of these mutants indicated that M485I and S514T within the HCN2 C-linker also have significant effects (Fig. 2, D–F; and Table S1). The strongest effect was found for mutation M485I (Fig. 2, E and H). A triple mutant containing substitutions M485I, G497D, and S514T within the C-linker activated with a V1/2 without cAMP of −124.2 ± 0.9 mV and displayed a cAMP-induced ΔV1/2 of 11.1 ± 0.5 mV, thus explaining ∼65% of the difference between WT HCN2 and the HCN2/1 chimera (Fig. 2, G and H).
Figure 2.
C-linker residues critical for isoform-specific modulation of HCN2 by cAMP. Top: Alignment of the C-linker of HCN1 and HCN2 illustrating in red the residues that were found to have effects on the response of HCN2 to cAMP. The remaining residues that differ between isoforms are shown in blue. (A–G) Normalized conductance–voltage curves in the presence and absence of cAMP obtained by measuring tail currents of WT HCN2 and various C-linker substitutions with equivalent HCN1 residues. Mutations that significantly decreased the cAMP-dependent ΔV1/2 are labeled red. (H) Summary of the shifts in the midpoints of activation (ΔV1/2) induced by cAMP for the mutants shown in A–G. *, P = 0.02; **, P < 0.00003 versus WT HCN2. The numbers of patches recorded per mutant were HCN2 (n = 19), D489E G493S (n = 21), D489E G497D G493S (n = 21), K534R (n = 18), M485I K534R (n = 14), S514T K534R (n = 19), and M485I G497D S514T (n = 18). Data presented are mean ± SEM.
CNBD residues V562A/S563G also contribute to functional differences between HCN1 and HCN2
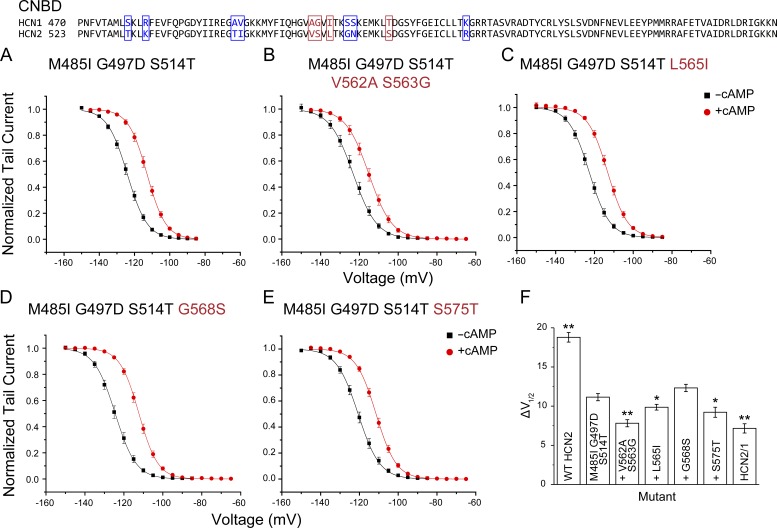
Mutants 13–21 (Table S1) allowed us to identify which substitutions are functionally relevant within the CNBD. Mutations V562A/S563G, L565I, and S575T had significant effects on the ΔV1/2 induced by cAMP (Fig. 3 and Table S1; mutants 14–17 were done in the background of mutant 12). The strongest effect was found for the double mutant V562A/S563G (Fig. 3, A and B). Combined with the nonneutral mutations in the C-linker, these two mutations resulted in a channel that activated with a V1/2 of −123.1 ± 1.2 mV without cAMP and ΔV1/2 of 7.8 ± 0.5 mV when cAMP was added (mutant 14; Fig. 3 B and Fig. 4, A and E). This ΔV1/2 was not statistically different from the full HCN2/1 chimera (P = 0.38; Fig. 3 F).
Figure 3.
CNBD residues critical for isoform-specific modulation of HCN2 by cAMP. Top: Alignment of the CNBD of HCN1 and HCN2 illustrating in red the residues that were found to have effects on the response of HCN2 to cAMP. The remaining residues that differ between isoforms are shown in blue. (A–E) Normalized conductance-voltage curves in presence and absence of cAMP obtained by measuring tail currents of HCN2 carrying various CNBD substitutions. Labeled red are CNBD mutations in the background of the previously identified nonneutral C-linker mutations. (F) Summary of the shifts in the midpoints of activation (ΔV1/2) induced by cAMP for the mutants shown in A–E. The background of the CNBD mutations tested (the triple mutant M485I G497D S514T) is abbreviated by a plus sign (+) in the mutant labels. *, P < 0.04; **, P < 0.00001 versus the triple mutant M485I, G497D, and S514T. The numbers of patches recorded per mutant were M485I G497D S514T (n = 18), M485I G497D S514T V562A S563G (n = 21), M485I G497D S514T L565I (n = 22), M485I G497D S514T L565I (n = 21), M485I G497D S514T S575T (n = 21), and HCN2/1 (n = 19). Data presented are mean ± SEM.
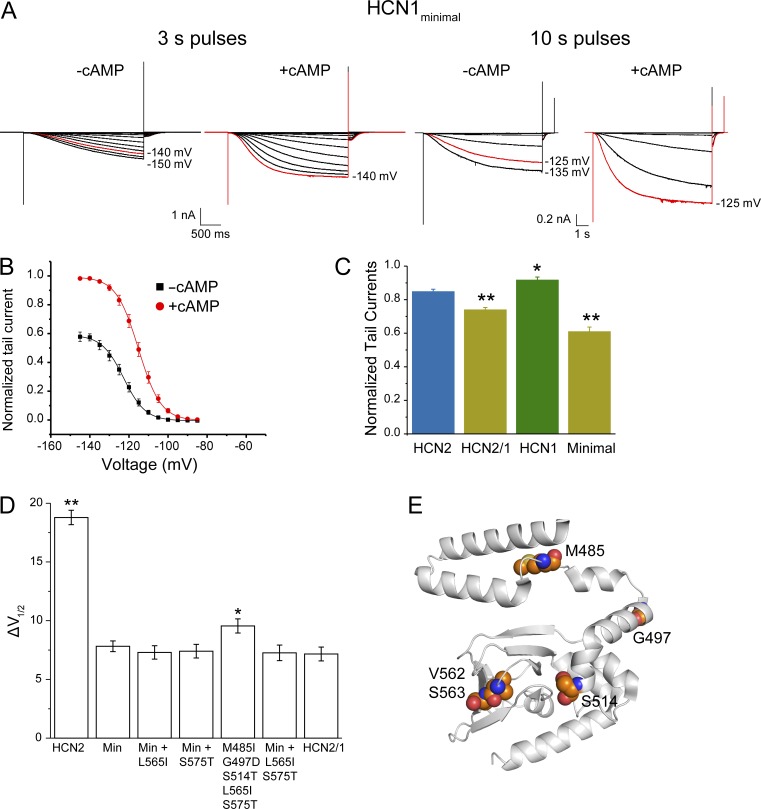
Figure 4.
The voltage-dependent modulation of the HCN1minimal mutant (with substitutions M485I, G497D, S514T, V562A, and S563G) is similar to the HCN2/1 chimera. (A) Representative traces of inside-out recordings for the HCN1minimal mutant in the absence and presence of 10 µM cAMP. For comparison, because of the slow kinetics in this mutant, recordings obtained with 10-s voltage pulses to ensure that the currents are saturated even in absence of cAMP are shown. (B) Conductance–voltage curves for the HCN1minimal mutant normalized to the maximum tail current in the presence of cAMP. (C) Tail currents at saturating voltages in absence of cAMP for WT HCN2 (n = 14 patches), WT HCN1 (n = 21), HCN2/1 (n = 19), and the HCN1minimal mutant (n = 21), calculated relative to the maximum tail current in saturating voltages and cAMP for each patch. *, P = 0.01; **, P < 0.00003 compared with WT HCN2. (D) Additional mutations L565I and S575T do not affect cAMP-dependent ΔV1/2 in the HCN1minimal (Min) background. n = 19 for WT HCN2, 21 for HCN1minimal, 19 for Min + L565I, 18 for Min + S575T, 17 for M485I G497D S514T L565I S575T, 20 for Min + L565I S575T, and 19 for HCN2/1. *, P = 0.03; **, P = 5 × 10−17 versus the HCN1minimal mutant. For conductance–voltage curves, see Fig. S3. Data presented are mean ± SEM. (E) HCN2 structure (PDB accession no. 3U10) showing the residues mutated in the HCN1minimal mutant (Lolicato et al., 2011).
Mutations L565I and S575T in the CNBD also produced significant reductions in the ΔV1/2 induced by cAMP (Fig. 3, C, E, and F; and Table S1), in contrast to mutation G568S (Fig. 3 D). The addition of L565I and S575T to mutant 14 did not produce further decrease in the cAMP-induced ΔV1/2 (mutant 21; Figs. 4 D and S3 and Table S1). Thus, the five residues substituted in mutant 14 are sufficient to account for the differences in the cAMP-induced ΔV1/2 between HCN2 and the HCN2/1 chimera, and we hereby refer to it as HCN1minimal mutant. As observed for the chimera, the maximal steady-state conductance and tail current at saturating voltages in the absence of cAMP is lower in the HCN1minimal mutant than in WT HCN2 (Fig. 4, B and C; and Fig. S2). In this construct, cAMP induced ∼40% larger maximal tail currents, which was highly statistically significant different from ∼15% in WT HCN2 (P = 2.6 × 10−9). The reductions in the maximal conductance achieved by voltage alone in the HCN1minimal mutant persisted when 10-s pulses were used to activate the channels (Fig. 4 A).
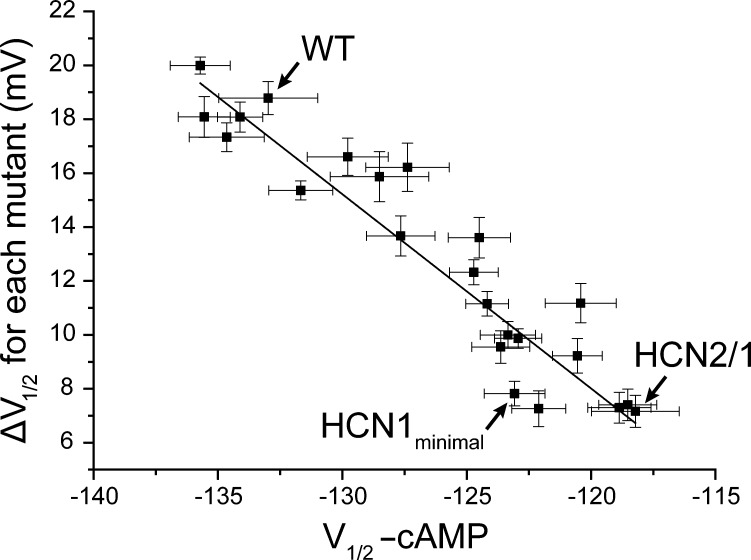
It has previously been suggested that cAMP acts on HCN channels by relieving the channel from the inhibition by unliganded CNDB (Zagotta et al., 2003; Zhou et al., 2004; Xu et al., 2010; Lolicato et al., 2011). Lower sensitivity to activation by cAMP in HCN1 and our mutants can be explained by changes in the behavior of either the liganded or the unliganded CNBD. In the first scenario, cAMP binding simply is not able to relieve the inhibition. Alternatively, mutations may relieve the inhibition by the unliganded CNBD, leading to a lack of effect of ligand binding. A plot of the V1/2 of the unliganded mutants with their corresponding ligand induced ΔV1/2 shows a strong correlation between the extent of modulation and the V1/2 of the unliganded channels (Fig. 5). Because cAMP-bound channels open at less hyperpolarized potentials, and the HCN1-like mutations make it easier to open the unliganded HCN2, these mutations must act by relieving the inhibition produced by the unliganded CNBD. Presumably, this is accomplished by altering the conformational state of the unliganded C-linker and CNBD domains or the coupling between the C-linker CNBD and the pore gates.
Figure 5.
The extent of cAMP-induced shifts correlates with intrinsic midpoints of activation of various mutants. Plot of the cAMP-induced shifts in V1/2 (ΔV1/2) against the V1/2 in the absence of cAMP for all mutants reported in this study. The correlation coefficient is 0.92.
Building an allosteric model of HCN channel gating by voltage and ligand
To gain a mechanistic understanding of the effects of HCN1 substitutions in the C-linker and CNBD of HCN2, we implemented allosteric models of gating using the binary elements approach described previously (Goldschen-Ohm et al., 2014). In a binary elements model, an ion channel is described by modules that represent distinct structural or functional domains in the protein. In the case of HCN2, our initial scheme included modules for pore, voltage sensor, and ligand-binding domain (Fig. S4 A and Scheme 1). Each of these modules is binary, existing in two conformations (nonactivated and activated). The interaction between any pair of binary elements is described by state-dependent changes in the kinetic rates of transition between the two states for each individual element. These changes can be defined by three energy terms, two of which describe a “catalytic” interaction-dependent change in the height of the activation barrier for each element’s transition to an activated state (ΔG‡); the third describes the change in interaction energy upon both elements undergoing a change of state (ΔG). Thus, the model parameters include two kinetic rates for each binary element and three interaction terms expressed as transition energies (Goldschen-Ohm et al., 2014).
The parameters to be used in the simplest model (Scheme 1) were calculated from the rate constants for the eight-state allosteric model described by Chen and colleagues (Chen et al., 2007; Goldschen-Ohm et al., 2014; Materials and methods). In this scheme, cAMP- and voltage-dependent gating are described by coupling interactions between the pore module with a ligand-binding module (CNBD) and the pore and one voltage-sensing module, respectively (Fig. S4 A and Table S2). This model accounted well for the steady-state voltage dependence of WT HCN2 with and without cAMP but failed to describe the activation kinetics. Notably, the sigmoidicity that is evident during the activation phase of HCN2 and HCN2/1 are not fitted by the eight-state allosteric model (Figs. S4 A and S5 A).
Next, we tested a more complex model containing four voltage sensors instead of only one (Fig. S4 B and Scheme 2). The rate constants for all voltage sensors and interaction energies between the pore and voltage sensors were kept equal for all voltage sensors. This model described well the activation kinetics and steady-state conductance–voltage curves of WT HCN2. Additionally, we tested a scheme that includes coupling interactions between the voltage sensor and the CNBD (Fig. S4 C and Scheme 3). This scheme only fitted our currents when the voltage sensor–CNBD interactions were relatively weak compared with the pore–CNBD interaction (Table S2).
Mechanistic dissection of the effects of C-linker and CNBD substitutions on ligand- and voltage-dependent gating
Kinetic modeling was used to dissect what parameters could account for the differences between WT HCN2, HCN2/1 chimera, and HCN1minimal mutant. We reasoned that mutations in the C-linker and CNBD should only affect either the ligand binding affinity of the CNBD or the interaction energies between CNDB, pore, and the voltage sensors. Because saturating concentrations of cAMP was used in this study (unpublished data; Chen et al., 2001; Wang et al., 2001), only the interaction energies between the CNDB and the pore or voltage sensors were changed to fit the traces from the HCN2/1 chimera using parameters derived for WT HCN2 in Schemes 1–3 (Table S3 and Fig. S5).
By definition, the interaction parameters considered in binary elements models are relative to a ground state, which is defined to be when the elements are both nonactivated (Goldschen-Ohm et al., 2014). The term ΔG‡Pore-CNBD describes the change in free energy for pore opening when the CNBD is bound to cAMP. Given that our substitutions primarily changed the voltage dependence of the currents in the absence of cAMP (Fig. 5 and Table S1), it is not surprising that it was not possible to fit the behavior of the HCN2/1 chimera by changing ΔG‡Pore-CNBD or ΔG‡VS-CNBD in Schemes 1–3 (Fig. S5).
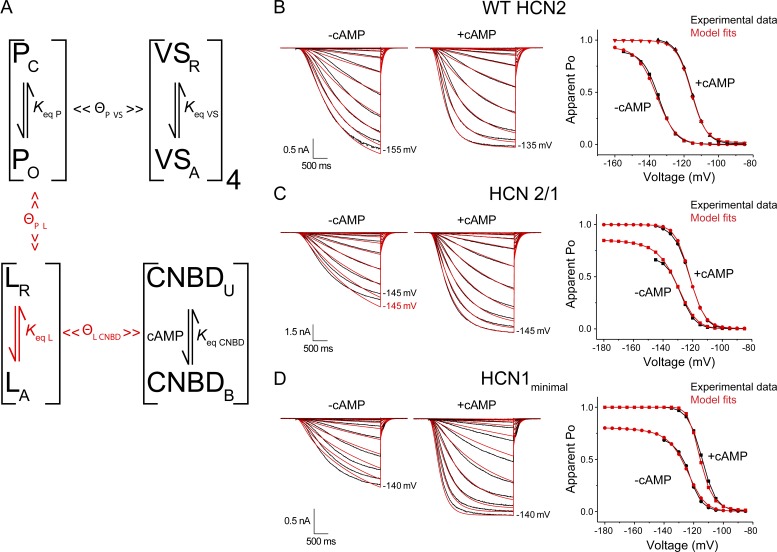
Given the current structural and functional understanding of the C-terminal domains in HCN channels, we reasoned that the C-linker constitutes a discrete module that can adopt at least two different states: a nonactivated or resting form that inhibits channel opening, and an activated form that relieves inhibition (Zagotta et al., 2003; Zhou et al., 2004; Xu et al., 2010; Lolicato et al., 2011). In Scheme 4, the channel pore interacts with the linker, but not the CNBD (Figs. 6 A and S6 A and Table S2). In Scheme 4, we only considered interactions between the pore and the linker in a fashion analogous to the modular model proposed by Craven and Zagotta (2006). In Scheme 5, we added interactions between the linker and the voltage sensors (Fig. S6 B). For WT HCN2, both schemes described the kinetics, voltage dependence, and cAMP responses very well (Figs. 6 B and S6). We then tested whether the effect of substitutions in the C-linker and CNBD could be described by the schemes containing a linker. As for Schemes 1–3, we focused on the model parameters that are expected to be affected by mutations in the C-linker and CNBD. First, we changed the rate constants of the linker and the interactions between the linker and the CNBD (Figs. S7 A and S8 A). These manipulations allowed a shift of the conductance–voltage curves in the absence and presence of cAMP to fit our data using Schemes 4 and 5 (Figs. S7 A and S8 A; and Table S3). As described above (see Figs. 1 A, 4 C, and S2), an unexpected feature of the HCN2/1 chimera and HCN1minimal mutant is that the maximal conductance at saturating voltages is significantly decreased in the absence of cAMP. Changing the rate constants of the linker to favor the activated configuration in the HCN2/1 chimera did not recapitulate this behavior (Figs. S7 A and S8 A).
Figure 6.
Allosteric models recapitulate the various voltage- and ligand-dependent properties of WT HCN2, the HCN2/1 chimera, and the HCN1minimal mutant. (A) Schematic representation of the various allosteric elements and interactions implemented in Scheme 4. Binary elements for the pore (P), voltage sensors (VS), linker (L), and binding domain (CNBD) are characterized by equilibrium constants (Keq) between two states. Coupling factors (Θ) characterize the interactions between elements. All the parameters, except those marked in red, were kept constant to fit the kinetic and steady-state data for WT HCN2, HCN2/1, and the HCN1minimal mutant. (B–D) Model fits (red) and experimental data (black) of current traces in response to voltage steps in the presence and absence of cAMP. Reference data for the apparent Po-voltage curves (right) were obtained from the steady-state conductances at the end of each pulse and are compared with the maximum probability of the open state calculated for the model. Refer to Tables S2, S3, and S4 for a complete list of all parameters.
To address the differences in the maximal conductance at saturating voltages, we changed the interaction energies between the linker and either the pore or voltage sensors in addition to the rate constants for the linker transition and the interaction between the linker and the CNBD (Figs. 6 A, S7 B, and S8 B). With these modifications, both Schemes 4 and 5 recapitulated the voltage dependence and response to cAMP of the HCN2/1 chimera. Increasing the inhibitory effect of the resting linker on the pore in Scheme 4 produced a dramatic improvement of the fits (Figs. 6 C and S7 B). Interestingly, we obtained equally good fits by removing the interaction between the linker and voltage sensors in Scheme 5 (Fig. S8 B), all with minimal changes in either the linker’s rate constants or the interactions between the linker and the pore (compare parameters in Tables S2 and S3). This result supports the idea that the C-linker and CNBD do not directly affect the rates of activation and deactivation of the voltage sensors despite the close proximity of the bottom of S4 and the C-linker in the cryo-EM structure of HCN1 (Lee and MacKinnon, 2017). Nevertheless, we tested whether the C-linker and CNBD substitutions affect the coupling of the voltage sensor and the pore. To model this effect, we changed the interaction energies between voltage sensors and pore using Schemes 4 and 5 (Figs. S7 C and S8 C and Table S3). Decreasing the interactions between the voltage sensor and the pore did not further improve the fits in either of the schemes.
The mutagenesis studies presented above indicate that five residues within the C-linker and CNBD of HCN2 explain most of the increased efficacy of cAMP in this isoform compared with HCN1. We then tested whether kinetic Schemes 4 and 5 can also describe the behavior of the HCN1minimal mutant. Only slight changes in the HCN2/1 chimera’s parameters were required to obtain close fits of the activation kinetics and voltage-dependent activation for this mutant (Fig. 6 D and Table S4).
Discussion
Previous studies of HCN1 and HCN2 chimeras suggest that the differences in response to cAMP between the two isoforms map entirely to the C-linker–CNBD region (Wang et al., 2001). Our results support this idea in a general sense, but a detailed comparison of the voltage dependence and maximal conductance of WT HCN2, WT HCN1, and the HCN2/1 chimera reveals two notable differences. First, the shifts in voltage activation induced by cAMP are not fully accounted by the residues in the C-linker and CNBD. The remaining difference in the shifts between WT HCN1 and the HCN2/1 chimera is quantitatively small (4 mV) but statistically significant (P = 2.4 × 10−6; Fig. 1 A). Second, the maximal conductance in the absence of cAMP at saturating voltages is lower in the HCN2/1 chimera and HCNminimal mutant than in both WT HCN1 and WT HCN2 (Figs. 1 A and S2).
The voltage dependence of activation of HCN2 channels without CNBD shifts in the direction of the fully liganded HCN2 channel (Wainger et al., 2001). This implies that the unliganded CNBD inhibit the activation of these channels and binding of cAMP relieves this inhibition. In vitro studies show that the monomeric C-linker–CNBD fragments of HCN2 and HCN4 tetramerize upon ligand binding (Zagotta et al., 2003; Zhou et al., 2004; Xu et al., 2010; Lolicato et al., 2011) and, indeed, the HCN1 fragments tetramerize more readily in absence of cAMP than do the equivalent HCN2 fragments (Lolicato et al., 2011). Because the HCN1minimal mutant is functionally almost identical to the HCN2/1 chimera, the straightforward prediction would be that the mutations identified in this study change the oligomerization dynamics of the HCN2 C-terminus to promote the activated state in unliganded channels. In addition, it is possible that at least some of the residues identified here also specifically alter the ability of the unliganded CNBD to transduce channel opening by altering the strength of coupling between these two allosteric modules.
We speculate that the difference in maximal open probability with and without cAMP at highly hyperpolarized potentials basically reflects the differences in allosteric coupling strength between the ligand binding domain and pore domain (interaction energies between the linker and the pore ΔG‡pore–linker and ΔGpore–linker). On the other hand, the voltage dependence reflects the activation equilibrium of the C-linker domain. The most important difference between HCN1 and HCN2 is that the HCN1 CNBD with C-linker is thought to be “preactivated.” In other words, the mutations may shift the linker equilibrium to activated states while not changing the coupling as much. Nevertheless, it is important to remember that the difference in maximal Po with and without cAMP is not large from an energetic standpoint, although it might be still physiologically relevant.
To gain further insights into how these mutations account for functional differences between the two isoforms, we tested various allosteric models. First, we tested a simple cyclic model proposed by Chen et al. (2007). This model involves a voltage-independent pore gate coupled to a single ligand binding and a voltage-sensing domain. Although this model accounted well for steady-state conductances, it did not provide a good fit for the kinetics of activation of HCN2 or the kinetics and response to cAMP of the HCN2/1 chimera (Figs. S4 A and S5 A). Our most parsimonious model involves four independent voltage sensors that are coupled to a single voltage-independent pore. In addition, the ligand-binding module is connected to the pore gates only through a linker module. In our model, cAMP binding activates the C-linker presumably by driving a change in the oligomerization dynamics of the C terminus, thereby relieving inhibition on the pore gate. The C-linker oligomerization is favored in the HCN2/1 chimera even when the CNBD is in unliganded state, and therefore, binding of cAMP has very little effect. Nevertheless, we find that to fully account for all the functional differences, the mutations must alter the strength of the coupling between pore gate and CNBD via C-linker.
The available HCN1 and HCN2 structures (Zagotta et al., 2003; Lolicato et al., 2011; Goldschen-Ohm et al., 2016; Lee and MacKinnon, 2017) provide some mechanistic insight into the possible effects of the minimal mutations. None of the five residues seem likely to interact directly with the loops between the transmembrane domains or the N terminus in full-length HCN1. Instead, the C-linker sites are located far from the intersubunit interface and appear to be involved in the stabilization of helices within the C-linker itself, whereas the CNBD sites probably contribute to the observed moderately higher affinity for cAMP in HCN1 (Chen et al., 2001; Wang et al., 2001; Lolicato et al., 2011).
Similarly to HCN2, HCN4 channels respond to cAMP with large shifts in the activation toward more depolarized potentials (Ludwig et al., 1999). Four of the five residues mutated in the HCN1minimal mutant (M485, S514, and V562/S563) are conserved between HCN2 and HCN4, suggesting that the same residues may account for the higher response to cAMP of HCN4 as well (Fig. 1 B). HCN3 responds to cAMP with either no shifts in the activation (Stieber et al., 2005) or a slight shift toward more hyperpolarized potentials (Mistrík et al., 2005). Surprisingly, two of the five residues mutated in the HCN1minimal mutant (M485 and S563) are also conserved between the highly responsive isoforms and HCN3. A chimera study between HCN4 and HCN3 indicated that the decrease in the response to cAMP of HCN3 is caused by the extreme C terminus of HCN3 distal to the CNBD (Stieber et al., 2005).
In summary, our study unambiguously identifies the minimal set of residues that contribute to the differences in efficacy between two HCN channel isoforms. These residues alter the transduction of the ligand-binding signal from the binding domain to the pore gates. Further studies focusing on these minimal set of residues should shed light on the detailed molecular forces responsible for these significant differences in spite of the apparent similarity in the amino acid residues substitutions.
Supplementary Material
Acknowledgments
We thank Dr. Michael C. Sanguinetti (University of Utah) for providing us with the WT mHCN2 plasmid and Dr. Steven A. Siegelbaum and Dr. Bina Santoro (Columbia University) for providing the WT mHCN1 plasmid. We are grateful to Dr. Marcel Goldschen-Ohm for his invaluable help with the modeling software, discussions of the results, and comments on the manuscript.
Funding was provided by the Training Program in Translational Cardiovascular Science (grant T32 HL-07936-15 to C.P. Alvarez-Baron), the American Heart Association (postdoctoral fellowship 17P0ST33411069 to C.P. Alvarez-Baron), and the National Institutes of Health (grant 1R01NS101723-01 to B. Chanda).
The authors declare no competing financial interests.
Author contributions: C.P. Alvarez-Baron designed the experiments, designed and performed molecular biology, performed all electrophysiology and modeling, analyzed the data, and wrote and edited the manuscript. V.A. Klenchin conceptualized research, designed the experiments, designed and performed molecular biology, and wrote and edited the manuscript. B. Chanda conceptualized research, supervised the project, and wrote and edited the manuscript.
Kenton J. Swartz served as editor.
References
- Bal R., and Oertel D.. 2000. Hyperpolarization-activated, mixed-cation current (I(h)) in octopus cells of the mammalian cochlear nucleus. J. Neurophysiol. 84:806–817. 10.1152/jn.2000.84.2.806 [DOI] [PubMed] [Google Scholar]
- Biel M., Wahl-Schott C., Michalakis S., and Zong X.. 2009. Hyperpolarization-activated cation channels: from genes to function. Physiol. Rev. 89:847–885. 10.1152/physrev.00029.2008 [DOI] [PubMed] [Google Scholar]
- Brown H.F., DiFrancesco D., and Noble S.J.. 1979. How does adrenaline accelerate the heart? Nature. 280:235–236. 10.1038/280235a0 [DOI] [PubMed] [Google Scholar]
- Cao X.J., and Oertel D.. 2011. The magnitudes of hyperpolarization-activated and low-voltage-activated potassium currents co-vary in neurons of the ventral cochlear nucleus. J. Neurophysiol. 106:630–640. 10.1152/jn.00015.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J., Mitcheson J.S., Lin M., and Sanguinetti M.C.. 2000. Functional roles of charged residues in the putative voltage sensor of the HCN2 pacemaker channel. J. Biol. Chem. 275:36465–36471. 10.1074/jbc.M007034200 [DOI] [PubMed] [Google Scholar]
- Chen S., Wang J., and Siegelbaum S.A.. 2001. Properties of hyperpolarization-activated pacemaker current defined by coassembly of HCN1 and HCN2 subunits and basal modulation by cyclic nucleotide. J. Gen. Physiol. 117:491–504. 10.1085/jgp.117.5.491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S., Wang J., Zhou L., George M.S., and Siegelbaum S.A.. 2007. Voltage sensor movement and cAMP binding allosterically regulate an inherently voltage-independent closed-open transition in HCN channels. J. Gen. Physiol. 129:175–188. 10.1085/jgp.200609585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiu P.L., Pagel M.D., Evans J., Chou H.T., Zeng X., Gipson B., Stahlberg H., and Nimigean C.M.. 2007. The structure of the prokaryotic cyclic nucleotide-modulated potassium channel MloK1 at 16 A resolution. Structure. 15:1053–1064. 10.1016/j.str.2007.06.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton G.M., Silverman W.R., Heginbotham L., and Morais-Cabral J.H.. 2004. Structural basis of ligand activation in a cyclic nucleotide regulated potassium channel. Cell. 119:615–627. 10.1016/j.cell.2004.10.030 [DOI] [PubMed] [Google Scholar]
- Colquhoun D., and Hawkes A.G.. 1995. A Q-matrix cookbook. In Single-Channel Recording. Sakmann B., and Neher E., editors. Springer US, Boston, MA: 589–633. 10.1007/978-1-4419-1229-9_20 [DOI] [Google Scholar]
- Craven K.B., and Zagotta W.N.. 2006. CNG and HCN channels: two peas, one pod. Annu. Rev. Physiol. 68:375–401. 10.1146/annurev.physiol.68.040104.134728 [DOI] [PubMed] [Google Scholar]
- DiFrancesco D. 2010. The role of the funny current in pacemaker activity. Circ. Res. 106:434–446. 10.1161/CIRCRESAHA.109.208041 [DOI] [PubMed] [Google Scholar]
- DiFrancesco D., and Tortora P.. 1991. Direct activation of cardiac pacemaker channels by intracellular cyclic AMP. Nature. 351:145–147. 10.1038/351145a0 [DOI] [PubMed] [Google Scholar]
- Golding N.L., and Oertel D.. 2012. Synaptic integration in dendrites: exceptional need for speed. J. Physiol. 590:5563–5569. 10.1113/jphysiol.2012.229328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldschen-Ohm M.P., Haroldson A., Jones M.V., and Pearce R.A.. 2014. A nonequilibrium binary elements–based kinetic model for benzodiazepine regulation of GABAA receptors. J. Gen. Physiol. 144:27–39. 10.1085/jgp.201411183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldschen-Ohm M.P., Klenchin V.A., White D.S., Cowgill J.B., Cui Q., Goldsmith R.H., and Chanda B.. 2016. Structure and dynamics underlying elementary ligand binding events in human pacemaking channels. eLife. 5:e20797 10.7554/eLife.20797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- James Z.M., Borst A.J., Haitin Y., Frenz B., DiMaio F., Zagotta W.N., and Veesler D.. 2017. CryoEM structure of a prokaryotic cyclic nucleotide-gated ion channel. Proc. Natl. Acad. Sci. USA. 114:4430–4435. 10.1073/pnas.1700248114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kesters D., Brams M., Nys M., Wijckmans E., Spurny R., Voets T., Tytgat J., Kusch J., and Ulens C.. 2015. Structure of the SthK carboxy-terminal region reveals a gating mechanism for cyclic nucleotide-modulated ion channels. PLoS One. 10:e0116369 10.1371/journal.pone.0116369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C.H., and MacKinnon R.. 2017. Structures of the Human HCN1 Hyperpolarization-Activated Channel. Cell. 168:111–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M., Zhou X., Wang S., Michailidis I., Gong Y., Su D., Li H., Li X., and Yang J.. 2017. Structure of a eukaryotic cyclic-nucleotide-gated channel. Nature. 542:60–65. 10.1038/nature20819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lolicato M., Nardini M., Gazzarrini S., Möller S., Bertinetti D., Herberg F.W., Bolognesi M., Martin H., Fasolini M., Bertrand J.A., et al. 2011. Tetramerization dynamics of C-terminal domain underlies isoform-specific cAMP gating in hyperpolarization-activated cyclic nucleotide-gated channels. J. Biol. Chem. 286:44811–44820. 10.1074/jbc.M111.297606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludwig A., Zong X., Jeglitsch M., Hofmann F., and Biel M.. 1998. A family of hyperpolarization-activated mammalian cation channels. Nature. 393:587–591. 10.1038/31255 [DOI] [PubMed] [Google Scholar]
- Ludwig A., Zong X., Stieber J., Hullin R., Hofmann F., and Biel M.. 1999. Two pacemaker channels from human heart with profoundly different activation kinetics. EMBO J. 18:2323–2329. 10.1093/emboj/18.9.2323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mistrík P., Mader R., Michalakis S., Weidinger M., Pfeifer A., and Biel M.. 2005. The murine HCN3 gene encodes a hyperpolarization-activated cation channel with slow kinetics and unique response to cyclic nucleotides. J. Biol. Chem. 280:27056–27061. 10.1074/jbc.M502696200 [DOI] [PubMed] [Google Scholar]
- Nimigean C.M., Shane T., and Miller C.. 2004. A cyclic nucleotide modulated prokaryotic K+ channel. J. Gen. Physiol. 124:203–210. 10.1085/jgp.200409133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santoro B., Liu D.T., Yao H., Bartsch D., Kandel E.R., Siegelbaum S.A., and Tibbs G.R.. 1998. Identification of a gene encoding a hyperpolarization-activated pacemaker channel of brain. Cell. 93:717–729. 10.1016/S0092-8674(00)81434-8 [DOI] [PubMed] [Google Scholar]
- Stieber J., Stöckl G., Herrmann S., Hassfurth B., and Hofmann F.. 2005. Functional expression of the human HCN3 channel. J. Biol. Chem. 280:34635–34643. 10.1074/jbc.M502508200 [DOI] [PubMed] [Google Scholar]
- Wainger B.J., DeGennaro M., Santoro B., Siegelbaum S.A., and Tibbs G.R.. 2001. Molecular mechanism of cAMP modulation of HCN pacemaker channels. Nature. 411:805–810. 10.1038/35081088 [DOI] [PubMed] [Google Scholar]
- Wang J., Chen S., and Siegelbaum S.A.. 2001. Regulation of hyperpolarization-activated HCN channel gating and cAMP modulation due to interactions of COOH terminus and core transmembrane regions. J. Gen. Physiol. 118:237–250. 10.1085/jgp.118.3.237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu X., Vysotskaya Z.V., Liu Q., and Zhou L.. 2010. Structural basis for the cAMP-dependent gating in the human HCN4 channel. J. Biol. Chem. 285:37082–37091. 10.1074/jbc.M110.152033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu F.H., Yarov-Yarovoy V., Gutman G.A., and Catterall W.A.. 2005. Overview of molecular relationships in the voltage-gated ion channel superfamily. Pharmacol. Rev. 57:387–395. 10.1124/pr.57.4.13 [DOI] [PubMed] [Google Scholar]
- Zagotta W.N., Olivier N.B., Black K.D., Young E.C., Olson R., and Gouaux E.. 2003. Structural basis for modulation and agonist specificity of HCN pacemaker channels. Nature. 425:200–205. 10.1038/nature01922 [DOI] [PubMed] [Google Scholar]
- Zhou L., Olivier N.B., Yao H., Young E.C., and Siegelbaum S.A.. 2004. A conserved tripeptide in CNG and HCN channels regulates ligand gating by controlling C-terminal oligomerization. Neuron. 44:823–834. 10.1016/j.neuron.2004.11.012 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.