Microtubules grow by the addition of bent guanosine triphosphate tubulin to the tips of curved protofilaments

How microtubules (MTs) grow during the addition of guanosine triphosphate (GTP) tubulin is not clear. McIntosh et al. now show that MTs elongating either in vivo or in vitro end in bent protofilaments that curve out from the microtubule axis, suggesting that GTP-tubulin is bent in solution and must straighten to join the MT wall.

Abstract

We used electron tomography to examine microtubules (MTs) growing from pure tubulin in vitro as well as two classes of MTs growing in cells from six species. The tips of all these growing MTs display bent protofilaments (PFs) that curve away from the MT axis, in contrast with previously reported MTs growing in vitro whose tips are either blunt or sheetlike. Neither high pressure nor freezing is responsible for the PF curvatures we see. The curvatures of PFs on growing and shortening MTs are similar; all are most curved at their tips, suggesting that guanosine triphosphate–tubulin in solution is bent and must straighten to be incorporated into the MT wall. Variations in curvature suggest that PFs are flexible in their plane of bending but rigid to bending out of that plane. Modeling by Brownian dynamics suggests that PF straightening for MT growth can be achieved by thermal motions, providing a simple mechanism with which to understand tubulin polymerization.

Introduction

The dynamics of microtubules (MTs) are unusual and of key importance for the roles these polymers play in cells (Kirschner and Mitchison, 1986). Moreover, both MT growth (Tilney and Porter, 1967) and shortening (Grishchuk et al., 2005) can do mechanical work. The remarkable ability of MTs to cycle between times of growth and shortening, termed dynamic instability (Mitchison and Kirschner, 1984), has been linked both to the state of the GTP molecules that bind reversibly to β-tubulin and to the structure of the tubulin protofilaments (PFs) at MT tips (Caplow and Shanks, 1990; Desai and Mitchison, 1997). This widely cited model proposes that GTP is required for tubulin polymerization, but GTP hydrolysis follows polymerization, making MTs intrinsically unstable. A cap of GTP-tubulin can maintain polymer stability unless hydrolysis of the bound nucleotide reaches the MT tip. Early electron cryomicroscopy of the growing and shrinking of polymers spontaneously initiated in vitro revealed mostly blunt ends on growing MTs and flared PFs on shortening ones (Mandelkow et al., 1991), providing a pleasingly simple way to explain the fact that GDP-tubulin will not polymerize. In this model, the minimum energy shape of GTP-tubulin is straight, and that of GDP-tubulin is bent, but the GDP-tubulin in the MT wall is held in a straight conformation by bonds with neighboring tubulins. This model provided a nice link between the polymerization-associated cycles of GTP hydrolysis, the shapes of MT ends, and dynamic instability, so it is found in many textbooks.

More recent structural information about the ends of MTs growing in vitro has been harder to reconcile with previous ideas about dynamic instability. Polymers of pure tubulin nucleated by isolated centrosomes end in long, gently curving sheets of PFs that are thought to curl up laterally as they form a patent tubule (Chrétien et al., 1995; Müller-Reichert et al., 1998; Vitre et al., 2008; Guesdon et al., 2016). Long, gently curving PF bundles at the ends of growing MTs have also been seen when tubulin is polymerized in the presence of a mutant allele of a kinesin 5 (Chen and Hancock, 2015). In this tubulin polymerization scenario, the link between GTP hydrolysis and dynamic instability is less clear, but these gently curving PF clusters are qualitatively consistent with structural work on tubulin dimers by x-ray crystallography. Several groups have found that both GDP- and GTP-tubulin appear bent, so both these forms of tubulin should form curving PFs. These atomic resolution studies provide convincing evidence for a bent configuration of the GTP-tubulin that was studied, but in each case, protein crystallization required some block to polymerization: a nonpolymerizing tubulin isoform (Rice et al., 2008), a drug (Buey et al., 2006), a mutation (Nawrotek et al., 2011), or a protein cofactor (Pecqueur et al., 2012). Thus, in spite of these multiple observations and some convincing biochemical research on the rates of ligand exchange with tubulin bound to either nucleotide (Brouhard and Rice, 2014), there remains some uncertainty about the true shape of GTP-tubulin in solution and thus how the ends of growing MTs should look.

Evidence about the shapes of MT ends in vivo has not clarified these issues; published images display a range of results. One study of kinetochore-associated MTs (KMTs) identified plus ends with either flared or straight PFs and assumed that those with straight PFs were elongating, whereas those with curled PFs were shortening (VandenBeldt et al., 2006). Other studies of KMTs, which used a more detailed approach to the structural characterization of each MT tip, found that the plus ends of essentially all KMTs displayed at least some flaring PFs regardless of whether they were growing or shrinking (McIntosh et al., 2008, 2013). Yet another study examined the ends of MTs recovering from drug-induced inhibition of tubulin polymerization and found flaring PFs on all these growing MTs (Hoog et al., 2011). Likewise, a study that used fluorescence imaging to follow MT dynamics in vivo and correlative EM to examine the end of a growing MT saw flaring PFs (Kukulski et al., 2011). However, each of these studies relied on a burst of very high pressure applied rapidly to the cells just before freezing to limit the ice crystal growth that can occur during freezing of big cells. High pressure is known to cause MTs to depolymerize (Tilney et al., 1966), so there is a possibility that even the ∼10-ms interval between the application of pressure and the onset of freezing was long enough to allow a depolymerization-related conformational change at the MT tip. Cultured mouse cells in interphase are, however, thin enough to be cryoimmobilized without ice crystal formation simply by plunging them into cryogen, thereby circumventing high-pressure treatment (Zovko et al., 2008). The MT ends described in that study showed a variety of shapes, but it was impossible to correlate the structures seen with the dynamic state of the MTs. It is noteworthy, though, that none of these studies described structures like the long, gently curving PF bundles found on MTs initiated by isolated centrosomes in vitro. Thus, there is no unanimity about the structure of growing MT plus ends either in vivo or in vitro.

We began our current study with an analysis of tip structures on MTs in the interzone of mitotic cells in anaphase B, a time when extensive evidence demonstrates that interpolar MTs (IPMTs) are elongating (McDonald et al., 1977; Saxton and McIntosh, 1987). We went on to undertake a quantitative comparison of PFs at the ends of growing MTs in cells prepared either by high-pressure freezing or by plunge freezing to determine the contribution that pressure might make to the PF shapes observed. Our results on growing MTs in cells from six species show flaring PFs whose shapes are incompatible with any of the published work on MTs growing in vitro, so we have gone on to examine MTs formed in vitro from pure tubulin using standard methods for electron cryotomography (cryoET) and detailed 3D sampling of each MT end. Again, our results are inconsistent with the interpretations given to all previously published studies, but controls suggest that our structures are valid. The existence of bent PFs at the tips of growing MTs motivates a significant change in the way one thinks about tubulin polymerization. In this study, we present and discuss these results and show that they provide a new way to think about the relationships between tubulin polymerization, MT structure, and dynamic instability.

Results

Tip structures of anaphase interzone MTs growing in vivo

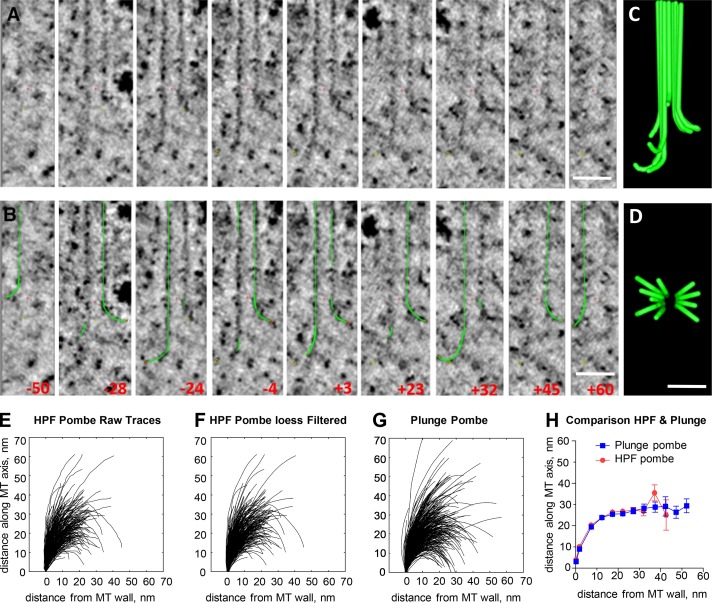
PtK₂ cells that were high-pressure frozen and fixed during mid–anaphase B were identified and oriented by light microscopy and then serial sectioned for study of their IPMTs by electron tomography (ET; Fig. S1 and Materials and methods). These MTs were elongating at ∼12 nm/s to maintain overlap while they slid apart during spindle elongation (Saxton and McIntosh, 1987). The shape of a representative MT from this region of an elongating spindle is shown in Fig. 1. These nine views of a single MT were obtained by rotating the plane of sampling about the MT axis and selecting orientations at which relatively clear PFs could be seen. A graphic object was then hand drawn on each PF (Fig. 1 B), allowing construction of the model shown in Fig. 1 (C and D). The outward flaring of most PFs at the end of this elongating MT plus end was not expected from existing data on the shapes of MTs growing in vitro or from current models for dynamic instability, raising questions about the validity of the images and the models drawn on them. The accuracy with which these traces represent the structure of a MT end is discussed in Materials and methods, and data on the reliability of the traces are presented in Fig. S2 (A–E′). More images and graphic models of IPMTs from the anaphase interzone of PtK₂ cells are shown in Fig. S1. Video 1 shows multiple views of a single MT during rotary sampling, and the legend to this video discusses the issue of accurate PF tracing.

Figure 1.

Angular sampling of the 3D structure of a growing MT end. (A) Nine slices through the end of an MT from the anaphase B interzone in a PtK₂ cell. All images contain the MT axis, but the orientation of the plane of sampling the 3D volume was changed to display flaring PFs. Red crosses mark the origins of the coordinate systems used. (B) The same images showing the angles at which the slices were taken and graphic objects drawn by hand on the image data. Red x's mark the tips of the graphic traces that represent the PFs. (C and D) Two orthogonal views of the graphic objects drawn on this MT end. Bars, 50 nm. (E) 346 PFs traced on the plus ends of 42 elongating IPMTs from four S. pombe (Pombe) cells in anaphase B that were cryoimmobilized by high-pressure freezing (HPF) and then prepared for EM. (F) The same traces after smoothing with a quadratic LOESS filter. (G) LOESS-filtered traces from 399 PFs from the plus ends of 45 IPMTs identified in four anaphase S. pombe cells cryoimmobilized by plunge freezing and then prepared for EM. (H) Means and SEMs for positions traced along all PFs from these two datasets to compare mean PF shapes after two methods of freezing.

Because these cultured cells were cryoimmobilized by high-pressure freezing before fixation by freeze substitution, one can worry that high pressure affected PF shape before freezing occurred. Mitotic PtK₂ cells are ∼10 µm thick in the region of the spindle, too thick to freeze well by simply plunging into cryogen; in most plunge-frozen cells of this kind, there is significant ice crystal damage. We therefore turned to anaphase fission yeast cells, which are ∼4 µm in diameter and can therefore be plunge-frozen effectively. Fig. 1 (E–H) compares 338 PFs traced on 42 IPMTs from four high-pressure–frozen anaphase fission yeasts with 373 PFs traced on 45 MTs from four plunge-frozen anaphase fission yeasts. Representative images and models of MT ends from these two datasets are shown in Fig. S2 (F and G). The distributions of PF lengths and the angles between adjacent line segments along the models drawn on all PFs from the two samples are displayed in Fig. S2 (H–K). Clearly, the PFs in both these preparations show considerable variation in shape. To minimize some of the inaccuracies that certainly arise during hand tracing, we have smoothed each trace and all other traces presented in this paper using quadratic local regression smoothing (LOESS) filtering (Fig. 1 E vs. Fig. 1 F; see also Materials and methods). Mean traces from each dataset were then prepared by calculating the mean and SEM of the vertical position for every horizontal position along the curving PFs from each of the two fission yeast datasets (Fig. 1 H). These data demonstrate that high-pressure freezing makes no observable difference to mean PF shape.

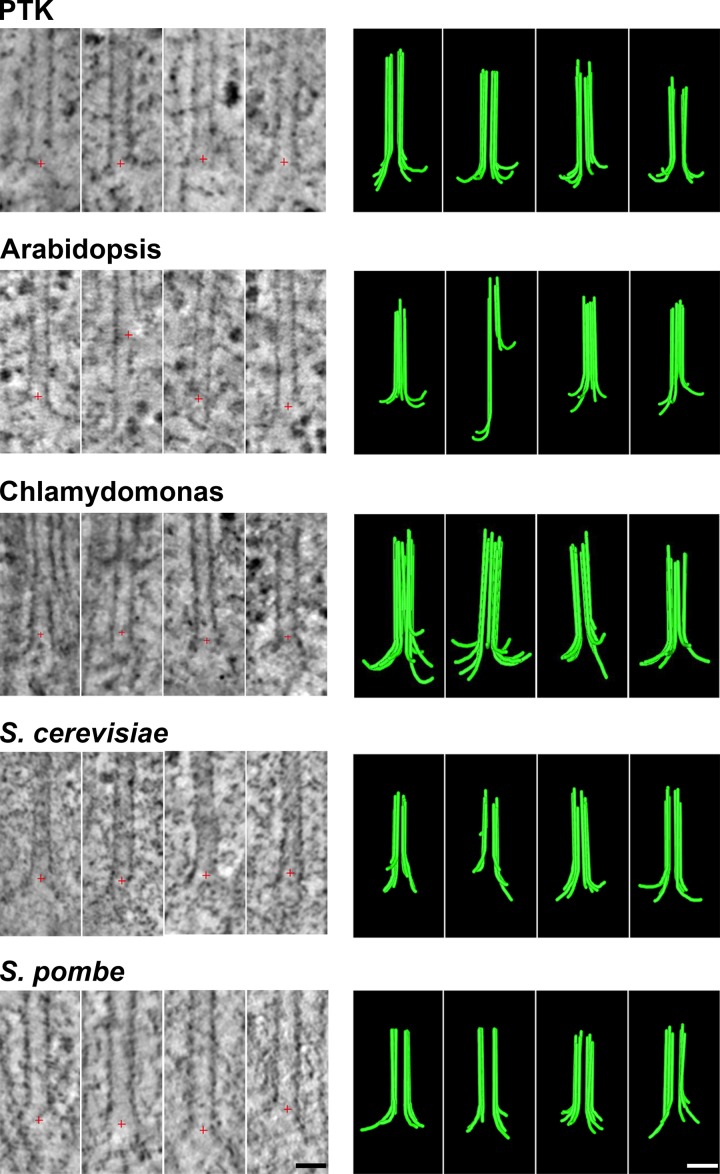
This result encouraged us to analyze the tips of anaphase IPMTs from multiple cell types that are thick enough to require high pressure for ice crystal–free freezing. Images of slices through the 3D structures of four MTs from anaphase B interzones in each of five species are shown in Fig. 2. Note that ET is based on images collected through only ±60° of tilt around one or two axes, so the reconstructions are not isotropic. At high tilt angles, the images were too distorted to allow reliable PF tracing, so only 6–10 PFs are available from any one MT, not the 13 that are actually present. Drawings of all PFs traced at the tips of MTs from the interzones in each of these species are shown in Fig. S3 (A–E), and quantitative characterizations of these PFs are shown either in Figs. 3 or S3 (F–K). The numbers of MTs studied and PFs traced along with the mean values and SDs for PF lengths and curvatures are shown in Table 1. We have pooled our tracings from plunge- and high-pressure–frozen fission yeast because there was no detectable difference between them. These images and data all support the contention that MTs in vivo grow by the addition of bent GTP-tubulin to the tips of individually curving PFs.

Figure 2.

Images and models of MTs growing in vivo. For each of five species names, the left column displays tomographic slices that contain the MT axis and show one or more PFs flaring out from the MT wall. Red crosses mark the origin of the coordinate system used for rotational sampling of the PFs. The right column displays models of these same MT ends showing traces of all the PFs detected by rotational sampling of the MT end as in Fig. 1 and Videos 1, 2, 3, 4, and 5. Bars, 25 nm.

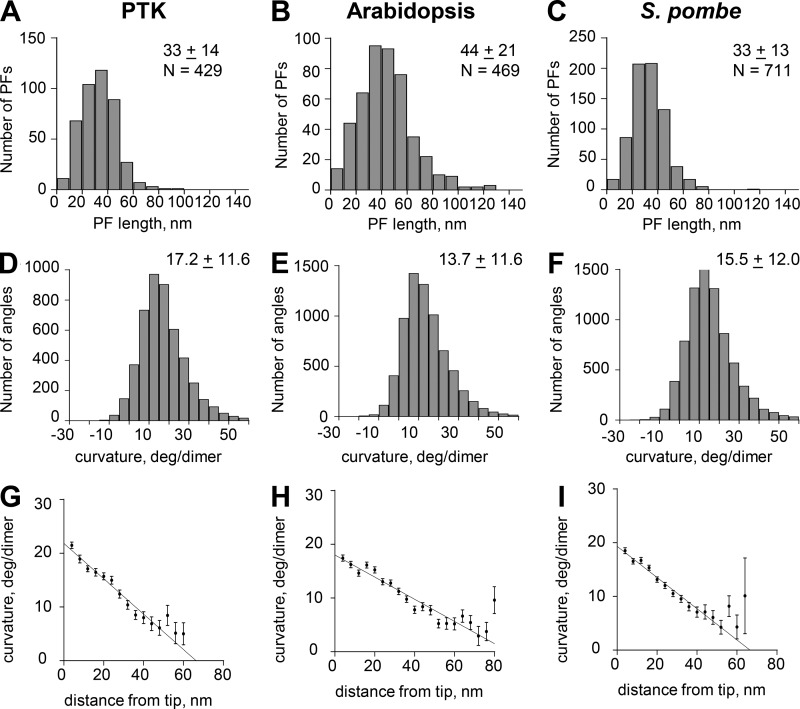
Figure 3.

Graphs depicting aspects of PF shape from three of the species studied. (A–C) Distributions of lengths for PFs from the species indicated. N, numbers of PFs traced. Other values are mean lengths ± SD. (D–F) Distributions of angles between consecutive line segments that connect adjacent points along all tracings for all PFs of each species shown. N, numbers of angles. Other values are means ± SD. (G–I) Distributions of mean angles between consecutive line segments plotted as functions of distance from the PF tip for each of the species studied. Error bars are SEM.

Table 1. Properties of PFs in IPMTs in vivo.

Dataset	PF length	PF curvature	# PFs	Approximate speed of growth	Reference
	nm	Deg/dimer		nm/s
IPMT-HPFPombe	30 ± 12	14.7 ± 12.6	338	∼12	Mallavarapu et al. (1999)
IPMT-PlungePombe	36 ± 13	16.3 ± 11.4	373	∼12	Mallavarapu et al. (1999)
IPMT-Pombe Combined	33 ± 13	15.5 ± 12.0	711	∼12	Mallavarapu et al. (1999)
IPMT-PTK	33 ± 14	17.2 ± 11.6	429	∼12	Saxton and McIntosh (1987)
IPMT-Arabidopsis	44 ± 21	13.7 ± 11.6	469	∼30	Reference for cultured tobacco because no data on Arabidopsis: Dhonukshe et al. (2006)
IPMT-Chlamy	36 ± 13	20.4 ± 14.4	329	∼6	Hepler (2016)
IPMT-Cerevisiae	32 ± 12	14.7 ± 13.0	128	∼9	Straight et al. (1998)

Tip structures of KMTs

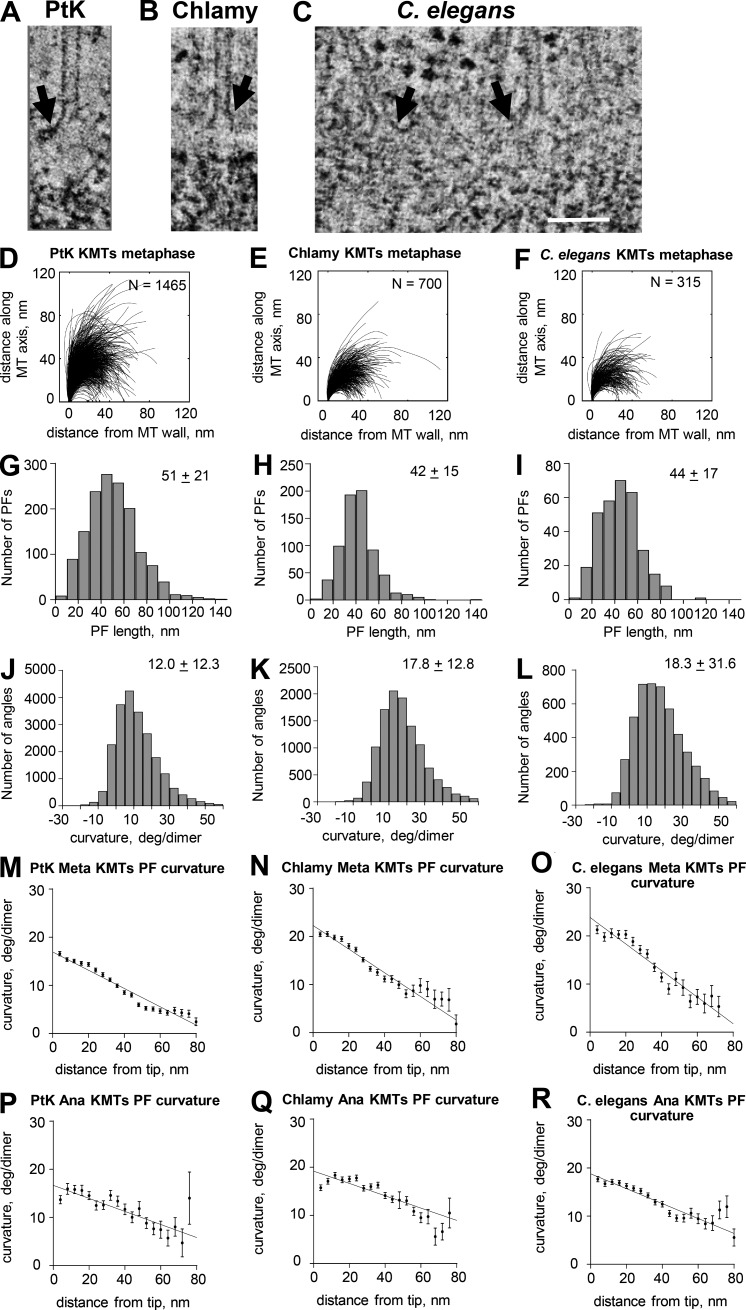
One can worry that the images presented above are not representative of normal MT growth in vivo because there is something unusual about the IPMTs in the anaphase interzone. From previous work, we had large numbers of 3D reconstructions of KMTs from several species at various stages of mitosis and prepared for EM in different ways (McIntosh et al., 2008, 2013). In the current study, we have reexamined some of those traces with our current methods. Fig. 4 shows representative images, smoothed PF traces, and distributions of both lengths and curvatures for PFs at the plus ends of KMTs from metaphase spindles in PtK₂ cells and Chlamydomonas reinhardtii along with blastomeres from embryos of Caenorhabditis elegans. These MTs are probably elongating, on average, thanks to MT flux toward the poles, which is well documented in mammalian spindles (Mitchison and Salmon, 1992), and some other spindles as well, albeit chromosome oscillations mean that there are probably some depolymerizing ends included in these samples. Uniformly shortening KMTs are available from cells in anaphase A, and KMTs from such spindles in three species are shown and characterized in Figs. S4 and 4 (P–R). The plus ends of KMTs displayed curving PFs in both metaphase and anaphase in all species studied. Data on PF lengths and curvatures for these species and for KMTs from budding yeasts are presented in Table 2. (No KMT information is presented for fission yeast because these MTs are too difficult to identify with confidence in this organism.) There are no consistent differences in PF structure between metaphase and anaphase, but the PFs at the tips of all in vivo MT ends show curvatures that decrease almost linearly with distance from the PF tips. These linear decreases are slower for anaphase KMTs than for other MTs (compare Fig. 3 [G–I] with Fig. 4 [M–R]), suggesting that MT function is reflected in some aspects of PF structure at the MT tip.

Figure 4.

Pictures and graphs describing the plus ends of metaphase KMTs. (A–C) Slices from tomograms of the plus ends of metaphase KMTs from the three species named. Arrows indicate flaring PFs. Bar, 100 nm. (D–F) Smoothed traces of PFs drawn on metaphase KMTs from each species. N, numbers traced. (G–I) Distributions of PF lengths. (J–L) Distributions of angles between adjacent line segments along PFs. Numbers are means ± SD. (M–O) Means and SEM of angles between adjacent segments along PFs plotted as a function of distance from the PF tips. (P–R) Similar graphs for PF from anaphase KMTs from the same species. Chlamy, Chlamydomonas.

Table 2. Properties of PFs on KMTs in vivo.

Dataset	PF length	PF curvature	# PFs
	nm	Deg/dimer
KMT-PTK-meta	51 ± 21	12.0 ± 12.3	1,465
KMT-PTK-ana	48 ± 18	13.7 ± 11.8	192
KMT-Chlamy-meta	42 ± 15	17.8 ± 12.8	700
KMT-Chlamy-ana	54 ± 14	16.3 ± 13.6	452
KMT-CE-meta	44 ± 17	17.9 ± 14.5	315
KMT-CE-ana	49 ± 18	22.9 ± 19.1	461
KMT-Cerevis-meta	27 ± 11	21.1 ± 17.5	449
KMT-Cerevis-ana	31 ± 12	24.6 ± 81.9	539

Almost all these cells were prepared for EM by high-pressure freezing and freeze-substitution fixation. Although the data in Fig. 1 H argue that pressure is not affecting mean PF shape, perhaps cells cannot be frozen fast enough to preserve MT tip shape, so all these images are compromised by a freezing artifact. As controls for this and related possibilities, we compared PFs on KMTs in cells that were chemically fixed with those that were high-pressure frozen and found no difference (McIntosh et al. [2008]. Tables S3 and S4 from that paper show that for 1,085 PFs from 186 MTs in high-pressure–frozen cells, mean length was 49 ± 23 nm, and mean curvature was 12° ± 7° per dimer, whereas 85 PFs from 15 MTs in a chemically fixed cell showed a mean length of 47 ± 20 nm and a mean curvature of 12° ± 2° per dimer). These data show that curving PFs at MT ends are not simply a result of freezing. Further controls for the possibility that pressure or freezing affect PF shape are presented in the section of Materials and methods called Additional controls for the impact of freezing.

Metaphase KMTs and growing IPMTs are strikingly similar. PFs on KMTs are commonly a little longer than the PFs on IPMTs, but the curvatures appear similar, suggesting that the properties we describe are generally valid for MTs in vivo. Moreover, PF lengths and curvatures for growing and shrinking MTs are quite similar, accepting the substantial variation in each population. Interestingly, all these PFs show a linear dependence of curvature on position, with the greatest curvature situated at the PF tip (Fig. 3, G–I; and Fig. 4, M–R). These results are consistent with the model that GTP-tubulin in solution is curved, thereby specifying the curvature at PF tips on growing MTs. However, PF curvature also decreases from the tip in anaphase KMTs, suggesting that PF shape depends on other factors as well.

Tip structures of MTs elongating in vitro

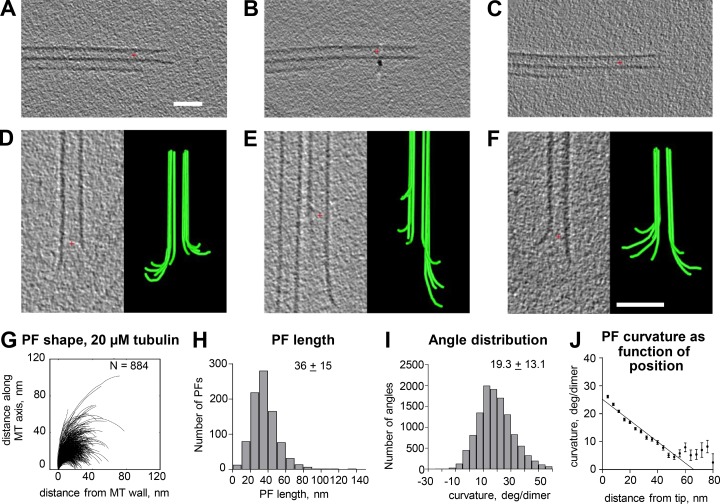
The addition of tubulin to MTs in vivo is accompanied by a group of proteins that associate specifically with growing MT tips (Gupta et al., 2014; Akhmanova and Steinmetz, 2015). The structures described above may therefore reflect the action of multiple proteins and not simply tubulin. To test this idea, we used cryoET to examine the ends of MTs elongating in vitro by the polymerization of purified tubulin. To assure that the ends we studied reflected the 13-PF MTs that commonly form in vivo, we used axonemes from Chlamydomonas to initiate tubulin polymerization on holy carbon-coated grids. Purified porcine brain tubulin (2 mg/ml) at 0°C in a standard polymerization buffer was then added to the axonemes and brought into the incubation chamber of a commercial plunge-freezing device (Materials and methods). Polymerization took place at 37°C for 3–8 min, and then samples were cryoimmobilized by rapid plunging into liquid ethane that was cooled to its freezing point by liquid nitrogen (Materials and methods). We identified growing MT tips and imaged them at a wide range of tilts. Tomograms were constructed and filtered, and then volumes that included just the MT plus ends were extracted for study. Fig. 5 (A–C) shows axonemal doublet MTs without tubulin added, Fig. 5 (D–F) shows representative images of growing MT ends, and Video 2 shows rotary sampling of a typical growing MT end. Fig. 5 G shows the shapes of 884 traces of PFs from MTs elongating in this way, and Fig. 5 (H–J) shows analyses of these PF traces analogous to those performed on PFs from MTs in vivo. Tomographic slices and models of additional MT ends are shown in Fig. S5 A. The similarity between these MT ends and those seen in vivo demonstrates that the flared PFs on MTs growing in cells are not a result of proteins that associate with tubulin in vivo.

Figure 5.

Shapes of plus ends of MTs elongating in vitro. (A–C) Slices through tomograms of three examples of the axonemal doublet MTs that served as seeds to nucleate the polymerization of purified porcine brain tubulin. (D–F) Tomographic slices and models of three representative MTs elongating from axonemal doublet MTs. Many of the PFs curve outward from the MT axis. Red crosses mark the origins of the coordinate systems used. Bars, 50 nm. (G) LOESS-smoothed traces of PFs from 60 growing MTs. N, numbers traced. (H and I) Distributions of lengths and angles for the PFs in G. (J) Means and SEM of angles between adjacent segments along PFs plotted as a function of distance from the PF tips.

Because these MT ends do not look like previous descriptions of tubulin polymerizing in vitro but do resemble depolymerizing MTs (Mandelkow et al., 1991; Chrétien et al., 1995; Müller-Reichert et al., 1998), we wondered whether there might be a flaw in our procedure that was leading the MTs we had grown in vitro to initiate depolymerization before they were frozen. We believe this was not the case for the following reasons: (A) We used a small thermocouple to measure the temperature in a drop of buffer taken through the polymerization procedure described above and found that it held steady at 37°C throughout the incubation period. Moreover, the longer the samples were left to incubate, the longer the MTs became, so tubulin was polymerizing in the incubation chamber of the plunge freezer as expected. (B) We have used cycles of concentration and dilution to exchange the GTP that comes with commercial tubulin for guanosine-5'-[(α,β)-methyleno]triphosphate (GMPCPP), an analogue known to make MTs more stable to dilution and thermally induced depolymerization (Hyman et al., 1992). Cryoimages of the ends of MTs grown in at least 100-fold more GMPCPP than GTP show similarly flared ends (Fig. 6 A). Additional images, models, and drawings of the 271 PFs we have traced on MTs grown in GMPCPP along with a quantification of their shapes are shown in Fig. S6 (B–F). Video 3 shows a rotary sampling of one representative GMPCPP-MT end. The similarities of these PFs to PFs on MTs formed in GTP suggest that curling PFs are not a freezing artifact.

Figure 6.

Shapes of plus ends of in vitro MTs elongating or prepared under stabilizing conditions. (A) Tomographic slices and models of MT ends plunge frozen while elongating in GMPCPP. (B) Tomographic slices and models of MTs fixed isothermally in first 0.2% and then 2% glutaraldehyde before plunge freezing. (C) Tomographic slices and models of MTs fixed isothermally in first 0.2% and then 2% glutaraldehyde and then negatively strained with uranyl acetate. Red crosses mark the origins of the coordinate systems used. Bar, 50 nm.

Our concern about artifact was increased, however, when we measured the temperatures in the hole at the bottom of the incubation chamber through which the samples fall when plunging from the incubation chamber into the vessel of cryogen. Although the temperature at the top of this hole (just below the moveable trap door) did not drop below room temperature, the close apposition of the chamber that contained freezing ethane with the underside of the incubation chamber immediately before sample plunging brought the bottom of that hole down to about −35°C. The sample passed through this colder region as it fell into the cryogen, taking ∼10 ms to get from places where the temperature should maintain a polymerizing state to the almost-freezing ethane, at which time its temperature dropped at ∼10⁶ degrees C per second (Dubochet et al., 1988; Dubochet, 2007). This might be sufficient exposure to cold for the PFs to change their shape, so we have taken an additional approach to minimizing the chances of a low-temperature artifact. We attached axonemes to EM grids, blotted, and again added 5 µl of 20 µM tubulin in polymerization buffer at 0°C as described above, but now the grids were placed on Parafilm in a Petri dish floating on a 37°C water bath. After 6 min of incubation, we fixed the sample with 2% glutaraldehyde at 37°C (Materials and methods). Some samples were then allowed to cool slowly to room temperature as they were taken to the plunge freezer and were then loaded, blotted, and plunged into freezing ethane. Other samples were rinsed with 2% uranyl acetate in water, blotted, and air dried without freezing for examination by ET of the negatively stained materials. Tomographic slices of samples prepared in each of these ways are shown in Fig. 6 B (fixed then frozen) and Fig. 6 C (fixed then negatively stained). Video 4 shows a rotary video of the end of an MT that was fixed and then frozen. Additional images of MTs prepared in these two ways are shown in Fig. S6 along with images of all PF traces and the distributions of PF lengths and curvatures. The means of the length and curvature distributions for all these in vitro assembly experiments are in Table 3. The similarity of the curvatures obtained with several methods of sample preparation suggests strongly that the curving PFs on MTs elongating with pure tubulin are not artifacts.

Table 3. Properties of PFs on MTs and of tubulin in vitro.

Dataset	PF length	PF curvature	# PFs
	nm	Deg/dimer
GTP	36 ± 15	19.3 ± 13.1	884
GMPCPP	38 ± 19	18.6 ± 12.8	271
Fixed-plunge	25 ± 13	19.9 ± 13.6	264
Fixed-NegStain	21 ± 10	20.5 ± 13.3	365
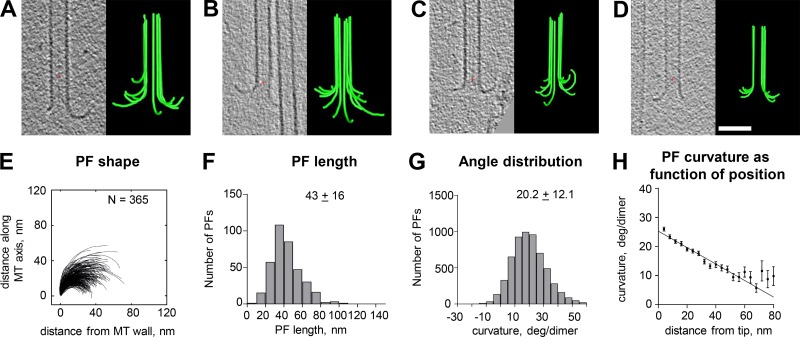
Depoly	43 ± 16	20.2 ± 12.1	365
Extrapolated tip curvature: GTP growth		23.6 ± 0.8
Extrapolated tip curvature: GMPCPP		22.3 ± 0.7
Extrapolated tip curvature: MT shorten		24.1 ± 0.6
GTP-tubulin–darpin complex		22	PDB ID 4DRX
GMPCPP-tubulin–stathmin complex		19	PDB ID 3RYH
GDP-tubulin–colchicine-stathmin		26	PDB ID 1SA0

Tip structure of MTs shortening in vitro

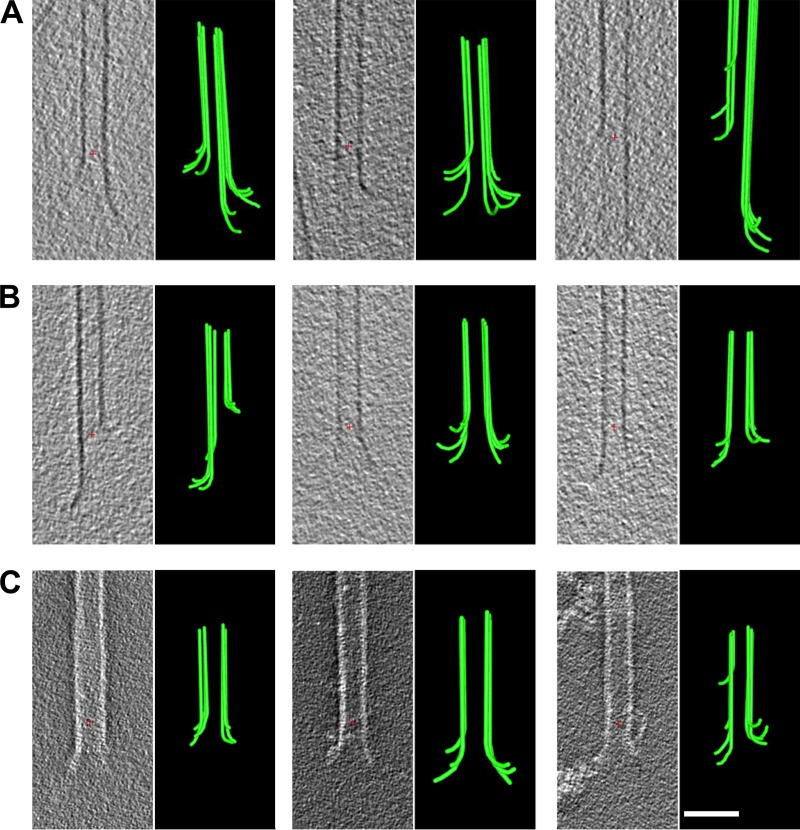
We were curious about the structure of MT tips on shortening polymers when viewed with our methods. To obtain appropriate specimens, we grew MTs as described above, opened a window on the incubation chamber of the plunge freezer, and used five volumes of tubulin-free polymerization buffer at 37°C to flush away the soluble tubulin. Within 1 min, essentially all MT elongations had disappeared from the axonemes, but if we waited only 20–30 s and then blotted and plunged the sample into liquid ethane, many dynamic MT ends were still visible. Images of such MT ends, models made from them, and graphs quantifying the shapes of traced PFs are shown in Fig. 7. A rotary sampling of one of these MT ends is shown in Video 5, and Table 3 includes a line that summarizes quantitative results from these samples. The PFs on these shortening MT ends were a little longer than those on the ends of growing MTs, but their curvatures were very similar; both parameters were well within the variances of the two populations.

Figure 7.

Shapes of plus ends of MTs shortening in vitro. (A–D) Tomographic slices and models showing flaring PFs of MTs frozen ∼20 s after isothermal dilution. Red crosses mark the origins of the coordinate systems used. Bar, 50 nm. (E) Traces of PFs on shortening MTs. (F–H) Graphs showing distributions of lengths, angles, and angles as a function of distance from the PF tips. Numbers and bars are as in Fig. 5. N, numbers traced. Error bars show SEM.

The formation of tubulin oligomers

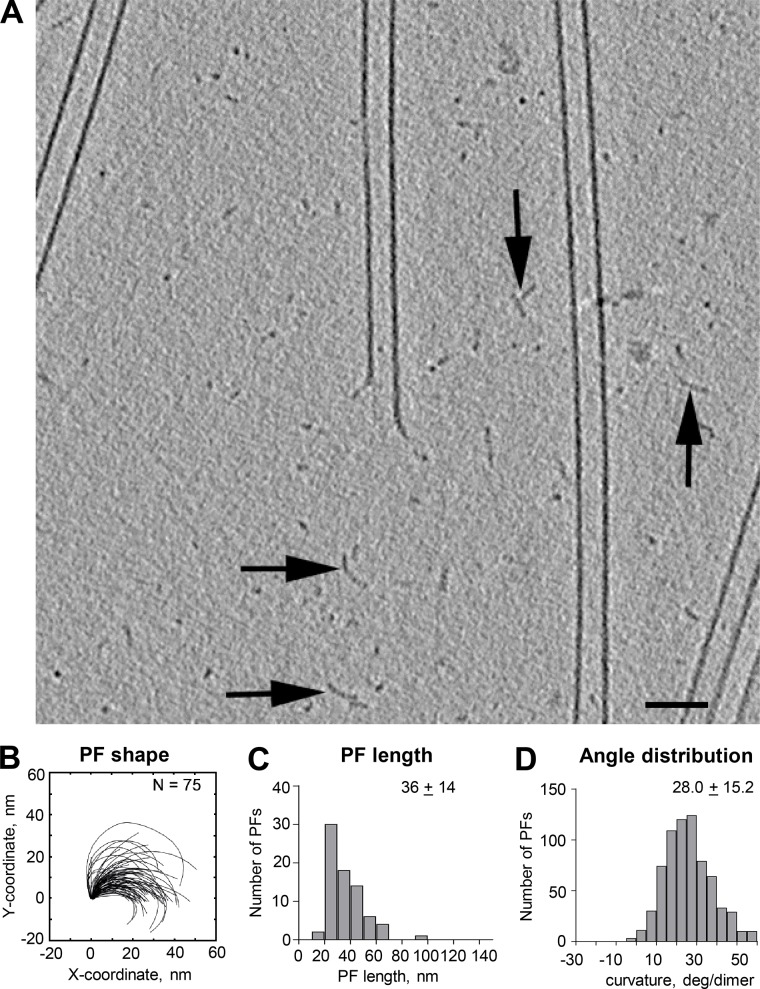
In our samples that favored tubulin polymerization, we frequently noticed small, curving structures in the ice between the growing MTs (Fig. 8). Similar structures were also seen in some previous work on MT dynamics in vitro (Mandelkow et al., 1991), but they were attributed to MT disassembly. Given the evidence that the MTs in our samples were growing, we think these structures were formed during tubulin polymerization. The curving structures were scattered widely, not localized near MT ends as one might expect if they were the products of disassembly. Many of these structures were shaped like PFs, so we quantified their curvatures and found that they were indeed similar to PFs on MT ends (Fig. 8, B–D). We did not attempt extensive characterization of these structures because our identification of them as probable tubulin oligomers depended on their being long enough to catch our eye. We also did not look for changes in curvature as a function of position along the oligomers because we could not detect PF polarity and therefore expected that any sampling we did would include mixed polarities and convey no position-dependent information. Nonetheless, the structures of these objects suggest strongly that they were oligomers of tubulin. We surmise that they formed in either or both of two ways: (1) GTP-tubulin in a polymerization buffer is wont to form longitudinal bonds, so oligomers formed, or (2) during the addition of tubulin to PFs on elongating MTs, polymerization is only one side of a reaction system, so there was always some dissociation. This might happen at any place along the curving PF, resulting in the release of tubulin oligomers from the tips of elongating MTs. The fact that the oligomers are curved is consistent with the idea that GTP-tubulin is bent in solution, as suggested by observations on crystalized material.

Figure 8.

Oligomers formed during tubulin polymerization. (A) 20-nm slice from a cryotomogram of an MT elongating in 20 µM tubulin for 6 min before plunge freezing. A large enough area of background is shown to reveal structures that we interpret as oligomers of tubulin (arrows) lying between the elongating MTs. Bar, 50 nm. (B–D) Tracings of these structures and distributions of their lengths and curvatures. N, numbers traced.

The flexibility of curving PFs

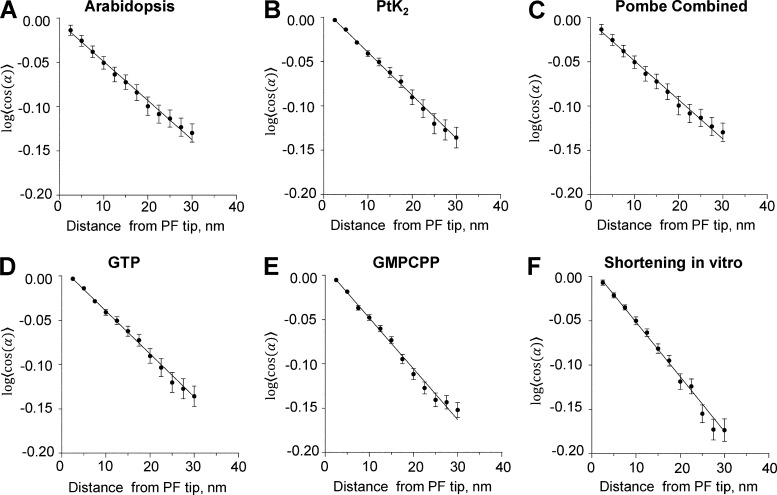
The significant range of PF shapes observed under all conditions used and in all species examined suggests that PFs are not stiff. However, the fact that PFs always bend almost entirely within a plane that contains the MT axis shows that they are quite rigid to bending in the direction perpendicular to those planes. We conclude that PFs are mechanically anisotropic. We assessed the extent to which PFs remain in a single plane by using tomograms to see whether one could follow a PF more clearly if one stepped around the MT as one followed the PF’s trajectory in 3D. The large majority of PFs could be traced well in a single plane. The maximal stepping out of the plane required to follow a PF was <4 nm over the 30–50 nm of PF length. Apparently, PFs are rigid to bending from a plane that contains the MT axis. Bending within that plane, however, seems quite easy. Under the assumption that the PFs are at thermal equilibrium at the time of freezing, one can use the theory of dynamic persistence length (Li et al., 2010) to assess their stiffness (Figs. 9 and S6, I–K; see also Materials and methods). The results are summarized in Table 4. These data imply that in their plane of bending, PFs are at least as rigid as an α-helical coiled coil.

Figure 9.

Data describing PF flexibility. (A–F) Plots of the logarithms of the cosines of mean differences between each measured angle between adjacent line segments and the means of all angles at that distance from the PF tip for each species listed. Error bars are SEM. Assuming thermal equilibrium, these data yield measures of persistence lengths as stated in Table 4. Pombe, S. pombe.

Table 4. Dynamic persistence of lengths of PFs.

Dataset	Persistence Length	# PFs
	nm
IPMT-Arabidopsis	227 ± 25	469
IPMT-Cerevisiae	234 ± 48	128
IPMT-Chlamy	165 ± 10	329
IPMT-PTK	206 ± 17	429
IPMT-Celegans	154 ± 25	123
IPMT-Pombe	162 ± 10	711
GTP	174 ± 10	884
GMPCPP	199 ± 16	271
Depoly	232 ± 15	365

Discussion

Our data suggest that the structures of growing and shortening MT ends are similar though not identical. There are quantitative differences in PF lengths, but the variations within each population of PFs obtained from different species or with different polymerization conditions are large enough that they almost match the differences between growing and shrinking polymers. Moreover, the ends of MTs identified as growing and shortening in cells are strikingly similar to the ends we describe in vitro. Thus, our observations correspond with either a persistent artifact or a unification of the structures for MT ends into a single form in which individual PFs flare out from the MT axis at the ends of both growing and shrinking polymers. Although we admit that our analysis of these many images with low signal-to-noise ratio is difficult and prone to errors in detail, we propose that the structures we describe are basically correct for the following reasons. (A) Essentially the same in vivo MT end structure has been found in six species as well as on cellular MTs prepared for study at two stages of mitosis and from two different parts of the mitotic spindle. The likelihood of artifact is small because we see quantitatively the same structures in cells that have been frozen with or without the application of high hydrostatic pressure to retard ice crystal formation, in PtK₂ cells that were chemically fixed without cooling (McIntosh et al., 2008), and on KMTs that were fixed first and then frozen. The flared end structures therefore do not require freezing, pressure, or dilution; they are found on MTs in any well-preserved cell.

(B) Our experiments on MT ends in vitro are similarly grounded in a range of methods. We have relied most heavily on plunge freezing into ethane cooled to its freezing point because this is regarded by most scientists as the method of choice for preserving biological structure. Given that the rate of freezing in this cryogen is on the order of −10⁶ degrees C per second (Dubochet, 2007), the time required to cool from ambient temperature to the glass transition temperature for water (−137°C) is ∼150 µs. Given also that the viscosity of super-cooled water rises sharply as its temperature drops (Dehaoui et al., 2015), the time required to immobilize the PFs during freezing is probably much less—perhaps 10 µs—which should make our images an accurate reflection of native structures. However, there is the concern about sample cooling before immersion in cryogen as discussed above. The facts that we have obtain quantitatively similar PF structures by plunge freezing, by chemical fixation and then freezing, or by chemical fixation and then negative staining (without freezing) suggest that the structures we describe are valid.

Why, then, have others obtained different results using similar methods in previously published work? For the shapes of MT plus ends in vivo, there may actually be no differences. The studies of MTs growing in fission yeast (Kukulski et al., 2011) and of the ends of MTs that were regrowing after drug-induced depolymerization (Hoog et al., 2011) described MT ends that were essentially the same as the ones we have seen in all species studied, although end shapes in those studies were not characterized with rotary sampling and detailed quantification. The MT ends seen in plunge-frozen interphase mammalian cells displayed a variation in end structure not unlike the range of structures we describe (Zovko et al., 2008), but again there was no rotary sampling of end structure and little quantification. Other studies of both KMTs in PtK₂ cells (VandenBeldt et al., 2006) and interzone MTs in Arabidopsis thaliana (Austin et al., 2005) used only a single orientation of sampling of MT end structure and may therefore have missed the flaring PFs we see so commonly.

Some recent evidence on the structure of MT ends formed in vitro is presented in a study of MT minus ends. Atherton et al. (2017) show tomographic slices through MT plus and minus ends, both of which look much like the ends described in our study. Atherton et al. (2017) also present data on the curvature of PFs seen in slices through multiple plus ends, and all are curved. However, most of the recent work on the ends of MTs growing in vitro has been done in the laboratory of D. Chrétien, who with multiple collaborators has described long, gently curving PF bundles at the ends of many MTs growing from isolated centrosomes in vitro (Guesdon et al., 2016). Although the earlier work from this group showed only these gentle curves, their most recent study, which used cryoET, revealed short, curling PFs at the tips of both the long, gently curving PF bundles and some shorter MTs as well (see Fig. 4 [a and d], Fig. S3 [f and h], Fig. S4 [b and d–k], and Fig. S5 [a–f, j, and k] in Guesdon et al., 2016). The appearance of sharper curls at the tips of long, gently curving PF bundles may be a result of Guesdon et al. (2016) using cryoET in that study but not in previous work. When the tips of frozen hydrated MTs are imaged with a single micrograph, the contrast along the side of a complete MT is quite high thanks to the superposition of multiple PFs into a single line along the MT wall. At the tip, where PFs flare out, the individual strands of tubulin scatter electrons individually and are therefore of significantly lower contrast. As such, they are easy to miss.

Guesdon et al. (2016) and others from the Chrétien group discuss the possibility that their gentle curves are mechanical equilibria between the intrinsic curvature of GTP-tubulin, which would form comparatively tight curves like the ones we see, that they display at the tips of some of their gentle curves, and the tendency for lateral interactions between PFs to straighten those tight curves (Jánosi et al., 1998). The question then becomes: why do they see so many MTs that elongate with a few PFs extending far beyond their neighbors, leading to the long and gentle curves? Most of the MTs we have seen show all of the PFs initiating their outward curve at approximately the same location along the MT axis. Granted, a few of the MT ends modeled in this study show some PFs extending along the MT axis farther than others (Fig. 2 for Arabidopsis, Fig. S5 B for GMPCPP tubulin, and four other MTs not depicted), but uneven PF lengths are the exceptions in our data, and they generally extend <300 nm. Moreover, all but two of the extensions we have seen are essentially straight rather than the gently curving ones seen by Guesdon et al. (2016). We do not know the reason for this difference, but one possibility is that the isolated centrosomes used as seeds by Guesdon et al. (2016) are biochemically complex. We suspect that proteins may wash from those organelles and interfere with the elongation of some PFs, allowing others to grow much longer then their neighbors. We know for sure that we have never seen these long, gently curving PF clusters in vivo.

The first description of the end structures on MTs growing and shrinking in vitro was performed using negative staining (Simon and Salmon, 1990). Figs. 1 (A and B), 2, and 3 (B and C) in that paper show curling PFs at the tips of elongating MTs. The original cryoEM work on growing and shrinking MTs (Mandelkow et al., 1991) took single images of each MT end without tomographic reconstructions, so they may have missed some curling PFs. Nonetheless, their images do show some curving PFs quite like the ones we describe. The fact that most of the growing ends they saw were blunt may be related to their conditions for polymerization, which were in part defined by their recent discovery of ways to make MT assembly oscillate; the concentration of tubulin used was 200 µM, 10-fold higher than we or others have used in vitro, and similarly higher than the concentration in cells. This might have an effect on the ways in which PFs straighten and cluster to form the MT wall.

Implications of MT end structure for the mechanisms of tubulin polymerization

Assuming that the structures we describe are correct, what do they imply about the mechanisms for tubulin assembly, disassembly, and dynamic instability? First, tubulin dimer addition must be at the tips of PFs. Thus, when tubulin assembles, the proteins interact initially with only a single polymerized dimer and by only a single longitudinal bond. This follows from the bending of all the PFs within planes that contain the MT axis and are separated by 360°/13 from their neighbors. We infer that GTP-tubulin changes its properties upon addition to a PF, increasing its affinity for dimers in solution. Were this not true, the fact that dimers are in vast molar excess over PF tips should lead to most of the tubulin assembling into oligomers rather than elongating existing MTs. The presence of oligomers during tubulin polymerization suggests that this is not an all-or-nothing difference but that the increased affinity must be sufficient to favor MT elongation. (Note that it is possible that all the oligomers we have seen were formed by the fragmentation of PFs at growing MT tips.) We suppose that this polymerization-associated structural change does not involve GTP hydrolysis given the substantial evidence that GTP-tubulin is present near the ends of growing MTs. The change is probably a subtle, binding-induced rearrangement in the tubulin fold analogous to the induced fit known to occur during the interaction of some enzymes with their substrate. Our data on shortening MTs are consistent with many published studies and suggest that tubulin loss during MT disassembly is through both the dissociation of tubulin dimers from PF tips and the separation of dimers within a PF, leading to the loss of tubulin oligomers from an already bending PF. Note that the observation of very long PFs at the ends of shortening MTs, the “ram’s horns” previously seen (Mandelkow et al., 1991; Müller-Reichert et al., 1998), depends on the addition of nonphysiologically high concentrations of divalent cations, which probably provide additional stabilization to the longitudinal interdimer bonds.

The second key point is that our evidence strongly supports the view that both GTP and GDP tubulins are bent, so their oligomers form curving PFs. This point is quantitatively consistent with observations on the structure of tubulin dimers by x-ray crystallography as seen in Table 3, where values of PF curvature/dimer have been estimated from dimer structure (Brouhard and Rice, 2014). Note, however, that computer-generated oligomers of tubulin built from the structures determined by crystallography are helical, not planar (e.g., Pecqueur et al., 2012). The fact that the PFs we see are essentially planar is an intriguing and significant difference, which may be another manifestation of structural changes that occur during the addition of dimers to elongating PFs.

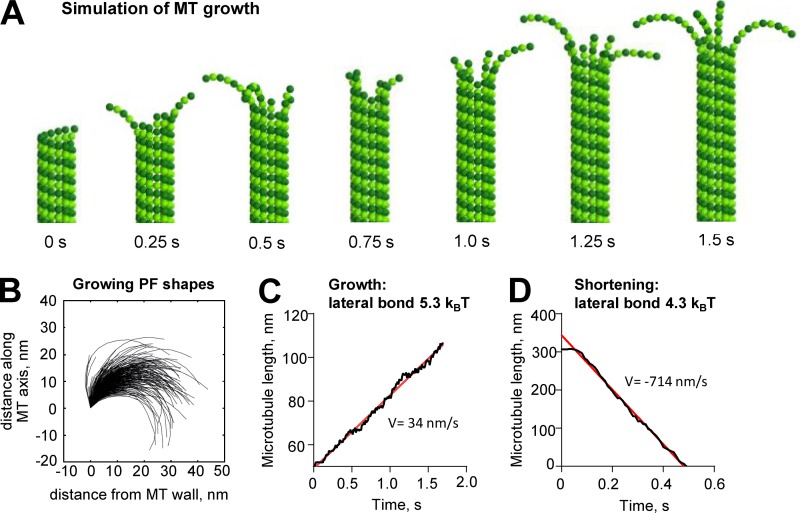
Why, then, will GTP-tubulin polymerize and GDP-tubulin not? It is possible that GTP- and GDP-tubulins differ in the strengths of the lateral and longitudinal bonds they can form, while having similar curvature and stiffness. To see whether such a hypothesis can explain our data, we used a published Brownian dynamics model for MT formation (Zakharov et al., 2015) modified so that the equilibrium shape of GTP-tubulin was bent. This theoretical structure allowed us to simulate MT growth with curved PFs at the tip. Assuming a PF stiffness comparable with that estimated from the observed variation of PF curvature (58 k_BT/rad² or 35 kcal/mol/rad²), we were able to reproduce MT growth with assembly rates and tip shapes similar to those seen in our experiments (Fig. 10, A–C; and Video 6). We found that strong longitudinal bonds and relatively weak lateral bonds were required to observe MT growth with fairly long PF curls at the tip (Fig. 10 B and Table 5; see also Materials and methods). Lowering lateral bond strength alone by only 1–2 k_BT (0.6–1.2 kcal/mol) was enough to switch MTs from growth to shortening with experimentally observed disassembly rates (Fig. 10 D). However, this produced overly long curls on shortening MTs (not depicted). It is therefore likely that both lateral and longitudinal bonds are weakened after GTP hydrolysis. Strikingly, this modeling predicts that at 37°C, PFs will vibrate so rapidly that the wall-proximal tubulin subunit near the origin of the curving PF will spontaneously straighten sufficiently to form lateral bonds at frequencies on the order of MHz, simply because of Brownian fluctuations. The rate of tubulin addition for normal rates of MT growth (1–10 µm/min) is only 2–20 dimers per second at each PF tip. Thus, a growing PF will have many chances to straighten and bond to its neighbors with every tubulin addition. This feature of the model is consistent with the fact that MTs elongate at a rate that is proportional to the concentration of soluble tubulin; the rate of tubulin addition to the PFs tips is rate limiting, not the process of PF straightening. Note, however, that PFs may be significantly stiffer than is implied by the analysis based on dynamic persistence length. Moreover, if they are straightening, binding to neighbors, and then frequently releasing, they may not be in thermal equilibrium. The shapes we have traced would then be defined in part by the intrinsic curvature of GTP-tubulin, in part by thermal oscillations, and in part the tendency of PFs to bind neighboring PFs when they are straight or almost straight. Under these circumstances, the assumptions of the theory for dynamic persistence length are not met, and our calculated stiffnesses may be too soft. However, even if PFs are 10-fold stiffer than our estimates from the calculated persistence lengths, the lateral bonds are predicted to form and break orders of magnitude more frequently than tubulin addition/loss, making the thermally driven mechanism for PF straightening effective for allowing MT growth.

Figure 10.

MT growth with curved PFs illustrated with a Brownian dynamics model. (A) MT growth in a model with curved GTP-tubulin. (B) Shapes of simulated PFs on the growing MT tip. (C) Dependence of MT length on time in simulation with lateral bond 5.3 k_BT yielding the polymerization rate V = 34 nm/s. Data in A–C correspond with Video 5. (D) Dependence of MT length on time in simulation with lateral bond 4.3 k_BT yielding the depolymerization rate v = 714 nm/s. Note that initial pause before rapid MT shortening is caused by the start of the simulation from the metastable configuration with blunt end. The pause was excluded from the linear fit. Red lines are linear fits to data.

Table 5. Parameters used to model MT growth.

Parameter	Description	Value
r0	Width of energy potential well characterizing the length of tubulin–tubulin bond	0.13 nm
alat	Energy parameter for lateral repulsion; corresponds with ∼2 × height of the energy barrier for lateral bond	15 kBT = 9 kcal/mol
blat	Depth of the potential well for lateral bonds	5.3 kBT = 3.2 kcal/mol for MT growth
		4.3 kBT = 2.6 kcal/mol for MT shortening
along	Energy parameter for longitudinal repulsion; corresponds with ∼2 × height of the energy barrier for longitudinal interdimer bond	15 kBT = 9 kcal/mol
blong	Depth of the potential well for longitudinal interdimer bond	16.6 kBT = 10 kcal/mol
k	Stiffness of longitudinal intradimer bond	517 kBT nm−2 = 310 kcal/mol nm−2
B	Flexural rigidity of PF bending	58 kBT rad−2 = 35 kcal/mol rad−2
χD0	Equilibrium angle between GDP-tubulin monomers	0.2 rad
χT0	Equilibrium angle between GTP-tubulin monomers	0.2 rad
ctub	Soluble tubulin concentration	10 µM
kon	On-rate constant for tubulin addition	8.3 µM−1s−1 per MT
T	Temperature	310 K
η	Viscosity	0.2 Pa · s
dt	time step for dynamic algorithm	10−10 s
Tkin	time step for kinetic algorithm	10−3 s

Many details of the model described above are not fleshed out. Moreover, there are experiments that can test predictions from the model such as the impact of MT growth rate on PF shape and the possibility of interdependence in the shape of neighboring PFs. There are also issues to consider about the unevenness of the positions at which PF bending begins and whether this depends on shortening versus growth or on the rate of growth. All these issues will be explored in future papers.

Materials and methods

Cell growth and the preparation of samples for microscopy

Mammalian cells (strain PtK₂) were plated on sapphire disks in McCoy’s medium at 37°C with 5% CO₂ and then cryoimmobilized by freezing under high pressure (McDonald et al., 2007). Schizosaccharomyces pombe was grown in rich medium (YES) at 25°C, collected by vacuum filtration onto EMD Millipore filters, and transferred by spatula to a planchette for high-pressure freezing (Giddings et al., 2017). For plunge freezing, S. pombe cells (strain CDC25-22) were grown at permissive temperature on nutrient agar covered with a thin Mylar film. Log-phase cells were frozen by rapid immersion of the Mylar into liquid ethane (Tanaka and Kanbe, 1986). Saccharomyces cerevisiae was grown in rich medium and then collected and frozen as described previously (Giddings et al., 2001). Arabidopsis was grown, and its root tips were harvested and then high-pressure frozen as described previously (Austin et al., 2005). Chlamydomonas (strain 137c) was grown in liquid culture at 25°C on a 12-h light/dark cycle to enrich for mitotic cells (Umen and Goodenough, 2001). The cells were collected by centrifugation after shifting to the dark and then high-pressure frozen essentially as described previously (Preble et al., 2001; O’Toole and Dutcher, 2014). Hermaphrodites of C. elegans were high-pressure frozen in M9 worm buffer containing 20% BSA as described previously (Muller-Reichert et al., 2008). All samples were fixed by freeze substitution at −90°C in acetone containing either glutaraldehyde and uranyl acetate or OsO₄ and then embedded in plastic as previously described (Muller-Reichert et al., 2008). Serial sections ∼250 nm thick were cut using an Ultracut microtome (Leica Biosystems), picked up on slot grids coated with a film of Formvar, and poststained with lead citrate and uranyl acetate. The sections were then strewn with particles of 15 nm colloidal gold to serve as markers for alignment of serial tilts.

Identification of cells whose MTs were growing

Cells were identified as suitable based on their stage in anaphase B (a time when spindles elongate) and the orientation of their spindle axes approximately parallel to their plane of sectioning. In all these cell types, anaphase B begins near the end of anaphase A, so cells with well-separated chromosomes were selected. In PtK cells, the number of MTs in the interzone stays approximately constant as the MTs slide and elongate (Fig. S1; McIntosh et al., 1975). Thus, all MTs in the anaphase B interzones of these cells were elongating at the time of freezing. The same appears to be true for Chlamydomonas, although the data are less complete. In Arabidopsis, MT number stays high until near the end of anaphase B, whereupon it decreases as the cell plate forms (Austin et al., 2005). Cells for study were therefore selected to be still in the spindle elongation phase of mitosis. In both yeasts, the number of interzonal MTs decreases during anaphase B, so some MTs must depolymerize as others elongate (Ding et al., 1993; Winey et al., 1995). Growing MTs were identified as those whose plus ends were still overlapping; other interzone MT ends were ignored. In blastomeres of C. elegans, there are very few MTs in the anaphase interzone (Muller-Reichert et al., 2008), so this organism was not used for studies of elongating IPMTs, only for examination of KMTs.

Identification of KMTs

KMTs were identified in PtK₂ cells, Chlamydomonas, and C. elegans as previously described (McIntosh et al., 2013). We did not include fission yeast KMTs in our analysis in part because there is no flux of spindle MTs toward the spindle poles, so these MTs are not growing in metaphase, in part because chromosome in fission yeast cells are hard to see by EM, and in part because the number of examples of fission yeast anaphase spindles combined with the low numbers of MTs per kinetochore meant that we did not have large enough numbers of MTs for a serious analysis of their shapes.

Preparation of electron tomograms and characterization of MT ends in vivo

Sections of suitable cells were imaged as tilt series ranging over ±60° about two orthogonal axes using the SerialEM image acquisition software (Mastronarde, 1997); 3D reconstruction was accomplished by back projection (Kremer et al., 1996). Electron tomograms of regions near the spindle midplane contained many overlapping MTs whose growing plus ends were easy to identify. Graphic models of these MT trajectories were made using the 3dmod program from the IMOD software package (Kremer et al., 1996). A subroutine in IMOD (mtrotlong) extracted volumes that contained each MT end.

Additional controls for the impact of freezing and high pressure on PF shape

As an additional control for the impact of freezing on MT structure, we have examined the plus ends of KMTs in metaphase PtK₂ cells that were chemically fixed with glutaraldehyde and then high-pressure frozen and further fixed by freeze-substitution before embedding, sectioning, and examination by ET in collaboration with the laboratory of J. DeLuca (Colorado State University, Fort Collins, CO). In this case, 264 PFs from 74 MTs showed a mean length of 43 ± 14 nm and a mean curvature of 14° ± 7° per dimer, further indicating that curving PFs are not a freezing artifact.

As final evidence that high pressure is not the cause for curving PFs in vivo, we have examined KMTs in one anaphase PtK₂ cell that was plunge frozen, a rare case in which ice crystal damage did not obscure structural detail in a mitotic mammalian cell (all anaphase KMTs are shown in Fig. S4 [A, D, G, and J], and the anaphase numbers for PtK₂ cells are shown as KMT-PtK-ana in Table 2). The similarities among these numbers support the contention that neither high pressure nor freezing is a factor in PF shape.

Growth and imaging of MTs in vitro

For the study of MT polymerization in vitro, pure porcine tubulin purchased from Cytoskeleton (t238p) was polymerized onto the MTs of axonemes prepared from Chlamydomonas flagella (Nicastro et al., 2006), a gift from M.E. Porter (University of Minnesota, Minneapolis, MN). Isolated axonemes were diluted into a buffer containing 80 mM Pipes, pH 6.9, supplemented with 1 mM GTP, EGTA, and MgCl₂ (BRB80) and then were applied as a 2–3-µl drop to a C-flat holy carbon-coated electron microscope grid (Electron Microscope Sciences) that had recently been glow discharged. Axonemes were given 30 s to attach to the carbon film, and then excess fluid was blotted away. 20 µM tubulin in BRB80 at 0°C was usually supplemented with a low titer of 10 nm colloidal gold, and then 5 µl of this mixture was immediately added to the grid, which was then drawn up into the prewarmed and hydrated chamber of a plunge-freezing device (Vitrobot; Thermo Fisher Scientific). Samples were incubated for 3–6 min at 37°C and 90% relative humidity. Both these chamber values were checked by independent measurement. Humidity was confirmed, but the temperature stated on the instrument’s console was ∼2°C higher than the temperature at the grid, as measured with a calibrated thermocouple. After sufficient time for MT growth, the grid was blotted with filter paper, plunged into liquid ethane, and then transferred to liquid nitrogen and kept under this liquid as it was transferred to a cryotransfer holder (910; Gatan) and inserted into a Tecnai F20 or F30 electron microscope from Thermo Fisher Scientific for examination at less than −170°C.

Shortening MTs were made by first growing MTs with the above procedure and then inducing depolymerization by isothermal dilution. Polymerization buffer without tubulin was warmed to 37°C, and then an aliquot of 25 µl was added to the 5-µl drop of tubulin-containing buffer on the grid. Because two or more drops fell from the grid during this addition, the final tubulin concentration was <3 µM. After ∼20 s, the grid was blotted and plunge frozen in liquid ethane.

In some experiments, GTP in the purchased tubulin was partially replaced with GMPCPP by cycles of dilution with 10 mM GMPCPP in BRB80 followed by reconcentration of the protein with a Vivicon 500 spin concentrator (Sartorius Stedim Biotech) following the manufacturer’s instructions. With two cycles of dilution and reconcentration, the initial concentration of 1 mM GTP was reduced to <40 µM, and GMPCPP was brought to 4 mM, so the final ratio of GMPCPP to GTP was >100.

In other experiments, we stabilized the structure of growing MTs by fixation before either freezing or negative staining. Glow-discharged holy carbon-coated grids were placed on a sheet of Parafilm in the top of a 10-cm plastic Petri dish accompanied by a small wad of paper towel saturated with distilled water (to maintain a hydrated atmosphere). The edge of each grid was pressed gently onto the Parafilm with the tip of sharp forceps to secure it to this support so that it would not rise up into a drop of liquid being added. Axonemes and then tubulin were added to the grid as described above, and then the Petri dish was covered with the bottom of the dish and floated top-side down in a 37°C water bath for 6 min. To terminate MT dynamics, 1/10 volume (0.5 µl) of 2% glutaraldehyde in BRB80 at 37°C was added to the 5-µl drop of tubulin solution on the grid. The grid was then plucked rapidly from the Parafilm and then rinsed in fresh 2% glutaraldehyde in BRB80 at 37°C and then in BRB80. In other experiments, the grids were fixed directly with 2% glutaraldehyde and then rinsed in BRB buffer. Each grid was then either allowed to cool slowly to room temperature and taken to the Vitrobot for rapid plunge-freezing, as described above, or was negatively stained with 2% uranyl acetate in water, blotted, and air dried.

Growing MTs were identified as extensions from axoneme doublet A tubules (Fig. 5); polymer ends that lay over holes were imaged with a bidirectional tilt series about a single axis, ranging first from 0° to about +60° and then from 0° to −60°. Microscope magnification was set to let the camera sample the specimen with 0.9-nm pixels. Images in a tilt series were collected at 2° tilt increments with a defocus of −4 µm; low-dose imaging conditions were used so that the total electron dose for a tilt series was ∼80 e/A². These images were again used for 3D reconstruction by back projection followed by filtering by nonlinear anisotropic diffusion. In some cases, image signal-to-noise ratio was improved by carrying out tomographic reconstructions using a simultaneous iterative reconstruction technique (SIRT)-like filter described by Zeng (2012).

Tracing PFs

The 3dmod slicer window was used to orient and position the axis of each MT collinear with the vertical axis of the viewing window. The slicer window was then tipped 90° about the horizontal axis so the MT was viewed in cross section. From this orientation, the origin of the coordinate system could be placed at the center of the MT with considerable precision. Now the slicer window was returned to an orientation parallel to the MT axis, and a 2–4-nm-thick sampling lamina was rotated about this axis, displaying the MT walls on either side of the rotation axis at each azimuthal orientation (Fig. 1 and Video 1). A contour was drawn on each PF both where it ran straight along the MT wall and where it curved outward from the MT axis (Fig. 1 A). Any place along a possible PF that showed a sharp change in curvature (e.g., 90° in a few pixels) or an obvious change in either thickness or stain density was interpreted as some nontubulin material associated with that PF rather than a continuation of the PF. PFs were sought at azimuthal angles separated by ∼27° (360°/13) because both MTs in vivo and those grown from axonemes contain 13 PFs. If no curving PF was found at an orientation where a PF should be, this position in the MT circumference was represented by a straight line drawn in the MT wall. The set of all such traces depicted the structure of each MT end (Fig. 1, C and D; and Fig. 2, right). We could never sample the full MT perimeter because of the limited range of tilt angles available for dual-axis ET, which results in a “missing pyramid” of data. These features of our imaging procedure increased the point-spread function in the direction along the beam axis, making resolution anisotropic (Mastronarde, 1997). Nonetheless, we were able to trace 4–10 PFs on multiple MTs from each species, yielding a clear characterization of most MT ends, which in turn permitted quantitative analysis of MT end structures.

Getting graphic objects whose structures accurately reflected the shape of the flaring PFs at the ends of MTs was sometimes straightforward and sometimes difficult. In vivo, all work was done by one experienced viewer of MTs, J.R. McIntosh. In vitro, the lack of cytoplasm made tracking somewhat easier, although the low signal-to-noise ratio of the low-dose images meant that tracking was still a challenge. In some cases, we obtained a better signal-to-noise ratio by applying a SIRT-like filter during reconstruction.

We have tried to assess the accuracy of our traces in several ways. Reproducibility was examined simply by retracing the same image data and comparing mean PF parameters. Initially, reproducibility was not good, but through trial and error, we identified the principal problem: finding the center of the MT to place the axis of rotation in the best position to allow accurate rotational samples of the MT end. The most successful method for this task was to use the slicer module in IMOD to sample the MT in cross section, raise the display magnification very high, and then fit a circle to the wall of the MT by eye. Because not all growing MTs were both circular and complete near their ends, this was an approximate process, but it served to position the coordinate system for rotations well enough that when two experienced MT trackers used the same method on the same MTs, their traces were pleasingly similar (Fig. S2, A–E′). This method was used for all in vitro–grown MTs presented in this study.

When a few PFs extended significantly beyond others on the MT end, they sometimes showed the gentle curvature described in the literature (Chrétien et al., 1995). Our interest in curvature at the growing tips of these PFs led us to digitize these structures in two ways. To make models that reflected MT tip structure, we digitized all these PFs with many points as seen in Figs. 2, (Arabidopsis), 5 E, S2 A, and S5 B. For quantitative analysis to tip PF curvature, we only digitized the portion of the PF near its end, where greater curvature was seen. The gentle curvatures found where several PFs were laterally associated was not analyzed.

Analysis of PF structure

The traces of each PF were analyzed in multiple ways. The “howflared” module of 3dmod package in IMOD assessed PF length by tabulating the total length from the point a PF began to curve out from the MT wall to its end. For PFs that show no curvature, this value was zero, but these zero values were not used in computation of the mean length of curved PFs. PF tracings were further processed using custom scripts written in MatLab (2015a; MathWorks). Although the vast majority of PFs were uniformly traced with a mean distance between consecutive points of ∼2–3 nm, some showed large gaps between adjacent points in tracings. These were filled in by linear interpolation. At the next step, six points were added to each of the PF tracings at their (MT-proximal) minus ends to represent MT walls. The resulting tracings were smoothed with the quadratic LOESS procedure using a 10-point span. After smoothing, the artificially added six points representing the MT wall were removed.

To determine PF curvatures, we calculated the angles between the consecutive pairs of line segments that connected adjacent points of the smoothed PF tracings. To assess curvature as a function of position along a PF, we aligned all PFs of each dataset at their tips and then computed their mean curvature as function of distance from PF tips. The resulting plots were fitted with a linear function by the method of weighted least squares with weights being the inverse squared SEM of the curvature at each position from tip.

For intrinsically curved filaments like tubulin PFs, the best measure of flexibility is their dynamic persistence length (Trifonov et al., 1988), which can be defined as distance along the filament at which the correlation between angular deflections of the filament from its equilibrium shape decays by a factor of e because of thermal fluctuations (Li et al., 2010). This definition can be expressed with the following formula:

$$\overrightarrow{\tau }\left(0\right)\mathrm{ }\overrightarrow{\tau }\left(s\right)= \cos (\delta \left(s\right)=\mathrm{ }{e}^{-\frac{s}{{\xi }_d}},$$ (1)

where $\overrightarrow{\tau }$(s) is tangent vector at position s along the filament, δ(s) is the filament’s position-dependent angular deflection from the mean curved shape, and ξ_d is the dynamic persistence length.

To measure the dynamic persistence length of tubulin PFs, the raw tracings with filled gaps were first smoothed using LOESS procedure with a seven-point span. Smoothed tracings were then aligned at their plus tips, and their averaged shape was calculated. Moving from segment to segment along each PF tracing starting at the plus tip toward MT wall, we computed the angles of orientation of each segment. From those angles, we subtracted the angles of orientation of the corresponding segments of the averaged PF shape to obtain the angular deflections δ(s). The logarithms of mean cosines of the angular deflections δ(s) across all PFs was plotted against position s along the PF and fitted with a straight line. As seen from Eq. 1, the inverse of the negative slope of that line produces a dynamic persistence length. To estimate errors in persistence length determination, n = 100 bootstrap sets of the same size as original dataset were generated by drawing PFs randomly with replacement. For each bootstrap set, the dynamic persistence length was measured as described above. SD of those measurements was reported as error in Table 4.

Brownian dynamic modeling

Simulations of MT assembly/disassembly were done using a previously published model (Zakharov et al., 2015) with some modifications. In brief, each tubulin monomer within MTs represented a sphere with interaction sites on its surface. The energy of tubulin–tubulin interaction was described by longitudinal and lateral potentials of the following shape:

$$v\left(r\right)=a\cdot \frac{r^2}{r_o^2}\cdot \exp (-\frac{r}{r_o})-b\cdot \exp (-\frac{r^2}{r_o^2})$$ (2)

Where r is the distance between corresponding interaction sites (lateral or longitudinal), r_o is width of energy potential well, and a and b define the height of the interaction barrier and the depth of the potential well, respectively. Longitudinal bonds within a dimer were modeled as unbreakable springs with quadratic potential energy u(r):

$$u\left(r\right)=\frac{1}{2}k·r^2,$$ (3)

where k is the stiffness of the tubulin–tubulin intradimer bond.

Bending energy g(r) associated with tubulin monomers’ rotation relative to one another was also described by an unbreakable quadratic function:

$$g\left(\chi \right)=\frac{B}{2}{(\chi -{\chi }_o)}^2,$$ (4)

where χ is the angle between neighboring tubulin monomers in a PF, χ₀ is the equilibrium angle between two monomers, and B is the flexural stiffness of the longitudinal tubulin–tubulin interface.

The evolution of the system was calculated by solving Langevin equations of motion (Ermak and McCammon, 1978) with 100-ps time steps for each of the three coordinates describing each tubulin sphere. Every millisecond, new tubulin subunits could be stochastically added to the MT tip, and tubulin oligomers could be removed from MT if their longitudinal interaction with the bottom tubulin neighbor became weaker than 0.1 k_BT because of a Brownian fluctuation.

All parameter values in the simulations are summarized in Table 5. Most of the values were the same as in Zakharov et al. (2015), with some modifications. Specifically, the equilibrium angle between longitudinally attached GTP-tubulin monomers was set to be 0.2 rad, i.e., the same as between GDP-tubulin monomers. Flexural rigidity of PF bending was 58 k_BT rad⁻². Depth of longitudinal bond, b_long, was 16.6 k_BT (10 kcal/mol). Hydrolysis probability was set to zero to explore regimes of pure assembly or disassembly. Depths of lateral bonds were selected to match experimental MT growth and shortening rates: b^GTP_lat = 5.3 k_BT (3.2 kcal/mol), and b^GDP_lat = 4.3 k_BT (2.6 kcal/mol).

Online supplemental material

Fig. S1 is an image and diagram showing the sites from which anaphase IPMTs were taken for analysis of elongating MTs as well as images of IPMTs from a PtK₂ cell in anaphase. Fig. S2 shows comparison of MT models traced by different observers and comparison of MT end structures in anaphase fission yeast cells prepared by high-pressure freezing or by plunging directly into liquid ethane. Fig. S3 shows traces of PFs on anaphase IPMTs from five species and distributions of PF shape parameters for anaphase IPMTs from S. cerevisiae and Chlamydomonas. Fig. S4 shows images and data describing the shapes of KMT plus ends in anaphase from three species. Fig. S5 is a gallery of images, models, traces, and data analyses for PFs at the ends of MTs growing in vitro in either 1 mM GTP or 4 mM GMPCPP and trace GTP. Fig. S6 shows images, models, and data describing the ends of MTs grown in GTP and then fixed in glutaraldehyde before either rapid freezing or negative staining as well as data that characterize the flexibility of PFs on IPMTs from three species. Video 1 shows rotary sampling of the end of an IPMT from the anaphase B interzone of a PtK₂ cell. Video 2 shows rotary sampling of the end of an elongating MT growing from an outer doublet MT from an axoneme of Chlamydomonas. Video 3 shows rotary sampling of the end of an elongating MT growing from an outer doublet MT from an axoneme of Chlamydomonas in the presence of 30-fold excess of GMPCPP. Video 4 shows rotary sampling of the end of an elongating MT that was fixed and then frozen. Video 5 shows rotary sampling of the end of a shortening MT that initially grew from an outer doublet MT from an axoneme of Chlamydomonas. Video 6 shows coarse-grained molecular dynamics showing MT growth by a mechanism that relies on thermal fluctuations of PFs to straighten these elongating oligomers.