“Resuscitation time bias”—A unique challenge for observational cardiac arrest research

Abstract

Observational studies are prone to a number of biases. One of these is immortal time bias. In this manuscript, we discuss immortal time bias as it pertains to post-cardiac arrest research and describes a related bias which we term “resuscitation time bias”. This bias can occur when studying exposures during cardiac arrest. In this unique situation, an exposure is more likely to occur the longer the cardiac arrest continues. Since length of resuscitation is strongly associated with worse outcome, this will bias the results toward a harmful effect of the exposure. We discuss this bias and present methods to account for it.

Introduction

Observational studies play an important role in cardiac arrest research. They are particularly important in this setting as randomized clinical trials might not be feasible for answering questions about cardiac arrest. This can be due to the complexity of consent and randomization during acute events, the relative rarity of cardiac arrests, and/ or requirements for very large sample sizes due to patient heterogeneity and relatively modest treatment effects. Unfortunately, observational studies suffer from a number of potential biases. In addition to the well-known bias introduced by confounding, selection bias and information bias may also be present [1].

Multiple methods have been developed to address the potential bias introduced by confounding (e.g. stratification, regression models, matching) and these are often used in observational studies. Other biases are less often explicitly addressed in observational studies. One potential bias that is often overlooked is “immortal time bias” [2]. This bias occurs when the outcome (most often mortality) cannot occur because exposure is defined in a way which implicitly assumes, but often does not acknowledge, that patients are essentially “immortal”until they receive the exposure [2].

A less well-known and described bias pertains to observational studies of exposures (e.g. drugs, airway management) during cardiac arrest. In this situation, an exposure is more likely to occur the longer the cardiac arrest continues. Since length of resuscitation is strongly associated with worse outcome [3–5], this will tend to bias the results toward a harmful effect. This bias can be considered the reverse of immortal time bias and will be termed “resuscitation time bias” in the current manuscript.

The aim of this manuscript is to provide a brief overview of immortal time bias with respect to cardiac arrest research and a comprehensive discussion related to resuscitation time bias. This includes a brief overview of the theoretical framework, real-word examples, and potential methods to deal with this type of bias. We hope this manuscript will provide a better understanding of these types of biases and provide a framework for future observational studies assessing intraand post-cardiac arrest interventions.

Immortal time bias

Immortal time bias occurs because exposure in observational studies is not defined at a discrete time point but rather occurs at some point over a period of time. As such, those who receive the exposure are, by definition, alive for the period of time until they receive the exposure. In contrast, those patients who die early will have a much lower likelihood of receiving the exposure. This biases the results towards a beneficial effect of the exposure [2].

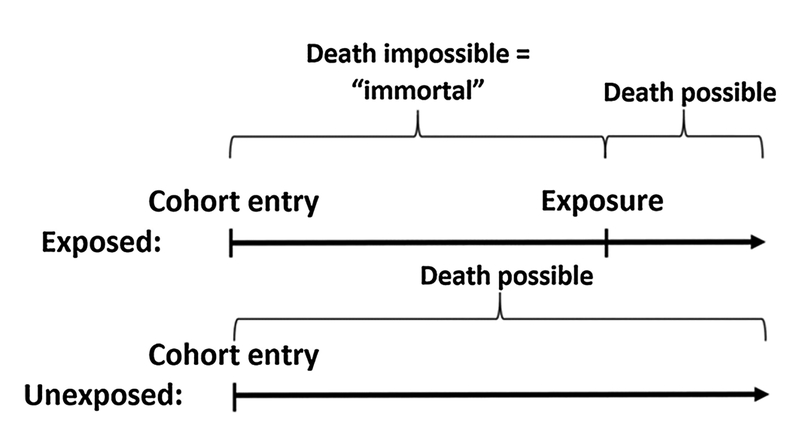
Immortal time bias is pertinent to many observational studies (e.g. studies of statin exposure [6,7]) and has been described in the critical care setting [8,9]. The concept of immortal time bias is illustrated in Fig. 1. When an exposure is defined after the patient enters the cohort, they will be “immortal” from the time of cohort entry until the exposure occurs. Had the patient died within this period of time, they would never have had received the exposure and would therefore have been classified as unexposed. This issue is particularly problematic when early death is common, such as in critical care settings.

Fig. 1.

Immortal time bias. Graphical example illustrating immortal time bias. Due to the way exposure is defined, patients in the exposed group are “immortal” until they receive the exposure. This artificially favors patients in the exposed group, biasing the results.

Immortal time bias can be a problem within post-cardiac arrest research since early death (i.e. within the first hours or days) is common. Consider the use of targeted temperature management (TTM) and a recent study from the American Heart Association’s Get With The Guidelines – Resuscitation registry [10]. In addition to other inclusion/ exclusion criteria, the authors included patients with in-hospital cardiac arrest (IHCA) with return of spontaneous circulation (ROSC). The authors then compared, using propensity score analyses, those patients receiving TTM to those not receiving TTM. However, as is clear from the above, immortal time bias is a concern here. If patients die early (within the first hours after ROSC) they are never at risk of exposure to TTM. Their default classification is the no TTM group. This is supported by the early (< 24 h) mortality in the TTM group of 29% vs. 45% in the no TTM group [10]. This issue would bias the results towards a beneficial effect of TTM. The authors’ main findings were a risk ratio of 0.88 (95%CI: 0.80, 0.97) for survival to hospital discharge favoring the no TTM group. In a sensitivity analysis excluding patients dying within the first 24 h, i.e. partly eliminating immortal time bias since early deaths are excluded, the risk ratio was 0.70 (95CI%: 0.64, 0.77) supporting the suspicion of immortal time bias. Limitations of this approach and methods to better address immortal time bias are presented below. Due to the observational nature of the Chan et al. study, which entails risk of confounding, and other specific limitations [11], these results should be interpreted with caution and are only included as an example.

Immortal time bias is a concern for all post-cardiac arrest interventions that can occur within the first days after ROSC. Coronary angiography is another specific example where immortal time bias is a major concern in observational studies [12,13].

Resuscitation time bias

While immortal time bias is an issue when analyzing post-cardiac arrest interventions in observational studies, a related problem arises when assessing intra-cardiac arrest interventions. This problem, which we term “resuscitation time bias” occurs because interventions during cardiac arrest (e.g. drug administration, endotracheal intubation) are related to time in three ways. First, interventions are more likely to be implemented the longer the duration of the cardiac arrest, i.e. the length of the cardiac arrest is causally related to the intervention. This is intuitively true and can also be shown using empirical data (see for example eFigure 2B in Andersen et al. [14]). Second, once ROSC is achieved or the cardiac arrest is terminated without ROSC, these intracardiac arrest interventions can no longer be performed. Third, these interventions may result in ROSC, thereby potentially shortening the duration of arrest. In fact, hastening ROSC is the clinical rationale for the majority of these interventions. Conversely, an adverse intervention could prolong the duration of arrest.

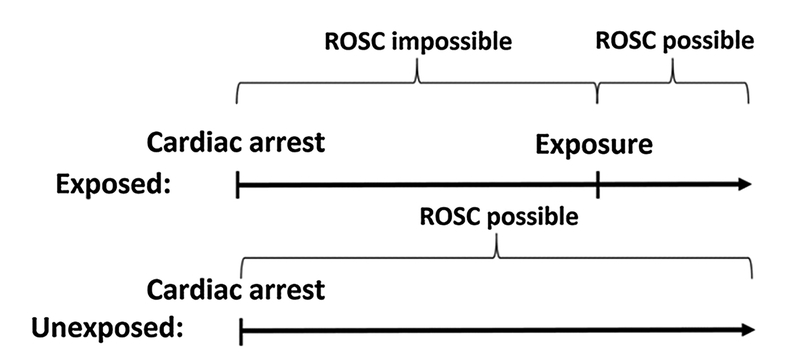
When these factors are considered in combination with the fact that longer duration of cardiac arrest is strongly associated with worse outcomes [3–5], the problem of resuscitation time bias is clear. Resuscitation time bias is conceptually similar to immortal time bias, although with reversed consequences. In the unique situation of cardiac arrest, patients are not “immortal” until they receive the exposure but are mortal (by definition) in the sense that they cannot achieve ROSC during this time period. This concept is illustrated in Fig. 2. Until patients receive the exposure, they cannot have ROSC. If they did, they would be categorized in the unexposed group. Technically, termination of resuscitation is also impossible when ROSC is impossible. However, termination of resuscitation without ROSC is rare in the early stages of cardiac arrest [15] and is generally not recommended within the first 20 min [16]. This therefore likely only plays a minor role.

Fig. 2.

Resuscitation time bias. Graphical example illustrating resuscitation time bias. Due to the way the exposure is defined, patients in the exposed group have longer cardiac arrest. Since longer cardiac arrests are associated with poor outcomes, this artificially favors the unexposed group, biasing the results.

The consequence of resuscitation time bias is that estimates of the effect of intra-cardiac arrest interventions will be biased toward a harmful effect. In short, this is because patients receiving an exposure are more likely to have a longer cardiac arrest (e.g. a patient successfully defibrillated after 2 min will never receive epinephrine) and because longer cardiac arrests are associated with worse outcomes. There is some limited empirical evidence to support this notion. A Japanese study from 2012 examined the association between epinephrine administration and outcomes in OHCA [17]. The authors performed propensity score matching and adjusted for a number of potential confounders. However, they did not account for the timing of epinephrine administration, which is likely to occur late in the OHCA setting in Japan given the nature of their pre-hospital ambulance system [18,19]. Their main result as it relates to 1-month survival was an odds ratio (OR) of 0.46 (95%CI: 0.42, 0.51) indicating worse survival with epinephrine administration. In a subsequent study by a different group using the same Japanese dataset, the authors adjusted for the timing of the epinephrine administration using a method as described in more detail below [20]. Their main results for 1-month survival were an OR of 1.36 (95%CI: 1.13, 1.63) for shockable rhythms and 1.78 (95%CI: 1.49, 2.13) for non-shockable rhythms leading to a profoundly different conclusion [20]. Although there were other differences between the two studies (e.g. patient inclusion/exclusion criteria and the time period of patient inclusion), these findings indicate that accounting for timing of interventions during cardiac arrest is important. Another, although more indirect, example comes from a 2012 study by Olasveengen et al. [21] Using data from a previous randomized clinical trial comparing intravenous drug administration to no intravenous drug administration during OHCA [22], they compared outcomes in patients when epinephrine was actually given to patients who never received epinephrine. Despite the fact that the original randomized trial showed increased admission to hospital with ROSC in the intervention group [22], the observational study found a longer duration of cardiac arrest in the epinephrine group (26 vs. 16 min, p < 0.001) [21] indicating that patients with a longer cardiac arrest are more likely to receive epinephrine and that this can bias the results.

Resuscitation time bias can occur for all interventions during cardiac arrest and especially those where the intervention is given late. The later the intervention is given and the more patients who have early ROSC, the more profound the bias will be. However, the magnitude of the bias is difficult to predict and will depend on other factors such as the strength of the association between duration of cardiac arrest and outcomes. In the next section, we will discuss methods to potentially deal with this issue.

Methods to deal with immortal and resuscitation time bias

There are various methods to deal with the potential biases discussed above. A common and simple method for partly addressing immortal time bias in post-cardiac arrest studies is to restrict the population to those surviving to a certain timepoint after ROSC (e.g. 24 h after ROSC as in the TTM study discussed above [10]). As shown above, this somewhat deals with the problem but is not always an ideal solution since patients who could have potentially benefitted from the intervention might have been excluded. Consider the case of early coronary angiography and percutaneous coronary intervention (PCI) after ROSC. If the cohort is restricted to patients who survived at least 24 h, patients who died without PCI but could have theoretically survived had they received PCI (e.g. a patient in cardiogenic shock due to a large myocardial infarction) are not included. Similarly, patients dying early as a consequence of the PCI (e.g. as a complication to the procedure) are excluded as well. As such, this approach can lead to unpredictable bias.

A related and equally problematic method to deal with resuscitation time bias is to adjust for the length of the cardiac arrest. However, since any intra-cardiac arrest intervention has the potential to causally effect the duration of cardiac arrest as discussed above, this is problematic. The intervention’s effect on the duration of cardiac arrest might mediate an effect on longer-term outcomes such as 30-day survival, i.e. the intervention leads to a shorter cardiac arrest which leads to a better longer-term outcome. By adjusting for a mediator (i.e. the duration of the cardiac arrest), results will be biased towards the null.

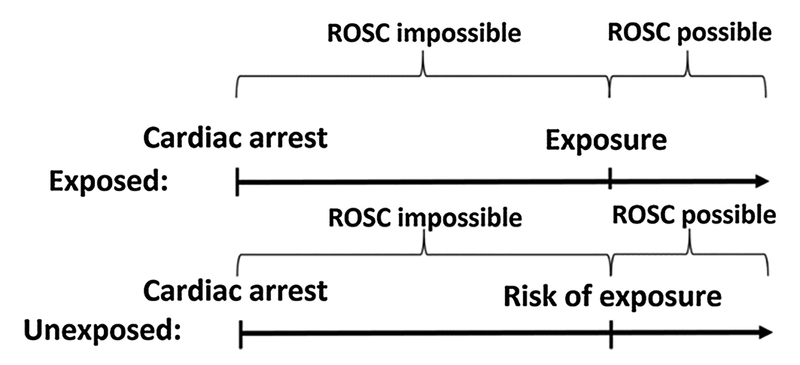
A relatively simple method to deal with both immortal time bias and resuscitation time bias is risk set matching. In traditional matching, an exposed patient is matched (using an algorithm) to a patient not exposed. With risk set matching, an exposed patient is matched to an unexposed patient, who at the time of the exposure in the exposed patient, is at risk of the exposure [23]. This approach (and is illustrated in Fig. 3) will essentially eliminate immortal time bias and resuscitation time bias for an intra-cardiac arrest intervention, provided the timing of the exposure is accurat.

Fig. 3.

Risk set matching. Graphical illustration of risk set matching. By comparing the exposed to unexposed who are at risk of the exposure (i.e. still in cardiac arrest), resuscitation time bias is essentially eliminated.

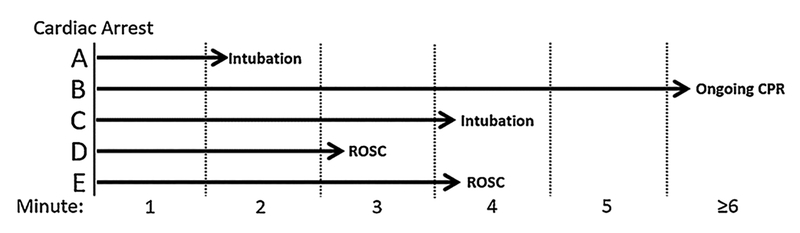
As an example, consider intubation during cardiac arrest [14,24]. Fig. 4 illustrates five hypothetical patients (adopted from Andersen and Donnino [25]). Patient A can be matched with all other patients since they are all at risk of intubation during minute 2, when Patient A is intubated. However, the only patient that patient C can be matched to is patient B, since patient B is the only patient at risk of intubation during minute 4. Patients at risk of intubation at any given minute includes those who are intubated later as the matching should not be dependent on future events [20,23,26]. If at-risk patients only included those never intubated, this would bias the results towards a harmful effect of intubation because those never intubated are more likely to have short duration of cardiac arrest as noted above.

Fig. 4.

Example of risk set matching. See text for details. Adopted with permission from Andersen and Donnino [25].

Because of this approach, the effect estimates obtained after risk set matching are different from those obtained from traditional matching. The effect estimates in this example (a risk ratio) should be interpreted as the risk of intubation at any given minute compared to the risk of no intubation at that given minute. This interpretation also provides a useful clinical interpretation since a clinician is unaware of future events at a given time. The question “Should this patient be intubated right now (as compared to not being intubated right now)?” is therefore of utmost relevance and equivalent to the “intention to treat” principle in clinical trials. However, since the unexposed group is a combination of patients never intubated and intubated later, the effect estimate would more likely be closer to one compared to a randomized trial strictly comparing intubation to no intubation (i.e. a “dilution” of the effect). This corresponds to an “intention to treat” analysis with a great deal of protocol deviations in the “no intubation” group, i.e. patients end up being intubated later. The magnitude of this “dilution” will depend heavily on the prevalence of the exposure. If the exposure is rare, the comparison will approximate exposed vs. never exposed whereas, if the exposure is common, the comparison will approximate exposed now vs. exposed later. While the previous mentioned study on epinephrine in OHCA from Japan [20] is an example of the former, studies by Andersen et al. [14,24] on IHCA intubation are examples of the latter.

Risk set matching deals with immortal time bias and resuscitation time bias, but not with traditional confounders including potential time-varying confounders. Although a detailed description is beyond the scope of the current commentary, a number of methods can be used in conjunction with risk set matching to adjust for potential confounders. Such methods include time-dependent propensity score matching [26] where the propensity score is calculated based on a Cox proportional hazards model [27] which is able to include time-varying covariates [28]. This methodology has been used in several cardiac arrest studies [14,20,24]. Others methods include marginal structural models where inverse probability of treatment weighting is used to account for confounding [29,30]. Importantly, none of these methods adjust for unmeasured confounders and, as always, observational studies should therefore be interpreted with caution.

Lastly, it is important to note that the use of risk set matching and the corresponding methods to deal with (time-varying) confounding require relatively large sample size and granular and accurate data which must include the timing of the exposure (e.g. timing of intubation or coronary angiography) and the timing of ROSC and/or death. Unfortunately, this is often not the case in large cardiac arrest registries which limits the use of these methods and therefore the ability to adjust for immortal time bias and resuscitation time bias. Consequently, registries should include this information if questions related to timedependent interventions are of interest.

Conclusion

This manuscript has discussed immortal time bias and a related bias which we have termed resuscitation time bias. Both are relevant for cardiac arrest research although the latter represents a challenge that is unique to this patient population. Future observational research should aim to address these biases analytically or acknowledge these issues in the limitations when not possible. Hopefully, addressing these biases will provide for a more valid interpretation of observational research and ultimately lead to better treatments and outcomes.