USING DEEP NEURAL NETWORKS FOR RADIOGENOMIC ANALYSIS

Abstract

Radiogenomic studies have suggested that biological heterogeneity of tumors is reflected radiographically through visible features on magnetic resonance (MR) images. We apply deep learning techniques to map between tumor gene expression profiles and tumor morphology in pre-operative MR studies of glioblastoma patients. A deep autoencoder was trained on 528 patients, each with 12,042 gene expressions. Then, the autoencoder’s weights were used to initialize a supervised deep neural network. The supervised model was trained using a subset of 109 patients with both gene and MR data. For each patient, 20 morphological image features were extracted from contrast-enhancing and peritumoral edema regions. We found that neural network pre-trained with an autoencoder and dropout had lower errors than linear regression in predicting tumor morphology features by an average of 16.98% mean absolute percent error and 0.0114 mean absolute error, where several features were significantly different (adjusted p-value < 0.05). These results indicate neural networks, which can incorporate nonlinear, hierarchical relationships between gene expressions, may have the representational power to find more predictive radiogenomic associations than pairwise or linear methods.

1. INTRODUCTION

Molecular profiling of aggressive tumors such as glioblastoma (GBM) require invasive surgery that is not always possible when tumors are near eloquent areas. Medical imaging, which is routinely collected, may provide an alternative approach to infer underlying molecular traits from imaging alone. Radiogenomic studies have suggested that biological heterogeneity is reflected radiographically through visible features on magnetic resonance (MR) imaging as enhancement patterns, margin characteristics, and shapes in GBM [1–4], liver [5], lung [6], and breast [7,8] cancer. These works show it may be possible to identify imaging-derived features that provide information about the underlying tumor biology. However, current radiogenomic studies use methods that do not fully represent the nonlinear relationships in gene expression [7]. Studies may also limit the scope of features to consider due to the high-dimensionality of radiogenomic data. For example, studies often perform feature selection [1, 4] or dimension reduction [3] prior to modeling. Neural networks such as multilayer perceptrons support hierarchical, nonlinear relationships and facilitates generation of complex features from high-dimensional input. Recently, the development of deep learning has enabled the training of deep neural networks that are scalable and have outperformed other methods in several common machine learning tasks [9] due to recent improvements in hardware and training procedures [10].

In -omics, various deep learning techniques have recently been applied to biological tasks, including convolutional neural networks [11], restricted Boltzmann machines and deep belief networks [12, 13], general deep neural networks [14], and autoencoders [15]. The motivation for using deep learning has been due to their ability to interpret low-level, high-dimensional data into features relevant for some prediction task.

In this work, we explore the use of deep neural network models to generate radiogenomic association maps between tumor gene expression profiles and their morphological appearance in MR images of GBM patients. Given their representational capacity, we hypothesize that neural networks may discover more predictive radiogenomic associations than current pairwise association or linear methods [1–4, 6–8].

2. METHODS

2.1. Datasets

2.1.1. Tumor gene expression

The GBM cohort contained 528 patients with untreated, primary tumor samples from The Cancer Genome Atlas (TCGA). The cohort’s gene expression profiles were produced by the Broad Institute using Affymetrix microarrays. Level 3 data were obtained from National Cancer Institute’s Genomic Data Commons; quantile normalization and background correction were already performed. Each expression profile had 12,042 genes, where each gene was standardized by subtracting its mean and dividing by its range.

2.1.2. Pre-operative imaging

Of the 528 patients, 109 had pre-operative MR imaging consisting of T1-weighted with contrast (T1WI+c), fluid-attenuated inversion recovery (FLAIR), and/or T2-weighted images (T2WI). Of these, 90 were segmented by raters from the Multimodal Brain Tumor Segmentation Challenge [16]. Briefly, images were co-registered to each patient’s T1WI+c, linearly interpolated to 1 mm³, and skull-stripped. Region-of-interests (ROIs) were manually segmented by 1–4 raters and approved by board-certified neuroradiologists. ROIs represent 3-dimensional volumes of two regions: contrast-enhancement from T1W1+c and peritumoral edema from FLAIR or T2WI. We segmented ROIs following a similar process via 1–4 trained raters for 19 cases, see Figure 1a.

Fig. 1.

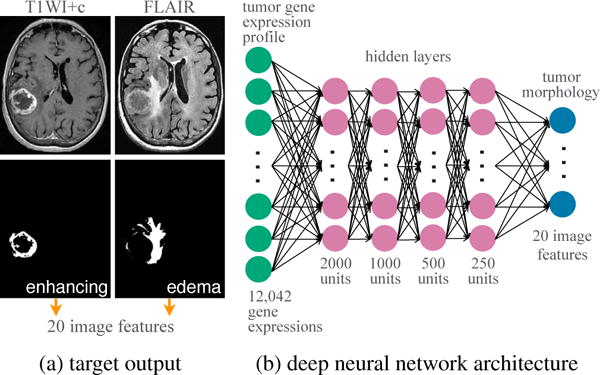
Modeling radiogenomics with a deep neural network. MR studies were segmented into two 3-dimensional ROIs.

For each ROI, 10 image-derived features were calculated and taken from [17–19], see Table 1. Morphological traits are commonly recognized as clinically indicative of tumor aggressiveness and are similar to previous radiogenomic studies [1–4, 6]. Features were calculated from the largest contiguously segmented area for each ROI using Matlab R2015b. Since image features had different ranges and units (e.g., volume versus sphericity), each feature was scaled by dividing by its maximum value.

Table 1.

Image features.

feature	description
volume (V)	volume by [18]
surface area (SA)	surface area by [18]
SA:V ratio	SA to V ratio: SA/V
sphericity	proximity to a sphere: $\frac{{\pi }^{3/2}{(6V)}^{2/3}}{SA}$ has values (0,1], where 1 is a perfect sphere
spherical disproportion	proximity from a sphere: $\frac{SA}{4\pi {[{(3V/4\pi )}^{1/3}]}^2}$ has values ≥ 1, where 1 is a perfect sphere
max diameter	max distance between any two voxels
major axis	largest major axis on axial slices
minor axis	minor axis to the major axis
compactness 1	proximity to the compactness of a perfect sphere: $V/\sqrt{\pi S{A}^3}$, has values (0, 0.053]
compactness 2	proximity to the compactness of a perfect sphere: 36πV2/SA3, has values (0, 1]

2.2. Radiogenomic neural network

2.2.1. Overall approach

The radiogenomic neural network, shown in Figure 1b, was trained in two phases: 1) pre-training with a deep autoencoder and 2) supervised learning with a deep neural network. All neural networks were fully connected, feed-forward models. We tuned the following hyperparameters: learning rate, decay, momentum, type of loss function, type of nonlinear activation function, and dropout [10]. Batch size was set to 10 and number of epochs to 200 for all models. Neural networks were optimized with stochastic gradient descent and trained using Keras [20] and Tensorflow [21] on a Nvidia GRID K520 GPU on Amazon Web Services. Implementation details, e.g., loss function and dropout, are defined in [20,21].

2.2.2. Deep autoencoder

An autoencoder is a neural network that is commonly used to compress data into smaller representations [22]. Here, each gene expression profile was an input. Both the input and output layers had 12,042 units. The model contained five sequential hidden layers with 2000, 1000, 500, 1000, and 2000 units, respectively. The model was trained using 528 gene expression profiles. The following hyperparameters were considered: five learning rates from 0.001 to 0.25; four decay factors from 0.01 to 1e⁻⁵; 0.2 momentum; mean squared error as the loss; and hyperbolic tangent and sigmoid activations.

2.2.3. Deep neural network

To learn radiogenomic associations, a deep neural network was trained using 109 patients with gene expression data and pre-operative MR studies. The model contained 12,042 input units, 20 output units, and four hidden layers, see Figure 1b. The first three hidden layers were initialized with the weights of the encoding layers transferred from the trained deep autoencoder. The following hyperparameters were considered: eighteen learning rates from 0.005 to 0.35; five decay factors from 0.01 to 1e⁻⁵; 0.5 momentum; dropout of 0.25 in the input and first three hidden layers; mean absolute error as the loss; and rectifier linear unit as the activation function. Network weights and biases were further constrained to be nonnegative to ensure predictions were also nonnegative.

2.2.4. Image feature prediction

Given a tumor’s gene expression profile (a vector of 12,042 genes), the deep neural network was given the task to simultaneously predict 20 image features corresponding to the tumor morphology of the enhancing and edema regions.

2.3. Linear regression

Regularized linear regression with L₁ and/or L₂ was used to predict a single image feature from gene expression data. Thus, 20 regression models were created. For each model, a combination of 4000 λ values and 21 α values were searched using the R package glmnet [23].

2.4. Evaluation

Models were evaluated using 10-fold cross-validation, which was repeated for the selection of hyperparameters when multiple values were considered. The hyperaparameters with the lowest average validation loss was selected.

For the deep autoencoder, its selected hyperparameters were used to retrained on all 528 gene expression profiles prior to being transferred to the deep radiogenomic neural network. In addition to the deep radiogenomic neural network that included the deep autoencoder (pre-training) and dropout, its selected hyperparameters were also used to train two more neural networks for comparison: 1) a neural network without pre-training and 2) a neural network with pre-training. For linear regression, λ and α were selected via R² in validation folds and intercept-only models were ignored.

Performance errors were calculated as the difference between the reference value of an image feature, y_i (e.g., measured volume of edema) and the predicted value by a model, ${\widehat{y}}_i$ (e.g., predicted volume of edema) in the 10 validation folds. Error was averaged over all N patients using mean absolute error (MAE) and mean absolute percent error (MAPE):

$$\mathit{MAE}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|y_i-{\widehat{y}}_i\right|},$$ (1)

$$\mathit{MAPE}=\frac{100\mathrm{\%}}{N}{\displaystyle \sum _{i=1}^N\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|.}$$ (2)

Statistical differences in prediction errors between neural network and linear regression models were obtained using a paired Wilcoxon signed-rank test with continuity correction and an α level of 0.05. The test was carried out for each image feature in R, where p-values were adjusted using the Bonferroni correction method ( p.adjust).

3. RESULTS

3.1. Overall performance

The deep autoencoder achieved optimal performance with the selected hyperparameters of 0.2 learning rate, 1e⁻⁵ decay, and the hyperbolic tangent as the activation function, producing 0.014 loss (mean squared error) after retraining. The deep neural network with pre-training and dropout was optimal when learning rate was 0.3 and decay was 5e⁻⁵; the mean training and validation losses (mean absolute error) were respectively 0.107 and 0.134, see Figure 2. Similarly, the mean training and validation losses were 0.021 and 0.143 for the neural network without pre-training and 0.022 and 0.146 for the neural network with pre-training.

Fig. 2.

Neural network learning curves from 10-fold cross-validation using selected hyperparameters.

On average, all neural networks had lower error than linear regression as measured by MAE and MAPE (see Table 2), where some features were significantly different, see Figure 3. A neural network pre-trained with a deep autoencoder and dropout had the lowest average MAE and the lowest average MAPE. This model was able to predict 80% and 100% more features at lower MAE and MAPE and had lower error than linear regression by 16.98% MAPE and 0.0114 MAE.

Table 2.

Overall performance.

pre-train:	neural network			linear regression
	no	yes	yes+drop
average MAE	0.1427	0.1455	0.1342	0.1456
average MAPE	68.32	69.47	52.53	69.51
features MAE†	11 (55%)	10 (50%)	16 (80%)	reference
features MAPE†	8 (40%)	7 (35%)	20 (100%)	reference

^†denotes the number (percent) of image features with lower error than linear regression.

Fig. 3.

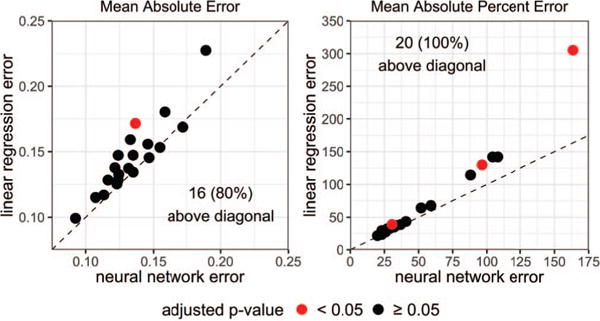
Predicting image features (dots) from gene expressions. The diagonal line indicates equal error. Dots above the line occur when neural network (with pre-training and dropout) error was lower than linear regression error.

3.2. Mean absolute error analysis

To interpret MAE in real physical dimensions, MAE was converted back to each image features’ original units in mm or cm in Table 3. The neural networks achieved the lowest MAE in 0, 2, and 15 features for models with no pre-training, with pre-training, and with pre-training and dropout, respectively. Linear regression outperformed neural networks in 3 features.

Table 3.

Scaled mean absolute error. All values were scaled back into original units in mm or cm.

	pre-train:		neural network			linear regression	measured values
			no	yes	yes+drop		min	max	mean
enhancing ROI	volume	cm3	16.8	17.2	16.3	16.2	1.0	111.2	29.3
	surface area	cm2	66.7	70.4	61.9	70.2	7.5	509.4	120.7
	SA:V ratio		0.136	0.141	0.130	0.140	0.218	1.214	0.456
	sphericity		0.134	0.132	0.124	0.133	0.128	0.851	0.434
	spherical disprop.		0.81	0.83	0.72	0.78	1.17	7.82	2.63
	max diameter	mm	14.2	14.7	13.2	14.4	20.3	97.7	57.6
	major axis	mm	15.4	15.9	13.8†	17.4	17.1	101.3	54.9
	minor axis	mm	11.5	11.9	10.6	10.4	11.9	61.5	34.8
	compactness 1		0.0072	0.0071	0.0066	0.0075	0.0024	0.0417	0.0159
	compactness 2		0.090	0.092	0.082	0.098	0.002	0.617	0.114
edema ROI	volume	cm3	37.6	38.3	37.1	44.6	4.9	196.1	69.8
	surface area	cm2	87.9	93.7	86.7	95.5	29.0	744.0	224.4
	SA:V ratio		0.142	0.145	0.128	0.127	0.145	0.828	0.387
	sphericity		0.089	0.085	0.087	0.090	0.179	0.700	0.370
	spherical disprop.		0.76	0.78	0.69	0.82	1.43	5.58	2.93
	max diameter	mm	16.5	16.9	15.3	16.3	36.6	123.1	88.3
	major axis	mm	16.5	17.6	16.0	16.3	33.0	129.8	86.6
	minor axis	mm	11.9	12.3	11.4	11.9	14.2	86.5	42.2
	compactness 1		0.00421	0.00416	0.00419	0.00417	0.00402	0.03105	0.0123
	compactness 2		0.0407	0.0392	0.0388	0.0400	0.0058	0.3426	0.063

^†adjusted p-value < 0.05.

Some differences were small between the two types of models. For example, predictions for the enhancing ROI’s maximum diameter differ by about 1 mm. On the other hand, neural networks were able to predict edema volume by an average of 7.5 cm³ more accurately than linear regression. However, the two models’ errors were only significantly different from each other when predicting the major axis of the enhanced ROI, also see Figure 3.

Several image features were challenging to predict by either model types. For example, linear regression had lower MAE in predicting enhancing volume but was still off by an average of 16.2 cm³ from the measured value. Note that the mean enhancing volume was 29.3 cm³.

3.3. Mean absolute percent error analysis

Neural networks achieved the lowest MAPE in predicting 0, 0, and 20 of the image features for the neural networks with no pre-training, with pre-training, and with pre-training and dropout, respectively (see Table 4). Linear regression under-performed neural networks in predicting all 20 features, where the enhancing ROI’s major axis and compactness 2 and the edema ROI’s volume were found to be significantly different, also see Figure 3.

Table 4.

Mean absolute percent error.

	pre-train:	neural network			linear regression
		no	yes	yes+drop
enhancing ROI	volume	154.9	156.6	104.2	141.9
	surface area	122.0	131.1	88.1	114.4
	SA:V ratio	31.0	32.6	28.6	32.3
	sphericity	37.3	37.0	31.5	36.0
	spherical disprop.	33.2	35.2	27.1	32.3
	max diameter	30.7	32.2	26.2	29.4
	major axis	36.5	37.7	30.6†	39.1
	minor axis	45.2	44.6	36.8	38.6
	compactness 1	66.3	64.6	51.9	64.3
	compactness 2	273.3	269.8	163.5†	305.1
edema ROI	volume	114.7	120.7	96.5†	129.9
	surface area	66.4	70.6	59.0	67.6
	SA:V ratio	42.0	43.8	33.8	37.4
	sphericity	27.4	26.3	25.9	27.3
	spherical disprop.	27.8	28.7	23.2	29.5
	max diameter	22.7	23.4	19.9	21.6
	major axis	24.7	26.5	22.9	23.4
	minor axis	36.0	37.9	32.1	34.8
	compactness 1	43.3	42.7	40.8	43.4
	compactness 2	131.1	127.3	108.0	141.9

^†adjusted p-value < 0.05.

Neural networks were able to predict the maximum diameter most accurately, achieving on average an error of just under 20% from the measured values. In analyzing the most incorrect predictions, neural networks had a MAPE over 100% for 3 features (both ROI’s compactness 2, and enhancing ROI’s volume), indicating that its prediction was often over- or underestimated. The linear regression model had a MAPE over 100% in 5 features.

4. DISCUSSION

We presented a novel approach to radiogenomic analysis utilizing autoencoders and deep neural networks, comparing their prediction error against linear regression. On average, neural networks had lower error than linear regression in predicting the morphology of enhancing and peritumoral edema in pre-operative MR images. A neural network pre-trained with a deep autoencoder and dropout was able to predict 16 image features with lower absolute error, where 1 feature was significantly different (adjusted p < 0.05) from linear regression’s predictions. This neural network also predicted all image features with lower absolute percent error, where 3 features were significantly different. We plan to apply activation maximization on our trained neural network models to identify specific gene expressions that were influential in the change of an image feature. Once these associations are found, image features can act as suggorates to infer the pattern of gene expressions that may be present in a tumor.

Our experiments indicated neural networks were better at determining the relative magnitude of an image feature, where the neural network’s MAPE was consistently the lowest. For example, neural networks was able to predict on average 8.5% closer to each patient’s measured enhancing ROI’s major axis length than linear regression, where differences were significant. Thus, neural networks can better differentiate small major axis lengths from large ones. Additionally, the inclusion of dropout always produced lower MAPE compared to the other two neural networks, suggesting their continued use in radiogenomic neural networks.

Previous radiogenomic studies utilized general linear models [3, 7, 8]. [3] used a similar dataset as ours to performed pair-wise association analysis between gene modules and MR features of 55 GBM patients. The MR features were based on 2-dimensional ROIs from a single slice, while the gene modules were co-expressed genes created from multiple types of molecular data. The authors reported the length measurements (size and minor axis) of the enhanced and edema ROIs as significantly correlated a gene module. In [1], the authors also reported a significant association between tumors with high enhancement and a gene module containing genes related to hypoxia in 22 GBM patients. A direct comparison between these findings and our model’s radiogenomic associations found via activation maximization is a part of future work. In comparison, we applied deep neural networks to perform both genomic feature generation and image feature prediction in one model.

A major limitation of this work was the sample size due to the small number of annotated pre-operative imaging studies with microarray data. Increasing the sample size with the added 19 patients segmented by our lab improved MAE by about a third in neural networks and a half in linear regressions. We also did not assess whether pre-training with an autoencoder was better than other types of dimensionality reduction methods (e.g., principal component analysis or gene module creation); this is part of future work. Similarly, we selected the hyperparameters based on the neural network with pre-training and dropout; there may have been other optimal hyperparameter for the later two models. While this study focuses on morphological features, other image features (e.g., radiomics) or ROIs (e.g., necrosis) could have been used. This study was also limited to comparing prediction performance between two different models. Other models, such as gradient boost trees should be evaluated.