Orbital shape in intentional skull deformations and adult sagittal craniosynostoses

Abstract

Intentional cranial deformations are the result of external mechanical forces exerted on the skull vault that modify the morphology of various craniofacial structures such as the skull base, the orbits and the zygoma. In this controlled study, we investigated the 3D shape of the orbital inner mould and the orbital volume in various types of intentional deformations and in adult non‐operated scaphocephaly – the most common type of craniosynostosis – using dedicated morphometric methods. CT scans were performed on 32 adult skulls with intentional deformations, 21 adult skull with scaphocephaly and 17 non‐deformed adult skulls from the collections of the Muséum national d'Histoire naturelle in Paris, France. The intentional deformations group included six skulls with Toulouse deformations, eight skulls with circumferential deformations and 18 skulls with antero‐posterior deformations. Mean shape models were generated based on a semi‐automatic segmentation technique. Orbits were then aligned and compared qualitatively and quantitatively using colour‐coded distance maps and by computing the mean absolute distance, the Hausdorff distance, and the Dice similarity coefficient. Orbital symmetry was assessed after mirroring, superimposition and Dice similarity coefficient computation. We showed that orbital shapes were significantly and symmetrically modified in intentional deformations and scaphocephaly compared with non‐deformed control skulls. Antero‐posterior and circumferential deformations demonstrated a similar and severe orbital deformation pattern resulting in significant smaller orbital volumes. Scaphocephaly and Toulouse deformations had similar deformation patterns but had no effect on orbital volumes. This study showed that intentional deformations and scaphocephaly significantly interact with orbital growth. Our approach was nevertheless not sufficient to identify specific modifications caused by the different types of skull deformations or by scaphocephaly.

Introduction

Intentional cranial deformation was a ubiquitous cultural practice especially prevalent in pre‐Columbian civilizations of Central and South America (Dingwall, 1931; Tiesler, 2014). Intentional cranial deformation consisted in modifying the shape of the skull vault using compressive devices such as tight bandages and/or wooden plates or flat stones, applied at least during the first year of life (Dingwall, 1931; Dembo & Imbelloni, 1938). Two subtypes of intentional cranial deformations are commonly described: anteroposterior deformations and circumferential deformations (Fig. 1).

Figure 1.

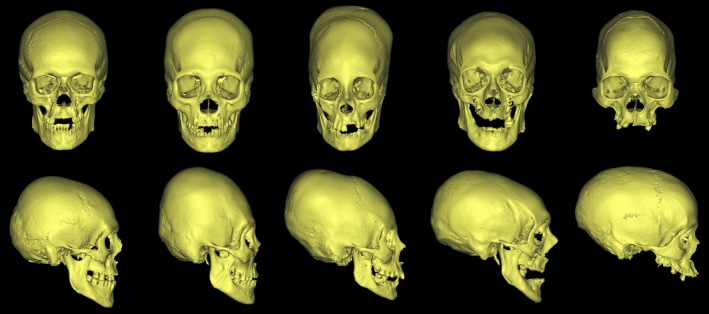
Frontal (upper row) and lateral (lower row) views of the five groups of skulls included in the study. From left to right: non‐deformed skull, antero‐posterior deformation, circumferential deformation, Toulouse deformation and adult scaphocephaly.

Non‐intentional cranial deformations can result from abnormal external mechanical constraints, such as in posterior positional plagiocephaly due to the supine sleep position recommended for newborns (Dec & Warren, 2011). Non‐intentional cranial deformations can also result from congenital disorders affecting the craniofacial skeleton, such as craniosynostoses. Craniosynostoses are defined by the premature fusion of one or more craniofacial sutures. The most common type of craniosynostosis is scaphocephaly, due to the premature isolated fusion of the sagittal suture (Twigg & Wilkie, 2015).

The case of Toulouse deformations – a type of induced cranial deformation from southwestern France resembling circumferential deformations in shape – is problematic, as these deformations may have been secondary to the practice of ‘bandeau’ and not strictly intentional (Dingwall, 1931). Practising the ‘bandeau’ consisted in tightly wrapping and padding the head of newborns, most probably in order to prevent trauma. In this study, we considered Toulouse deformations as intentional cranial deformations.

In previous studies by our group, we demonstrated the influence of intentional cranial deformation on the thickness of the skull vault (Khonsari et al. 2013), the position of the zygoma (Ketoff et al. 2017), the structure of the skull base (Cottin et al. 2017) and the shape of the orbits and maxillary sinuses (Khonsari et al. 2013) by developing orbital cephalometry approaches and orbital volume measurement methods (Nyström et al. 2011; Khonsari et al. 2013, 2016; Nysjö, 2016; Levasseur et al. 2017). The growth correlations between the skull and the face are acknowledged by maxillofacial and craniofacial surgeons in daily clinical practice, but limited scientific data support these interactions (Enlow, 1968; Lieberman, 2011). More precisely, we have little understanding of how the mechanical constraints are transmitted from the vault to the face (Ketoff et al. 2017).

The aim of this study was to investigate the influence of various types of intentional and non‐intentional cranial deformations on orbital growth in order to explore the integration between the two functional modules formed by the brain/braincase and the eye/orbit (Enlow, 1968; Lieberman, 2011).

Materials and methods

The study sample consisted of 32 adult skulls with intentional cranial deformation, 21 adult skulls with sagittal suture craniosynostosis and 17 adult non‐deformed skulls. All skulls were part of the collections of the Muséum national d'Histoire naturelle (Musée de l'Homme) in Paris.

Intentional cranial deformations were divided into three groups: Toulouse deformations (six skulls), circumferential deformations (eight skulls) and antero‐posterior deformations (18 skulls). This classification followed previous definitions of circumferential and antero‐posterior deformations (Antón, 1989; Cheverud et al. 1992; Kohn et al. 1993). All antero‐posterior and circumferential deformed skulls were from Bolivia. All Toulouse deformations were from southwestern France (see Cottin et al. 2017 for sample details). Non‐deformed skulls were sampled from the same two regions. Information on gender was generally not available and therefore not taken into account. Age data were not available; nevertheless, all skulls had fused spheno‐occipital synchondroses and were thus from adult individuals. All skulls with craniosynostosis had non‐syndromic scaphocephaly due to an isolated premature fusion of the sagittal suture. Other conditions affecting the bone and taphonomical deformations were ruled out based on a palaeopathological assessment of every skull.

CT scans of skulls with intentional cranial deformations and non‐deformed skulls had already been acquired for a previous study, using a standard medical CT scan protocol adapted to dry skulls (Badawi‐Fayad et al. 2005; Khonsari et al. 2013). CT scans for skulls with scaphocephaly were performed at the Radiology Department of the Ambroise Paré Hospital in Boulogne, France. A United Healthcare Facial skeleton multi‐detector computed tomography device was used with a tube voltage at 120 kV and a tube current of 300 mAs, an acquisition matrix of 512 512 and a 230‐mm display field‐of‐view. Each CT scan was reconstructed with a slice thickness of 0.33 mm using ultra‐high‐resolution mode. All orbits were segmented using a previously described semi‐automatic segmentation technique based on deformable models and haptic interaction (Nyström et al. 2011; Khonsari et al. 2013, 2016; Nysjö, 2016). The mean orbital size and shape models for all groups were automatically generated from the segmented orbits through registration‐based landmarking (Frangi et al. 2002). In brief, we used iterative closest point (ICP) registration (Besl & McKay, 1992) and free‐form deformation (Rueckert et al. 1999; Schnabel et al. 2001) to establish landmark correspondences on the orbits, followed by Procrustes alignment (Goodall, 1991) of the landmarks in order to obtain the mean size and shape. Further details about the shape model generation are provided in Levasseur et al. (2017).

We compared the mean and individual orbits vs. mean orbits from varying reference groups (non‐deformed and all other groups) by alignment, computation and visualization of the surface‐to‐surface distance and spatial overlap using colour‐coded distance maps and semi‐transparent overlays. Quantification of shape discrepancy was obtained by computing the mean absolute distance (MAD), the maximum absolute distance – or Hausdorff distance (HD) (Aspert et al. 2002), and the Dice similarity coefficient (DSC) (Zou et al. 2004). These parameters have been previously used for the characterization of the orbital shape in various craniofacial deformations and malformations (Khonsari et al. 2016; Levasseur et al. 2017).

MAD indicates how similar two aligned orbits A and B are on average. For instance, if the MAD between A and B is 1.5 mm, then every point on A is located on average 1.5 mm from the closest point on B (Supporting Information Fig. S1, first row). The Hausdorff distance represents the largest distance between two corresponding points on the orbits and is useful for detecting local shape deviations. If both the MAD and the Hausdorff distance are small, then the orbits are on average similar to each other, but they may have local shape deviations. If both the MAD and the Hausdorff distance are large, then the orbits differ substantially in shape and/or size (Fig. S1, second row). The DSC complements the distance measures by providing a spatial (volume) overlap index between two orbits. This overlap index is useful for assessing global shape similarity and symmetry. DSC values range from 0 (no overlap) to 1 (complete overlap), higher values indicating higher shape similarity (Fig. S1, third row).

From a statistical point of view, the specificity of MAD, HD and DSC was that these parameters were by definition comparisons with reference values (here, non‐deformed skulls), as they quantified the distance between a specific deformed orbit and a control, non‐deformed, mean orbit. All statistical tests were thus performed on groups of ‘distances to normal values’ and assessed whether a specific deformation type (for instance Toulouse) was less or more distant from non‐deformed orbits compared with a specific group (for instance, circumferential). We used a hierarchical linear model to take into account two measurements per individual (left and right orbits) and therefore the measures were not independent. A random effect on the intercept was introduced on the individual. The coefficients associated with each of the five groups (antero‐posterior, circumferential, Toulouse, scaphocephaly and non‐deformed) were compared, as well as the covariances. Model comparisons were made using maximum likelihood studies and the Akaike information criterion (AIC)/Bayesian information criterion (BIC). The five groups were compared by changing the reference class successively. The model parameters were compared with zero (the null hypothesis) using Student tests. Histograms were computed for each variable of interest (DSC, HD and MAD) and for each reference group. Left–right symmetry and orbital volumes were also studied, and the coefficients associated with each deformation group were compared. Hypotheses of normality and homoscedasticity of errors were verified. We did not take the inflation of the alpha risk into account when changing the reference class. The analyses were carried out with r (R Core Team, R Foundation for Statistical Computing, Vienna, Austria, 2017, https://www.R-project.org) and two specific packages were used: (i) nlme for mixed models (Pinheiro et al. 2018) and (ii) ggplot2 for plots (Wickham, 2009).

We performed two cephalometric measurements to assess skull height and skull length. Skull length was approximated using the distance between (i) the three‐dimensional (3D) Enlow point M (mid‐M), which corresponded to the mid‐point of the left and right junctions of the frontal, nasal and maxillary bones (Lee et al. 2014) and (ii) the intersection of the two lambdoid sutures (Supporting Information Figs S2 and S3). Skull height was approximated using the C3 line as defined in Delaire's cephalometric analysis, a standard analysis used in orthodontics and orthognathic surgery (Lee et al. 2014). To measure skull height C3, we first traced C2 as the line segment passing through Mid‐Cp, the midpoint of the left and right posterior condylar (Cp) points and bounded by the two following endpoints: (i) previously defined mid‐M and (ii) the occipital inferior point (Oi). C3 was the line segment of the perpendicular bisector of C2 bounded by: (i) the midpoint of C2 and (ii) the intersection of the perpendicular bisector of C2 with the external table of the skull vault (Sc) (Lee et al. 2014). We then used skull length and skull height to compute an index reflecting cranio‐orbital proportions [(skull length × skull height)/orbital volume] and compared the values of this index in different deformation groups with values from the non‐deformed group using a multivariate model.

Results

Raw data – volume measurements, morphological assessment using DSC, MAD and HD and symmetry assessment using DSC – are provided in Supporting Information Table S1.

Volume measurements

Orbital volumes were measured in all groups. Left and right orbital volumes were considered as dependent variables. We could not show volume differences between scaphocephaly and non‐deformed skulls, between Toulouse deformations and non‐deformed skulls or between scaphocephaly and Toulouse deformations. The orbital volume in circumferential deformations and antero‐posterior deformations was significantly smaller than in non‐deformed skulls (Table 1 and Fig. 2). Furthermore, orbital volumes in circumferential deformations were significantly smaller than in antero‐posterior deformations (Supporting Information Table S2).

Table 1.

Orbital volume values for non‐deformed (ND) skulls, intentional deformations and scaphocephaly

	Value	SE	P‐value
ND	27.387046	0.8414094	NA
S	27.22637	1.1318516	0.8876
C	21.09555	1.4874157	<0.001a
AP	22.53344	1.1732893	<0.001a
T	24.779	1.6473870	0.1182

AP, antero‐posterior deformations; C, circumferential deformations; NA, not applicable; ND, non‐deformed skulls; S, scaphocephaly; SE, standard error; T, Toulouse deformations.

The P‐value stands for the comparison of the volume of all the groups with non‐deformed skulls.

^aSignificantly different from non‐deformed skulls.

Figure 2.

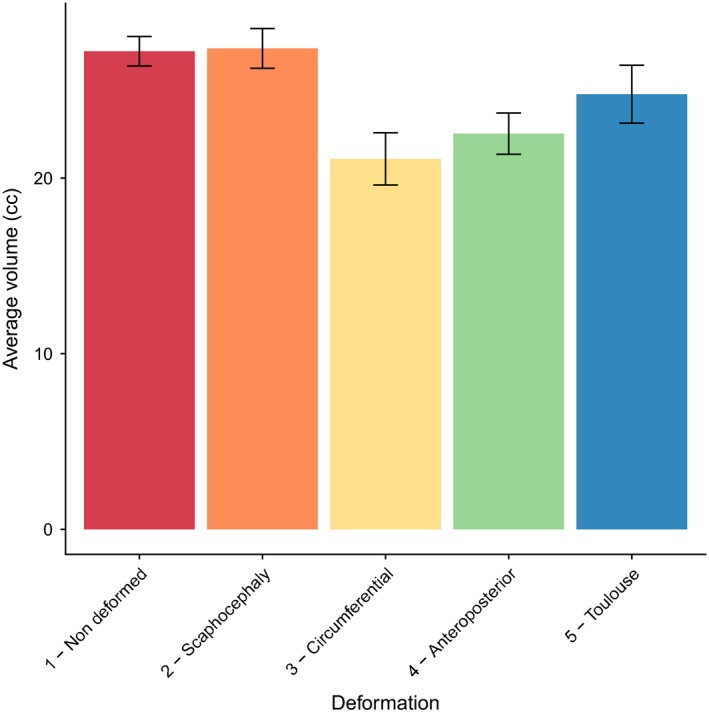
Average orbital volumes in intentional deformations and adult scaphocephaly. The volume was significantly smaller than in non‐deformed skulls for the antero‐posterior and circumferential deformation groups. Volume values in mL. The results of the statistical tests comparing groups are given in Table 1.

Orbital morphology

DSC, MAD and HD were computed for each deformation group taking each other group as a reference. The results when non‐deformed orbits were considered as a reference are provided in Fig. 3 and Tables 2, 3, 4. The results when the other groups were chosen as references have less obvious interpretations and are provided for information in Supporting Information Figs [Link], [Link], [Link], [Link] and Table S3.

Figure 3.

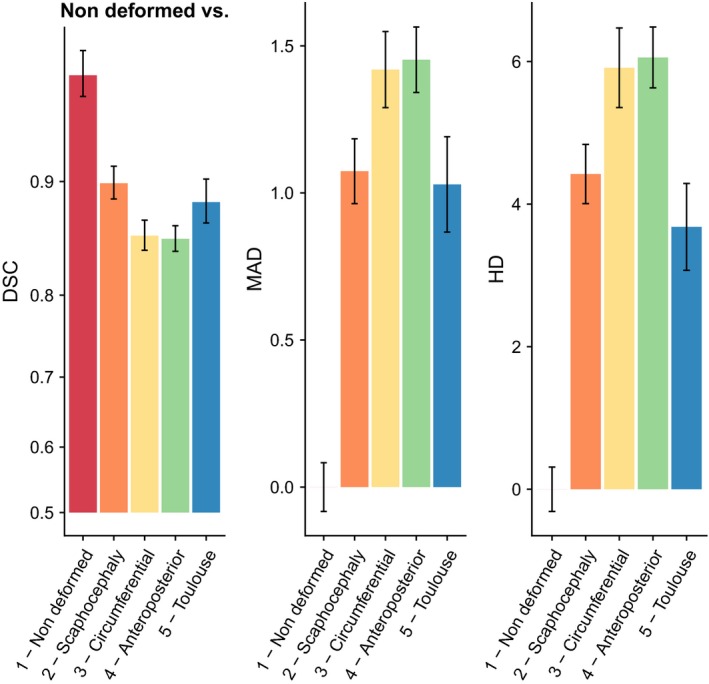
Orbital morphology in intentional deformations and adult scaphocephaly. Dice similarity coefficient (DSC), mean absolute distance (MAD) and Hausdorff distance (HD) computed with non‐deformed skulls taken as a reference. DSC, MAD and HD revealed a similar pattern of orbital modifications: orbits in intentional deformations and adult scaphocephaly were significantly different than those of control skulls but neither antero‐posterior and circumferential deformations or Toulouse deformations and scaphocephaly were significantly different. The results of the statistical tests comparing groups are given in Tables 2, 3, 4.

Table 2.

Comparison of Dice similarity coefficient (DSC) values with non‐deformed (ND) skulls taken as a reference; P‐values. For instance, P = 0.862 refers to the comparison of DSC(T‐ND) with DSC(S‐ND). Same abbreviations as in Table 1

	ND	S	C	AP	T
ND	NA	–	–	–	–
S	<0.001*	NA	–	–	–
C	<0.001*	0.002*	NA	–	–
AP	<0.001*	<0.001*	0.764	NA	–
T	<0.001*	0.862	0.014*	0.005*	NA

S, Scaphocephaly.

Table 3.

Comparison of mean absolute distance (MAD) values with non‐deformed skulls taken as a reference; P‐values. For instance, P = 0.776 refers to the comparison of MAD(T‐ND) with MAD(S‐ND). Same abbreviations as in Table 1

	ND	S	C	AP	T
ND	NA	–	–	–	–
S	<0.001*	NA	–	–	–
C	<0.001*	0.007*	NA	–	–
AP	<0.001*	<0.001*	0.716	NA	–
T	<0.001*	0.776	0.026*	0.009*	NA

S, Scaphocephaly.

Table 4.

Comparison of Hausdorff distance (HD) values with non‐deformed skulls taken as a reference; P‐values. For instance, P = 0.214 refers to the comparison of HD(T‐ND) with HD(S‐ND). Same abbreviations as in Table 1

	ND	S	C	AP	T
ND	NA	–	–	–	–
S	<0.001*	NA	–	–	–
C	<0.001*	0.007*	NA	–	–
AP	<0.001*	<0.001*	0.773	NA	–
T	<0.001*	0.214	0.002*	<0.001*	NA

S, Scaphocephaly.

For instance, in Table 2, P = 0.002 corresponded to the test comparing the DSC between circumferential deformations and non‐deformed skulls [DSC(C‐ND)] vs. the DSC between scaphocephaly and non‐deformed skulls [DSC(S‐ND)]. The difference between these two distances was significant. We found that the absolute value of DSC(S‐ND) was 0.9058, which is closer to 1 than 0.8579, which was the absolute value of DSC(C‐ND) (Table S3). Furthermore, we know that as DSC(A‐B) gets closer to 1, the volume overlap between A and B increases. Thus, the fact that DSC(C‐ND) and DSC(S‐ND) were significantly different meant that the volume overlap between scaphocephaly and non‐deformed skulls was greater than the volume overlap between circumferential deformations and non‐deformed skulls, which could be understood as a ‘more different’ orbital shape in circumferential deformations than in scaphocephaly relative to non‐deformed skulls. The same approach applies to MAD (Table 3) and HD (Table 4), except for the fact that increasing MAD and HD values refer to increasing shape differences.

In brief, when non‐deformed skulls were chosen as a reference for the distance calculations, we could show that scaphocephaly, Toulouse deformations, antero‐posterior deformations and circumferential deformations were all different compared with non‐deformed skulls based on DSC, MAD and HD. Antero‐posterior deformations and circumferential deformations clustered together in a group that was more different from non‐deformed skulls than were scaphocephaly and Toulouse deformations, which formed another cluster. This second cluster was significantly different from non‐deformed skulls but closer in absolute values to non‐deformed skulls than the was the cluster formed by antero‐posterior deformations and circumferential deformations. In brief, DSC, MAD and HD could not differentiate (i) antero‐posterior deformations from circumferential deformations and (ii) scaphocephaly from Toulouse deformations.

Colour maps in Fig. 4 illustrate the same point and show the cluster formed by antero‐posterior deformations and circumferential deformations (first and second rows), and the cluster formed by scaphocephaly and Toulouse deformations. Scaphocephaly and Toulouse deformations each seemed to have a specific shape visually but were not distinguishable based on DSC, MAD or HD.

Figure 4.

Distance maps between mean non‐deformed orbits (red) and mean deformed orbits (grey) in three‐quarter view. Orbits are superimposed with a partial transparency effect for the non‐deformed orbits after mean alignment. Distance maps have a colour code ranging from –5 mm (blue) to +5 mm (red). First row, antero‐posterior deformation: shorter and smaller orbits than in non‐deformed skulls. Second row, circumferential deformation: shorter and smaller orbits than in non‐deformed skulls. Third row, Toulouse deformation: slightly shorter orbits than in non‐deformed skulls. Fourth row, adult scaphocephaly: minimal contour differences compared with non‐deformed orbits.

Orbital symmetry

Based on left–right volume overlap quantification using DSC, we showed that non‐deformed skulls, scaphocephaly and all deformed groups were symmetrical, without any group being less or more asymmetrical than another (Supporting Information Fig. S8 and Table S4).

Cranio‐orbital index within deformation groups

The cranio‐orbital index [(skull length × skull height)/orbital volume] was significantly increased in all intentional deformation groups. This index was not significantly different in adult scaphocephaly compared with the non‐deformed groups (Supporting Information Fig. S9 and Tables S5 and S6).

Discussion

Orbital volumes

In a previous study (Khonsari et al. 2013), we could not show any difference in orbital volumes between non‐deformed skulls, antero‐posterior deformations, circumferential deformations and Toulouse deformations. Interestingly, we had previously shown, using cephalometric methods, that orbital shape modifications were maximal in circumferential deformations (Khonsari et al. 2013). In the present study we considered left and right orbits together in the volume assessment by taking laterality into account as a repeated measurement per individual for each orbit. By increasing the number of orbits included into the statistical tests, we were able to show a significant decrease of orbital volume in circumferential deformations and antero‐posterior deformations, whereas Toulouse deformations and scaphocephaly were similar in volume to non‐deformed skulls.

The globe is most probably the main driving factor of orbital growth (Enlow, 1968; Lieberman, 2011). Nevertheless, our results show that extreme external mechanical forces exerted early on the skull vault can interfere with orbital expansion. Scaphocephaly corresponds to an abnormal fusion of the sagittal suture, which is located between the parietal bones and is generally associated with frontal bossing and temporal narrowing. Scaphocephaly can thus potentially affect orbital shape and volume. Nevertheless, we show here that the orbital effects of scaphocephaly are less pronounced than the orbital effects of circumferential deformations and antero‐posterior deformations, and resemble the moderate orbital effects of Toulouse deformations. Interestingly, frontal bossing is very different in scaphocelphaly and intentional deformations – especially antero‐posterior deformations – where frontal flattening and frontal bone thinning are secondary to the pressure exerted by the deformation devices (Khonsari et al. 2013).

Orbital shape and symmetry

Orbital shape is significantly modified in all deformation types and in scaphocephaly. These results are in line with our previous study using 3D cephalometric methods (Khonsari et al. 2013). 3D cephalometric approaches and geometric morphometric methods provide complementary data that can contribute to a better description of non‐trivial shapes such as the orbital cavity (Khonsari et al. 2016; Levasseur et al. 2017).

Interestingly, the deformation pattern of the orbital cavity was not specific to the deformation type. We had previously shown that similar cephalometric parameters were modified in circumferential deformations, antero‐posterior deformations and Toulouse deformations (Khonsari et al. 2013). Here we showed that antero‐posterior deformations and circumferential deformations were not distinguishable based on DSC, MD and HD. Similarly, scaphocephaly and Toulouse deformations were not distinguishable based on the same indices, even though the gross aspect of their orbital cavity seemed qualitatively different (Fig. 4). These results could indicate that our morphometric indices were not refined enough to distinguish orbital cavity shapes from one another in these four deformation types. Nevertheless, based on the fact that two different approaches (cephalometry and geometric morphometrics) provide similar results concerning the way the orbit is modified in different types of deformations, we can also hypothesize that the orbital cavity reacts in a standardized way to external mechanical stimulations, due to the characteristics of the functional matrix formed by its bony scaffold and its contents. Antero‐posterior deformations and circumferential deformations result from different forces exerted on the skull vault, but they induce a similar pattern of orbital deformation, varying only in intensity. Similarly, we have previously shown that intentional deformations induce zygomatic retrusion, the difference between the various types of deformations being the extent of the retrusion. This retrusion was maximal in antero‐posterior deformations, followed by circumferential deformations and Toulouse deformations (Ketoff et al. 2017).

Finite element analyses would be of great interest in this context and would help to determine whether (i) different force distributions (antero‐posterior deformations, circumferential deformations, Toulouse deformations and scaphocephaly) exerted on the skull vault converge towards a unique force field around the orbit due to local anatomical specificities or (ii) the force fields transmitted to the orbit are different in various deformation groups but the orbital response to these constraints is standardized due to the properties of the orbital contents, and more specifically of the globe. The fact that the orbital deformations are symmetrical in all four groups despite the many factors that could cause asymmetrical vault deformations (for instance, the position of the deformation devices and the movements of the newborn) (Dingwall, 1931) is in favour of the second hypothesis; the globe is in fact a good candidate when counter‐balancing minor asymmetrical effects of the ongoing deformation during the first years of life.

Interestingly, the computation of a cranio‐orbital index defined by [(skull length × skull height)/orbital volume] indicated that intentional deformations induced an orbito‐cranial disproportion, whereas scaphocephaly had no measurable effect on this parameter. This point is also in favour of a standard reaction of the growing skull to abnormal external mechanical constraints.

Similar results are reported by several authors for skull base angles and their correlation with deformation types. A large number of studies indicate that both antero‐posterior and circumferential deformations are associated with an increase in the posterior skull base angle (Oetteking, 1924; McNeill & Newton, 1965; Hanzel, 1977; Antón, 1989; Pereira da Silva et al. 1990; Cussenot et al. 1992); however, recent investigations question this and have found divergent effects of circumferential and antero‐posterior deformations on the skull base (Cottin et al. 2017). These inconsistencies could result from differences in the classification of antero‐posterior deformed skulls (Cottin et al. 2017) and further studies, especially in 3D, are required to solve this issue. Nevertheless, there may be a ‘standard’ behaviour of the skull base independent of the deformation forces exerted on the skull, similar to what we have suggested for the orbit.

Authors’ contributions

R.S. performed the orbital segmentations, Q.H. performed the statistical analyses, J.N. designed the orbital segmentation methods and performed the morphometric assessment, G.R. acquired the scaphocephaly data, M.F. provided the anthropological data and R.H.K. supervised the study and wrote the paper. The authors report no conflict of interest.

Supporting information

Fig. S1. Geometrical meaning of mean absolute distance (MAD), Hausdorff distance and Dice similarity coefficient (DSC). MAD models the mean shape similarity, Hausdorff distance is an indicator of local morphological differences and DSC reflects the global volume overlap. First row: small MAD, small HD and high DSC. Second row: small MAD, large HD and average DSC. Third row: large MAD, large HD and low DSC. After Khonsari et al. (2016).

Fig. S2. Main three‐dimensional (3D) landmarks used for computing skull height and skull length: mid‐M (3D Enlow point) = midpoint of the left and right M points; mid‐Cp = midpoint of the left and right posterior condylian points (respectively, LCp and RCp). For further details see Lee et al. (2014).

Fig. S3. Main three‐dimensional (3D) landmarks used for computing skull height and skull length; lamb: intersection of the two lambdoid sutures; SC: intersection of C3 with the external table of the skull vault. Skull height (C3) was defined as [Sc – mid(Oi‐mid‐M)] and skull length was defined as [mid‐M – lamb]. For other abbreviations see Fig. S7. For further details see Lee et al. (2014).

Fig. S4. Orbital morphology in intentional deformations and adult scaphocephaly. Dice similarity coefficient (DSC), Mean absolute distance (MAD) and Hausdorff distance (HD) computed with adult scaphocephaly taken as a reference. The results of the statistical tests comparing groups are given in Supporting Information Table S3.

Fig. S5. Orbital morphology in intentional deformations and adult scaphocephaly. Dice similarity coefficient (DSC), mean absolute distance (MAD) and Hausdorff distance (HD) computed with circumferential deformations taken as a reference. The results of the statistical tests comparing groups are given in Supporting Information Table S3.

Fig. S6. Orbital morphology in intentional deformations and adult scaphocephaly. Dice similarity coefficient (DSC), mean absolute distance (MAD) and Hausdorff distance (HD) computed with anterioposterior deformations taken as a reference. The results of the statistical tests comparing groups are given in Supporting information Table S3.

Fig. S7. Orbital morphology in intentional deformations and adult scaphocephaly. Dice similarity coefficient (DSC), mean absolute distance (MAD) and Hausdorff distance (HD) computed with Toulouse deformations taken as a reference. The results of the statistical tests comparing groups are given in Supporting Information Table S3.

Fig. S8. Inter‐orbital symmetry assessment in intentional deformations and adult scaphocephaly using the computation of the Dice similarity coefficient (DSC) between one orbit and the mirror image of the contralateral orbit for each sample. All values were similar to non‐deformed controls.

Fig. S9. Cranio‐orbital index = [(skull length × skull height)/orbital volume] in intentional deformations and adult scaphocephaly.

Table S1 . Raw data for each individual skull included into the study: orbital volumes, symmetry assessment using the Dice similarity coefficient (DSC) and computation of the DSC, the mean absolute distance (MAD) and the Hausdorff distance (HD) with each consecutive group (scaphocephaly, non‐deformed skulls, circumferential deformations, antero‐posterior deformations, Toulouse deformations) taken as a reference.

Table S2. Intergroup comparisons of orbital volumes. * Significantly different from control; ND, non‐deformed skulls; S, scaphocephaly; C, circumferential deformations; AP, antero‐posterior deformations; T, Toulouse deformations; NA, not applicable.

Table S3. Comparisons of Dice similarity coefficient (DSC), mean absolute distance (MAD) and Hausdorff distance (HD) values with all other groups respectively taken as a reference.

Table S4. Absolute DSC values and intergroup comparisons for symmetry assessment.

Table S5. Skull length and skull height in intentional deformations and adult scaphocephaly.

Table S6. Cranio‐orbital index = [(skull length × skull height)/orbital volume] in intentional deformations and adult scaphocephaly.