Spectral Ripples in Round-Window Cochlear Microphonics: Evidence for Multiple Generation Mechanisms

Abstract

The cochlear microphonic (CM) results from the vector sum of outer hair cell transduction currents excited by a stimulus. The classical theory of CM generation—that the response measured at the round window is dominated by cellular sources located within the tail region of the basilar membrane (BM) excitation pattern—predicts that CM amplitude and phase vary little with stimulus frequency. Contrary to expectations, CM amplitude and phase-gradient delay measured in response to low-level tones in chinchillas demonstrate a striking, quasiperiodic pattern of spectral ripples, even at frequencies > 5 kHz, where interference with neurophonic potentials is unlikely. The spectral ripples were reduced in the presence of a moderate-level saturating tone at a nearby frequency. When converted to the time domain, only the delayed CM energy was diminished in the presence of the saturator. We hypothesize that the ripples represent an interference pattern produced by CM components with different phase gradients: an early-latency component originating within the tail region of the BM excitation and two delayed components that depend on active cochlear processing near the peak region of the traveling wave. Using time windowing, we show that the early, middle, and late components have delays corresponding to estimated middle-ear transmission, cochlear forward delays, and cochlear round-trip delays, respectively. By extending the classical model of CM generation to include mechanical and electrical irregularities, we propose that middle components are generated through a mechanism of “coherent summation” analogous to the production of reflection-source otoacoustic emissions (OAEs), while the late components arise through a process of internal cochlear reflection related to the generation of stimulus-frequency OAEs. Although early-latency components from the passive tail region typically dominate the round-window CM, at low stimulus levels, substantial contributions from components shaped by active cochlear processing provide a new avenue for improving CM measurements as assays of cochlear health.

INTRODUCTION

Nearly 90 years ago, Wever and Bray (1930) observed that an electrode placed near the cochlea picks up an alternating current potential that faithfully mirrors the waveform of the acoustic stimulus. This potential, which came to be known as the cochlear microphonic (CM), is generated primarily by the summed receptor currents of the outer hair cells (OHCs) responding to basilar membrane (BM) displacement (e.g., Dallos and Cheatham 1976). Because the CM can be measured in an intact cochlea with far-field monopolar electrodes (e.g., by electrodes placed on the round window or eardrum), it provides a potentially important assay of OHC health and function (Russell 2008). Nevertheless, CMs are perhaps the least utilized indices of OHC performance due to difficulties interpreting the responses in terms of local (i.e., place-specific) cochlear function (e.g., Cheatham et al. 2011).

In the common view, the poor place specificity of the far-field CM derives from a combination of two factors. First, the voltage measured by the electrode depends on a weighted sum of OHC transducer currents whose effects decrease with distance from the electrode, as in a simple cable model where the decrease is exponential (Patuzzi 1987). Thus, for an electrode placed at the round window (RW), the CM primarily reflects the activity of the most proximal cells—those located near the basal end of the cochlea—even when one employs a low-frequency stimulus whose response peaks near the apical end (Patuzzi et al. 1989). Second, because the individual hair cells contributing to the CM evoked by a tonal stimulus are excited by the BM traveling wave, contributions from different cells add with different phases. In particular, the rapid phase variation near the peak of the traveling wave causes the currents from neighboring sources to largely cancel one another; consequently, hair cells in the peak region contribute little to the total CM. As a result, the measured CM is dominated by contributions from cells located in the passive tail region of the BM response, where the phase varies little with location and currents sum constructively (Dallos 1973). Although several studies have proposed ways of overcoming the limited place specificity of monopolar CM measurements, and thereby improving their utility as assays of OHC health (Ponton et al. 1992; Chertoff et al. 2014; Charaziak et al. 2017), the classical theory is widely believed to capture the mechanisms shaping CM responses at the round window (Cheatham et al. 2011; He et al. 2012). Here, we describe previously unreported features of the round-window CM and interpret the results as indicating that mechanisms unaccounted for in the classical theory also play an important role in generating the cochlear microphonic.

Specifically, we show that when measured in response to low-level probe tones in fine frequency steps, CM amplitude and phase-gradient group delays demonstrate a striking quasiperiodic pattern of local maxima and minima, referred to here as spectral ripples. When the probe tone is presented together with another tone of moderate level at a nearby frequency, the spectral ripples are almost completely abolished, confirming their cochlear origin. We describe these phenomena in chinchillas for probe frequencies above 5 kHz, where interference with delayed neurophonic responses is unlikely (Verschooten and Joris 2014). The presence of spectral ripples in CM responses appears inconsistent with the classical view of CM generation, where the response is dominated by contributions from cells located near the round window in the tail region of the BM excitation pattern. By analogy with mechanisms responsible for spectral ripples in distortion-product otoacoustic emission (DPOAE fine structure; Shera and Guinan 1999), we hypothesize that CM spectral ripples represent an interference pattern produced by CM components with different phase gradients: an early-latency (“classical”) component with a shallow phase gradient and one or more delayed components with rapidly rotating phases. We explore this possibility using a model of CM generation in which additional delayed components are created within the active, peak region of the BM displacement wave as a consequence of the existence of cochlear roughness (i.e., random spatial mechanical and/or electrical irregularities). When they are of sufficient magnitude, these delayed components interfere with the early-latency components, resulting in spectral ripples in the round-window CM. Our results suggest a promising new avenue for exploring the utility of the CM in extracting place-specific information on the active function of OHCs. Furthermore, our modeling efforts suggest a link between CM and otoacoustic emission responses evoked with pure tones (i.e., stimulus-frequency otoacoustic emissions, SFOAEs) that can help to unify our understanding of cochlear mechanics.

METHODS

Animal Preparation

The procedures for animal preparation are detailed elsewhere (Charaziak and Siegel 2015; Charaziak et al. 2017). In brief, adult chinchillas were anesthetized (induction: ketamine hydrochloride, 20 mg/kg; maintenance: diallylbarbituric acid, 50 mg/kg, in urethane, 200 mg/kg; supplemental maintenance doses of 20 % of the initial one were given to eliminate limb withdrawal reflex), tracheotomized, and secured in a head holder. The pinna and lateral portion of the ear canal were dissected so that the tip of the sound delivery system could be sealed within ~ 2 mm of the eardrum. The bulla was opened, the tendon of the tensor tympani was sectioned, and in some animals, the stapedius muscle was paralyzed through sectioning of the facial nerve (Songer and Rosowski 2005). A silver ball electrode was placed on the round window, the reference electrode was inserted in the skin of the contralateral ear, and the ground electrode was attached to the head holder. The rectal temperature was kept at ~ 37 °C. The status of the preparation was monitored via recordings of compound action potential (CAP) thresholds. The data collection involved experiments that were part of another study (Charaziak and Siegel 2015). Experimental protocols were approved by the Animal Care and Use Committee of Northwestern University.

Instrumentation

All measurements were carried out in an electrically shielded sound-attenuating booth. Stimulus waveforms were generated and responses acquired and averaged digitally using 24-bit sound card (Card Deluxe-Digital Audio Labs; sampling rate 44.1 kHz) controlled with EMAV software ver. 3.24 (Neely and Liu 2011). The RW electrode signal was differentially amplified (40 dB), band-pass filtered (0.1–30 kHz), and corrected for the acoustic delay of the sound delivery system, as well as for the delay of the preamplifier filter. The stimuli were presented via two modified Radio Shack RS-1377 Super Tweeters coupled via plastic tubing to the probe-microphone system (a modified ER-10A OAE probe, Etymōtic Research, Elk Grove, IL). The speakers were grounded and shielded with heavy steel boxes to minimize electrical and magnetic radiation. Any contamination of the CM signals from the speakers occurred at levels below the system noise floor for all stimulus conditions. Stimulus levels were calibrated in situ to maintain a constant sound-pressure level at the probe microphone, whose output voltages were corrected for the frequency-dependent sensitivity of the microphone (Siegel 2007).

Measurements

The RW signal was measured in response to pure tone(s) of ~ 1.57 s duration, including 10-ms onset/offset ramps. The stimuli consisted of 30-dB SPL probe tones (f_p, varied from 0.5 to 16 kHz) presented together with an additional, 65-dB SPL saturating tone (f_s = f_p-43 Hz) on alternate runs. The probe frequency was varied in fine steps (86 Hz) to avoid phase unwrapping errors. The probe level was kept low to limit the spread of BM excitation toward the base that typically occurs at higher stimulus levels. Each condition was immediately repeated, and the responses stored in separate buffers (A and B). The two response buffers were averaged ($\frac{\mathrm{A}+\mathrm{B}}{2}$) and subtracted ($\frac{\mathrm{A}-\mathrm{B}}{2}$) to obtain estimates of either the CM or the noise amplitude at the frequency of the probe (obtained via fast Fourier transform), respectively. In both cases, the first and last 46.4 ms of the response buffer was skipped to prevent contamination from responses to onset and offset transients (e.g., CAP). The microphone response was measured simultaneously with the RW signal and was used to eliminate data where probe slippage was suspected (i.e., deviations in the measured probe SPL from its target value).

RESULTS

Data from 19 chinchillas (of 22 tested) showed no signs of probe slippage throughout the measurements (i.e., stable ear-canal pressure) and were included in the analyses. In all cases, CAP thresholds were considered normal (i.e., typically within 20 to 40 dB SPL in the mid frequencies, rising above 60 dB SPL above ~ 12–18 kHz), and both round-window CMs and robust OAE responses (distortion-product and stimulus-frequency OAEs) were obtained.

At low frequencies, the RW electrode signal contains phase-locked auditory nerve action potentials (auditory neurophonics) as well as hair-cell potentials (e.g., Henry 1995; He et al. 2012; Lichtenhan et al. 2013). Interference between the neurophonic and the CM might result in sharp peaks and notches in the CM levels. To avoid confusion between interference patterns that may include neural components, we analyze data only at higher frequencies (5–16 kHz) where contamination from neurophonic potentials is highly unlikely due to the low-pass nature of neural phase locking (Johnson 1980; Weiss and Rose 1988)_.

Spectral Ripples in the CM Responses

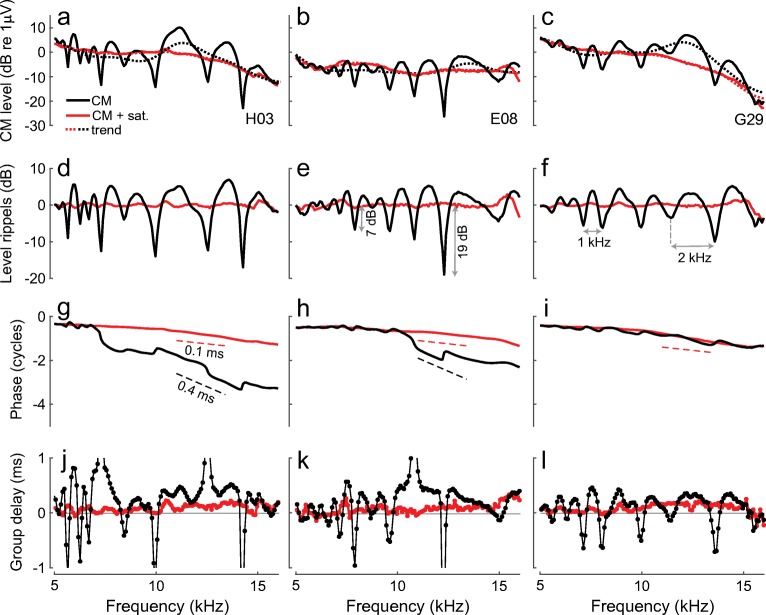
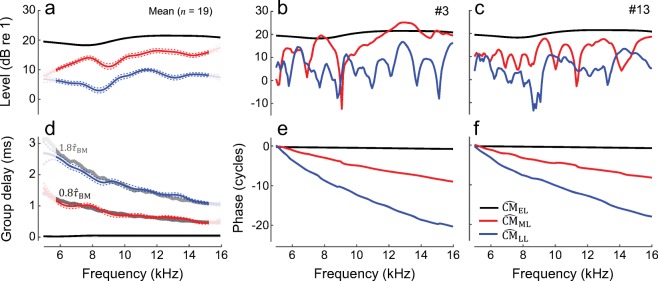
Figure 1 shows examples of the round-window CM responses to low-level tones (solid black) for three representative animals (columns). In all cases, the CM levels (a–c) exhibit a striking quasiperiodic pattern of peaks and notches (i.e., ripples). The spectral ripples in the CM levels can be better appreciated following detrending (d–f; the subtracted trend levels are shown in a–c with black dotted lines). Although the level rippling pattern varies idiosyncratically from animal to animal, the ripple spacing (e.g., horizontal arrows in Fig. 1) and ripple depth (vertical arrows) typically increase with probe frequency (on average from ~ 1 to ~ 2 kHz and from ~ 5 to ~ 20 dB over 5 to 16 kHz range, respectively; also see Fig. 7, black). The unwrapped CM phase demonstrates subtle ripples as well (g–i), although these are better visualized following calculation of the local phase slope (i.e., group delay; j–l). Within an animal, the patterns of spectral ripples observed in the CM levels and phase-gradient group delays are similar (e.g., f vs. l), with discrepancies most often observable near CM level minima, where lower signal-to-noise ratios could have compromised the phase estimate (e.g., deep level notches in d and e tend to line up with discontinuities in group delays in j and k, respectively). In some animals, the CM phase not only demonstrates subtle ripples but also exhibits regions with steeper slope that translate to longer group delays (~ 0.4 ms; e.g., H03 and E08 in Fig. 1g, h). Such steep phase slopes are inconsistent with the classical view of the round-window CM responses, which predicts that the CM phase gradient should approximate the sum of the stimulus delay (here ~ 6 μs) and the forward middle-ear delay (~ 0.05–0.08 ms as in Slama et al. 2010; Robles et al. 2015) due to dominance by potentials generated at the basal end of the BM excitation pattern, most proximal to the electrode (but see also the “DISCUSSION” for an alternative interpretation of the shallow phase of the classical CM component). The presence of the spectral ripples in the CM level and phase is suggestive of interference between early and delayed CM components with shallow and steep phase slopes, respectively. In some cases, such delayed components may even dominate the overall CM response, as exemplified by the regions of steep phase slopes (e.g., g, h).

Fig. 1.

Probe frequency CM measured in response to tones presented either in isolation (black) or in the presence of an additional, moderate-level saturating tone at a nearby frequency (red) for three chinchillas (columns). CM levels and unwrapped phases are shown in a–c and g–i, respectively. Corresponding noise levels are typically below − 30 dB (re 1 μV) and are omitted for clarity. To extract the level rippling pattern (d–f), we subtracted the corresponding trend (dotted lines, a–c) from the CM level. Trend lines were obtained by smoothing the CM levels with a low-pass filter. Phase-gradient delays are shown in j–l. The vertical arrows (e) show the level ripple depth and the horizontal arrows (f) mark the ripple spacing

Fig. 7.

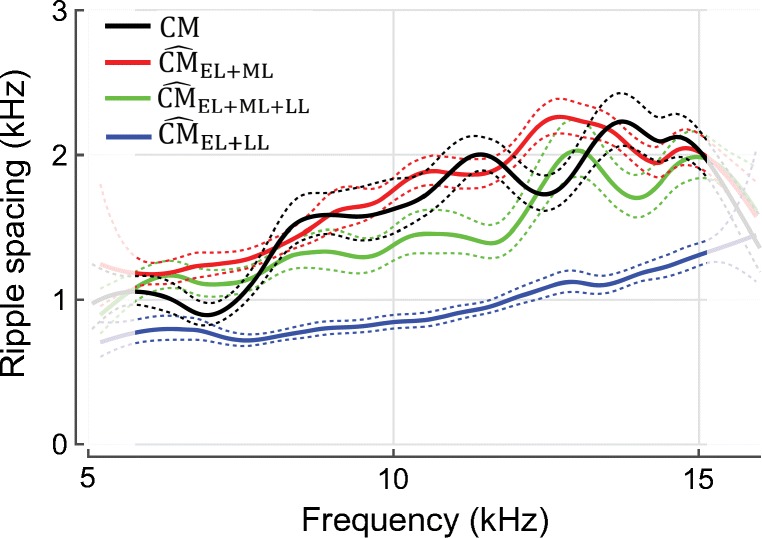
The mean ripple spacing (solid) of measured (black) and simulated (colored; see legend) round-window microphonics for 19 ears. Ripple spacings were estimated by taking the reciprocal of the instantaneous period of the rippling pattern “waveform” (e.g., Fig. 1d) obtained from its Hilbert transform. This automated procedure yields estimates of ripple spacing nearly equivalent to the spacings extracted by hand (see horizontal arrows in Fig. 1f). The means were gently smoothed by computing loess trend lines and the 95 % CIs of the trend were calculated by bootstrapping (dashed lines). Due to edge effects of the smoothing, the results at the extreme frequencies are less reliable (see lighter colors). For simulations of ${\widehat{\mathrm{CM}}}_{\mathrm{EL}+\mathrm{LL}}$, the rippling pattern was artificially enhanced by increasing the value of γ_m threefold [see Eq. (3)] so that the early and late components had more similar magnitudes

When a moderate-level saturating tone is swept together with the probe at a nearby frequency, the CM response becomes smoother, and no ripples are evident in either the CM levels or phase gradients (Fig. 1, red). As a result, the CM phase has a consistently shallow and nearly constant slope across frequency, corresponding to group delays of ~ 0.05–0.1 ms. Evidently, the saturating tone removes contributions from delayed CM components with steep phase slopes that would otherwise interfere with CM components with shallow phase slopes, producing the pattern of spectral ripples clearly observed in the CM levels and phase-gradient group delays. Because the saturating tone is believed to act primarily on OHC currents arising near its CF place (Geisler et al. 1990; Charaziak et al. 2017)—which is close to that of the probe tone—the delayed CM components are likely to originate within the peak region of the BM response to the probe. In contrast, the saturating tone has little effect on the global trend in CM levels (compare solid red and dashed black lines in a–c), although small reductions or enhancements (typically within ± 5 dB) are sometimes observed (Nuttall and Dolan 1991). (Small increases or decreases in CM level can be explained by the classical view of the CM generation; see “DISCUSSION”). These patterns indicate that CM components having shallow phase slopes are largely unaffected by near-probe saturating tones, consistent with their domination by sources located basal to the CF place of the probe. In other words, the CM measured in the presence of the near-probe saturating tone displays characteristics expected from the classical theory of CM generation.

Unmixing CM Components in the Pseudo-Time Domain

We test for CM components having different phase gradients by trying to separate them using a time-windowing method. Similar signal processing strategies have been used previously to unmix OAE components having different phase-gradient group delays (Kalluri and Shera 2001; Knight and Kemp 2001; Shera et al. 2008). If the semiregular pattern of CM ripples arises due to interference between CM components with different phase slopes, then an inverse Fourier analysis of the CM signal should reveal components with different latencies. Complete or partial separation of such components can be achieved using time windows. However, due to cochlear frequency dispersion, the CM components may be smeared in time, rendering them more difficult to separate by time windowing. To compensate for this dispersion, we performed the Fourier analysis with respect to a transformed frequency coordinate derived from the empirical place map of chinchilla near-CF basilar membrane group delays, τ_BM (for details, see Shera et al. 2008). The CM measurements were interpolated to frequencies spaced at intervals inversely proportional to τ_BM, where ${\tau }_{\mathrm{BM}}\left(f\right)=a+b{\left(\frac{f}{f_0}\right)}^c$, with parameters a, b, c, and f₀ set to 0.496 ms, 1.863 ms, − 0.771, and 1 kHz, respectively (Siegel et al. 2005). The same strategy has been applied to unmix stimulus-frequency OAE components in chinchillas (Shera et al. 2008).

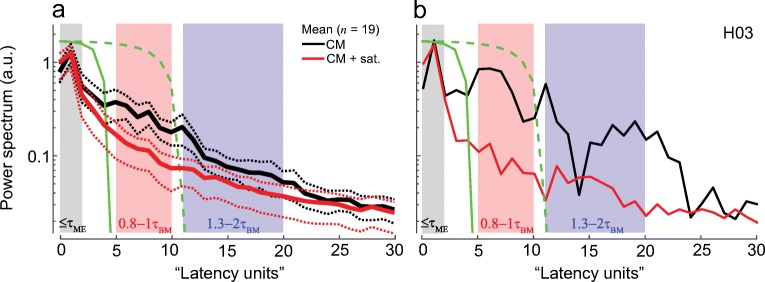
Figure 2 shows the latency-domain representation of the round-window CM signal for one chinchilla (b, black) together with the mean CM latency function obtained from 19 animals (a). Because of the quasi-power-law transformation applied before Fourier analysis, the conjugate “latency units” (lu) along the abscissa have no simple physical interpretation. On average, the latency demonstrates a single prominent peak centered at ~ 1 lu (Fig. 2a, black). In the individual data, however, several distinct peaks can be observed at longer latencies (b, black). Because the delayed peaks in the latency domain do not align perfectly for different animals, they tend to smear out through the averaging process. Nevertheless, in all cases, the energy at later latencies (> 3 lu) is considerably reduced when a near-probe saturating tone is presented concomitantly with the probe (Fig. 2, red). In contrast, the saturator has little effect on the amplitude of the early peak centered at ~ 1 lu. These results are consistent with the existence of delayed CM components with steep phase slopes.

Fig. 2.

Chinchilla CM latency functions for signals measured with and without the saturating tone (red and black, respectively). Panel a shows mean (solid) latency functions together with 95 % confidence intervals (CIs, dotted, calculated through bootstrapping) for 19 animals, while b plots an individual example. The shaded boxes mark the ranges of latencies over which an artificial signal with the specified phase-gradient delay, τ_AS, exhibits significant peaks. The ranges are based on either middle ear (ME) or near-CF basilar membrane (BM) group delays (see description within each box). The solid green line shows the matched window duration used to separate putative early-latency from delayed CM components. The delayed CM components were subsequently unmixed into middle- and long-latency components using the second window (green dashed lines)

To clarify how the units along the latency axis (lu) relate to cochlear travel times (i.e., to place of origin) and thereby facilitate the choice of unmixing windows, we created artificial signals with known phase-gradient delays (τ_AS) and transformed them to the latency domain so that the location of their respective peaks could be identified (see shaded areas in Fig. 2). The latency function of artificial signals that mimic pure middle-ear delays (τ_AS = τ_ME = 0.05–0.1 ms) peaks within the first 2 lu (gray box). Thus, the first prominent peak in the data (at ~ 1 lu) presumably represents CM sources located near the basal end of the cochlea, as predicted by the classical theory. When τ_AS matches forward BM travel time (range from 0.8 to 1.0 times τ_BM), the latency function peaks between 5 and 10 lu (red box). [The τ_BM was set as the near-CF basilar membrane group delay in chinchillas derived by Siegel et al. (2005) and Shera et al. (2010).] In about half the animals, distinct peaks at longer latencies are also observed (Fig. 2b). Simulations indicate that latency functions with τ_AS in the range 1.3–2.0 times τ_BM peak from 11 to 20 lu (blue box). Thus, these long-latency CM components have latencies roughly corresponding to the round-trip travel time of the BM excitation to and from the CF place.

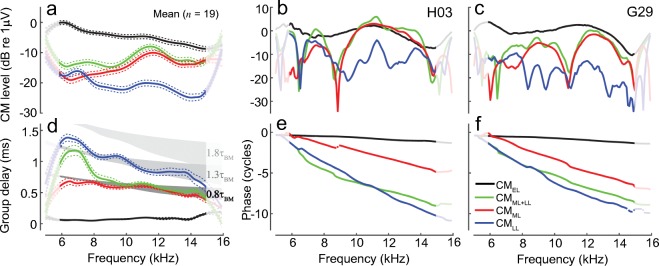
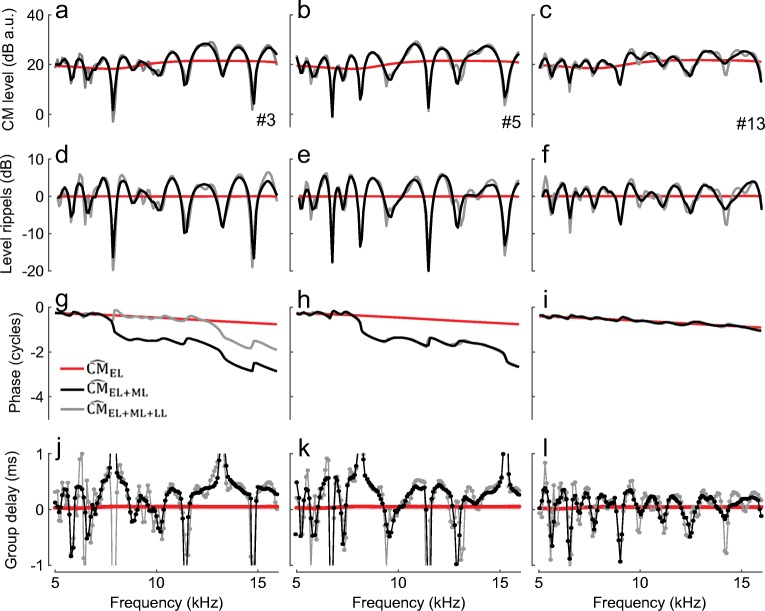
To separate putative CM components in the latency domain we used 10th-order recursive exponential windows (Shera and Zweig 1993). The windowed signals were then converted back to the frequency domain with a Fourier transform. The early components were separated from the delayed components using a window with half-power duration of 4 lu (Fig. 2, green solid). As shown in the examples in Fig. 3 (middle and right columns), the early-latency components (CM_EL) have a shallow phase slope and a level that varies smoothly with frequency. The phase-gradient delays average 0.05–0.08 ms (d, black), values which agree well with the range of middle-ear delays in chinchillas. On average, CM_EL levels decrease with frequency at a rate of 5–6 dB/oct. This trend may reflect stimulus attenuation due to middle-ear transmission, where a local decrease in sensitivity (by ~ 7 dB) is typically observed as frequency increases from ~ 6 to ~ 14 kHz despite the transfer functions having relatively broadband characteristics otherwise (also see Dallos et al. 1974, for middle-ear effects on CM measurements; Robles et al. 2015). Furthermore, the decrease in CM_EL level with frequency may relate to cochlear “end effects” (e.g., for probe frequencies peaking near the basal end of the cochlea, the tail region of the BM excitation pattern shortens and currents through fewer OHCs can add in phase). In general, the overall characteristics of CM_EL agree with the predictions of the classical theory of the CM generation.

Fig. 3.

CM components obtained by time-windowing of the CM latency function. The initial unmixing produces early-latency components (black, CM_EL, < 4 lu) and delayed components (green, CM_ML + LL, > 4 lu); the delayed components are subsequently unmixed into middle- (red, CM_ML, 4–10 lu) and late-latency components (blue, CM_LL, > 10 lu). The first column shows gently smoothed (loess) mean component magnitudes (a) and phase-gradient group delays (d) together with 95 % CIs (dotted, calculated through bootstrapping) for 19 animals. The noise level averaged − 40 dB re 1 μV and rarely exceeded − 30 dB within an animal (not shown). Mean group delays were calculated from data points with SNR > 6 dB. The gray shaded areas in d mark regions corresponding to 0.8τ_BM, 1.3τ_BM, and 1.8τ_BM [darker to lighter gray, respectively; chinchilla near-CF τ_BM from Siegel et al. (2005) marks the upper area limit, while estimates from Shera et al. (2008) mark the lower limit]. The second and third columns show examples of the component magnitudes and phases for two animals (same as in Fig. 1). The signal processing (smoothing and time-windowing) renders the results at the edges of the frequency range less reliable (see lighter colors at the edges)

In contrast, the delayed CM (> 4 lu) level does not vary smoothly with frequency and demonstrates idiosyncratic patterns of magnitude peaks and notches (Fig. 3b, c, green). Typically, the delayed CM is lower in level than the early CM (Fig. 3a), although exceptions occur at higher frequencies (b), because, unlike the CM_EL, the delayed components tend to increase in level with increasing probe frequency. The delayed CM phase rotates rapidly with frequency, with slope changing abruptly from ~ 1.3τ_BM (mid gray area in d) to ~0.8τ_BM (dark gray area) below and above ~ 8 kHz, respectively, as if components with different phase gradients are dominating the response at low vs. high frequencies. To test that possibility, we further unmixed the delayed CM using a 10-lu window duration (Fig. 2, dashed green). The resulting middle-latency (4–10 lu) and late-latency (> 10 lu) components are shown in Fig. 3 (red and blue, respectively). The late components (CM_LL) are small in magnitude (~ 20 dB below CM_EL), exhibit an idiosyncratic pattern of magnitude microstructure (Fig. 3b, c, blue), and decrease in level with increasing frequency at a rate similar to the CM_EL (Fig. 3a). Throughout the frequency range, the CM_LL has phase-gradient delays corresponding to estimated otoacoustic round-trip travel times in chinchillas [~ 1.3τ_BM, (Shera et al. 2008)]. This suggests that the late-latency components arise through a process of internal reflections of the traveling pressure-difference wave between the CF place and stapes (Shera and Cooper 2013). In contrast, the levels of the middle-latency components (CM_ML) increase with frequency (Fig. 3a, red), so that CM_ML are lower/higher in magnitude compared to CM_LL at frequencies, respectively, below/above 8 kHz. Although CM_ML levels also exhibit an animal-specific microstructure (Fig. 3b, c, red), the pattern of peaks and notches does not align with the microstructure of the late CM (blue). Furthermore, CM_ML phase-gradient group delays are slightly shorter than the cochlear forward travel time to the CF place (~0.8τ_BM, Fig. 3d). This suggests that the middle CM arises from regions slightly basal to the probe-tone CF place. The differences in CM_ML and CM_LL magnitude microstructures, group delays, and global changes in level with frequency suggest that these two components arise via different mechanisms, rather than CM_LL being simply a “delayed reflection” of CM_ML.

The results of the component unmixing are robust to reasonable variations in the analysis parameters, specifically to changes in the form, order, and duration of the unmixing windows (the latter by ± 1 lu), despite the limited resolution of the latency-domain function (note the proximity of the colored boxes in Fig. 2). Using recursive exponential windows of high order allows for relatively clean separation of the unmixed signals in the latency domain, although some energy leaking across windows cannot be avoided unless rectangular windows are used. Rectangular windows, however, introduce spectral artifacts when converting the unmixed signals back to the frequency domain. We tested the “leakage” of the recursive exponential windows by applying the unmixing strategy to signals synthesized from the data to include only the early- and late-latency components (i.e., the middle-latency component was absent). If the component separation were perfect, then no middle-latency component would be obtained from the synthesized signals. Although the middle-latency components unmixed from the synthesized signals were nonzero, their amplitudes were ~ 15 dB below those seen in the data, indicating that energy leakage between windows is relatively low. We selected the window durations based on average BM near-CF group delays, as estimated from auditory nerve fiber data in a different group of animals (Siegel et al. 2005; Shera et al. 2010). Although this strategy facilitates interpretation in terms of cochlear travel times, it neglects possible differences in cochlear travel times in individual animals, so that the chosen window durations may have not been optimal in each case (e.g., Fig. 2b). Finally, we tested our unmixing strategy on artificial signals that contained either all three components or only the early-latency component. If the delayed components were not present in the analyzed signal, the unmixed delayed signals were at least 35 dB lower in level compared to when all three components were present (i.e., unmixing “noise”). Importantly, the trends we describe do not depend sensitively on the details of the signal-processing strategy—we obtained similar results using an alternative unmixing method based on the continuous wavelet transform (Moleti et al. 2012).

CM Model Description

We explore the origin of the various CM components by modifying the classical theory of CM generation to include effects of possible cochlear irregularities (i.e., “roughness”). In general, we assume that the local complex-valued CM voltage produced by the ionic current flowing through a hair cell is proportional to the local BM displacement (D_BM), and that the voltage spreads instantaneously throughout the cochlea, reaching the electrode with no additional delay (He et al. 2004; Cheatham et al. 2011; Charaziak et al. 2017). The CM at the round window is calculated as the vector sum of all the local sources, weighted exponentially with distance from the source to mimic the effects of electrical attenuation. Because we are concerned only with responses to low-level stimuli, and simulations show that inclusion of the nonlinear hair-cell transducer function has negligible effects on the results, we omit nonlinear elements in the model (see “DISCUSSION”).

According to the classical theory of CM generation, the round-window $\widehat{\mathrm{CM}}$ at probe frequency f_p represents a vector sum of the individual voltage sources excited by the forward traveling wave on the BM, weighted according to their distance (x) from the round window:

$$\widehat{\mathrm{CM}}\left(f_{\mathrm{p}}\right)\cong \sum _i{V}_{0}w\left(x_i\right)D_{\mathrm{BM}}\left(x_i,f_{\mathrm{p}}\right),$$ 1

where D_BM(x, f_p) is the normalized complex-valued spatial excitation pattern of BM displacement produced by the probe frequency f_p, V₀ represents the intrinsic strength of the local voltage sources (assumed independent of x), and w(x) is the weighting function that controls the attenuation with distance from the source (e.g., Cheatham et al. 2011; Charaziak et al. 2017). We used $w\left(x\right)={10}^{\frac{-\mathit{Ax}}{20}},$ with attenuation rate A in decibels per millimeter. (All modeled CM components are marked with a hat to distinguish them from measured data.)

We now extend the classical model to include plausible effects of small, cochlear irregularities on the CM generation process. For generality, we distinguish two possible types of irregularity in the cochlea: “micromechanical” irregularities (r_m) that represent spatial perturbations in the micromechanics of the organ of Corti and “microelectrical” irregularities (r_e) that represent spatial variations in the strength of the OHC voltage sources, although the two may be closely related. If one adds both irregularities to the model, two things happen. First, the traveling wave is scattered by the micromechanical roughness, creating a reverse traveling wave via a process described by the coherent reflection theory of OAE generation (Zweig and Shera 1995). Second, the constant V₀ becomes V₀[1 + γ_er_e(x)], where γ_e is a microelectrical scaling factor introduced for convenience. The assumption here is that the strength of the voltage sources, previously assumed constant (or at least smoothly varying), acquires an irregular or random component. So, to first order, the equation for the round-window CM becomes:

$$\begin{array}{c}\widehat{\mathrm{CM}}\left(f_{\mathrm{p}}\right)\cong \sum _i{V}_{0}w\left(x_i\right)1+{\gamma }_{\mathrm{e}}{r}_{\mathrm{e}}\left(x_i\right)\left(+R\left(f_{\mathrm{p}}\right)\left(1+R_{\mathrm{s}}\right)\right]D_{\mathrm{BM}}\left(x_i,f_{\mathrm{p}}\right),\end{array}$$ 2

where R_s represents the reflection coefficient for reverse waves at the stapes and the cochlear reflectance R describes the reflection of the forward traveling wave near its CF place. The cochlear reflectance is as approximated by:

$$\begin{array}{c}R\left(f_{\mathrm{p}}\right)={\gamma }_{\mathrm{m}}\sum _i{r}_{\mathrm{m}}\left(x_i\right)D_{\mathrm{BM}}^2\left(x_i,f_{\mathrm{p}}\right),\end{array}$$ 3

where γ_m is a micromechanical scaling factor (chosen so that |R| < 1). Equation (3) simplifies the physics by assuming that the cochlear reflection near the CF place is proportional to the square of the BM displacement wave, rather than to the square of the pressure-difference wave (Shera et al. 2008). Derivation of the pressure difference from the BM displacement requires estimates of the BM impedance (or, equivalently, the wavenumber). Since these are not available for our BM displacement patterns (see below), we adopted the simplified expression for R. The main consequence of this simplification is that the model predicts a round-trip OAE travel time of ~ 1.8τ_BM, somewhat larger than the value of ~ 1.3τ_BM obtained using the pressure-difference wave (Shera et al. 2008). The Shera et al. (2008) predictions match well the estimated cochlear round-trip travel times from stimulus-frequency (SF) OAE and BM measurements.

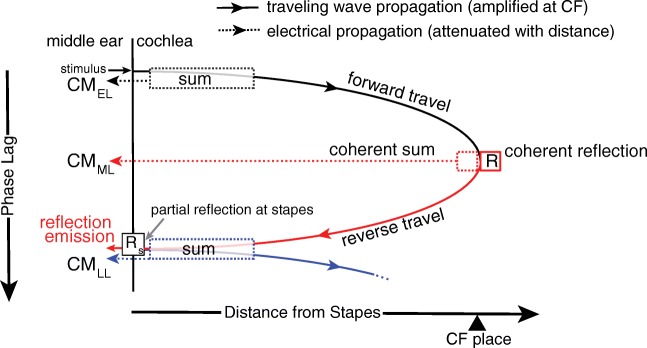
One can immediately see that our extension of the classical theory to include the two kinds of irregularity predicts that the CM has three components, as schematically depicted in Fig. 4. The first component is simply the classical CM, which is dominated by basal sources producing an early-latency response [${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$; Eq. (1)]. The second component is due to the microelectrical roughness, and we show that it produces a “middle-latency” response due to coherent electrical summation at the peak [i.e., ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}\cong \sum V_{0}w{\gamma }_{\mathrm{e}}{r}_{\mathrm{e}}{D}_{\mathrm{BM}}$]. The third component is due to internal reflection of the traveling wave and produces a long-latency response [i.e., ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}\cong \sum V_0\mathit{wR}\left(1+R_{\mathrm{s}}\right)D_{\mathrm{BM}}$].

Fig. 4.

Schematic diagram illustrating the generation of CM components. The diagram shows phase lags relative to the stimulus at the stapes (lag increasing downward) of traveling waves (solid) and electrical signals (dotted). The electrical signals spread instantaneously throughout the cochlea (i.e., no additional phase lags) but decay exponentially with distance from the source. As in the classical model, the early-latency component arises in the tail region of the stimulus-evoked forward traveling wave, where BM phase varies slowly with location and currents from the hair cells sum constructively (black dotted box). The resulting CM component reaches the round window with essentially no delay (black dotted arrow). Although local CM currents are large near the peak of the forward traveling wave, the classical model predicts that rapid BM phase variations cause near total cancelation of the CM from this region. However, the introduction of cochlear electrical irregularities allows a region of coherent summation of CM sources to emerge (red dashed box). As a result, CM components with delays close to the forward travel BM time to the CF place (middle latency) reach the round window. Near the CF place, through a process of coherent reflection (R) from micromechanical irregularities, a reverse traveling wave arises (solid red) that is partially transmitted to the middle ear (OAEs) and partially reflected toward the cochlea (R_s), giving rise to a secondary forward traveling wave (solid blue). The late-latency components (dotted blue) represent the sum of currents produced by the cells located in the overlapping tail regions of the reverse and the secondary forward traveling waves (dotted blue box)

As in the classic theory, the early-latency component is dominated by the contributions from the tail region of the primary forward traveling wave (Fig. 4, black solid arrow), where the phase varies slowly and the BM moves nearly in unison (dashed black box), while contributions from the CF region are largely canceled out. In contrast, the middle-latency component arises predominantly within the CF region through an electrical analog of “coherent reflection” (Zweig and Shera 1995). Specifically, when the microelectrical irregularities include spatial-frequency components that match the wavelength of the traveling wave, the resulting voltage potentials combine coherently. Sources within the peak region that would normally tend to cancel one another then sum in phase (i.e., coherent summation; red dashed box in Fig. 4). Because this CM component originates within the peak region of the primary forward traveling wave, its latency should be close to the forward BM travel time to the CF place. (Recall that the reverse travel is electrical and therefore effectively instantaneous.) The long-latency component arises due to the internal reflection of cochlear traveling waves. The micromechanical irregularities scatter the primary forward traveling wave (black solid arrow, Fig. 4) and the resulting reflected wavelets combine coherently near the wave peak when the irregularities contain spatial-frequency components matching half the wavelength of the traveling wave (Zweig and Shera 1995). The process of coherent reflection creates the reverse traveling wave that propagates back toward the stapes (red solid arrow; Zweig and Shera 1995), where it is represented by the cochlear reflectance, R. At the stapes, part of the reverse wave energy is transmitted through the middle ear to the ear canal, where it can be measured as a reflection-source emission (SFOAE). The other part is reflected back into the cochlea (with reflection coefficient, R_s), giving rise to a secondary forward traveling wave (blue solid arrow, Fig. 4). Just as for the primary traveling wave, the current sources excited by the BM displacement resulting from the reverse wave and the secondary forward wave add constructively in the tail region of the combined excitation pattern (blue dashed box), giving rise to CM components with latencies equivalent to the round-trip travel time to and from the CF place. Although these long-latency components are dominated by CM sources located in the tail region of the BM excitation pattern, their amplitudes depend on the size of the reverse traveling wave and are therefore related to the OAE. For example, because the amplitude of the reverse wave depends on cochlear amplification at the CF place, a reduction in this amplification (e.g., resulting from high stimulus levels, damage, or a saturating tone) decreases the relative amplitude of the long-latency CM components. Unlike the classical, early-latency component, the new roughness-related middle- and long-latency components depend on cochlear activity near the CF place.

To compute CM components using the model, we derived estimates of longitudinal BM displacement profiles [D_BM(x, f_p)] from published chinchilla data (Rhode 2007b; Ruggero et al. 1997, 2000). We converted frequency responses at a single location (30-dB SPL tones at CFs ranging from 6.6 to 10 kHz) to spatial profiles at fixed probe frequency using scaling. All derived displacement profiles were normalized to their peak value and interpolated to a resolution of 2.4 μm over a BM length of 10 mm. (For comparison, the width of a single hair cell is about 10 μm.) To simulate responses over a range of frequencies, BM displacement profiles were translated using the chinchilla frequency-position map (Muller et al. 2010), with the CF varied from 5 to 16 kHz in 86-Hz steps. Although simulations were performed for each of four different BM displacement profiles obtained from different cochleae [(Rhode 2007b) for chinchillas N92 and N157; (Ruggero et al. 1997) for L113; and (Ruggero et al. 2000) for L208], we show only those results obtained for cochlea L208 for brevity; similar patterns were obtained in all cases.

Because the BM displacement and CM data were obtained from different groups of animals, and because irregularity patterns in individual animals remain unknown, only qualitative comparisons between model predictions and CM data are currently possible. To simulate data from individual “ears,” we computed CM components for 19 different realizations of the roughness. For computational convenience, we assumed that the micromechanical and microelectrical irregularities have the same spatial pattern (r = r_m = r_e). The common roughness function, r(x), was obtained by drawing random numbers from a zero mean normal distribution with a standard deviation of 0.2. The unknown stapes reflectance (R_s) was assumed frequency-independent and set equal to 0.9. Adjusting the complex value of R_s modulates the amplitude and phase of the reflected wave but has no qualitative effect on the model conclusions. The value of V₀ was set arbitrarily to 1 V. The remaining free parameters of the models (A, γ_m, and γ_e) were initially varied until the relative component levels visually mimicked major trends observed in the data (Fig. 3a) and were then fixed at these constant values. The electrical attenuation constant A was set to 2 dB/mm for all simulations; this value agrees with estimates of the attenuation rate suggested by Charaziak et al. (2017) and produces an increase in ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ level with frequency that matches the trends observed in the data (Fig. 3a). Although the early and late CM components are insensitive to the value of A, the middle components are strongly attenuated and contribute little to the round-window response at larger values of A (A > 4 dB/mm). The scaling parameters γ_m and γ_e determine the relative amplitudes of the various CM components and were fixed at the values 24 and 5, respectively; these values provide good approximations to the trends in the data (i.e., $\mid {\widehat{\mathrm{CM}}}_{\mathrm{ML}}\mid \le \mid {\widehat{\mathrm{CM}}}_{\mathrm{EL}}\mid$ and $\mid {\widehat{\mathrm{CM}}}_{\mathrm{LL}}\mid \ll \mid {\widehat{\mathrm{CM}}}_{\mathrm{EL}}\mid$).

CM Model Results

Model-Predicted CM Components

Figure 5 shows early, middle, and late CM components simulated for two roughness profiles (middle and right columns) together with mean results computed for 19 profiles (left). The ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ component does not depend on roughness and therefore remains unchanged across the different “ears,” so long as the BM displacement profile used in the simulations remains fixed (as here).

Fig. 5.

Model-predicted early-, middle-, and late-latency CM components are shown in black, red, and blue, respectively, averaged for 19 “ears” (a, d) and for example individual ears (b, c, e, f). To simulate the different “ears,” we used different roughness profiles while keeping all other model parameters unchanged. The mean values were gently smoothened by computing loess trend lines (solid), and 95 % CIs for the trend were calculated via bootstrapping (dashed), with loess edge effects estimated as 25 % of the span (lighter colors at the edges). The gray lines in d correspond to 0.8${\widehat{\tau }}_{\mathrm{BM}}$ and 1.8${\widehat{\tau }}_{\mathrm{BM}}$, where ${\widehat{\tau }}_{\mathrm{BM}}$ was calculated directly from simulated near-CF BM displacement phase gradients. Because the model is perfectly scaling symmetric (aside from end effects), the predicted ${\widehat{\tau }}_{\mathrm{BM}}$ diverges from the real ear delay estimates, τ_BM, toward lower frequencies, where deviations from scaling symmetry are more apparent

The simulated ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ has nearly zero phase-gradient delay (< 0.05 ms, Fig. 5d, black) and levels that vary little with frequency (a–c). Thus, ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ resembles both the CM measured in the presence of the near-probe saturator (Fig. 1, red) and the unmixed early-latency component, CM_EL (Fig. 3, black). However, ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ level does not vary systematically with frequency and its group delays are shorter than those of CM_EL. These discrepancies are likely due to the absence of a middle-ear model in the simulations. Furthermore, cochlear “end effects” may have been underestimated in the simulations, since different frequencies were simulated by simply translating the BM displacement profiles uniformly along the cochlear length with no accompanying change in shape. Stronger end effects are observed when the simulations are extended to frequencies approaching 20 kHz; in these cases, the level of the simulated CM decreases with increasing frequency due to the considerable shortening of the tail region of the BM excitation profile (in the model x = 0 mm was set to have a CF = ~ 30 kHz). Finally, because ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ is dominated by contributions from sources located in the tail region of the BM excitation pattern, its level is not sensitive to changes in the attenuation constant, A [Eq. (1)], whose value primarily affects currents originating at more apical locations. However, a small increase in ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ phase slope is observed for A > 0 dB/mm (see “DISCUSSION”).

Like the early-latency component, the late component in the model arises from basal sources. The key difference is the identity of the wave driving the OHCs: Whereas the early component is driven by the stimulus-induced forward traveling wave, the late component is driven by the reverse traveling (OAE) wave combined with its reflection at the stapes. Because both ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ and ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ arise from basal sources, ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ levels generally parallel ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ levels across frequency (Fig. 5a, blue vs. black), as seen in the data (Fig. 3a, blue vs. black). Unlike ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$, however, the phase of the late component rotates rapidly with frequency—the ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ delay equals the round-trip travel time derived from the model (~ 1.8${\widehat{\tau }}_{\mathrm{BM}}$; blue vs. light gray in Fig. 5d)—and its level exhibits idiosyncratic spectral structure (e.g., notches) similar to SFOAEs. Thus, the features of ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ qualitatively match those of the long-latency components unmixed from the data (Fig. 3, blue).

The middle-latency component in the model arises from CM sources located near the peak of the BM excitation pattern (Fig. 4). Overall ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ levels are therefore strongly influenced by the attenuation rate, particularly for lower frequency stimuli. As a result, when A is nonzero, ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ levels tend to increase gradually with increasing frequency (Fig. 5a, red). ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ group delay matches ~ 0.8${\widehat{\tau }}_{\mathrm{BM}}$ (Fig. 5d, red vs. dark gray), as if the region of coherent summation is centered slightly basal to the probe CF place [as also observed for coherent reflection, e.g., (Shera and Guinan 2003)]. Finally, ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ displays idiosyncratic patterns of magnitude microstructure (b, c, red). All these features agree well with the properties of the unmixed middle-latency components seen in the data (Fig. 3, red).

Importantly, even though we used the same roughness profiles for the calculation of both ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ and ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ (r = r_m = r_e), their spectral microstructures appear uncorrelated (Fig. 5b, c, red vs. blue). This occurs because the coherent summation of ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ and OAE sources depends on different spatial-frequency components in the pattern of irregularities. Because ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ depends on the product rD_BM (i.e., on D_BM raised to the first power), irregularity components whose spatial period matches the wavelength of the traveling wave at its peak contribute most to ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}.$ By contrast, the cochlear reflectance R depends on $r{D}_{\mathrm{BM}}^2$ (i.e., on D_BM raised to the second power), and therefore, the dominant spatial-frequency components for both SFOAEs and ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ are those whose period is half the wavelength of the traveling wave.

In summary, the modeling results agree remarkably well with the data. The model correctly predicts that the overall levels of the early and late components change in parallel across frequency, while the middle-latency component level exhibits an opposing trend (compare Figs. 3a and 5a). Although inclusion of the electrical attenuation with distance from the RW explains the gradual increase of the middle-component level with frequency, the simulations do not reproduce the opposite trend seen in the data for the early and late components unless higher frequencies, peaking near the simulated cochlear base, are included. The phase-gradient delays of the model components match the trends observed in the unmixed data. [Note that the total phase accumulation of the delayed model components is larger than seen in the data (Figs. 3e, f and 5e, f); this is due to the perfect scaling symmetry assumed in the model, which results in longer BM group delays than observed experimentally across the range of frequencies. Thus, it is more meaningful to compare the component group delays relative to the underlying BM group delays (e.g., Figs. 3d and 5d) than to compare the unwrapped phase lags.] Although the ratio of τ_LL/τ_BM is closer to ~ 1.3 in the data (Fig. 3a), as opposed to the predicted ~ 1.8 ratio in the model (Fig. 5d), this discrepancy is the expected consequence of adopting a simplified form for the cochlear reflectance, R(f_p) [Eq. (3)]. Our model results are consistent with the predictions of Shera et al. (2008), who used a more accurate form of Eq. (3) based on the traveling pressure-difference wave rather than D_BM. According to Shera et al., the coherent reflection model predicts OAE round-trip travel times of ~ 1.3τ_BM, in agreement with the data, at least for the basal end of the cochlea (in chinchillas > 3–4 kHz). Thus, the delay of the unmixed CM_LL component agrees well with the theory of its origin in the reverse OAE wave. Finally, the simulations predict highly individualized, uncorrelated patterns of spectral microstructure in the middle and late components (Fig. 5b, c), while the early components vary relatively little from ear to ear as long as the underlying BM excitation patterns are similar (as assessed for BM displacement profiles derived from four cochleae; data not shown). The unmixed data indicate similar trends (Fig. 3b, c).

Total CM at the Round Window

Figure 6 shows examples of modeled total round-window microphonics for various possible compositions of the $\widehat{\mathrm{CM}}$ (see legend). In the classical theory, only the early-latency components (${\widehat{\mathrm{CM}}}_{\mathrm{EL}})$ are included, and no spectral ripples in either CM magnitude (red, top rows) or group delay (bottom) are observed. When the middle-latency component is added to the early component (${\widehat{\mathrm{CM}}}_{\mathrm{EL}+\mathrm{ML}})$, an ear-specific rippling pattern emerges in both the total microphonic level and its group delay (Fig. 6, black). As observed in the data (Fig. 1, black), the ripple depth varies from ear to ear depending on the relative magnitudes of the two components. In ear no. 3, for example, the levels of ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ and ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ are similar (Fig. 5b, black and red), creating deep notches (~ 20 dB) in the total CM magnitude and regions of steep and shallow phase slopes (Fig. 6d, g, black). This example resembles the data for animal H03 (Figs. 1 and 3). When ${\widehat{\mathrm{CM}}}_{\mathrm{ML}}$ is lower in level than ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ (no. 13, Fig. 5c), the rippling pattern in total CM is less pronounced (Fig. 6f, i, black), similar to the pattern observed for animal G29 (Figs. 1 and 3). Because the modeled late component is typically lower in level than the middle component (Fig. 5a), inclusion of ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ in the total $\widehat{\mathrm{CM}}$ (Fig. 6, gray) introduces a small modulation to the ripple spacing but does not appreciably alter the ripple depth.

Fig. 6.

Model-derived $\widehat{\mathrm{CM}}$ at the RW for different “ears” (columns; ear #3 and #13 are the same as those used in Fig. 5). The total $\widehat{\mathrm{CM}}$ was obtained by summing different components: red—early-latency component only; black—sum of the early- and middle-latency components; gray—sum of the early-, middle-, and late-latency components. The data are arranged as in Fig. 1

The spacing between ripples can be quantified by extracting it from the total microphonic using signal processing (Fig. 7). When the simulated $\widehat{\mathrm{CM}}$ includes all three components (green), the ripple spacing tends to be narrower than when $\widehat{\mathrm{CM}}$ is computed without the late component. Comparison with the ripple spacing obtained from the total measured CM (black) shows that the simulations nicely capture the change in ripple spacing across frequency. In the mid-frequency range, the data agree better with the spacing predicted for ${\widehat{\mathrm{CM}}}_{\mathrm{EL}+\mathrm{ML}}$ responses (red) than for ${\widehat{\mathrm{CM}}}_{\mathrm{EL}+\mathrm{ML}+\mathrm{LL}}$ (green), plausibly due to our overestimation of round-trip travel times in the ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ model computations (see above). The ripple spacing is determined by the relative delay between the contributing components. This concept can be better visualized if the ripple spacing of the $\widehat{\mathrm{CM}}$ consisting of early- and late-latency components (blue) is compared to the spacing obtained for a mixture of early- and middle-latency components (red). Because the phase of the long-latency component rotates more rapidly with frequency than the phase of the middle-latency component, the ${\widehat{\mathrm{CM}}}_{\mathrm{LL}}$ is in and out of phase with ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ at narrower frequency intervals, resulting in narrower ripple spacing (Fig. 7, blue).

DISCUSSION

Further Evidence for Origin of the Delayed CM Components in the Peak Region of the BM Excitation

The interference pattern observed in the round-window CM (Fig. 1) suggests contributions from components with different phase-gradient delays (Fig. 2) that may originate in different cochlear regions. The delayed CM components, but not the early-latency CM, are effectively diminished in magnitude in the presence of a near-probe saturating tone (Fig. 2). This result suggests that the delayed CM components originate in the active peak region of the BM response to the probe tone where nonlinear two-tone interactions are strong (Rhode 2007a). The additional data reproduced in Fig. 8, obtained as a part of another experiment (Charaziak et al. 2017), further support this conclusion. The data show that the spectral ripples observed in the CM responses to low-level tones (black) are diminished (1) at higher probe levels (dotted red; linearly scaled down), (2) in the presence of a near-probe saturating tone (solid red), and (3) following acoustic trauma that causes a mild threshold elevation (dashed gray; see caption for details). In each of these three experimental conditions, the cochlear gain at the CF place is known to be decreased (Robles and Ruggero 2001), and the reduced rippling patterns suggest that the delayed components, but not necessarily the early ones, are diminished in magnitude. In contrast, the spectral ripples are affected relatively little with a tendency for small increase in the ripple depth when the frequency of the saturating tone is set more than an octave above the probe tone (blue). Such remote saturating tones do not suppress cochlear gain at the CF place (Rhode 2007a) and are therefore unlikely to affect the CM components originating in that region. Instead, a decrease in the overall CM level is observed in the presence of the remote saturator, consistent with suppression of sources located in the tail region of the BM response to the probe tone, where large early-latency components originate. While these preliminary results reveal promising trends, a more systematic study of dependence of different latency CM components on active cochlear processing is warranted. Better understanding of how different CM components are shaped by active cochlear processing could improve interpretation of changes in CM seen due to activation of the efferent system, application of ototoxic drugs or genetic mutations (Gifford and Guinan 1987; Fitzgerald et al. 1993; Cheatham et al. 2011; Elgueda et al. 2011). Measurements with intracochlear electrodes placed near the CF place of the stimulus support the existence of “active” CM potentials demonstrating nonlinear growth and, at low levels, sharp tuning with rotating phase characteristics (Dallos et al. 1974; Fridberger et al. 2002, 2004; Dong and Olson 2013). Whether these intracochlearly measured nonlinear CM potentials correspond to the delayed CM components seen at the RW needs further investigation.

Fig. 8.

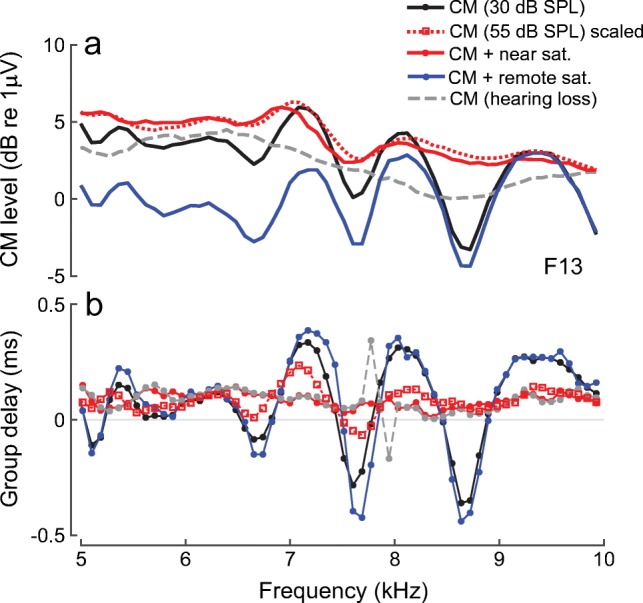
a, b Round-window CM measured in response to 30-dB SPL tones in a normal cochlea (solid black) and following acute acoustic trauma causing a mild threshold elevation (~ 20–30 dB CAP threshold shift over the 3–10-kHz range; dashed gray). The solid colored lines show responses for a normal cochlea measured when the probe stimulus is presented together with 55-dB SPL saturating tone fixed at either nearby (f_s ≈ f_p; red) or an octave higher frequency (f_s = 2.1f_p; blue). The red dotted line shows the CM, scaled down by 25 dB, measured and plotted at the frequency of the 55-dB SPL saturating tone. It is assumed that the responses to the 55-dB SPL saturating tone are not affected by the presence of a 30-dB SPL probe tone. All data from animal F13 as in Charaziak et al. (2017)

Spectral Ripples in CM Responses and in Ear-Canal Pressure

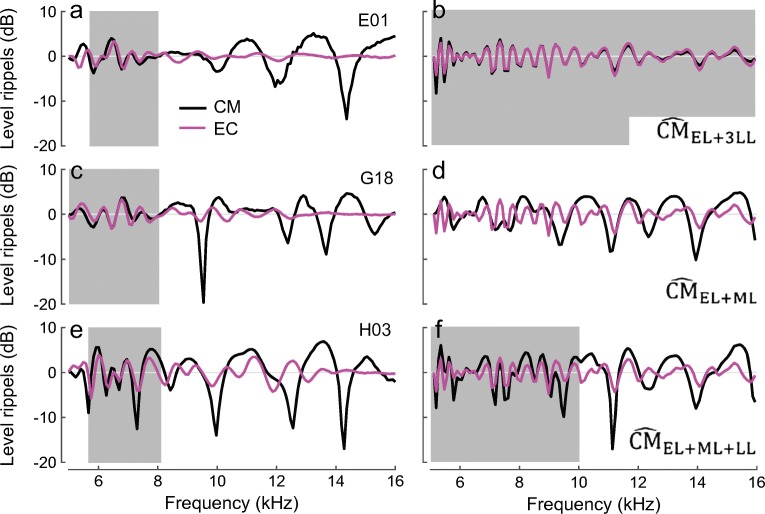
Are all three components necessary to explain the existence of spectral ripples in the round-window CM? In theory, the spectral ripples can emerge in the CM response as interference between the early components and either late- or middle-latency components (Fig. 9b, d, black). Additional insights into that problem can be provided by comparing the CM ripples with the rippling pattern observed in the ear-canal pressure. It is well known that the quasiperiodic ripples in the ear-canal pressure are due to interference between the evoking tone and the delayed SFOAE (e.g., Kemp and Chum 1980; Zwicker and Schloth 1984; Shera and Zweig 1993). Because middle-ear delays are small compared to cochlear round-trip travel times, the model predicts that the pattern of spectral ripples evident in ear-canal pressure should be correlated with the ripples observed in the round-window CM due to interference between early and late CM components, as simulated in Fig. 9b. This is because our model predicts that late CM originates through a process of internal cochlear reflection closely related to the generation of SFOAEs. In the data, we observed a good match between the CM and ear-canal pressure rippling patterns in about 50 % of the animals, but only at lower frequencies (Fig. 9, the gray boxes in the left-side plots). This observation agrees with the results of the component unmixing, where the late-latency components are typically larger than the middle-latency components at the lowest frequencies (Fig. 3a) as they are less susceptible to the effects of the electrical attenuation with distance. For higher frequencies, where the middle-latency components contribute more to the CM response, the CM rippling pattern does not correlate with the ear-canal pressure ripples, as predicted by the simulations (Fig. 9d, f). The rather abrupt change in the correlation between the CM and ear-canal rippling patterns with frequency provides independent evidence of the existence of at least two delayed CM components with different phase gradients that mix with the early-latency CM.

Fig. 9.

Spectral ripples in the total CM (black) and ear-canal pressure (EC, magenta) levels measured in three animals (a, c, e) and simulated for three different CM compositions (b, d, f). The level ripples were extracted as in Fig. 1. The gray boxes identify the frequency ranges where CM and EC ripples appear to be well correlated. The EC pressure was simulated as a mixture of constant stimulus pressure and SFOAE [with SFOAE(f_p) ~ R(f_p)(1 + R_s) and R given by Eq. (3)]. The CM at the RW was simulated as a mixture of different combinations of early-, middle-, and late-latency components, as indicated on each panel. Note that in b the relative magnitude of the late component was adjusted (increased threefold) to produce visible ripples in the total response. Because we employed a simplified version of Eq. (3) (see text), round-trip delays for the SFOAE and late-latency CM are overestimated in the simulations, resulting in generally closer spacing of the ripples compared to the data (e.g., magenta in a and b)

Species Differences

To the best of our knowledge, high-resolution CM measurements of the type used here to test models of CM generation are not available in other species, with the partial exception of gerbils. In contrast to the round-window CM in chinchillas, the CM in gerbils does not appear to exhibit strong rippling patterns, even at low stimulus levels (He et al. 2012). However, the CM measurements extend only to the relatively low (for gerbils) frequency of 10 kHz. Based on the chinchilla data, the largest contribution to the round-window CM from middle-latency components occurs for tones with CFs mapped to basal cochlear locations due to their proximity to the electrode. This agrees with observations in mice, where round-window CM suppression tuning curves are sharply tuned only at very high probe frequencies, as would be expected if the place-specific middle-latency component dominated the measured signal (Cheatham et al. 2011). Furthermore, CM rippling patterns resulting from interference with late-latency CM components are expected in species with strong intracochlear reflections such as chinchillas and humans (Dhar et al. 2002; Siegel et al. 2011; Shera and Cooper 2013). In contrast, relatively weak reflection-source OAEs in gerbils and mice (Kemp 1986; Siegel et al. 2011) suggest such reflections may be small, if present at all in these species. While high-resolution CM measurements in other species will undoubtedly provide additional insights into CM generation, species differences in cochlear frequency maps, in electrical attenuation constants, and in the length and shape of the cochlea (e.g., the number of turns) all complicate interspecies comparisons.

Interpretation of CM Phase: Place- and Wave-Fixed Components

In the classical theory of CM generation, the frequency invariance of round-window microphonic phase has been ascribed to the dominance of contributions from CM sources located in the basal region of the cochlea (He et al. 2012). We suggest, however, that the shallow phase gradient of the classical CM derives primarily from the presumed mechanism rather than from the place of CM generation. In other words, because the classical theory ignores the role of micromechanical and microelectrical irregularity, it predicts that CM phase gradients are shallow no matter where the sources are located. A useful analogy here is to “wave-fixed” OAE sources—the phase of wave-fixed OAEs is nearly independent of frequency in a scaling-symmetric cochlea (e.g., Kemp and Brown 1983; Shera and Guinan Jr 1999). When combined with an exponential cochlear frequency-position map, scaling symmetry implies that traveling wave excitation patterns are locally translation-invariant, with the number of wavelengths in the traveling wave remaining nearly independent of frequency. Thus, even though a low-frequency wave travels farther than a high-frequency wave to reach its CF place, both waves travel the same number of wavelengths, and their total phase accumulation is therefore the same (Shera and Guinan 2008). As a result, the phase of wave-fixed components—whether they be components of OAEs or components of the CM—cannot vary with frequency. Wave-fixed mechanisms, no matter where they operate in the cochlea, must give rise to early-latency components.

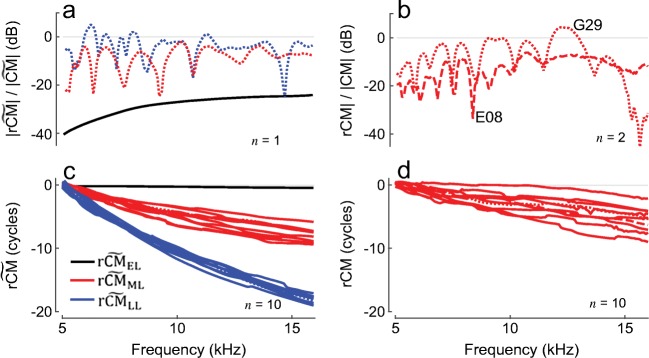
To validate this reasoning computationally, we use the classical model to evaluate contributions to ${\widehat{\mathrm{CM}}}_{\mathrm{EL}}$ arising from the CF region—such contributions can arise due to incomplete cancelation of sources within the peak region. According to the wave-fixed hypothesis, peak region contributions to the classical CM should have a shallow phase slope despite their more apical origin. In the model, these peak region components can be extracted by simply restricting the summation to locations near the CF place. Alternatively, the peak region components can be also extracted with a help of a near-probe saturating tone (Charaziak et al. 2017). Because this additional tone saturates the transducer currents of the hair cells located near its own CF place (Geisler et al. 1990), contributions from these cells to the total response can be gauged by deriving the complex difference between probe-tone responses obtained with and without the saturating tone (i.e., residual CM). In the limit that the saturating tone has no effect on the probe-frequency CM sources, the residual CM (rCM) is ideally zero (in the absence of noise). In the opposite limit, the saturating tone completely suppresses all sources, and rCM equals the probe-alone response. In practice, because of phase-interference effects, the round-window probe response can either decrease or increase in the presence of the saturating tone, even though the saturator always reduces the local source currents (see also Nuttall and Dolan 1991). In the model, the residual CM response closely resembles the features of the peak components extracted by simply restricting the summation to the CF region in Eq. (1). Because the rCM can also be obtained from experimental data, only the modeled results of extracting the peak region components with a saturating tone are discussed in the subsequent paragraphs.

To simulate two-tone interactions in the classical model, we modified Eq. (1) so that the local source excitation becomes proportional to the local BM displacement fed through a saturating transducer function. Specifically,

$$\begin{array}{c}{\widetilde{\mathrm{CM}}}_{\mathrm{EL}}\left(f_{\mathrm{p}}\right)=\sum _i{V}_{0}w\left(x_i\right)\widehat{N}\left[D_{\mathrm{BM}}\left(x_i,f_{\mathrm{p}}\right)\right],\end{array}$$ 4

where the diacritical “~” indicates the nonlinear model and $\widehat{N}$[∙] is an operator that converts the Fourier coefficient D_BM(x, f_p) into the corresponding time waveform d_BM(x, t), combines that waveform with an optional saturating tone, passes the sum through a saturating transducer function [a second-order Boltzmann function; see Eq. (3) in (Charaziak et al. 2017) for details], and then extracts the modified Fourier component at frequency f_p from the distorted waveform. We derived the residual microphonic ($\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$) by calculating ${\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$ for BM displacement profiles obtained for single- (probe-alone) or two-tone (probe+saturating tone) stimuli. The saturating tone parameters were set to approximate those used in the measurements [L_s = L_p + 30 dB and f_s = f_p-86 Hz], with all other parameters set as in (Charaziak et al. 2017).

Figure 10a, c shows model results for $\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$ magnitude and phase, respectively (black). The $\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$ levels are 30–40 dB below the probe-alone ${\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$ level, indicating that the peak region of the BM excitation pattern contributes to the round-window CM, but that these contributions are relatively small (Fig. 10a, black), especially at low frequencies, due both to their attenuation with distance and the mutual phase cancelation that occurs among sources located near the CF region. Most importantly, even though $\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$ components originate near the peak region of the BM excitation (Charaziak et al. 2017), $\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$ phase is nearly independent of frequency, implying close to zero phase-gradient delay (Fig. 10c, black). Thus, because it assumes wave-fixed CM sources, the classical model of CM generation cannot produce CM components with long delays, even when the sources are located in the peak region of the traveling wave. Small but nonzero phase gradients for the early-latency CM component can be introduced by imperfect scaling at the level of the BM, by the effects of electrical attenuation with distance (which violate “electrical scaling”), and, perhaps most significantly, by delays associated with stimulus transmission though the ear canal and middle ear. In agreement with this latter view, He et al. (2012) showed in gerbils that round-window CM phase, when referenced to the stapes motion, is essentially independent of frequency across a wide range of frequencies. In summary, the classical model predicts that CM phase gradients are shallow no matter where the sources are located.

Fig. 10.

Examples of modeled (a, c) and measured (b, d) CM suppression residuals. Residual levels are expressed relative to corresponding smoothed probe-alone response levels. Exemplary residual CM levels measured in two chinchillas are shown in b (E08, G29) and 10 randomly chosen unwrapped phase functions are shown in d. Modeled CM residuals for early-, middle-, and late-latency CM components (black, red, and blue, respectively) are shown for one “ear” in a and 10 randomly chosen phase functions in c. The CM residuals were calculated as described in Charaziak et al. (2017). Attenuation with distance was assumed at a rate of 2 dB/mm, and BM displacement profiles for tone and saturator stimuli were modeled after 30- and 60-dB SPL responses from cochlea L208

Contrasting $\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{EL}}$ with measured CM residuals (Fig. 10b, d) reinforces the failure of the classical (wave-fixed) model to fully account for the CM generation process. Unlike the small peak region components predicted by the classical model, those present in the data (rCM) can have magnitudes approaching the level of the probe-alone CM. In addition, rather than varying smoothly with frequency, as predicted by the classical model, the measured rCM manifests a quasiperiodic pattern of peaks and notches and shows considerable phase accumulation with frequency (from 2 to 9 cycles over the displayed range). To generate peak region components with the observed characteristics, the classical model must be extended to incorporate the effects of cochlear irregularities [Eq. (2)]—just as with OAEs, longer latency CM components require place-fixed mechanisms (e.g., micromechanical and/or microelectrical irregularity). Although the two roughness-dependent CM components (the middle- and late-latency components) arise by different mechanisms, both depend on BM responses near the peak region of the traveling wave, and their respective residuals ($\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{ML}}$ and $\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{LL}}$) are therefore of substantial magnitude [Fig. 10a, c, red and blue; to simulate suppression, we modified Eq. (2) by analogy with Eq. (4)]. These two CM components behave in a fashion similar to “place-fixed” OAEs, for which the source phase is tightly linked to the intracochlear location of the source. For $\mathrm{r}{\widetilde{\mathrm{CM}}}_{\mathrm{LL}}$, the relationship between the component phase and the underlying place of origin is indirect. Just as with the early-latency CM components, the late-latency components are dominated by potentials produced by hair cells located in the tail region of the total BM excitation pattern. But the hair cells that generate the late potentials are responding not directly to the primary forward traveling wave but to a reverse traveling (OAE) wave that originates in the peak region of the BM excitation and its stapes reflection (Fig. 4). Thus, suppressing the reverse wave with a near-probe saturating tone diminishes the long-latency CM through this indirect route. Furthermore, the model predicts that the long-latency CM, but not the middle component, should be also suppressible by remote saturating tones, similar to the early-latency CM. Unfortunately, the data at hand obtained with both remote and near-probe saturating tones (Fig. 8) suffer from too poor resolution in the latency domain to clearly observe the predicted patterns.

Model Limitations

We developed our model of CM generation with the goal of explaining the various components seen in the data rather than providing a complete account of the many complexities involved in CM generation. The model ignores the complicated electroanatomy of the spiral cochlea and its possible implications for round-window responses (e.g., Dallos 1984; Chertoff et al. 2012; Ayat et al. 2015). For instance, the spiral shape of the cochlea may affect the effective electrical attenuation factor, which may not be an entirely monotonic function of longitudinal distance (Chertoff et al. 2012). Furthermore, the model assumes a simple proportionality between the local CM response and BM displacement. Although this proportionality is well documented in the tail region of the traveling wave, cochlear potentials near the CF place appear more in phase with BM velocity (Dong and Olson 2013). As a result, an abrupt ¼ cycle relative phase shift occurs in local CM responses near the boundary between the tip and tail. Our simulations are robust against inclusion of this phase shift, but we cannot exclude the possibility that abrupt phase shifts may have important effects on CM summation patterns in more realistic models. Lastly, the majority of our simulations have assumed a linear cochlea. Although inclusion of a saturating transducer function in the model allows qualitative simulation of nonlinear two-tone interactions in CM responses, our implementation does not capture the full, mutually dependent relationship between active BM responses and hair-cell transduction. For example, the nonlinearities measured in cochlear potentials do not simply mirror those seen in BM vibrations (Dong and Olson 2013); these differences may well affect the degree of suppression seen in the various CM components. Despite these limitations, our simple model of CM generation reproduces the trends in the data reasonably well; additional data that reveal discrepancies with model predictions may provide motivation for the development of more comprehensive models.

Summary

This study demonstrates that chinchilla round-window CM measured in response to low-level tones exhibits an idiosyncratic pattern of spectral ripples in magnitude and phase-gradient delay (Fig. 1, black). We show that the spectral ripples are reduced both in the presence of a near-probe saturating tone (Fig. 1, red) and after removing delayed CM components in the latency domain (Fig. 3, black). These results are consistent with the hypothesis that spectral ripples are caused by the interference between CM components with shallow and steep phase gradients. Further dissection of the delayed CM in the latency domain reveals middle- and long-latency components, CM_ML and CM_LL(Fig. 3). Although both delayed components are diminished in the presence of the near-probe saturating tone (Fig. 2), consistent with their origin in the active peak region, they depend differently on probe frequency: whereas CM_ML levels increase with frequency, CM_LL levels show the opposite pattern (Fig. 3a).

By extending the classical model of CM generation to include the effects of cochlear irregularities—both mechanical and electrical—we predict two additional mechanisms of CM generation. These two mechanisms give rise to middle- and late-latency CM components (Figs. 4 and 5) that mix with the early-latency CM at the RW, producing spectral ripples (Fig. 6). In the model, the middle-latency components originate via the novel mechanism of coherent summation of CM sources near the CF place, while the late-latency components arise through the internal reflection of cochlear traveling waves that produces SFOAEs. Both mechanisms require that the BM traveling wave interacts with some sort of cochlear roughness or irregularity distributed along the partition (Zweig and Shera 1995). The model suggests that, unlike the early-latency components, the delayed CM components depend on cochlear responses in the active near-CF region of the probe response and could therefore be utilized as place-specific assays of cochlear function. Despite its simplicity, the model replicates the trends in the data remarkably well (e.g., compare Figs. 1 and 3 and Figs. 5 and 6; also Fig. 7). While our results reveal the existence of additional, previously unnoticed CM components, our data do not contradict the notion that the round-window CM is usually dominated by cellular sources located within the tail region of the BM excitation pattern, particularly at high stimulus levels (Fig. 8).