Diffusion Compartmentalization Using Response Function Groups with Cardinality Penalization

Abstract

Spherical deconvolution (SD) of the white matter (WM) diffusion-attenuated signal with a fiber signal response function has been shown to yield high-quality estimates of fiber orientation distribution functions (FODFs). However, an inherent limitation of this approach is that the response function (RF) is often fixed and assumed to be spatially invariant. This has been reported to result in spurious FODF peaks as the discrepancy of the RF with the data increases. In this paper, we propose to utilize response function groups (RFGs) for robust compartmentalization of diffusion signal and hence improving FODF estimation. Unlike the aforementioned single fixed RF, each RFG consists of a set of RFs that are intentionally varied to capture potential signal variations associated with a fiber bundle. Additional isotropic RFGs are included to account for signal contributions from gray matter (GM) and cerebrospinal fluid (CSF). To estimate the WM FODF and the volume fractions of GM and CSF compartments, the RFGs are fitted to the data in the least-squares sense, penalized by the cardinality of the support of the solution to encourage group sparsity. The volume fractions associated with each compartment are then computed by summing up the volume fractions of the RFs within each RFGs. Experimental results confirm that our method yields estimates of FODFs and volume fractions of diffusion compartments with improved robustness and accuracy.

1 Introduction

Diffusion magnetic resonance imaging (DMRI) is a powerful imaging modality due to its unique ability to extract microstructural information by utilizing restricted diffusion to probe compartments that are much smaller than the voxel size. One important goal of DMRI is to estimate axonal orientations, tracing of which will allow one to gauge connectivity between brain regions. For estimation of axonal orientations, a widely used method, constrained spherical deconvolution (CSD) [1], estimates the fiber orientation distribution function (FODF) by deconvolving the measured diffusion-attenuated signal with a spatially-invariant kernel representing the signal response function (RF) of a single coherent fiber bundle. Unlike the multi-tensor approach, CSD does not require the specification of the number of tensors to fit to the data. However, it has been recently reported that a mismatch between the kernel used in CSD and the actual fiber RF can cause spurious peaks in the estimated FODF [2]. Although CSD has been recently extended to include RFs of not only the white matter (WM), but also the gray matter (GM) and the cerebrospinal fluid (CSF) [3], these RFs remain spatially fixed and similar shortcomings as reported in [2] apply.

In this paper, we propose to estimate the WM FODF and the volume fractions of the GM and CSF compartments by using response function groups (RFGs). Each RFG is a collection of exemplar RFs aimed at capturing the variations of the actual RFs. Unlike the conventional approach of using fixed RFs, the utilization of RFGs will allow tolerance to RF variations and hence minimize estimation error due to RF and data mismatch. Several RFGs are included to cater to the WM, GM, and CSF compartments. The WM is represented by a large number of directional RFGs with orientations distributed uniformly on the unit sphere. Each WM RFG consists of a set of unidirectional axial-symmetric diffusion tensors with a range of typical axial and radial diffusivities. The GM and CSF RFGs consist of isotropic tensors with diffusivities of GM RFs set lower than CSF RFs, consistent with what was reported in [3]. The FODF and compartmental volume fractions for each voxel are estimated by solving a group cardinality (i.e., l₀-“norm”) penalized least-squares problem that aims to preserve the group structure of the RPGs while at the same time encourage sparsity. Our work is an integration of concepts presented in [3–5] with a novel estimation framework.

Recently, Daducci et al. [6] linearize the fitting problem of ActiveAx and NODDI to drastically speed up axon diameter and density estimation by a few orders of magnitude. They achieve this by solving an l₁ minimization problem with a design matrix containing instances of the respective biophysical models generated with a discretized range of parameters. The results reported in [6] are supportive of the fact that variation of diffusion signals should be explained not only in terms of varying volume fractions but also in terms of varying model parameters. Similar to [6], we observe that by using RFGs containing RFs of varying parameters, the data can be explained with greater fidelity than by using RFs with a single fixed set of parameters. Dissimilar to [6], our work (i) is not limited to single fiber populations and explicitly considers fiber crossings, (ii) solves a cardinality penalized problem instead of the l₁ problem, and (iii) explicitly considers the natural coupling between RFs via sparse-group estimation, similar but not identical to [7].

We propose here to directly minimize the cardinality penalized problem instead of resorting to reweighted ℓ₁ minimization as performed in [8]. By doing so, we (i) overcome the suboptimality of reweighted minimization, and (ii) improve estimation speed greatly by avoiding having to solve the l₁ minimization problem (especially the sparse-group problem [7]) multiple times to gradually improve sparsity. We will describe in this paper an algorithm based on iterative hard thresholding (IHT) to effectively and efficiently solve the cardinality penalized sparse-group problem.

2 Proposed Approach

2.1 Response Function Groups (RFGs)

At each voxel, the diffusion-attenuated signal $S(b,\widehat{\mathbf{g}})$, measured for diffusion weighting b and at direction $\widehat{\mathbf{g}}$, can be represented as a mixture of N models: $S(b,\widehat{\mathbf{g}})={\displaystyle {\sum }_{i=1}^N{f}_i{S}_i}(b,\widehat{\mathbf{g}})+\epsilon (b,\widehat{\mathbf{g}})$, where f_i is the volume fraction associated with the i-th model S_i and $\epsilon (b,\widehat{\mathbf{g}})$ is the fitting residual. In the current work, we are interested in distinguishing signal contributions from WM, GM, and CSF and choose to use the tensor model $S_i(b,\widehat{\mathbf{g}})=S_0\exp (-b{\widehat{\mathbf{g}}}^{\mathrm{T}}{\mathbf{D}}_i\widehat{\mathbf{g}})$, where S₀ is the baseline signal with no diffusion weighting and D_i is a diffusion tensor. This model affords great flexibility in representing different compartments of the diffusion signal. Setting D = λI, the model represents isotropic diffusion with diffusivity λ. When λ = 0 and λ > 0 the model corresponds to the dot model and the ball model, respectively [9]. Setting $\mathbf{D}=({\mathrm{\lambda }}_{\Vert }-{\mathrm{\lambda }}_{\perp })\widehat{\mathbf{v}}{\widehat{\mathbf{v}}}^{\mathrm{T}}+{\mathrm{\lambda }}_{\perp }\mathbf{I},{\mathrm{\lambda }}_{\Vert }>{\mathrm{\lambda }}_{\perp }$, the model represents anisotropic diffusion in principal direction $\widehat{\mathbf{v}}$ with diffusivity λ_║ parallel to $\widehat{\mathbf{v}}$ and diffusivity λ_⊥ perpendicular to $\widehat{\mathbf{v}}$. When λ_⊥ = 0 and λ_⊥ > 0 the model corresponds to the stick model and the zeppelin model, respectively. In our case, each of these tensor models is a representation of an RF.

The solution to SD [1] can be obtained in discretized form by including in the mixture model a large number of anisotropic tensors uniformly distributed on the unit sphere with fixed λ_║ and λ_⊥ and solving for {f_i} by minimizing the error in the least-squares sense with some appropriate regularization, giving us the FODF. In this work, instead of fixing λ_║ and λ_⊥, we allow them to vary across a range of values. Therefore, each principal direction is now represented by a group of RFs, forming a RFG. Additional isotropic RFGs are included to account for signal contributions from GM and CSF. Formally, the representation can be expressed as

$$S(b,\widehat{\mathbf{g}})=\underset{\widehat{S}(b,\widehat{\mathbf{g}})}{\underbrace{{\displaystyle \sum _{i=1}^{N_{\text{WM}}}{S}_i^{\text{WM}}(b,\widehat{\mathbf{g}})+S^{\text{GM}}(b,\widehat{\mathbf{g}})+}{S}^{\text{CSF}}(b,\widehat{\mathbf{g}})}}+\epsilon (b,\widehat{\mathbf{g}}),$$ (1)

where we have N_WM WM RFGs, a GM RFG, and a CSF RFG with $S_i^{\text{WM}}(b,\widehat{\mathbf{g}})={\displaystyle {\sum }_{j=1}^{K_{\text{WM}}}{f}_{i,j}^{\text{WM}}\exp (-b{\widehat{\mathbf{g}}}^{\mathrm{T}}{\mathrm{D}}_{i,j}^{\text{WM}}\widehat{\mathbf{g}})}$, $S^{\text{GM}}(b,\widehat{\mathbf{g}})={\displaystyle {\sum }_{j=1}^{K_{\text{GM}}}{f}_j^{\text{GM}}}\exp (-b{\widehat{\mathbf{g}}}^{\mathrm{T}}{\mathbf{D}}_j^{\text{GM}}\widehat{\mathbf{g}})$, $S^{\text{CSF}}(b,\widehat{\mathbf{g}})={\displaystyle {\sum }_{j=1}^{K_{\text{CSF}}}{f}_j^{\text{CSF}}\exp (-b{\widehat{\mathbf{g}}}^{\mathrm{T}}{\mathbf{D}}_j^{\text{CSF}}\widehat{\mathbf{g}})}$ and ${\mathbf{D}}_{i,j}^{\text{WM}}=({\mathrm{\lambda }}_{\Vert ,j}^{\text{WM}}-{\mathrm{\lambda }}_{\perp ,j}^{\text{WM}}){\widehat{\mathbf{v}}}_i{\widehat{\mathbf{v}}}_i^{\mathrm{T}}+{\mathrm{\lambda }}_{\perp ,j}^{\text{WM}}\mathbf{I},{\mathbf{D}}_j^{\text{GM}}={\mathrm{\lambda }}_j^{\text{GM}}\mathbf{I},{\mathbf{D}}_j^{\text{CSF}}={\mathrm{\lambda }}_j^{\text{SCF}}\mathbf{I}$. Given the signal $S(b,\widehat{\mathbf{g}})$, we need to estimate the volume fractions $\left\{f_{i,j}^{\text{WM}}\right\}$, $\left\{f_j^{\text{GM}}\right\}$, and $\left\{f_j^{\text{CSF}}\right\}$. Note that we have dropped S₀ here because it can be absorbed into the volume fractions. The normalized volume fractions can be recovered by dividing the unnormalized volume fractions by S₀. It is easy to see that if we take a Fourier transform of (1), these volume fractions are in fact weights that decompose the ensemble average propagator (EAP) of the overall signal as a weighted sum of the EAPs of the individual tensors. The overall volume fractions associated with WM, GM, and CSF are $f^{{\text{WM}}_i}={\displaystyle {\sum }_{j=1}^{K_{\text{WM}}}{f}_{i,j}^{\text{WM}}}$, $f^{\text{GM}}={\displaystyle {\sum }_{j=1}^{K_{\text{GM}}}{f}_j^{\text{GM}}}$, $f^{\text{CSF}}={\displaystyle {\sum }_{j=1}^{K_{\text{CSF}}}{f}_j^{\text{CSF}}}$. The set $f^{{\text{WM}}_i}$ over i gives the WM FODF. For notation simplicity, we group the volume fractions into a vector $\mathbf{f}=[{\mathbf{f}}^{{\text{WM}}_1};\dots ;{\mathbf{f}}^{{\text{WM}}_{N_{\text{WM}}}};{\mathbf{f}}^{\text{GM}};{\mathbf{f}}^{\text{CSF}}]$.

2.2 Estimation of Volume Fractions

To obtain an estimate of the volume fractions, we solve the following optimization problem: ${min}_{\mathbf{f}\ge 0}\left\{\varphi (\mathbf{f})={\Vert S(b,\mathbf{g})-\widehat{S}(b,\mathbf{g})\Vert }_2^2+\alpha \gamma {\Vert \mathbf{f}\Vert }_0+(1-\alpha )\gamma \left[{\displaystyle {\sum }_{i=1}^{N_{\text{WM}}}\mathrm{ℐ}({\Vert {\mathbf{f}}^{{\text{WM}}_i}\Vert }_2)+\mathrm{ℐ}({\Vert {\mathbf{f}}^{\text{GM}}\Vert }_2)+\mathrm{ℐ}({\Vert {\mathbf{f}}^{\text{CSF}}\Vert }_2)}\right]\right\}$, where $\mathrm{ℐ}(z)$ is an indicator function returning 1 if z ≠ 0 or 0 if otherwise. The l₀-“norm” gives the cardinality of the support, i.e., ||f||₀ = |supp(f)| = |{k : f_k ≠ 0}|. Parameters a ∈ [0, 1] and γ > 0 are for penalty tuning, analogous to those used in the sparse-group LASSO [7]. Note that α = 1 gives the l₀ fit, whereas α = 0 gives the group l₀ fit. The problem can be written more succinctly in matrix form: ${min}_{\mathbf{f}\ge 0}\left\{\varphi (\mathbf{f})={\Vert \mathbf{A}\mathbf{f}-\mathrm{s}\Vert }_2^2+\alpha \gamma {\Vert \mathbf{f}\Vert }_0+(1-\alpha )\gamma {\displaystyle {\sum }_{g\in G}\mathrm{ℐ}({\Vert {\mathbf{f}}_g\Vert }_2)}\right\}$, where f_g denotes the subvector containing the elements associated with group $g\in G=\left\{{\text{WM}}_1,\dots ,{\text{WM}}_{N_{\text{WM}}},\text{GM},\text{CSF}\right\}$. If s is the signal vector acquired at D (b, g)-points, A = [A^WM|A^GM|A^CSF] is a D × N matrix (N = N_WM K_WM + K_GM + K_CSF) with columns containing all the individual WM, GM, and CSF tensor models sampled at the corresponding D points. To the best of our knowledge, the solution to this problem has not been described elsewhere. We will therefore provide next the details of our algorithm.

2.3 Optimization

The problem we are interested in solving has the following form: min_f≥0{ϕ(f) = l(f)+r(f)}, where in our case $l(\mathbf{f})={\Vert \mathbf{A}\mathbf{f}-\mathrm{s}\Vert }_2^2$ is smooth and convex and $r(\mathbf{f})=\alpha \gamma {\Vert \mathbf{f}\Vert }_0+(1-\alpha )\gamma {\displaystyle {\sum }_{g\in G}\mathrm{ℐ}}({\Vert {\mathbf{f}}_g\Vert }_2)$ is non-convex, non-smooth, and discontinuous. Note that the solution is trivial, i.e., f* = 0, when $\gamma \ge {\Vert \mathrm{s}\Vert }_2^2$. We will solve this problem using an algorithm called non-monotone iterative hard thresholding (NIHT), as described in the following.

Non-monotone Spectral Projected Gradient

Choose factor τ > 1, step size constants L_min < L_max, line search constant η > 0, stopping tolerance ∊ > 0, and integer-valued non-monotone descent parameter M > 0. For iteration k = 0, set $L_0^{(0)}=1$ and initial solution to f⁽⁰⁾. Then proceed with the following steps to obtain the solution:

1. Set $L^{(k)}=L_0^{(k)}$.

   • 1a)
     Solve the subproblem

     $${\mathbf{f}}^{\left(k+1\right)}\in \text{Arg}\underset{\mathbf{f}\ge 0}{min}\left\{l\left({\mathbf{f}}^{(k)}\right)+\nabla l{\left({\mathbf{f}}^{(k)}\right)}^{\mathrm{T}}\left(\mathbf{f}-{\mathbf{f}}^{(k)}\right)+\frac{L^{(k)}}{2}{\Vert \mathbf{f}-{\mathbf{f}}^{(k)}\Vert }_2^2+r(\mathbf{f})\right\}.$$
   • 1b)
     If $\varphi \left({\mathbf{f}}^{\left(k+1\right)}\right)\le {max}_{{[k-M]}^{+}\le i\le k}\varphi \left({\mathbf{f}}^{\left(i\right)}\right)-\frac{\eta }{2}{\Vert {\mathbf{f}}^{\left(k+1\right)}-{\mathbf{f}}^{\left(k\right)}\Vert }_2^2$ is satisfied, then go to Step 2.
   • 1c)
     Set L^(k) ← τL^(k) and go to Step 1a.

2. If |ϕ(f^(k+1)) − ϕ(f^(k))|/max(ϕ(f^(k+1)), 1) < ε is satisfied, then return f^(k+1) as a solution. Otherwise, go to Step 3.

3. Set $L_0^{\left(k+1\right)}=max\left\{L_{min},min\left\{L_{max},\frac{\Delta l^{\mathrm{T}}\Delta \mathbf{f}}{{\Vert \Delta \mathbf{f}\Vert }_2^2}\right\}\right\}$, where Δf = f^(k+1) − f^(k) and Δl = ∇l(f^(k+1)) − ∇l(f^(k)).

4. Set k ← k + 1 and go to Step 1.

The algorithm above seeks the solution via gradient descent using a majorization-minimization (MM) formulation of the problem. Step 1a minimizes the majorization of the objective ϕ(·) at f^(k). It can be shown that the minimization involves a gradient descent step with step size 1/L^(k) (more details in the next section). The parameters L_min and L_max constrain the step size so that it is neither too aggressive nor too conservative (Step 3). We choose the initial step size $1/L_0^{(k)}$ as proposed by Barzilai and Borwein in [10], using a diagonal matrix $1/L_0^{(k)}$ I to approximate the inverse of the Hessian matrix of l(f) at f^(k) (Step 3). A suitable step size is determined via backtracking line search, where the step size is progressively shrunk by a factor of 1/τ (Step 1c). Parameter η makes sure that the backtracking line search results in a sufficient change of the objective. Since the problem is non-monotone, i.e., the objective function is not guaranteed to decrease at every iteration, we require the objective to be slightly smaller than the largest objective in M previous iterations (Step 1b). For M > 0, the algorithm may increase the objective occasionally but will eventually converge faster than the monotone case with M = 0. Parameter ε controls the stopping condition (Step 2). We divide |ϕ(f^(k+1)) − ϕ(f^(k))| by max(ϕ(f^(k+1)), 1) to compute the relative change or the absolute change of the objective, whichever is smaller. In this work, the following parameters were used: L_min = 1 × 10⁻², L_max = 1 × 10⁸, η = 1 × 10⁻⁴, τ = 2, = 1 × 10⁻³, and M = 10.

Solution to Subproblem

The subproblem is group separable and can be shown to be equivalent to solving the problem separately for each group g ∈ G. With some algebra, the subproblem associated with group g can be shown to be equivalent to ${\mathbf{f}}_g^{\left(k+1\right)}\in \text{Arg}{min}_{{\mathbf{f}}_g\ge 0}\left\{{\varphi }_g\left({\mathbf{f}}_g\right)={\Vert {\mathbf{f}}_g-{\mathbf{z}}_g^{\left(k\right)}\Vert }_2^2+\frac{2}{L^{\left(k\right)}}r\left(\mathbf{f}\right)\right\}$, where z^(k) = f^(k) − ∇l(f^(k))/L^(k) = f^(k) − 2A^T(Af^(k) − b)/L^(k) and ${\mathbf{z}}_g^{\left(k\right)}$ is a subvector of z^(k) associated with group g. If we let ${\stackrel{\sim }{\mathrm{\gamma }}}_1^{\left(k\right)}=2\alpha \mathrm{\gamma }/L^{(k)}$, and ${\stackrel{\sim }{\mathrm{\gamma }}}_1^{\left(k\right)}=2\left(1-\alpha \right)\mathrm{\gamma }/L^{(k)}$, the solution to the problem can be obtained by hard thresholding. If $\stackrel{\sim }{\mathbf{z}}={\text{hard}}_{+}\left({\mathbf{z}}_g^{\left(k\right)},{\stackrel{\sim }{\mathrm{\gamma }}}_1^{\left(k\right)}\right)$, where hard₊ (z, γ)_i = z_i if if $z_i>\sqrt{\mathrm{\gamma }}$ and 0 otherwise, the solution to the subproblem is ${\mathbf{f}}_g^{\left(k+1\right)}=\stackrel{\sim }{\mathbf{z}}$ if ${\Vert \stackrel{\sim }{\mathbf{z}}\Vert }_2^2>{\stackrel{\sim }{\mathrm{\gamma }}}_1^{\left(k\right)}{\Vert \stackrel{\sim }{\mathbf{z}}\Vert }_0+{\stackrel{\sim }{\mathrm{\gamma }}}_2^{\left(k\right)}$ and 0 otherwise. Note that the sparse-group LASSO [7] can be implemented in a similar fashion by replacing the above solution with a soft-thresholding version.

3 Experimental Results

3.1 Data

For reproducibility, diffusion weighted (DW) data from the Human Connectome Project (HCP) were used. The 1.25 × 1.25 × 1.25 mm³ data were acquired with diffusion weightings b = 1000, 2000, and 3000 s/mm² each applied in 90 directions. 18 baseline images with low diffusion weighting b = 5s/mm² were acquired.

3.2 Diffusion Parameters

The parameters of the RFGs were set to cover the typical values of the diffusivities of the WM, GM, and CSF voxels in the above dataset: ${\mathrm{\lambda }}_{\Vert }^{\text{WM}}=1\times {10}^{-3}{\text{mm}}^2/s$, ${\mathrm{\lambda }}_{\perp }^{\text{WM}}=\left[0.1:0.1:0.3\right]\times {10}^{-3}{\text{mm}}^2/s$, λ^GM = [0.00 : 0.01 : 0.80] × 10⁻³ mm²/s, and λ^CSF = [1.0 : 0.1 : 3.0] × 10⁻³ mm²/s. The notation [a : s : b] denotes values from a to b, inclusive, with step s. Note that in practice, these ranges do not have to be exact but should however cover the range of possible parameter variation. The WM RFGs are distributed evenly on 321 points on a hemisphere, generated by subdivision of the faces of an icosahedron.

3.3 Comparison Methods

We compared the proposed method (L200-RFG) with the following methods: L0-RF: l₀ minimization using a single RF each for WM, GM, and CSF [3]. Similar to [3], WM-GM-CSF segmentation was used to help determine the parameters for the RFs. The axial and radial diffusivities of the WM RFs were determined based on WM voxels with fractional anisotropy (FA) greater than 0.7. The diffusivity of the isotropic GM/CSF RF was determined based on GM/CSF voxels with FA less than 0.2. L211-RFG: Sparse-group LASSO [7] using RFGs identical to the proposed method. Similar to [8], we executed sparse-group LASSO multiple times, each time reweighing the l₂₁-norm and the l₁-norm so that they eventually approximate their l₀ counterparts. The tuning parameter γ was set to 1 × 10⁻⁴ for all methods. In addition, we set α = 0.05 for the proposed method.

3.4 Results

Volume Fractions

The top row of Fig. 1 shows that the proposed method, even with no spatial regularization, is able to produce WM, GM, CSF volume fraction estimates that match quite well with the anatomy shown by the T₁-weighted image. The second row of the figure shows color-coded volume-fraction images generated by convex combinations of green, blue, and red using the WM, GM, and CSF volume fractions, respectively, as the weights. The results confirm the benefits of using RFGs over just RFs for the WM, GM, and CSF compartments. Compared with l₁ penalization, our method based on cardinality penalization yields cleaner volume fraction estimates especially for cortical GM.

Fig. 1.

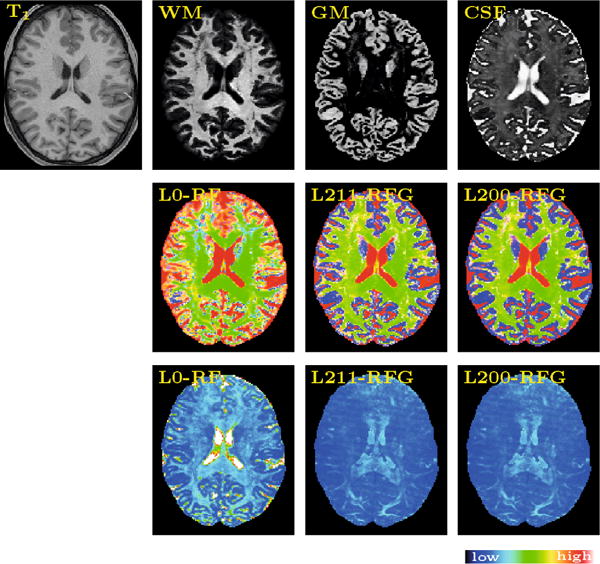
(Top) Volume fractions of WM, GM, and CSF obtained by the proposed method. The T₁-weighted image is provided for reference. (Middle) Color-coded volume fraction images and (Bottom) fitting-residual images obtained by the various methods.

Fitting Residuals

The last row of Fig. 1 indicates that using only a RF for each compartment is inadequate for explaining the data sufficiently, resulting in large fitting errors for some voxels. This also indicates that there is a mismatch between the RFs and the data. By using RFGs, the fitting residuals are smaller and relatively uniform spatially.

FODFs

The FODFs at the WM-GM interface are significantly affected by partial volume effect, with the signal being a mixture of contributions from WM and GM. Fig. 2 shows an example of the WM FODFs estimated at a WM-GM interface. The GM and CSF compartments are discarded and not shown. The proposed method in general yields FODFs that penetrate deeper into the GM when compared with L0-RF and that have a smaller amount of false-positive peaks when compared with L211-RFG. These observations indicate that the proposed method is able to effectively extract directional information that is buried within confounding signals.

Fig. 2.

WM FODFs at WM-GM interface. The glyphs are normalized to have unit integral.

4 Conclusion

We have shown that the estimation of the WM FODF and the GM and CSF volume fractions can be improved by using response function groups in a cardinality-penalized estimation framework. Our method provides the flexibility of including different diffusion models in different groupings for robust microstructural estimation. Future work includes incorporating complex diffusion models [9] for estimation of subtle properties such as axonal diameter. We will also apply our method to the investigation of pathological conditions such as edema.