A Class of Semiparametric Cure Models with Current Status Data

Abstract

Current status data occur in many biomedical studies where we only know whether the event of interest occurs before or after a particular time point. In practice, some subjects may never experience the event of interest, i.e., a certain fraction of the population is cured or is not susceptible to the event of interest. We consider a class of semiparametric transformation cure models for current status data with a survival fraction. This class includes both the proportional hazards and the proportional odds cure models as two special cases. We develop efficient likelihood-based estimation and inference procedures. We show that the maximum likelihood estimators for the regression coefficients are consistent, asymptotically normal, and asymptotically efficient. Simulation studies demonstrate that the proposed methods perform well in finite samples. For illustration, we provide an application of the models to a study on the calcification of the hydrogel intraocular lenses.

1 Introduction

Current status data occur in many biomedical and health studies, where the exact onset of the event of interest cannot be observed directly and we only know whether or not the event has occurred at the time the sample is collected. For example, in a tumorigenicity experiment that involves lung tumors in mice (Hoel and Walburg, 1972), only an indicator of lung tumor presence or absence at time of death was observed. A second example is the Calcification study of the hydrogel infraocular lenses (IOL), which is an infrequently reported complication of cataract treatment (Yu et al, 2001). The exact time to the occurrence of calcification is not observable. Instead, the calcification status was observed at the time of examination.

Current status data have been investigated extensively in literature. Groeneboom and Wellner (1992) derived the nonparametric maximum likelihood estimator (NPMLE) of the survival function of time to event. Methods for the regression analysis of current status data include the Cox proportional hazards model (Huang, 1996), the proportional odds model (Rossini and Tsiatis, 1996; Huang and Rossini, 1997), and the additive hazard model (Lin et al, 1998). More recently, partly linear accelerated failure time (AFT) model and partly linear transformation models were proposed by Xue et al (2004) and Ma and Kosorok (2005), respectively. There is an inexplicit assumption in all the aforementioned methods that the event will eventually occur for all subjects given a sufficient long time of follow-up.

In many studies, it is observed that a proportion of subjects never experiences the event of interest, i.e., they are cured or not susceptible to the event of interest. The aforementioned standard survival analysis techniques may no longer be appropriate in such situations. Alternatively, survival models that allow for a cured subgroup are more desirable. Such models generally are referred to as “cure models”. Under the cure model, the survival function, denoted by S, is allowed to be improper, i.e., S(∞) > 0. There is an abundant literature on cure rate models incorporating a cure fraction for right censored data. Perhaps the most commonly used cure rate model is the mixture model first introduced by Berkson and Gage (1952). This model assumes that the underlying population consists of a cured sub-population and a sub-population not being cured. This mixture cure model and its extensions have been studied by many investigators, including Farewell (1982, 1986), Gray and Tsiatis (1989), Kuk and Chen (1992), Taylor (1995), Sy and Taylor (2000), Peng and Dear (2000), Betensky and Schoenfeld (2001), and Lu and Ying (2004), among others. A comprehensive discussion of the mixture cure model is given in Maller and Zhou (1996).

The mixture cure model, however, does have several drawbacks both from a frequentist and Bayesian perspective as noted by Chen et al (1999) and Ibrahim et al (2001). One particular drawback is that the mixture cure model does not appear to describe the underlying biological process generating the failure time in the context of cancer relapse. The test of the effects of one covariate (on the cure fraction and the hazard rate in the uncured sub-population) has a degree of freedom of two and consequently can potentially compromise the power of the test. Furthermore, the EM-algorithm is often used to estimate the unknown parameters in the mixture cure models, which may increase the computation burden especially when there are no closed form solutions in the M-step. Additionally, in the Bayesian inference, the mixture cure model can yield improper posterior distributions for many non-informative improper priors, including the uniform prior for regression coefficients.

Alternatively, Yakovlev and Tsodikov (1996) proposed the promotion time cure model, which was further studied by Tsodikov (1998), Chen et al (1999), and Tsodikov et al (2003), among others. This model has a proportional hazards structure, a desirable feature of survival models, yields proper posterior distributions under a wide class of non- informative improper priors for the regression coefficients, and also has biological motivations (Chen et al, 1999). In this model, the population survival function for a subject with covariates Z is given by

$$S_{\text{pop}}(t\mid \mathbf{Z})=exp\{-e^{{\mathit{\beta }}^T\mathbf{Z}}F(t)\},$$ (1)

where F(t) is a distribution function. This model integrates the survival function for either cured subjects or non-cured subjects into one single formulation and assumes that the cured subjects have survival time equal to infinity. The hazard function corresponding to (1) is λ_pop(t|Z) = e^βTZf(t), where f(t) = dF(t)/dt. The cure rate under model (1) is lim_t→∞ S_pop(t|Z) = exp(−e^βTZ). The promotion time cure model is also referred to as the proportional hazards cure model. As a matter of fact, the above promotional time cure model can be derived from a biological process generating the relapse time in cancer patients. For a cancer patient, let N denote the number of carcinogenic cells, which is assumed to follow a Poisson distribution with mean θ. Here θ may depend on some covariates, e.g., θ = e^βTZ. We denote by Y_i the random time for the ith carcinogenic cell to produce a detectable cancer mass. We assume that Y_i’s are i.i.d. with a distribution function F(·) and are independent of N. It then can be shown that the probability of cancer free by time t for the patient is exp{−θF(t)}, which takes the same form as the survival function in (1).

To further increase the flexibility of the promotional time cure model, Zeng et al (2006b) proposed the following class of cure rate models by using Box-Cox type of transformations

$$S_{\text{pop}}(t\mid \mathbf{Z})=G_{\gamma }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(t)\},$$ (2)

where

$$G_{\gamma }(x)=\{\begin{array}{ll}{(1+\gamma x)}^{-1/\gamma },\hfill & \gamma >0\hfill \\ e^{-x},\hfill & \gamma =0.\hfill \end{array}$$

This class of models include the proportional hazards cure model and the proportional odds cure model as special cases. When γ = 0, model (2) reduces to the proportional hazards cure model; when γ = 1, model (2) has the proportional odds structure. This class of cure models have sound biological basis and provide flexible alternatives to the mixture cure models.

The studies of cure rate models for current status data are relatively limited. Lam and Xue (2005) considered a partly linear AFT model for susceptible subjects and used a sieve maximum likelihood approach. Ma (2008) and Ma (2009) used additive risk model and linear or partly linear Cox models (Cox, 1972), respectively, to model the event time in the susceptible population. In all three papers, the authors considered mixture cure rate models. Cook et al (2008) also considered parametric and semiparametric mixture cure models but focused on the estimation of covariates effects on the cure rate only. Liu and Shen (2009) considered the proportional hazards cure model for interval-censored data and proved the strong consistency of the maximum likelihood estimators under the Hellinger distance.

In this article, we investigate current status data with a cure fraction. Particularly, we consider the class of transformation models (2). Although this class of models have been well studied for right-censored data, such models have not been used to analyze current status data and the extension is far from trivial. Our research aims to fill in this gap both theoretically and practically. In the next section, we derive the likelihood function and propose using maximum likelihood approach for estimation. In section 3 we establish the asymptotic properties of the proposed maximum likelihood estimators (MLEs). In Section 4 we conduct simulation studies to evaluate the finite-sample properties of the estimators and also illustrate the proposed model with the Calcification data. We conclude with a brief discussion in Section 5 and provide technical details for the proofs in the Appendix.

2 Maximum Likelihood Estimation

Suppose that there are n i.i.d. observations. For i = 1, …, n, we observe {Y_i, Δ_i = I(T_i ≤ Y_i), Z_i}, where T_i is the failure time for member i, Y_i is the random censoring or inspection time, Z_i is a vector of bounded covariates, and I(·) is the indicator function. The first component of Z_i is 1. We assume that the inspection time Y_i is conditionally independent of T_i given Z_i.

We consider model (2). The observed-data likelihood function for the parameters (β, F) can be expressed, for fixed γ, as

$$L_n(\mathit{\beta },F)-\prod _{i=1}^n{\left[1-G_{\gamma }\{e^{{\mathit{\beta }}^T{\mathbf{Z}}_i}F(Y_i)\}\right]}^{{\mathit{\Delta }}_i}{\left[G_{\gamma }\{e^{{\mathit{\beta }}^T{\mathbf{Z}}_i}F(Y_i)\}\right]}^{1-{\mathit{\Delta }}_i}.$$

We wish to to obtain the maximum likelihood estimators of (β, F) by maximize the above likelihood function over the parameter space

$$\mathit{\Theta }=\{(\mathit{\beta },F):\mathit{\beta }\text{is}\text{in}\mathrm{a}\text{compact}\text{set},\Vert \mathit{\beta }\Vert \le B,F(·)\text{is}\mathrm{a}\text{cumulative}\text{distribution}\text{function}\text{on}[0,\infty )\}.$$

It is obvious that the MLEs exist since the likelihood function is bounded from above by 1 and Θ is weakly compact. The MLEs, however, are not unique since the likelihood function depends on F only through the its values at the observed times Y_i, i = 1, …, n. Thus we focus on the maximization of L_n(β, F) over all nondecreasing step functions with jumps at the Y_i’s for F(t). We denote the MLEs of β and F by β̂_n and F̂_n. Furthermore, we claim that F̂_n can only have jumps at those Y_i’s with Δ_i = 1. Let s₁ < ··· < s_m denote the ordered distinct time points of Y_i, i = 1, …, n with associated Δ_i = 1. For a subject with Δ_i = 0 and s_k < Y_i < s_k+1, consider two distribution functions F₁ and F₂, which have the same values at all time points except that F₁(Y_i) = F₁(s_k) and F₂(Y_i) > F₁(s_k). Since G_γ(·) is a decreasing function, it can be easily shown that L_n(β, F₁) > L_n(β, F₂). Therefore, F̂_n can have positive jumps only at s_k, k = 1, …, m. Similarly, we can show that F̂_n(s_m) = 1 since F is a proper distribution function. Therefore we maximize the likelihood function subject to the constraint that 0 ≤ F(s₁) ≤ ··· ≤ F(s_m) = 1.

The pool-adjacent-violator (PAV) approach (Barlow et al, 1972; Robertson et al, 1988) is often used in the optimization problems with monotone constraints, e.g., see Groeneboom and Wellner (1992), van der Laan and Jewell (2001), and Ma (2008, 2009). Alternatively, in this paper we use the following transformation

$$F(s_k)=1-e^{-{\sum }_{j=1}^k{e}^{{\alpha }_j}},k=1,\dots ,m-1$$

and the constrained optimization problem reduces to the maximization of the likelihood function over (β, α₁, …, α_m−1) without constraints. For small m, Newton-Raphson algorithm can be used to solve the score equations for β and {α_k, k = 1, …, m − 1}. When m is large, we use the quasi-Newton method of Broyden, Fletcher, Goldfarb and Shanno (or the so-called BFGS algorithm) as described in Press et al (1992) to search for the optimum. The BFGS algorithm refines an approximation of the inverse Hessian matrix at each iteration via a rank-one update. Therefore, although the number of parameters under the proposed model increases with sample size, the computation burden for obtaining the NPMLEs increases linearly with sample size. In our experience, the BFGS algorithm performs well even when there are thousands of parameters. This algorithm has been successfully applied in optimization problems with a large number of parameters, e.g., see Diao et al (2013) and Yuan and Diao (2014). It is well known that for interval-censored data, the MLE of the distribution function may have zero mass at some inspection times even with Δ = 1. Numerically, the estimates of the jumps of F are negligible (< 10⁻⁶) at those time points. The same transformation technique was also used by Zeng et al (2006a) to estimate the cumulative hazard function under the semiparametric additive risks model for interval-censored data.

3 Asymptotic Properties

We first impose the following assumptions:

• (C1)Covariates Z_i are bounded with probability one. Furthermore, if there exists a constant vector β such that β^TZ_i = 0 almost surely, then β = 0.
• (C2)Conditional on Z_i, the inspection time Y_i is independent of T_i.
• (C3)There exists a constant t₀ < ∞ such that P(T_i > t₀|Z_i) = P(T_i = ∞|Z_i) > 0 almost surely. Furthermore, the inspection time Y_i is a random variable from a distribution with support [τ_l, τ_u] with 0 ≤ τ_l < t₀ ≤ τ_u < ∞ and P(Y_i ≥ t₀|Z_i) > 0.
• (C4)
  The true values of β, denoted by β₀, belong to the interior of a known compact set,

  $$\mathcal{B}=\{\mathit{\beta }:\Vert \mathit{\beta }\Vert \le B\text{for}\text{some}\text{constant}B\},$$

  where ||·|| is the Euclidean norm.

• (C5)
  The true promotion time cumulative distribution function F₀ belongs to the space

  $$\mathcal{F}=\{F:F\text{is}\mathrm{a}\text{cumulative}\text{distribution}\text{function}\text{on}[0,\infty )\text{and}\text{has}\text{strictly}\text{positve}\text{first}\text{order}\text{derivatives}\text{on}[{\tau }_l,t_0]\}.$$

Remark 1

Condition (C1) is the usual linear independence condition of Z_i in regression settings. Conditions (C2), (C4), and (C5) are standard assumptions in semiparametric inferences with failure time data. Condition (C3) assumes that no new cases occur after t₀ and that t₀ is in the support of inspection time. Under this assumption, all censored observations beyond t₀ are treated as “T_i = ∞” (i.e., observed to be cured) and we can discriminate between cured and un-cured observations. The constant t₀ serves as the “cure threshold” defined in Zeng et al (2006b). This condition is needed to ensure the identifiability of the unknown parameters (β, F). Note that for a parametric cure rate model, the condition that some subjects are observed to be cured is not needed. More details on the identifiability of cure models are provided in Li et al (2001). For practical data analysis, we can set t₀ = s_m or choose a threshold value suggested by clinicians. In the mixture cure rate model setting, Ma (2008, 2009) set Λ̂(t) = ∞ for t > max{Y_i : i = 1, …, n}, where Λ is the baseline cumulative hazard function for the un-cured sub-population. This technique is essentially the same as setting t₀ = s_m.

Remark 2

For right-censored failure time data, Zeng et al (2006b) imposed the assumption P(Y_i = ∞|Z_i) > 0. However with current status data Y_i = ∞ implies Δ_i = 1 regardless of whether T_i = ∞ or not therefore such observations are not informative.

Under conditions (C1) – (C3), the parameters β and F are identifiable. Suppose that two sets of parameters, (β, F) and (β̃, F̃), give the same likelihood function for the observed data, i.e., if for almost all (Z, Y),

$${[1-G_{\gamma }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\}]}^{\mathit{\Delta }}{[G_{\gamma }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\}]}^{1-\mathit{\Delta }}={[1-G_{\gamma }\{e^{{\stackrel{\sim }{\mathit{\beta }}}^T\mathbf{Z}}\stackrel{\sim }{F}(Y)\}]}^{\mathit{\Delta }}{[G_{\gamma }\{e^{{\stackrel{\sim }{\mathit{\beta }}}^T\mathbf{Z}}\stackrel{\sim }{F}(Y)\}]}^{1-\mathit{\Delta }},$$

we claim that β = β̃ and F(t) = F̃(t) for every t ∈ [τ_l, t₀]. In fact, by condition (C3), F(t) = F̃(t) = 1 for any t ≥ t₀. Let Y = t₀, we have G_γ(e^βTZ) = G_γ(e^β̃TZ). Then, from the monotonicity of G_γ, it follows that β^TZ = β̃^T Z for almost all Z. Thus condition (C1) gives β = β̃. Furthermore, by letting Δ = 1 and Y = t, τ_l ≤ t < t₀, we have G_γ{e^βTZF(t)} = G_γ{e^βTZ F̃(t)}. It then follows that F(t) = F̃(t) for any t ∈ [τ_l, t₀].

We establish the consistency of the MLEs in the following theorem.

Theorem 1. (Consistency)

Under conditions (C1), (C3) and (C4), ||β̂_n−β₀|| → 0 and sup_t∈[τl,t0] |F̂_n(t) − F₀(t)| → 0 almost surely.

We outline the proof here and defer the details to Appendix A.1. Let

$$p(Y,\mathbf{Z},\mathit{\Delta }\mid \mathit{\beta },F)={\left[1-G_{\gamma }\left(e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\right)\right]}^{\mathit{\Delta }}{\left[G_{\gamma }\left(e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\right)\right]}^{1-\mathit{\Delta }},$$

and

$$m(Y,\mathbf{Z},\mathit{\Delta }\mid \mathit{\beta },F)=log\frac{p(Y,\mathbf{Z},\mathit{\Delta }\mid \mathit{\beta },F)}{p(Y,\mathbf{Z},\mathit{\Delta }\mid {\mathit{\beta }}_0,F_0)}$$

be the log-likelihood ratio. Let d((β, F), (β₀, F₀)) = ||β−β₀||+sup_t∈[τl,b0] |F(t)− F₀(t)|, and ℳ = {m(Y,Z,Δ|β, F) : (β, F) ∈ ℬ×ℱ}. We show that ℳ is a P-Glivenko-Cantelli class, and m(Y,Z,Δ|β, F) satisfies some other conditions. If follows from Theorem 5.8 in van der Vaart (2002) that

$$d(({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n),({\mathit{\beta }}_0,F_0))\stackrel{a.s.}{\to }0.$$

This gives the desired result.

With the consistency result, we can establish the following result on convergence rate of the MLEs.

Lemma 1. (Convergence rate)

Under conditions (C1), (C3) and (C4),

$$d(({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n),({\mathit{\beta }}_0,F_0))=O_p(n^{-1/3})$$

Groeneboom and Wellner (1992) established that the best convergence rate for estimates of the nonparametric distribution function with one-sample current status data is n^1/3. Huang (1996) and Ma (2008, 2009) obtained similar results for the estimates of the baseline cumulative hazard function in the Cox model (Cox, 1972) and the mixture cure rate model, respectively. Lemma 1 indicates that the optimal convergence rate can be achieved under the proposed cure rate model. The detailed proof of Lemma 1 is given in Appendix A.2.

Before stating the result for the asymptotic normality of β̂_n, we derive the efficient score function for β. The log-likelihood for a single observation X ≡ (Y, Δ, Z), denoted by l(β, F), takes the form

$$l(\mathit{\beta },F)=\mathit{\Delta }log[1-G_{\gamma }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\}]+(1-\mathit{\Delta })log[G_{\gamma }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\}].$$

The score function for β is the first derivative of l(β, F) with respect to β and takes the form

$$l_{\beta }(\mathit{\beta },F)=\mathbf{Z}F(Y)Q(X;\mathit{\beta },F),$$

where

$$Q(X;\mathit{\beta },F)=e^{{\mathit{\beta }}^T\mathbf{Z}}{G}_{\gamma }^{\prime }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\}\left[-\frac{\mathit{\Delta }}{1-G_{\gamma }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\}}+\frac{1-\mathit{\Delta }}{G_{\gamma }\{e^{{\mathit{\beta }}^T\mathbf{Z}}F(Y)\}}\right]$$

and $G_{\gamma }^{\prime }$ is the first derivative of G_γ. For a function g in [τ_l, τ_u] with bounded total variation, the score function for F along the direction of g is given by

$$l_F(\mathit{\beta },F)[g]=g(Y)Q(X;\mathit{\beta },F).$$

Project the score function of β onto the space generated by l_F (β, F)[g], and for g = (g₁, …, g_d) with d = dim(β), denote l_F (β, F)[g] = (l_F (β, F)[g₁], …, l_F (β, F)[g_d])^T. We obtain the efficient score function for β at the true parameter

$$l_{\beta }^{\ast }({\mathit{\beta }}_0,F_0)=l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }],$$

where

$${\mathbf{g}}^{\ast }(Y)=F_0(Y)\frac{E(\mathbf{Z}{Q}^2(\mathbf{X};{\mathit{\beta }}_0,F_0)\mid Y)}{E(Q^2(\mathbf{X};{\mathit{\beta }}_0,F_0)\mid Y)}.$$

Write $I_{\beta }({\mathit{\beta }}_0,F_0)=E[l_{\beta }^{\ast }({\mathit{\beta }}_0,F_0)l_{\beta }^{\ast T}({\mathit{\beta }}_0,F_0)]$. In the appendix, we will show that I_β(β₀, F₀) is positive definite and component-wise bounded.

With the derived convergence rate and the efficient score function for β, we can obtain the following asymptotic normality results for β̂_n.

Theorem 2. (Asymptotic normality)

Under conditions (C1)–(C4), $\sqrt{n}({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)$ converges weakly to a zero-mean normal distribution with variance $I_{\beta }^{-1}({\mathit{\beta }}_0,F_0)$.

Theorem2 states that although the convergence rate of (β̂_n, F̂_n) is considerably slower than the n^1/2 rate for right censored data, we can still obtain the $\sqrt{n}$ consistency and asymptotic normality of β̂_n. Furthermore, we conclude that β̂_n is the most efficient estimator for β₀ as $I_{\beta }^{-1}({\mathit{\beta }}_0,F_0)$ attains the semiparametric efficiency bound for β₀. The proof of Theorem 2 is provided in Appendix A.3.

Let 𝔹(·) be the two-sided Brownian motion originating from zero: a mean zero Gaussian process on R with 𝔹(0) = 0, and E(𝔹(s) − 𝔹(h)² = |s − h| for all s, h ∈ R. Denote $\stackrel{D}{\to }$ for convergence in distribution. Let w_n be the random variable that given the Z_i’s, w_n takes $e^{-{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}{G}_{\gamma }^{-1}(1-i/n)-e^{-{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_{i+1}}{G}_{\gamma }^{-1}(1-(i+1)/n)$ with probability 1/n. Denote w = w(Z) for its asymptotic version conditioning on Z. Let f₀(·) be the derivative of F₀(·).

To derive the asymptotic distribution of F̂_n, we make two additional assumptions.

• (C6)Function G_γ satisfies $0<{lim}_{x\to \infty }{G}_{\gamma }^{-1}(1/x)/x<\infty$.
• (C7)The density function of Y, g(t) > 0 with t ∈ [τ₁, t₀].

Theorem 3

Assume (C1)–(C7), then ∀t ∈ [τ₁, t₀],

$$n^{1/3}({\widehat{F}}_n(t)-F_0(t))\stackrel{D}{\to }{\left(\frac{4{\eta }^2(t)f_0(t)}{g(t)}\right)}^{1/3}arg\underset{h\in R}{min}\{\mathbb{B}(h)+h^2\},$$

where η₂(t) = E[(I(T ≤ t)w(Z) − F₀(t))²].

The distribution of arg min_h∈R{𝔹(h)+h²} is called Chernoff distribution, the density function of which was derived in Groeneboom (1989). It has no closed form and is not easy to evaluate. Kosorok (2008) proposed a sampling method to evaluate this distribution. The proof of Theorem 3 is in Appendix A.4.

Remark 3

The inference above is based on the selected model with the transformation parameter γ fixed. To select the best model, we may choose the transformation which minimizes the Akaike information criterion (AIC), which is defined as twice the negative log-likelihood function plus twice the number of parameters. It is theoretically possible to accounting for the variation due to the model selection procedure. The computation, however, may be demanding or unstable. Furthermore, whether this kind of variation should be accounted for is up to debate (Box and Cox, 1982). In the subsequent simulation studies, we will fix the transformation whereas in the data application, we will use the AIC to select the best transformation.

4 Numerical Studies

4.1 Simulation

We conducted simulation studies to examine the finite sample performance of our proposed methodology. We generated data from model (2) with Z = (1, Z₁, Z₂)^T, where Z₁ is a uniform random variable in [0, 1], and Z₂ is a Bernoulli random variable with a success probability 0.5. The true parameter values of β = (β₀, β₁, β₂) are are set to be (−0.5, 1, −0.5); and F(t) = 1 − {exp(−t) − exp(−t₀)}I(t ≤ t₀)/{1−exp(−t₀)}, where t₀ = 4. The inspection time was set to be the minimum of 4 and an exponential variable with mean 2. We considered five different models by varying the values of γ from 0 to 1. The average cure rate ranged from 0.45 to 0.56 as α changed from 0 to 1, whereas the censoring proportion among those un-cured subjects was about 0.26 for all five models.We considered sample sizes of 200 and 400 for each model. For each simulation set-up, we generated 1,000 data sets. The quasi-Newton algorithm implemented in C language was applied to maximize the log-likelihood function. The initial values of the regression parameters were set to be 0 and the initial jump sizes of F were set to be 1/m at s₁, …, s_m. The convergence of the quasi-Newton algorithm was very fast and it took about 0.3 second to analyze one data set with 400 subjects on a Dell PowerEdge 2900 server.

Table 1 summarizes the results for each combination of γ and n. The column labeled as “Mean” denotes the sampling mean of the parameter estimator from the true parameter value; “SE” is the sampling standard error of the parameter estimator; “SEE” is the mean of the standard error estimator, which is calculated based on the inverse of the observed information; and “CP(%)” is the coverage probability of the 95% confidence interval based on the asymptotic normal approximation. The proposed estimators appear to be unbiased. The estimate of the standard error reflects accurately the true variation, and for moderate sample size and cluster size the confidence intervals have proper coverage probabilities. As the sample size increases from 200 to 400, the standard deviations of the estimates shrink at approximately the $\sqrt{2}$ rate.

Table 1.

Summary Statistics for the Maximum Likelihood Estimators

Model	n	Parameter	True value	Estimate	SE	SEE	CP(%)
γ = 0	200	β1	1	1.047	0.436	0.427	94.7
		β2	−0.5	−0.538	0.249	0.245	94.9
	400	β1	1	1.029	0.302	0.294	94.1
		β2	−0.5	−0.522	0.168	0.169	94.9
γ = 0.25	200	β1	1	1.048	0.481	0.471	95.0
		β2	−0.5	−0.540	0.275	0.270	93.3
	400	β1	1	1.031	0.334	0.325	94.5
		β2	−0.5	−0.523	0.183	0.187	95.2
γ = 0.5	200	β1	1	1.044	0.525	0.511	94.4
		β2	−0.5	−0.54	0.298	0.293	94.3
	400	β1	1	1.026	0.367	0.353	94.0
		β2	−0.5	−0.524	0.199	0.203	95.7
γ = 0.75	200	β1	1	1.048	0.569	0.550	93.8
		β2	−0.5	−0.541	0.321	0.315	95.4
	400	β1	1	1.030	0.395	0.379	94.1
		β2	−0.5	−0.525	0.215	0.218	95.0
γ = 1	200	β1	1	1.054	0.602	0.587	94.2
		β2	−0.5	−0.547	0.344	0.336	95.1
	400	β1	1	1.032	0.417	0.404	94.4
		β2	−0.5	−0.529	0.234	0.232	94.3

The next line of simulation studies concerned about the performance of the commonly used proportional hazards cure model and the proportional odds cure model when data were generated from a different model. Specifically, we used the same setting for generating data in the simulation studies described earlier. The model with γ = 1/2 corresponds to a model between the proportional hazards cure model and the proportional odds cure models. For each simulation setting, we generate 1,000 replications with sample size of n = 400. The results are summarized in Table 2. We observe when the true model is the proportional hazards cure model, the regression parameters from the proportional odds cure model are overestimated, whereas the parameters from the proportional hazards cure model are underestimated when the proportional proportional odds cure model is true. In general, when the transformation parameter is between 0 and 1, the proportional hazards cure model tends to bias towards 0, whereas the opposite is observed for the proportional odds cure model. Note that both models estimate the direction of the coefficients correctly under misspecified transformation. We also observe that standard error estimates of the regression coefficients corresponding to the covariates appear to be correct although the parameter estimates are biased.

Table 2.

Simulation Results Under Misspecified Transformation

Model	Parameter	True value	Estimate	SE	SEE	CP(%)
True transformation: G(x) = e−x
Proportional odds model	β1	1	1.396	0.415	0.405	84.6
	β2	−0.5	−0.706	0.228	0.231	86.7
True transformation: G(x) = (1+x)−1
Proportional hazards model	β1	1	0.806	0.325	0.316	89.7
	β2	−0.5	−0.414	0.185	0.183	92.9
True transformation: G(x) = (1+x/2)−2
Proportional hazards model	β1	1	0.889	0.317	0.305	92.1
	β2	−0.5	−0.455	0.174	0.176	95.2
Proportional odds model	β1	1	1.168	0.420	0.402	92.6
	β2	−0.5	−0.595	0.226	0.230	93.9

4.2 Application to the Calcification Study

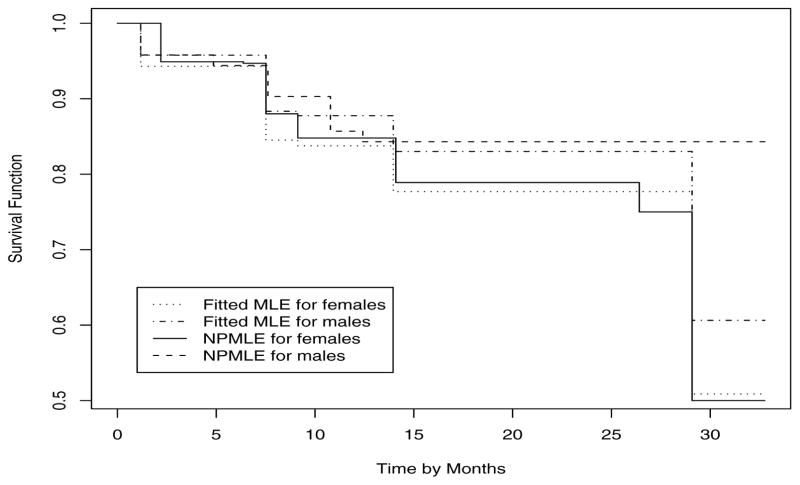
As an illustration, we applied our proposed model to the Calcification study of Yu et al (2001). The objective of the study was to investigate the effects of certain clinical factors on the time to IOL calcification after implantation. The status of calcification for each of the 379 patients in the study was determined by an experienced ophthalmologist at a random time ranging from 0 to 36 months after implantation. Covariates of interest include incision length, gender, and age at implantation. One individual with missing measurement on incision length was excluded from the analysis. Of the remaining 378 individuals, 48 experienced calcification before examination time. The nonparametric maximum likelihood estimates of the survival functions for males and females at the end of study were 0.844 and 0.5, respectively.

In our data analysis, we included incision length, gender, and age at implantation as covariates in the cure models. Let Z₁ be the incision length, Z₂ be gender that takes values 0 and 1 for female and male patients, respectively, and Z₃ be the age at implantation divided by 10. We fit the proposed model (2) with Z = (1, Z₁, Z₂, Z₃)^T. We compared the proportional hazards cure model and the proportional odds cure model, and those models in between. As suggested by Zeng et al (2006b), we selected the proportional odds cure model which maximizes the Akaike information criterion (AIC). The AIC is defined as the twice log-likelihood function minus twice the number of parameters. The results under the proportional odds cure model are presented in Table 3. We see that males and older people are more likely to be cured and increase in incision length leads to an decrease in cure rate, although their effects are not significant. Our findings agree well with those of Lam and Xue (2005). Furthermore, to give a graphical comparison, Figure 1 plots the separate nonparametric estimates of the survival curve and the model-fitted survival curve for each gender group. The model-fitted survival function is calculated as the empirical average of the predicted survival functions. The dotted and dot-dashed lines in Figure 1 present the predicted survival functions; these in general agree quite well with the nonparametric estimates of the survival curves. The big difference between the fitted survival function and the nonparametric estimate of the survival function for males at the tail is due to that the largest inspection time in male patients with the occurrence of calcification was 17.6 months. Therefore the nonparametric estimate of the survival function for males is flat whereas the MLE of F₀ in the fitted model has jumps beyond that time point. Figure 1 indicates that the proportional odds cure model fits the data well.

Table 3.

Maximum Likelihood Estimates of Regression Coefficients in the Proportional Odds Cure Model for the Calcification Data

Covariate	Estimate	SE	Est/SE	p-value
Intercept	0.354	0.075	4.689	<0.001
Incision length	0.447	0.260	1.719	0.086
Gender (male)	−0.310	0.343	−0.906	0.365
Age/10	−0.136	0.216	−0.626	0.531

Fig. 1.

Nonparametric estimates and proportional odds cure model-fitted survival functions of time to IOL calcification. The model-fitted survival function is calculated as the empirical average of the predicted survival functions for each gender group.

5 Discussion

We have considered a class of semiparametric cure models by imposing the Box-Cox type transformation on the population survival function for the analysis of current status data with a cured proportion in the population. This class includes the well-known proportional hazards and proportional odds structures as two special cases and has great potential in clinical trials and for modeling survival data with a cure fraction. We have developed efficient likelihood-based estimation and inference procedures and shown that the MLEs of the regression parameters are consistent, asymptotically normal and asymptotically efficient. The inference in this paper is based on the selected model with the transformation parameter fixed. As suggested by Zeng et al (2006b) we use the AIC to select the best model. It would be of interest to estimate the variances of the MLEs of the regression parameters accounting for the variation due to the model selection procedure in semiparametric inference. Future research is warranted.

We have developed an efficient algorithm implemented in C language for calculating the MLEs and standard error estimates of the MLEs under the proposed models. The computation is substantially faster than the PAV approach under the mixture cure model in Ma (2009). This significant improvement makes it possible to apply our methods to genetic studies in which linkage or association tests are performed at hundreds of thousands of genetic markers. Our computer program is available upon request.

As noted by Taylor (1995), Fang et al (2005), and Lam et al (2005), applications of cure models are restricted to problems in which there is strong scientific evidence for the existence of the cured population or a clear level plateau of the survival function is observed. Identifiability problem may arise when the cure probability is very close to one or zero. In our experience, the numerical computation of the MLEs may not be stable if the cure fraction is small.

Appendix

A.1. Proof of Theorem 1

Let p(Y,Z,Δ|β, F) = [1 − G_γ(e^βTZF(Y))]^Δ[G_γ(e^βTZF(Y))]^1−Δ, and

$$q(Y,\mathbf{Z},\mathit{\Delta }\mid \mathit{\beta },F)=log\frac{p(Y,\mathbf{Z},\mathit{\Delta }\mid \mathit{\beta },F)}{p(Y,\mathbf{Z},\mathit{\Delta }\mid {\mathit{\beta }}_0,F_0)}$$

be the log-likelihood ratio. Let P be the probability measure of p(Y,Z,Δ|β₀, F₀), Pq(Y,Z,Δ|β, F) = ∫ q(Y,Z,Δ|β, F)dP(Y,Z,Δ), the true mean of q; and let $P_{n}q(Y,\mathbf{Z},\mathit{\Delta }\mid \mathit{\beta },F)=(1/n){\sum }_{i=1}^{n}q(Y_i,{\mathbf{Z}}_i,{\mathit{\Delta }}_i\mid \mathit{\beta },F)$, the empirical mean of q based on the data {(Y_i,Z_i,Δ_i): i = 1, …,n}. Note that Pq(Y,Z,Δ|β, F) is the negative Kullback-Leibler divergence of p(Y,Z,Δ|β, F) from p(Y,Z,Δ|β₀, F₀), and as a function of (β, F), it is always non-positive, attaining its maximum value of 0 at (β, F) = (β₀, F₀). Let Θ be the range of β and ℱ be the collection of all distribution functions on R⁺. Recall that (β̂_n, F̂_n) is the MLE of (β₀, F₀), i.e.,

$$({\mathit{\beta }}_0,F_0)\in arg\underset{(\mathit{\beta },F)\in (\mathit{\Theta },\mathcal{F})}{max}{P}_{q(y,\mathbf{z},\delta \mid \mathit{\beta },\mathbf{F})},\text{and}({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)\in arg\underset{(\mathit{\beta },F)\in (\mathit{\Theta },\mathcal{F})}{max}{P}_{n}q(y,\mathbf{z},\delta \mid \mathit{\beta },F).$$

Let d((β, F), (β₀, F₀)) as given before the Lemma (recall definitions of τ_l and t₀ given in condition (C3)). By our model specification, Pq(Y,Z,Δ|β, F) is continuous with respect to (β, F); also, with (C3), the model is identifiable, and so (β₀, F₀) is the unique maximizer of Pq(Y,Z,Δ|β, F). Thus for all η > 0,

$$\begin{gathered} \underset{(\mathit{\beta },F)\in (\mathit{\Theta },\mathcal{F}):d((\mathit{\beta },F),({\mathit{\beta }}_0,F_0))>\eta }{sup}{P}_q(Y,\mathbf{Z},\mathit{\Delta }\mid \mathit{\beta },F)<P_q(Y,\mathbf{Z},\mathit{\Delta }\mid {\mathit{\beta }}_0,F_0) \\ \text{and}\text{by}\text{definition}\text{of}\text{MLE},P_{n}q(Y,\mathbf{Z},\mathit{\Delta }\mid {\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)\ge P_{n}q(Y,\mathbf{Z},\mathit{\Delta }\mid {\mathit{\beta }}_0,F_0), \end{gathered}$$

so if we show that 𝒬 = {q(Y,Z,Δ|β, F): (β, F) ∈ (Θ,ℱ)} is a P-Glivenko- Cantelli class, then by Theorem 5.8 in van der Vaart (2002, p.386),

$$d(({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n),({\mathit{\beta }}_0,F_0))\stackrel{a.s.}{\to }0.$$

This gives the desired result. Note that F̂_n is estimated by data points s₁, …, s_m.

Now we show that 𝒬 is P-Glivenko-Cantelli. For any function g, let ||g||_L1(P) = ∫ |g(y, z, δ)|dP(y, z, δ), and N_{[ ]}(ε,𝒬, L₁(P)) be the minimum number of ε-brackets needed to cover 𝒬 under norm ||·||_L1(P). We first show that N_{[ ]}(ε,𝒬, L₁(P)) is finite ∀ε > 0.

By our specification of p(Y,Z,Δ|β, F) and with (C1), it can be checked that q(Y,Z,Δ|β, F) is boundedly differentiable with respect to β, and boundedly Gáteaux differentiable with respect to F. Consequently, by Taylor expansion, there are constants 0 < C_j < ∞ (j = 1, 2), such that

$$\begin{gathered} {\Vert q(Y,\mathbf{Z},\mathit{\Delta }\mid {\mathit{\beta }}_1,F_1)-q(Y,\mathbf{Z},\mathit{\Delta }\mid {\mathit{\beta }}_2,F_2)\Vert }_{L_1(P)}\le C_1\Vert {\mathit{\beta }}_1-{\beta }_2\Vert +C_2{\Vert F_1-F_2\Vert }_{L_1(P)}, \\ \forall ({\mathit{\beta }}_1,F_1),({\mathit{\beta }}_2,F_2)\in (\mathit{\Theta },\mathcal{F}).\text{So}, \\ {N}_{[]}(\epsilon ,\mathcal{Q},{\Vert ·\Vert }_{L_1(P)})\le N_{[]}(\frac{\epsilon }{2C_1},\mathit{\Theta },\Vert ·\Vert )\times N_{[]}(\frac{\epsilon }{2C_2},\mathcal{F},{\Vert ·\Vert }_{L_1(P)}),\forall \epsilon <0. \end{gathered}$$

By (C4), N_{[ ]}(ε/(2C₁),Θ, ||·||) = O(1/ε^d), with d = dim(Θ). Since ℱ is a collection of bounded monotone functions, by Theorem 2.7.5 in van der Vaart and Wellner (1996, p.159), for some constant 0 < C < ∞,

$$N_{[]}(\epsilon ,\mathcal{F},{\Vert ·\Vert }_{L_1(P)})\le exp\{\frac{C}{\epsilon }\},\forall \epsilon >0.$$

Thus, for some generic constant 0 < C < ∞,

$$\begin{gathered} N_{[]}(\epsilon ,\mathcal{Q},{\Vert ·\Vert }_{L_1(P)})\le N_{[]}(\frac{\epsilon }{2C_1},\mathit{\Theta },\Vert ·\Vert )\times N_{[]}(\frac{\epsilon }{2C_2},\mathcal{F},L_1(P)) \\ \le \frac{C}{{\epsilon }^d}exp\{\frac{C}{\epsilon }\}<\infty ,\forall \epsilon >0, \end{gathered}$$

and so by Theorem 2.4.1 in van der Vaart and Wellner (1996, p.122), 𝒬 is a Glivenko-Cantelli class with respect to P.

A.2 Proof of Lemma 1

Denote S = (Y,Z,Δ), let p(S|β, F), P and P_n as given in the proof of Theorem 1, ℓ(β, F|S) = log p(S|β, F) be the log-likelihood, and D_n be the set of all the observed data. Define

$${\mathbb{M}}_n(\mathit{\beta },F)=P_n\ell (\mathit{\beta },F\mid S)\text{and}\mathbb{M}(\mathit{\beta },F)=P\ell (\mathit{\beta },F\mid S).$$

Since (β̂_n, F̂_n) ∈ (Θ,ℱ) is the MLE of (β₀, F₀), it is the M-estimator based on the log-likelihood ℓ(β, F|D_n) on the parameter space (Θ,ℱ), and so ${\mathbb{M}}_n({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)\ge {\mathbb{M}}_n(\mathit{\beta },F)\ge {\mathbb{M}}_n(\mathit{\beta },F)-O_p(r_n^{-2})$, for any (β, F) ∈ (Θ,ℱ) and any positive sequence r_n →∞.

Let d(β̂_n − β₀, F̂_n − F₀) = ||β̂_n − β₀|| + || F̂_n − F₀||_L2. Since conditions of Theorem 1 are satisfied, in its proof change sup_t∈[τl,t0] | F̂_n(t) − F₀(t)| to ||F̂_n − F₀||_L2, we get $d({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0,{\widehat{F}}_n-F_0)\stackrel{P}{\to }0$.

Note that (β₀, F₀) = arg sup_{(β,F)∈(Θ,ℱ)} 𝕄(β, F). Denote by ${\ell }_{\mathit{\beta }}^{(1)}({\mathit{\beta }}_0,F_0\mid S),{\ell }_F^{(1)}({\mathit{\beta }}_0,F_0\mid S)[F-F_0],{\ell }_{\mathit{\beta }\mathit{\beta }}^2({\mathit{\beta }}_0,F_0\mid S),{\ell }_{\beta ,F}^2{\mathit{\beta }}_0,F_0\mid S)[F-F_0],{\ell }_{F,\mathit{\beta }}^2({\mathit{\beta }}_0,F_0\mid S)[F-F_0]{\ell }_{F,F}^{(2)}({\mathit{\beta }}_0,F_0\mid S)[F-F_0,F-F_0]$ the partial derivatives of ℓ(β, F|S) with respect to (β, F). The derivative with respect to F is in the Gáteaux sense. By our specification of model, these quantities exist. Note that $E_{({\mathit{\beta }}_0,F_0)}{\ell }_{\mathit{\beta }}^{(1)}({\mathit{\beta }}_0,F_0\mid S)=\mathbf{0}$, and $E_{({\mathit{\beta }}_0,F_0)}{\ell }_F^{(1)}({\mathit{\beta }}_0,F_0\mid S)[F-F_0]=0$. Denote by Q⁽²⁾(β, F|S)[F − F₀, F − F₀] the (d + 1) × (d + 1) matrix of all the second order partial derivatives. Therefore,

$$\mathbb{M}(\mathit{\beta },F)-\mathbb{M}({\mathit{\beta }}_0,F_0)=\frac{1}{2}{E}_{({\mathit{\beta }}_0,F_0)}\left({(\mathit{\beta }-{\mathit{\beta }}_0,1)}^T{Q}^{(2)}(\overline{\mathit{\beta }},\overline{F}\mid S)[F-F_0;F-F_0](\mathit{\beta }-{\mathit{\beta }}_0,1)\right)<0$$

and is of order O(d²(β − β₀, F − F₀), where (β̄, F̄) is an intermediate value between (β, F) and (β₀, F₀). Under some general conditions, the above can be upper bounded by −Cd²(β − β₀, F − F₀) for some 0 < C < ∞, in small neighborhood of (β₀, F₀). So for any 0 < η_n → 0 and any τ with η_n < τ ≤ η < ∞, for some 0 < C < ∞,

$$\underset{\tau /2<d(\mathit{\beta }-{\mathit{\beta }}_0,F-F_0)\le \tau ,(\mathit{\beta },F)\in (\mathit{\Theta },\mathcal{F})}{sup}\mathbb{M}(\mathit{\beta },F)-\mathbb{M}({\mathit{\beta }}_0,F_0)\le -C{\tau }^2.$$

Next we show, with E^* for outer expectation,

$$E^{\ast }\underset{\tau /2<d(\mathit{\beta }-{\mathit{\beta }}_0,F-F_0)\le \tau ,(\mathit{\beta },F)\in (\mathit{\Theta },\mathcal{F})}{sup}\sqrt{n}\mid ({\mathbb{M}}_n-\mathbb{M})(\mathit{\beta },F)-({\mathbb{M}}_n-\mathbb{M})({\mathit{\beta }}_0,F_0)\mid \le {\varphi }_n(\tau ),$$ (A.0)

for some decreasing function ϕ_n(·) to be given.

For this, let N_{[ ]}(ε, (Θ,ℱ),L₂(P)) be defined in the proof of Theorem 1, we showed N_{[ ]}(ε, (Θ,ℱ),L₂(P)) = O(1/ε^d exp{C/ε}) = O(exp{C/ε}). Let C be some generic finite positive constant, and

$$\begin{gathered} J_{[]}(\tau ,(\mathit{\Theta },\mathcal{F}),L_2(P))={\int }_0^{\tau }\sqrt{1+log{N}_{[]}(\epsilon ,(\mathit{\Theta },\mathcal{F}),L_2(P))}d\epsilon \\ ={\int }_{-\infty }^{log\tau }{e}^t\sqrt{1+C{e}^{-t}}dt\le C{\int }_{-\infty }^{log\tau }{e}^t{e}^{-t/2}dt=C{\tau }^{1/2}. \end{gathered}$$

In the above we used the fact that for small τ > 0, log τ < 0, so e^−t > 1 and 1 + Ce^−t ≤ (1 + C)e^−t on (−∞, log τ).

Let 𝒬₁ = {q(·|β, F): (β, F) ∈ (Θ,ℱ), τ/2 < d(β − β₀, F − F₀) ≤ τ}, ${\mathbb{G}}_{n}q=\sqrt{n}(P_n-P)q$, ||𝔾_n||_𝒬1= sup_q∈𝒬1|𝔾_nq|. Then the left hand side of (A.0) is upper bounded by 2||𝔾_n||_𝒬1.

Note that since 𝒬₁ is a subset of the 𝒬 defined in the proof of Theorem 1, so N_{[ ]}(ε,𝒬₁, L₂(P)) ≤ N_{[ ]}(ε,𝒬, L₂(P)) ≤ N_{[ ]}(ε, (Θ,ℱ),L₂(P)) and consequently, J_{[ ]}(τ,𝒬₁, L₂(P)) ≤ J_{[ ]}(τ, (Θ,ℱ), L₂(P)) ≤ Cτ^1/2.

Also, it is easy to see that, with our specification of the likelihood, Pq² < Cτ² and ||q||_∞ < C for all q ∈ 𝒬₁, for some 0 < C < ∞. Thus, by Lemma 3.4.2 in van der Vaart and Wellner (1996, p.324),

$$E^{\ast }{\Vert {\mathbb{G}}_n\Vert }_{{\mathcal{Q}}_1}\le J_{[]}(\tau ,\mathcal{Q},L_2(P))\left(1+\frac{J_{[]}(\tau ,\mathcal{M},L_2(P))}{{\tau }^2\sqrt{n}}C\right)\le C{\tau }^{1/2}(1+{\tau }^{-3/2}{n}^{-1/2}),$$

which implies (A.0) with ϕ_n(τ) = Cτ^1/2(1 + τ^−3/2n^−1/2). Take r_n = n^1/3, then

$$r_n^2{\varphi }_n\left(\frac{1}{r_n}\right)=C{n}^{1/3}\le \sqrt{n}.$$

Now, all conditions of Theorem 3.4.1 in van der Vaart and Wellner (1996, p.322) are satisfied, so by this Theorem, r_nd(β̂ _n − β₀, F̂_n − F₀) = n^1/3d(β̂_n − β₀, F̂_n − F₀) = O_p(1).

A.3 Proof of Theorem 2

Recall that l_β(β, F) is the score for β, l_F (β, F)[g] = ∂l(β, F + λg)/∂λ|_λ=0 is the score operator for F at direction g, with $g(y)={\int }_0^{y}h(x)dF(x)$ and $h\in L_2^0(F)$, where $L_2^0(F)=\{h:\int \mathit{hdF}=0,\int h^{2}dF<\infty \}$. Denote $\mathcal{G}=\{g:g(·)=\int \mathit{hdF},h\in L_2^0(F)\}$. Note that $l_{\beta }^{\ast }({\mathit{\beta }}_0,F_0)=l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]$ be the efficient score, where ${\mathbf{g}}^{\ast }={(g_1^{\ast },\dots ,g_d^{\ast })}^T(d=\mathit{dim}(\mathit{\beta }))$,

$$l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]={(l_F({\mathit{\beta }}_0,F_0)[g_1],\dots ,l_F({\mathit{\beta }}_0,F_0)[g_d])}^T,$$

and g^* is determined by

$$\begin{gathered} \mathbf{0}=E\left((l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }])l_F({\mathit{\beta }}_0,F_0)[g]\right) \\ =E\left(E\left[\left(\mathbf{Z}{F}_0(Y)-{\mathbf{g}}^{\ast }(Y)\right)Q^2(\mathbf{X};{\mathit{\beta }}_0,F_0)|Y\right]\right),\forall g\in \mathcal{G}. \end{gathered}$$ (A.1)

This gives g^*(Y) = F₀(Y)E[ZQ²(X;β₀, F₀)|Y ]/E[Q²(X;β₀, F₀)|Y ].

Let l_n(β, F) = logL_n(β, F) be the log-likelihood, l_β,n(β, F) = ∂l_n(β, F)/∂β and l_F,n(β, F)[g] be the sample score operator for F at direction g, and define l_F,n(β, F)[g^*] similarly. Since (β̂_n, F̂_n) is the MLE, we have l_β,n(β̂, F̂_n) = 0 and l_F,n(β̂, F̂_n)[g^*] = 0. Additionally, it is obvious that Pl_β(β₀, F₀) = 0 and Pl_F (β₀, F₀)[g^*] = 0. Let ℳ₁ = {l_β(β, F): β ∈ ℬ, F ∈ ℱ} and ℳ₂ = {l_F (β, F)[g^*]: β ∈ ℬ, F ∈ ℱ}. Since ℬ is bounded and ℱ is collection of bounded monotone functions, using the entropy computations in the proof of Theorem 1, it is easy to show that they are Donsker classes. It can be shown that for fixed X, l_β(β, F) and l_F (β, F) are Lipchitz in (β, F), so ℳ₁ and ℳ₂ are also Donsker classes. Since by Theorem 1, ||β̂_n − β₀||+ sup_t∈[τl,t0] |F̂_n −F₀| → 0 almost surely, condition (C1) and the given model imply that l_β(β, F) and l_F (β₀, F₀)[g^*] are continuous in (β, F) and with finite second moments, thus by Corollary 2.3.12 in van der Vaart and Wellner (1996), we have

$$\left|\sqrt{n}(P_n-P)l_{\beta }({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)-\sqrt{n}(P_n-P)l_{\beta }({\mathit{\beta }}_0,F_0)\right|=o_p(1)$$

where the o_p(1) is in the vector sense, and

$$\left|\sqrt{n}(P_n-P)l_F({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)[{\mathbf{g}}^{\ast }]-\sqrt{n}(P_n-P)l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]\right|=o_p(1).$$

From these facts we get

$$-\sqrt{n}P{l}_{\beta }({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)-\sqrt{n}{P}_n{l}_{\beta }({\mathit{\beta }}_0,F_0)=o_p(1)$$ (A.2)

and

$$-\sqrt{n}P{l}_F({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)[{\mathbf{g}}^{\ast }]-\sqrt{n}{P}_n{l}_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]=o_p(1).$$ (A.3)

Denote l_β,β(β, F) = ∂l(β, F)/(∂β∂β^T),

$$l_{\beta ,F}(\mathit{\beta },F)[g]=\partial l_{\beta }(\mathit{\beta },\int (1+\lambda g)dF)/\partial {\lambda \mid }_{\lambda =0},$$

and define l_F,β(β, F)[g] and l_F,F (β, F)[g₁, g₂] similarly. Using Taylor expansion, and note that ||β̂_n−β₀||²+|| F̂_n−F₀||² is bounded, so by Lemma 1 and dominated convergence E(||β̂_n − β₀||² + ||F̂_n − F₀||²) = O(n^−2/3), and so

$$\begin{gathered} P{l}_{\beta }({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)-P{l}_{\beta }({\mathit{\beta }}_0,F_0)-P{l}_{\beta ,\beta }({\mathit{\beta }}_0,F_0)({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)-P{l}_{\beta ,F}({\mathit{\beta }}_0,F_0)[{\widehat{F}}_n-F_0] \\ =OE({\Vert {\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0\Vert }^2+{\Vert {\widehat{F}}_n-F_0\Vert }^2)=(n^{-2/3}). \end{gathered}$$

The above and (A.2) give

$$-P_n{l}_{\beta }({\mathit{\beta }}_0,F_0)-P{l}_{\beta ,\beta }({\mathit{\beta }}_0,F_0)({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)-P{l}_{\beta ,F}({\mathit{\beta }}_0,F_0)[{\widehat{F}}_n-F_0]=o_p(n^{-1/2}).$$ (A.4)

Similarly,

$$P{l}_F({\widehat{\mathit{\beta }}}_n,{\widehat{F}}_n)[{\mathbf{g}}^{\ast }]-P{l}_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]-P{l}_{F,\beta }({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)-P{l}_{F,F}({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast },{\widehat{F}}_n-F_0]=O({\Vert {\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0\Vert }^2+{\Vert {\widehat{F}}_n-F_0\Vert }^2)=O_p(n^{-2/3}).$$

The above and (A.3) give

$$-P_n{l}_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]-P{l}_{F,\beta }({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)-P{l}_{F,F}({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast },{\widehat{F}}_n-F_0]=o_p(n^{-1/2}).$$ (A.5)

It is known that $P\left(l_{\beta }({\mathit{\beta }}_0,F_0)l_{\beta }^T({\mathit{\beta }}_0,F_0)\right)=-P{l}_{\beta ,\beta }({\mathit{\beta }}_0,F_0)$. By the same way, −Pl_β,F (β₀, F₀)[g] = P(l_β(β₀, F₀)l_F (β₀, F₀)[g]) for all g, and −P(l_F,F (β₀, F₀)[g₁, g₂]) = P(l_F (β₀, F₀)[g₁]l_F (β₀, F₀)[g₂]) for all g₁ and g₂. Note that (A.1) holds for any g. Thus,

$$\begin{gathered} P{l}_{\beta ,F}({\mathit{\beta }}_0,F_0)[{\widehat{F}}_n-F_0]-P{l}_{F,F}({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast },{\widehat{F}}_n-F_0] \\ =-P(l_{\beta }({\mathit{\beta }}_0,F_0)l_F({\mathit{\beta }}_0,F_0)[{\widehat{F}}_n-F_0])+P(l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]l_F({\mathit{\beta }}_0,F_0)[{\widehat{F}}_n-F_0]) \\ =-P\left((l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }])l_F({\mathit{\beta }}_0,F_0)[{\widehat{F}}_n-F_0]\right)=\mathbf{0}. \end{gathered}$$

Now, subtracting (A.4) from (A.5) we get

$$\sqrt{n}P(l_{\beta ,\beta }({\mathit{\beta }}_0,F_0)-l_{F,\beta }({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }])({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)=\sqrt{n}{P}_n(l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[g^{\ast }])+o_p(1).$$ (A.6)

Note that, since $P\left((l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }])l_F^T({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]\right)=\mathbf{0}$, so

$$\begin{gathered} P(l_{\beta ,\beta }({\mathit{\beta }}_0,F_0)-l_{F,\beta }({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }])=-P\left(l_{\beta }({\mathit{\beta }}_0,F_0)l_{\beta }^T({\mathit{\beta }}_0,F_0)-l_{\beta }({\mathit{\beta }}_0,F_0)l_F^T({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]\right) \\ =-P\left(l_{\beta }({\mathit{\beta }}_0,F_0){(l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }])}^T\right) \\ =-P\left((l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }]){(l_{\beta }({\mathit{\beta }}_0,F_0)-l_F({\mathit{\beta }}_0,F_0)[{\mathbf{g}}^{\ast }])}^T\right) \\ =-P\left(l_{\beta }^{\ast }({\mathit{\beta }}_0,F_0){(l_{\beta }^{\ast }({\mathit{\beta }}_0,F_0))}^T\right)=-I_{\beta }({\mathit{\beta }}_0,F_0). \end{gathered}$$

This and (A.6) give

$$\sqrt{n}({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)=I_{\beta }^{-1}({\mathit{\beta }}_0,F_0)\sqrt{n}{P}_n{l}_{\beta }^{\ast }({\mathit{\beta }}_0,F_0)+o_p(1),$$

which gives the desired result.

A.4 Proof of Theorem 3

Since (β̂_n, F̂_n) is the MLE, we have

$${\widehat{F}}_n=arg\underset{F\in \mathcal{F}}{max}\sum _{i=1}^n\left({\mathit{\Delta }}_{i}log\left[1-G_{\gamma }\{e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}F(Y_i)\}\right]+(1-{\mathit{\Delta }}_i)log\left[G_{\gamma }\{e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}F(Y_i)\}\right]\right).$$

Let R(y|z, F) = 1 − G_γ{β̂^T zF(y)}, then R(·|z, F) is a distribution function. Let ℛ = {R(·|z,F): F ∈ ℱ}, and R̂_n(·|z) be the MLE of R(·|z, F), i.e.,

$${\widehat{R}}_n=arg\underset{R\in \mathcal{R}}{max}\sum _{i=1}^n\left({\mathit{\Delta }}_{i}logR(Y_i\mid {\mathbf{Z}}_i,F)+(1-{\mathit{\Delta }}_i)log[1-R(Y_i\mid {\mathbf{Z}}_i,F)]\right)$$

and it is straightforward that R̂_n(·|z) = R(y|z, F̂_n).

Recall that the common current status model with log-likelihood

$$\sum _{i=1}^n\left({\mathit{\Delta }}_{i}logF(Y_i)+(1-{\mathit{\Delta }}_i)log[1-F(Y_i)]\right)$$

and it is known (e.g., see Example 3.2.15 in van der Vaart and Wellner (1996)) that the NPMLE F̌_n(·) of F₀(·) is the slope function of the greatest convex minorant of F_n(·), which is the cumulative- sum diagram on [0, 1] with jump Δ_i/n at Y_i. i.e.

$$F_n(t)=\frac{1}{n}\sum _{j\le i}{\mathit{\Delta }}_i,t\in n^{-1}(i-1,i],(i=1,\dots ,n).$$

and F̌_n(·) is the slope of greatest convex minorant of F_n(·), and for a ∈ R,

$${\check{F}}_n(Y_i)\le a\text{if}\text{and}\text{only}\text{if}arg\underset{s}{min}\{{\check{V}}_n(s)-a{\check{G}}_n(s)\}\ge Y_i,$$

where ${\check{V}}_n(s)=n^{-1}{\sum }_{i=1}^n{\mathit{\Delta }}_{i}I(Y_i\le s)$, and ${\check{G}}_n(s)=n^{-1}{\sum }_{i=1}^{n}I(Y_i\le s)$.

In our case, similarly, R̂_n(·|Z) is the greatest convex minorant of R_n(·|Z), cumulative- sum diagram on [0, 1], where the latter has constant jump of Δ_i/n. Thus the corresponding F_n(·) in this case must be a we weighted cumulativesum diagram with weight w_i at the Y_i’s, where the w_i’s are determined by w_i ≥ 0, ${\sum }_{i=1}^n{w}_i=n$. Then F̂_n(Y_i) = Σ_j≤i w_i:= W_i. Assume the $e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}{W}_i$’s are arranged in an increasing order. With (C6), $W_n=e^{-{\widehat{\mathit{\beta }}}_n^T{\mathbf{z}}_n}{G}_{\gamma }^{-1}(1/n)$ with 0 < lim_n W_n/n < ∞ in probability. Since W_i = 0 for Δ_i = 0, we can arrange the W_i’s such that {w_i/n = (W_i+1 − W_i)/n: i = 1, …,n} are probability weights. Then as for the common current status model, the log-likelihood in our case will be maximized with the W_i’s satisfying

$$W_1=0,1-G_{\gamma }\left(e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_{i+1}}{W}_{i+1}\right)=1-G_{\gamma }\left(e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}{W}_i\right)+\frac{{\mathit{\Delta }}_i}{n},(i=1,\dots ,n-1).$$

Thus, $e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}{W}_i=G_{\gamma }^{-1}(1-i/n)$, and

$$w_i=G_{\gamma }^{-1}(1-\frac{i+1}{n})e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_{i+1}}-G_{\gamma }^{-1}(1-\frac{i}{n})e^{{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}.$$

In our case, the above equality may not be achieved for some of the Δ_i’s.

Let

$$F_n(y)=\frac{1}{n}\sum _{j\le i}{\mathit{\Delta }}_i{w}_i,y\in n^{-1}(i-1,i],(i=1,\dots ,n).$$

then F̂_n(·) is the slope of greatest convex minorant of F_n(·), and for a ∈ R,

$${\widehat{F}}_n(Y_i)\le a\text{if}\text{and}\text{only}\text{if}arg\underset{s}{min}\{V_n(s)-a{G}_n(s)\}\ge Y_i,$$

where $V_n(s)=n^{-1}{\sum }_{i=1}^n{\mathit{\Delta }}_i{w}_{i}I(Y_i\le s)$ and $G_n(s)=n^{-1}{\sum }_{i=1}^{n}I(Y_i\le s)$.

Then as in Example 3.2.15 in van der Vaart and Wellner (1996), at every fixed point t,

$${\widehat{F}}_n(t)\le a\text{if}\text{and}\text{only}\text{if}arg\underset{s}{min}\{V_n(s)-a{G}_n(s)\}-t\ge 0.$$

To evaluate the distribution of n^1/3(F̂_n(t) − F₀(t)), we need to compute the probability of the event {n^1/3(F̂_n(t)−F₀(t)) ≤ r}for each r ∈ R. Take a = F₀(t)+ rn^−1/3, then {n^1/3(F̂_n(t)−F₀(t))≤ r} = {F̂_n(t) ≤ a} = {n^1/3(arg min_s {V_n(s)− aG_n(s)} − t)≥ 0}, and by the change of variable s ↦ t + n^−1/3h,

$$\begin{gathered} n^{1/3}\left(arg\underset{s}{min}\{V_n(s)-a{G}_n(s)\}-t\right) \\ =arg\underset{h}{min}\{V_n(t+n^{-1/3}h)-(F_0(t)+r{n}^{-1/3})G_n(t+n^{-1/3}h)\} \\ =arg\underset{h}{min}\{P_n(\mathit{\Delta }wI(Y\le t+n^{-1/3}h])-(F_0(t)+r{n}^{-1/3})P_{n}I(Y\le t+n^{-1/3}h]\} \\ =arg\underset{h}{min}\{P_n([\mathit{\Delta }w-F_0(t)]I[Y\le t+n^{-1/3}h])-r{n}^{-1/3}{P}_n[I(Y\le t+n^{-1/3}h)]\} \\ =arg\underset{h}{min}\{P_n([\mathit{\Delta }w-F_0(t)]I(t\le Y\le t+n^{-1/3}h])+P_n([\mathit{\Delta }w-F_0(t)]I(Y\le t])-r{n}^{-1/3}{P}_n(I(t\le Y\le t+n^{-1/3}h])-r{n}^{-1/3}{P}_{n}I(Y\le t]\} \\ =arg\underset{h}{min}\{P_n([\mathit{\Delta }w-F_0(t)]I[t\le Y\le t+n^{-1/3}h])-r{n}^{-1/3}{P}_{n}I[t\le Y\le t+n^{-1/3}h]\} \\ =arg\underset{h}{min}\{n^{2/3}{P}_n([\mathit{\Delta }w-F_0(t)]I[t\le Y\le t+n^{-1/3}h])-r{n}^{1/3}{P}_{n}I[t\le Y\le t+n^{-1/3}h]\} \\ =arg\underset{h}{min}\{n^{2/3}(P_n-P)([\mathit{\Delta }w-F_0(t)]I[t\le Y\le t+n^{-1/3}h])+n^{2/3}P([\mathit{\Delta }w-F_0(t)]I[t\le Y\le t+n^{-1/3}h])-r{n}^{1/3}{P}_{n}I[t\le Y\le t+n^{-1/3}h]\} \\ :=arg\underset{h}{min}\{B_{1,n}(h)+B_{2,n}(h)+B_{3,n}(h)\}. \end{gathered}$$ (A.6)

Let g(·) be the density function of Y,

$$B_{3,n}(h)~-r{n}^{1/3}P[I(t\le Y\le t+n^{-1/3}h]~-r{n}^{1/3}g(t)n^{-1/3}h=-rg(t)h.$$

As a random variable, given the Z_i’s, w takes $e^{-{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_i}{G}_{\gamma }^{-1}(1-i/n)-e^{-{\widehat{\mathit{\beta }}}_n^T{\mathbf{Z}}_{i+1}}{G}_{\gamma }^{-1}(1-(i+1)/n)$ with probability 1/n. Without confusion, we also denote w = w(Z) for its asymptotic version conditioning on Z. Note that Y and (T,Z) are independent, and ||β̂_n − β₀|| = O_p(n^−1/2), and with condition (C6), we show that

$$P(w)=E[e^{-{\mathit{\beta }}_0^T\mathbf{Z}}]\sum _{i=1}^n\frac{1}{n}\left(G_{\gamma }^{-1}(1-\frac{i+1}{n})-G_{\gamma }^{-1}(1-\frac{i}{n})\right)=E[e^{-{\beta }_0^T\mathbf{Z}}]\frac{G_{\gamma }^{-1}(\frac{1}{n})}{n}-1.$$

and

$$\begin{gathered} B_{2,n}(h)~n^{2/3}P([\mathit{\Delta }-F_0(t)]I[t\le Y\le t+n^{-1/3}h]) \\ =n^{2/3}{\int }_t^{t+n^{-1/3}h}(F_0(y)-F_0(t))g(y)dy~n^{2/3}{f}_0(t)g(t){\int }_t^{t+n^{-1/3}h}(y-t)dy \\ =n^{2/3}{f}_0(t)g(t)n^{-2/3}\frac{1}{2}{h}^2=\frac{1}{2}{f}_0(t)g(t)h^2. \end{gathered}$$

Now we evaluate B_1,n(h). For h < 0, the notation I(t ≤ Y ≤ t + hn^−1/3) means I(t + hn^−1/3 ≤ Y ≤ t). Let

$$f_{n,h}(Y_i,{\mathbf{Z}}_i)=n^{1/6}(\mathit{\Delta }w({\mathbf{Z}}_i)-F_0(t))I(t\le Y_i\le t+h{n}^{-1/3}).$$

Then

$$B_{1,n}(h)=n^{-1/2}\sum _{i=1}^n[f_{n,h}(Y_i,{\mathbf{Z}}_i)-P{f}_{n,h}(Y_i,{\mathbf{Z}}_i)].$$

Let ℱ_n = {f_n,h(·, ·): |h| ≤ K}, for some K > 0. By (C1) and (C4), the w(Z_i)’s are uniformly bounded, thus ℱ_n has an envelope function F_n(y, x, z) = n^1/6CI(t− Kn^−1/3 ≤ Y ≤ t + Kn^−1/3, with some 0 < C < ∞. Obviously,

$$P{F}_n^2(Y,\mathbf{Z})=O(1),P\left[F_n^{2}I(F_n>\eta \sqrt{n})\right]\to 0,\forall \eta >0,$$

and for some 0 < C < ∞,

$$\begin{gathered} P{\left(f_{n,s}-f_{n,h}\right)}^2=n^{1/3}E\left[{({\mathit{\Delta }}_{i}w({\mathbf{Z}}_i)-F_0(t))}^{2}I(t+(s\wedge h)n^{-1/3}\le Y_i\le t+(s\vee h)n^{-1/3})\right] \\ ~C{n}^{1/3}{\int }_{t+(s\wedge h)n^{-1/3}}^{t+(s\vee h)n^{-1/3}h}g(y)dy~O(1)\mid s-h\mid . \end{gathered}$$

It follows that for any totally bounded semimetric ρ(·, ·) on [−K,K],

$$\underset{(s,h):\rho (s,h)\le {\delta }_n}{sup}P{\left(f_{n,s}-f_{n,h}\right)}^2~O(1)\mid s-h\mid \to 0,\forall {\delta }_n\to 0.$$

Thus the three conditions in Theorem 2.11.21 of van der Vaart and Wellner (1996) are satisfied.

Let ℱ_n,δ = {f_n,s − f_n,h: ρ(s, h) ≤ δ}. Then ℱ_n,δ and ${\mathcal{F}}_{n,\delta }^2$ are P-measurable in the sense of Definition 2.33 in van der Vaart and Wellner (1996). Furthermore, for fixed h,

$$\begin{gathered} P{f}_{n,h}=n^{1/6}E\left[(\mathit{\Delta }w(\mathbf{Z})-F_0(t))I(t\le Y\le t+h{n}^{-1/3})\right] \\ ~n^{1/6}E\left[\{(\mathit{\Delta }-F_0(t))+o(1)\}I(t\le Y\le t+h{n}^{-1/3})\right] \\ =O(n^{1/6}{n}^{-2/3}{h}^2)+o(1)n^{1/6}g(t)n^{-1/3}h=O(n^{-1/2}{h}^2)+o(n^{-1/6}h)\to 0, \end{gathered}$$

and

$$\begin{gathered} P{f}_{n,s}{f}_{n,h}=n^{1/3}E\left[{(\mathit{\Delta }w(\mathbf{Z})-F_0(t))}^{2}I(t\le Y\le t+(s\wedge h)n^{-1/3})\right] \\ =n^{1/3}{\int }_t^{t+(s\wedge h)n^{-1/3}}E\left[{(I(T\le Y)w(\mathbf{Z})-F_0(t))}^2\mid Y=y\right]g(y)dy \\ ~n^{1/3}E\left[{(I(T\le t)w(\mathbf{Z})-F_0(t))}^2\right]g(t)(s\wedge h)n^{-1/3}:={\eta }^2(t)g(t)(s\wedge h). \end{gathered}$$

Therefore as n → ∞, (Pf_n,sf_n,h − Pf_n,sPf_n,h) → η²(t)g(t)(s ∧ h). Note that E[𝔹(s) − 𝔹(h)]² = |s − h|, where 𝔹(·) is the two-sided Brownian motion process, originating from zero. It follows that Pf_n,sf_n,h − Pf_n,sPf_n,h converges to the covariance function of the process g^1/2(t)η(t)𝔹(·).

For a probability measure Q, let N(ε,ℱ_n, L₂(Q)) be the number of -balls needed to cover ℱ_n under the metric of L₂(Q). It is easy to see that

$$\underset{Q}{sup}N(\epsilon {\Vert F_n\Vert }_{Q,2},{\mathcal{F}}_n,L_2(Q))=O(1/\epsilon ),$$

where the supreme is over all probability measures. Thus, ∀ η_n → 0,

$$\begin{gathered} \underset{Q}{sup}{\int }_0^{{\eta }_n}\sqrt{N(\epsilon {\Vert F_n\Vert }_{Q,2},{\mathcal{F}}_n,L_2(Q))}d\epsilon \\ ~{\int }_0^{{\eta }_n}\sqrt{-log\epsilon }d\epsilon =2{\int }_{\sqrt{-log{\eta }_n}}^{\infty }x{e}^{-x^2}dx\to 0. \end{gathered}$$

By Theorem 2.11.22 in van der Vaart and Wellner (1996), we obtain

$$B_{1,n}(·)\stackrel{D}{\to }\sqrt{{\eta }^2(t)g(t)}\mathbb{B}(·),\text{in}{l}^{\infty }([-K,K]),$$

where l^∞([−K,K]) is the space of all bounded real functions on [−K,K] equipped with the supremum metric.

Now collecting results from (A.6), we have that the event {n^1/3(F̂_n(t) − F₀(t))≤ r} is asymptotically equivalent to

$$\begin{gathered} \left\{arg\underset{h}{min}\{\sqrt{{\eta }^2(t)g(t)}\mathbb{B}(h)+\frac{1}{2}{f}_0(t)g(t)h^2-rg(t)h\}\ge 0\right\} \\ =\left\{arg\underset{h}{max}\{-\sqrt{\frac{{\eta }^2(t)}{g(t)}}\mathbb{B}(h)-\frac{1}{2}{f}_0(t)h^2+rh\}\ge 0\right\} \\ =\left\{arg\underset{h}{max}\{\sqrt{\frac{{\eta }^2(t)}{g(t)}}\mathbb{B}(h)-\frac{1}{2}{f}_0(t)h^2+rh\}\ge 0\right\}. \end{gathered}$$

In the above we used the fact that $-\mathbb{B}(h)\stackrel{D}{=}\mathbb{B}(h)$. Using problem 3.2.5 in van der Vaart and Wellner (1996), the above is re-written as

$$\begin{gathered} \left\{{\left(\frac{4{\eta }^2(t)f_0(t)}{g(t)}\right)}^{1/3}arg\underset{h}{max}\{\mathbb{B}(h)-h^2\}+r\ge 0\right\} \\ =\left\{{\left(\frac{4{\eta }^2(t)f_0(t)}{g(t)}\right)}^{1/3}arg\underset{h}{min}\{-\mathbb{B}(h)+h^2\}\ge -r\right\} \\ =\left\{{\left(\frac{4{\eta }^2(t)f_0(t)}{g(t)}\right)}^{1/3}arg\underset{h}{min}\{\mathbb{B}(h)+h^2\}\ge -r\right\} \\ =\left\{{\left(\frac{4{\eta }^2(t)f_0(t)}{g(t)}\right)}^{1/3}arg\underset{h}{min}\{\mathbb{B}(h)+h^2\}\le r\right\},\forall t,r. \end{gathered}$$

In the above we used the fact that −𝔹(·) and 𝔹(·) have the same distribution, and that W = arg min_h {𝔹(h) + h²} is symmetrically distributed about 0, thus P(CW ≥ −b) = P(CW ≤ b). This gives the desired result for h ∈ [−K,K]. Below we prove that the result is actually true on R. Let ĥ_n = arg min_h{V_n(h) − aG_n(h)} − t. We need to show that ĥ_n is bounded in probability. Thus for large n, ĥ_n will be in [−K,K] for some 0 < K < ∞ in probability, and so the desired result is true on R. For this, we only need to show n^1/3d(ĥ_n, ĥ) = O_p(1) for some distance d(·, ·). The method is similar to that in the proof of Lemma 1 and is omitted.