Is a constant low-entropy process at the root of glycolytic oscillations?

Abstract

We measured temporal oscillations in thermodynamic variables such as temperature, heat flux, and cellular volume in suspensions of non-dividing yeast cells which exhibit temporal glycolytic oscillations. Oscillations in these variables have the same frequency as oscillations in the activity of intracellular metabolites, suggesting strong coupling between them. These results can be interpreted in light of a recently proposed theoretical formalism in which isentropic thermodynamic systems can display coupled oscillations in all extensive and intensive variables, reminiscent of adiabatic waves. This interpretation suggests that oscillations may be a consequence of the requirement of living cells for a constant low-entropy state while simultaneously performing biochemical transformations, i.e., remaining metabolically active. This hypothesis, which is in line with the view of the cellular interior as a highly structured and near equilibrium system where energy inputs can be low and sustain regular oscillatory regimes, calls into question the notion that metabolic processes are essentially dissipative.

Electronic supplementary material

The online version of this article (10.1007/s10867-018-9499-2) contains supplementary material, which is available to authorized users.

Introduction

When glucose in the growth medium is depleted and mitochondrial metabolism is blocked (for example, by cyanide or anaerobiosis), Saccharomyces cerevisiae will use externally added glucose in such a way that the concentration of the central products of glycolysis, namely NADH and ATP, will follow a well-established waveform. These glycolytic oscillations have been the object of research for seven decades now [1–3]. The term oscillation refers to a temporal oscillation, which is defined as the strictly periodic repetitive variation in time of some measure about a central value.

Although the enzymes and reactions of glycolysis have been characterized in detail, and the conditions under which oscillations take place are well known, an adequate explanatory framework remains elusive, i.e., the generative principles of such oscillations are still unclear as are the attendant questions of why oscillations arise and what they reveal about the complex relationship between the various levels of description of life processes—physical, chemical, and physiological. This is likely due to the fact that canonical models aiming to understand why glycolysis oscillates have generally approached the pathway largely in isolation from the rest of the cell. Most of these models build on the in vitro regulatory properties of the glycolytic enzymes as classically studied by biochemists; others have proposed that glycolysis involves autocatalysis with respect to ATP [4–6], which may give rise to oscillations without invoking delicate in vitro regulatory properties of (some) enzymes catalyzing the reactions [7]. Also, it has been suggested that oscillations have evolved to reduce energy dissipation so as to make the process more thermodynamically efficient [3]. All these approaches implicitly rely on the assumption that van’t Hoff’s dilute solution theory is applicable to the cellular interior. Specifically, they assume that the cytosol can be treated as a mostly dilute isotropic aqueous solution where the relevant components—enzymes and metabolites—diffuse and react following mass action kinetics.

An important and generally overlooked observation, however, is that it is not only a few cellular metabolites (e.g., NADH, ATP) that oscillate during glycolysis, but a large number of cellular properties including intracellular pH, electrical potentials, intracellular water dynamics, and heat [8–12], in ways that strongly suggest that general principles of coupling are at play and that glycolysis as an enzymatic pathway both influences and is influenced by the rest of the cell. This coupling of glycolysis with a host of other cellular phenomena is not adequately described under the assumptions of a largely isolated system of reactions occurring under conditions akin to a dilute solution.

Moreover, the cell interior is an extremely crowded environment due to the high concentration of macromolecules, many of them polyelectrolytes, estimated to be around 200–350 mg/ml [13, 14]. In such conditions, the intracellular milieu is unlikely to share the properties of dilute solutions where enzymes are generally characterized. In fact, there is a long-standing controversy about the state of water in intact cells. While some reports suggest that most intracellular water is in a liquid state [15, 16], others claim that it is altered, in an H-bonded polymer-based gel-like state [17–20]. Therefore, it is still an open question to what extent mass action kinetics is a valid framework on which to build a more complete understanding of the processes occurring in the cell cytoplasm.

A thermodynamic approach

Chemical transformations of the living cell are conceived in terms of Onsager’s theory of dissipative chemical processes [21, 22]. In this approach, non-equilibrium chemical reactions are approximated by a linear matrix between fluxes and thermodynamic forces, where the coefficients constitute the symmetric part of the phenomenological matrix. This formalism, valid close to equilibrium, is generally applied to describe irreversible processes (e.g., diffusion and heat dissipation); far-from-equilibrium systems still display a coupling between fluxes and forces, however the coupling is no longer linear because the entropy constitutes a non-harmonic potential.

In a recent paper [23], Onsager’s theory was revised in depth, and a new formalism proposed that also considers the antisymmetric part of the phenomenological matrix, which relates to isentropic processes. In such situations, the behavior of a system may include not just dissipative regimes but also oscillations near equilibrium [23], i.e., oscillating chemical reactions can be associated with isentropic processes. This new formalism predicts that in addition to changes in concentrations of metabolites other (extensive and intensive) macroscopic variables, such as heat, volume, and, most important, temperature, must oscillate in a coupled way if the system is to remain isentropic (for more details see Nonequilbrium-thermodynamics theory section below).

In order to explore this possibility, we measured heat, cellular volume, and temperature in a series of experiments in suspensions of non-dividing oscillating yeast displaying glycolytic oscillations. As a consequence, we propose an alternative framework of interpretation for the emergence of oscillating processes in biological systems, namely, that oscillations arise as a consequence of a nearly isentropic state of non-dividing S. cerevisiae cells using fermentation as the sole source of energy. Based on previous results from our laboratory [9, 12], it seems entirely plausible that the coupling principles that link chemical transformations with the thermodynamics of the system may be fruitfully approached as a natural consequence of the highly structured nature of cytoplasm, conceptualized in terms of the association-induction hypothesis (AIH) proposed by G.N. Ling [24] (recently discussed in [25]), where ATP production and the dynamics of intracellular water are mechanistically linked (see Discussion section).

Nonequilibrium-thermodynamics theory

The first law of thermodynamics for conversions between equilibrium states can be written as

$$\mathit{dS}=\left(\frac{1}{T}\right)\mathit{dE}+\left(\frac{p}{T}\right)\mathit{dV}-\left(\frac{\psi }{T}\right)\mathit{dq}+\dots -\sum \left(\frac{{\mu }_i}{T}\right)d{n}_i$$ 1

where the quantities in brackets define the intensive variables, and the differential terms represent changes in the extensive variables. In a nonequilibrium system, gradients or differences of the terms in brackets define the thermodynamic forces driving the system back to equilibrium [26].

Einstein proposed that entropy can be expanded in a Taylor series around the equilibrium value [27]. Close to equilibrium, the entropy potential can be approximated as a harmonic potential such that

$$S=S_0-\frac{1}{2}{\sum }_i{g}_{\mathit{ij}}{\xi }_i{\xi }_j+···$$ 2

where ξ_i is the deviation of an extensive variable from the equilibrium value, and the positive definite matrix g_ij defines the metric of that potential. Entropy production in this potential is given by

$$\frac{\mathit{dS}}{\mathit{dt}}=\sum _i\underset{\text{force}{X}_i}{\underbrace{\frac{\partial S}{\partial {\xi }_i}}}·\underset{\text{flux}{J}_i}{\underbrace{\frac{\partial {\xi }_i}{\partial t}}}$$ 3

The change of an extensive variable ξ_i in time defines the flux J_i (e.g., flow of matter, an electrical current, or a change along a reaction coordinate). The gradient of the entropy potential defines the conjugated forces X_i (e.g., pressure gradients, voltage or chemical affinity). In linear nonequilibrium thermodynamics, the fluxes J are linear functions of the forces X.

$$J\_=\underset{\_}{\underset{\_}{L}}\underset{\_}{X},$$ 4

where $\underset{\text{\_}}{J}$ is the vector of fluxes, and $\underset{\text{\_}}{X}$ is the vector of the conjugated forces. Common examples for fluxes proportional to a force are Stokes law for the motion of a sphere in a viscous fluid and Ohm’s law (current along an electrical potential gradient). According to Lars Onsager, $\underset{\text{\_}}{\underset{\text{\_}}{L}}$ is a positive definite symmetric matrix [21, 22]. The symmetry is known as the ‘reciprocal relations’.

Combining Eq. (3) with Eq. (4) yields

$$\frac{\mathit{dS}}{\mathit{dt}}=\sum _{\mathit{ij}}{L}_{\mathit{ij}}{X}_i{X}_j.$$ 5

Recently, one of us has proposed that the coupling matrix $\underset{\text{\_}}{\underset{\text{\_}}{L}}$ does not have to be symmetric [23]. Any matrix can unambiguously be written as the sum of a symmetric and an antisymmetric matrix, $\underset{\text{\_}}{\underset{\text{\_}}{L}}={\underset{\text{\_}}{\underset{\text{\_}}{L}}}^S+{\underset{\text{\_}}{\underset{\text{\_}}{L}}}^A$. It can easily be seen that in Eq. (5) defining entropy production, $\sum _{\mathit{ij}}{L}_{\mathit{ij}}^A{X}_i{X}_j$ does not contribute because all terms in the sum cancel. Therefore, dissipation is exclusively governed by the symmetric matrix as derived by Onsager. It follows that the antisymmetric part describes entropy-conserving phenomena such as oscillations of a spring or an electrical LC circuit, and also chemical oscillations. In the presence of a symmetric matrix, one obtains damped oscillations.

In Heimburg’s formalism, it is argued that entropy-conserving oscillations of the extensive variables determined by the matrix ${\underset{\text{\_}}{\underset{\text{\_}}{L}}}^A$ must lead to oscillations of all thermodynamic forces. Independent of their nature and according to Eq. (1), the oscillations of these thermodynamic forces are always accompanied by oscillations in temperature [23]. They are the consequence of oscillations in internal energy in an adiabatically shielded system. This intrinsic feature of all adiabatic oscillations can be considered a fingerprint of such processes. While in far-from-equilibrium processes the approximations above are no longer valid, non-equilibrium processes will nevertheless be represented by combinations of dissipative and adiabatic processes. Importantly, the indicator for the adiabatic process will be a periodic change in temperature.

Materials and methods

Chemicals

Zymolyase^® 20 T was obtained from Amsbio (Abingdon, UK). All other chemicals were from Sigma (Munich, Germany).

Yeast strains and growth

The yeast strain used in this study was the S. cerevisiae BY4743 strain, which was obtained from EUROSCARF (Frankfurt am Main, Germany). Cells were grown essentially as described previously [28, 29], i.e., under semi-aerobic conditions at 30 °C, on a rotary shaker, 180 rpm, in a medium containing 10 g l⁻¹ glucose, 6.7 g l⁻¹ yeast nitrogen base (Bacto) and 100 mM potassium phthalate (Sigma-Aldrich, Steinhem, Germany) at pH 5.0. The medium was further supplemented with 60 mg l⁻¹ histidine, 60 mg l⁻¹ methionine, 80 mg l⁻¹ leucine, 80 mg l⁻¹ lysine and 80 mg ml⁻¹ uracil. Yeast cells were harvested at the point when glucose was completely depleted as measured with a glucose test strip (Macherey-Nagel, Düren, Germany). The cells were washed twice with 100 mM potassium phosphate buffer (Merck, Darmstadt, Germany), pH 6.8 (centrifugation, 5 min at 4066 × g, GSA, Sorvall, Newtown, CT, USA), re-suspended in the same buffer to a cell density of 10% by weight and starved for 3 h on a rotary shaker at 30 °C.

Zymolyase treatment

To measure volume changes by light scattering, the yeast cell wall was removed using zymolyase treatment. Briefly, a zymolyase stock was prepared by dissolving this compound in PBS buffer plus 2 mM MgCl₂, pH 7.5, to a final concentration of 1 mg/ml. The cells were diluted in 100 mM potassium phosphate buffer, pH 7.5, to a density of 2 mg dry weight per ml. Then, 10 ml of zymolyase solution was mixed with 30 ml of cell suspension, 50 ml of PBS buffer plus 2 mM MgCl₂ and 10 ml milliQ water (total volume 100 ml) and incubated at 30 °C for 2 h in rotary shaker (150 rpm). Finally, the cells were sedimented by centrifugation for 5 min at 4066 × g (GSA, Sorvall, Newtown, CT, USA) and re-suspended in 100 mM potassium phosphate buffer to a cell density of 10% by weight (unless indicated).

Measurements of light scattering

Changes in cell size/shape were measured as light scattering using a 636.2 nm picosecond pulsed diode laser (Edinburgh Instruments, Edinburgh, Scotland), (1 μs between pulses) mounted on an Edinburgh FL920 Spectrofluorometer (Edinburgh Instruments, Edinburgh, Scotland) equipped with a temperature-controlled cuvette holder (Quantum Northwest). Sample volume was 2 ml and the temperature was 25 °C. For these measurements, the spectrofluorometer was operated in dark-mode, i.e., with the lamp switched off. Measurements were done in (at least) triplicates.

Fluorescence measurements

Measurements of NADH fluorescence were conducted in an Edinburgh FL920 spectrofluorometer (Edinburgh Instruments, Edinburgh, Scotland) equipped with a temperature-controlled holder as described above. Sample volume was 2 ml and the temperature was 25 °C. NADH was excited at 366 nm (slit 3 nm) and emission was measured at 450 nm (slit 10 nm). Measurements were done in (at least) triplicates.

Calorimetry experiments

The calorimetric measurements where conducted in a TA nanoDSC (TA Instruments, New Castle, DE, USA), which where keep at a constant temperature of 25 °C. The yeast suspension was mixed with 30 mM glucose and then loaded into the running DSC. After 60 s, the 5 mM KCN solution was added and the measurements were continued until the oscillations had stopped. The obtained data have been corrected by subtraction of a transient that arises because addition glucose and cyanide has to be done from outside the calorimeter and, therefore, it takes some time for the instrument to equilibrate. Measurements were done in (at least) triplicates.

Determination of the period of the oscillations

The period of the oscillations in NADH, light scattering, and heat flux were obtained using fast Fourier transform (FFT) analysis using either MATLAB or the Berkeley Madonna algorithm.

Measurements of temperature oscillations and analysis

Measurements of temperature were conducted using a Fluke 1523 handheld thermometer equipped with a 152-mm secondary reference thermistor (Fluke 5610–6, diameter 3.2 mm). A glass beaker (12 cm in height, 1 cm in diameter) containing a magnetic stirrer, was placed in a closed Styrofoam box on top of a magnetic stirrer, and filled with 10 ml 20% (w/v) suspension of untreated BY4743 yeast cells in 100 mM potassium phosphate, pH 6.8 to cover the temperature sensor. The temperature sensor connection and the needle of a Hamilton syringe were fed to the suspension through two tightly fitting holes in the lid of the Styrofoam box. Measurements were initiated by turning on the magnetic stirrer, when after a baseline was established, 30 mM glucose, and 60 s later, 5 mM KCN was introduced through the syringe. Temperatures were recorded from the thermometer by a custom-made LabVIEW program at 2 Hz. Subsequent data analysis was done by using a custom-made MATLAB script. Oscillatory parts of the raw data were cut out and smoothed over ten measurements through the built-in Smooth function, which removes short-term random noise variations while maintaining trends over longer periods. From these data, the Fourier spectrum was calculated using the fast Fourier transform (FFT) function. Control experiments were performed in i) milliQ water (without cells) before and after addition of glucose and KCN and ii) yeast cell suspensions without addition of glucose and KCN; all these controls failed to show any oscillations in temperature. All measurements were done in (at least) triplicate.

Results

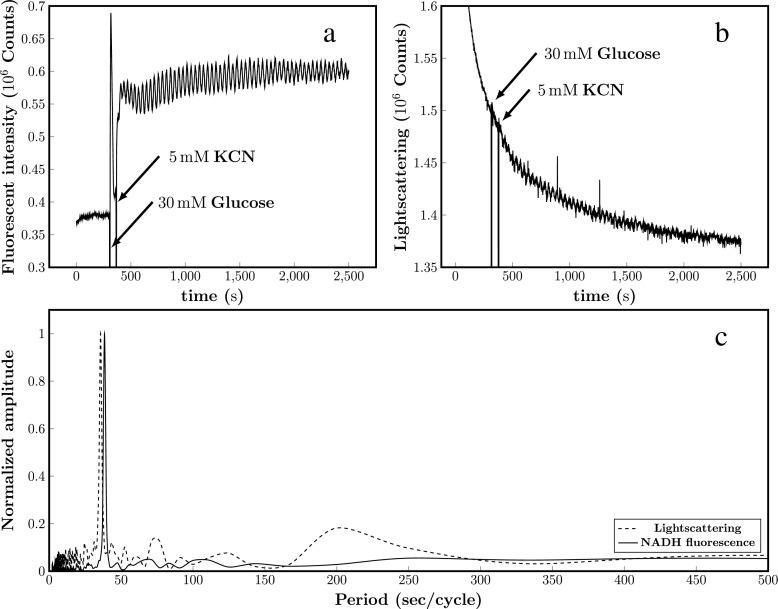
Figure 1 shows oscillations in NADH (Fig. 1a) and oscillations measured using 90° light scattering (Fig. 1b) of yeast spheroblasts (that is, cells without cell walls; removed with Zymolyase^®). Since there are no shape changes in the spheroblasts under the conditions of the experiment, we interpret the data in Fig. 1b to be oscillations in cell volume. Fig. S1B in the Electronic Supplementary Material shows a control experiment showing that there are no oscillations in light scattering in suspensions of cells with intact cell walls although these cells do display NADH oscillations, which suggests that the rigid cell wall predictably precludes detection of volume changes. The period of the scattering oscillations is essentially identical to that of NADH (Fig. 1c; prevailing peaks with a period of 37–38 s in the power spectra), suggesting that oscillations in metabolites and cell volume are coupled.

Fig. 1.

Representative oscillations in NADH (a) and light scattering (b) obtained in suspensions of B4743 yeast cells treated with Zymolyase^®. Yeast cells (10% w/v) treated with Zymolyase^® as described in the Materials and methods section were suspended at in 100 mM potassium phosphate, pH 6.8. At the indicated arrows, 30 mM glucose and (60 s later) 5 mM KCN were added to the cell suspension to induce oscillations in glycolysis. Measurement temperature was 25 °C. c Fast Fourier transform (FFT) analysis of the NADH fluorescence (solid line) and light scattering (dotted line) oscillations

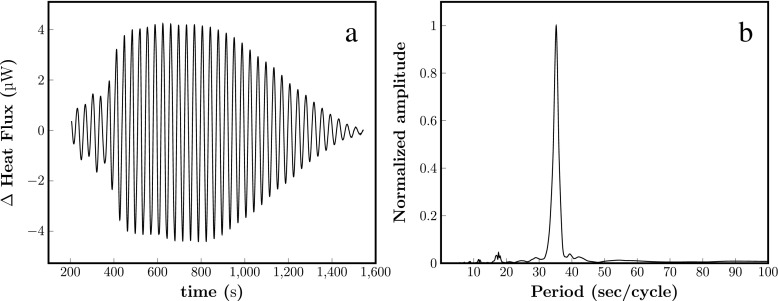
Fluctuations in thermodynamic variables such as mass and volume may be associated with fluctuations in heat flux. Oscillations in heat flux have been already reported by Teusink et al. in suspension of yeasts [8] and reproduced by us in a suspension of S. cerevisiae B4743 cells (Fig. 2a). Interestingly, the power spectrum of the heat flux oscillations (Fig. 2b) shows a peak corresponding to 38 s, which is the same as the period of oscillations in NADH and cell volume during oscillating glycolysis.

Fig. 2.

Representative oscillations in heat flux obtained in suspensions of B4743 yeast cells (a). Yeast cells (10% w/v) were suspended at in 100 mM potassium phosphate, pH 6.8. At time zero, 30 mM glucose and (60 s later) 5 mM KCN were added to the cell suspension to induce oscillations in glycolysis. Measurement temperature was 25 °C. b Fast Fourier transform (FFT) analysis of the oscillations shown in a

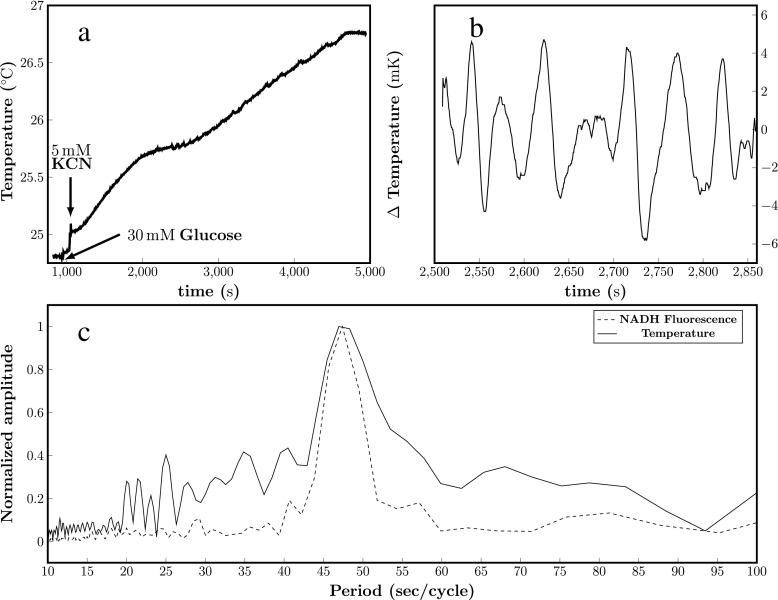
If the hypothesis being examined [23] is even partly valid for our system, the antisymmetric phenomenological matrix does not contribute to dissipation and oscillations in temperature should involve cyclic release and absorption of heat. The experiments presented in Fig. 2 cannot provide information about the absorption/release of heat during the oscillations. This is because adiabatic conditions are broken in the experiment, i.e. the calorimeter compensates the temperature changes making the system partially isothermal. Therefore, we conducted a series of experiments where we measured temperature instead of heat flux. The results are shown in Fig. 3b and the raw temperature data in Fig. 3a. We note from Fig. 3a that temperature increases steadily throughout the experiment evidencing some dissipation, but also that there is a critical region where the temperature cyclically moves up and down from a quasi-constant temperature value, evidencing that heat is released and absorbed. According to Heimburg’s formalism, this signals a contribution from an entropy-conserving (adiabatic) process. The power spectrum of this critical region shows a peak corresponding to a period of 47 s, identical to the period of NADH oscillations (Fig. 3c), which we measured in parallel in a fluorometer using a sample of the same yeast suspension removed from the temperature chamber after addition of glucose. It has been previously shown that the period of the glycolytic oscillations is dependent on the concentration of yeast cells [30], and in a previous study we observed the same 47-s frequency for NADH and 6-acetyl-2-dimethylaminonaphthalene (ACDAN) oscillations when measured in the microscope, without stirring [9, 12]. Furthermore, theoretical calculations using the measured heat flux (Fig. 2), which assume that heat oscillations are linear with yeast density and that the specific heat capacity and density of the system are similar to water, predict temperature oscillations of the same order of magnitude to those experimentally observed (not shown).

Fig. 3.

Representative oscillations in temperature obtained in suspensions of BY4743 yeast cells. Yeast cells were suspended in 100 mM potassium phosphate, pH 6.8 (20% w/v) in a long narrow beaker containing a magnetic stirrer, and placed in a closed polystyrene box with holes for a thermometer and an injection needle. Temperature was monitored at 2 Hz (see Materials and methods). a Raw data. At the indicated arrows in 30 mM glucose and, 60 s later, 5 mM KCN was added to the cell suspension to induce oscillations, which started after roughly an additional 1000 s. b Temperature oscillations are clearly visible in the region 2500 s to 2850 s after transient subtraction and smoothing as described in the Materials and methods section. c Solid line: Fourier spectrum of temperature oscillations; Dotted line: Fourier spectrum of NADH fluorescence oscillations obtained from a sample taken from the temperature chamber after addition of glucose. The NADH oscillations were inducing by addition of KCN once the sample was placed in the fluorometer

Discussion

The intensive variables important in chemical oscillations and in metabolism are mostly associated to the chemical potentials, $\frac{-{\mu }_i}{T}$. This implies that the concentrations of the reactants of a chemical oscillation will oscillate (for glycolysis [10, 28, 31, 32]). However, other variables such as volume, osmotic pressure, internal energy, pH, heat, cellular volume, and voltage (across membranes) will also oscillate, as anticipated in Heimburg’s formalism [23], in line with previous work [8, 11, 31] and the results presented in this paper. Importantly, these coupled oscillations are accompanied by oscillations in temperature, as well as dissipative contribution that leads to an overall continuous change in temperature on top of the oscillation (Fig. 3).

In recent studies, we established that glycolytic oscillations are tightly coupled with the global state of intracellular water and that this phenomenon is scale-independent (i.e., it is observed for cellular sub-volumes, whole cells and cell populations) [9, 12, 33]. Specifically, we demonstrated that there is an optimum dynamical state of the major component of the cell cytosol, water, modulated by ATP levels and a functional actin network, associated with the emergence of the metabolic oscillations. This strongly supports the view of a highly coherent and ordered cellular interior, with properties similar to a responsive hydrogel [34]. In fact, the observed oscillations in water dynamics (using the fluorescent probe ACDAN [9, 12, 33]) can be linked to the temperature experiments presented here because the magnitude of the temperature oscillation depends on the heat capacity of the system; the larger the heat capacity, the smaller the amplitude of the temperature oscillations. In biological (and aqueous chemical) systems, the heat capacity is mostly that of the aqueous medium. For this reason, a fluorescent dye sensitive to water relaxation dynamics such as ACDAN will indirectly monitor temperature changes. To the best of our knowledge, these observations have not been reported before in this system. Temperature oscillations have been found in chemical systems, e.g., the Belousov–Zhabotinsky [35–37] and the Briggs–Rauscher reactions [38]. This is strong evidence that chemical oscillations contain reversible adiabatic contributions. Reversible temperature changes have also been found in nerve pulses, which indicates that adiabatic processes are also possible in biology (for a review see [39]).

Taken together, our results on the oscillatory coupling between cellular volume, heat, metabolites (NADH in this case), and temperature support the idea that an isentropic state is maintained during glycolytic oscillations. This is rarely considered in biological systems, in which dissipative processes are assumed to dominate all functional aspects of cellular phenomena.

A search for a mechanistic model

Considering the breadth of coupled phenomena, an adequate explanatory framework cannot be limited to a description of the well-known waveform of cyclic accumulation and consumption of metabolites (NADH, ATP, etc.) of oscillating glycolysis; it must incorporate principles that explain the global cellular nature (scale independence) of the oscillations, including previously observed oscillations in water dynamics [9, 12] and thermodynamic variables such as those measured by us an others.

As Heimburg [23] points out, Onsager’s choice to focus on the symmetrical coupling matrix is justified in such systems where motion is dominated by random thermal collisions. This would be consistent with a cytoplasm described in terms of steady-state energetics because of the assumed liquid state of intracellular water and freely diffusing ions [25]. Given the highly dynamic and structured cellular interior, however, it is not clear that thermal randomness dominates the way in which particles move and react throughout the cytoplasm. If water is taken into account, not as a passive medium dominated by random thermally driven collisions but as a reversibly dynamically structured active participant, then general coupling principles naturally follow, such that heat is not dissipated during oscillations but can be stored and moved around in the system to minimize further energy consumption as suggested in Heimburg formalism [23].

The view of orderly (or highly structured) biological systems was classically discussed by Schrödinger [40]. Citing Max Planck, Erwin Schrödinger found it useful to distinguish between “statistical” and “dynamical” types of physical law, and proceeded to extend this thinking into, in his words, “The orderliness encountered in the unfolding of life (...)” [40]. To him, the apparently mechanical (dynamical) aspects of life processes emerge from statistical properties that are, simultaneously, similar and different from exemplary mechanical devices such as pendulums and clocks. Regularity of behavior emerges in dynamical (mechanical) devices because their parts are solid (ordered) and with very low sensitivity to thermal (statistical) fluctuations. Regularity can be maintained for very long periods with very low energy inputs (say, a small spring) because entropy is largely maintained at very low levels, the oscillation itself is a reversible process, and the little dissipation that occurs can be easily compensated. Furthermore, Schrödinger convincingly argues that when looked at in detail, even the dynamical laws that govern a mechanism such as a clock are statistical in nature ([40], pp. 81–84).

Moving into cellular metabolism, a similar perspective may be useful in that the cellular interior may, by virtue of structure, contribute a “dynamical” level (in Planck’s sense) where thermal randomness is mostly obliterated. This stands in contrast to approaches in which the cellular interior is thought of as a dilute solution, where thermally governed free diffusion must be constantly compensated in an energy-intensive, dissipative steady-state. In a highly structured system constrained around equilibrium, sensitivity to thermal randomness is reduced and energy inputs can be low, as in an escapement of a clock, and sustain regular, i.e., oscillatory, regimes that have the property of maintaining low entropy (“orderliness” in Schrödinger’s view) while minimizing energy input.

The association-induction hypothesis (AIH)

The AIH (introduced by G.N. Ling; see [24, 41]) developed a rigorous statistical mechanics framework to explain precisely these principles of general cell-wide coupling. Very briefly, Ling proposed that fluctuations in the chemical activity of key metabolites (e.g., ATP, but also others) during an active metabolic process alter the conformational states of fibrillar proteins (e.g., the cytoskeleton) through association and inductive effects. This in turn modulates the binding affinity of intracellular water (described by the polarized-oriented multilayer theory of cell water), ions and metabolites for proteins [19, 41] and, therefore, the way numerous molecular actors move in the cell. In the particular case of ATP, Ling demonstrated that its centrality in cellular activity resides in its capacity to modulate the bulk properties of the intracellular milieu as an integrated water–protein–solute system. Contrary to the view that the resting cell is in a steady state, the A-I hypothesis quantitatively approaches the living state as a near equilibrium system that requires relatively small energy inputs to maintain its highly constrained dynamical properties.

Ling’s insights provide, in our view, a valid explanation for our (previous and current) observations during the glycolytic oscillations, namely:

1. Using fluorescent probes sensitive to water dipolar relaxation phenomena [9, 12], we confirmed one of the AIH’s central tenets: that water is an active participant in the coherent behavior of the cell and that it is dynamically “structured”. Specifically, we demonstrated that there is an optimum dynamical state of the major component of the cell cytosol, water, modulated by ATP levels and a functional actin network (the central mechanism of Ling’s AIH), associated with the emergence of the oscillations.

2. The AIH offers a valid explanation for the maintenance of a (quasi) constant low cell entropy state since the motion of particles is directed by a structured cellular matrix conceptually equivalent to the inertia of the pendulum of a clock. This is consistent with Heimburg’s extension of Onsager’s work, which suggests that if particle motion is directed, as opposed to random, entropy can be preserved. In other words, during glycolytic oscillations the periodic fluctuations in the chemical activity of ATP modulate changes in the dynamical state of the water–protein–solute system, offering a reservoir of (reversibly) stored energy preventing dissipation, the hallmark of an isentropic process.

Conclusions

The experimental data presented here confirm important predictions of Heimburg’s formalism [23] concerning the emergence of isentropic processes, in this case in a well-known biological system. The approach may be reasonably generalized to other cellular processes known to operate in near-equilibrium oscillatory regimes, as opposed to wholly dissipative steady states far from equilibrium.

The AIH treats the cellular interior as highly structured, and resting cells as systems near equilibrium. In this situation, energy inputs can be low, as in an escapement of a clock, and sustain regular, i.e., oscillatory, regimes in the context of cellular coherence. Oscillatory glycolysis is, in our interpretation, a requirement of yeast cells to maintain viability—remain metabolically active—while in a state of low and quasi-constant entropy.

Cyclic processes, such as the metabolic oscillations studied here, offer a unique window into dynamical regularity at the cellular level. This regularity, in turn, is uniquely adapted to the extrication of generative principles that, while simple and necessarily limited in scope, are the essential scaffold on which more rigorous explanations can be constructed.

Funding

This study was funded by a grant from the Danish Council for Independent Research|Natural Sciences (grant # DFF - 4002-00465).

Compliance with ethical standards

The authors declare that they have no conflicts of interest.