Diameter-Dependent Optical Absorption and Excitation Energy Transfer from Encapsulated Dye Molecules toward Single-Walled Carbon Nanotubes

Abstract

The hollow cores and well-defined diameters of single-walled carbon nanotubes (SWCNTs) allow for creation of one-dimensional hybrid structures by encapsulation of various molecules. Absorption and near-infrared photoluminescence-excitation (PLE) spectroscopy reveal that the absorption spectrum of encapsulated 1,3-bis[4-(dimethylamino)phenyl]-squaraine dye molecules inside SWCNTs is modulated by the SWCNT diameter, as observed through excitation energy transfer (EET) from the encapsulated molecules to the SWCNTs, implying a strongly diameter-dependent stacking of the molecules inside the SWCNTs. Transient absorption spectroscopy, simultaneously probing the encapsulated dyes and the host SWCNTs, demonstrates this EET, which can be used as a route to diameter-dependent photosensitization, to be fast (sub-picosecond). A wide series of SWCNT samples is systematically characterized by absorption, PLE, and resonant Raman scattering (RRS), also identifying the critical diameter for squaraine filling. In addition, we find that SWCNT filling does not limit the selectivity of subsequent separation protocols (including polyfluorene polymers for isolating only semiconducting SWCNTs and aqueous two-phase separation for enrichment of specific SWCNT chiralities). The design of these functional hybrid systems, with tunable dye absorption, fast and efficient EET, and the ability to remove all metallic SWCNTs by subsequent separation, demonstrates potential for implementation in photoconversion devices.

Single-walled carbon nanotubes (SWCNTs), and in particular their semiconducting species (s-SWCNTs), show great promise for solar photoconversion schemes, that is, photovoltaic and photocatalytic systems, due to their large absorption coefficients, enhanced stability (photochemical, thermal, etc.), and high exciton diffusion and charge carrier mobility.^1,2 The optical absorption properties of SWCNTs are determined by the quasi-one-dimensional (1D) structure with a highly delocalized π-electron network, resulting in discrete, narrow, and chirality-dependent excitonic transitions spanning the infrared to the UV.^3,4 The same quasi-1D π-conjugated structure, along with a small reorganization energy,⁵ enables the facile transport of charges and excitons over long distances,⁶⁻⁸ a clear advantage for the efficient conversion of solar photons to useful work.

Despite strong absorption in the near-infrared and visible regions, the narrow excitonic transitions of semiconducting SWCNTs only cover a small part of the solar spectrum (depending on the specific diameter distribution). In recent years, filling of SWCNTs with functional molecules has become a powerful strategy to create new optical and electronic properties, for example, amphoteric doping of the SWCNTs through encapsulation of electron donor/acceptor molecules,⁹ tuning of the SWCNT properties through modification of the internal dielectric environment of the SWCNTs,¹⁰⁻¹⁴ observation of giant Raman cross sections for confined dyes,¹³ and strong second-order nonlinear optical response due to specific head-to-tail alignment of elongated dipolar molecules inside the SWCNTs hollow core.¹² Furthermore, the 1D hollow core of SWCNTs can provide an elegant approach to control molecular orientations¹⁵ and aggregation through tuning of the SWCNT diameter and, accordingly, the strength of confinement. For example, Gaufrès et al. demonstrated that large-diameter SWCNTs facilitated the formation of strongly coupled J-aggregates of α-sexithiophene molecules.^13,16 Beyond these effects, encapsulation of sensitizing chromophores offers a powerful strategy to complement light absorption in SWCNT systems through energy transfer to the SWCNTs.^17,18

In this work, we exploit the inner hollow space of SWCNTs to encapsulate 1,3-bis[4-(dimethylamino)phenyl]-squaraine (SQ) dye molecules that can strongly sensitize SWCNT excitation in the visible region of the solar spectrum so that energy transfer of photoexcitation from the dye to the SWCNTs enhances their excitation in regions outside of the distinct excitonic absorption transitions. SQ is an ideal SWCNT photosensitizer owing to its large extinction coefficient (2.25 × 10⁵ L mol^–1 cm^–1 at the peak absorption wavelength in chloroform), appropriate size for SWCNT encapsulation (inset of Figure 1a and see further Figure 7) and its peak absorption wavelength of ca. 630 nm, which matches well with the energy gap between the second (S₂₂) and third (S₃₃) van Hove transitions of the s-SWCNTs with diameters that can accommodate the dye (vide infra).

Figure 1.

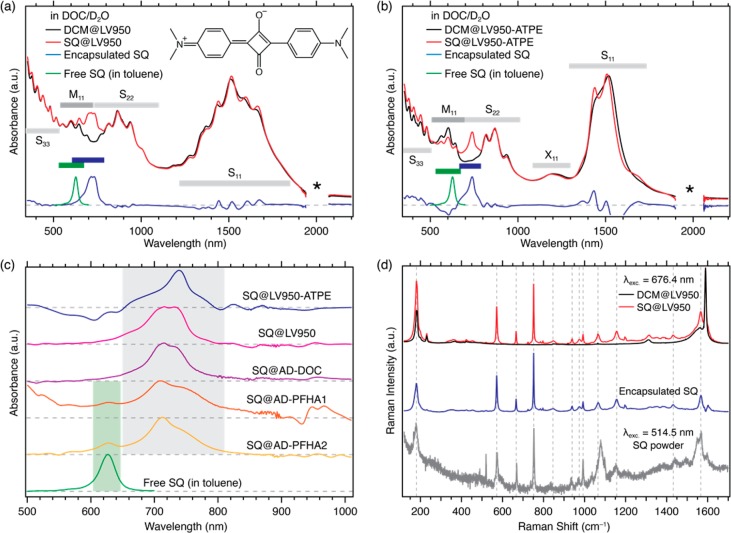
Optical absorption and RRS characterization of SQ encapsulation in SWCNTs. Normalized absorption spectra of the (a) LV950 and (b) LV950-ATPE samples. SQ@SWCNT samples are denoted by red traces and reference DCM@SWCNT samples by black traces. The spectrum for the encapsulated SQ dye, obtained by subtraction of the DCM@SWCNT spectrum from the SQ@SWCNT spectrum, is identified by the blue traces. The spectrum for free SQ dye in toluene is denoted by the green trace. Ranges for the excitonic transitions for semiconducting (S₁₁, S₂₂, S₃₃) and metallic (M₁₁) SWCNTs and phonon side bands (X₁₁) are indicated, and the region where a strong D₂O absorption band complicates the background subtraction is identified by an asterisk. (c) Absorbance contribution due to encapsulated SQ for all five SWCNT samples, estimated by subtraction of the DCM@SWCNT spectrum from the SQ@SWCNT spectrum and compared to the absorption spectrum of SQ freely dissolved in toluene. (d) Raman spectra of the SQ@LV950 (red trace) and DCM@LV950 (black trace) samples excited at 676.4 nm. The spectrum of encapsulated SQ (blue trace) is obtained by subtracting the Raman spectra of DCM@LV950 from the SQ@LV950 spectrum (see SI, section 6, for other excitation wavelengths). The Raman spectrum of the pure SQ powder (gray trace) obtained at 514.5 nm is also shown.

Figure 7.

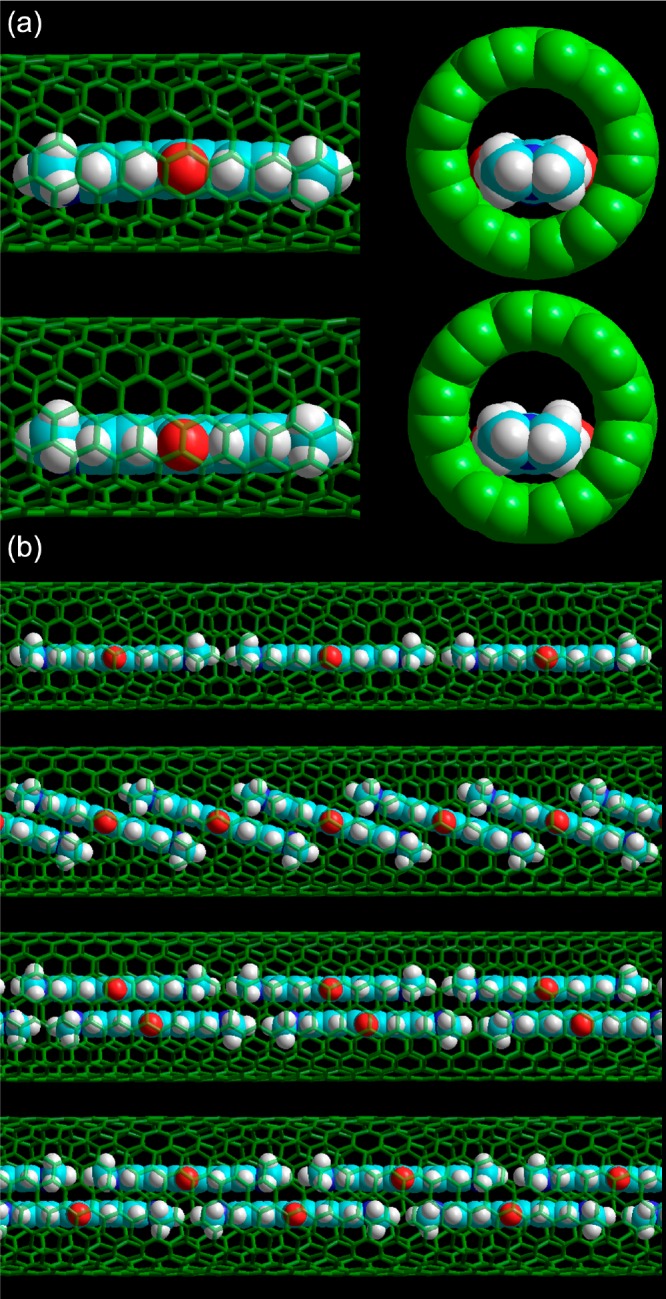
Possible SQ stacking geometries in different diameter SWCNTs. (a) Calculated structure of a single SQ molecule in a (9,7) SWCNT, as optimized at the semiempirical level using the PM6 Hamiltonian with D3H4 correction (top) and using the PM7 Hamiltonian (bottom). (b) Qualitative models of possible stacking of SQ molecules in different diameter SWCNTs, based on the calculated intermolecular distances in π-stacked and head-to-tail SQ dimers. Top to bottom: 1D array of SQ in a (9,7) SWCNT; tilted single-file SQ array and double-file array with small slip-shift between π-stacked monomers are both plausible structures in a (10,9) SWCNT; and a staggered double-file array of SQ molecules in a (12,8) SWCNT would explain the even larger redshift. In panel a, spheres represent atom’s standard van der Waals radii.

The solution-phase synthesis of SQ-filled SWCNTs has been demonstrated previously and fast EET to the SWCNTs was observed.¹⁸ Here, we encapsulated SQ dye molecules in a wide range of SWCNT samples with different diameter distributions to characterize in detail the diameter-dependent ultrafast energy transfer in these hybrid structures using an extensive combination of dedicated spectroscopic techniques and postsynthesis diameter and electronic type separation.

We first generated hybrid structures of SQ dye molecules encapsulated in SWCNTs with many different diameters, originating from different SWCNT synthesis methods. These SQ@SWCNT nanohybrids were subsequently sorted by either aqueous two-phase extraction (ATPE)¹⁹⁻²¹ or highly selective polymer wrapping with polyfluorene-based polymers,²² allowing selection of subsets of SWCNT diameters and/or pure semiconducting (s-)SWCNT samples, respectively. Separation of filled SWCNTs by chirality²³ or metallicity²⁴ has been performed before using density gradient ultracentrifugation (DGU), but being based on density, this requires the separation protocols to be adapted for the specific filler molecule. Since the encapsulated molecules should not significantly alter the outer wall properties of the SWCNTs, the separation techniques of ATPE²⁵ and selective polymer wrapping used here, which rely on the chirality-specific interaction with the outer SWCNT wall, can be directly transferred to filled SWCNTs. We utilize steady-state absorption, two-dimensional photoluminescence excitation (2D PLE), and wavelength-dependent resonant Raman scattering (RRS) experiments to prove (in a chirality-selective way) the encapsulation of the dye molecules and identify the minimal SWCNT diameter needed to accommodate the dye. 2D PLE mapping demonstrates efficient diameter-dependent EET to the SWCNTs, showing that the quasi-1D supramolecular architectures formed by the encapsulated dyes strongly depend on the SWCNT diameter since the 1D arrays of confined dyes feature drastically shifted absorption spectra with respect to the free dye absorption. Transient absorption (TA) spectroscopy, following the excited state dynamics of both SWCNT and dye, reveals ultrafast sub-picosecond EET for all filled diameters studied. These results suggest that diameter- and chirality-selected SWCNT “nanoencapsulants” can guide the structure of molecular aggregates for hybrid light-absorbing materials.

Results and Discussion

In this study, we spectroscopically interrogate five primary sample types, prepared from two different SWCNT raw materials, either SWCNTs synthesized at NREL by laser vaporization at a furnace temperature of 950 °C (LV950) or commercially available arc discharge (AD) SWCNTs, corresponding to smaller and larger SWCNT diameters, respectively. SWCNTs were opened by chemical processing, and SQ-filling was achieved by refluxing the SWCNTs in a saturated solution of SQ in dichloromethane (DCM) (see Experimental Methods for details and Supporting Information (SI), section 1). The LV950 SWCNTs were dispersed in D₂O with sodium deoxycholate (DOC), corresponding to a sample with a relatively broad diameter range. To investigate in detail those SWCNT diameters in which a single file of dye molecules narrowly fits (as determined from characterization of the broad diameter distribution samples, see below), an ATPE separation protocol for enriching these LV950 SWCNTs with a mean diameter of ca. 1.195 nm and dominated by the (9,8), (10,8), and (11,6) chiralities was developed (see Experimental Methods) and afterward applied to the filled SWCNTs. The AD SWCNTs were either dispersed in D₂O with DOC (AD-DOC) or dispersed with two different molecular-weight PFH-A polymers in toluene to extract either a large-diameter s-SWCNT sample strongly enriched with near-armchair SWCNT chiralities (AD-PFHA1)²² or a broader distribution of large-diameter s-SWCNTs (AD-PFHA2). The five samples are detailed in Table 1; in all cases, we will refer to squaraine-filled SWCNTs as “SQ@sample_name”.

Table 1. Summary of SWCNT Samples Investigated in This Study.

sample name	SWCNT source	polymer/surfactant	solvent	enrichment	diameter rangea (nm)
LV950	LV 950 °C	DOC	D2O	none	0.945–1.445
LV950-ATPE	LV 950 °C	DOC	D2O	diameter-enriched	1.135–1.255
AD-DOC	arc discharge	DOC	D2O	none	1.08–1.42
AD-PFHA1	arc discharge	PFH-A (MW = 39 kDA)	(d-)toluene	>99.98% s-SWCNTs26 mostly near-armchair	1.02–1.36
AD-PFHA2	arc discharge	PFH-A (MW = 125 kDA)	(d-)toluene	s-SWCNTs	1.15–1.53

^aDiameter range determined as the smallest and largest diameter yielding a measurable signal in PLE and used to extract the EET peak positions (see further). Note that for surfactant-solubilized samples in D₂O, the absorption of D₂O limits the PL detection from larger-diameter SWCNTs (λ_em < 1750 nm), while deuterated toluene enables measurements at longer PL wavelengths (transparent throughout the entire sensitive area of the detector up to 2200 nm).

Since the encapsulation procedure is performed in the presence of dichloromethane (DCM), DCM is also potentially encapsulated in the SWCNTs (for example, in SWCNTs too narrow to be filled by the dye). We therefore prepared appropriate control samples by repeating the filling procedure without the presence of the dye (DCM@sample_name). Afterward the same sorting protocols were applied on the DCM-filled SWCNTs. We also repeated the same refluxing procedure in the presence of the dye with partially closed SWCNTs, to distinguish dye encapsulation from residual adsorption on their outer walls (see further and SI, Figure S3).

In the first part of this article, we prove the encapsulation of the SQ molecules and then focus on the observed excitation energy transfer (EET) by TA for the ATPE-enriched LV950 sample (i.e., comparing DCM@LV950-ATPE and SQ@LV950-ATPE), since this sample contains a very narrow diameter distribution centered around the thinnest SWCNTs that can accommodate the dyes. Such a small set of SWCNT chiralities simplifies in particular the TA analysis. Finally, we turn to a detailed treatment of PLE maps of all samples that permits in-depth characterization of diameter-dependent EET from encapsulated dyes to the SWCNTs.

Spectroscopic Characterization of Squaraine Encapsulation in SWCNTs

To prove the encapsulation of the SQ dyes inside the SWCNT samples, we employ a combination of different spectroscopic techniques, as demonstrated in previous work.¹² A first indication of dye encapsulation is obtained from optical absorption spectroscopy. Figure 1a,b compares the absorption spectra of the SQ- and DCM-filled LV950 and LV950-ATPE SWCNTs. Figure S2 in the SI shows the same comparison for the other samples. The absorption spectra feature excitonic transitions for s-SWCNTs (S₁₁, S₂₂, and S₃₃), metallic SWCNTs (M₁₁), and phonon side bands (X₁₁).²⁷ In the SQ@SWCNT samples, an additional absorption band appears near 700–740 nm, corresponding to the encapsulated SQ dye molecules. This dye absorption is completely absent for the reference samples prepared with closed SWCNTs (Figure S3), proving that the dye is encapsulated inside the SWCNTs and not adsorbed on the outer walls.

Subtracting the absorption spectra of the reference DCM@SWCNT from the spectra of the SQ@SWCNT samples (blue traces in Figure 1a,b and plotted for all samples in Figure 1c) and comparing this with the absorption spectrum of the dye molecules dissolved freely in toluene (green traces in Figures 1a–c) highlight a strong bathochromic shift (∼220 meV), and spectral broadening upon encapsulation, indicating that the dye molecules experience a very different environment relative to the solvent. Moreover, Figure 1c demonstrates that SQ molecules in the five different SWCNT samples have different absorption spectra. In particular, for the ATPE-extracted SWCNTs (blue curve in Figure 1c), containing just a few chiralities with similar (and relatively small) diameters, the dye absorption displays the strongest redshift and narrowest line width. The other samples contain larger diameters and a broader diameter range, and accordingly the SQ absorption envelope broadens and shifts to shorter wavelengths. These results suggest that the absorption shift of encapsulated SQ molecules is directly tied to the diameter of the SWCNTs in which they are encapsulated (vide infra). Figure 1c also shows that the polymer-wrapped SWCNTs exhibit a weak absorption band near 625 nm associated with free SQ dyes in solution, indicating that a small fraction of the encapsulated dye molecules redisperses into the toluene. We also found that polyfluorene-wrapped SWCNTs enable the SQ dye molecules to be (reversibly) encapsulated into SWCNTs after preparing dispersions, since the dye is soluble in toluene. Figure S4 (SI Section 4) demonstrates this postdispersion filling. In contrast, the dye leaching does not occur in aqueous suspensions because the SQ dye is not soluble in water, and the absorption spectra of these aqueous suspensions were found to be stable for at least 18 months. Thanks to strong quenching of the dye emission after encapsulation, it is furthermore possible to measure the RRS spectrum of the encapsulated dye throughout the entire absorption wavelength range (Figure 1d and S5, SI).

As detailed in the SI (sections 2, 6, and 7), an extensive combination of absorption, RRS, and PLE experiments (see also below) with comparative reference samples with DCM-filled and closed SWCNTs, indicates that SQ molecules are successfully incorporated into all the samples outlined in Table 1. Importantly, this suite of experiments also demonstrates that both the ATPE-sorting and PFH-A wrapping protocols, used to select specific SWCNT chiralities, are not hampered by the presence of encapsulated dye molecules. This result confirms the expectation that encapsulated dyes are shielded from interactions with the environment by the SWCNT wall and implies that numerous separation methods developed for raw SWCNTs can be directly applied to dye-filled SWCNTs.

Tracking Energy Transfer with PLE and Transient Absorption Spectroscopy

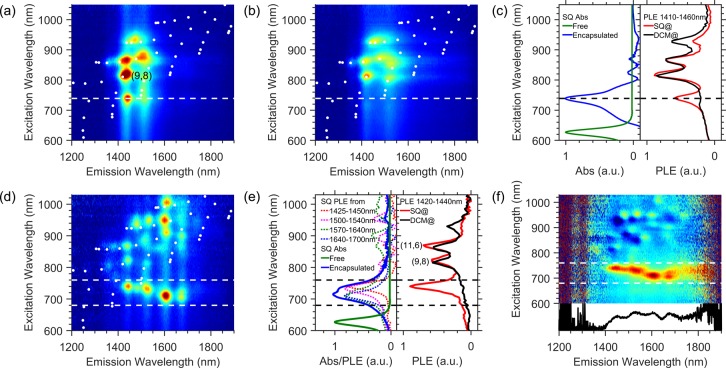
2D PLE spectroscopy and TA spectroscopy are used to characterize EET in the SQ@SWCNT nanohybrids. Figure 2a,b presents PLE maps of the SQ-filled and DCM-filled LV950-ATPE samples, respectively, and Figure 2d presents a PLE map obtained from the SQ@AD-DOC sample. PLE maps of other samples can be found in the SI (Figure S7–S11) and will be discussed in more detail in the next section (vide infra). By comparing the PLE maps in Figure 2a,b, we can distinguish two important regions. In the excitation wavelength range of ca. 800–1050 nm, s-SWCNTs are excited through direct excitation at their S₂₂ optical transitions. The specific peak positions and line widths associated with the different SWCNTs are clearly influenced by the dye-filling, as was also observed in previous work for a dipolar dye molecule encapsulated inside SWCNTs.¹² At a shorter excitation wavelength, highlighted by the dashed line in Figure 2a,b, the SQ-filled SWCNTs clearly exhibit an additional peak compared to the DCM-filled reference sample. The near-IR emission observed here is clearly associated with the SWCNTs but is observed upon excitation of the encapsulated dye molecules (ca. 740 nm) and is therefore a direct manifestation of energy transfer from the dye molecules to the SWCNTs. Such peaks will henceforth be referred to as EET peaks. Figure 2c demonstrates that the EET peak extracted from the PLE map by integrating excitation slices from 1410 to 1460 nm overlays very well with the absorption of the encapsulated dye species (from Figure 1c), confirming that the EET arises from the encapsulated dye molecules.

Figure 2.

PLE spectroscopy of SQ-filled SWCNTs. (a,b) PLE maps of (a) SQ@LV950-ATPE and (b) DCM@LV950-ATPE. White points indicate possible peak positions obtained from empirical relations for empty SWCNTs,²⁸ and the white dashed line highlights the position of the additional EET peak. (c) Comparison of free SQ absorbance in toluene (green), encapsulated SQ absorbance (blue, see Figure 1c), and PL excitation spectra of SQ@LV950-ATPE (red) and DCM@LV950-ATPE (black) obtained from the PLE maps by integrating over emission wavelengths from 1410 to 1460 nm. (d) PLE map of SQ@AD-DOC with the two dashed lines highlighting the EET excitation window. (e) PL excitation spectra of SQ@AD-DOC and DCM@AD-DOC integrated over emission wavelengths 1420–1440 nm and comparison between SQ absorption of the free and encapsulated molecules (colors as in panel c), as well as obtained by integrating excitation spectra of SQ@AD-DCM@AD for indicated emission wavelength ranges (dotted curves). The absorption envelope of the encapsulated dyes clearly originates from a superposition of EET peaks for different host SWCNTs (for an enlarged version see SI, Figure S12). (f) Normalized difference PLE map (see main text) clearly highlighting the EET and prominently showing the onset of EET at an emission wavelength of about 1420 nm and the variation of dye excitation wavelength with SWCNT diameter (hence emission wavelength). The bottom panel represents the integrated intensity of the normalized EET band, integrated over excitation wavelengths 690–750 nm.

More pronounced EET peaks were found for the SQ@AD-DOC sample in the excitation range between 690 and 750 nm as highlighted by the dashed lines in the Figure 2d. Since this sample represents a broader diameter range than the SQ@LV950-ATPE sample, we now observe EET peaks with different (dye) absorption wavelengths at different (SWCNT) emission wavelengths (see also Figure 2e, which compares different excitation slices with each other).

In order to better visualize the EET band and compare its relative intensity as a function of the encapsulating SWCNTs (emission wavelength), it is useful to subtract the DCM@SWCNT PLE map (pure SWCNT signals) from the SQ@SWCNT PLE map, after normalization over the intrinsic SWCNT signals, to eliminate the influence of SWCNT chirality dependent abundance and PL efficiency (see SI section 8 and ref (12)). The obtained map (Figure 2f, top), containing solely EET peaks, clearly shows the dependence of the EET peak position on the SWCNT emission wavelength. Plotting its integrated intensity (over excitation wavelengths 690–750 nm) as a function of emission wavelength (Figure 2f, bottom) clearly shows an onset of the EET band at about 1420 nm, corresponding to the emission of the (9,8) and (11,6) chiralities. SWCNTs with smaller diameters, that is, shorter emission wavelengths, do not show any EET as they appear to be too narrow in diameter to accommodate the dye. Note that we find a much smaller critical diameter for SQ-filling than in previous work,¹⁸ which may be ascribed to the more efficient SWCNT opening procedure used here, including air oxidation, acid treatment, and high-temperature annealing. In particular the latter step removes any functional groups, for example those formed during oxidation, and results in clean, open SWCNT ends.¹²

Steady-state PL studies also indicate that the SQ emission is quenched by a factor of ∼10⁵ by encapsulation within SWCNTs (see SI, section 5). Reports of fluorescence quantum yield of SQ range from 0.65 to 0.85,²⁹ showing that the SQ excited state decays primarily via a radiative process for the isolated molecule. This near-quantitative PL quenching implies a strong interaction between the dye molecules and the SWCNTs that leads to rapid nonradiative excited state deactivation, consistent with the intense EET peaks observed in SWCNT PLE maps. Indeed, when comparing the PL excitation spectra to the absorption spectra, the intensity of the SQ (EET) and S₂₂ excitation bands is of the same order of magnitude, indicative of a high EET efficiency (Figure S12). However, this does not allow for a quantitative determination of EET efficiency due to the diameter-dependent PL efficiency of the SWCNTs. Since quenching of SQ emission alone cannot distinguish between EET and other nonradiative decay pathways, we turn to TA spectroscopy to characterize the excited-state dynamics of encapsulated dye molecules and SWCNTs.

The ATPE sorted sample allows us to thoroughly track the well-isolated spectral signatures of s-SWCNTs with diameters close to 1.195 nm, effectively removing the spectral congestion present in more polydisperse samples. Furthermore, the absorption energy of the encapsulated SQ dye species is even better separated from SWCNT exciton transitions (for both metallic and semiconducting species). Thus, in contrast to previous TA studies,¹⁸ where SQ molecules were encapsulated in unsorted SWCNTs and the SQ dynamics were not directly probed, the SWCNT enrichment we demonstrate here allows us to probe the excited state dynamics for the encapsulated SQ with minimal overlap with SWCNT excited state TA features.

TA spectra for the SQ@LV950-ATPE and DCM@LV950-ATPE samples, taken at relatively short probe delays (∼400 fs) following a 748 nm pump pulse, that is, at the long-wavelength side of the dye absorption, are shown in Figure 3a. There are two primary differences between the spectra: (1) there is clear SQ ground-state bleach (GSB) at ca. 750 nm in the SQ@LV950-ATPE sample that is absent for the DCM@LV950-ATPE sample, and (2) the S₁₁ and S₂₂ signal intensities (∼1400–1600 nm and 800–1000 nm, respectively) are enhanced for the SQ@LV950-ATPE sample relative to the DCM@LV950-ATPE sample. Figure 3b displays the GSB dynamics of SQ molecules either in toluene (green trace) or encapsulated in SWCNTs (blue trace). The SQ GSB for isolated molecules decays with a lifetime of 2.1 ± 0.1 ns, consistent with the measured photoluminescence lifetime (2.0 ± 0.1 ns) for the integrated fluorescence decay over the wavelength range 590–760 nm (Figure S19). Figure 3b illustrates that the encapsulated SQ excited-state lifetime, measured via the GSB at 748 nm, is dramatically reduced compared to isolated SQ molecules. The dominant decay component (∼92%) is 205 ± 12 fs, obtained after deconvolution with the instrument response function (IRF, ∼200 fs), and hence not limited by it. There is a second, low-amplitude component (∼8%) with a 1.9 ± 0.3 ps decay time. When probing the decay of the complete SQ spectrum, as presented in Figure 4, we find that at early times (dominated by the 205 fs component) the GSB peaks at 748 nm and excited-state absorption peaks at 720 nm. At later times, the transient spectrum changes to a derivative-like spectrum with a node at 748 nm that lasts for tens of picoseconds (Figure 4b) indicating a shifted absorption spectrum. To investigate the origin of these different components, we first turn to the GSB kinetics of the surrounding SWCNTs.

Figure 3.

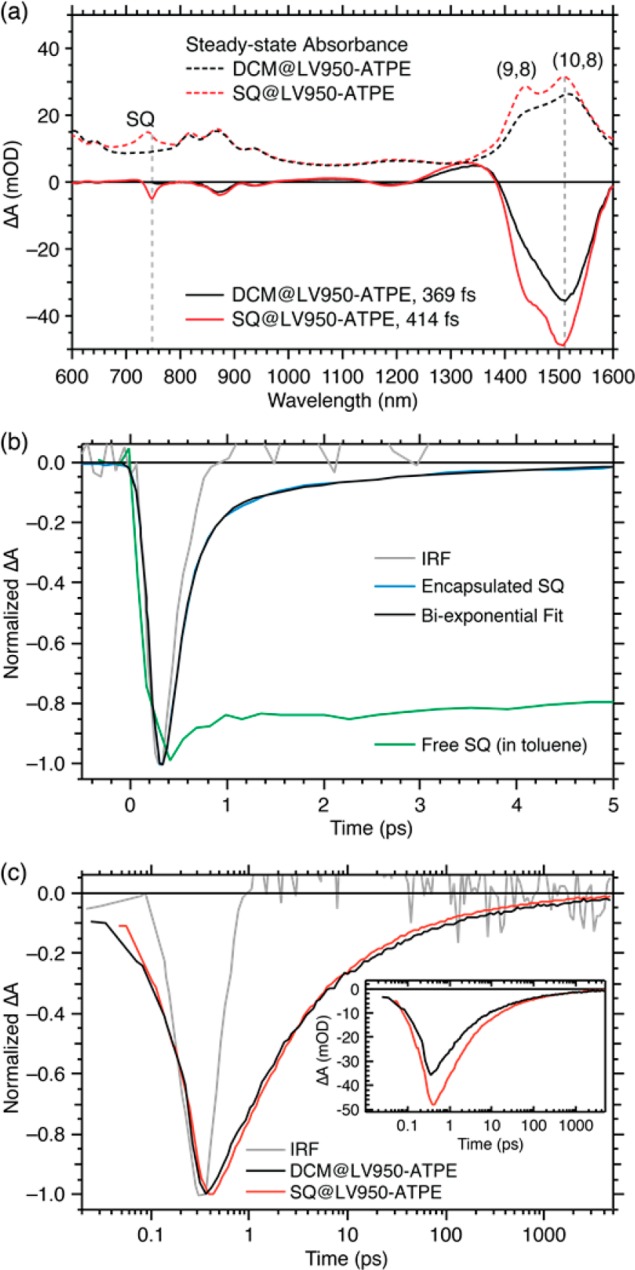
TA spectroscopy of ATPE-sorted LV950 SWCNTs pumped at 748 nm (i.e., in the SQ absorption band). (a) Peak transient absorption spectra at early times (solid traces) and steady-state absorption spectra (dashed traces) of DCM-filled (black traces) and SQ-filled (red traces) SWCNTs. Dashed vertical lines indicate the probe wavelengths at which the kinetic slices in panel b, that is, 748 nm (also the pump wavelength) and in panel c, that is, 1511 nm were obtained. (b) Kinetic slices for the SQ ground state bleach at 748 nm (blue trace), with the corresponding biexponential fit (black trace). The kinetic traces for free SQ dye in toluene (green trace) and the instrument response function, IRF (gray trace), are shown for reference. A probe-wavelength-dependent TA map is presented in Figure 4. (c) Kinetic slices at the peak (1511 nm) of the NIR ground state bleach dominated by the (10,8) S₁₁ transition for the SQ@LV950-ATPE (red trace) and reference DCM@LV950-ATPE (black trace). The kinetic trace for the IRF (gray trace) is shown for reference. Inset: Non-normalized kinetics with same color scheme as main panel.

Figure 4.

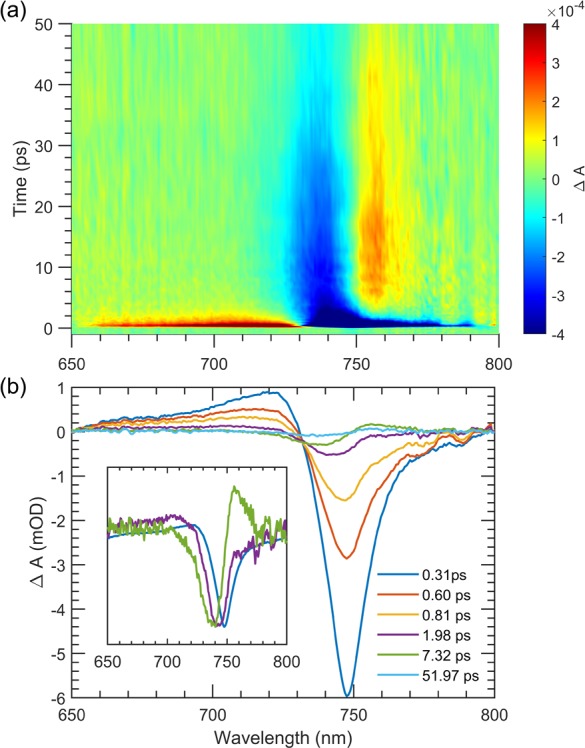
Focus on TA of the SQ@LV950-ATPE sample near the SQ absorption. (a) 2D TA map showing the spectral evolution of the encapsulated SQ absorption. (b) Selected TA spectra for short (sub-ps), medium (ps), and long (tens of ps) time scales. Inset shows a few selected normalized TA spectra (see also Figure S23 for kinetic slices at different probe wavelengths).

Figure 3c compares the GSB kinetics at 1511 nm, primarily probing the exciton generation and decay dynamics of the (10,8) s-SWCNTs. The increased intensity of the GSB peaks of s-SWCNTs within the SQ@LV950-ATPE sample compared to DCM@LV950-ATPE, seen in both spectral (Figure 3a) and kinetic (Figure 3c, inset) traces, indicates increased exciton populations in the s-SWCNTs following photoexcitation of encapsulated SQ molecules, consistent with the EET peaks observed in the PLE maps. The dynamics of both the rise and decay of the GSB features associated with the S₁₁ exciton envelope, through comparison of direct excitation of the s-SWCNT in the DCM@LV950-ATPE reference sample to excitation of encapsulated SQ in the dye-filled sample, allow us to better understand the dynamics related to the EET process. The fact that this increased GSB intensity is observed instantaneously suggests that EET from encapsulated SQ to the (10,8) species occurs on a time scale similar to the IRF (see SI Figure S23 for direct comparison of SQ and CNT GSB kinetics). This strongly suggests that the 205 fs component of the SQ decay (reported in Figure 3b) reflects the EET time. The normalized transients (Figure 3c) also illustrate that the SWCNT exciton dynamics are nearly indistinguishable in the two samples. This overlap suggests that none of the slower components in the SQ decay contribute significantly to the SWCNT dynamics and, hence, cannot be attributed to EET. Otherwise, this would be observed as an apparent slowing of the GSB decay of the SQ-filled SWCNTs with respect to the reference sample (due to a superimposed rise of GSB intensity from the hypothetical slower EET process on top of the decay from recombination of excitons already excited in or transferred to the s-SWCNTs).

Since the slower components do not appear to be related to EET from SQ to s-SWCNTs, we undertook other analyses to try to better understand their origin. The absorption spectrum in Figure 1b demonstrates that the LV950-ATPE sample contains reduced but still appreciable amounts of metallic SWCNTs. It is thus conceivable that the slower SQ GSB recovery results from EET (or another induced nonradiative decay pathway) associated with SQ molecules within metallic SWCNTs. Therefore, to ensure that metallic SWCNTs do not significantly affect the dynamics, we also performed TA measurements on PFH-A extracted s-SWCNTs (SQ@AD-PFHA1), where the metallic SWCNT content is expected to be less than 0.02%.²⁶ The results for the SQ@AD-PFHA1 (see SI, section 13) are similar to those for the SQ@LV950-ATPE sample, confirming that the slower components are not related to SQ interactions within metallic SWCNTs. Similar ultrafast S₁₁ intensity enhancements observed for the two SQ-filled samples confirms that the ca. 205 fs process corresponds to EET.

Taken as a whole, the ability to probe simultaneously the SQ and SWCNT dynamics as presented in Figures 3 and 4 suggests that excitation of the encapsulated SQ dye leads to EET to the surrounding s-SWCNT on a time scale of ca. 205 fs, consistent with several previous literature studies of EET from dyes to SWCNTs.^17,18,30,31 In addition, the broadband probe spectral window utilized here allows determination of the encapsulated SQ kinetics, which exhibit minor components with a shifted absorption spectrum with lifetimes greatly exceeding the IRF (Figure 3b and 4b). One possible origin for the 1.9 ps component in the SQ GSB would be that a subpopulation of SQ molecules does not undergo EET but decays nonradiatively to the ground state on a picosecond time scale. However, it could also be (perhaps more likely) that the EET leaves the SQ molecules in a vibrationally hot ground electronic state and that the 1.9 ps component corresponds to relaxation within the vibrational manifold of this state, which would also explain why this component is not observed in the SWCNT decay. Yet, the exact origin of the 1.9 ps component is difficult to assign and warrants further investigation.

The longer 34 ps component of the SQ decay shows a derivative-like TA spectrum, indicating a redshift of the SQ ground state absorption, which could be caused by charge carriers present in the surrounding SWCNTs (i.e., Stark effect) that are generated either from excitons directly created in the SWCNTs or transferred from SQ. Indeed, components in this time range seem to be present in the GSB decay of the SWCNTs but are superimposed on a much slower (nanosecond) decay, which was previously attributed to, for example, triplet excitons³² or phonon thermalization,³³ both of which would be consistent with the absence of a long-lived Stark shift of the SQ absorption. While we do not have direct evidence for the creation of charges in the SWCNTs studied here, charge generation in neat PFO-wrapped SWCNT samples has been observed in several other studies.³⁴⁻³⁶ Such charge generation has also been invoked to explain Stark shifts observed previously for higher-energy excitons of the SWCNTs themselves³⁷ and implies that encapsulated molecules could potentially serve as probes for the excited-state SWCNT properties. We summarize the states explored by TA and the rates between them in Scheme 1.

Scheme 1. Photophysical Scheme Illustrating the Excited State Manifold Present for the SQ@SWCNT Samples.

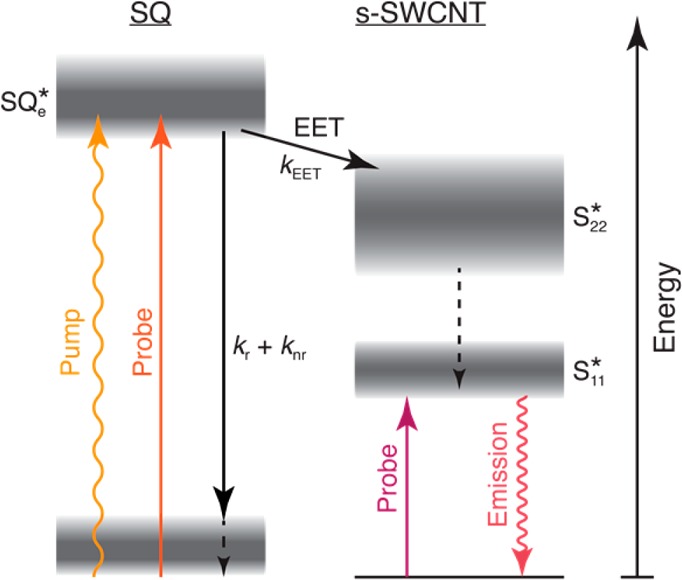
The pump pulse generates the excited state of encapsulated squaraine molecules (SQ_e*). TA measurements probing directly at the SQ_e* energy track the total excited state decay of SQ_e* by radiative and non-radiative decay (k_r + k_nr) or energy transfer to SWCNTs (k_EET). Arrival of excitons in SWCNTs via energy transfer is probed either by TA or PLE measurements at the energy of the first exciton, S₁₁*.

The quantum yield of EET (ϕ_EET) can be estimated in many ways. First, the near-quantitative quenching (≥99.999%) of SQ fluorescence after encapsulation (see section 5 in SI) suggests that all SQ excited states decay nonradiatively, either through EET or other nonemissive pathways. If we assume that EET is the dominant nonradiative decay pathway for encapsulated SQ molecules, then the PL quenching result suggests ϕ_EET ≥ 99.999%.

Second, whereas fluorescence only monitors emissive states, the SQ GSB kinetics track the entire excited-state population, including both emissive and dark states resulting from encapsulation. Thus, the measured rates of SQ excited state decay pathways can be used as a second means to estimate ϕ_EET:

1

where k_EET is the rate coefficient for EET and the denominator sums all rate coefficients for decay from the encapsulated SQ excited state, including EET (Figure 3d). If we assume that the dominant decay pathway(s) competing against EET do not change for SQ molecules upon encapsulation (although decay times can change upon aggregation^38,39), then the 2.1 ns lifetime of free SQ molecules in toluene with respect to the GSB recovery time constant of encapsulated SQ molecules (i.e., τ = 205 fs) results in ϕ_EET ≅ 99.99%. If, as mentioned above, the 1.9 ps component stems from a separate SQ excited-state population not undergoing EET, then using the amplitude of the biexponential fit of the SQ kinetics gives an approximate efficiency, ϕ_EET ≅ 92%.

As a final method for estimating ϕ_EET, one can use the enhanced TA signal intensities of the SQ-filled SWCNTs with respect to the DCM-filled reference sample combined with the fraction of light absorbed by the SQ at the pump wavelength to estimate the ϕ_EET. This method is described in detail in section 12 of the SI, but it suffers from a finite, unknown contribution of SWCNT absorption at the pump wavelength. This uncertainty means that estimates using this approach result in 64% ≤ ϕ_EET ≤ 100%.

Chirality-Dependent SQ Excitation Energy Transfer

We now turn to an extensive investigation of the diameter-dependent excitation wavelength of the encapsulated SQ molecules, using the full range of samples with varying diameter distribution. The first implication of strong interchromophore coupling comes from the large bathochromic absorbance shift for encapsulated SQ molecules (∼220 meV), observed in absorption and PLE measurements (Figure 1c and Figure 2). In general, bathochromic shifts of the dye absorption can originate from a change in dielectric environment or intermolecular electronic coupling in dimers or aggregate structures.⁴⁰ The SWCNT internal cavity by itself is known to act as a very apolar environment⁴¹ and thus cannot explain the redshift. Moreover, the redshift (∼220 meV) observed for SQ molecules in the SQ@LV950-ATPE sample is much larger than typically observed for changes in dielectric environment of isolated SQ molecules in solution: the wavelength of maximum absorbance for SQ dissolved in acetonitrile (ε = 37) and toluene (ε = 2.93) differs by less than 10 meV (see Figure S13). Similarly, a reaction field of induced molecular dipoles of neighboring molecules in the 1D encapsulated array forming a polar environment, somewhat analogous to that described previously for an array of molecules with a large permanent dipole moment,¹² cannot account for the magnitude of the redshift observed here. Intermolecular transition dipole coupling between the dye molecules is therefore more likely to be the dominant cause of the large absorbance shifts here, as is well described for J-aggregates. Previous work has shown that such interactions can indeed be induced by SWCNT encapsulation, leading to, for example, α-sexithiophene J-aggregates.^13,16,31 The magnitude and sign of the electronic shift induced by such aggregation should strongly depend on the particular geometry of stacking that the molecules adopt, that is, H-like and J-like aggregates.^40,42,43 Studies on SQ thin films (in the absence of SWCNTs) demonstrate that the formation of SQ J-aggregates shifts the absorption to a broad wavelength range between ca. 700 and 780 nm,³⁹ consistent with the shift observed here for all SQ@SWCNT samples (Figure 1c). Of course, the inclusion of solvent molecules in addition to dye molecules cannot be excluded, yet the strong redshift (which moreover is maximal for small diameter tubes as expected, vide infra) shows that dye–dye interactions are large (much larger than solvent effects on these molecules), and thus no significant spacing by solvent molecules occurs. Encapsulation of SQ molecules within the internal SWCNT pore hence offers a strategy for hybrid optical materials wherein the diameter of the SWCNT may act to guide or constrain the particular aggregate geometries available to the molecules, tuning the properties of the exact same molecules.

The PLE maps presented in Figure 2 provide a robust platform for unraveling such diameter-dependent interactions since the selectivity in excitation and emission wavelengths disentangles the electronic transitions of each SWCNT chiral species on a two-dimensional map. Figure 2d displays a PLE map of the SQ@AD-DOC sample, which contains a relatively broad range of both small and large diameter s-SWCNTs. Strikingly, as we briefly discussed above, the excitation wavelength of the EET peaks, that is, the one corresponding to the dye absorption, varies strongly with emission wavelength; hence SWCNT structures with shorter emission wavelengths (smaller diameters) generally correspond to longer EET excitation wavelengths.

The diameter-dependent SQ absorption can be analyzed in more detail by taking vertical slices (excitation spectra) from the 2D PLE maps and integrating the emission intensity between two emission wavelengths, hence selectively probing only a small subset of SWCNT chiralities (those emitting in this specific wavelength range). The right panel of Figure 2e compares excitation spectra for emission wavelengths between 1420 and 1440 nm, corresponding to the emission of the (9,8) and (11,6) chiralities, for the DCM@AD-DOC (black curve) and SQ@AD-DOC (red curve) samples. The presence of the dye absorption at ∼739 nm can be clearly observed in the SQ@AD-DOC sample and is the signature of EET to the (9,8) and (11,6) s-SWCNTs. By subtracting the excitation spectra for the DCM-filled sample from those for the SQ-filled sample (after scaling to match the intrinsic S₂₂ excitation peak amplitudes), for various emission ranges, we obtain the contribution of encapsulated SQ to the excitation slices, shown in the left panel of Figure 2e (see Figure S12 in the SI for more detail). The EET excitation peaks (dotted curves) are narrower than, and fall within the range of, the overall absorption spectrum of the encapsulated SQ molecules (solid blue curve) and are all clearly redshifted with respect to the absorption of the free dye in toluene (solid green curve).

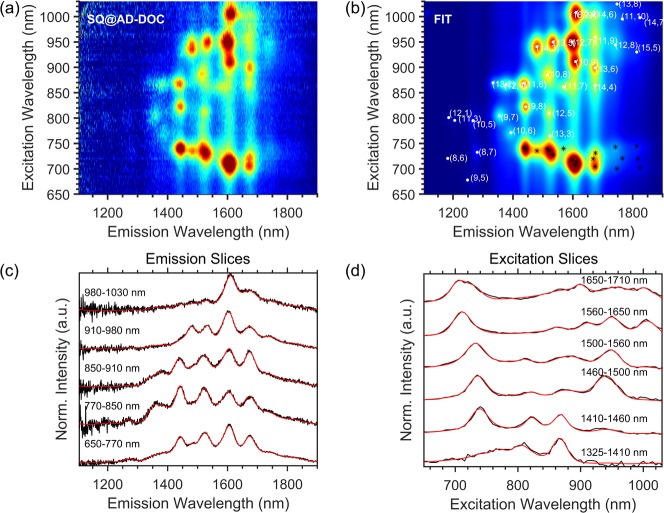
While these vertical slices of the PLE maps already convincingly demonstrate the diameter dependence of the EET peaks, much more accurate information can be deduced by a detailed two-dimensional fitting of the PLE maps. To this end, we adapted the previously developed fitting routine, which was successfully employed to extract peak positions, line widths, and amplitudes for the intrinsic SWCNT peaks in the PLE maps¹² and is based on an accurate model for the complicated excitation line shape associated with both excitonic and band-to-band excitations as well as phonon side bands for the SWCNTs. Here, in addition, for each SQ-filled SWCNT chirality, we included an EET peak which was modeled by the experimental absorption spectrum of the free dye molecules in toluene and spectrally shifted and contracted to match the EET peaks for each different chirality (see SI, section 10 for more details).

Interestingly, although the PFH-A-wrapped SWCNTs experience a different outer environment compared to the DOC-dispersed SWCNTs, hence yielding different SWCNT (S₁₁/S₂₂) peak positions and line widths, the corresponding chirality-dependent EET excitation peak positions and excitation line widths are identical to those obtained for the DOC-dispersed SWCNTs (while emission peaks and line widths do shift with environment). This confirms that the specific EET excitation wavelength (i.e., the absorption) of the encapsulated dyes, is solely determined by the diameter of the SWCNT in which the dye molecules are encapsulated, and not the dielectric environment provided by the solvent. In addition, the SWCNT peak positions of the DOC-dispersed SQ@LV950 and SQ@AD samples vary slightly, due to different filling fractions in these samples (PLE peak positions of empty and filled SWCNTs are different^10,28 but not resolved in partially filled samples, resulting in effective average peak positions), but the EET excitation peak positions and line widths remain the same in both samples. Therefore, the 2D fits were obtained by fitting the SQ@AD-DOC, SQ@LV950, and SQ@AD-PFHA2 samples simultaneously, with different SWCNT peak positions but the same EET excitation peak positions, allowing for a more accurate determination of the chirality-dependent EET peak positions. The simultaneous fit of samples with different relative abundance of SWCNT chiralities helps in disentangling information on those chiralities with nearly identical emission wavelengths. For chiralities that differ ∼15 nm or more in emission wavelength, the chirality assignment of the EET excitation peak position is unambiguous, but for chiralities that differ much less in emission wavelength, a possible interchange of chirality assignment of the EET cannot be excluded (e.g., for the (14,6) and (11,9) chiralities). The latter is not included in the error bars on the EET excitation wavelengths that are directly obtained from the fit. In addition, it should be noted that the model also includes the assumption that the EET line width is the same for all chiral structures. While we cannot ensure the validity of this assumption, fixing the line width helps to minimize the number of free fit parameters, while still yielding an excellent fit. Interestingly, the absorption of dyes within one single chiral structure is significantly narrower (∼24% ± 3%) than the absorption of freely isolated dyes in solution (see SI, Figure S18), which is also consistent with the formation of J-aggregates.⁴⁴ While the narrowing may not be as extensive as many prototypical J-aggregate systems,⁴⁴ such differences may reflect differences in the extent of exciton delocalization rather than the physical extent of the aggregate. Note that Yanagi et al.(18) previously used the broadening in absorption as evidence against J-aggregate formation. However, by disentangling the SQ absorption for every single chirality through analysis of the EET, we see that the apparent broadening in absorption is due to the broad diameter distribution of the SWCNTs and the associated range of aggregate geometries (vide infra).

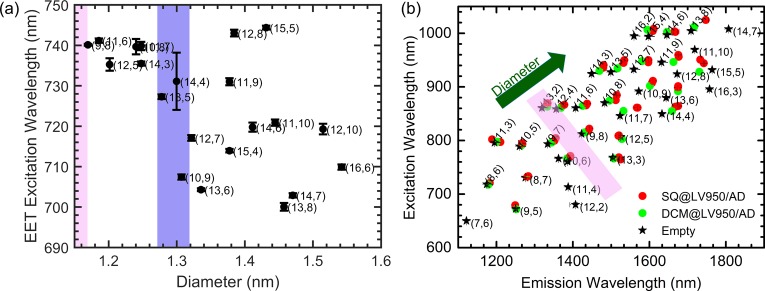
Figure 5 presents a representative example of a 2D fit of the PLE maps (see SI, section 10, for 2D PLE fits for all samples), demonstrating the excellent correspondence between the empirical model and the experimental data, and Figure 6 presents the peak positions extracted from these fits. Figure 6a presents the obtained EET peak positions for different chiralities as a function of SWCNT diameter and Figure 6b presents the electronic transitions (S₁₁ and S₂₂) of the SWCNTs, from which we can observe that the (9,8) chirality is one of the smallest diameter SWCNTs that shows a significant bathochromic shift of the SWCNT absorption/excitation (S₂₂) and emission (S₁₁) with respect to the DCM-filled SWCNT. This observation is in good agreement with the fact that this chirality is also the smallest diameter SWCNT that exhibits an EET peak (Figure 2f), establishing the (9,8) chirality as the smallest diameter (d = 1.15 nm) for which filling with SQ molecules is clearly observed. Also the (9,7) chirality (d = 1.09 nm) shows a notable shift of the SWCNT transitions, but no detectable EET peak; hence most likely only a small fraction of the (9,7) SWCNTs are filled, similar to what was observed before for a different dye near the critical diameter for filling.¹² While for the smallest filled diameters the EET peak position shows a large but constant redshift, at diameters larger than or equal to the (13,5) SWCNT (d = 1.26 nm; highlighted by the purple shaded area in Figure 6a), a more complex dependence of the SQ EET peak position on diameter is observed, indicating additional variations in stacking.

Figure 5.

2D spectral analysis PLE map of the SQ@AD-DOC sample. (a) Experimental PLE map of SQ@AD-DOC. (b) 2D fit of the PLE map, including both the intrinsic SWCNT PLE peaks (white dots) and the respective EET peaks (indicated by black stars). (c,d) Selected emission and excitation slices for the denoted excitation/emission wavelength ranges, showing the excellent correspondence between experimental data (black traces) and fit (red traces).

Figure 6.

(a) Position of the EET excitation peak, extracted from the 2D spectral analysis of the dye-filled PLE maps, as a function of the s-SWCNT diameter. The pink shaded area (in both panels a and b) represents the minimal encapsulation diameter range, and the purple shaded area represents the diameter range after which a more complex behavior is found with the diameter of the SWCNTs increasing according to the green arrow in panel (b) (see also main text). (b) Peak positions of empty (black stars), SQ-filled (red circles), and DCM-filled (green circles) SWCNTs as obtained from the PLE fits. A clear change in S₁₁/S₂₂ peak position between the SQ- and DCM-filled samples can be observed for SWCNTs with diameters similar or larger than the (9,8) SWCNT, indicative of filling with the SQ-molecules, also highlighted by the pink shaded area.

One can understand the dependence of SQ stacking on SWCNT diameter by considering the degrees of geometric freedom available to the SQ molecules. The exciton splitting energy, defined as the energy difference between the upper and lower excited states associated with simple dimer formation between interacting molecular monomers,⁴⁵ within a simple point dipole model, depends on the acute “slip-stack” angle formed between the transition dipole of one molecule, the line joining the centers of the transition dipoles, and the distance between monomers. Since all the observed shifts are bathochromic relative to the monomer absorption, the dominant behavior for encapsulated SQ molecules appears to be the formation of J-like aggregates.⁴⁵ The largest redshift is expected for molecules arranged in a head-to-tail fashion (i.e., slip-stack angle ∼0), which would be expected for SWCNTs with the minimum diameter that allows SQ encapsulation. Indeed, the (9,8) and other similarly small diameters show among the longest wavelength SQ excitation peaks.

To further support this conclusion, we performed quantum-chemical modeling of SQ molecules within SWCNTs. To computationally estimate the minimal encapsulation diameter of an array of SQ molecules, we first optimized the structure of an individual SQ molecule in vacuum using quantum-chemical calculations at the Hartree–Fock level with the semiempirical Hamiltonian PM7^46,47 (MOPAC).⁴⁸ The minimal diameter of a cylinder surrounding this optimized molecular structure was calculated (0.7546 nm, essentially determined by the O–O distance of the squaraine unit of SQ), taking into account standard van der Waals radii⁴⁹ and the van der Waals radius of the SWCNT carbon atoms (taken to be half the interlayer spacing of graphite, i.e., 0.1677 nm) was added (twice) to account for the inner van der Waals surface of the SWCNT. Using this approach, we obtain an estimated minimal encapsulation diameter of 1.09 nm, precisely corresponding to the diameter of the (9,7) SWCNT, which indeed shows a shift in SWCNT emission, but slightly smaller (by 0.06 nm) than the diameter of the (9,8) chirality, which is the smallest diameter for which EET is observed (see above). This is in line with previous work,¹² where we found that near the critical diameter SWCNTs are filled only partially, because of which the approximation by van der Waals radii seems to slightly underestimate the minimal encapsulation diameter. This is, perhaps, not surprising, since the molecules need to enter through the open ends of the SWCNTs, which might be slightly smaller due to the end structure, and filling near the critical diameter may also be kinetically limited.

We also calculated the structure of a (single) SQ molecule inside a (9,7) SWCNT (finite, hydrogen terminated section) at the semiempirical Hartree–Fock level using both the PM6-D3H4 and PM7 levels (Figure 7a). In both cases, we find that the molecule sits off-center in the SWCNT, in agreement with the structure previously determined using X-ray diffraction for SWCNTs with a larger diameter distribution.¹⁸ However, the PM7 calculation yields a significantly smaller distance between the SQ molecule and SWCNT wall. Note that although for molecular structure calculations PM7 is expected to perform slightly better than PM6, dispersion corrections are intrinsically incorporated in the PM7 Hamiltonian, while for PM6 these are applied as separate corrections (D3H4 includes both corrections for hydrogen bonding⁵⁰ and Grimme’s D3 correction for dispersion),⁵¹ which is the more established method for modeling van der Waals interactions in semiempirical calculations. To obtain a representative spacing for a 1D array in a narrow SWCNT, while avoiding the complications of the periodic potential of specific chirality SWCNTs, we also calculated the geometry of a SQ head-to-tail dimer by restricting the nitrogen atoms to lie on a straight line, yielding a lattice spacing of 1.90 nm.

The minimized diameter for double-file encapsulation was then estimated by the above method of calculating the narrowest cylinder surrounding the optimized structure, yielding a minimal encapsulation diameter of 1.188–1.217 nm, depending on the specific relative stacking orientation with respect to each other (i.e., close to cofacial or more slipped with respect to each other). Considering the small empirical offset as for the monomer in the (9,8) SWCNT, this amounts to a minimum SWCNT diameter of 1.267–1.296 nm.

Hence, at diameters larger than this threshold, additional variations in stacking may be expected, for example, slightly tilted versus two staggered parallel rows. We have highlighted this threshold with a purple band in Figure 6a, which agrees with the onset of a more complex dependence of the SQ EET peak position on diameter, while for smaller diameters a more monotonic dependence is observed. Interestingly, H-aggregate formation, that is, blue-shifted absorption with respect to the free dyes in solution, is not observed experimentally, suggesting that intermolecular geometries (i.e., paired parallel rows or large tilt angles) that result in significant oscillator strength for absorption to the upper manifold of the split excited states, while in principle possible from a purely geometrical point of view in larger diameters, seem not to occur. However, note that the usual point-dipole approximation may differ significantly from the actual interactions between molecules having charge centers near their ends (nitrogen atoms), which implies that head-to-tail interactions tend to dominate in many of the possible 1D stacking geometries.

Of course, the geometrical degrees of freedom are too large (especially with increasing diameter; the energy landscape exhibiting a vast number of local minima) to deterministically predict the exact stacking of SQ molecules in SWCNTs with the semiempirical approach. Based on the theoretically calculated intermolecular distances in π-stacked and head-to-tail SQ dimers and wall-to-dye distance for a SQ monomer inside a (9,7) SWCNT, a qualitative picture of possible stacking geometries of SQ in different diameter SWCNTs was obtained (Figure 7b). For (9,7) and similarly small diameters, a restriction to a 1D head-to-tail stacking is consistent with the large and nearly constant redshift of SQ absorption. For the wider (10,9) SWCNTs, either a tilted SQ array or a double-file array with small slip offset between π-stacked pairs may explain the smaller redshift observed experimentally (J-aggregate-type head-to-tail interaction partly compensated by H-aggregate-type interaction between π-stacked neighbors). For the (12,8) tubes, a double-file stacking with large slip offset would be consistent with the extra-large redshift observed, by the cooperative effects of J-aggregate type interactions between both π-stacked and head-to-tail neighbors.

While many uncertainties regarding intermolecular interactions (e.g., coherence length⁴³ and inter- or intrachromophore charge transfer interactions⁵²), as well as the fact that different stacking arrangements could lead to the same redshift, preclude us from assigning particular SQ transition energies to specific stacking arrangements, the simple qualitative framework discussed above provides insights into the role of the SWCNT diameter in dictating the stacking and electronic properties of the encapsulated SQ molecules. Our data are all consistent with SQ molecules interacting to a variable extent as J-aggregates within SWCNTs, where the precise stacking and associated absorption energies of encapsulated SQ molecules depend sensitively upon the surrounding SWCNT diameter.

Conclusions

In this work, we demonstrate that squaraine molecular dyes encapsulated inside the hollow cores of SWCNTs experience strong interchromophore interactions that are consistent with the formation of J-aggregates and undergo ultrafast EET to surrounding SWCNTs. Extensive simulation of 2D PLE maps demonstrates that the SQ absorption envelope is narrowed, relative to the free dye, and that the precise SQ absorption energy is linked to the diameter of the SWCNT in which the dyes are encapsulated. Transient absorption measurements demonstrate that the majority of SQ excited states undergo ultrafast EET to the surrounding nanotubes, with a characteristic time constant of ca. 205 fs. The near-complete fluorescence quenching and the comparison of the excited state lifetimes of free and encapsulated dye, along with analysis of SWCNT TA intensities, are all consistent with close to quantitative EET efficiency. Furthermore, we demonstrate that molecular encapsulation is fully compatible with multiple separation and extraction techniques. This compatibility should facilitate the incorporation of broadly tunable molecules into chirality-enriched and purely semiconducting SWCNT distributions for optoelectronic device applications, such as photodetectors and photovoltaic devices targeting specific spectral regions for energy harvesting. Such nanohybrids will also serve as important model systems for understanding the effects of spatial confinement and collective interactions between chromophores on dynamic excited state processes such as energy transfer, exciton delocalization, and charge transfer and transport.

Experimental Methods

SQ Encapsulation in SWCNTs

Two different SWCNT batches were used: commercial raw arc-discharge SWCNTs from Raymor (batch no. RNL 12-010-113, abbreviated here as AD) and in-house produced laser vaporization SWCNTs synthesized at 950 °C (LV950). To open the SWCNTs before filling, we employed a similar procedure to that described previously.^12,18 First, the raw SWCNT powders were oxidized in air. The oxidation temperature and envisaged weight loss was selected based on thermogravimetric analysis of the starting raw material (see SI, section 1) and amounted to 300 °C (18% weight loss) for the LV950 tubes and 460 °C (55% weight loss) for the AD SWCNTs. Second, the remaining SWCNTs were sonicated for 1 h in concentrated HCl (37 wt % in water) at 60 °C (bath sonicator, Bransonic 1510E-MTH, 70 W, 42 kHz) followed by thorough washing with deionized water to neutralize the SWCNTs. Finally, SWCNTs were annealed in high vacuum at 800 °C to remove any remaining functional groups at the SWCNT ends or (acid) filling inside their hollow core.

Filling of each of these opened SWCNT batches was performed by refluxing in a saturated solution of 1,3-bis[4-(dimethylamino)phenyl]-squaraine or in short Squarylium III dye (SQ, Aldrich, 90% purity, chemical structure presented in Figure 1a) in dichloromethane (DCM, Acros 99.6%, ACS reagent grade, typically 15 mg in 25 mL), followed by repeated rinsing with dichloromethane (∼500 mL) over a filtration membrane (Zefluor supported PTFE, 0.5 μm) with short (∼1 min) bath sonication between the subsequent washing cycles to remove any excess dye adsorbed on the outer SWCNT walls, while maintaining the dye in the endohedral SWCNT volume. These samples are further referred to as SQ@AD and SQ@LV950, where “@” refers to endohedral inclusion. As a reference sample for distinction from potential encapsulation of the reflux-solvent dichloromethane inside the SWCNTs, the same “filling” procedure was repeated on the same SWCNT soot without the presence of the SQ dye: DCM@AD and DCM@LV950. To distinguish encapsulation from any external adsorption, a closed SWCNT reference sample was also prepared (see SI, section 3).

Solubilizing the SWCNT Hybrids

To analyze the samples by optical spectroscopy, the SQ@SWCNT hybrids were isolated in solution. SQ- and DCM-filled SWCNTs were solubilized in a 1% w/v sodium deoxycholate (DOC, Acros Organics, 99%) solution in D₂O (Cortecnet, 99.8 atom % D). The samples were bath sonicated for 1 h on the first 3 days and subsequently magnetically stirred for 3 weeks, after which a short (1 h) centrifugation at 16000g (Sigma 2-16KCH, with swing-out rotor) was performed to remove undissolved species.

In Raman and 2D PLE measurements, selectivity in excitation allows for samples with a broad diameter distribution to be analyzed, yielding a wealth of information on the many individual SWCNT chiralities present. To this end, individual filled SWCNTs were thoroughly isolated from bundles by density gradient ultracentrifugation (DGU) in an Optima MAX tabletop ultracentrifuge (MLS50 swing out rotor operated at 218 000g for at least 18 h) as discussed previously,¹² and afterward the gradient medium was removed by dialysis in an ultrafiltration cell equipped with 30 kDa membranes. For comparison of spectral peak positions, empty, closed SWCNTs of each of the different SWCNT batches were also extracted by DGU, after gentle solubilization of the unopened (raw) SWCNTs powders according to previous work.²⁸

Sorting of SQ Filled SWCNTs

While this polydispersity in SWCNT diameter provides a wealth of information in the above-mentioned (2D selective) steady-state spectroscopy, the same heterogeneity generates severe spectral congestion that obscures the interpretation of transient absorption spectra (and hence the kinetics extracted from these spectra). To obtain a narrow chirality distribution, we followed two different and complementary approaches. We utilized chiral sorting by aqueous two-phase extraction (ATPE) of the thinnest SWCNTs that are filled with the SQ dye, that is, enriching the (9,8) chirality (see further). The sorting protocol was developed as a two-step procedure, similar to that previously reported for (6,5) and (7,5) SWCNTs.²¹ More critical for future photovoltaic applications, we applied selective polymer wrapping to achieve a narrow diameter distribution and at the same time remove all metallic SWCNTs from the sample.²² Both methods are described below.

ATPE Sorting of SQ@LV950 SWCNTs

Poly(ethylene glycol) (PEG, Alfa Aesar, MW 6 kDa) and dextran (Tokyo Chemical Industry Co., MW 40 kDa) were dissolved in D₂O in 15.3% w/w solutions. For the first separation step, 700 μL of 15.3% w/w PEG and 300 μL of 15.3% w/w dextran were mixed together with 12 μL of a 4.33% w/w DOC solution, 24 μL of a 4.33% w/w sodium dodecylbenzenesulfonate (SDBS, Acros, 88%) suspension, 60 μL of the SWCNT solution (0.9% w/w DOC), and 104 μL of D₂O. Benchtop centrifugation was performed (10 min at 5000g in an Eppendorf MiniSpin Plus centrifuge) to separate both phases. For the second step, a stock solution of 332 μL of 15.3% w/w PEG, 59.2 μL of 15.3% w/w dextran, 45.8 μL of 0.9% w/w DOC, and 18 μL of 8.3% w/w SDBS solution was prepared. A 75 μL portion of the bottom phase after step 1 was mixed with 175 μL of this stock solution, followed by a short centrifugation. Note that this separation can be easily scaled up to obtain several milliliters of sorted samples. In the first step, the (9,8) SWCNT together with most smaller diameter SWCNTs separate in the bottom phase. In the second step, the surfactant concentrations are slightly different, so that preferentially the (9,8) SWCNT chirality migrates to the top phase, while the other chiralities remain in the bottom phase. The top phase is then extracted and dialyzed in an ultrafiltration cell (100 kDa membranes) to a 1 wt %/V DOC/D₂O suspension. All separations were performed at room temperature, 21 °C.

Polymer Wrapping of SQ@AD SWCNTs

Polymer wrapping, using polymers based on the fluorene moiety, has emerged as one of the best methods for producing highly pure, isolated s-SWCNTs with narrow chirality distributions. Importantly, these polymers are highly selective and can result in metallic SWCNT impurity levels of <0.02%,²⁶ and the precise subset of s-SWCNTs can be targeted by judicious choice of the starting SWCNT raw material and the chemical structure of the fluorene-based polymer.²² To generate s-SWCNT samples with a small subset of s-SWCNT species here, we employ poly[(9,9-dihexylfluorenyl-2,7-diyl)-co-(9,10-anthracene)] (PFH-A) as the wrapping polymer since it yields high selectivity for large-diameter semiconducting SWCNTs with a narrow distribution of s-SWCNT species under appropriate processing conditions.²²

SQ- and DCM-filled AD SWCNT hybrids were dispersed in a solution containing PFH-A in 10 mL of toluene (2 mg mL^–1) using a 0.5 in. probe tip sonicator (Cole-Parmer CPX 750) operating at 40% power and held at a temperature of 18 °C using a bath of cool flowing water for 30 min. The resulting dispersion was centrifuged at 13 200 rpm using a SW32Ti rotor (Beckman Coulter), and the supernatant was collected for absorption and 2D PLE spectroscopy. For 2D PLE experiments, samples were exchanged to deuterated toluene (Aldrich, 99.6 atom % D), for its better IR transparency, by first drying the toluene suspension and afterward redispersing the as-formed film in deuterated toluene using short bath sonication. Two different samples were prepared with different molecular weight PFH-A, so that either a broad diameter distribution of only semiconducting tubes is formed (high MW = 125 kDa) or a small subset of near-armchair semiconducting SWCNTs is selected (lower MW = 39 kDa).

Spectroscopic Methods

Absorbance measurements were acquired on a Cary 500 spectrophotometer using cuvettes with a 5 mm path length or a Cary 5000 using a microcell with a 3 mm path length and 60 μL sample volume. 2D PLE maps were collected in an in-house developed dedicated spectrometer consisting of a pulsed Xe lamp (Edinburgh Instruments, Xe900-XP920) for excitation and a liquid-nitrogen cooled extended InGaAs array detector (Princeton Instruments OMA V:1024) sensitive up to 2.2 μm. Spectra were recorded in 90° geometry in a 3 mm microcell, with 5 nm steps in excitation wavelength. All 2D PLE maps were corrected for detector and spectrograph efficiency, filter transmission, and temporal variations of the excitation intensity.

Raman spectra were collected in backscattering geometry using a Dilor XY800 triple-grating spectrometer equipped with a liquid nitrogen cooled CCD detector. Excitation at various wavelengths was afforded by Ar⁺ (514.5 nm), Kr⁺ (647.1 and 676.4 nm), and tunable Ti:sapphire (700–900 nm) lasers. Individual spectra were corrected for detector and spectrograph efficiency and obtained with sub-wavenumber spectral resolution.

All transient absorption data were collected using an optical setup utilizing a Coherent Libra amplifier to pump visible and mid-IR OPAs (Light Conversion TOPAS-C) and an Ultrafast Systems Helios transient absorption spectrometer for collecting data. Each pulse was 100–150 fs long, giving an IRF near 200 fs. Specifically, the Libra output 3 mJ of 800 nm light at 1 kHz. For visible probing (∼400–800 nm), a small fraction of the 800 nm beam light is used to generate continuum probe light in a 2 mm sapphire crystal; for NIR probing (∼800–1600 nm), a small fraction of the 800 nm is sent into a thick 1 cm sapphire crystal to generate the probe. The mid-IR OPA pumped by the Libra was used to generate mid-IR probe light with ∼75 nm bandwidth; several probes were used to cover the range ∼1600–1800 nm. In all experiments, the visible TOPAS was used to excite the samples.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.8b02213.

• Thermogravimetric analysis, absorption, RRS, and PLE maps and fits for all samples, quenching of encapsulated SQ fluorescence, solvatochromism of SQ, SQ time-resolved PL in toluene, and EET efficiency estimation from TA (PDF)

Author Contributions

^# S.v.B. and D.H.A. contributed equally.

The authors declare no competing financial interest.