Detection of widespread horizontal pleiotropy in causal relationships inferred from Mendelian randomization between complex traits and diseases

Abstract

Horizontal pleiotropy occurs when the variant has an effect on disease outside of its effect on the exposure in Mendelian randomization (MR). Violation of the ‘no horizontal pleiotropy’ assumption can cause severe bias in MR. We developed the Mendelian Randomization Pleiotropy RESidual Sum and Outlier (MR-PRESSO) test to identify horizontal pleiotropic outliers in multi-instrument summary-level MR testing. We showed using simulations that MR-PRESSO is best suited when horizontal pleiotropy occurs in <50% of instruments. Next, we applied MR-PRESSO, along with several other MR tests to complex traits and diseases, and found that horizontal pleiotropy: (i) was detectable in over 48% of significant causal relationships in MR; (ii) introduced distortions in the causal estimates in MR that ranged on average from −131% to 201%; (iii) induced false positive causal relationships in up to 10% of relationships; and (iv) can be corrected in some but not all instances.

Epidemiological studies have established correlations between numerous exposures and complex diseases¹. Drawing causal inferences from these studies can be challenging due to reverse causation, confounding and/or other biases².

Mendelian randomization (MR) is a commonly-used human genetics approach that can be used to infer causality of an exposure for a complex disease outcome^3,4. MR presents a number of advantages over observational epidemiology, including the ability to control for non-heritable environmental confounders in such analyses and the use of genetic instruments to evaluate the impact of an exposure without necessitating the collection of that exposure in the outcome group. MR uses genetic variants as instrumental variables (IVs) that are robustly associated with the exposure of interest and tests whether the effects of the variants on the exposure result in proportional effects on the outcome.

In response to the advent of the genome-wide association (GWA) study and subsequent identification of thousands of trait-associated loci, multiple MR methods that leverage GWA summary statistics have been developed. These multi-instrument MR methods aggregate estimates from multiple IVs, testing for a causal relationship between a given exposure and outcome in a linear regression framework where the variants’ effects on the outcome are regressed on the same variants’ effects on the exposure^5,6.

A fundamental assumption of MR is the ‘no horizontal pleiotropy’ assumption (also called exclusion restriction criterion) which requires that the IV used for MR analysis acts on the target outcome exclusively through the exposure of interest². Horizontal pleiotropy occurs when the variant has an effect on other traits outside of the pathway of the exposure of interest and has an impact on the target outcome, or when the variant has a direct effect on the target outcome⁷. As a violation of the ‘no horizontal pleiotropy’ assumption, horizontal pleiotropy can distort MR tests, leading to inaccurate causal estimates, loss of statistical power, and potential false positive causal relationships.

Emerging evidence has supported a pervasive role of pleiotropy amongst loci identified from GWA studies. Studies have shown that many traits are genetically correlated with each other⁸. Furthermore, studies have shown that hundreds of individual variants identified from GWA studies are associated with multiple traits^9–14.

As a result, there has recently been discussion regarding the potentially serious consequences horizontal pleiotropy may have on the validity of previous and current MR studies. Some have raised skepticism about the MR approach due to the pervasiveness of pleiotropy amongst trait-associated variants¹⁵, while others have defended MR by noting that horizontal pleiotropy has long been known to impose limits on MR¹⁶. Regardless, the fact remains that the extent to which horizontal pleiotropy affects causal relationships inferred by MR is currently unknown. Importantly, a systematic evaluation of horizontal pleiotropy has not been performed.

Here, we conduct a systematic evaluation of the role of horizontal pleiotropy in MR. We developed the Mendelian Randomization Pleiotropy RESidual Sum and Outlier (MR-PRESSO) approach to detect and correct for horizontal pleiotropic outliers in multi-instrument summary-level MR testing. In extensive simulations, we then evaluate the performance of MR-PRESSO and compare it to other complementary methods including methods that measure and correct for an average horizontal pleiotropic effect across all variants, and outlier-robust methods. Finally, we apply these methods to 4,250 MR tests of complex traits and diseases derived from 82 summary level GWA datasets.

Results

We developed MR-PRESSO to evaluate horizontal pleiotropy in multi-instrument summary-level MR. In brief, MR-PRESSO has three components (Online Methods and Figure 1), including: a) detection of horizontal pleiotropy (MR-PRESSO global test); b) correction for horizontal pleiotropy via outlier removal (MR-PRESSO outlier test); and c) testing of significant differences in the causal estimates before and after correction for outliers (MR-PRESSO distortion test). MR-PRESSO relies on a regression framework where the variants’ effects on the outcome are regressed on the same variants’ effects on exposure, with the slope of the regression line providing an estimate of the causal effect of the exposure on the outcome. The MR-PRESSO global test evaluates overall horizontal pleiotropy amongst all IVs in a single MR test by comparing the observed distance of all the variants to the regression line (residual sum of squares) to the expected distance under the null hypothesis of no horizontal pleiotropy. The MR-PRESSO outlier test evaluates the presence of specific horizontal pleiotropic outlier variants by using the observed and expected distributions of the tested variant. Finally, the MR-PRESSO distortion test evaluates the significance of the distortion between the causal estimate before and after removal of the horizontal pleiotropic outlier variants (detected from the outlier test of MR-PRESSO).

Figure 1: Description of the Mendelian Randomization Pleiotropy RESidual Sum and Outlier (MR-PRESSO) method.

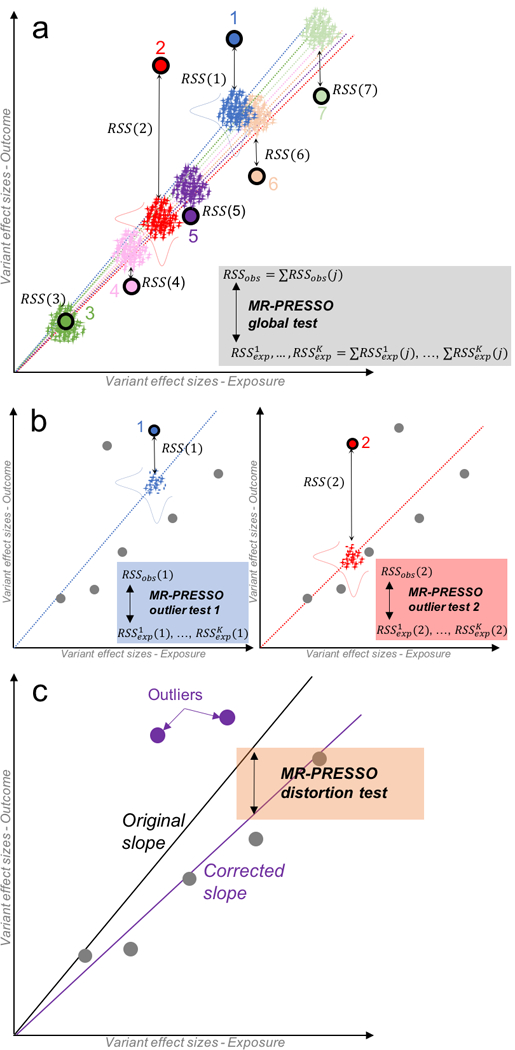
MR-PRESSO is comprised of three components. Panel a represents the global test. For each variant j, a slope, representing the causal estimate, is computed without the variant using standard inverse variance weighted meta-analysis (seven colored dotted lines; each color of the regression line corresponds to the line obtained by excluding the variant of the same color). The observed residual sum of squares RSS_obs(j) is computed as the squared difference between the observed effect size of variant j on the outcome and the effect size predicted using the slope computed without j. In addition, K pairs of random effect sizes for the exposure (x-axis) and the outcome (y-axis) (represented as crosses) are drawn from two Gaussian distributions (horizontal and vertical bell curves respectively for the exposure and outcome) from the predicted effect sizes and standard errors using the slope computed without j. A distribution of K expected ${\text{RSS}}_{\text{exp}}^{\text{k}}\left(\text{j}\right)$ is then calculated. By summing up the J RSS_obs(j), we calculate a global statistic that is compared to the K expected sum of ${\text{RSS}}_{\text{exp}}^{\text{k}}\left(\text{j}\right)$. Panel b represents the outlier test. A test is performed for each variant j by comparing the observed RSS_obs(j) to the K expected ${\text{RSS}}_{\text{exp}}^{\text{k}}\left(\text{j}\right)$. Here, only variants (1 and 2) are shown for simplicity. Panel c represents the distortion test. The panel shows how removing significant outliers detected by the MR-PRESSO outlier test (variant 1 and 2) leads to an unbiased slope (causal estimate).

Comparison of statistical properties of MR methods

We assessed the statistical performances of several methods designed to either detect (MR-PRESSO global test, the Q test^17,18, Q (modified) test¹⁹, Q’ test ^17,18 and Q’ (modified) test¹⁹) or correct for horizontal pleiotropy (correction of the global average horizontal pleiotropic effect using MR-Egger regression^20,21 or Multi-variable MR^22,23; outlier detection and removal approaches using MR-PRESSO outlier test, Cook’s distance^24,25, Studentized residuals²⁴, Q (modified) outlier test or Q’ (modified) outlier test) in multi-instrument summary-level MR. For these comparisons, we performed 10,000 simulations under different scenarios using the model described in Supplementary Figure 1b. We varied several parameters in the simulations including the main causal effect (β_causal = 0, 0.1, 0.2, 0.5 with β_pleiotropic = 0.1), the percentage of horizontal pleiotropic outlier variants (0, 2, 4, 10, 50, 90%), the type of horizontal pleiotropy (positive or balanced) and whether or not we assume the Instrument Strength Independent of Direct Effect (InSIDE) condition²⁰ (Online Methods; Supplementary Note).

False positive rate/power to detect horizontal pleiotropy

Using simulations, we first assessed the false positive rate (type 1 error) and power (1 – type 2 error) of the above MR methods that detect horizontal pleiotropy, including the MR-PRESSO global test, the Q test^17,18, Q (modified) test¹⁹, Q’ test^17,18 and Q’ (modified) test¹⁹ (Online Methods; Supplementary Note).

Under the null hypothesis of no horizontal pleiotropy (Supplementary Table 1), the MR-PRESSO global test, the Q (modified) test and Q’ (modified) test had controlled false positive rates (~5%) whereas the rates of the original Q and Q’ tests were inflated (between 5 and 25%). Since the Q and Q’ tests were found to be inflated, we proceeded with the MR-PRESSO global test, the Q (modified) test and the Q’ (modified) test in power analyses. The power to detect horizontal pleiotropy was similar for the MR-PRESSO global test and the Q (modified) test (Table 1). We observed acceptable power to detect horizontal pleiotropy across all three tests under simulations when the percentage of horizontal pleiotropic variants was ≥ 10% (which corresponds to 5 horizontal pleiotropic variants out of 50). Similar results were observed across all magnitudes of causal estimates, including instances in which there was no causal relationship (β_causal = 0) (Table 1). In addition, we conducted several sensitivity analyses (violation of the InSIDE condition, percentage of horizontal pleiotropic variants ≥ 50% and perfectly overlapping samples to estimate the effect sizes on the outcome and exposure) to further evaluate the robustness of these methods. All three tests had high power to detect horizontal pleiotropy under a wide range of these parameters; however, simulations showed a reduction in power in those with perfectly overlapping samples (Supplementary Results and Supplementary Tables 2–4).

Table 1:

Power to detect horizontal pleiotropy in Mendelian randomization for different methods.

Causal effect	Percent	Pleiotropy	MR-PRESSO global test	Q (modified) test	Q’ (modified) test
0	2	balanced	25.34	25.40	22.04
0	2	positive	25.01	25.01	22.00
0	4	balanced	51.79	51.96	47.80
0	4	positive	50.88	51.32	47.34
0	10	balanced	95.53	95.58	94.47
0	10	positive	94.27	94.26	92.85
0.1	2	balanced	24.10	24.41	21.58
0.1	2	positive	23.60	23.89	20.96
0.1	4	balanced	51.17	51.49	47.51
0.1	4	positive	50.67	50.59	46.69
0.1	10	balanced	95.56	95.56	94.31
0.1	10	positive	93.73	93.77	92.08
0.2	2	balanced	22.42	22.70	19.74
0.2	2	positive	22.95	22.92	19.97
0.2	4	balanced	48.37	48.29	44.45
0.2	4	positive	46.89	46.82	43.18
0.2	10	balanced	94.08	94.11	92.78
0.2	10	positive	91.85	91.91	90.24
0.5	2	balanced	16.72	16.70	14.90
0.5	2	positive	16.76	16.55	15.15
0.5	4	balanced	33.71	33.79	31.00
0.5	4	positive	32.52	32.66	29.93
0.5	10	balanced	81.15	81.22	79.07
0.5	10	positive	76.99	77.09	74.75

A total of 50 variants was simulated in each case. The InSIDE (Instrument Strength Independent of Direct Effect) condition is satisfied in all reported scenarios. MR-PRESSO: Mendelian Randomization Pleiotropy RESidual Sum and Outlier.

Evaluation of bias in the causal estimates

We investigated how the causal effect estimate (bias) and corresponding standard deviation (precision) of the MR-PRESSO outlier test were affected by horizontal pleiotropy. We then compared MR-PRESSO to other established MR methods that can correct for horizontal pleiotropy, including those that correct for a global average horizontal pleiotropic effect across all variants (e.g. inclusion of the intercept in MR-Egger regression^20,21, adjustment for multiple exposures in Multi-variable MR (MMR)^22,23), horizontal pleiotropic outlier detection methods (Cook’s distance^24,25, Studentized residuals²⁴, Q (modified) outlier test, Q’ (modified) outlier test) and outlier-robust methods (weighted median²⁶, mode-based estimate²⁷) (Online Methods).

The MR-PRESSO outlier test and Cook’s distance had similar power to identify the correct horizontal pleiotropic outliers whereas Studentized residuals had low power (Supplementary Table 5; Supplementary Note). However, Cook’s distance had lower specificity to identify the correct horizontal pleiotropic outliers compared to the MR-PRESSO outlier test (inflated false positive rate (family-wise error rate), > 97% when there was no horizontal pleiotropy). The false positive rate (family-wise error rate) and power of the Q (modified) outlier test and the Q’ (modified) outlier test were very similar to the MR-PRESSO outlier test (Supplementary Table 5).

MR-Egger regression generally had lower precision than the MR-PRESSO outlier test and MMR. The $I_{GX}^2$ index, which informs on when MR-Egger regression should be employed (i.e. $I_{GX}^2$>90%), was lower than 90% on average in most settings (Supplementary Table 6; Supplementary Results).

Cook’s distance and Studentized residuals had similar bias and precision in the causal estimate compared to the MR-PRESSO outlier test (Supplementary Table 7). The weighted median had less bias but also less precision in the causal estimate compared to the MR-PRESSO outlier test, particularly when the percentage of horizontal pleiotropic variants was < 50%. The mode-based estimate generally had very low precision compared to the other methods.

All four methods (mode-based estimate, weighted median, Cook’s distance and Studentized residuals) had similar limitations as the MR-PRESSO outlier test (e.g. inflated causal estimates and low precision) when there was a very high percentage of horizontal pleiotropic variants (≥ 50%) (Supplementary Table 7; Supplementary Note). Our simulations showed that when the InSIDE assumption was invalid, all methods exhibited bias in the causal estimate (Supplementary Tables 8 and 9; Supplementary Note).

The standard IVW approach showed an expected bias in the causal estimate due to horizontal pleiotropy. When the InSIDE assumption was valid and the percentage of horizontal pleiotropic variants was small (≤ 10%), the causal estimate of the MR-PRESSO outlier adjustment was less biased and had better precision (smaller standard deviation) than IVW, MR-Egger and MMR. However, when the percentage of horizontal pleiotropic variants was high (≥ 50%), the opposite was found. These trends were expected since outlier detection methods such as the MR-PRESSO outlier test require, as a baseline assumption, that at least 50% of the genetic variants to be valid instruments (no horizontal pleiotropy), have balanced pleiotropy and for the InSIDE assumption to be valid. Conversely, methods that correct for a global average horizontal pleiotropic effect amongst all variants (either by including the regression intercept in MR-Egger or covariate adjustment in MMR) are best suited when there is a large percentage of horizontal pleiotropic variants (> 50%).

Horizontal pleiotropy detection in MR for complex traits

We applied the MR-PRESSO global test, along with two methods (Q (modified) test, Q’ (modified) test) that can detect horizontal pleiotropy in MR to all possible pairs of 82 complex traits and diseases retrieved from publicly available GWA datasets (Table 2; Online Methods). In total, we conducted 4,250 tests for each of the three MR approaches. We accounted for multiple testing of the 4,250 tests using the Bonferroni correction. We note that this correction is overly stringent since many of the traits and diseases are correlated. Using a Bonferroni-corrected threshold of P < 1.17 × 10⁻⁵, the MR-PRESSO global test was statistically significant in 21.69% (n = 922) of the 4,250 tests. When restricting to statistically significant causal estimates in the IVW meta-analysis, we detected significance of the MR-PRESSO global test at a higher rate of 48.69% (n = 93 of 191 tests). Both the Q (modified) test and the Q’ (modified) test provided similar estimates. As a sensitivity analysis, we restricted to a subset of traits and diseases that were less correlated (e.g. Pearson r < 0.30). We observed that 24.17% of MR tests were statistically significant for the MR-PRESSO global test amongst significant causal relationships (Supplementary Table 10).

Table 2:

Application of methods to detect horizontal pleiotropy in Mendelian randomization analysis from 82 summary-level genome-wide association traits and diseases.

	4,250 pairs		191 ‘putatively causal’ pairs
	Percentage	Counts	Percentage	Counts
MR-PRESSO global test	21.69%	922	48.69%	93
Q (modified) test	20.59%	875	45.03%	86
Q’ (modified) test	18.85%	801	42.93%	82

MR-PRESSO: Mendelian Randomization Pleiotropy RESidual Sum and Outlier. ‘Putatively causal’ pairs are exposure-outcome pairs with a statistically significant causal estimate in the inverse variance weighted meta-analysis (at the Bonferroni-corrected cut-off).

Horizontal pleiotropy correction in MR for complex traits

We evaluated five methods to correct for horizontal pleiotropy in MR (Table 3). This included: 1) removing outliers detected by the MR-PRESSO outlier test, Q (modified) outlier test and Q’ (modified) outlier test (at Bonferroni-corrected threshold); and 2) adjusting for significant covariates individually or all together from the main MR test (e.g. significant causal effect in IVW meta-analysis at Bonferroni-corrected threshold). As shown in the simulations, the MR-PRESSO global test can be used to determine if there is any remaining horizontal pleiotropy after applying correction strategies to minimize initial horizontal pleiotropy in the MR test (Supplementary Note; Supplementary Table 11). In Table 3, we observed that the outlier removal approach using the MR-PRESSO outlier test was effective in eliminating statistical significance in the MR-PRESSO global test in 46% of the 922 tests. The Q (modified) outlier test and Q’ (modified) outlier test provided similar estimates. Furthermore, the covariate adjustment approach – defined by accounting for traits that were shown to have a significant causal effect on the same outcome – eliminated significance in the MR-PRESSO global test in 22% (n = 20) of the 93 tests when adjusting for a single covariate. When adjusting for all significant covariates in the same model, the covariate adjustment approach eliminated significance in 34% (n = 22) of the 42 tests. Taken together, these two correction strategies (MR-PRESSO outlier removal and MMR) were successful in 47% (n = 438) of the 922 tests total. Furthermore, we note that the covariate adjustment approach is limited in that it requires a priori knowledge of the trait responsible for the horizontal pleiotropic effect.

Table 3:

Correction for horizontal pleiotropy in Mendelian randomization using two different approaches: MR-PRESSO outlier test and covariate adjustment for 922 exposure-outcome pairs with significant horizontal pleiotropy.

	MR-PRESSO outlier test	Q (modified) outlier test	Q’ (modified) outlier test	Single-covariate adjustment (MMR)	All-covariate adjustment (MMR)
Total corrected	422	354	356	20	22
Total remaining horizontal pleiotropy	500	511	445	73	42
Fraction corrected horizontal pleiotropy	46%	41%	44%	22%	34%

MR-PRESSO: Mendelian Randomization Pleiotropy RESidual Sum and Outlier; MMR: Multi-variable Mendelian Randomization.

Outliers effect on the distortion of MR causal estimates

We evaluated the extent to which outliers cause distortion in the causal estimates resulting from MR. Using the MR-PRESSO distortion test, we compared the causal estimates from the IVW meta-analysis before and after removal of outlier variants detected by the MR-PRESSO outlier test (Online Methods). Using a Bonferroni-corrected threshold, we observed a significant distortion (of −93% and 35%) in 2.5% (n = 2) of significant causal estimates (n = 81 total). Since the Bonferroni correction is overly stringent, we considered the commonly-used nominal threshold of P < 0.05 that the majority of MR studies to date have used for statistical significance. A significant distortion was observed in almost 10% (n = 22) of the causal relationships (n = 229 total) with a distortion between −131% and 201% on average (Figure 2).

Figure 2: Distribution of the distortion of causal estimates before and after correction for horizontal pleiotropy using the MR-PRESSO distortion test.

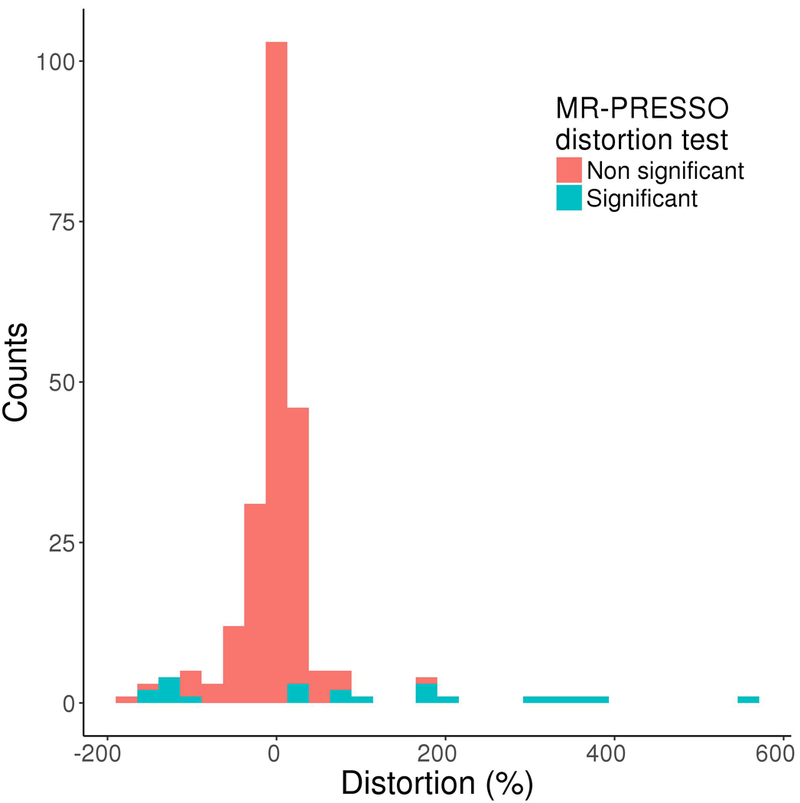
The distortion coefficient was calculated for all exposure-outcome pairs with a significant causal estimate (P < 0.05) using an inverse variance weighted meta-analysis (n = 229). The distortion coefficients were then tested using MR-PRESSO (Mendelian Randomization Pleiotropy RESidual Sum and Outlier) distortion test which provides an empirical P-value. The distortion coefficients are colored according to whether the distortion is statistically significant (blue) or not (red) at a Bonferroni-corrected threshold of P < 0.05 / 229 in the MR-PRESSO distortion test. The distortion estimate represents the change in the causal estimate as a result of horizontal pleiotropic outlier variants (Online Methods). A positive distortion represents a decrease in the outlier-corrected causal estimate.

Below, we provide one example to highlight the role of pleiotropy in MR (Supplementary Figure 2). We observed that the causal effect of body mass index (BMI) on C-reactive protein was estimated to be 0.39 (P = 7.02 × 10⁻⁸) by IVW. The MR-PRESSO global test showed statistical significance (P < 10⁻⁶) and the MR-PRESSO outlier test identified one significant outlier variant (P < 10⁻⁶, rs2075650 in the APOE locus). Examining this further, we observed that this variant was highly pleiotropic, having associations with several traits and diseases including Alzheimer’s Disease, body mass index, C-reactive protein, high-density lipoprotein cholesterol, low-density lipoprotein cholesterol, plasma triglycerides, waist circumference, hip circumference and waist-hip ratio at P = 6 × 10⁻⁴ (Bonferroni-corrected P = 0.05 / 82; Supplementary Table 12). Furthermore, this variant was associated with several other traits and diseases in the public NHGRI-EBI GWAS catalog²⁸ (P < 5 × 10⁻⁸; Supplementary Table 13). We believe some of these genetic associations with other traits and diseases will be due to horizontal pleiotropy while others will be in the same causal pathway (e.g. vertical pleiotropy). After removing this outlier variant, we observed a lower estimation of the causal estimate for BMI on C-reactive protein (β_causal = 0.35, P = 3.45 × 10⁻¹⁶) with this single variant alone causing a 12% distortion in the causal estimate (Supplementary Figure 2).

Outliers effect on false positive causal relations in MR

We evaluated the extent to which outliers (as detected by the MR-PRESSO outlier test) can induce false positive causal relationships. A false positive causal relationship was defined as an exposure-outcome pair in which the causal estimate was no longer statistically significant in the outlier-corrected IVW model but was previously significant in the naïve IVW model. According to this definition, we identified false positive relationships in 10% of putatively causal relationships (n = 24 out of 229 total tests) using the common nominal P < 0.05 threshold and 1.2% (n = 1 out of 81 total tests) using the stringent Bonferroni-corrected threshold (P < 1.17 × 10⁻⁵). We note that the outlier removal approach decreases the power of the outlier-corrected IVW model test because a smaller number of variants is included after removal of horizontal pleiotropic outlier variants. Therefore, we expect that a small number of false positive causal relationships may be due to reduced statistical power.

Causal relationships inferred from MR testing

We identified 191 significant causal relationships out of a total number of 4,250 MR tests using the Bonferroni-corrected threshold of P < 0.05 / 4,250 < 1 × 10^-5. We note that many of the traits examined are closely related to each other (e.g. BMI/waist circumference/hip circumference, and low-density lipoprotein cholesterol (LDL-C)/total cholesterol) and therefore the tests are not completely independent of each other. After correcting for horizontal pleiotropy via outlier removal using the MR-PRESSO outlier test, we validated known causal relationships including LDL-C on coronary artery disease (CAD) (β_causal = 0.52, P = 5.15 × 10⁻¹²)²⁹, systolic blood pressure on CAD (β_causal = 0.05, P = 1.78 × 10⁻⁶)^30–32, BMI on type 2 diabetes (β_causal = 0.76, P = 2.19 × 10⁻⁹)³³ and BMI on C-reactive protein (β_causal = 0.35, P = 3.45 × 10⁻¹⁶), amongst the strongest findings. Furthermore, we observed an effect of BMI on uric acid (β_causal = 0.31, P = 3.29 × 10⁻¹⁵)³⁴ and plasma triglycerides (β_causal = 0.20, P = 6.9 × 10⁻¹⁵)¹², although these are significant for the MR-PRESSO global test even after correction via outlier removal.

Discussion

In summary, we have evaluated horizontal pleiotropy in the context of MR testing across pairwise comparisons of a large number of complex traits and diseases. We have: i) developed the MR-PRESSO method to detect and correct for horizontal pleiotropic outliers in MR and compared it to several established methods; (ii) applied several of these MR methods to complex traits and diseases, and showed that horizontal pleiotropy occurs in over 48% of causal relationships between complex traits and diseases inferred by MR; (iii) observed average distortion between −131% and 201% in the causal estimates of MR due to horizontal pleiotropy; and (iv) showed that horizontal pleiotropy can be minimized and corrected in some cases through outlier detection and/or secondary phenotype adjustment when the mediating trait is known.

By applying the MR-PRESSO global test to detect horizontal pleiotropy in a wide array of complex traits and diseases, we observed horizontal pleiotropy in approximately over 48% of inferred causal relationships. This is consistent with emerging evidence that many disease-associated variants identified from GWA studies have effects on multiple traits¹⁰. Since these variants are used as IVs in multi-instrument MR, it is likely that a non-negligible number of these variants do not meet the ‘no horizontal pleiotropy assumption’ in MR. Furthermore, Hemani et al.³⁵ have evaluated horizontal pleiotropy in a study concomitant to the present study. The study proposed a mixture-of-experts machine learning framework to select the most appropriate MR method amongst a variety of standard and horizontal pleiotropy-robust MR methods associated with an IV selection procedure. The framework selected a method that involved horizontal pleiotropy (pleiotropy-robust method or IV filtering) in 90% of the MR tests. These results indicate that horizontal pleiotropy is commonplace and highlight the need to evaluate horizontal pleiotropy for variants acting as instrumental variables as a necessary and standard test when performing MR.

Horizontal pleiotropy in MR has direct implications for genetics-guided drug discovery and validation. Accurate estimates of causal effects between biomarkers and diseases can inform dose-response curves for drug efficacy and safety³⁶. In the present study, we show that horizontal pleiotropy can induce distortion in the causal estimates in MR and that this distortion is pervasive amongst many causal relationships. Secondly, there is increasing interest in using surrogate endpoints for drugs in clinical trials. Identifying true causal relationships using MR can pinpoint biomarkers that are causal and hence identify those surrogate endpoints that are most relevant to disease³⁷.

The current study has several strengths. Outlier detection methods are useful because they work within the framework of IVW. Furthermore, the MR-PRESSO global test (as well as the Q (modified) test and Q’ (modified) test) is adequately powered to detect horizontal pleiotropy amongst even a small subset of loci. Finally, outlier detection methods can be used in several different MR tests including IVW, MMR and even within the framework of MR-Egger regression. The MR-PRESSO method also has limitations. There were instances for which correction strategies (outlier removal or covariate adjustment) could not completely remove horizontal pleiotropy as detected by the MR-PRESSO global test. Possible reasons include violation of the InSIDE condition (as shown in the simulations) which is untestable, a percentage of horizontal pleiotropic outlier variants that is not suitable for the particular correction strategy (outlier detection method with > 50% of horizontal pleiotropic variants), no applicable covariate adjustment, or other sources of heterogeneity in the effect sizes other than horizontal pleiotropy such as gene-gene and gene-environment interactions. Furthermore, several GWA consortia use the same cohorts and study samples; therefore, some GWA summary statistics may have overlapping samples. In simulations, we evaluated the effect of perfectly overlapping samples on the power of our global test across a range of scenarios. A reduction in power for detecting horizontal pleiotropy was observed in the model with perfectly overlapping samples. Finally, because MR-PRESSO requires simulations, the processing time to apply the method can be slower compared to other methods.

In summary, we have shown through a series of analyses, that horizontal pleiotropy is pervasive in MR testing between complex traits and diseases, highlighting the need to employ approaches that minimize horizontal pleiotropy. Rigorous analysis and careful interpretation of causal inference testing in MR is warranted as a result of these observations.

Online Methods

General assumptions of Mendelian randomization

MR relies on genetic variants that are robustly associated with the tested exposure. A variant can be used as an instrumental variable (IV) through its effect size on the exposure and its proportional effect on the outcome. The causal estimate is an inferred estimate of the predicted response of the outcome caused by a modification of the exposure. Supplementary Figure 3 illustrates a standard MR framework (Supplementary Note). The single instrument approach can be extended to multiple instruments. Multi-instrument MR can be performed using an inverse variance-weighted, fixed effects meta-analysis³⁸ (IVW meta-analysis). IVW meta-analysis consists of fitting a weighted linear regression with a fixed intercept of 0 between the set of effect sizes on the outcome (either continuous or dichotomous response) and the effect sizes on the exposure (either continuous or dichotomous predictor), with the inverse of the variance of the effect sizes on the outcome as weights. When the intercept is fixed to 0, the slope of the regression then provides an estimate of the causal effect of the exposure on the outcome⁵.

The validity of MR analysis relies on three assumptions (Supplementary Figure 3): 1) the variant (i.e. IV) is associated with the exposure; 2) the variant is independent of all confounders of the exposure-outcome relationship; and 3) the variant is independent of the outcome conditional on the exposure and all confounders of the exposure-outcome association (i.e. exclusion restriction criterion). Violation of the third assumption, the exclusion restriction criterion, is a direct consequence of horizontal pleiotropy (Supplementary Figure 1).

Existing methods to detect and correct for horizontal pleiotropy in MR

Several existing methods have been developed to detect horizontal pleiotropy in MR. Methods to detect horizontal pleiotropy include the Q test and the Q’ test, as well as the recently proposed modified versions of these tests¹⁹, which are traditionally used to identify over dispersion and have been applied in the context of MR¹⁷.

Several existing MR methods have also been designed to correct for horizontal pleiotropy. Methods that we evaluated in the current study are described below.

Outlier methods:

Traditional methods to detect outliers have been applied in the context of MR to detect and remove invalid IVs²⁴. We applied Cook’s distance where we defined outliers using a threshold of greater than four divided by the number of variants²⁵. We also applied Studentized residuals where we performed Student tests on the Studentized residuals and defined outliers using a Bonferroni-corrected P-value threshold (0.05 divided by the number of variants). Finally, the Q (modified) outlier test and the Q’ (modified) outlier test use a χ²distribution with one degree of freedom to test each variant separately¹⁹ in association with a Bonferroni-corrected P-value threshold (0.05 divided by the number of variants).

Correction of the average horizontal pleiotropic effect methods:

The intercept of MR-Egger regression²⁰ can correct for the average horizontal pleiotropic effect across all IVs. The $I_{GX}^2$ index, which encapsulates the collective strength of a set of variants, can be used to inform on the use of MR-Egger regression²¹. MMR (Multi-variable MR)^22,23 takes into account known causal exposures to the outcome (E₂ in Supplementary Figure 1b). If the IV is subject to horizontal pleiotropy and has a significant effect on not only the tested exposure E₁ but also on a second exposure E₂, then MMR allows to adjust for this secondary horizontal pleiotropic effect. In practice, MMR is implemented by fitting a weighted linear regression by regressing ${\stackrel{\wedge }{\Gamma }}_{1,j}$ on both ${\widehat{\gamma }}_{1,j}$ and ${\widehat{\gamma }}_{2,j}$ (with the inverse of the variance of the effect sizes on the outcome as weights). The ${\widehat{\gamma }}_{2,j}$ are the genetic effects of the variants on the known secondary causal exposure E₂. The model can be extended to include multiple exposures. In this study, a fixed intercept of 0 was used in all MMR models.

Outlier-robust methods:

Additional methods are naturally robust to horizontal pleiotropic outlier variants in MR. The weighted median²⁶ estimator provides a consistent estimate of the causal effect when up to 50% of genetic variants are invalid instruments. The mode-based estimate (MBE) method²⁷ uses the property that valid instruments should provide the largest number of similar individual-instrument causal estimates even if the majority of instruments is invalid.

MR-PRESSO: MR Pleiotropy RESidual Sum and Outlier

We developed the MR Pleiotropy RESidual Sum and Outlier (MR-PRESSO) test to detect and correct for horizontal pleiotropic outliers. MR-PRESSO is comprised of three components (Figure 1):

• a)detection of horizontal pleiotropy (and violation of the exclusion restriction assumption, Supplementary Figure 1) in MR (global test);
• b)correction by removal of offending IVs that are due to horizontal pleiotropy (outlier test);
• c)testing of significant differences in the causal estimates before and after outlier removal (distortion test).

MR-PRESSO extends the framework of IVW meta-analysis and is based on the following rationale. IVW meta-analysis consists of fitting a weighted linear regression between the set of effect sizes on the outcome and the effect sizes on the exposure. The slope of the regression provides an estimate of the causal effect of the exposure on the outcome. Under the null hypothesis where horizontal pleiotropy does not exist, all variants are expected to be close to the regression line (i.e. to have small residuals in the regression). However, when a variant is subject to horizontal pleiotropy, the effect size on the outcome can be larger or smaller than the effect size mediated by the exposure in question and therefore the variant can deviate from the true slope of the regression line. MR-PRESSO is designed to detect whether a subset of variants is significantly deviating from the regression line. The MR-PRESSO outlier test requires that at least 50% of the variants are valid instruments and relies on the InSIDE (Instrument Strength Independent of Direct Effect) condition²⁰, which states that the effect sizes of the variants on the exposure should not depend on the horizontal pleiotropic effects on the outcome.

MR-PRESSO global test

The MR-PRESSO global test evaluates for the presence of horizontal pleiotropy and is comprised of four steps (Figure 1a):

• 1)for each variant j, we removed the variant in question and refit a IVW regression. This allows us to calculate the slope of the regression line on the remaining variants, denoted ${\widehat{\beta }}_{-j}$ which represents the causal estimate without variant j;
• 2)the estimated causal effect (slope) without variant j is used to predict the expected effect size on the outcome as the product of${\widehat{\beta }}_{-j}$ and the effect size of the same variant on the exposure ${\widehat{\gamma }}_j$. Then, we calculated the observed residual sum of squares (RSS) as the difference between the observed effect size of the variant on the outcome (${\widehat{\Gamma }}_j$) and the predicted effect size of the same variant on the outcome $RS{S}_{obs}\left(j\right)={\left({\widehat{\Gamma }}_j-{\widehat{\beta }}_{-j}{\widehat{\gamma }}_j\right)}^2$. The global observed RSS is then obtained by summing over the J $RS{S}_{obs}\left(j\right)$: $RS{S}_{obs}={\displaystyle \sum }_{j}RS{S}_{obs}\left(j\right)={\displaystyle \sum }_j{\left({\widehat{\Gamma }}_j-{\widehat{\beta }}_{-j}{\widehat{\gamma }}_j\right)}^2$;
• 3)the observed RSS is compared to a simulated expected distribution of RSSs. The expected distribution is simulated under the null hypothesis (0% of variants are outliers). First, we simulated a distribution of effect sizes on the exposure ${\widehat{\gamma }}_j^{random}$ from a Gaussian distribution $\mathcal{N}\left({\widehat{\gamma }}_j,\mathbb{V}\left({\widehat{\gamma }}_j\right)\right)$. Second, we simulated a distribution of effect sizes on the outcome ${\widehat{\Gamma }}_j^{}$_random around the predicted effect size on the outcome (${\widehat{\beta }}_{-j}{\widehat{\gamma }}_j$) by drawing in a Gaussian distribution $\mathcal{N}\left({\widehat{\beta }}_{-j}{\widehat{\gamma }}_j,\mathbb{V}\left({\widehat{\Gamma }}_j\right)\right)$. The expected RSS is then obtained as ${\displaystyle \sum }_{j}RS{S}_{exp}\left(j\right)={\left({\widehat{\Gamma }}_j^{random}-{\widehat{\beta }}_{-j}{\widehat{\gamma }}_j^{random}\right)}^2$. The procedure was repeated multiple times (K) to obtain a null distribution of the K expected RSSs, $RS{S}_{exp}^k={\displaystyle \sum }_{j}RS{S}_{exp}^k\left(j\right)={\displaystyle \sum }_j{\left({\widehat{\Gamma }}_{jk}^{random}-{\widehat{\beta }}_{-j}{\widehat{\gamma }}_{jk}^{random}\right)}^2$;
• 4)an empirical P-value is computed as the number of expected RSSs greater than the observed RSS divided by the total number of times the procedure is repeated:$P=\frac{{{\displaystyle \sum }}_k{1}_{>RS{S}_{obs}}\left(RS{S}_{exp}^k\right)}{K}$.

K corresponds to the number of random drawings used to generate the expected distribution. The magnitude of K depends on the desired precision of the P-value which is 1/K. We recommend to use at least K = 1,000, which will produce a precision of at least 10⁻³.

MR-PRESSO outlier test

The MR-PRESSO outlier test allows for the detection of specific horizontal pleiotropic outlier variants. For a given variant j, we compared the observed j^th RSS $RS{S}_{obs}\left(j\right)$ (obtained in step 2 of the global test) with the distribution of K expected j^th RSSs $RS{S}_{exp}^k\left(j\right)$ (obtained in step 3 of the global test). Finally, an empirical P-value is computed as $P_j=\frac{{{\displaystyle \sum }}_k{1}_{>RS{S}_{obs}\left(j\right)}\left(RS{S}_{exp}^k\left(j\right)\right)}{K}$ (Figure 1b) which is then multiplied by the number of variants J to account for multiple testing using the Bonferroni correction.

Given that J outlier tests are performed, we recommend to use a Bonferroni correction of the J P-values.

MR-PRESSO distortion test

The MR-PRESSO distortion test quantifies the distortion in the causal estimate due to significant horizontal pleiotropic outlier variants (Figure 1c). Distortion (D) is defined as the percentage of the causal estimate that is due to significant horizontal pleiotropic outlier variants. It is calculated as$D=100\times \frac{{\widehat{\beta }}_{causal,o}-{\widehat{\beta }}_{causal}}{\left|{\widehat{\beta }}_{causal}\right|}$, with ${\widehat{\beta }}_{causal,o}$the original causal effect estimated using all variants and $\widehat{\beta }$_causal the corrected causal estimate obtained after removing outliers identified by MR-PRESSO. Normalizing by the absolute value of the corrected causal estimate provides a direction for the magnitude of D. To test for statistical significance of D, we calculated an empirical P-value by generating a null distribution (the null hypothesis corresponds to the expected distortion due to a random set of variants). We defined $n_O$ as the number of variants detected as outliers by the MR-PRESSO outlier test and $n_E$ as the total number of variants robustly associated with the exposure. The null distribution is generated by substituting $n_O$ variants detected as outliers by the MR-PRESSO outlier test with $n_E-2n_O$ non-outliers, which are drawn with replacement from the entire set of non-outlier variants. This results in the total number of variants being fixed at $n_E-n_O$. We repeated this procedure K times to generate the null distribution. An empirical P-value is then calculated as the number of times that the observed distortion is greater than the expected distortion under the null hypothesis divided by K.

Simulation framework

We performed simulations to evaluate the statistical properties (false positive rate and power) to detect and correct for horizontal pleiotropy. We simulated the standard MR framework shown in Supplementary Figure 1b with an outcome as well as two exposures E₁ and E₂. A total of 50 variants was simulated per case. Horizontal pleiotropy was induced by a certain percentage of the 50 variants G_j having a significant effect on both E₁ (through ${\text{γ}}_{1,j}$) and E₂ (through ${\text{γ}}_{2,j}$). We varied the following parameters:

• the main causal effect (of exposure 1 on the outcome), β_causal> = 0 (no main causal effect) or β_causal = 0.1, 0.2, 0.5 whereas the causal effect of exposure 2 was always set to β_pleiotropic= 0.1;

• percentage of horizontal pleiotropy (0, 2, 4, 10, 50, 90);

• type of horizontal pleiotropy: positive (all ${\text{γ}}_{2,j}$ positive) or balanced horizontal pleiotropy (approximately half of the ${\text{γ}}_{2,j}$ positive and half negative);

• verification of the InSIDE²⁰ (Instrument Strength Independent of Direct Effect) assumption (Supplementary Note).

For each scenario, 10,000 simulations were performed.

Collection of genome-wide association (GWA) summary statistics

We retrieved publicly available genome-wide association (GWA) summary statistics data for 82 complex traits and diseases (Supplementary Note). We performed the following steps to ensure that all datasets were uniform and standardized. For each, we retrieved the appropriate variant annotation (build, rsid, chromosome, position, reference and alternate alleles) and summary statistics (effect size, standard errors, P-values and sample size of the study). All variant coordinates (chr, pos) were lifted over to hg19 using the UCSC Genome Browser LiftOver Tool. We imputed Z-scores of variants using ImpG³⁹ using 1000 Genomes Phase 3 European panel⁴⁰ (n = 503) as a reference panel. Effect sizes, standard errors and P-values were then calculated using the variance of the trait estimated from genotyped variants and allele frequencies calculated on the same subset of individuals from the 1000 Genomes reference panel. Sets of GWA-significant variants were manually retrieved from the corresponding GWA manuscripts. In total, we retrieved GWA summary statistics for 82 traits and diseases (Supplementary Table 14).

Detection and correction of horizontal pleiotropy using MR-PRESSO or covariate adjustment in MMR

We applied MR-PRESSO to all possible exposure-outcome pairs of 82 traits and diseases, and then compared the results of this test to those obtained from other MR methods. In total, we performed 4,250 MR tests. Only 53 distinct traits had a sufficient set of genome-wide significant variants that could be used as instrumental variables. This led to 53 × (82–1) = 4,293 possible exposure-outcome pairs. The remaining pairs were removed because of missing values in the summary data, which led to a total of 4,250 MR tests. We compared these results to other approaches including the Q (modified) test¹⁹ and Q’ (modified) test¹⁹ as well as MR-Egger regression^20,21. Next, we evaluated five strategies to correct for significant horizontal pleiotropy detected from our MR-PRESSO global test. The first approach included covariates in our MMR model, either one by one or all at the same time. We considered only covariates with a statistically significant causal effect (causal estimate of the IVW meta-analysis using a Bonferroni-corrected cut-off). Furthermore, to account for co-linearity, we also included only covariates with a correlation coefficient < 0.3. We note that not all pairs were eligible for MMR analysis due to either a lack of relevant covariates to adjust on in the one by one model or too many covariates to adjust on in the full model. The second approach corrected for horizontal pleiotropy by removing offending variants that are statistically significant outliers according to the MR-PRESSO outlier test. The MR-PRESSO global test was performed on the adjusted MR models to determine if there was any remaining horizontal pleiotropy. Finally, in a similar fashion, the Q (modified) outlier test and Q’ (modified) outlier test were used to correct for horizontal pleiotropy by removing significant outliers and the Q (modified) test and Q’ (modified) test were respectively applied to test for any remaining horizontal pleiotropy. 1,000,000 simulations to calculate the empirical P-values were performed for the MR-PRESSO global and outlier tests to obtain a precision of P = 10⁻⁶ which allows for a Bonferroni-corrected cut-off of P = 0.05/4,250 = 1.17×10^-5. 10,000 simulations were computed to calculate the empirical P-values for the MR-PRESSO distortion test.