Abstract
Population ecologists have traditionally focused on the patterns and causes of population variation in the temporal domain for which a substantial body of practical analytic techniques have been developed. More recently, numerous studies have documented how populations may fluctuate synchronously over large spatial areas; analyses of such spatially extended time-series have started to provide additional clues regarding the causes of these population fluctuations and explanations for their synchronous occurrence. Here, we report on the development of a phase-based method for identifying coupling between temporally coincident but spatially distributed cyclic time-series, which we apply to the numbers of muskrat and mink recorded at 81 locations across Canada. The analysis reveals remarkable parallel clines in the strength of coupling between proximate populations of both species—declining from west to east—together with a corresponding increase in observed synchrony between these populations the further east they are located.
Keywords: spatial time-series|population fluctuations|predator–prey interactions|external climatic factors
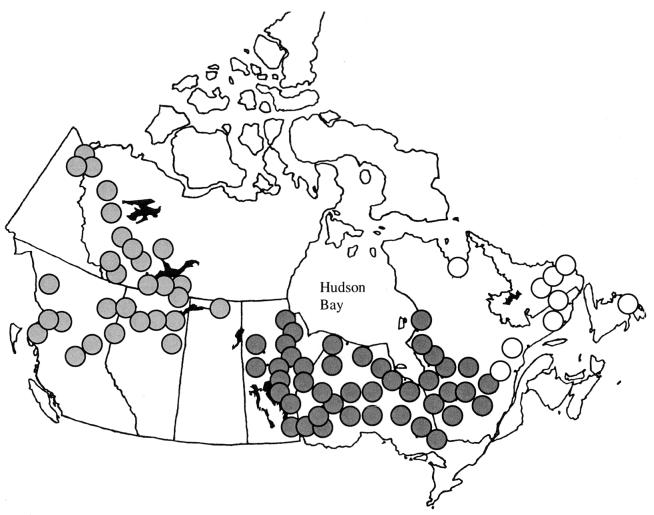
Large-scale synchrony in animal populations has become a key issue in ecology (1–6) and many cyclic populations have been shown to fluctuate more or less synchronously on the basis of cross-correlation analyses, bispectral analysis, and other methods (7–11). Documenting patterns in the spatiotemporal dynamics of populations is an essential prerequisite to developing an understanding of underlying processes (12). However, to achieve this understanding, mechanistically discriminating models need to be developed and fitted to these spatiotemporal data to assess which of the various processes contribute the most to the maintenance of large-scale synchrony (3, 13, 14). For instance, is synchrony primarily maintained at a uniformly high level because of some constant level of coupling between populations (by which we mean any process by which cycling populations are moved toward synchrony)? Or, are populations mostly uncoupled? Do they drift out of synchrony, but occasionally are brought back into high levels of synchrony by intermittent extremes in environmental conditions? A method for distinguishing between such processes would facilitate the identification of the ultimate underlying explanations for observed patterns in spatiotemporal population dynamics. By using fur-return records of mink (Mustela vison) and muskrat (Ondatra zibethicus) from the Hudson Bay Company collected at 81 stations across Canada from 1925 to 1949 (Fig. 1, refs. 15 and 16, and Fig. 4, which is published as supporting information on the PNAS web site, www.pnas.org.), we explore phase-coupling and synchrony in this predator–prey system.
Figure 1.
Map indicating the locations of the 81 trading stations. The western group (29 populations) is indicated in light gray, the central group (43 populations) in dark gray, and the eastern group (9 populations) in white. Western and central population cycles have an average period of 8–9 years, whereas populations in the east cycle with a shorter period, close to 4 years (15, 16).
One approach to the measurement of synchrony among cycling populations relies on the computation of correlations of the counts (or their logs). A problem with this method is that phase effects are confounded by the correlation structure of the amplitudes within the collection of time-series. If these amplitudes are fairly uniform or highly correlated, then phase correlation may be measurable by this method. Otherwise, the method breaks down, because phase synchrony is masked by amplitude variation. Another shortcoming of the method is that it fails to measure the dynamics of phase coupling.
To avoid the confounding effect of amplitudes, our approach is first to transform each time-series of counts into a time-series of phases. We ask whether phase increments at each station proceed independently of each other, or whether phase increments are coupled to phase increments in other populations of the same species. Evidence of spatial coupling is indicated if populations that are lagging behind the regional average show a tendency to catch up, or if those leading the regional average tend to be pulled back. Note that this coupling is not simply related to any interaction between the predator with prey. The frequency of coupling, which may occur annually or less frequently, then may be identified. The details of the analysis are reported in (17); hence, only a brief outline is presented here.
When a cyclic time-series, Xt (t = 1 … n), is plotted in a state-space defined by (log Xt, log Xt+1), it is represented by a series of orbits. The phase, φi,t(0 ≤ φi,t <1), of the population of each species at the ith station (i = 1 … s) at time t is measured as the proportion of the orbital circumference circumscribed by time t as measured relative to the position on the orbit of the last cyclic trough. We assume the discrete time-phase increment (in this case, assumed to occur annually) is described by a deterministic function denoted gi,t, with an identical and independently distributed noise term denoted by η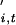 , thus we can write:
, thus we can write:
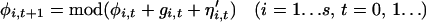 |
1 |
Let Δ(φi,t,x) denote the phase difference between φi,t and phase x (which will be positive if φi,t leads x and negative if φi,t lags x). We introduce a definition of central (or mean) phase, 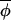 t, defined to be a solution of ∑
t, defined to be a solution of ∑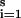 Δ(φi,t, φ̄t) = 0, over a collection of phases φi,t(i = 1, … , s, for each fixed t).
Δ(φi,t, φ̄t) = 0, over a collection of phases φi,t(i = 1, … , s, for each fixed t).
We can now introduce coupling between the s stations which we assume to be constant in strength at each of the discrete time-points (or in the intervals between time-points) and uniform among stations. This coupling may be expressed as a link between the overall mean phase across the s stations and the phase at each station and has the effect of drawing back populations that lead the overall average and pulling forward populations lagging behind the overall phase. Coupling between each population and the average of all populations can be shown to be equivalent to the more familiar form: (c/s) (∑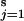 φj,t − φi,t) (e.g., ref. 5) suggestive of corrective flows of individuals from populations of higher density to those of lower density. With these assumptions, we can write the annual phase increment of each population as:
φj,t − φi,t) (e.g., ref. 5) suggestive of corrective flows of individuals from populations of higher density to those of lower density. With these assumptions, we can write the annual phase increment of each population as:
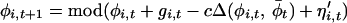 |
2 |
 |
The coupling parameter c is 0 in the absence of any coupling, whereas 0 < c ≤ 1 indicates coupling of phases. If coupling is of constant and uniform strength, then a recursive equation for the time-evolution of Δ(φi,t,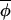 t) may be written as:
t) may be written as:
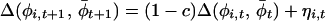 |
3 |
where ηi,t now represents a noise term related to the original noise term in the annual phase increment. When c = 0, Eq. 3 expresses that the change in Δ(φi,t,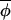 t) from t to t+1 is random. When c > 0, phases leading the average phase tend to be drawn back toward this average, and phases lagging behind tend to be pulled forward toward the average. Eq. 3 defines a vector-valued variant of a first-order autoregressive process, and estimators applicable to standard first-order autoregressive processes may be used to estimate (1−c) and the variance of the noise term, σ
t) from t to t+1 is random. When c > 0, phases leading the average phase tend to be drawn back toward this average, and phases lagging behind tend to be pulled forward toward the average. Eq. 3 defines a vector-valued variant of a first-order autoregressive process, and estimators applicable to standard first-order autoregressive processes may be used to estimate (1−c) and the variance of the noise term, σ , from the regression of Δ(φi,t+1,
, from the regression of Δ(φi,t+1,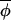 t+1) on Δ(φi,t,
t+1) on Δ(φi,t,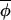 t).
t).
Because values of Δ(φi,t,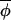 t) are centered, the expression
t) are centered, the expression
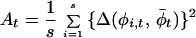 |
4 |
is a variance measure of phase asynchrony over the set of s stations at each time t. If populations are fully phase-randomized, then their distribution over the unit phase would be uniform with variance 1/12. The extent to which the quantity 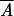 , the average of At over the time-series, is less than 1/12 is, thus, a measure of overall asynchrony in the phase data.
, the average of At over the time-series, is less than 1/12 is, thus, a measure of overall asynchrony in the phase data.
We observe coupling from Eq. 3 and measure synchrony by Eq. 4. If At is small, there are three possible explanatory hypotheses, identifiable in terms of the autoregressive process, that, either alone or in some combination, could contribute to phase synchronization:
Hypothesis 1. Synchrony may be maintained by invariant coupling of phases, in which case |Δ(φi,t+1,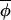 t+1)| generally would be less than |Δ(φi,t,
t+1)| generally would be less than |Δ(φi,t,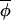 t)|, and regressing Δ(φi,t+1,
t)|, and regressing Δ(φi,t+1,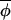 t+1) on Δ(φi,t,
t+1) on Δ(φi,t,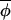 t) would result in a slope less than 1, with residuals distributed symmetrically around this best-fitting-line (Fig. 2A).
t) would result in a slope less than 1, with residuals distributed symmetrically around this best-fitting-line (Fig. 2A).
Figure 2.
Schematic illustration of two different ways in which phase synchrony might be maintained. (A) A continuous series of phase corrections such that |Δ(φi,t+1,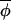 t+1)|<|Δ(φi,t,
t+1)|<|Δ(φi,t,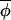 t)|, and points lie symmetrically around a line of slope less than 1. (B) The majority of phase increments proceed independently of the overall average phase, giving rise to points that fall around a line of slope 1, but a few outliers arise from infrequent occasions on which|Δ(φi,t+1,
t)|, and points lie symmetrically around a line of slope less than 1. (B) The majority of phase increments proceed independently of the overall average phase, giving rise to points that fall around a line of slope 1, but a few outliers arise from infrequent occasions on which|Δ(φi,t+1,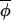 t+1)|≪|Δ(φi,t,
t+1)|≪|Δ(φi,t,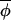 t)|, which result in the best fitting regression line having a slope of less than one. However, on eliminating points associated with large standardized residuals from the regression analysis, a slope of ≈1 would be recovered. A third possibility (not shown) is that the regression indicates no evidence of coupling at all, and the observed synchrony between phases must have arisen from synchronizing events that occurred before the interval over which data were collected. (C) The regression of Δ(φi,t+1,
t)|, which result in the best fitting regression line having a slope of less than one. However, on eliminating points associated with large standardized residuals from the regression analysis, a slope of ≈1 would be recovered. A third possibility (not shown) is that the regression indicates no evidence of coupling at all, and the observed synchrony between phases must have arisen from synchronizing events that occurred before the interval over which data were collected. (C) The regression of Δ(φi,t+1,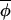 t+1) on Δ(φi,t,
t+1) on Δ(φi,t,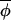 t) for muskrat in the eastern region. The slope of the best-fitting-line is 0.906, which is significantly less than 1 (see Table 1), indicating a coupling strength of 0.094. The dotted line indicates the line of slope 1. (D) The change in asynchrony, At, with time for mink (dotted line) and muskrat (solid line) in the three regions studied. Because phase can be estimated only from completed cycles, At cannot be calculated for the entire duration of the time-series data. A plot of the empirical function At reveals a significant upward trend (using the Newey-West test for the trends; ref. 25) in the west (but not in central and eastern regions) for both mink (slope = 0.0024, F1, 15 = 40.5, P < 0.0001) and muskrat (slope = 0.0015, F1, 14 = 37.2, P < 0.0001).
t) for muskrat in the eastern region. The slope of the best-fitting-line is 0.906, which is significantly less than 1 (see Table 1), indicating a coupling strength of 0.094. The dotted line indicates the line of slope 1. (D) The change in asynchrony, At, with time for mink (dotted line) and muskrat (solid line) in the three regions studied. Because phase can be estimated only from completed cycles, At cannot be calculated for the entire duration of the time-series data. A plot of the empirical function At reveals a significant upward trend (using the Newey-West test for the trends; ref. 25) in the west (but not in central and eastern regions) for both mink (slope = 0.0024, F1, 15 = 40.5, P < 0.0001) and muskrat (slope = 0.0015, F1, 14 = 37.2, P < 0.0001).
Hypothesis 2. Individual populations' dynamics may proceed independently of each other most of the time (in which case |Δ(φi,t+1,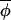 t+1)|≈|Δ(φi,t,
t+1)|≈|Δ(φi,t,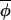 t) )| and most points on the regression fall around a line of slope 1, but populations may be brought back into synchrony by intermittent but more substantial phase-coupling events resulting in some outliers on the regression plot that would act to reduce the slope of the best-fitting-line (Fig. 2B). Elimination of these outlying points would result in recovery of a slope closer to 1.
t) )| and most points on the regression fall around a line of slope 1, but populations may be brought back into synchrony by intermittent but more substantial phase-coupling events resulting in some outliers on the regression plot that would act to reduce the slope of the best-fitting-line (Fig. 2B). Elimination of these outlying points would result in recovery of a slope closer to 1.
Hypothesis 3. The phases of the populations are observed to be synchronized, but the autoregressive process (Eq. 3) has a slope of 1 and no outliers, reflecting no coupling of any sort. In this case, a coupling agent may have acted before the period over which data are available. The population phases then would show decreasing synchrony over time, i.e., At would increase.
The 81 stations were divided into three groups (western, central, and eastern) according to their similarity in dynamic structure, which also corresponds to distinct geographic locations (ref. 18; unfortunately, the variation in the number of populations assigned to each group results in uneven statistical power available for estimating coupling across the continent). Cyclic minima for each station were identified from temporally smoothed data for each station. For some cycles, multiple potential “trough years” were identified. One candidate point would be selected randomly for each cycle for each station, and phases, phase deviations, coupling, and synchrony would be estimated; the process was repeated with a new sample of potential candidate minima 2,000 times.
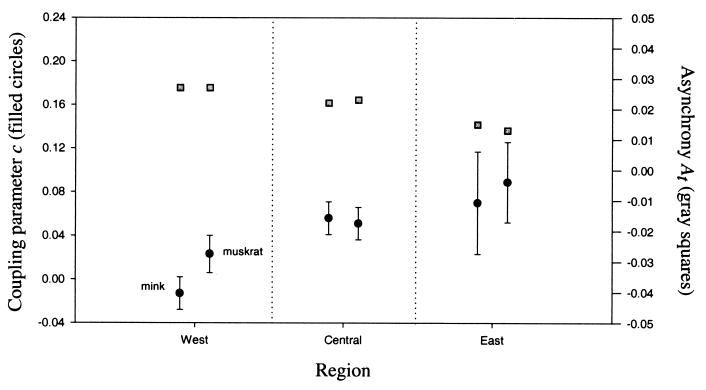
Our analysis reveals that muskrat and mink populations exhibit strikingly similar geographical patterns in their dynamics. For both muskrat and mink populations, the dynamics (within each species) seem to be essentially spatially uncoupled in the west, but become increasingly coupled along a gradient running west to east (Table 1, Fig. 3). Elimination of significant outliers does not alter the estimated coupling strengths (Table 1); thus, where coupling is detectable, it seems to be constant, which is consistent with Hypothesis 1. The regression analyses (see Fig. 2C for an example) reveal no patterns consistent with Hypothesis 2 in which synchrony might be maintained by intermittent but more substantial coupling (Table 1).
Table 1.
Estimated parameters of the phase model
| Species | Region | (1 − c)* | Sig.† | (1 − c)‡ | (1 − c)§ | Sig.,¶ % | σ ‖ ‖
|
Ā** |
|---|---|---|---|---|---|---|---|---|
| Mink | ||||||||
| West | 1.026 (0.0145) | NS | 1.028 | 1.013 (0.015) | NS (0) | 0.0025 | 0.027 (0.017–0.047) | |
| Central | 0.969 (0.0134) | P < 0.05 | 0.971 | 0.944 (0.015) | P < 0.05 (100) | 0.0031 | 0.022 (0.015–0.035) | |
| East | 0.945 (0.0397) | NS | 0.983 | 0.930 (0.047) | NS (0) | 0.0032 | 0.015 (0.007–0.047) | |
| Muskrat | ||||||||
| West | 0.992 (0.0163) | NS | 1.000 | 0.977 (0.0171) | NS (0) | 0.0027 | 0.027 (0.017–0.047) | |
| Central | 0.957 (0.0145) | P < 0.05 | 0.960 | 0.949 (0.0149) | P < 0.05 (100) | 0.0027 | 0.023 (0.015–0.037) | |
| East | 0.906 (0.0385) | P < 0.05 | 0.915 | 0.911 (0.0369) | P < 0.05 (100) | 0.0020 | 0.013 (0.006–0.039) |
The coupling parameter estimated using a choice of cycle troughs that minimizes the error-mean-square of the regression model (with standard error of slope estimated from regression in the usual way) based on a search of 2,000 resamples of cycle minima.
Significance of the coupling parameter reported in previous column (based on a t test of (c/SE(c)).
The slope of the same regression analysis with points associated with standardized residuals greater than |1.96| eliminated from the analysis (significance levels are unchanged).
The average coupling parameter from 2,000 resamples of cycle minima (in parentheses, standard error, computed as square-rooted averaged squared standard error of parameter estimates from each choice).
Significance of the coupling parameter reported in previous column (based on a t test of (c/SE(c)). The figure in parentheses is the % of trough resamples yielding slopes significantly less than 1.
The variance of the residuals (σ ) associated with the best fitting regression model (almost identical to the average variance of residuals).
) associated with the best fitting regression model (almost identical to the average variance of residuals).
The averaged measure of asynchrony along the time-series evaluated using the 2,000 resamples. The upper 95% confidence intervals of these variances (in parentheses) are all less than 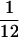 .
.
Figure 3.
Estimates of the coupling parameters c, and  for mink (left-most points) and muskrat (right-most points) populations in the three geographic regions. The error bars shown are one square-rooted average of the squared standard-error terms for parameters estimated from 2,000 resamples of candidate cyclic minima.
for mink (left-most points) and muskrat (right-most points) populations in the three geographic regions. The error bars shown are one square-rooted average of the squared standard-error terms for parameters estimated from 2,000 resamples of candidate cyclic minima.
Consistent with these results is a pattern of increasing spatial synchrony between populations from west to east for both muskrat and mink (Table 1). Among western populations of mink and muskrat, At is 1/3 of its maximum value expected under the hypothesis of fully phase-randomized populations, and among eastern populations, At is almost 1/6 of this maximum value (Fig. 3).
In the absence of phase coupling, we would predict that synchrony levels would decrease along the time-series in the west, but not in the central and eastern regions. Analysis reveals that spatial synchrony does, indeed, decrease linearly over time in the west for both mink and muskrat, but no such trends are exhibited by either species in central and eastern regions (Fig. 2D), which is exactly the pattern anticipated if coupling was, indeed, weakest in western populations and strongest in central and eastern populations.
Our analysis reveals remarkable parallels in the spatial dynamics of muskrat and mink populations. First, there is a cline in the phase coupling between sets of populations in the three identified geographic regions of Canada that increases from west to east. Second, consistent with this observation, populations of both species are less synchronous in the west than they are in central and eastern regions. Third, as expected in the absence of coupling, synchrony seems to decline significantly in the west over time in both species, whereas in central and eastern regions, where coupling is identified, synchrony levels are stable over time.
As is the case for the other regions, western populations exhibit significantly less asynchrony than expected under the hypothesis of random phase alignment (Table 1), yet our analysis reveals no significant evidence of coupling having occurred over a 25-year period in the western region. Hence, coupling in the west seems to be infrequent but might be substantial when it occurs. In the absence of coupling, asynchrony starts to accumulate in an initially synchronous population at the rate of approximately σ per year, suggesting that the last synchronization event in the west may have been up to 5 years before the start of data collection, or sometime between 1920 and 1925 (data from British Columbia indicate that the 2nd largest increase in mink returns last century occurred over the years 1920 and 1921, which is suggestive of some real phenomenon).
per year, suggesting that the last synchronization event in the west may have been up to 5 years before the start of data collection, or sometime between 1920 and 1925 (data from British Columbia indicate that the 2nd largest increase in mink returns last century occurred over the years 1920 and 1921, which is suggestive of some real phenomenon).
Observed values of σ suggest that fully synchronized populations will become randomly phase-aligned within about 3 decades in the absence of any coupling. In the central region, spatial coupling seems to be more continuous in nature, becoming stronger still in eastern regions. Observed levels of coupling here result in the elimination of about 15% of phase asynchrony per year (in the absence of phase noise, residual phase asynchrony would have a half-life of about 5 years).
suggest that fully synchronized populations will become randomly phase-aligned within about 3 decades in the absence of any coupling. In the central region, spatial coupling seems to be more continuous in nature, becoming stronger still in eastern regions. Observed levels of coupling here result in the elimination of about 15% of phase asynchrony per year (in the absence of phase noise, residual phase asynchrony would have a half-life of about 5 years).
Our analysis addresses, of course, only the proximal causes of these differences in regional phase dynamics—the ultimate explanations require further study. Significantly higher cross-correlation coefficients between the time-series of these fur returns from stations less than 450 km from each other have been identified (19), implying some localized basis for coupling. Whereas there are no latitudinal trends evident in the data, there are longitudinal differences in the length of time that mink dynamics lag behind those of muskrat: in the east, the two species cycle in phase, whereas in central and western regions, mink lag 1–2 years behind muskrat in their 8–10 year periodic density cycles (19, 20). This fact is indicative of differences in the predator–prey relationship between the two species. However, the very similar patterns of coupling identified in populations of these two species is highly suggestive of some common synchronizing agent.
The North Atlantic Oscillation (NAO) is known to affect climate and related ecological processes differently in the three regions (21). Mechanistically, the effect of the NAO may work through its determination of spring conditions. During years of this analysis, Charles Elton coordinated the mailing of questionnaires to each Hudson's Bay fur post regarding causes for changes in the abundance of furbearers (see ref. 7). The most common comment recorded among eastern posts was the occurrence of declines in muskrat numbers during spring floods in years of heavy ice. The timing of thawing and flooding will influence the duration of the available breeding season, which will bear directly on the breeding success of muskrat (whereas mink have only one litter per year, muskrat may have as many as five; ref. 22). Covariation between the NAO and winter temperature is negative in eastern Canada, positive in central Canada, but not significant in western Canada, which would be influenced by the Pacific climate system. Interestingly, a regime shift (relating to precipitation of run-off from rivers along the Pacific coast) occurred during the period 1920–25 (23, 24)—the period during which we have hypothesized that some synchronizing agent may have acted on western populations (a similar shift occurred toward the end of the period for which we have data but which, presumably for this reason, is not reflected in our data). These observations are, however, only an indication of the possible role of climate in the determination of synchronization, which should be explored further with additional data and analyses. There is no doubt that the three regions are quite distinct topographically as well as climatically; perhaps the more mountainous terrain of western Canada disrupts coupling between populations that serves to maintain synchrony in the more permeable landscapes further east.
It remains possible that if climatic conditions across sites are more highly correlated in the east than in the west—perhaps caused by the presence of large-scale climatic variations such as the NAO—trapping conditions also might be correlated similarly, thereby influencing the ease with which both muskrat and mink are captured across neighboring sites. Unfortunately, such a mechanism is not easily distinguished from one in which the NAO affects mink and muskrat numbers directly, so this hypothesis remains only speculation.
In conclusion, we have demonstrated a clear geographic structure in the coupling and resulting synchrony of both muskrat and mink populations across Canada. We consider it likely that climate, demonstrated to have been influential over the dynamics of other populations in these ecosystems (21), is the most likely determinant of these patterns, but that topography may also play an important role. The insight provided by this study will be of value when developing mechanistically based models for explaining geographic patterns in the synchrony and coupling of these populations.
Supplementary Material
Acknowledgments
We acknowledge the stimulating influence of Prof. Howell Tong who provided the impetus for discussions between N.C.S. and P.E.G. on synchrony of animal populations. We thank Alun Lloyd, Ben Bolker, Hildegunn Viljugrein, and Tero Klemola for commenting on an earlier version of the paper, Darren Shaw for preparing the supplementary information, and Jim Hurrell, Dan Cayan, and Larry Riddle for useful discussions regarding climate history. D.T.H. was supported by the Wellcome Trust (U.K.). N.C.S. thanks the Norwegian Science Council, the University of Oslo, and the Biotechnology and Biological Sciences Research Council/Engineering and Physical Sciences Research Council (U.K.); M.S.B. and P.E.G. thank the Natural Sciences and Engineering Research Council (Canada); P.E.G. acknowledges also the Peter Wall Institute for Advanced Studies at the University of British Columbia.
Abbreviation
- NAO
North Atlantic Oscillation
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Grenfell B T, Wilson K, Finkenstadt B F, Coulson T N, Murray S, Albon S D, Pemberton J M, Clutton-Brock T H, Crawley M J. Nature (London) 1998;394:674–677. [Google Scholar]
- 2.Lambin X, Elston D A, Petty S J, MacKinnon J L. Proc R Soc London Ser B. 1998;265:1491–1496. doi: 10.1098/rspb.1998.0462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bjørnstad O N, Stenseth N C, Saitoh T. Ecology. 1999;80:622–637. [Google Scholar]
- 4.Bjørnstad O N, Ims R A, Lambin X. Tree. 1999;14:427–432. doi: 10.1016/s0169-5347(99)01677-8. [DOI] [PubMed] [Google Scholar]
- 5.Blasius B, Huppert A, Stone L. Nature (London) 1999;399:354–359. doi: 10.1038/20676. [DOI] [PubMed] [Google Scholar]
- 6.Lundberg P, Ranta E, Ripa J, Kaitala V. Tree. 2000;15:460–464. doi: 10.1016/s0169-5347(00)01981-9. [DOI] [PubMed] [Google Scholar]
- 7.Elton C, Nicholson M. J Anim Ecol. 1942;11:215–244. [Google Scholar]
- 8.Smith C H, Davies J M. J Biog. 1981;8:27–35. [Google Scholar]
- 9.Smith C H. Can Field Nat. 1983;97:151–160. [Google Scholar]
- 10.Ranta E, Kataila V, Lindstrom J, Linden H. Proc R Soc London Ser B. 1995;262:113–118. [Google Scholar]
- 11.Ranta E, Kaitala V, Lindstrom J. Ecography. 1997;20:454–460. [Google Scholar]
- 12.MacArthur R H. Geographic Ecology. Patterns in the Distribution of Species. Princeton: Princeton Univ. Press; 1972. [Google Scholar]
- 13.Bjørnstad O N, Bolker B. Proc R Soc London Ser B. 2000;267:1787–1794. [Google Scholar]
- 14.Bjørnstad O N, Falck W. Environ Ecol Stat. 2001;8:53–70. [Google Scholar]
- 15.Erb J, Stenseth N C, Boyce M S. Can J Zool. 2000;78:1009–1016. [Google Scholar]
- 16.Erb J, Boyce M S, Stenseth N C. Oikos. 2001;93:365–375. [Google Scholar]
- 17.Haydon D T, Greenwood P E. Theor Popul Biol. 2000;58:239–254. doi: 10.1006/tpbi.2000.1489. [DOI] [PubMed] [Google Scholar]
- 18.Yao Q, Tong H, Finkenstadt B, Stenseth N C. Proc R Soc London Ser B. 2000;267:2459–2467. doi: 10.1098/rspb.2000.1306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Viljugrein H, Lingjaerde O C, Stenseth N C, Boyce M S. J Anim Ecol. 2001;70:671–682. [Google Scholar]
- 20.Bulmer M G. J Anim Ecol. 1974;43:701–718. [Google Scholar]
- 21.Stenseth N C, Chan K S, Tong H, Boonstra R, Boutin S, Krebs C J, Post E, O'Donoghue M, Yoccoz N G, Forchhammer M C. Science. 1999;285:1071–1073. doi: 10.1126/science.285.5430.1071. [DOI] [PubMed] [Google Scholar]
- 22.Errington P L. Muskrat Populations. Ames: Iowa State Univ. Press; 1963. [Google Scholar]
- 23.Mantua N J, Hare S R, Zhang Y, Wallace J M, Francis R C. Bull Amer Meterol Soc. 1997;78:1069–1079. [Google Scholar]
- 24.Minobe S. Geophys Res Lett. 1997;24:683–686. [Google Scholar]
- 25.Newey W, West K. Econometrica. 1987;55:703–708. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.