Cooperative Contraction Behaviors of a One-Dimensional Cell Chain

Abstract

Collective behaviors of multiple cells play important roles in various physiological and pathological processes, but the mechanisms of coordination among cells are highly unknown. Here, we build a one-dimensional cell-chain model to quantitatively study cell cooperativity. Combining experimental and theoretical approaches, we showed that the matrix stiffness, intercellular adhesion strength, and cell-chain length have a significant effect on the cooperative contraction of the cell chains. Cells have strong cooperativity, i.e., exhibiting a united contraction mode, in shorter cell chains or on softer matrix or with higher intercellular adhesion strength. In contrast, cells would exhibit a divided contraction when the cell chain was long or on stiffer matrix or with weaker adhesion strength. In addition, our quantitative results indicated that the cooperativity of cells is regulated by the coupling between matrix stiffness and intercellular adhesion, which can be quantified by an explicit parameter group. These results may provide guidelines for regulating the cooperativity of cells in their collective behaviors in tissue morphogenesis and tissue engineering in biomedical applications.

Introduction

Collectivity is a main feature of multiple cell behaviors that is crucial in physiological and pathological processes, such as tissue morphogenesis, wound healing, and cancer invasion (1, 2, 3). Compared with the behavior of single cell, collective cell behavior is a complex multibody phenomenon in which the cooperation and orchestration among cells take crucial roles. For example, due to the cell cooperation through cell-cell contact, there is vortex formation in the cell sheet during collective cell migration (4). In the wound-healing process, there is rosette-like pattern formation at the wound edge through coordinated migration of epithelial cells (5). The coordination among cells is also observed in the collective migration of neural crest cells at the neural plate border during neurulation (6). Recently, it is reported that collective invasion represents a predominant invasion mode in breast cancer that associates with distant metastasis, suggesting a critical role in systemic dissemination (7). Although the coordination in collective cell behaviors has been extensively observed, it still remains unclear how cells communicate with each other and coordinately function during the processes.

The cell-cell interaction is the key to the collective cell behaviors. Based on this interaction, the tension, represented by the in-plane stresses, would be developed in the cell layer due to the contractility of cytoskeleton (8, 9). It has been shown that the in-plane stresses play significant roles in the collective behaviors. For instance, cells would align and polarize along the maximal principal stress, driven by the in-plane maximal shear stress (9). For cells migrating on a strip-like substrate, the vortex-like pattern in a wide strip changed to a contraction-elongation type in a narrow strip due to the reduction of the width of the cell sheet, which changed the cell-cell interaction (4). Human keratinocytes formed suspended multicellular bridges over nonadherent areas through cell-cell interaction when these cells migrated along functionalized micropatterned surfaces comprising alternating strips of extracellular matrix (ECM) and nonadherent polymer (10). But such behaviors would disappear when the cell-cell interaction was inhibited or weakened. For example, when the cell-cell interaction was disrupted, the epithelial-bridge formation was inhibited when cells were cultured and migrated in a low-Ca²⁺ medium (10), and the cells would migrate in a highly uncoordinated and random fashion (4). But how the cell-cell interaction influences the cell coordination has remained unknown.

Cell-matrix interaction is the other key factor that influences the collective cell behaviors, and it is coupled with cell-cell interaction. For example, the development and distribution of traction force at the cell-matrix interface is mediated by cell-cell interaction (11), and it was shown that when the intercellular interaction was strong, the traction force scaled with the size of cell colony (12, 13), but if the interaction was weak, then this correlation would disappear. There are several factors that can affect cell-matrix interaction. Besides the geometric properties, the stiffness of the substrate takes a crucial role in regulating cell behaviors. For instance, cells adhere (14, 15, 16, 17, 18, 19, 20) and spread (14, 16, 21, 22) better on stiff substrates than on soft ones. Cell proliferation rate is positively correlated with substrate stiffness (16, 23). Moreover, cells preferentially polarize and migrate toward the stiffer substrates (14, 24, 25). In particular, cell migration speed depends on substrate stiffness in a biphasic manner (26, 27, 28, 29, 30, 31). Recent studies have demonstrated that increasing substrate stiffness enhances the persistence and directionality of the collective cell migration (32). And we have recently shown that the substrate stiffness can biphasically influence the collective polarization and alignment of cells on patterned substrate. For example, there is an optimal stiffness for maximal polarization and optimal alignment (33). However, how the matrix stiffness quantitatively regulates the cooperativity among cells by mediating force transmission and distribution among cells is still unclear.

To quantitatively study the influences of substrate stiffness and intercellular adhesion strength on the coordination/cooperativity among cells, we tested the contraction mode, traction force distribution, and in-plane tension distribution of the cell chain on a one-dimensional (1D) adhesive pattern. The advantage of using the 1D cell-chain model is that it simplifies the mathematic modeling of cell-cell and cell-matrix interaction in such a simple configuration of multiple cells (34). In fact, the ECM environments in vivo are often composed of single ECM fibers or bundles of aligned fibers (35), which is well worth studying. For example, aligned ECM fibers are key factors to regulate cell behaviors and function during embryonic development (36) and myocardial tissue development and reconstruction process (37), as well as tumor progression and metastasis (38, 39, 40). We found that cells exhibited united contraction mode when they had high intercellular adhesion strength or adhered on soft substrate. Increasing the cell-chain length caused a decrease of cell cooperativity and the proportion of united contraction mode. This study provided a deeper understanding of collective cell behaviors.

Materials and Methods

Micropatterning and cell seeding

The micropatterned substrate was prepared using soft lithography techniques, followed by a microcontact printing. Briefly, the pattern with the designed geometric features was first fabricated on a mask, which was then replicated on a master with an AR-P3210 photoresist layer (ALLRESIST GmbH, Strausberg, Germany) of 5 μm in thickness on a silicon wafer exposed to ultraviolet (UV) radiation. The master was placed in a vacuum drying oven (Beijing Zhongke Huanshi Apparatus Co. Ltd., Beijing, China) and fluorosilanized with fluoroalkyl silane (chemical abstracts service: 78560-44-8) to facilitate casting (41). The mixture of Dow Corning 184 gel (Dow Corning Corporation, Midland, MI) and curing agent (10:1) were poured onto the master in a petri dish, which was further vacuumized for 1 hr and permitted to cure at 80°C for 2 hr. After being peeled off from the master, the cured polydimethylsiloxane was cut into square stamps. The 1D adhesive zones on stamps had a width of 25 μm and lengths of 100, 200, 300, and 400 μm. The stamp was washed with 75% alcohol in a bath sonicator (Kunshan Ultrasonic Instruments Co. Ltd., Kunshan, China), dried with nitrogen gas, and treated with oxygen ion sputtering to make it hydrophilic. A droplet of comb polymer, nonadhesive to cells (42), was placed on the stamp surface and uniformed by centrifugation at 1500 rotations per minute. The stamp with the comb polymer was immediately pressed onto polyacrylamide gel with precoated collagen. The micropatterned gel was sterilized by UV for 15 min before seeding cells. Fig. 1 shows the process of fabricating 1D adhesive patterns and seeding cells on them.

Figure 1.

Fabrication of the 1D strip-like pattern. (A) A schematic drawing of the processes of fabricating the 1D polydimethylsiloxane stamp is shown. (B) A schematic drawing of patterning antiadhesive molecular (comb polymer) on PAA gel surface and seeding cells on it is shown. To see this figure in color, go online.

Osteoblast-like MC3T3-E1 cells (ATCC, Manassas, VA) were cultured with α-MEM medium (Hyclone, Logan, UT) containing 10% fetal bovine serum (Gibco, Carlsbad, CA) and 1% penicillin/streptomycin (Invitrogen, Carlsbad, CA) at 5% CO₂, 37°C. MDCK (NBL-2) cells were cultured with Dulbecco’s modified eagle medium-high glucose (Hyclone) containing 10% fetal bovine serum (Gibco) and 1% penicillin/streptomycin (Invitrogen) at 5% CO₂, 37°C. After reaching 70% confluence, these cells were trypsin treated and seeded onto the 1D micropatterned surfaces. The cells were then cultured at 37°C and 5% CO₂ for 12–16 hr.

Preparation of polyacrylamide gel substrates

The 10 and 30 kPa polyacrylamide substrates were prepared according to protocols in the literature (33, 43). In brief, a slide was pretreated with a drop of 0.1 mol/L NaOH and allowed to dry in air, and then a drop of three-aminopropyltrimethoxysilane was smeared evenly on the surface. After 4–5 min, the slide was washed extensively with distilled water and then incubated with 0.5% glutaraldehyde in phosphate-buffered saline for 30 min. Then the slide was washed extensively with distilled water and dried in air. Acrylamide and N,N-methylene-bis-acrylamide were mixed with fluorescent beads and curing agent. The mixture of 50 μL was sandwiched between the activated slide and a blank coverslip, allowing the formation of a flat gel layer of ∼100 μm in thickness. The resulting sandwich assembly was turned upside down. After polymerization, the surface of gel substrate was washed with HEPES and applied with sulfosuccinimidyl 6-(4'-azido-2'-nitrophenylamino)hexanoate under UV irradiation for 30 min. After being washed with HEPES, 200 μL of 0.2 mg/mL type-I collagen solution was coated on the substrate and stayed at 4°C overnight. Then the gel substrate was washed extensively with phosphate-buffered saline, drained off, and dried at 37°C for 15 min before micropatterning.

Cell staining and imaging

Nuclei of living cells were stained by a Hoechst 33342 solution of concentration 0.166 μg/mL and incubated for 1 hr. After that, images were taken by using a Leica DMI6000B (Leica, Wetzlar, Germany) microscope that was equipped with a Leica live-cell station. We used a Leica 20 ×/0.40 HC PL FLUOTAR L objective (Leica) to take phase contrast and fluorescent images.

Measurement of traction force

Firstly, to measure the traction force at various cell-cell interaction strengths, the surface deformation of the substrate should be measured. Briefly, a fluorescent image of the patterned substrate with fluorescence beads embedded was recorded. Then, ethylene glycol-bis(β-aminoethyl ether)-N,N,N',N'-tetraacetic acid (EGTA) solution for chelating calcium and weakening cell-cell junction was added into the petri dish with a final concentration of 4 mM (9). The second and third fluorescence images, respectively, were recorded after EGTA treatment for 20 min and removing cells with trypsin. Based on these three fluorescent images, the displacement field of the surface of the pattern before and after EGTA treatment was calculated using the digital image correlation method (33, 44).

Secondly, constrained Fourier transform traction microscopy (FTTC) (45) was used to calculate the traction force, which consists of the following procedures. 1) Calculate the traction field using unconstrained FTTC. Briefly, the displacement field in Fourier space was first calculated using the fast Fourier transform; then, multiplying the transformed displacements by the inverse of the Fourier transform of the Green function, i.e., the Boussinesq solution, to get the transformed traction; and then, taking the inverse Fourier transform of the result to obtain the traction. 2) Define a new traction field by setting the traction outside the boundary of the cell chain to zero. Calculate the displacement field by this new traction field. 3) Define a new displacement field by replacing the calculated displacement field within the cell-chain boundary by the experimentally measured displacements. 4) Repeat steps 1–3 until convergence is reached at a given level of tolerance. We chose to terminate the iteration when the relative variation in maximal magnitude of the tractions was less than 0.001 on succeeding steps. A flow chart of calculation of the traction force with FTTC was provided in Fig. S1.

Analysis of cell traction mode

The contour of cell chain in phase contrast image was manually picked by using the spline function in MATLAB software (The MathWorks, Natick, MA) for traction-force calculation using constrained FTTC. The X component of traction force (along the cell chain) was adopted in a traction-force curve for judging the contraction mode of the cell chain. In the plot, the positive traction force stands for cells contracting toward the right, whereas the negative one stands for cells contracting toward the left. A united contraction mode was defined when the traction force on both sides of cells chain was significantly larger than that in the interior region and the traction force curve only has one intersection point with the x axis. Otherwise, the cell chain was thought of as a divided contraction. Considering the system error of measurement in experiments, we considered it as a united contraction mode if there were more than 1 intersection point in the interior region, but the magnitude of error is limited in a fairly small range. For a specific condition, more than 10 replicas of the test were performed. A united contraction mode for specific cell number and substrate stiffness was defined when the ratio of united contraction mode was larger than 50%.

The 1D cell chain model

Fig. 2 A shows a model of a 1D cell chain on the substrate. Cells are connected to each other via cadherin molecules, where the stiffness of the molecules is defined as k_c, and cells adhere to substrate via integrin molecules with an effective stiffness k_s (considering the stiffness of both adhesive molecules and the substrate). In this study, we model the cell chain as a 1D continuum rod (Fig. 2 B), and its constitutive equation is given by

$$\mathit{\sigma }=E_c\left(\mathit{\epsilon }+{\epsilon }_0\right)\text{,}$$ (1)

where σ and ε are stress and strain in cell chain, respectively; E_c is Young’s modulus of cell chain; and ε₀ represents prestrain generated by myosin contraction. For the 1D cell chain, its equilibrium equation is

$$l_p^2\frac{d^2{u}_n}{d{x}^2}-u_n=0.$$ (2)

Normalizing Eq. 2 gives

$$\frac{d^2{\overline{u}}_n}{d{\overline{x}}^2}-{\overline{u}}_n=0\text{,}$$ (3)

where u_n represents the displacement of the nth cell (2 ≤ n ≤ N − 1), as shown in Fig. 2, and ${\overline{u}}_n=u_n/l_p$, $\overline{x}=x/l_p$, and $l_p^2=E_{c}h/k_s$. The boundary conditions of Eq. 3 are written as

$$\{\begin{array}{c}{\overline{\sigma }}_1\left(0\right)=0\\ {\overline{\mathit{\sigma }}}_n\left(n\overline{L}\right)={\overline{\sigma }}_{n+1}\left(n\overline{L}\right)=\lambda \left({\overline{u}}_{n+1}-{\overline{u}}_n\right)\\ {\overline{\sigma }}_N\left(N\overline{L}\right)=0\end{array}\text{,}$$ (4)

in which $\overline{L}=L/l_p$, $\overline{\sigma }=\sigma /E_c$, and $\lambda =k_c\sqrt{h/E_c{k}_s}$.

Figure 2.

1D cell chain. (A) Cells (in green) were connected to each other via cadherin molecules with stiffness k_c. Cells adhere to substrate via integrin molecules with an effective stiffness of k_s. (B) A theoretical model of the 1D cell chain is shown. To see this figure in color, go online.

Solving Eq. 3, we obtained the solution as

$${\overline{u}}_n=C_{1n}{e}^{\overline{x}}+C_{2n}{e}^{-\overline{x}}\text{.}$$ (5)

According to the boundary condition (4), we calculated the coefficients in Eq. 5. Thus, we obtained the intracellular stress as

$${\overline{\sigma }}_n=\frac{\partial {\overline{u}}_n}{\partial \overline{x}}+{\epsilon }_0\text{,}$$ (6)

intercellular tensile stress was

$${\overline{\sigma }}_{cn}=\lambda \left({\overline{u}}_n-{\overline{u}}_{n-1}\right)\text{,}$$ (7)

and the traction force (shear stress) between cells and substrate was

$$\frac{{\tau }_n}{k_s}=l_p{\overline{u}}_n\text{.}$$ (8)

Equation 8 provides information on the deformation mode of the cell chain.

Results

MC3T3-E1 cell chain on substrates of different stiffness

Here, we first adopted MC3T3-E1 fibroblast cells for studying the contraction behaviors of a cell chain on 10 and 30 kPa substrates. Constrained by micropatterns, cells aligned and polarized along the 1D adhesive zone and formed a 1D cell chain. Fig. 3 shows the typical traction-force distribution and contraction mode of MC3T3-E1 cells on 10 kPa polyacrylamide (PAA) gel. Fig. 3, A, D, and G show the cell morphology, traction-force distribution, and traction-force plots, respectively, of a cell chain composed of two cells. Fig. 3 A was a phase-contrast image merged with a fluorescence image of the cell nucleus of the cell chain. Fig. 3 D shows the traction force distribution associated with Fig. 3 A, in which the color indicates the magnitude of the traction force. As we can see, the maximal traction force is located at the ends of the chain. This kind of traction-force distribution was similar to that of a single cell (46). Fig. 3 G shows not only the magnitude of the traction but also the direction of the traction: the positive value stands for the traction force pointing toward the right, and the negative one for the force pointing toward left. We can see that the traction force always pointed to the center of the cell chain, suggesting that the cells in the chain contracted simultaneously as a unit (like a single cell), which we called united contraction. Fig. 3, B, E, and H show the results of the three-cell chain. Similar to the two-cell chain, it had maximal traction force at both ends that pointed to the center of the chain and also showed a united contraction mode. Fig. 3, C, F, and I show the results of the four-cell chain. However, Fig. 3 I shows that the traction force is fairly large in the interior region, and there are multiple intersection points with the x axis, suggesting that the cells in the chain somehow contracted independently, different from the contraction mode of the two-cell and three-cell chains, indicating a divided contraction mode. Fig. S2 shows the contraction behaviors of the five-cell chain, which indicates that the traction force of the cell chain is large in the interior region (Fig. S2 C), suggesting a divided contraction mode as well.

Figure 3.

Contraction behaviors of MC3T3-E1 cell chain composed of two to four cells on 10 kPa PAA gel. (A)–(C) A merged phase-contrast image with a fluorescence image of the cell nucleus of the cell chain is shown. The contour of the cell chain is plotted in yellow, and the cell nucleus is shown in blue. (D)–(F) The traction-force field of cell chains is shown. (G)–(I) The plot of distribution of the traction force along the x axis is shown. Positive value stands for traction force pointing toward the right, and negative value for pointing toward the left. The black line is for traction force measured before EGTA treatment, and the red line is for that measured after EGTA treatment for 20 min. (G) and (H) show the united contraction mode, whereas (I) shows the divided contraction mode. Scale bars, 25 μm. To see this figure in color, go online.

Fig. 4 shows typical results of contraction behaviors of MC3T3-E1 cells on 30 kPa PAA gel. For example, Fig. 4, A, D, and G were cell morphology, traction-force field, and traction-force plots of a two-cell chain on this stiffer substrate, respectively. As we can see, the traction-force field and plots show similar contraction behaviors as those at 10 kPa substrate, i.e., the maximal traction force is located at the ends of the cell chains, and thus the chain exhibited a united contraction mode. Fig. 4, B, E, and H were the results of the three-cell chain, also suggesting a united contraction mode. However, the four-cell chain shown in Fig. 4, C, F, and I exhibited a divided contraction mode. As we can see, Fig. 4 I shows that there were a few large peak values of traction force in the interior region, indicating that cells in the chain contracted independently, different from the contraction mode of the two-cell and three-cell chains. Fig. S2, D–F show the results of the five-cell chain on the 30 kPa substrate. According to Fig. S2, E and F, there are apparently multiple peak values of traction force, indicating a divided contraction mode.

Figure 4.

Contraction mode of MC3T3-E1 cell chains composed of two to four cells on 30 kPa PAA gel. (A)–(C) A merged phase-contrast image with a fluorescence image of the cell nucleus of the cell chains on 30 kPa substrate is shown. The cells’ contour is plotted in yellow, and the cell nucleus is shown in blue. (D)–(F) The traction-force field of cell chains is shown. (G)–(I) The plots of traction-force curves are shown. The black line is traction force measured before EGTA treatment, and the red line is for that after EGTA treatment for 20 min. (G) and (H) show the united contraction mode, whereas (I) shows the divided contraction mode. Scale bars, 25 μm. To see this figure in color, go online.

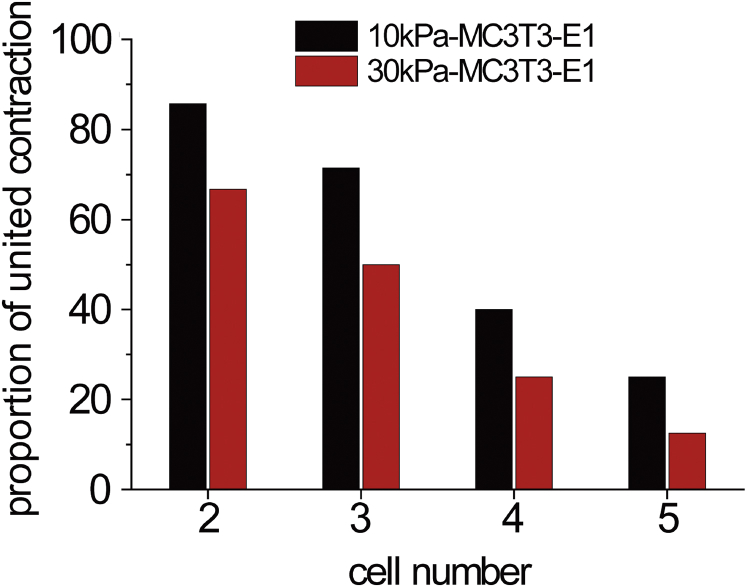
To compare the contraction behaviors of MC3T3-E1 cell chains on 10 and 30 kPa gel and test the effect of the substrate stiffness, we calculated the proportion of united contraction mode of cell chains on the soft and stiff substrates. Fig. 5 shows that the cell chain on 10 kPa gel had a higher proportion than on 30 kPa substrate, and the proportion decreased with the increase of cell number on both of the two types of substrate. Although the two- and three-cell chains exhibited united contraction on both of the two substrates, the three-cell chain on 30 kPa substrate had a proportion of united contraction only slightly higher than 50%. In addition, the four-cell and five-cell chains had divided contraction on both substrates.

Figure 5.

Effect of substrate stiffness and cell number on cell contraction behaviors. The proportion of united contraction mode on 10 kPa gel is higher than on 30 kPa gel. The two- and three-cell chains showed united contraction mode, and the four- and five-cell chains showed divided contraction mode. To see this figure in color, go online.

Effect of inhibition/enhancement of intercellular adhesion

To study how intercellular adhesion strength affects cell contraction mode and traction force distribution, we added the calcium-ion-chelating agent EGTA into culture media (the concentration of EGTA was 4 mmol/L) and treated the cells for 20 min to decrease the intercellular adhesion strength. The traction force of cell chains decreased after the EGTA treatment on 10 kPa substrate, as shown in Fig. 3, G–I. Moreover, the synergistic behavior of cells decreased, e.g., multiple intersecting points with the x axis appeared on the red curve of the traction-force plot shown in Fig. 3 G, suggesting that the contraction mode of the cell chains was changed from the united contraction to the divided contraction. On the 30 kPa substrate, we also observed a decrease of traction force and change of contraction mode of the cell chain (Fig. 4, G and H). EGTA treatment did not significantly affect the magnitude of traction force of the cell chain with divided contraction (Figs. 3 I and 4 I). Taken together, on both soft and stiff substrate, EGTA treatment reduced the cooperativity of contraction of cells.

Moreover, to test the effect of enhancement of intercellular adhesion, we transfected MC3T3-E1 cells with N-cadherin-EGFP (a gift from Valeri Vasioukhin (plasmid #18870; Addgene, Cambridge, MA)) to overexpress the N-cadherin. Fig. S3 shows the proportion of population of united contraction of five- and six-cell chains with N-cadherin overexpression. As we can see, the overexpression of N-cadherin significantly increased the proportion of united contraction of the cell chain, e.g., the proportion of the five-cell chain increased from 10 to 30%, and that of the six-cell chain increased from less than 2% to more than 10% compared with the control.

Contraction behaviors of MDCK cell chain on substrates of different stiffness

To test the effect of cell type on the contraction mode, we also cultured MDCK cells on the 1D patterned substrate. Our results showed that on the 10 kPa substrate, the cell chain composed of two to four cells exhibited united contraction mode (Fig. S4), whereas the five-cell chain (Fig. S6, A–C) exhibited divided contraction. In comparison, on the 30 kPa substrate, although the two-cell chain (Fig. S5, A, D, and G) and three-cell chain (Fig. S5, B, E, and H) exhibit united contraction mode, the four-cell chain (Fig. S5, C, F, and I) showed a divided contraction, which is different from that on the 10 kPa substrate. Of course, the five-cell chain also had a divided contraction mode like on the 10 kPa substrate, as expected (Fig. S6, D–F).

Fig. S7 shows the comparison of proportion of united contraction mode of MDCK cell chains on 10 and 30 kPa substrates. As we can see, the proportion of united contraction on the 10 kPa substrate is higher than that on the 30 kPa substrate, suggesting that MDCK cell chains on the soft substrate had stronger cooperativity than on the stiff substrate.

To compare the contraction behaviors of MC3T3-E1 and MDCK cells, we analyzed the proportion of united contraction of MC3T3-E1 and MDCK cells in Fig. 6. Fig. 6 A shows the comparison of proportion of united contraction of the cell chain between MDCK and MC3T3-E1 cells on 10 kPa substrate, and Fig. 6 B shows the comparison on 30 kPa substrate. As we can see, for the same substrate stiffness and cell number, MDCK cells showed a higher proportion of united contraction (higher synergy) than MC3T3-E1 cells. This might be attributed to the difference in intercellular adhesion property between these two kinds of cells. For example, cell-cell adhesion among MC3T3-E1 cells was mediated via N-cadherin and OB cadherin, whereas that of MDCK cells was mediated via E-cadherin.

Figure 6.

Comparison of proportion of united contraction of cell chains between MDCK and MC3T3-E1 cells on 10 and 30 kPa PAA gels. (A) The 10 kPa substrate comparison is shown. (B) The 30 kPa substrate comparison is shown. Cells on softer substrate showed a higher proportion of united contraction than on stiffer substrate for specific cell number. MDCK cells had a higher proportion of united contraction than MC3T3-E1 cells. To see this figure in color, go online.

Theoretical predictions

With our theoretical model, we analyzed the effect of intercellular adhesion stiffness and substrate stiffness on the tensile stress and traction force of the cell chain to predict how these parameters influence the cooperativity of cells during the contraction. Here, we introduced two parameter groups: $\lambda =k_c\sqrt{h/E_c{k}_s}$ determines the distribution feature of the tensile stress/tension and traction, and $l_p=\sqrt{E_{c}h/k_s}$ determines the magnitude of the tension and traction. Note that $\lambda =k_c\sqrt{h/E_c{k}_s}$ is the function of both cadherin stiffness k_c and substrate stiffness k_s. It suggests that there existed a competition between the effect of cell-cell interaction and cell-substrate interaction, and this competition was determined by the magnitude of the parameter group λ. At constant $l_p=\sqrt{E_{c}h/k_s}$ (i.e., constant k_s), Fig. 7 A shows that when λ is small (i.e., the cadherin stiffness is low, e.g., λ = 0.5), the normalized tensile stress σ_n/E_c is small, and the distribution is periodic like with multiple periods—there is one peak of the tensile stress curve in the center of each cell and a trough at the edges of the individual cell. With the increase of the value of λ (λ = 1, 2), the stress increased, and the difference between the peak and trough values decreased, i.e., the distribution of tensile stress became more uniform. And when the value of λ was very high (λ = 10), the curve of tensile stress had only one peak in the center of the whole cell chain like a single cell, suggesting a united contraction.

Figure 7.

Effect of stiffness of cell-cell interaction and stiffness of substrate on the tensile normal stress in cell chain and the traction force at the cell-matrix interface. $\lambda =k_c\sqrt{h/E_c{k}_s}$ describes a competition between the effects of cell-cell interaction and cell-substrate interaction on the contraction behaviors of the cell chain. (A) The effect of λ (i.e., k_c) on the distribution of tensile stress in the cell chain at constant substrate stiffness k_s is shown. (B) The effect of λ on traction force at given k_s is shown. (C) The effect of λ (i.e., K_s) on the distribution of tensile stress in the cell chain at a given stiffness of cell-cell interaction k_c is shown. (D) The effect of λ on traction force at a constant k_c is shown. The unit of l_p is μm. To see this figure in color, go online.

Regarding the traction force (Fig. 7 B), when λ was small (e.g., λ = 0.5), the distribution of traction was periodic like—its magnitude was approximately zero at the center of each individual cell, whereas it increased to a maximal value at the ends of each cell. In this way, there was a step-like change of the traction at the boundary of neighboring cells. When the value of λ was very high (λ = 10), the traction became continuous at the boundary, i.e., there was no peak value in individual cells, and the maximal value only occurred at the ends of the whole cell chain, whereas the traction was close to zero at the chain center. The mechanism is that when the cadherin stiffness was large enough, there would be a perfect interface at cell-cell contact; therefore, the displacement within the cell chain become smoothly continuous, and the multicells act as a unity. But when the cadherin stiffness was small, cell-cell contact became weak, and the contraction mode of the cell chain would change from a united contraction to a divided one, resulting in multiple peaks of traction force in the cell chains. This result was consistent with the experiments of this study and others such as Jasaitis and Mertz (11, 12, 13).

At constant k_c, large λ and l_p (e.g., λ = 10, l_p = 200 μm) correspond to a low substrate stiffness, whereas small λ and l_p (e.g., λ = 0.5, l_p = 10 μm) correspond to a high substrate stiffness. In the experiment, we chose the substrate stiffness as 10 and 30 kPa, and their corresponding values of λ are 2 and 1, respectively. As you can see from Fig. 7, C and D, when we increase the substrate stiffness (e.g., λ from 2 to 1), the tension (contractility) of individual cell will increase rapidly compared with the intercellular tension (at cell-cell junction), and as a result, the traction pattern shifts from a united contraction pattern to a divided one.

Discussion

Effect of cell-chain length on contraction behaviors

Cell-chain length was a key geometric factor that affects cell cooperativity in collective cell behaviors. We tested the relation of the chain length and population proportion of the united contraction for MC3T3-E1 and MDCK cells (see Fig. 5; Fig. S7). Both types of cells showed that with an increase in the chain length, the proportion of united contraction decreased, i.e., cell cooperativity was reduced. For example, for MC3T3-E1 cells, the two- and three-cell chains exhibited united contraction, whereas the four- and five-cell chains exhibited divided contraction (see Figs. 3, 4, and 5). This size effect in the 1D cell chain was consistent with that of a two-dimensional cell sheet. For example, the cell sheet showed united contraction (traction force was scaled with the size of the cell sheet) when its size was comparatively small (12). However, it hardly showed a united contraction when its size was large. Besides, the size of the vortex (47) formed via cooperativity among cells in collective cell migration is found to be always smaller than a critical value, suggesting that the cooperativity of cells is size dependent.

Note that there is an intrinsic length in our model, i.e., $l_p=\sqrt{E_{c}h/k_s}$, which might be responsible for the length-dependence behaviors of the cell chain. If we continuously increase the cell chain length L (from 60 to 120 μm), the cell chain would have a switch of contraction behavior from a united contraction to a divided contraction, as shown in Fig. S8.

Effect of intercellular adhesion strength

Intercellular adhesion strength should affect force transmission among cells and interaction between cells and substrate and thus changed collective cell behaviors. When the adhesion strength is high, force transmission among cells will be efficient, which then enhances the coordination among cells in their collective behaviors. But if the adhesion strength is low, then the coordination among cells should be inefficient. For example, EGTA treatment weakened the adhesion strength and thus impaired the ability of force transmission among cells via cadherin. Our results showed that when intercellular adhesion was weakened, cells’ contraction mode changed from the united contraction to the divided contraction, i.e., the degree of cooperativity among cells decreased (Figs. 3, 4, S4, and S5). In contrast, if we increase the adhesion strength with cadherin overexpression, the cooperativity would be enhanced (Fig. S3). Moreover, our model predictions (Fig. 7 B) showed that when cadherin stiffness was high, i.e., the cell-cell interaction was strong, the cell chain contracted like an entirety with strong synergy. But when the cadherin stiffness was low, the cell chain contracted with a divided contraction mode, resulting in traction force increasing in the inner domain of the cell chain and decreasing at the edges of the chain. Previous experiments also showed that the intercellular adhesion strength could affect collective cell behaviors, e.g., knocking down the expression of cadherin-connected α-catenin or culturing cells in low-calcium media caused intercellular adhesion to be unstable, so that cells migrated randomly and lost cooperativity among cells with decreased migration speed of cell front (4).

In addition, we showed that different kinds of cells might have different intercellular adhesion strength and thus exhibit different collective cell behaviors. We studied the contraction mode and traction force distribution of MC3T3-E1 and MDCK cell chains and showed that the MDCK cell chain exhibited stronger cooperativity among cells and a higher proportion of united contraction mode than the MC3T3-E1 cell chain (Fig. 6). For example, the two- and three-cell chains of MC3T3-E1 cells on the 10 kPa substrate exhibited united contraction, whereas the four- and five-cell chains exhibited divided contraction. But for MDCK cells on the 10 kPa substrate, even the four-cell chain showed united contraction. This result might be attributed to the difference in intercellular adhesion strength of these two kinds of cells. Among MC3T3-E1 cells, N-cadherin and OB-cadherin are the main types of adhesion molecules (48), and N-cadherin plays a more important role (49). In contrast, E-cadherin was the main type of adhesion molecule among MDCK cells, and adhesion strength between E-cadherin molecules was at least two times larger than that between N-cadherin (50). Therefore, MDCK cells that mainly express E-cadherin had stronger intercellular adhesion strength than MC3T3-E1 cells that mainly mediate by N-cadherin. This might explain why MDCK cells had higher proportion of population of united contraction mode than MC3T3-E1 cells.

Effect of substrate stiffness

Substrate stiffness also significantly impacted cell contraction behaviors. Previous studies showed that substrate stiffness influences cell spreading, polarization, and migration, and recent studies showed that the substrate stiffness affects the collective cell polarization and orientational arrangement. The mechanism is that the substrate stiffness can directly affect cell-matrix adhesion, which then influences the magnitude and distribution of the traction force and thus influences cell behaviors. In this study, we showed that the substrate stiffness affected the cell contraction mode of a 1D cell chain. We found that both MC3T3-E1 cells (Fig. 5) and MDCK cells (Fig. S7) showed stronger cooperativity on softer substrate, i.e., the proportion of united contraction on softer substrate was higher than on stiffer substrate for specific chain length and intercellular adhesion strength. Our model predictions (Fig. 7 D) also showed that the magnitude of fluctuation of traction force in the inner domain of the cell chain increased with an increase of substrate stiffness, resulting in the cell contraction mode transforming from the united contraction to a divided one. Our results were consistent with existing experimental observations, e.g., when the microenvironment of myocardial cells was stiffened, the degree of intercellular cooperativity was decreased correspondingly, resulting in an increase of traction force and reappearance of focal adhesion adjacent to the cell-cell interface (i.e., showing divided contraction) (51). It was also found that migrating cells had strong cooperativity and formed a large swirl on soft substrate, but they showed weak cooperativity and formed a small swirl on stiff substrate (47).

Effect of cellular contractility on cell cooperativity

Note that in our theory, we assumed a constant prestrain. But it would be interesting to discuss the effect of change of cellular contractility on the cooperativity of cells. In the experiments, we can reduce/increase the contractility of cells by blebbistatin/calyculin A treatments, respectively. The decrease of contractility by the blebbistatin treatment corresponded to the reduction of the prestrain in our cell-chain model. It predicted that the traction force of the cell chain became more continuous after the blebbistatin treatment, although its amplitude decreased compared with that of the control, and thus the cell chain showed a united contraction behavior (Fig. S9). Our theoretical results were consistent with the experiments (Fig. S10). For example, the statistical analyses showed that the proportion of united contraction mode increased with blebbistatin treatment compared with that of the control (Fig. S10 F).

Similarly, the increase of contractility by calyculin A treatment corresponded to the increase of the prestrain in the model. Our predictions showed that the traction force of the cell chain became more discontinuous after the treatment, although its amplitude increases compared with the control, and thus the cell chain showed a divided contraction behavior (Fig. S11). Our theoretical results are in good agreement with experiments with calyculin A treatment (Fig. S12), and the statistical analyses showed that the proportion of united contraction mode decreases with calyculin A treatment compared with the control (Fig. S12 F).

Conclusions

By culturing cells on 1D hydrogel micropatterns to build a 1D cell chain, we studied the effect of substrate stiffness, intercellular adhesion strength, and the chain length on the contraction mode of the cell chain. Our experiments demonstrated that matrix stiffness had a significant impact on the cell contraction mode and traction-force distribution of the cell chain. Cells preferred to show a united contraction mode on soft substrate rather than on the stiff one. At the same time, intercellular adhesion strength also plays an important role in the collective contraction of the cell chain. A strong cell-cell interaction resulted in a united contraction mode, whereas a weak interaction preferred a divided one. We also found that the contraction mode depended on the cell-chain length. When it was small, the cell chain exhibited a united contraction mode; but when it was large, the cell chain preferred a divided one.

We also built a mathematical model of the cell chain and studied how cadherin stiffness and substrate stiffness influence the contraction mode. We found that there was a competitive relationship between the effect of cadherin stiffness and substrate stiffness on the contraction mode. For example, stronger intercellular adhesion or softer substrate resulted in stronger intercellular coordination, which allows cells to contract as a unit. On the contrary, if intercellular adhesion was weak or cells were on stiff substrate, cells contracted independently due to weak intercellular interaction. Besides, a cell has stronger coordination in the short cell chain than the long one. These results allow us to have a deeper understanding of collective behaviors of cells and provide guidelines for design of tissue materials for biomedical applications.

Author Contributions

S.H. and B.J. designed the research. X.L., J.X., and P.L. performed the experiment. S.H. contributed the analytical model. X.L., J.X., S.H., and B.J. analyzed data. X.L., S.H., and B.J. wrote the article. All authors reviewed the manuscript.

Editor: Cynthia Reinhart-King.