Towards a Quantified Network Portrait of a Population

Abstract

Computational network analysis has enabled researchers to investigate patterns of interactions between anatomical regions of the brain. Identification of subnetworks of the human connectome can reveal how the network manages an interplay of the seemingly competing principles of functional segregation and integration. Despite the study of subnetworks of the human structural connectome by various groups, the level of expression of these subnetworks in each subject remains for the most part largely unexplored. Thus, there is a need for methods that can extract common subnetworks that together render a network portrait of a sample and facilitate analysis of the same, such as group comparisons based on the expression of the subnetworks in each subject. In this paper, we propose a framework for quantifying the subject-specific expression of subnetworks. Our framework consists of two parts, namely subnetwork detection and reconstructive projection onto subnetworks. The first part identifies subnetworks of the connectome using multi-view spectral clustering. The second part quantifies subject specific manifestations of these subnetworks by nonnegative matrix decomposition. Positivity constraint is imposed to treat each subnetwork as a structure depicting the connectivity between specific anatomical regions. We have assessed the applicability of the framework by delineating a network portrait of a clinical sample consisting of children affected by autism spectrum disorder (ASD), and a matched group of typically developing controls (TDCs). Subsequent statistical analysis on the intra- and inter-subnetwork connections, revealed decreased connectivity in ASD group between regions of social cognition, executive functions, and emotion processing.

1 Introduction

Identifying patterns of structural and functional connectivity in the human brain aids in the understanding of the neural substrates of the mind, its cognitive computations and its outward expressions in behavior [1]. Hence, research on the human connectome, with a goal of identifying interpretable motifs of interactions between anatomical regions has drawn extensive attention in the neuroscience community. Methodologies developed for computational network analysis [2] have enabled researchers to investigate the overall communication design of the human brain by defining networks over a set of anatomical regions and their connections. This was established by advances in in vivo imaging techniques such as functional MRI and diffusion MRI, in conjunction with improvement in tools depicting connectivity between anatomical regions such as tractography [3].

While the overall attention directed to network analysis has increased at every level of study [4–6], studies performed at meso-scale currently form the main line of investigation. Meso-scale structures refer to grouping of anatomical regions based on their distinctive connectivity patterns. In brain networks, the identification of meso-scale structures can reveal how the network manages an interplay of seemingly competing principles of functional segregation and integration [7], thereby how specific communication pathways between set of regions contribute to behavior. One of the best known examples of a meso-scale structure is a module [8]. In the context of this paper, we adopt the term subnetwork instead of module since it has a broader scope that encompasses any cluster of anatomical regions with a distinctive connectivity pattern. Henceforth, the term meso-scale architecture will refer to decomposition of connectome into subnetworks, rendering a network portrait of a subject or a sample.

Although the extraction of subnetworks of the human connectome has been studied by various groups [6, 7, 9, 10], subsequent studies on identified subnetworks suffer from a common methodical deficiency. That is, the subnetworks are determined with the goal of architectural characterization i.e. characterizing the overall aggregation/segregation of regions. Other than a few exceptions [4, 11], the expression of these subnetworks in each subject followed by their quantification and subsequent comparison, remains for the most part largely unexplored. Thus, there is a need for methods that can extract the meso-scale architecture of a sample and facilitate analysis of the same, such as group comparisons based on the magnitude of expression of subnetworks in subjects.

In this paper, we propose a framework for quantifying the subject-specific expression of subnetworks, by decomposing connectomes into a basis set that is explicitly defined by these subnetworks. This is an important advancement since the proposed framework not only extracts subnetworks, but also quantifies their presence in a subject, enabling subsequent statistical comparison of individuals and different groups of individuals (e.g., cases vs. controls). Similar approaches have been explored in [4, 11], with critical differences in the way subnetworks were extracted and defined. In [11], the authors extracted subnetworks that corresponded to the most dominant sets of connections that were not spatially/anatomically correlated. This approach is useful for identifying important connections, but does not lend itself well to identify how anatomical regions contribute to function by their segregation and integration. This was improved in [4] where a subnetwork (or hub as the authors refer to it) consists of a set of anatomical regions and their intra-connections. However, subnetworks are not necessarily defined by sparse sets of regions and a thresholding is required to determine the final membership of regions to subnetworks.

Our framework separates the stage of subnetwork identification from the stage of quantification of their expression in each subject. Hence, subnetworks that are extracted by different approaches such as community detection [8] or clustering [10] can be incorporated into our framework, making it a generic methodology for network analysis. The result is a quantified network portrait of a sample that renders a comprehensive low dimensional representation that is common to each subject, facilitating population studies. Additionally, subnetworks and their corresponding weights are estimated under non-negativity constraints, leading to easily interpretable results since each subnetwork is a connectivity matrix on its own.

We assessed the applicability of this framework by first identifying subnetworks in a clinical sample consisting of children affected by autism spectrum disorder (ASD), and a matched group of typically developing controls (TDCs). The coefficients that quantify the expression of these subnetworks in each subject were estimated. Subsequent statistical analysis on these coefficients revealed group differences between TDC and ASD groups, in terms of differing connectivity patterns.

2 Method and Materials

The proposed methodology consists of two parts, namely subnetwork detection and reconstructive projection onto subnetworks. The first part identifies subnetworks of the connectome by assigning anatomical regions into different clusters based on their connectivity. We use multi-view spectral clustering [12] to extract a meso-scale architecture that is common to all subjects of a group. This facilitates a decomposition of the connectome into common subnetworks. The second part quantifies subject specific manifestations of these subnetworks. This is achieved by nonnegative matrix decomposition [13] to calculate the strength of expression of each subnetwork. Positivity constraint is imposed to get nonnegative components and coefficients so that each subnetwork is a connectivity matrix on its own. This enables us to treat each subnetwork as a structure depicting the connectivity between specific anatomical regions. The output is a subject specific vector of coefficients corresponding to weights of identified subnetworks in this subject (depicting both intra- and inter-connectivity). These coefficients, inherently, can be used for subsequent statistical analyses such as group differences.

2.1 Multi Subject Subnetwork Detection

Subnetwork detection in the human connectome aims at finding grouping of anatomical regions depicting the meso-scale architecture of the brain [4]. Each group consists of several regions that are densely connected to each other and sparsely connected to regions outside their group. Several methods have been proposed to extract subnetworks in the human connectome either by utilizing algorithms specifically developed for complex network analysis such as modularity maximization [8] or by using domain general clustering algorithms such as spectral clustering [10]. Recently, a few approaches have been also proposed to extract structures that are common to a group of subjects [10, 14, 15]. In this work, we adapt multi-view spectral clustering approach [12] that identifies both common clusters and subject-level variations, to extract subnetworks from a sample.

The classical spectral clustering for a single subject starts with the construction of the normalized (or un-normalized) Laplacian (L) of the connectivity (adjacency) matrix A of the subject. A is a symmetric matrix where the element A_ij is the connectivity between the regions i and j. Then, a simple clustering technique such as k-means is used on the eigenvectors (U) corresponding to the smallest k eigenvalues of L to determine groupings of nodes. This can be formulated as the following minimization problem:

$${\text{min}}_U\mathit{\text{ tr}}(U^{T}LU),\text{subject to }{U}^{T}U=I.$$ (1)

Solution of (1) is to choose the aforementioned eigenvectors of L. The centroid based co-regularization approach as proposed by Kumar et al. [12] formulates the problem of finding a common architecture among multiple subjects, by minimizing the disagreement between subject specific subnetworks and the common subnetworks. Similar to the formulation of spectral clustering, we have the following minimization problem:

$${\text{min}}_{U_1,\dots ,U_N,U_c}{\sum }_{s=1}^N\mathit{\text{ tr}}(U_s^T{L}_s{U}_s)-{\sum }_{s=1}^N{\lambda }_s\mathit{\text{tr}}(U_s{U}_s^T{U}_c{U}_c^T),$$ (2)

where the centroid eigenvector matrix U_c encodes the common set of subnetworks. Eigenvector matrices U_s correspond to individual subnetworks of subjects (s = 1…N). λ_s‘s are the weights of each regularization term. Once this problem is solved for U_c, k-means clustering is applied on U_c to get the common k subnetworks. The solution is obtained by a two-step iterative scheme after initializing U_c: (a) solve for U_s by fixing U_c and (b) solve for U_c by fixing U_s. This is repeated until convergence is achieved for U_c. Given U_c, U_s are determined by solving

$${\text{min}}_{U_1,\dots ,U_N}{\sum }_{s=1}^N\mathit{\text{tr}}(U_s^T(L_s-{\lambda }_s{U}_c{U}_c^T)U_s).$$ (3)

This is equivalent to calculating eigenvectors corresponding to the smallest k eigenvalues of the modified Laplacian ${\tilde{L}}_s=L_s-{\lambda }_s{U}_c{U}_c^T$. Then by fixing U_s, U_c is determined by solving

$${\text{max}}_{U_c}{\sum }_{s=1}^N{\lambda }_s\mathit{\text{tr}}(U_s{U}_s^T{U}_c{U}_c^T),$$ (4)

that is again equivalent to finding the eigenvectors corresponding to the largest k eigenvalues of ${\sum }_{s=1}^N{\lambda }_s{U}_s{U}_s^T$.

2.2 Reconstructive Projection onto Subnetworks

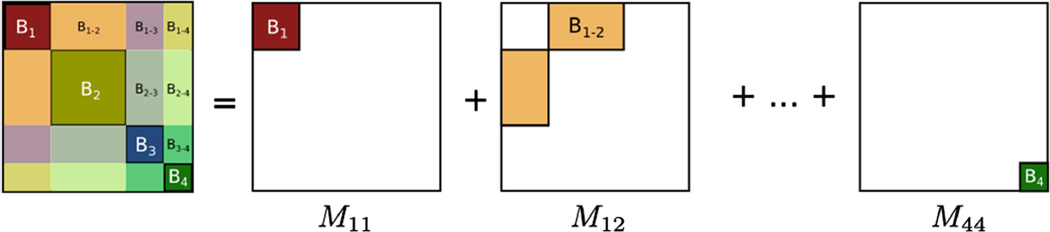
Subnetwork detection determines membership of each anatomical region to a specific subnetwork. Based on these memberships, a connectivity matrix of a subject can be decomposed into blocks (after reordering rows and columns), each corresponding to connections in a subnetwork or between two subnetworks. This is illustrated in Fig. 1. The block structure of a connectivity matrix, as illustrated in Fig. 1, naturally defines a generative model for the multiple subject case: for each block we define a common basis (M_ij) that includes connections in a subnetwork or between two subnetworks, and subject specific coefficients $({\alpha }_{ij}^s)$.

Fig. 1.

Decomposition of a connectivity matrix into blocks corresponding to connections in a single subnetwork (B₁, B₂, B₃, B₄) or between two subnetworks (B_1–2, B_1–3, …). Each matrix M_ij includes zeros everywhere except at the region corresponding to the encoded block. Note that in case of a single subject, this decomposition defines an exact reconstruction of the original connectivity matrix.

Then the connectivity matrix A^s of a subject s is assumed to be generated as

$$A^s={\alpha }_{11}^s{M}_{11}+{\alpha }_{12}^s{M}_{12}+\dots +{\alpha }_{22}^s{M}_{22}+\dots +{\alpha }_{kk}^s{M}_{kk},$$ (5)

where M_ij (corresponding to a block in Fig. 1) defines a common basis of connections in the subnetwork i (if i = j) or between subnetworks i and j (if i ≠ j), including zeros everywhere except at the region corresponding to the connections encoded by M_ij. The coefficients ${\alpha }_{ij}^s$ are subject specific weights. The estimation of each M_ij can be done independently since they do not share any connection. Thus, each basis component and corresponding coefficients are determined by solving

$${\text{min}}_{m,p}f(m,p)={\Vert X-m{p}^T\Vert }_F^2,\text{ subject to }m>0,p>0$$ (6)

where the s^th column of matrix X has the elements of matrix A^s in the block corresponding to M_ij. m is a vector including only non-zero elements of M_ij. p is a vector including the coefficient ${\alpha }_{ij}^s$ as its s^th element. This is solved independently for each M_ij by a projected gradient descent algorithm for nonnegative matrix factorization [13]. The solution is found iteratively by updating the current estimate of parameters θ^t ≡ (m^t, p^t) as

$${\theta }^{t+1}=P[{\theta }^t-{\beta }^t{\nabla }_{\theta }f({\theta }^t)],$$ (7)

$$P[x]\underset{¯}{\underset{¯}{\text{def}}}\{\begin{array}{cc}x\hfill & \mathit{\text{if }}l<x<u,\hfill \\ u\hfill & \mathit{\text{if }}x\ge u,\hfill \\ l\hfill & \mathit{\text{if }}x\le l,\hfill \end{array}$$ (8)

$${\nabla }_{\theta }f\underset{¯}{\underset{¯}{\text{def}}}((m{p}^T-X)p,m^T(m{p}^T-X)).$$ (9)

The step size parameter β^t is selected so that the following inequality is satisfied.

$$f({\theta }^{t+1})-f({\theta }^t)\le \sigma {\nabla }_{\theta }f{({\theta }^t)}^T({\theta }^{t+1}-{\theta }^t),$$ (10)

where σ is any value between 0 – 1. The projection function P[x] projects the value of x into the range defined by the lower and upper bounds l, u.

2.3 Population Studies

The coefficients of generative model (5), ${\alpha }_{ij}^s$, are subject-specific and encode the overall strength of connections in a subnetwork or between subnetworks. These coefficients that provide a comprehensive low dimensional representation of each subject facilitate population studies. Similar to edge-wise comparison of groups [5], we can compare two groups, such as controls vs. Patients, on a subnetwork-wise basis i.e. we can identify which group has higher/lower expression of a subnetwork or connections of an inter-subnetwork communication. This approach also increases statistical power by lowering the dimensionality of the comparison. Instead of comparing each edge individually, we divide the connectome into subnetworks and compare only coefficients that depict the overall communication pattern of these subnetworks, reducing the problem of multiple comparisons.

2.4 Dataset

Our clinical sample consists of 172 male participants, including 97 children (age: 12.6 ± 2.9 years) affected by autism spectrum disorder (ASD), and a matched group of typically developing controls (TDCs) (age: 12.2 ± 3.3 years). Participants with a community diagnosis of an ASD were recruited in part through autismMatch (https://autismmatch.org), and diagnoses were confirmed using diagnostic instruments and expert consensus clinical judgment by two independent psychologists following Collaborative Programs of Excellence in Autism (CPEA) diagnostic guidelines.

Diffusion tensor imaging was acquired in two epochs on the same scanner with different scanner parameters. In the first set, DTI was acquired using a monopolar+ sequence, with repetition time (TR)/echo time (TE) = 11000/75 ms, resolution = 2 × 2 × 2 mm, collecting 30 directions with b-value = 1000 s/mm2 and 1 b = 0 image on a Siemens Verio 3T scanner. In the second epoch, DTI TR/TE was 11000/76 ms using a monopolar sequence. DTI measures of FA and MD were verified not to vary between scans within the two epochs. T1-weighted (TR/TE = 1900/2.54) MRI images with resolution 0.4 × 0.4 × 0.9 mm were also acquired. The T1 image of each subject was segmented into 95 anatomical regions of interest (ROIs) of the Desikan atlas [16] using Freesurfer [17]. FSL’s bedpostx was fit to each voxel in the DTI image, and FSL’s probtrackx was used to perform tractography seeded from each of the 95 ROIs and going to the others [18]. A 95 × 95 connectivity matrix A was created for each subject, where A_ij = (S_ij/S_i) · R_i. In this formula, S_ij represents the number of fibers connecting seed region i to target j, and S_i represents the total number of fibers emanating from region i. R_i, the surface area of region i, accounts for the different sizes of the 95 ROIs.

3 Results

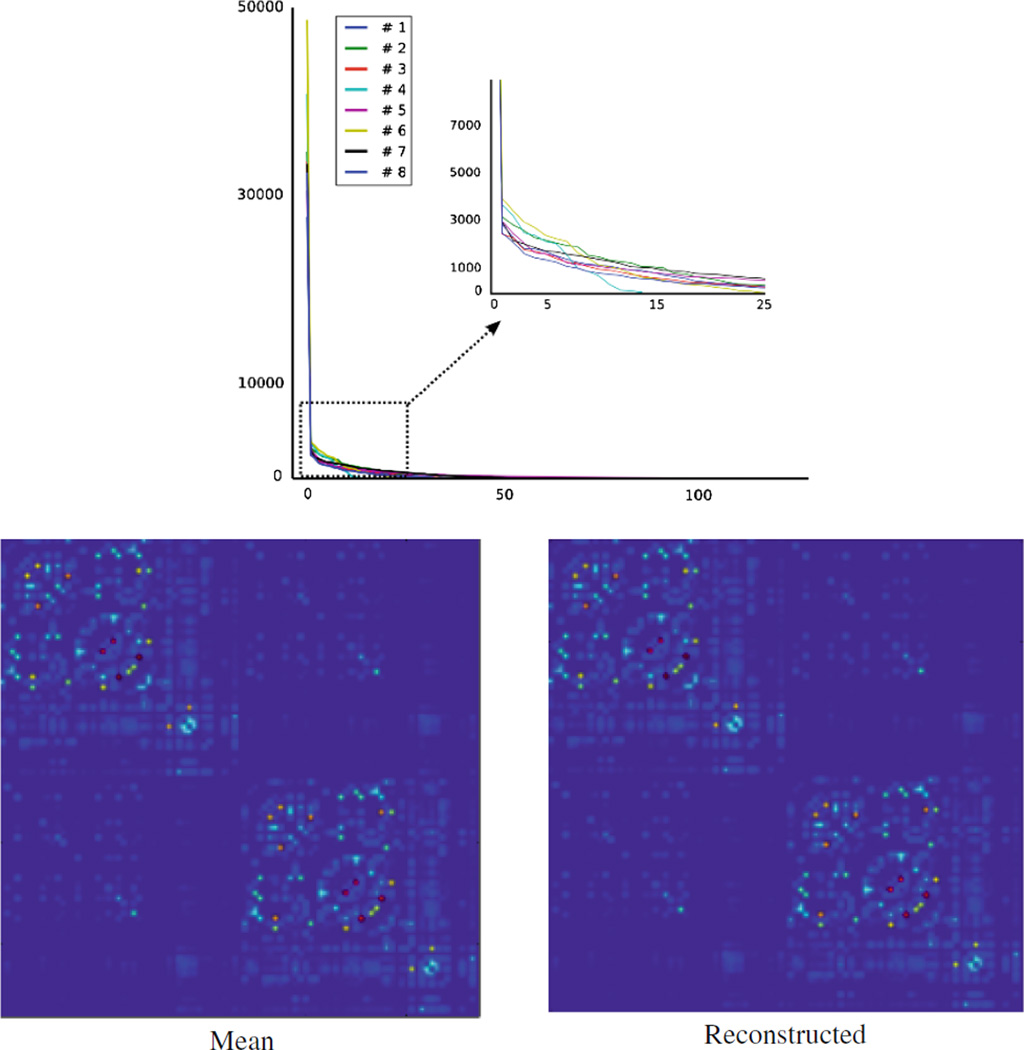
Here, we first review our projection approach introduced in Sect. 2.2. Then, experimental results for group comparison will be presented. In the generative model (5), we assume a single common basis M_ij for each block of the connectivity matrix (see Fig. 1). Estimating M_ij in (6) corresponds to finding a single basis for connections that are included in M_ij. The feasibility of this assumption can be easily validated by observing singular values¹ of the matrix X in (6). This is illustrated in Fig. 2 (top) where our dataset was used to identify eight common subnetworks. The matrix X for each subnetwork has only one dominant singular value and the remaining singular values diminish quickly. One expects to have even clearer dominance as the number of subnetworks increases, since with increasing number of subnetworks, variation of connection strength in each subnetwork tends to decrease. In Fig. 2 (bottom left and right), the connectivity matrix that was reconstructed by the estimated components M_ij and mean coefficients ${\alpha }_{ij}^s$ is compared to the average connectivity matrix of our dataset. Overall agreement between two matrices, thereby the quality of reconstruction is clear.

Fig. 2.

Top: Singular values of X in Eq. (6), for eight subnetworks. For each subnetwork, we have one clearly dominant singular value. Bottom left: Mean connectivity matrix of our clinical sample. Bottom right: Reconstructed mean connectivity matrix using (5). Similarity between the two is easily noticeable, illustrating the reliability of reconstruction.

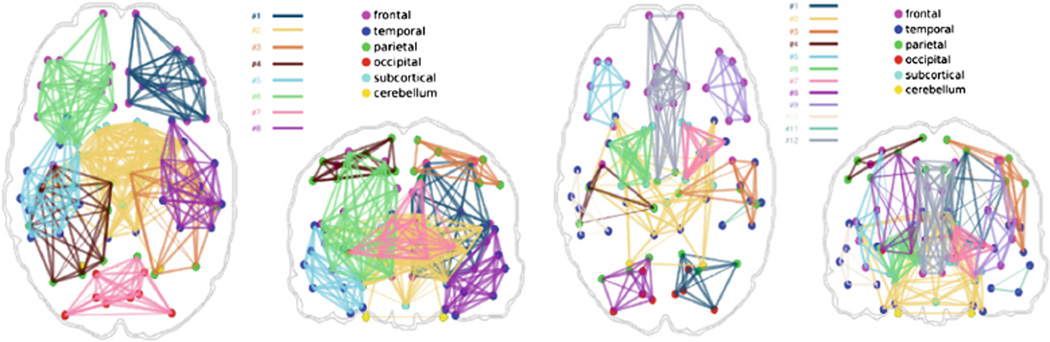
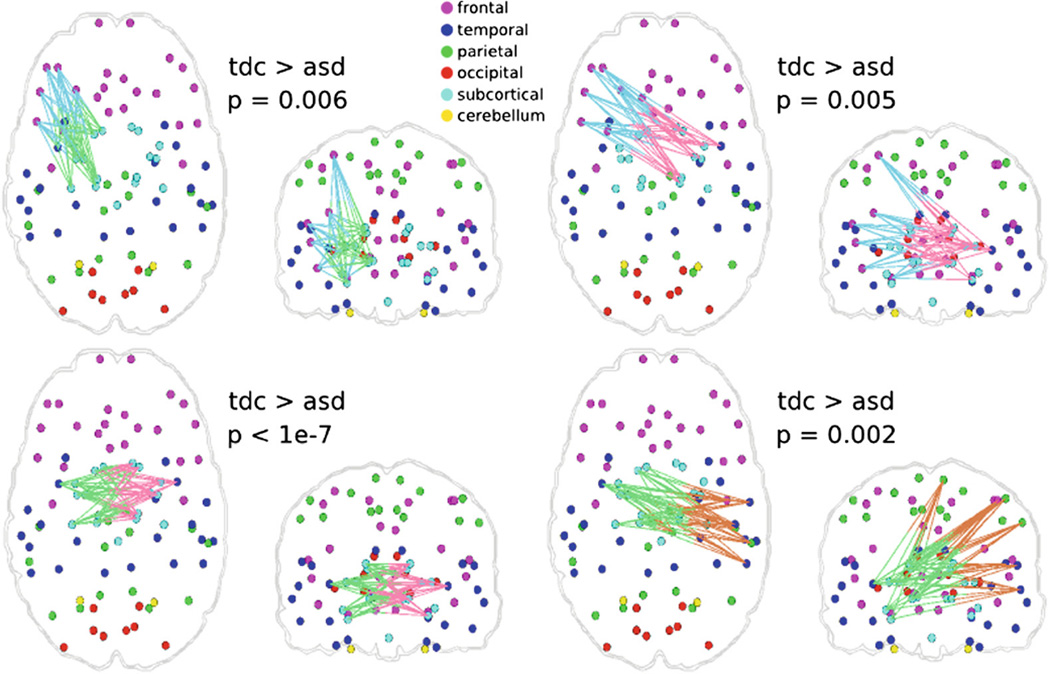
In order to use our framework for group comparisons, we first extracted the mesoscale architecture of the sample. We created several network portraits consisting of different numbers of subnetworks. The actual choice of the number depends on the level of detail required for the hypothesis being investigated. Figure 3 illustrates two network portraits consisting of 8 and 12 subnetworks that are common to all subjects, to provide a representation of how subnetworks are formed at different resolutions. Statistical analysis was performed on the coefficients ${\alpha }_{ij}^s$ that describe the expression of these subnetworks in each of the subjects. Figure 4 shows sets of connections that differ significantly between TDC and ASD groups (p < 0.01), when the 12-subnetwork portrait was used to describe the population. For the remainder of the paper where we discuss extracted subnetworks, we refer to the subnetworks of the 12-subnetwork portrait, unless otherwise stated.

Fig. 3.

Common meso-scale architectures of our clinical sample, depicting network portraits of 8 (left) and 12 (right) subnetworks. Only intra-subnetwork connections are displayed (Color figure online).

Fig. 4.

Connections with significant (p < 0.01) group differences between TDC and ASD samples, for the 12 subnetwork case. Colors of edges correspond to the subnetworks that they are part of (see Fig. 3). They are all two-colored since they are connections between two subnetworks. Connections that are significantly different are between subnetworks #3 (brown), #5 (blue), #6 (green), and #7 (pink) (Color figure online).

Overall symmetry of the meso-scale architectures in Fig. 3 conforms to previously published findings on the structural core of human connectome [9]. Meso-scale architectures (both for 8 and 12 subnetworks) define spatially correlated subnetworks, each characterized mostly by local (short-range) connections. This is consistent with the fact that cortical communication in the human brain is dominantly characterized by short-range connections [19]. Inter-hemispheric connections (Subnetworks #2 and #12) exist between bilateral temporal lobes and sub-cortical regions (Subnetwork #2), or within frontal lobe (Subnetwork #12). We should note that the meso-scale architectures illustrated in Fig. 3 only shows intra-subnetwork connections. More inter-hemispheric connections appear when statistically analyzing the inter-subnetwork communication.

Four sets of connections related to inter-subnetwork communication were found to be significantly lower in ASD group (Fig. 4). Lower structural connectivity supports the underconnectivity hypothesis for ASD [20]. Specifically, connections related to the regions involved in social cognition such as amygdala, insula, caudate (Subnetworks #6 and #7) [21] and regions involved in executive functions as well as social cognition such as left orbitofrontal cortex and left middle frontal cortex (Subnetwork #5) [20], [22] were found to be lower in the ASD group. In addition, connections related to the regions involved in emotion processing such as right superior temporal and supramarginal cortex (Subnetwork #3) [23] were significantly lower in the ASD group. Accordingly, identified group differences revealed decreased connectivity between regions of social cognition, executive functions, and emotion processing, which is very consistent with common conceptualization of ASD [24].

4 Conclusion

We have developed a framework for creating a quantified network portrait of a population. Our framework quantifies the subject-specific expression of subnetworks, by decomposing connectomes into a basis set that is explicitly defined by these subnetworks. The approach introduced here separates the subnetwork extraction that is usually performed with community detection or clustering methods from the stage of quantification of identified subnetworks in each subject. Hence, subnetworks that are extracted by different approaches can be incorporated. Our framework provides a novel way of identifying subnetworks, and subsequent analysis both at the population and subject level. Subject level coefficients can be correlated with clinical measures to identify the imaging correlates of clinical manifestations.

The resulting meso-scale architecture of the sample renders a comprehensive low dimensional representation that is common to each subject, facilitating population studies. This approach also increases statistical power since we divide the connectome into subnetworks and compare only coefficients that depict the overall communication pattern of these subnetworks, instead of comparing each edge individually, alleviating the problem of multiple comparisons.

The applicability of the framework was assessed on a clinical sample consisting of children affected by ASD and a matched group of TDCs. The extracted meso-scale architecture of the sample was consistent with previously published findings on the structural core of human connectome. Subsequent statistical analysis on the intra- and inter-subnetwork connections revealed decreased connectivity between regions of social cognition, executive functions, and emotion processing. Overall, the results support the underconnectivity hypothesis for ASD.

Group differences at the level of meso-scale structures reveal important changes in integration/segregation of anatomical regions, which would not be possible with traditional edge-wise analyses. Our results provide insights on how overall communication between cortical clusters pertaining to different faculties such as social cognition, executive functions, and emotion changes between TDC and ASD groups.