A Novel Zernike Application to Differentiate Between Three-dimensional Corneal Thickness of Normal Corneas and Corneas With Keratoconus

Abstract

PURPOSE

To evaluate a novel Zernike algorithm to differentiate 3-dimensional (3-D) corneal thickness distribution of corneas with keratoconus (KC) from normal corneas.

DESIGN

A retrospective development and evaluation of a diagnostic approach.

METHODS

Corneal tomography with Scheimpflug imaging was performed in normal (43 eyes) and KC (85 eyes) corneas. Axial and tangential cone location magnitude index (axial CLMI and tangential CLMI, respectively) of the anterior and posterior surface were calculated. The aberrations of the anterior corneal surface were analyzed with Zernike polynomials. Pachymetric Zernike analyses (PZA) were used to map the 3-D thickness distribution of the cornea. Logistic regression was performed to develop a diagnostic procedure for KC using CLMI, PZA, and aberrations. A receiver operating characteristic curve was constructed for each regression model. Corneal volume was also compared between normal and KC corneas. Only the central 5 mm zone was used for all analyses.

RESULTS

Among the PZA coefficients, second- and third-order root mean squares of PZA coefficients were the best predictors of KC corneas (P < .0001). Among the CLMI variables, axial CLMI of anterior and tangential CLMI of posterior surface were the best predictors of KC (P < .0001). Among the Zernike corneal aberration coefficients, second- and third-order root mean squares of coefficients were the best predictors of KC (P < .0001). Sensitivity and specificity of Zernike corneal aberrations, CLMI, and PZA logistic regression model were similar (P > .05).

CONCLUSIONS

The entire 3-D corneal thickness was mapped with Zernike. The PZA method was comparable to CLMI and anterior corneal wavefront aberrations in detecting KC.

Corneal tomography and biomechanics play an important role in detection and treatment of keratoconus.^1,2 A multitude of approaches are used to classify grades of keratoconus, including slit-lamp microscopic features, corneal tomography, corneal aberrations, and corneal biomechanics.^3–10 Custom indicators beyond maximum keratometry and minimum thickness of the cornea have been developed for improved detection of keratoconus and the more diagnostically challenging subclinical cases.^3–10 These custom indicators have comparable value in predicting keratoconus among different study groups.^3–10 Total corneal and epithelial thickness have also been shown to be sensitive indicators of keratoconus.^8,11–17 Epithelial thickness may be particularly useful in diagnosis of severity of keratoconus because of its compensatory relationship to the steepness of the stroma.^12,13,16

Spatial variation of corneal thickness may be an important marker of keratoconus as well.^8,11–17 Recent studies have shown that corneal thickness distribution and change (percentage progression in thickness) are useful in diagnosis of keratoconus.^8,11–17 However, the mathematical formulations used were limited to quadratic or cubic-order polynomials that reduced the complex corneal 3-dimensional (3-D) thickness distribution, which varies as a function of both radius and meridian, to a function of just the radius by averaging the thickness distribution over all the meridians.^15–17 The objective of this study was to introduce a novel application of the Zernike transform to map the 3-D spatial distribution of corneal thickness measured by Scheimpflug imaging. Further, Zernike coefficients, similar to Zernike transform of corneal aberrations, were defined and analyzed in normal and keratoconus patients using an automated classification system.

METHODS

THIS RETROSPECTIVE, OBSERVATIONAL STUDY WAS approved by the institutional research and ethics committee of Narayana Nethralaya multi-specialty hospital, India, and conducted in accordance with the tenets of the Declaration of Helsinki. Only the preoperative data of patients who underwent collagen cross-linking and/or topography-guided ablation were included in this retrospective study. The selection criteria of corneas with keratoconus that underwent treatment are detailed below.

STUDY POPULATION

Patients between 18 and 60 years of age were included in the study. The diagnosis of keratoconus was based on evidence of stromal thinning, focal protrusion, or increase in corneal curvature, Fleischer ring, Vogt striae, scissoring of the red reflex, an abnormal retinoscopy, and curvature asymmetry leading to abnormal corneal astigmatism. The exclusion criteria were ocular hypertension, corneal inflammation, prior eye surgery, and current topical medication use. The severity of keratoconus was assessed using mean keratometry (Kmean). Three keratoconus grades and a normal grade, designated as grade 0, were defined: grade 1, Kmean < 48 diopters (D); grade 2, 48 D ≤ Kmean < 52 D; grade 3, Kmean ≥ 52 D.^18,19 For “normal” eyes, manifest spherical error and astigmatism were limited to ±2 D.

STUDY DESIGN

Corneal topography (flat [K1] and steep [K2] axis keratometry, maximum keratometry [Kmax], and Kmean of the anterior surface) and thickness measurements were performed using Scheimpflug imaging (Pentacam; Oculus Optikgeräte GmbH, Wetzlar, Germany). If any normal or keratoconus subject was using contact lenses prior to treatment, tomography was measured after the subject was off contact lenses for at least 2 weeks. Anterior corneal wavefront aberrations were computed by Pentacam using ray tracing (software version 6.07r29). The wavefront aberrations were analyzed using Zernike polynomials up to 12th order²⁰ and an analysis zone size of 5 mm of the central cornea. A 5 mm analysis zone size was chosen because in most eyes functional vision is limited by the pupil size and the location of the cone was within the central 3 mm cornea in all the patients included in this study. The location of the cone was evaluated as the location of the steepest point on the tangential curvature map.¹⁹ The Zernike polynomials can be expressed as:

$$\mathrm{W}\left(\rho ,\theta \right)={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{m}}^{\mathrm{i}}{\mathrm{Z}}_{\mathrm{m}}^{\mathrm{i}}}$$ (1)

In eq. (1), W = wavefront error, ρ = nondimensional radius (0 ≤ ρ ≤ 1), θ = meridian in radians, a = Zernike co-coefficients (defocus, coma, etc), Z = Zernike polynomials, i = order of Zernike polynomial, and m = −n, −n+2,…, n − 2, n. In this study, eq. (1) was modified to map the 3-D thickness distribution, p, as follows:

$$\mathrm{p}\left(\rho ,\theta \right)={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{b}}_{\mathrm{m}}^{\mathrm{i}}{\mathrm{Z}}_{\mathrm{m}}^{\mathrm{i}}}$$ (2)

In eq. (2), p was the thickness spatial distribution. Henceforth, the method described by eq. (2) is referred to as “pachymetry Zernike analyses,” or PZA. By converting eq. (2) to the conventional quadratic matrix form (eq. 3), all ${\mathrm{b}}_{\mathrm{m}}^{\mathrm{i}}$ were computed. Thus, ${\mathrm{b}}_{\mathrm{m}}^{\mathrm{i}}$ were the PZA Zernike coefficients.

$$\left[\mathrm{b}\right]={\left({\left[\mathrm{Z}\right]}^{\mathrm{T}}\left[\mathrm{Z}\right]\right)}^{-1}\left({\left[\mathrm{Z}\right]}^{\mathrm{T}}\left[\mathrm{p}\right]\right)$$ (3)

Thus, eqs. (2) and (3) were simply a nonlinear regression of the 3-D thickness distribution as a function of Zernike polynomials. To assess the quality of the nonlinear regression, a root mean square (pRMS in eq. 4) of the difference between the measured (p) and estimated $\left(\widehat{\mathrm{p}}\right)$ at all the evaluation points (k) on the anterior surface of the cornea in the central 5 mm was computed.

$$\text{pRMS}=\sqrt{\frac{{\displaystyle {\sum }_{\mathrm{j}=1}^{\mathrm{k}}{\left(p_{\mathrm{j}}-{\widehat{p}}_{\mathrm{j}}\right)}^2}}{\mathrm{k}}}$$ (4)

To compute the PZA Zernike coefficients for the 3-D corneal thickness, the corneal tomography maps were exported from Pentacam as comma-separated value files. These files were analyzed in a custom script written in Python v2.6. Using the estimated thickness distribution, corneal volume of the central 5 mm was computed by eq. 5:

$$\text{Volume}\text{of}\text{cornea}={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{1}{\int }}\widehat{\mathrm{p}}\rho {\mathrm{R}}^2\mathrm{d}\rho \mathrm{d}\theta }}$$ (5)

In eq. 5, R = 2.5 mm. PZA Zernike coefficients and volume of the cornea were computed for the normal and keratoconus grades. Additionally, the cone location magnitude index (CLMI) of the anterior and posterior corneal surface using both axial and tangential curvature maps was computed using the algorithm described previously.^4,5

STATISTICAL ANALYSIS

All continuous indices were reported as median (95% confident interval). The following indices were analyzed: (a) K1, K2, Kmax, Kmean; (b) central corneal thickness (CCT) and minimum corneal thickness; (c) root mean square of second-order, third-order, and higher-order PZA Zernike coefficients; (d) root mean square of second-order, third-order, and higher-order corneal anterior wavefront aberration Zernike coefficients; (e) axial CLMI and tangential CLMI – axial and tangential curvature CLMI, respectively.¹¹ Only the root mean square form of Zernike coefficients was chosen for analysis to neutralize contrasting sign (negative or positive) arising from enantiomorphism of left and right eye in a subject.⁸ The curvature indices were compared among the grades using the Kruskal-Wallis nonparametric test. Curvature, PZA, and corneal anterior wavefront aberration indices were analyzed using stepwise logistic regression to establish a machine-based classification system. Receiver operating characteristic (ROC) curves of the significant indices obtained from stepwise logistic regression were used to define a probability of presence of disease index (PPI).⁵ Thus, PPI = 0 and 1 indicated a normal and keratoconic cornea, respectively. The sensitivity and specificity of the ROC curves were compared using the Z-test statistic. A P value < .05 was considered statistically significant. Sample size was estimated using Kmean and a type I/II error of .05 (P value)/0.2 (80% power). The required sample size to detect difference between the groups was only 3. All statistical analyses were performed in MedCalc v14.10.2 (MedCalc Inc, Ostend, Belgium) and G*Power 3.1.9.2 (Universitat Kiel, Kiel, Germany).

RESULTS

TABLE 1 SHOWS THE MEDIAN (95% CONFIDENCE INTERVAL) of all the variables. Only 1 eye selected randomly from each subject was included. The numbers of subjects in grades 1, 2, and 3 of keratoconus were 36, 27, and 22 eyes, respectively. The number of normal eyes was 43. The median age was 26, 26, 24.5, and 25.8 years in normal eyes and in grades 1, 2, and 3 of keratoconus, respectively. Further, the male-to-female ratio was 0.5, 1.4, 1.3, and 0.77 in normal eyes and in grades 1, 2, and 3 of keratoconus, respectively. Thus, the study sample size was adequate. K1, K2, Kmean, and Kmax were significantly different among grades (P < .0001) as well as between normal and disease (P < .0001). Figure 1 shows the frequency histogram of root mean square of second-order, third-order, and higher-order PZA Zernike coefficients in normal (Left column) and keratoconus (Right column) eyes. Distinction between normal and keratoconus eyes was evident; for example, the root mean square of second-order PZA Zernike coefficients ranged from 10 to 22 and from 10 to 80 in normal (Top left in Figure 1) and keratoconus (Top right in Figure 1) eyes, respectively. Similarly, volume of the central 5 mm cornea in normal (Left) and keratoconus (Right) eyes is shown in Figure 2. There was considerable overlap between normal and keratoconus eyes (ie, volume of cornea ranged from 9.5 mm³ to 12.5 mm³ and from 8.5 mm³ to 12.5 mm³, respectively). The pRMS was similar among normal (median = 0.282, 95% confidence interval: 0.281–0.284) and keratoconus grades (median = 0.282, 95% confidence interval: 0.281–0.283) (P = .42).

TABLE 1.

Median (95% Confidence Interval) of Clinical and Custom-Derived Indices in Normal and Keratoconus Eyes

	Normala	Keratoconusa
Age (y)	24 (22–28)	25 (24–26)
K1 (D)	42.6 (42.3–43.0)	46.9 (46.0–48.2)
K2 (D)	43.6 (43.1–44.2)	51.7 (49.8–53.6)
Kmax (D)	44.1 (43.6–44.6)	58.7 (56.6–59.6)
Kmean (D)	43.2 (42.6–43.5)	49.4 (47.2–50.4)
Minimum corneal thickness (μm)	522 (516–528)	443 (436–455)
Central corneal thickness (μm)	526 (520–536)	454 (446–467)
Root mean square of second-order PZA Zernike coefficients (μm)	15.76 (14.84–16.31)	24.24 (23.78–25.48)
Root mean square of third-order PZA Zernike coefficients (μm)	1.39 (1.09–1.67)	5.62 (4.38–6.36)
Root mean square of higher-orderb PZA Zernike coefficients (μm)	1.42 (1.17–1.97)	7.29 (4.73–9.18)
Root mean square of second-order anterior corneal wavefront Zernike coefficients (μm)	0.77 (0.67–0.89)	3.78 (3.24–4.58)
Root mean square of third-order anterior corneal wavefront Zernike coefficients (μm)	0.15 (0.13–0.20)	1.91 (1.59–2.33)
Root mean square of higher-order anterior corneal wavefront Zernike coefficients (μm)	0.47 (0.42–0.52)	0.94 (0.87–1.06)
Axial curvature CLMI of anterior surface (D)	0.53 (0.43–0.66)	7.83 (6.03–10.78)
Axial curvature CLMI of posterior surface (D)	0.15 (0.12–0.18)	1.91 (1.52–2.35)
Tangential curvature CLMI of anterior surface (D)	1.62 (1.31–1.99)	12.36 (10.55–13.50)
Tangential curvature CLMI of posterior surface (D)	0.28 (0.18–0.57)	2.75 (2.22–3.16)

CLMI = cone location magnitude index; D = diopter; K1 = flat axis keratometry; K2 = steep axis keratometry; Kmax = maximum keratometry; Kmean = mean keratometry; PZA = pachymetry Zernike analysis.

^aAll variables were statistically significant between normal and keratoconus eyes with P < .0001. A P value < .05 was considered statistically significant.

^bZernike order 4 and greater.

FIGURE 1.

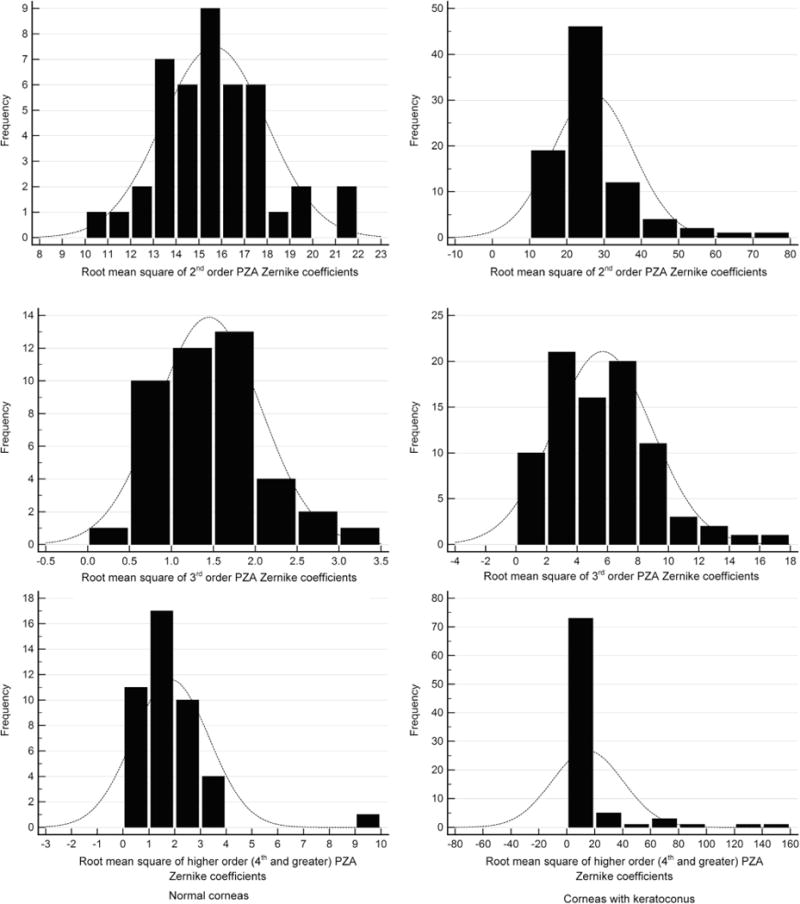
Frequency distribution of pachymetry Zernike analysis (PZA) coefficients in normal (Left column) and keratoconus (Right column) eyes. (Top left) Frequency distribution of root mean square of second-order PZA Zernike coefficients in normal eyes. (Top right) Frequency distribution of root mean square of second-order PZA Zernike coefficients in keratoconus eyes. (Middle left) Frequency distribution of root mean square of third-order PZA Zernike coefficients in normal eyes. (Middle right) Frequency distribution of root mean square of third-order PZA Zernike coefficients in keratoconus eyes. (Bottom left) Frequency distribution of root mean square of higher-order (fourth order and higher) PZA Zernike coefficients in normal eyes. (Bottom right) Frequency distribution of root mean square of higher-order PZA Zernike coefficients in keratoconus eyes.

FIGURE 2.

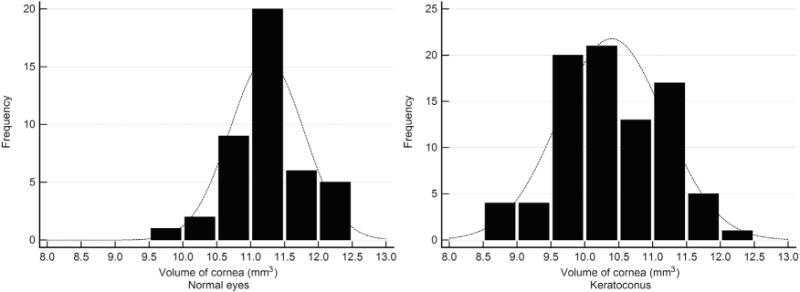
Frequency distribution of central 5 mm volume of the cornea in (Left) normal and (Right) keratoconus eyes.

Stepwise logistic regression of corneal anterior wavefront aberration Zernike coefficients yielded only root mean squares of second- and third-order coefficients as significant determinants of keratoconus (P < .0001). The logistic regression model using the corneal anterior wavefront aberration Zernike coefficients was as follows:

$$\begin{gathered} \log \left(\frac{{\text{PPI}}_{\mathrm{a}}}{1-{\text{PPI}}_{\mathrm{a}}}\right)=-15.17+2.86 \\ \times \text{second-order}\text{root}\text{mean}\text{square} \\ +42.65\times \text{third-order}\text{root}\text{mean}\text{square} \end{gathered}$$ (6)

In eq. (6), PPI_a was the probability of presence of keratoconus index based on corneal anterior wavefront aberration. The cut-off, area under the ROC curve, and sensitivity and specificity of PPI_a were 0.35, 0.998 ± 0.002, and 98.8% and 97.7%, respectively. Figure 3 shows the distribution of PPI_a among grades (Left) and the resulting ROC curves (Right), respectively. PPI_a of normal was significantly different from that of all keratoconus grades (P < .0001). PPI_a of grades 2 and 3 were similar (P > .05) but different from grade 1 (P < .0001). Stepwise logistic regression of CLMI variables yielded axial CLMI of the anterior surface and tangential CLMI of the posterior surface as significant determinants of keratoconus (P < .0001). The logistic regression model using the CLMI variables was as follows:

$$\begin{gathered} \log \left(\frac{{\text{PPI}}_{\text{CLMI}}}{1-{\text{PPI}}_{\text{CLMI}}}\right)=-7.89+11.48\times \text{axial}\text{CLMI} \\ +1.19\times \text{tangential}\text{CLMI} \end{gathered}$$ (7)

FIGURE 3.

Results of logistic regression analyses. (Left) Box-whisker plot of presence of probability of disease index (PPI) in normal eyes and eyes with grades (1, 2, 3) of keratoconus. Variables plotted include cone location magnitude indices (CLMI), corneal anterior wavefront aberration Zernike coefficients, and pachymetry Zernike analyses (PZA) Zernike coefficients from logistic regression analyses. (Right) Receiver operating characteristic curves of the same indices plotted at left.

In eq. (7), PPI_CLMI was the probability of presence of keratoconus index based on CLMI. The cut-off, area under the ROC curve, and sensitivity and specificity of PPI_a were 0.26, 0.998 ± 0.001, and 98.8% and 97.7%, respectively. Figure 3 shows the distribution of PPI_CLMI among grades (Left) and the resulting ROC curves (Right), respectively. PPI_CLMI of normal was significantly different from all keratoconus grades (P < .0001). PPI_CLMI of grades 1 and 2 were similar (P > .05) but different from grade 3 (P < .0001).

Stepwise logistic regression of PZA Zernike coefficients yielded minimum corneal thickness and root mean square of second-order and third-order coefficients as significant determinants of keratoconus (P < .0001). The logistic regression model using the PZA Zernike coefficients was as follows:

$$\begin{gathered} \log \left(\frac{{\text{PPI}}_{\mathrm{p}}}{1-{\text{PPI}}_{\mathrm{p}}}\right)=4.92+-0.03\times \text{minimum}\text{thickness} \\ +0.43\times \text{second-order}\text{root}\text{mean}\text{square} \\ +1.35\times \text{third-order}\text{root}\text{mean}\text{square} \end{gathered}$$ (8)

In eq. (8), PPI_p was the probability of presence of keratoconus index based on corneal thickness Zernike coefficient variables. The cut-off, area under the ROC curves, and sensitivity and specificity of PPI_a were 0.47, 0.980 ± 0.01, and 95.0% and 96.0%, respectively. Figure 3 shows the distribution of PPI_p among grades (Left) and the resulting ROC curves (Right), respectively. PPI_p of normal was significantly different from all keratoconus grades (P < .0001). PPI_p of grades 1, 2, and 3 were significantly different from each other (P < .0001). The ROC curve of PPI_a was similar to the ROC curve of PPI_CLMI (P = .76). Similarly, the ROC curve of PPI_p was similar to the ROC curve of PPI_a (P = .06) and of PPI_CLMI (P = .06). Table 2 shows the median (95% confidence interval) of variables that were significant in the stepwise logistic regression models.

TABLE 2.

Median (95% Confidence Interval) of Clinical and Custom-Derived Indices in Grades of Keratoconus Eyes That Were Significant in Stepwise Logistic Regression

	Grade 1	Grade 2	Grade 3
Root mean square of second-order anterior corneal wavefront Zernike coefficients (μm)	2.27 (1.65–2.98)	4.42 (3.41–4.69)	7.38 (5.0–9.33)
Root mean square of third-order anterior corneal wavefront Zernike coefficients (μm)	1.0 (0.57–1.66)	1.93 (1.59–2.62)	2.75 (2.08–3.28)
Axial curvature CLMI of posterior surface (D)	1.42 (0.96–1.94)	1.75 (1.14–2.33)	2.99 (2.49–3.75)
Tangential curvature CLMI of anterior surface (D)	8.13 (5.35–11.42)	12.43 (9.58–14.54)	18.72 (16.32–23.22)
Minimum corneal thickness (μm)	475 (459–495)	442 (434–446)	400.5 (375–428)
Root mean square of second-order PZA Zernike coefficients (μm)	20.54 (18.36-22.0)	24.70 (23.94–26.98)	35.47 (31.52–43.39)
Root mean square of third-order PZA Zernike coefficients (μm)	3.57 (2.60–5.24)	5.73 (4.36–6.20)	7.41 (6.25–8.48)

CLMI = cone location magnitude index; D = diopter; PZA = pachymetry Zernike analysis.

Volume of cornea had significantly lower diagnostic ability than curvature, PZA, and corneal anterior wavefront analyses. The cut-off, area under the ROC curve, and sensitivity and specificity were <10.68 mm³, 0.812 ± 0.037, and 63.2% and 90.9%, respectively. The ROC curve of volume of the cornea was significantly different from the PPI_a, PPI_p, and PPI_CLMI ROC curves (P < .05). Volume of cornea of normal eyes was significantly different from that of all grades (P < .0001). However, volume of cornea of grades 1 and 2 were similar (P > .05). Figure 4 shows the variation in the volume of the cornea among normal and keratoconus grades (Left), along with the ROC curve (Right). Figure 5 shows an example of measured (Top left), PZA interpolation (Top middle), and difference (Top right) between measured and PZA interpolation of 3-D thickness distribution in a normal cornea. The bottom row of Figure 5 shows an example of measured (Top left), PZA interpolation (Top middle), and difference (Top right) between measured and PZA interpolation of 3-D thickness distribution in a grade 1 keratoconus cornea. Figure 6 shows an example of measured (Top left), PZA interpolation (Top middle), and difference (Top right) between measured and PZA interpolation of 3-D thickness distribution in a grade 2 keratoconus cornea. The bottom row of Figure 6 shows an example of measured (Top left), PZA interpolation (Top middle), and difference (Top right) between measured and PZA interpolation of 3-D thickness distribution in a grade 3 keratoconus cornea. Thus, the same level of accuracy was achieved in all the corneas as the difference plots were similar in all the grades and in normal cornea (third column in Figures 5 and 6).

FIGURE 4.

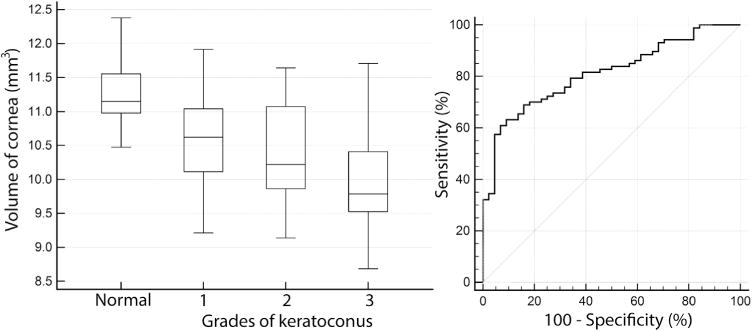
Analyses of volume of cornea as a diagnostic index to detect keratoconus. (Left) Box-whisker plot of central 5 mm volume of cornea in normal eyes and eyes with grades (1, 2, 3) of keratoconus. (Right) Receiver operating characteristic curve of central 5 mm volume of cornea plotted at left.

FIGURE 5.

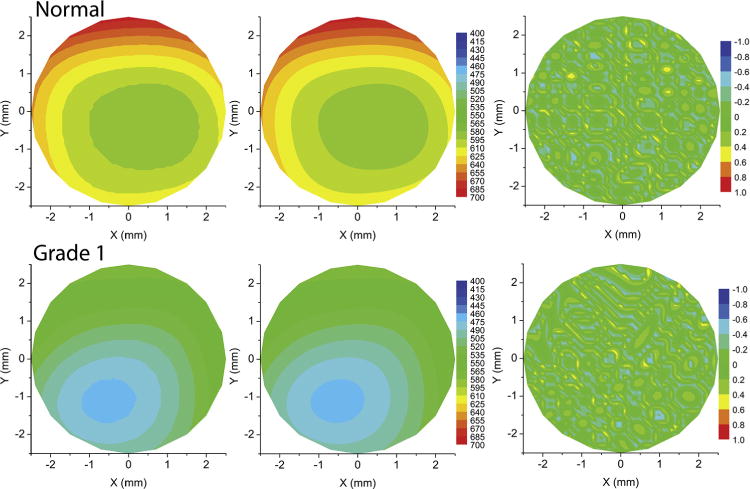
Comparison of actual and Zernike interpolated thickness in a normal and grade 1 keratoconus cornea. (Top left) Contour plot of measured thickness of a normal cornea. (Top middle) Contour plot of pachymetry Zernike analyses (PZA) interpolated thickness of the normal cornea. (Top right) Contour plot of difference between the measured and PZA interpolated thickness of the normal cornea. (Bottom left) Contour plot of measured thickness of a grade 1 keratoconus cornea. (Bottom middle) Contour plot of PZA interpolated thickness of the grade 1 keratoconus cornea. (Bottom right) Contour plot of difference between the measured and PZA interpolated thickness of the grade 1 keratoconus cornea.

FIGURE 6.

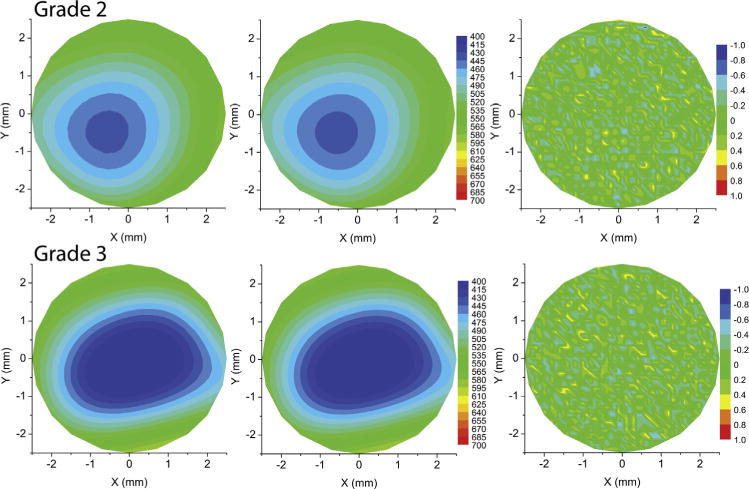
Comparison of actual and Zernike interpolated thickness in a grade 2 and grade 3 keratoconus cornea. (Top left) Contour plot of measured thickness of a grade 2 keratoconus cornea. (Top middle) Contour plot of pachymetry Zernike analyses (PZA) interpolated thickness of the grade 2 keratoconus cornea. (Top right) Contour plot of difference between the measured and PZA interpolated thickness of the grade 2 keratoconus cornea. (Bottom left) Contour plot of measured thickness of a grade 3 keratoconus cornea. (Bottom middle) Contour plot of PZA interpolated thickness of the grade 3 keratoconus cornea. (Bottom right) Contour plot of difference between the measured and PZA interpolated thickness of the grade 3 keratoconus cornea.

DISCUSSION

THERE IS CONSIDERABLE EVIDENCE THAT DIAGNOSIS OF keratoconus based on corneal topography alone may not represent the totality of the morphologic features of keratoconus.^{4–6,12,15,16} Corneal topography data have been leveraged to define indices based on several techniques such as neural network base detection³ and CLMI.^4,5 Corneal wavefront aberrations have also been shown to differ between subclinical and clinical keratoconus.^6,8,9 Corneal thickness distribution was introduced into the detection scheme later, once enabling imaging tools became available.² Several newer indices were developed to assess the rate of change of thickness in the cornea from the center to the periphery or from the cone center to the periphery to diagnose keratoconus.^12,15,17 However, the rate of change of thickness suffered from a parametric limitation, as no single mathematical formulation was available to describe the entire 3-D thickness distribution as composite indices; for example, the spatial profile along different meridians was averaged and fitted with quadratic or cubic-order polynomials to define an averaged representation of the thickness distribution with several custom indices.^16,17 Although these indices showed high sensitivity and specificity, interpretation of these indices in the context of a 3-D structure with meridional asymmetry is complex and may contribute to discordant conclusions between studies using different methods of thickness distribution analyses.^15,16

On the other hand, the concept of Zernike polynomials and its application to quantify corneal and ocular aberrations is well known. Corneal aberrations have been successfully used to classify keratoconus with high sensitivity and specificity.^6,8,9 By simply modifying eq. (1) to eq. (2), the Zernike polynomial method was adapted to describe the 3-D thickness distribution of the cornea in normal and keratoconus grades with the same level of accuracy (Figure 5). The Zernike polynomial was also able to map the Scheimpflug 3-D thickness measurement with sub-micrometer accuracy in both normal corneas and corneas with keratoconus (third column in Figures 5 and 6). The higher the magnitude of the PZA indices, the greater was the rate of change of the thickness—in other words, the greater was the severity of the disease. Further, comparisons of the ROC curves showed that PZA indices were similar to CLMI and corneal anterior wavefront aberrations with respect to sensitivity and specificity in this study. Similar to recent studies, the combination of anterior and posterior CLMI was a better diagnostic indicator of the disease than either of them used alone in this study.⁵

Since the PZA method demonstrated a high degree of spatial resolution necessary for corneal tomography,²⁰ it can be easily extended to evaluate thickness distribution in other conditions, including post–collagen cross-linking and post–refractive surgery. The present analyses can also be extended to map the thickness of the epithelium, since it can also be mapped as a function of radius and thickness.^12,13,21,22 Mapping of the 3-D epithelium thickness with Zernike polynomials may have better sensitivity and specificity than mapping of the corneal thickness, since it is more uniform in magnitude in normal corneas and more nonuniform with focal thinning in keratoconus eyes.^12,13 Thus, by combining corneal wavefront aberrations and 3-D corneal and epithelium thickness mapping with the PZA method, there may be the possibility of defining an aggregate index to complement corneal topography and biomechanics^7,10 for the diagnosis of keratoconus. The repeatability of estimation of the PZA indices needs to be established in future studies. The present method also needs to be evaluated with different methods of measurement of corneal and epithelium thickness, such as Schiempflug and optical coherence tomography.^21,22 In this study, a central analysis zone size of 5 mm was sufficient to differentiate between normal corneas and corneas with keratoconus with high sensitivity and specificity. In future studies, the diagnostic efficacy of the PZA method may also be investigated with an analysis zone size greater than 5 mm in eyes where the cone may be located closer to the limbus (eg, pellucid marginal degeneration).

The Pentacam provides several indices to assess the corneal thickness change from the center to the periphery.^2,17 These indices should be compared with the PZA method. This study included only the anterior corneal surface aberrations in the logistic regression model. Posterior corneal surface aberrations need to be assessed in future studies.⁸ However, in this study the area under the ROC curve of the logistic regression model based on corneal anterior wavefront aberrations was 0.998, leaving little room for improvement of the model by adding posterior corneal surface wavefront aberrations. Thus, the logistic regression model based on anterior corneal surface aberrations may be adequate for diagnosing keratoconus from normal eyes. In future studies, the PZA method also needs to be assessed prospectively for diagnosing subclinical keratoconus, including the clinical features (eg, Fleischer ring, Vogt striae, etc) used for diagnosing keratoconus.

Biographies

Dr Rohit Shetty is Senior Consultant, Cornea and Refractive, and Vice-Chairman at Narayana Nethralaya multi-specialty hospital in Bangalore, India. Dr Shetty earned his MD from Kempegowda Institute of Medical Sciences, Bangalore and Diplomate of National Board certification from St. Johns medical College, Bangalore. He then became Fellow of Royal College of Surgeons from University of Glasgow, UK in 2006. He has research interests in the area of cornea and refractive surgery. He has more than 40 peer-reviewed journal publications to his credit.

Dr Abhijit Sinha Roy is Chief Scientist, Imaging and Biomechanics at the Narayana Nethralaya Foundation, Bangalore, India. He received his MS and PhD degree from University of Cincinnati, USA. Subsequently, he completed his post-Doctoral fellowship from Cleveland Clinic Cole Eye institute, USA and was a research scientist at the same institute until 2013. He has broad research interests related to ocular imaging and biomechanics and has more than 30 peer-reviewed journal publications to his credit.