Abstract
The analysis of the structural organization of lipid bilayers is generally performed across the direction normal to the bilayer/water interface, whereas the surface properties of the bilayer at the interface with water are often neglected. Here, we present PackMem, a bioinformatic tool that performs a topographic analysis of the bilayer surface from various molecular dynamics simulations. PackMem unifies and rationalizes previous analyses based on a Cartesian grid. The grid allows identification of surface regions defined as lipid-packing defects where lipids are loosely packed, leading to cavities in which aliphatic carbons are exposed to the solvent, either deep inside or close to the membrane surface. Examples are provided to show that the abundance of lipid-packing defects varies according to the temperature and to the bilayer composition. Because lipid-packing defects control the adsorption of peripheral proteins with hydrophobic insertions, PackMem is instrumental for us to understand and quantify the adhesive properties of biological membranes as well as their response to mechanical perturbations such as membrane deformation.
Introduction
Lipid membranes are one of the main building blocks of cells, and as such, they have been the focus of scientific investigations for a very long time. Although their primary function is to define the boundaries of cellular compartments, their extraordinary diversity in composition, notably in lipid species (1, 2), is also decisive for numerous cellular events. Therefore, there is a growing interest in understanding the connections between lipid membrane composition and function.
One of the consequences of the remarkable lipid heterogeneity of cellular membranes is the imperfect arrangement of their lipids in the form of a bilayer. These imperfections create spots in the membrane at which the hydrophobic core of the bilayer is exposed to the surrounding aqueous environment, whether it is lumen, cytosol, or the extracellular milieu. These voids, often referred to as lipid-packing defects, are too small to lead to membrane poration, yet their size is sufficient to selectively promote the binding of peripheral proteins harboring hydrophobic or amphipathic sequences to the membrane (3, 4, 5). In the case of amphipathic helices, the lipid-packing defects tend to coalesce after initial amino acid insertion to accommodate the full hydrophobic face of the helix (6). Therefore, the nature and initial abundance of lipid-packing defects are critical for the kinetics of protein binding, but other factors are at play in the thermodynamics of adsorption (5). Nevertheless, in the few examples studied so far, there is a very good match between the abundance and depth of lipid-packing defects, as assessed by Cartesian methods, and the adsorption of model amphipathic helices (7, 8).
Due to their small size and the intrinsic fluidity of lipid bilayers, lipid-packing defects are difficult to characterize experimentally. In general, their existence and their features are deduced from indirect observations, such as the preferential partitioning of amphipathic proteins to defined subcellular organelles or artificial membranes. Computational methods such as molecular dynamics (MD) simulations, on the other hand, have proven to be a powerful tool for investigating this property with atomistic detail and in a quantitative manner (6, 9, 10).
Most of the analyses that are routinely performed on MD simulations of lipid bilayers focus on transbilayer properties (e.g., density profiles, order parameters, lateral pressure profiles, etc.) but neglect the characterization of the surface of lipid bilayers at the molecular level (8, 9, 11). This bias arises for two reasons. First, integral membrane proteins (in contrast to peripheral membrane proteins) have been the main focus of computational efforts to characterize biological membranes; see, for example, (12). Second, the analysis of surface properties requires new computational tools to quickly extract information on lipid-packing defects. Tools that are used to identify cavities in proteins such as surface-accessible area calculations provide an alternative to identify lipid-packing defects (6). However, they are very time consuming at the scale of a lipid membrane and do not provide information on the depth of the defects.
We have recently developed a computational approach to identify lipid-packing defects based on mapping of the membrane surface according to a Cartesian grid. This method has allowed us to investigate the effect of various membrane parameters on interfacial properties, including acyl chain mono- and polyunsaturation (8, 13, 14), membrane curvature (7), and the presence of conical lipids or of molecules against lipointoxication (15). The pivotal role of interfacial voids has been suggested by a number of recent investigations on disparate topics, including membrane remodeling processes such as bending, fusion, and fission (8, 16, 17, 18, 19) as well as the binding of peripheral proteins, disaccharides, and nanoparticles (8, 14, 20).
Here, we present PackMem, a greatly optimized version of this computational tool, with which interfacial voids in any MD simulation of a lipid membrane or of an equivalent interface can be readily characterized, both in size and depth, and quantified. We have improved the source code to 1) strongly reduce the computation time (a few seconds per membrane frame) and 2) make the tool versatile; i.e., adaptable to different membrane types, including different force fields (FFs) and different lipids. Considering the ever-growing interest in cellular membranes and their interactions with proteins and nanoparticles, PackMem should provide a useful tool for investigating membrane interfacial properties at the structural level to a large community of computational scientists.
Materials and Methods
Algorithm
Lipid-packing defects are defined as surface voids—that is, cavities between lipid polar heads where aliphatic atoms are accessible to external molecules. By their very nature, these voids correspond to a volume but can be also defined in terms of area upon projection on a surface. The driving idea of the algorithm is to map the membrane surface according to a grid parallel to the plane of the bilayer (Figs. 1 and 2). Looking at the grid from above, we assign a value of 0 to each grid cell in which the first atom that is vertically met is an aliphatic atom. Conversely, we assign a value of 1 to all other cells—that is, cells in which the first atom met vertically is a polar atom. In our analysis, only lipids are considered (water, ions, and any other molecules are ignored), and each leaflet is treated separately.
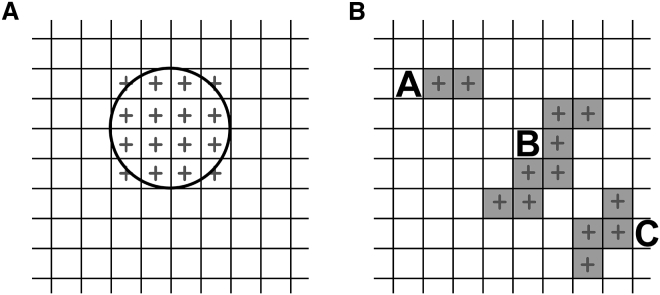
Figure 1.
Cartesian rules for atom mapping. (A) The definition of grid points overlapping with an atom is shown. The grid is represented by black lines, a random atom projected on the surface of the grid is represented as a black circle, and the overlapping grid points are marked with gray crosses. Any grid point partially or fully overlapping with the atom will be ticked by a gray cross. Each gray cross represents a grid point in which the algorithm will add 0.001 (if the atom is aliphatic and not too deep below the glycerol) or 1 (if the atom is polar) (see Algorithm description). (B) An example of clusters of elementary defects found by the connected component algorithm is shown. Once PackMem has computed the three matrices M_deep, M_shallow, and M_all (see Algorithm), each matrix will present elementary defects (represented by gray crosses), and some of them will be contiguous. The purpose of the connected component algorithm is to merge these neighboring elementary defects into clusters. Each cluster is then considered as a packing defect whose area can be computed. In general, a grid point of 1 Å2 is used. Thus, cluster A is 2 Å2, cluster B is 7 Å2, and cluster C is 4 Å2 in this example. Note that the algorithm uses an eight-connectivity (two grid points located diagonally are considered neighbors).
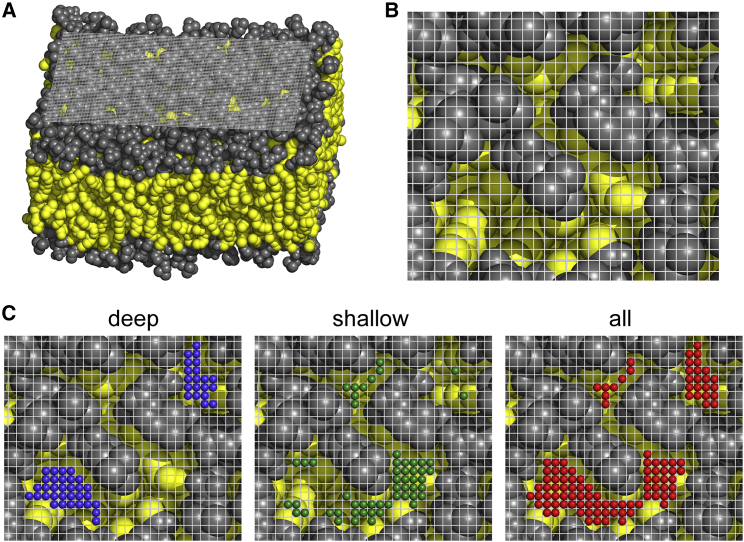
Figure 2.
Example of packing defect analysis for a pure POPC bilayer. In all panels, the light gray grid represents the matrix M at 1 Å resolution. The aliphatic atoms are colored in yellow, and the other atoms are colored in gray (including polar head and glycerol group). (A) A three-dimensional view is shown. (B) A top view is shown of a patch of upper leaflet. (C) The same view as in (B) with the coordinates of the various elementary packing defects is shown. Deep, shallow, and all packing defects are colored in blue, green, and red, respectively.
Instead of looping over all grid cells and checking the nature (polar/apolar) of the atom(s) in each cell, which is an approach that would be too computationally expensive (because it would require a double-nested loop over all grid cells and all atoms), we opted to loop over all atoms and check which grid cells overlap with each atom. In detail, the algorithm starts by constructing a grid of 1 × 1 Å resolution and follows these steps in pseudo-code:
initialize a matrix M (representing the grid) with 0
for atom in all lipid atoms of one leaflet
if atom z coordinate is below d Å of the central glycerol atom
of the same lipid
go to next iteration # the grid cells overlapping the atom
# (M[i,j]) stay at the same value
else
if atom is aliphatic
add 0.001 to the grid cells (M[i,j]) overlapping the atom
else
# the atom is polar
add 1 to the grid cells (M[i,j]) overlapping the atom
endif
endif
endfor
Note that this pseudo-code applies to the upper leaflet but can be used for the lower leaflet by reversing the z direction. The grid spacing is fixed to 1 Å, which is computationally tractable and sufficiently fine to have a precise measure of packing defects.
PackMem determines lipid-packing defects from the top of the leaflet and uses a z-value corresponding to the maximal depth level. This value is not fixed for each grid cell but is dependent on the central glycerol atom of the examined lipid plus a specific distance d. As such, the maximal depth is dependent on each lipid z-position, making PackMem adapted to moderately deformed membranes (such as bilayers undergoing undulations). The choice of the d-value defines the threshold between deep and shallow packing defects. In general, we recommend setting d = 1 Å, which is a choice that has provided a good match with experimental data in previous studies (7, 13).
The algorithm needs a list of aliphatic and nonaliphatic atoms. For common phospholipids, all carbon atoms below the ester moieties of the sn-1 and sn-2 chains are considered to be aliphatic. Another key parameter in the algorithm is the definition of overlap: for a given atom, all grid points that are within its radius are considered to be overlapping grid points (Fig. 1 A). Therefore, a list of atom radii has to be provided to the program. We recommend using the minimum of the Lennard-Jones function (corresponding to Rmin distance) for the radii, as in previous studies (7, 13).
PackMem provides the list of aliphatic atoms as well as the atom radii for many common all-atom phospholipids and sterols (ergosterol and cholesterol), but the user can easily add new lipids by including these two parameters.
At the end of the procedure, the program builds a matrix “M” filled in with numbers (n), which can be interpreted in the following way:
Grid cells for which n = 0. This value implies that no atom (polar or aliphatic) has been encountered up to d Å below the glycerol (this value is configurable; it is set at d = 1 Å by default). Therefore, these grid cells correspond to deep voids where aliphatic atoms are deeper than d Å below the central atom of glycerol and vertically accessible from the outside. These grid cells are assigned as “deep” elementary defects (see Fig. S1).
Grid cells for which 0 < n < 1. This range implies that some aliphatic atoms have been encountered between z_max_lipid (the highest z-value for each lipid) and d Å below the glycerol level. Therefore, these grid cells correspond to accessible aliphatic atoms that are not very deep within the membrane interior. These grid cells are assigned as “shallow” elementary defects (see Fig. S1).
Grid cells for which n ≥ 1. Such a value implies that a polar atom has been encountered. The corresponding cells, which represent the vast majority of the surfaces under inspection, do not represent any elementary defect.
In our algorithm, deep and shallow defects are treated separately. From the initial matrix M and the lipid-packing defect type chosen by the user, PackMem builds one of the following binary matrices. Matrix “M_deep” assigns 1 for grid cells with n = 0 and 0 for all other cells. Matrix “M_shallow” assigns 1 for grid cells with 0 < n < 1 and 0 for all other cells. Last, matrix “M_all” ignores the difference between deep and shallow defects and is built from the union of M_deep and M_shallow. We call these defects “all.” The user will choose the type of lipid-packing defect (deep, shallow, or all) to be processed with the PackMem tool. In all cases, we merge adjacent elementary defects using a connected component algorithm (21) to obtain the actual defects—that is, membrane patches made by grid cells that are contiguous and that display the same binary value (see Fig. 1 B).
At the end, our program provides the following outputs:
-
1)
A list of defects (with an identification for each one).
-
2)
The area and the approximate (x,y) position of each defect.
-
3)
Output files in Protein Data Bank (PDB) format for each leaflet containing the coordinates of all elementary defects. The PDB field “resSeq” is used to store the defect identification. Note that the z-coordinate of each elementary defect is assigned to the highest z-value of all lipid atoms. This arbitrary assignment allows the user to watch the defects and the membrane at the same time using a molecular visualization software such as visual MD (22) or PyMOL (23).
-
4)
A PDB file for each leaflet in which the B-factor column is used to list all n-values from the initial matrix M.
The area in (2) is used to determine the statistical distribution of the size of lipid-packing defects (see Statistical Analysis). Because the number of lipid-packing defects obtained from a single bilayer snapshot is too low to give robust statistics, the analysis is performed on many snapshots of MD trajectories (see below). The PDB file (3) is used to overlay the packing defects with the PDB of the bilayer (Fig. 2 C; Fig. S2). The PDB file (4) allows the user to represent the full initial matrix “M” as a two-dimensional image in which the B-factor color settings of the chosen molecular graphics program (e.g., PyMOL) are used to represent the n-value (Fig. S2).
PackMem is written in the Python language and provides specific libraries. Python version 2.6 or above is needed to execute the script PacMem.py. The source code of the PackMem tool package can be obtained from the following GitHub repository: https://github.com/rogautier/packmem. Several PDB files of membranes as well as parameters files for different FFs are provided in the archive.
The code has been optimized to strongly reduce the calculation time. This was achieved through rewriting several functions, optimizing memory resources, handling exceptions, and collecting different data formats (text or PDB). For example, the average calculation time on a regular work station for a membrane frame (250 dimyristoyl-phosphatidylcholine (DMPC) lipids with Berger force field) was 17.7 ± 0.4 s with the previous method compared to 2.68 ± 0.06 s with PackMem, corresponding to a sixfold gain in speed. Overall, the analysis of a trajectory of 300 ns corresponding to 3000 frames requires 2 hr 15 min with PackMem, as compared to 15 hr with the previous method.
In the PackMem website (http://packmem.ipmc.cnrs.fr), we provide scripts to concatenate the outputs of PackMem and to extract the π constant. We also provide a “mini-HOWTO” on how to build new input files for lipids not provided here. Last, we provide parameters files for several lipids and for three lipid FFs: united-atom as Berger (24), all-atom as Chemistry at Harvard Macromolecular Mechanics 36 (CHARMM36) (25), and coarse-grained as Martini (26). Note that for this last force field, the user should carefully select the glycerol level, which is only represented by two beads. We recommend selecting the GL2 bead (often the lowest of both). By comparing various bilayers simulated by different FFs, we observed an excellent correlation between the lipid-packing defect distribution in all-atom/united-atom FFs and in coarse-grained FFs except for shallow defects, which are overestimated in the Martini force field (7, 27).
Statistical analysis
The goal of PackMem is to provide the distribution of packing defect areas according to a given lipid composition and set of conditions (temperature, pressure, ionic strength, curvature, surface tension, etc.). Fig. 3, A and B show some examples of distribution for flat membranes under standard conditions. To obtain robust statistics for a given lipid composition and set of conditions, one typically needs to collect the packing defects from a few thousand snapshots. Such snapshots can be extracted from an individual MD trajectory of a few hundred nanoseconds (see below). After a given equilibration time (typically a few tens to hundreds of nanoseconds), all packing defects from frames separated by 100 ps of a trajectory are determined, and their area is accumulated in a single vector (for both upper and lower leaflets). From this vector, a histogram of packing defect areas is then computed. The histogram bin width has to be carefully chosen to ensure a fair comparison between different simulations. Because the grid resolution is 1 Å2, we generally recommend the use of 1 Å for the bin width.
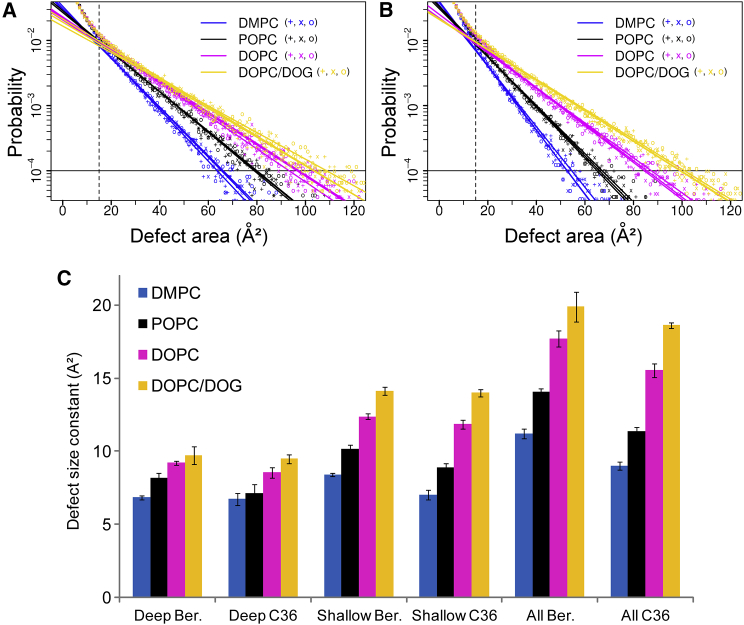
Figure 3.
Lipid-packing defect probability versus lipid-packing defect size. The plots were determined from thousands of MD snapshots for DMPC (blue), POPC (black), DOPC (magenta), and DOPC/DOG (yellow) bilayers using a Berger force field (A) or a CHARMM36 FF (B). The trajectories were divided into three parts (+, x, and o) using the block-averaging method. Straight lines are linear fits for defects larger than 15 Å2 and for probabilities of ≥10−4. The packing defect type is all (deep plus shallow). (C) Defect size constants for deep, shallow, and all packing defects are shown as determined from linear fits similar to that shown in (A) and for bilayers of the indicated composition with different FFs (Ber = Berger; C36 = CHARMM36).
The lipid-packing defect area follows an exponential distribution and can be conveniently fitted to a monoexponential decay (6, 13):
| (1) |
where p(A) is the probability of finding a lipid-packing defect with an area A, b is the pre-exponential factor (a value that we do not use any further in the analysis), D is the exponential decay in units of Å−2, and π is the packing defect constant in units of Å2.
The fit is independently performed for the three types of packing defects (deep, shallow, and all). Indeed, some membranes are more prone to forming deep lipid-packing defects, whereas others are more prone to forming shallow lipid-packing defects (8). Note that D and π are interchangeable parameters (π is the inverse of D). We prefer to report the packing defect constant π (Fig. 3), which has a more intuitive meaning, as it corresponds to a surface. The higher the π constant, the more abundant are the large lipid-packing defects. Because very small defects tend to be equally distributed whatever the conditions (e.g., lipid composition, curvature, etc.) and defects with low probability converge very slowly, we recommend performing the fit on defects larger than 15 Å2 and for probabilities of ≥10−4. Using these rules, πdeep typically ranges between 6 and 10 Å2, πshallow ranges between 7 and 15 Å2, and πall ranges between 9 and 20 Å2 for phospholipid bilayers made of a single lipid species (see Fig. 3). An example of the effect of temperature is shown in Fig. 4.
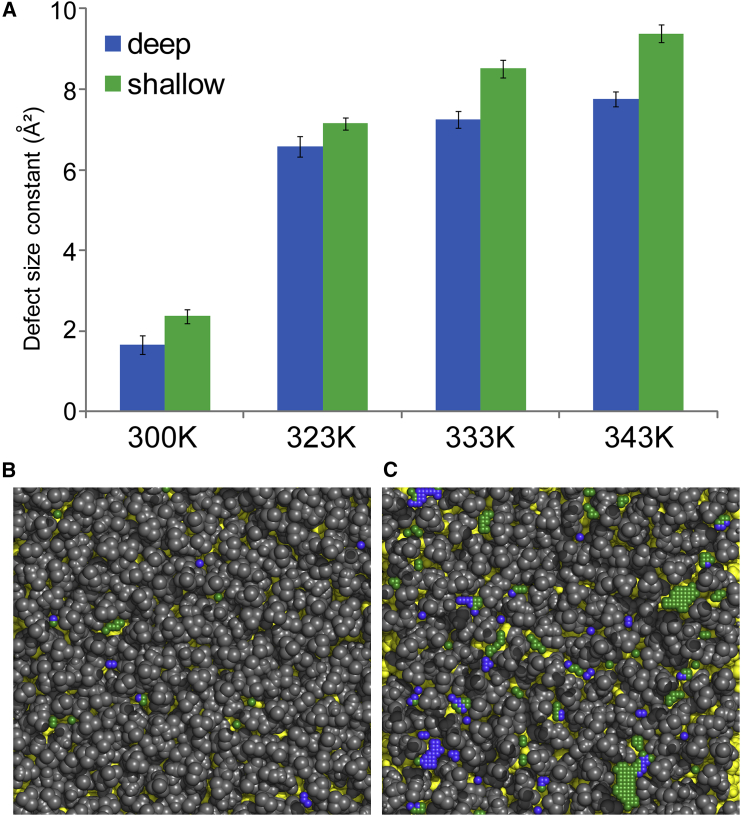
Figure 4.
Effect of temperature on lipid-packing defects. (A) A plot of lipid-packing defect size constants (deep in blue, shallow in green) for DPPC membrane simulations is shown at different temperatures. (B and C) The top view of a membrane patch of DPPC is shown at gel phase ((B); 300 K) and in the liquid disordered state ((C); 333 K) with coordinates of every elementary deep and shallow packing defect colored in blue and green, respectively. Aliphatic atoms are colored in yellow. All other lipid atoms are in gray.
In previous work (7, 13, 15, 28), the error on π was determined from the error on the linear fit of the logarithmic plot, thus considering the logarithmic value of p(A). However, we believe that an error determined by block averaging, as reported here, is more reliable, and we encourage the users to follow this procedure in the future. The trajectory is divided into three equal blocks, and the error is the SD over the three blocks. Note that each block has to be long enough (see below) to give robust results.
The statistical significance of the packing defect calculation depends on the size and length of the MD simulations. To obtain reasonable error values by block averaging (typically below 0.5–0.6 A2 for deep defects), the total number of defects found in the two leaflets over a trajectory has to be at least 105. For a given number of lipids and simulation lengths, this number varies according to the bilayer composition and external conditions. Importantly, the user has to carefully monitor deep lipid-packing defects, which are less abundant and thus much slower at converging than shallow or “all” lipid-packing defects. As a guideline, we recommend simulating membranes composed of at least 128 lipids per monolayer and performing the analysis for at least 300 ns (after proper equilibration for a few tens of nanoseconds). We also recommend a temporal resolution of one PDB file every 100 ps to ensure the absence of correlation between the defects from different frames because the lifetime of lipid-packing defects is typically <20 ps. The lifetime of lipid-packing defects was calculated from 50 ns simulations with a 1 ps sampling step. With this time step, the defects can be readily tracked from consecutive time frames so that we do not miss them by diffusion. The analysis was performed on packing defects with an average size above 15 Å2 and with a lifetime above 5 ps (Fig. S3). Using these settings, the user can obtain robust statistics on fluid bilayers using all-atom FFs. For example, a palmitoyl-oleoyl-phosphatidylcholine (POPC) bilayer of 288 lipids simulated for 300 ns (after 100 ns of equilibration) displayed a total of 174,599 deep packing defects for the whole trajectory (3000 frames, including the upper and lower leaflets).
Results and Discussion
Three examples of the use of PackMem are given here to illustrate how this tool can provide insight into membrane surface properties.
Membrane simulations using different FFs
We used PackMem to compare how two widely used FFs (namely Berger (24) and CHARMM36 (25)) describe the interfacial properties of membranes of defined composition. This is particularly timely because the choice of a particular force field is a key step in membrane simulations. Several comparisons have been recently discussed (29, 30, 31).
We used four bilayer systems (288 lipids, 144 by leaflet): pure DMPC (C14:0/C14:0), pure POPC (C16:0/C18:1), pure dioleoyl-phosphatidylcholine (DOPC) (C18:1/C18:1), and mixed DOPC:dioleoylglycerol (DOG) at a 85:15 molar ratio. The Berger model (24) in combination with the half-e double-pairlist optimized potentials for liquid simulations method (32) was used for all lipids. The parameters for DOG were validated in a previous study (9). These MD simulations were performed using the software GROMACS (Groningen Machine for Chemical Simulations) 4.6 (33) with the same parameters as those used previously (13, 14).
We used the CHARMM36 force field (FF) (25) to create the same systems using the CHARMM graphical user interface (CHARMM-GUI) tool (34) and the software GROMACS 5 (35). The DOG topology for the CHARMM36 FF was constructed in the same manner as before (9). The duration of the simulations was 400 ns, and the analysis was performed on the last 300 ns. For the MD simulations with GROMACS 5.0.6, we used the parameters recommended in CHARMM-GUI (34): we used the transferable intermolecular potential with three points water model (36), and the simulations were integrated with a 2 fs timestep. Van der Waals interactions were switched to zero between 1.0 and 1.2 nm, and particle mesh Ewald was used to evaluate electrostatic interactions. All bonds to hydrogen were constrained using the linear constraint solver algorithm (37). The v-rescale thermostat (38) was used to maintain temperature with a coupling time constant of 1.0 ps. The Parrinello-Rahman barostat (39) was used to maintain a pressure of 1.0 bar with a compressibility of 4.5 × 10−5 and a coupling time constant of 5.0 ps. The pressure was maintained semi-isotropically.
The averages and error bars were determined according to the block-averaging method (see above).
Fig. 3, A and B show the frequency of all lipid-packing defect versus lipid-packing defect size, as determined from thousands of MD snapshots using the Berger FF (Fig. 3 A) and CHARMM36 FF (Fig. 3 B) for DMPC (blue), POPC (black), DOPC (magenta), and DOPC/DOG (orange) bilayers. Fig. 3 C reports the defect size constants π in the corresponding simulations for each packing defect type (πdeep, πshallow, and πall). The two FFs show a similar trend. First, there is an increase in lipid-packing defects as a function of the number of monounsaturated C=C bonds (DPMC < POPC < DOPC). Second, DOG, a lipid with a small polar head, increases the abundance of lipid-packing defects (DOPC < DOPC/DOG). Fig. S4 shows representative snapshots of packing defects on different membranes and the gradual increase in the surface area of the defects from DMPC (A) to DOPC/DOG (D). The π values are similar for the CHARMM36 FF compared to the Berger FF but with slightly lower values for the Berger FF. The small differences observed between both FFs are probably due to the unsaturation parameters (DMPC, POPC, and DOPC with 0, 1, and 2 monounsaturations, respectively) used in both FFs and may be a consequence of the fact that CHARMM36 FF has all-atom resolution, including hydrogen atoms, whereas the Berger FF has united-atom resolution (with hydrogen atoms not explicitly included). These small differences notwithstanding, PackMem appears to be an efficient tool for determining lipid-packing properties independently of the force field. In the future, it should provide an additional approach to comparing various lipid species in terms of packing properties as well as help in the development of new lipid FFs.
Packing defects at different temperatures
As a second application, we computed lipid-packing defects in dipalmitoylphosphatidylcholine (DPPC) bilayers for varying temperatures. The DPPC simulations are based on the CHARMM36 force field (25) and the initial structure provided on the LipidBook website (40) for the gel simulation and on the CHARMM-GUI website (34) for the other simulations. The systems contained 400 DPPC molecules for the gel (or 300 K) simulation and 288 DPPC for the simulations at 323, 333, and 343 K. All simulations were carried out for 400 ns (the analysis was carried out on the last 300 ns) using GROMACS 5.0.6 (35) and with the same parameters as those used in the previous section.
As shown in Fig. 4 A, πdeep and πshallow increase with temperature as expected because of the effect of thermal motion on lipid packing. We observe a sharp difference between 300 vs. 323, 333, and 343 K. Indeed, DPPC formed a gel phase (Lβ) at 300 K, explaining the very low π constants, whereas DPPC was in the liquid disordered state (Lα) at 323, 333, and 343 K. The convergence of the π constants for the gel phase was low for deep defects because the chosen thresholds (defect area >10 Å2 and probability ≥10−4) are more adapted to the fluid phase and thus lead to poor statistics for such a system. However, it is important to keep the same thresholds when comparing different systems. Raising the temperature to 323 K results in the appearance of lipids in the liquid disordered state (Lα), which translates into a sudden jump of the π constants. This jump is larger than what is observed from 323 to 333 K or 333 to 343 K, at which the whole DPPC membrane remains in the liquid disordered state (Lα). Fig. 4, B and C show representative snapshots of both deep (blue) and shallow (green) packing defects during the simulation in the gel phase at 300 K (Fig. 4 B) and in the liquid disordered state at 333 K. We observe much fewer packing defects (in terms of number and size) for the gel phase (300 K) than the liquid disordered state at 333 K. In summary, PackMem reproduces an expected result: in the gel phase, lipids are tightly packed, resulting in very few and small packing defects.
Packing defects in membranes of complex composition
As a last application, we used PackMem to determine the distribution of lipid-packing defects in more biologically relevant membrane simulations. Klauda and co-workers have created computational models aimed at mimicking three specific organelles from the yeast Saccharomyces cerevisiae: the plasma membrane (PM), which acts as the cell’s protective barrier; the endoplasmic reticulum (ER), where many complex synthesis reactions take place; and the trans-Golgi network (TGN), an organelle in which an intense exchange of material takes place (41). These model membranes differ by the relative amounts of ergosterol, phosphatidic acid, phosphatidylcholine, phosphatidylethanolamine, phosphatidylserine, and phosphatidylinositol as well as by the acyl chain composition of the various phospholipids, as determined by experimental methods. We used PackMem to compare the packing defects in the PM, TGN, and ER simulations.
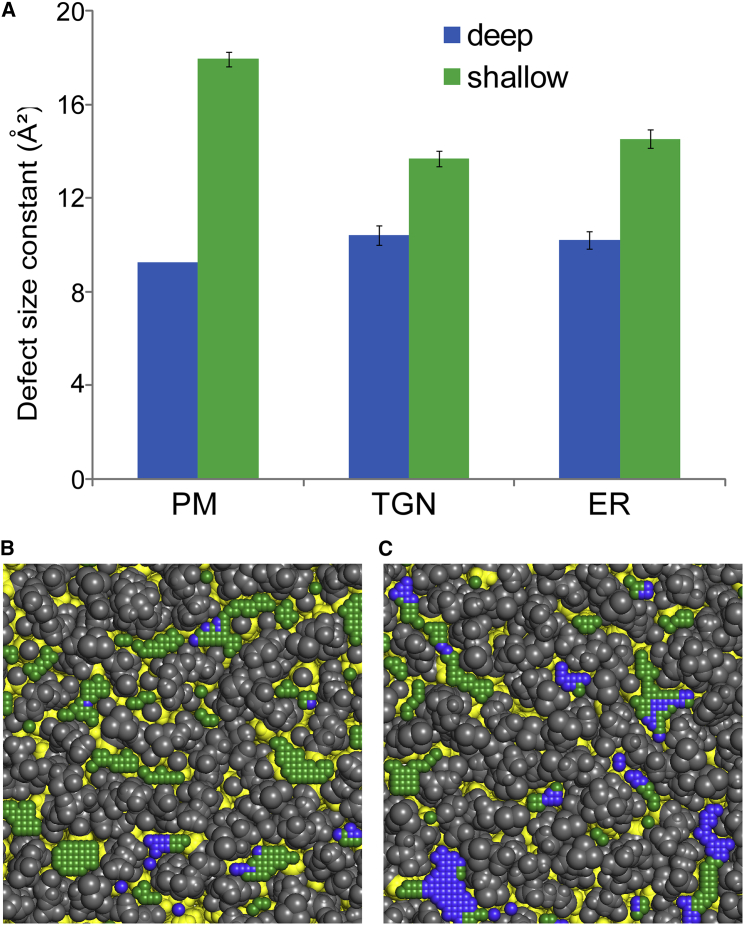
Fig. 5 A shows the values of πdeep and πshallow for the three simulations. We observe the same trend for TGN and ER membranes. πdeep is higher at the TGN/ER than at the PM, whereas an opposite trend is observed for πshallow, which is higher at the PM than at the TGN/ER. Thus, the TGN and ER are more prone to displaying deep voids in their interfacial membrane region, whereas the PM is more prone to displaying regions of shallow hydrophobic exposure. Fig. 5 B shows the mapping of both packing defects (deep and shallow in blue and green, respectively) for a frame during the PM simulation. We observe many shallow defects with large size and few deep defects with small size. The opposite is observed with the TGN frame (Fig. 5 C). Importantly, these contrasting traits fit very well with the different capacities of the two organelles to host peripheral proteins with amphipathic helices, as observed experimentally (42). Proteins with helices of the amphipathic lipid-packing sensor motif family (43, 44) insert preferentially in vesicles arising from the Golgi. In contrast, α-synuclein adsorbs at the surface of vesicles arising from the PM (8). At the molecular level, this difference is explained by the different chemistry of these two amphipathic helices. The hydrophobic face of amphipathic lipid-packing sensor motifs is made of bulky residues, which should readily insert into deep lipid-packing defects, such as those found at the TGN. The hydrophobic face of α-synuclein contains small residues, which should be more adapted to shallow lipid-packing defects, such as those found at the PM (45). Thus, PackMem is able to analyze complex membrane systems and provides unique information regarding their interfacial properties. It must be noted that these membrane simulations are not asymmetric in terms of leaflet composition. It will be interesting to use PackMem on asymmetric membranes to be closer to more realistic biological membranes.
Figure 5.
Lipid-packing defects in biological membranes. (A) A plot of packing defect size constants (deep in blue, shallow in green) in membranes of complex compositions (PM, plasma membrane; TGN, trans-Golgi network; ER, endoplasmic reticulum). (B) The top view of a PM patch is shown with the coordinates of every elementary packing defect. Blue, deep; green, shallow. (C) The same as in (B) is shown for a TGN membrane patch. The aliphatic atoms are colored in yellow, and all other lipid atoms are in gray.
Conclusions
PackMem identifies some striking differences between membranes of different shape or composition that cannot be deduced from other types of analyses. It puts the emphasis on the interfacial region and does not time-average the behavior of lipid atoms in this region but rather takes advantage of many snapshots. Given the complexity of biological membranes and their exposure to many external constraints (e.g., tension, curvature, heat, pH, etc.), PackMem should improve our understanding at the molecular level of the adaptation between membrane composition and membrane function.
Author Contributions
R.G. conceived the method. R.G. and A.B. developed the PackMem tool, and P.F.F. contributed the connected component routine. A.B. performed the packing defects at different temperatures. R.G. performed the force field comparison and the packing defects in membranes of complex composition. M.L.T. analyzed the packing defect lifetime. P.F.F. performed the different tests for the error analysis. R.G., P.F.F., S.V., and B.A. wrote the article. All authors read and commented on the article.
Acknowledgments
We thank J. Klauda and V. Monje-Galvan for sharing the yeast membrane trajectories.
This work was supported by the European Research Council (advanced grant ERC 268 888) and by the Agence Nationale de la Recherche (ANR-11-LABX-0028-01 and ANR-13-BSV2-0013). S.V. acknowledges support by the Swiss National Science Foundation (#163966). This work was performed using high-performance computing resources from Grand Equipement National de Calcul Intensif – Centre Informatique National de l’Enseignement Supérieur (grants c2016077362 and A0020707362).
Editor: Ana-Suncana Smith.
Footnotes
Four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30762-8.
Supporting Material
References
- 1.Holthuis J.C., Levine T.P. Lipid traffic: floppy drives and a superhighway. Nat. Rev. Mol. Cell Biol. 2005;6:209–220. doi: 10.1038/nrm1591. [DOI] [PubMed] [Google Scholar]
- 2.van Meer G., Voelker D.R., Feigenson G.W. Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008;9:112–124. doi: 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang L., Rajendram M., Cui Q. Ionic hydrogen bonds and lipid packing defects determine the binding orientation and insertion depth of RecA on multicomponent lipid bilayers. J. Phys. Chem. B. 2016;120:8424–8437. doi: 10.1021/acs.jpcb.6b02164. [DOI] [PubMed] [Google Scholar]
- 4.Jackson C.L., Walch L., Verbavatz J.M. Lipids and their trafficking: an integral part of cellular organization. Dev. Cell. 2016;39:139–153. doi: 10.1016/j.devcel.2016.09.030. [DOI] [PubMed] [Google Scholar]
- 5.Hatzakis N.S., Bhatia V.K., Stamou D. How curved membranes recruit amphipathic helices and protein anchoring motifs. Nat. Chem. Biol. 2009;5:835–841. doi: 10.1038/nchembio.213. [DOI] [PubMed] [Google Scholar]
- 6.Cui H., Lyman E., Voth G.A. Mechanism of membrane curvature sensing by amphipathic helix containing proteins. Biophys. J. 2011;100:1271–1279. doi: 10.1016/j.bpj.2011.01.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vanni S., Hirose H., Gautier R. A sub-nanometre view of how membrane curvature and composition modulate lipid packing and protein recruitment. Nat. Commun. 2014;5:4916. doi: 10.1038/ncomms5916. [DOI] [PubMed] [Google Scholar]
- 8.Pinot M., Vanni S., Barelli H. Lipid cell biology. Polyunsaturated phospholipids facilitate membrane deformation and fission by endocytic proteins. Science. 2014;345:693–697. doi: 10.1126/science.1255288. [DOI] [PubMed] [Google Scholar]
- 9.González-Rubio P., Gautier R., Fuchs P.F. Amphipathic-lipid-packing-sensor interactions with lipids assessed by atomistic molecular dynamics. Biochim. Biophys. Acta. 2011;1808:2119–2127. doi: 10.1016/j.bbamem.2011.05.006. [DOI] [PubMed] [Google Scholar]
- 10.Andersson M., Ulmschneider J.P., White S.H. Conformational states of melittin at a bilayer interface. Biophys. J. 2013;104:L12–L14. doi: 10.1016/j.bpj.2013.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bera I., Klauda J.B. Molecular simulations of mixed lipid bilayers with sphingomyelin, glycerophospholipids, and cholesterol. J. Phys. Chem. B. 2017;121:5197–5208. doi: 10.1021/acs.jpcb.7b00359. [DOI] [PubMed] [Google Scholar]
- 12.Mesbahi-Vasey S., Veras L., Kurnikova M.G. All atom NMDA receptor transmembrane domain model development and simulations in lipid bilayers and water. PLoS One. 2017;12:e0177686. doi: 10.1371/journal.pone.0177686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vamparys L., Gautier R., Fuchs P.F. Conical lipids in flat bilayers induce packing defects similar to that induced by positive curvature. Biophys. J. 2013;104:585–593. doi: 10.1016/j.bpj.2012.11.3836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vanni S., Vamparys L., Antonny B. Amphipathic lipid packing sensor motifs: probing bilayer defects with hydrophobic residues. Biophys. J. 2013;104:575–584. doi: 10.1016/j.bpj.2012.11.3837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ferru-Clément R., Spanova M., Ferreira T. Targeting surface voids to counter membrane disorders in lipointoxication-related diseases. J. Cell Sci. 2016;129:2368–2381. doi: 10.1242/jcs.183590. [DOI] [PubMed] [Google Scholar]
- 16.Erkut C., Penkov S., Kurzchalia T.V. Trehalose renders the dauer larva of Caenorhabditis elegans resistant to extreme desiccation. Curr. Biol. 2011;21:1331–1336. doi: 10.1016/j.cub.2011.06.064. [DOI] [PubMed] [Google Scholar]
- 17.Simunovic M., Manneville J.B., Callan-Jones A. Friction mediates scission of tubular membranes scaffolded by BAR proteins. Cell. 2017;170:172–184.e11. doi: 10.1016/j.cell.2017.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ben M’barek K., Ajjaji D., Thiam A.R. ER membrane phospholipids and surface tension control cellular lipid droplet formation. Dev. Cell. 2017;41:591–604.e7. doi: 10.1016/j.devcel.2017.05.012. [DOI] [PubMed] [Google Scholar]
- 19.Read J., Clancy E.K., Duncan R. Reovirus FAST proteins drive pore formation and syncytiogenesis using a novel helix-loop-helix fusion-inducing lipid packing sensor. PLoS Pathog. 2015;11:e1004962. doi: 10.1371/journal.ppat.1004962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Magdeleine M., Gautier R., Antonny B. A filter at the entrance of the Golgi that selects vesicles according to size and bulk lipid composition. eLife. 2016;5 doi: 10.7554/eLife.16988. Published online July 26, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pfaltz J.L. Sequential operations in digital picture processing. J. Assoc. Comput. Mach. 1966;13:471–494. [Google Scholar]
- 22.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
- 23.Schrödinger, LLC. 2010. The PyMOL Molecular Graphics System, Version 1.3r1.
- 24.Berger O., Edholm O., Jähnig F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997;72:2002–2013. doi: 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Klauda J.B., Venable R.M., Pastor R.W. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Marrink S.J., Risselada H.J., de Vries A.H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 27.Bacle A., Gautier R., Vanni S. Interdigitation between triglycerides and lipids modulates surface properties of lipid droplets. Biophys. J. 2017;112:1417–1430. doi: 10.1016/j.bpj.2017.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Garten M., Prévost C., Vanni S. Methyl-branched lipids promote the membrane adsorption of α-synuclein by enhancing shallow lipid-packing defects. Phys. Chem. Chem. Phys. 2015;17:15589–15597. doi: 10.1039/c5cp00244c. [DOI] [PubMed] [Google Scholar]
- 29.Piggot T.J., Piñeiro Á., Khalid S. Molecular dynamics simulations of phosphatidylcholine membranes: a comparative force field study. J. Chem. Theory Comput. 2012;8:4593–4609. doi: 10.1021/ct3003157. [DOI] [PubMed] [Google Scholar]
- 30.Sandoval-Perez A., Pluhackova K., Böckmann R.A. Critical comparison of biomembrane force fields: protein-lipid interactions at the membrane interface. J. Chem. Theory Comput. 2017;13:2310–2321. doi: 10.1021/acs.jctc.7b00001. [DOI] [PubMed] [Google Scholar]
- 31.Pluhackova K., Kirsch S.A., Böckmann R.A. A critical comparison of biomembrane force fields: structure and dynamics of model DMPC, POPC, and POPE bilayers. J. Phys. Chem. B. 2016;120:3888–3903. doi: 10.1021/acs.jpcb.6b01870. [DOI] [PubMed] [Google Scholar]
- 32.Jorgensen W.L., Maxwell D.S., Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 33.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 34.Lee J., Cheng X., Im W. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2016;12:405–413. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Abraham M.J., Murtola T. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. [Google Scholar]
- 36.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 37.Hess B. P-LINCS: a parallel linear constraint solver for molecular simulation. J. Chem. Theory Comput. 2008;4:116–122. doi: 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- 38.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 39.Parrinello M., Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. [Google Scholar]
- 40.Domański J., Stansfeld P.J., Beckstein O. Lipidbook: a public repository for force-field parameters used in membrane simulations. J. Membr. Biol. 2010;236:255–258. doi: 10.1007/s00232-010-9296-8. [DOI] [PubMed] [Google Scholar]
- 41.Monje-Galvan V., Klauda J.B. Modeling yeast organelle membranes and how lipid diversity influences bilayer properties. Biochemistry. 2015;54:6852–6861. doi: 10.1021/acs.biochem.5b00718. [DOI] [PubMed] [Google Scholar]
- 42.Pranke I.M., Morello V., Jackson C.L. α-Synuclein and ALPS motifs are membrane curvature sensors whose contrasting chemistry mediates selective vesicle binding. J. Cell Biol. 2011;194:89–103. doi: 10.1083/jcb.201011118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bigay J., Gounon P., Antonny B. Lipid packing sensed by ArfGAP1 couples COPI coat disassembly to membrane bilayer curvature. Nature. 2003;426:563–566. doi: 10.1038/nature02108. [DOI] [PubMed] [Google Scholar]
- 44.Drin G., Casella J.F., Antonny B. A general amphipathic alpha-helical motif for sensing membrane curvature. Nat. Struct. Mol. Biol. 2007;14:138–146. doi: 10.1038/nsmb1194. [DOI] [PubMed] [Google Scholar]
- 45.Bigay J., Antonny B. Curvature, lipid packing, and electrostatics of membrane organelles: defining cellular territories in determining specificity. Dev. Cell. 2012;23:886–895. doi: 10.1016/j.devcel.2012.10.009. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.