Cost and conflict in animal signals and human language

Abstract

The “costly signaling” hypothesis proposes that animal signals are kept honest by appropriate signal costs. We show that to the contrary, signal cost is unnecessary for honest signaling even when interests conflict. We illustrate this principle by constructing examples of cost-free signaling equilibria for the two paradigmatic signaling games of Grafen (1990) and Godfray (1991). Our findings may explain why some animal signals use cost to ensure honesty whereas others do not and suggest that empirical tests of the signaling hypothesis should focus not on equilibrium cost but, rather, on the cost of deviation from equilibrium. We use these results to apply costly signaling theory to the low-cost signals that make up human language. Recent game theoretic models have shown that several key features of language could plausibly arise and be maintained by natural selection when individuals have coincident interests. In real societies, however, individuals do not have fully coincident interests. We show that coincident interests are not a prerequisite for linguistic communication, and find that many of the results derived previously can be expected also under more realistic models of society.

How do organisms communicate honestly despite the temptation to deceive one another when interests conflict? Over the past quarter-century, the “costly signaling” hypothesis—that signal honesty can be ensured by appropriate signal cost—has emerged as the dominant explanation for this puzzle. First proposed by Zahavi (1, 2) to explain elaborate ornaments such as the peacock's tail, this hypothesis was later formalized by Grafen (3) and Godfray (4). A proliferation of theoretical models (5–15) and empirical tests (reviewed in refs. 16–19) has ensued.

The main theoretical results in signaling theory predict that high signal costs will be observed when communication occurs between individuals with conflicting interests. Empirical studies are more equivocal, with costs often but not always detected (see ref. 20). In Part I of this paper, we show that, although the cost of out-of-equilibrium signals plays an important role in stabilizing honest signaling, the signals actually used at equilibrium do not have to be costly. Therefore, even unrelated individuals with conflicting interests can communicate honestly by using cost-free or very cheap signals. Contrary to the “handicap principle,” waste is not required to ensure honest signals. We illustrate this principle by constructing examples of cost-free signaling equilibria for the two paradigmatic signaling games of Grafen (3) and Godfray (4). Although these results are of central importance to signaling theory, readers who are more interested in the relevance to human language may wish to skim the mathematical details of this section on a first reading. This paper is structured so that its two parts can be read independently or in sequence.

Although human language is commonly used among individuals with conflicting interests, it usually involves very cheap signals. Consequently, signaling theory has had little to contribute to the study of linguistic communication. In Part II of this paper, we use the results of Part I to forge an explicit connection between signaling theory and language. Recently, both within the field of linguistics and more broadly, there has been great interest and progress in studying the evolution and structure of human language by formulating linguistic interactions as evolutionary games (21–29). These studies have shown that several important properties of language can plausibly arise and be maintained by natural selection when individuals have coincident interests (30). However, human language almost certainly did not evolve in an Eden of coincident interests (31). We imagine that conflicting interests would have been frequent during the origin of language (as they are now), and that the problem of honesty would have exerted a continuing influence on the development of language. We ask the following: Can language evolve and be maintained under common biological scenarios of noncoincident interest? We find that coincident interests are not a prerequisite for language and explore the structural features that are to be expected of the languages used in societies with noncoincident interests. Many of the results derived previously also arise under these more realistic models of society.

Part I: Honesty Does Not Require Waste

A signal can be defined as a behavior or phenotype produced by one individual (the signaler) that serves to influence the behavior of a second individual (the signal receiver) by transmitting information. As discussed by Maynard Smith and Harper (32)—who consider in detail the terms and definitions associated with signaling—this definition highlights two important aspects of signaling. First, signals carry information from a signaler to a receiver. Second, signals influence receiver behavior. Thus, communication can be viewed as a game theoretic process. A signaler, who has private information about some aspect of the world, selects a signal to send to a signal receiver; the receiver, in response, then selects an action to take. The payoffs depend on the choices of both individuals.

Communication will be stable, at least in the short-term, when the signaler and receiver pursue strategies (choice of signal given the private information, and choice of response given the signal) that together comprise a signaling equilibrium. Given a set of possible signals, a signaling equilibrium is simply a pair of signaler and receiver strategies such that neither party gains from unilateral change in strategy (20). At a signaling equilibrium, signalers benefit from signaling and receivers benefit from heeding their signals (32, 33). From this principle, it follows that signalers, in some sense (34), must be conveying reliable information about the world; on average, the incentive to the signaler to misrepresent the state of the world must be outweighed by the incentive not to do so.

But why would that result occur? When the interests of signaler and signal receiver coincide, the signaler has no incentive to deceive the receiver. But when interests conflict, the signaler will have an incentive to misrepresent the world. For the signals to be reliable, this incentive must be balanced by a countervailing incentive against misrepresentation. Much of signaling theory focuses on understanding the source and form of this countervailing incentive. The critical idea behind Zahavi's original formulation of the handicap principle (1, 2) is that the necessary incentives come from the costs of signaling. When signaling is costly—and differentially costly according to the meaning and/or validity of the message—signalers can be relied upon to report aspects of their condition or of the environment (3–5, 8, 9).

Formally, this scenario is commonly described along the following lines: a signaler's condition, or quality, is q. She knows the value of q, but the receiver does not. The signaler selects a signal s = T(q) and pays a display cost d = D(q,s). Upon receiving a signal s, the receiver takes an action r = R(s). The payoff to the signaler, H(q,r), depends on her quality and the action taken by the receiver. The payoff to the receiver, G(q,r), depends on the same parameters. The “strategies” in this game are simply the signaler's choice of what signal to send, given by the function T(q), and the receiver's choice of how to respond to each signal, given by the function R(s). At equilibrium, a signaler of quality q will not benefit from sending a signal different from T(q) while paying the appropriate cost. The receiver will not benefit by responding to a signal s with an action other than R(s).

Two types of signaling equilibrium have been described in the literature: In a separating equilibrium, signalers of different qualities always send distinct signals, and thus the receiver can infer perfectly the quality of the signaler. In a semipooling equilibrium, signalers of different qualities might send identical signals, and thus the receiver cannot infer completely the signaler quality from the signal (35). It has been shown already that certain semipooling equilibria can be arbitrarily cheap (20), allowing inexpensive transfer of limited information. Signals that merely facilitate verification of physical traits (e.g., striped coloration emphasizing body size) need not involve production costs either (36–38). Their only costs come from the information that they reveal (39). However, separating equilibria lie at the heart of costly signaling theory (3, 4), and these equilibria were thought to require substantial “strategic” cost. Here, we show that separating equilibria can be arbitrarily cheap. This result obtains because signaling equilibria are stabilized by the costs of out-of-equilibrium signals, not by the costs of equilibrium signals; as long as the former are sufficiently costly, the latter can be virtually zero for all signalers. Therefore, signal cost is never necessary at equilibrium; contrary to the primary tenet of costly signaling theory (1–4, 12, 40, 41), waste is not necessary.

A simple toy model illustrates the basic reason behind this claim. As above, signalers communicate quality to signal receivers; with all else held equal, signalers benefit from being seen as higher quality, whereas receivers benefit from accurately assessing signalers. In our toy model, the signal-cost function D(q,s) used has the following structure:

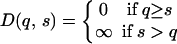Here, it is cost-free to signal up to true quality but lethal to signal above it. At equilibrium, in this signaling game, all signalers will signal their true quality with zero cost. Of course, this game is just a toy model and display costs are unlikely to take this form in the real world, but such a drastic cost function is unnecessary for cheap signaling. Indeed, separating equilibria exist in which equilibrium signals are arbitrarily cheap, despite display costs that are continuous and continuously differentiable with respect to both quality and signal intensity.

To prove this formally, consider a basic communication scenario, parameterized as the signaling game described above. Given the continuously differentiable payoffs for signaler and receiver, H(q,r) and G(q,r), we ask whether there exists a continuously differentiable cost function D(q,s) for which the equilibrium signals will be completely honest and yet cheap or free. At a separating equilibrium, receivers can infer precisely the condition of any signaler (3, 14); therefore, we shall identify signals with the qualities that they advertise. The receiver will have some optimal response r = z_r(q) to a signaler in condition q. By definition, at a separating equilibrium, a signaler with quality q will advertise quality q, and will get the highest payoff from this choice of signal. To standardize the meaning of “cost”, we define the cost to be 0 for sending some arbitrary signal q₀, no matter what the actual quality q of the signaler is. This value can be seen as the cost of not signaling (42). All other signals have a nonnegative cost. Then the net payoff to the signaler

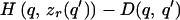will have a maximum at q′ = q, i.e., for any alternative signal q′ ≠ q,

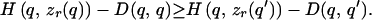1

Because H and D are continuously differentiable, this inequality implies that

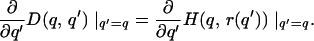2

Because D(q,q₀) = 0 by definition, it follows from basic calculus that

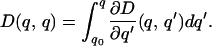3

We can choose D such that for all q, equation (2) is met but

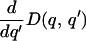is arbitrarily small for q′ < z_r(q). Therefore, we can construct a smooth cost function D with arbitrarily small signal costs at equilibrium.

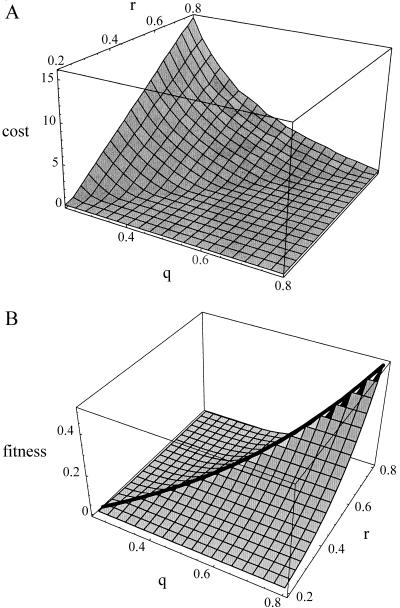
Fig. 1 shows a cost function that ensures a very low cost for a signaling scenario, as in Grafen's model of signaling to prospective mates. The sharp nick near the signaling optimum is characteristic of cost functions that allow low-cost signaling at equilibrium. Indeed, one can show that the second derivative of the cost function imposes a lower bound on the signal cost at equilibrium. In the Appendix, we derive this signaling equilibrium and an analogous almost-free signaling equilibrium for Godfray's model of parent–offspring communication (4).

Figure 1.

Cheap (cost < 0.01) signaling in Grafen's model: signal cost (A) and signaler's net fitness when eliciting response r in state q (B). Receiver's equilibrium response z_r(q) is shown by the solid line in B.

If signals can be arbitrarily cheap at equilibrium—that is, if there is no a priori mathematical reason that signal honesty requires signal cost—should we expect that signal costs in nature will always be very close to zero? Our answer is: not necessarily. Cost-free signaling will not be stable unless a specific relationship obtains between signaler quality and the cost of signal production, i.e., unless the cost function D(q,s) takes a specific form. In some cases, it may be reasonable to assume constraints on the form of the signal-cost function. In the begging baby birds scenario modeled by Godfray, for example, signal cost could come largely from predation risk and thus be independent of signaler condition (as Godfray quite reasonably assumes; ref. 4). Under such circumstances, the models do predict that honest signals will be costly at equilibrium.

By contrast, cheap or cost-free signaling can occur when there is great flexibility in the relation D of cost to signal. This flexibility is essential to impose high costs on signalers who send “wrong” signals, while allowing very low costs for those sending the “right” signals. The more abruptly a cost function changes with small changes in the signal sent, the higher will be its curvature and the lower will be signal costs at equilibrium. Equilibrium signal cost will depend critically on the ability of signaling systems to “find” cost functions for which costs change abruptly with signal intensity around equilibrium.

Part II: The Evolution of Language

Now, we will lead into human language with a pair of examples based on peacock and sparrow-signaling behavior. Our aim is neither to provide realistic models of peacock and sparrow signals nor to reconstruct a hypothetical chain of steps by which language evolved; we focus on these idealized systems because of their utility as models to help us see the connections between costly signaling theory and human language.

The Peacock and the Sparrow.

The peacock's elaborate tail is perhaps the most commonly invoked example of costly signaling. This trait is typically explained as follows: the male peafowl expends a great deal of energy and effort to produce, maintain, and live with a flamboyant tail. Female peafowl preferentially mate with males who have spectacular tails, because a large tail is a reliable indicator of high genetic quality. Peacocks weigh the marginal viability costs of increasing tail size against the marginal gains in mating success from doing so to select an optimal tail length; higher quality peacocks end up “choosing” to produce longer tails, and thus quality is honestly conveyed (3, 12).

Peacocks pay signal costs that are direct consequences of the effort involved in signal expression. Signal cost is intertwined with physiology, and there will almost invariably be constraints on the shape of the signal cost function. As a consequence, there will almost inevitably be costs associated with signaling at equilibrium.

Just as peacocks' tails are the paradigmatic costly signals, the dominance badges of passerines—for example, the black “bibs” of male sparrows—serve as the classic (if somewhat contentious) example of conventional signaling (7, 43, 44). In these signaling systems, relatively minor and inconspicuous variations in plumage, such as variable throat bibs or forehead patches, serve as reliable indicators of aggressiveness, fighting ability, or other correlates of resource-holding potential (RHP). Birds with “dominant” badges are more likely to win agonistic interactions, whereas “cheats”—birds that exaggerate their own RHP in their choice of badge—are attacked and punished by conspecifics (43, 45–48). The actual production costs of these signals are very low. The cost on the producer's side is only that needed to convey the message—the efficacy cost (7). Any strategically necessary costs required to keep signaling honest arise as a consequence of the receivers' actions (11, 32).

Because both peacocks and sparrows signal some aspect of quality to receivers with noncoincident interests, why do peacocks use costly signals, whereas sparrows use free signals? The answer lies not in the meanings of the signals but rather in the relative ability of receivers to verify the integrity of messages. In our peacock example, the advertised trait—some form of genetic quality—only manifests itself stochastically and far in the future, in terms of viability and fecundity of the offspring. A signal receiver cannot verify the signal within the time frame of her decision, nor can she identify and punish deception should it occur. Consequently, the costs to deception cannot be imposed through the social interaction. Instead, the mechanism of signal reliability must involve differential costs intrinsic to signal production. Costly signals such as the peacock's tail may not be as efficient as cost-free signals, but peafowl have no alternative.

In the sparrow example, by contrast, the signal serves primarily as a shortcut to facilitate assessment of RHP. Receivers can verify the signal with relative ease, should they choose to do so. All they have to do is approach more closely or, at worst, start a fight. Because the signals are so easily verified (and because receivers punish severely signalers with misleading badges), production costs are not needed to ensure reliable signaling. The comparison between this pair of examples leads us to the following prediction: “conventional” signals will be used when communicating about (i) coincident interests or (ii) verifiable aspects of conflicting interests; “costly” signals will be used otherwise.

Precision and Cost in Conventional Signaling.

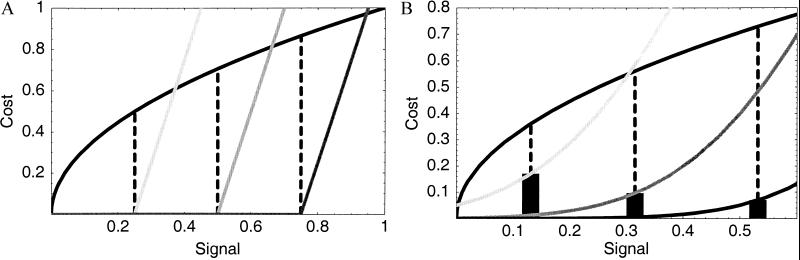
We have shown that to keep equilibrium signal costs low, cost functions must rise sharply around the signaling equilibrium. This finding raises a new problem for socially imposed costs. When the costs are imposed socially, the signaler doesn't pay the costs associated with the signal level that he chose: rather, he pays the costs associated with the signal level that the receiver thinks that he chose. A misunderstanding can be very costly if the signal-cost function rises sharply near the equilibrium signal level. For example, if sparrows commonly “misread” the status badges of conspecifics, costly fights will be common even if all badges are honest. If signalers can reduce the chance of signaling error or perceptual error, they can lower the costs at equilibrium. When costs are imposed socially, selection will favor precise and accurate signals to reduce costly errors. Fig. 2 illustrates this principle.

Figure 2.

Imprecision increases signaling costs in conventional signaling systems. Upper black curve, benefit to signaler of being perceived as quality x; lower gray curves, cost of signaling quality x to signalers of low quality (light gray), medium quality (gray), and high quality (dark gray); dashed lines, equilibrium signals. (A) No perceptual error. Receivers punish signalers who signal above true quality, generating kinked cost functions. If receivers make no mistakes, signalers will signal their true qualities and equilibrium signal costs will be zero. (B) Perceptual error (here, normally distributed with μ = 0, σ = 0.2) “rounds out” the kinked cost functions, as receivers sometimes mistakenly punish honest signalers. This event decreases the curvature of the signal-cost function and raises equilibrium signal costs (shown as black bars).

Evolutionary Stability.

Socially imposed signal costs also may be more resistant to breakdown over evolutionary time. When signal costs are intrinsic to signal production, natural selection actively works to destabilize a signaling system. Signalers are selected to find cheaper ways of sending equivalent signals; over time, they are likely to acquire evolutionary innovations that reduce signaling costs. Although the evolutionary dynamics that follow such an innovation can be extremely complicated, a series of innovations could plausibly destabilize a signaling system (16, 49).

When costs arise through the receiver response, signal costs are no longer under the evolutionary control of those who pay them. The only individuals able to reduce signal costs (the receivers) are unlikely to have an evolutionary incentive to do so. Natural selection will not necessarily favor innovations that reduce signal costs. As a consequence, the destabilizing pressure of selection for reduced signal costs will not threaten equilibrium stability.

Human Language.

Linguistic communication is often modeled as an evolutionary game played among individuals with coincident interests. This approach addresses many important features of communication, but defers some of the associated strategic considerations. What role have strategic issues played in shaping language? Must we assume coincident interests to explain the evolutionary stability of language? Here, we apply the insights obtained from the peacock and sparrow to understand how the features of human language can be evolutionarily stable despite conflicting interests among the communicating parties.

Arbitrary Signal–Meaning Association.

In human language, the relationship between signal and meaning is largely arbitrary (50). Although the capacity for speech may itself be costly, once language has been acquired the production costs vary little among alternative signals. In models of costly signaling, this is not the case; in these models, noncoincident interests require that signal meaning be related to the signal's production costs (35). This discrepancy has led some authors to dismiss Zahavian handicap arguments as not pertinent to human language (51).

Our first challenge, in applying costly signaling theory to human language, is to explain how arbitrary meanings can be assigned to signals in a stable way, despite conflicts of interest and without signal cost. The sparrow analogy, taken alongside the results from Part I, suggests a three-step explanation: (i) reliable signaling can be maintained by a Zahavian mechanism without signal cost at equilibrium, so long as the cost function takes the appropriate form; (ii) social enforcement of signal costs may be particularly likely to give rise to this form, where the cost of the signal is exquisitely sensitive to the quality signalled around the point of true quality; and (iii) when costs arise through social enforcement, the signal–meaning association can be arbitrary, so long as it is properly understood by the signal receiver.

Conversely, precise linguistic communication with socially imposed sanctions against liars provides one example of how cost functions can take on forms similar to those in Figs. 1A and 3A. Social punishment of liars may often impose cost functions that rise sharply on one side of the equilibrium “honest” signal, whereas they remain essentially flat on the other. Receivers can generally distinguish between misleading signals that are, and are not, helpful to the signaler and/or harmful to themselves; if a signal is misleading but not harmful, it probably will not merit punishment. Suppose, for example, that a used car dealer is trying to sell me a car that gets 20 miles per gallon. If the dealer tells me that the car gets 30 miles per gallon and I later discover the truth, I will probably be angry. I may even take some sort of retaliatory action, be it a lawsuit, a fist-fight, or a verbal smearing of the dealer's reputation. If, instead, the dealer tells me that the car gets 10 miles per gallon, and I later discover the truth, I am unlikely to be angry. Nor am I likely to punish the dealer in any way even though, strictly speaking, the initial claim is every bit as false as if the dealer had claimed 30 miles per gallon. What matters more is the implication of a claim rather than honesty per se.

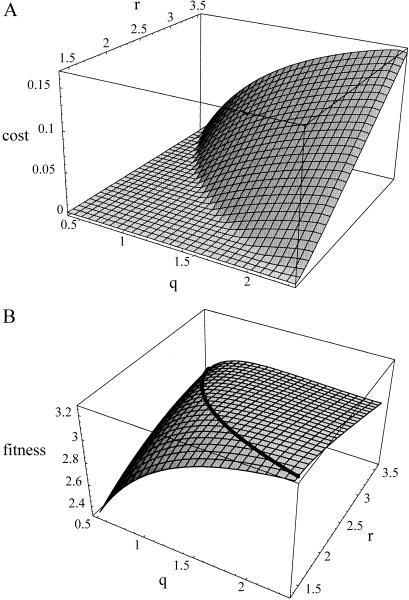
Figure 3.

Cheap (cost < 0.001) signaling in Godfray's model. (A) Signal cost and (B) signaler's net fitness when eliciting response r in state q. The receiver's equilibrium response z_r(q) is shown by the solid line in B and, indeed, optimizes signaler fitness.

Language may also facilitate social enforcement by allowing the referential communication necessary for sharing information about others' reliability. Among humans, individual reputations as liars or as good sources of information may provide important incentives for useful communication and against deception (52). Although reputations can emerge even without communal “discussion” of an individual's reliability (53–55), language facilitates the spread of reputations by allowing individuals to share information about others' reliability.

These comments constitute merely a sketch of the argument, and further work is needed. A full “demonstration of possibility” would include (i) a formal model by which signal and meaning take on arbitrary associations and are maintained stably by social enforcement, and (ii) a formal explanation of why the particular acts of social enforcement needed to stabilize the signaling system are themselves evolutionarily stable (56–58).

Selection for Precision and Accuracy.

Language—with its assembly of phonemes into words and words into sentences—facilitates precise, accurate, high-volume communication. This fact is a good thing, at least when interests coincide. When interests diverge, reductions in precision can be favored. A switch from separating to semipooling equilibria can reduce drastically signal costs, leaving all parties better off despite the reduction in the precision of the information conveyed (35). Even reductions in accuracy can sometimes be favored (35).

Nevertheless, we expect that in the course of language evolution, increased communication efficiency will be favored even when interests diverge. To the degree that communication is beneficial to both parties, the advantages to improved communication that are described by Nowak et al. (26–29) will persist. Moreover, language favors two distinct types of precision. First, when costs are imposed by signal receivers, or when the constraints on cost functions are otherwise relaxed, more information can be shared without increased costs by shifting from relatively uninformative semipooling equilibria to more informative alternatives. Second, when costs are socially imposed, misunderstandings become more costly. These results will select for the more careful and redundant signals that become possible through linguistic communication.

Language Requires Dissociation of Meaning and Cost.

In Zahavian systems, signaling is kept honest by an intrinsic relationship between the meaning of a complete signal (hereafter, a sentence) and the production cost for this sentence. In human language, meaningful sentences are constructed combinatorially out of smaller discrete units that have their own referents. How can this type of combinatorial communication be stabilized by a Zahavian mechanism?

Consider an absurdly simple example, a Wittgensteinian language game, in which an individual solicits food for his family from a somewhat sympathetic kinsman by using a six-word language. His request is made as follows. He first names the type of food item that he needs—“goat,” “rabbit,” or “apple”—and then specifies how many of that item he needs, “one,” “two,” or “three”. With just six signals, this language could conceivably be used to convey nine different requests. But in this system, how can costs be assigned to individual words to ensure reliable communication? For example, how much more should it cost to use the word “two” than to use the word “one”? If communication is to be reliable, the cost of using the word “two” must be sufficient to deter an individual who needs one goat but not two from saying “goat, two” instead of “goat, one”. But if this is the case, the word “two” will be too expensive to use in reference to the lesser food items, rabbits and apples. When stabilizing costs are assigned to individual words, several of the nine possible “food, number” sentences (e.g., “apple, two”) will be so expensive that they are not worth sending. There is no way to associate words and costs so as to facilitate full yet reliable use of this “language.”

More complex languages will employ negation, conjunctions, and other complex grammatical constructs, and consequently will face even greater difficulties of this sort. To employ a Zahavian mechanism to stabilize reliable signaling, then, signal cost will somehow have to be associated not with the component phonemes or words but instead with each sentence as a whole. Although difficult when signal costs arise from the physiology of signal production, association between whole-sentence meaning and signal cost more easily obtains when costs are imposed by the individuals receiving and interpreting the signals, as in the sparrow example.

Therefore, we argue that the transition from peacock-like costly signals to sparrow-like conventional signals is a prerequisite for the evolution of combinatorial sentence meaning. To reap the benefits of building sentences from words, a signaling system must separate the meaning of a signal from the mechanism that keeps its use honest. How can this happen? When the signal receivers impose the stabilizing costs, these costs can be associated with sentences rather than phonemes.

Costly Forms of Human Communication.

Not all human communication is linguistic, despite the many advantages of this mode. As Thorstein Veblen (59) noted over a century ago, humans make liberal use of costly signals in their myriad displays of conspicuous consumption. Why do people resort to this inefficient form of communication?

In comparing the peacock and the sparrow, we predicted that conventional signals will be used when talking about either coincident interests or verifiable qualities; otherwise, costly signals will be used. Because of the social context in which human linguistic communication often occurs (structured populations with repeated interactions), much of human communication falls into the former domain. However, not all human interactions will meet these criteria; under circumstances that do not, we might expect to see the use of costly signals. In particular, we might expect humans to use costly signals (i) in one-time interactions, (ii) when communicating about otherwise unverifiable properties, or (iii) when the expected gains from deception exceed the expected costs from community-imposed or individually imposed sanction or punishment.

Conclusions

In Part I of this paper, we showed that honest communication does not require signal cost at equilibrium; waste is not a prerequisite for signal honesty. It is the derivative of signal cost, and not signal cost itself, that serves to maintain honesty. This result has important implications for future empirical studies of honest signaling. In particular, measurement of cost at equilibrium is not sufficient to test costly signaling hypotheses. Equilibrium cost tells us very little because many different costs (even zero cost) are possible at equilibrium under the revised theory. Instead, the theory's strong and unambiguous predictions involve the consequences of deviations from equilibrium; manipulation experiments in which signal magnitudes are experimentally altered may be necessary. In addition, our findings remove the discrepancy between models of discrete and continuous games, as arbitrarily cheap signaling previously was known to be possible in the former (10, 13) but thought to be impossible in the latter (1, 3, 4, 12).

Over the past decade, a number of authors have explored language evolution with models from evolutionary game theory and have shown (i) that arbitrary meanings can be assigned to signals in an evolutionarily stable manner, and (ii) that the various higher-level structures of language can emerge by evolution. These arguments typically have assumed coincident interests among the communicating parties. In Part II of this paper, we have strengthened considerably these prior results. By using signaling theory, we showed that the results derived under the assumptions of coincident interest hold under much less restrictive conditions, including environments of conflicting interest as would have been present during language evolution. Moreover, signaling theory can predict when signals will be costly and when they will not and can explain the form of signals, both costly and free. It predicts that even with social enforcement signals still may not be cost-free, depending on the details of how the social enforcement works (i.e., the form of the signal-cost function). Finally, signaling theory can offer a framework in which to explore the dynamics of language origin and evolution under conflicting interests. For all of these reasons, we expect that signaling theory and evolutionary game theory more broadly will provide a useful foundation for further analysis of human linguistic communication.

Appendix.

We derive cost functions that allow arbitrarily cheap signaling in Godfray's model of signaling among relatives (4) and in a game analogous to Grafen's sexual selection model (3).

Godfray's Model.

In Godfray's model, an offspring of quality q ∈ [0.5, 2.5] (where low q implies high hunger level) signals to elicit resource transfer from its parent. The offspring receives a personal fitness benefit 1 − e^−rq for response r; the parent receives a personal fitness benefit of 1 − 0.08r. To handle the relatedness between two players, Godfray employs Hamilton's rule: signaler and receiver each attempt to maximize their inclusive fitnesses, i.e., the sum of their personal fitnesses weighted by relatedness. Net payoffs are, therefore, H(q,r) = (1 + k) − e^−rq − 0.08rk and G(q,r) = 2 − e^−rq − 0.08r (see ref. 4). When subsequent offspring will be full sibs, k = 1/2. Thus, the parent's optimum response curve is given by z_r(q) = (1/q) log (q/0.08), and δH/δr = −0.04 − qe^−qr = 0.04 everywhere along the equilibrium path. By (2) we need to find a smooth cost function C with a partial derivative of cost with respect to induced response of δC/δr = 0.04 everywhere along equilibrium path and with C[q,z_r(q)] = E(q) < ɛ for all q. One such function has a partial derivative δC/δr that is a smooth approximation to a step function and is given by δC/δr = a + (2a/π) Arctan [b(ɛ,q)r − z_r(q)], where a = δH/δr = 0.04 and b can be found numerically such that the necessary conditions are met. Such a cost function is shown in Fig. 3 for ɛ = 0.0001, i.e., for which signal cost never exceeds 0.0001 at equilibrium.

Grafen's Model.

In Grafen's model, a male signals his quality q ∈ [0.2, 0.8] to a prospective mate, who selects a response (e.g., inclination to mate) r. The signaler's payoff is given by w(s,r,q) = r^0.3q^s. The signal receiver's optimal response curve is z_r(q) = q. Here, the benefit and cost to the signaler are not linearly independent. In this game, however, we can determine the optimal strategic behavior for the signaler by maximizing any monotone increasing transformation of payoff; here, we choose to use log w(s,r,q) = 0.3 log r + s log q. At this point, we can see that one of Grafen's seemingly innocuous assumptions, that signal cost takes the form F(q,s) = q^s, is actually a strong and arbitrary constraint. To treat a more general class of signaling games (as Godfray did), Grafen could have used the payoff function w(s,r,q) = r^0.3q^F(q,s), or equivalently, log w(s,r,q) = 0.3 log r + F(q,s) log q. Grafen's payoff function is a special case of this function. Define H(q,r) to be the first term and D(q,r) = C[F(q,z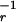(r)] to be the second term (parameterized in terms of the equilibrium response rather than the signal). As above, we construct a cost function with partial derivative δD/δr = a(q) + [2a(q)/π] Arctan [b(ɛ,q)r − z_r(q)], where

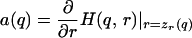and where b is determined numerically. Such a cost function is shown in Fig. 1 for ɛ = 0.01.

From these figures, we see that whereas the relation between signal cost and signaler quality can stabilize honest signaling, signals need not be expensive at equilibrium. Indeed, previous authors concluded that cost was necessary only because they imposed specific constraints on the form of the signal function. In Godfray's case, this constraint is the implicit assumption that all signalers pay the same cost to send any given signal, regardless of their own condition. In Grafen's model, this constraint is that signal cost takes the form q^s, where q is the quality of the signaler and s is the magnitude of the signal.