Kernelized rank learning for personalized drug recommendation

Abstract

Motivation

Large-scale screenings of cancer cell lines with detailed molecular profiles against libraries of pharmacological compounds are currently being performed in order to gain a better understanding of the genetic component of drug response and to enhance our ability to recommend therapies given a patient's molecular profile. These comprehensive screens differ from the clinical setting in which (i) medical records only contain the response of a patient to very few drugs, (ii) drugs are recommended by doctors based on their expert judgment and (iii) selecting the most promising therapy is often more important than accurately predicting the sensitivity to all potential drugs. Current regression models for drug sensitivity prediction fail to account for these three properties.

Results

We present a machine learning approach, named Kernelized Rank Learning (KRL), that ranks drugs based on their predicted effect per cell line (patient), circumventing the difficult problem of precisely predicting the sensitivity to the given drug. Our approach outperforms several state-of-the-art predictors in drug recommendation, particularly if the training dataset is sparse, and generalizes to patient data. Our work phrases personalized drug recommendation as a new type of machine learning problem with translational potential to the clinic.

Availability and implementation

The Python implementation of KRL and scripts for running our experiments are available at https://github.com/BorgwardtLab/Kernelized-Rank-Learning.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

One of the key goals of precision medicine is the ability to suggest personalized therapies to patients based on their molecular profiles. This approach is particularly interesting for cancer treatment given the heterogeneous nature of this disease, with somatic alterations in cancer genes shown to be the determinants of a patient's response to therapy (Chapman et al., 2011). For the development of targeted treatments, large collections of patients with recorded clinical outcomes and molecularly profiled tumor samples are needed. However, the cost of such a medical records knowledge bank is currently prohibitive except for a few encouraging examples (Gerstung et al., 2017). Therefore, pre-clinical biological models, such as cultured human cancer cell lines, are a relatively inexpensive alternative approach for finding biomarkers. Recently, several large-scale drug sensitivity screens of genomically profiled cell lines ranging different cancer (sub)types have been established (Barretina et al., 2012; Iorio et al., 2016; Seashore-Ludlow et al., 2015). One of the current challenges lies in building accurate predictive models and translating these models into the clinic.

A number of regression models (Costello et al., 2014; Jang et al., 2014) have been proposed to predict drug sensitivity measured by the half maximal inhibitory concentration (${\text{IC}}_{50}$) or the area under the fitted dose response curve (AUC). These methods typically build a predictor for each drug individually (Aben et al., 2016; Barretina et al., 2012; Iorio et al., 2016), use multi-task learning (Ammad-ud-din et al., 2016; Gönen and Margolin, 2014) or combine genomic profiles with information about the drug's chemical structure (Ammad-ud-din et al., 2014; Menden et al., 2013; Zhang et al., 2015). However, there are three potential problems with these approaches. Firstly, medical records knowledge banks are much sparser than cell line panels, meaning that only a few therapies are recorded for each patient compared to a comprehensive screen of tens to hundreds of drugs for each cell line. Secondly, these therapies are carefully selected by experienced doctors based on their expert judgment. Finally, the regression-based methods are not directly optimized for the prediction of the clinically relevant case in which a clinician needs to know a few most-suited drugs for a given patient.

Here, we phrase the personalized drug recommendation as a ranking problem (Section 2) and propose a method, named Kernelized Rank Learning (KRL), that is directly optimized for the clinically relevant scenario of personalized drug recommendation illustrated above. To this end, we extend the approach of Weimer et al. (2007) and Teo et al. (2010) in Section 3. The key difference between KRL and the available regression approaches is that for a given cell line (patient), KRL directly predicts the top ranking drugs rather than the exact sensitivity values for all potential drugs. Our experimental evaluation using a dataset of cancer cell lines (Section 4) shows that KRL outperforms competing approaches, particularly in the realistic scenario when only a few training examples per cell line are available. Next, using publicly available patient data and the gene expression homogenization pipeline of Geeleher et al. (2014, 2017), we show that even when KRL is trained on cell line models, it can produce plausible recommendations for cancer patients. Finally, we summarize our findings and suggest potential directions for future work in Section 5.

2 Problem statement

We are given $\mathit{X}\in {ℝ}^{\mathit{n}\times \mathit{p}}$, a set of n samples (cell lines or patients) where each of them is represented with a molecular profile (e.g. gene expression) with p variables. Furthermore, we are given $\mathit{Y}\in {ℝ}^{\mathit{n}\times \mathit{m}}$, a set of drug response measurements to m distinct drugs. Importantly, the majority of values in $\mathit{Y}$ might be missing since the response of each individual sample is known only for a few of all potential drugs. Given $\mathit{X}$ and $\mathit{Y}$ as described above, and a molecular profile of a new sample, not present in $\mathit{X}$, our goal is to rank drugs based on their efficacy so that the most effective drug is ranked first. This goal is thus different from predicting the exact value of the drug response (as done by drug sensitivity prediction methods). Here we focus on the relative ordering (ranking) of a few, most effective, drugs.

From a machine learning perspective, drug recommendation can be framed into a problem of learning a weight matrix $\mathit{W}\in {ℝ}^{\mathit{p}\times \mathit{m}}$ and then recommending drugs based on the predicted ranking vector $\mathit{f}=\mathit{xW}$. Here $\mathit{x}\in {ℝ}^{\mathit{p}}$ is the molecular profile of a new sample, and $\mathit{f}\in {ℝ}^{\mathit{m}}$ is a ranking vector which entails the predicted ranking scores for each of the m distinct drugs. Finally, the ranking of the drugs is obtained as a permutation $\mathit{\pi }$ which sorts the drugs in the decreasing order of $\mathit{f}$ (thus, ${\mathit{\pi }}_1=\mathit{i}$ such that $\mathit{max}\left(\mathit{f}\right)={\mathit{f}}_{\mathit{i}}$, that is, ${\mathit{\pi }}_1$ gives the identity of the first recommended drug, the one with the largest ranking score in $\mathit{f}$).

The weight matrix $\mathit{W}$ can be viewed as containing weights of all molecular features towards each drug. Since we are interested in relative ordering of the drugs, $\mathit{W}$ needs to be learned jointly across all drugs rather then for each drug individually. Learning $\mathit{W}$ can be formulated as the following minimization problem:

$$\underset{\mathit{W}}{\mathit{min}}\mathcal{L}(\mathit{XW},\mathit{Y})+\mathit{\lambda }\mathcal{R}\left(\mathit{W}\right)$$ (1)

where $\mathcal{L}(\mathit{XW},\mathit{Y})$ is a loss function, $\mathcal{R}\left(\mathit{W}\right)$ is a regularization term with λ controlling the effect of the regularization (regularization is necessary to avoid over-fitting to the training set).

2.1 Normalized discounted cumulative gain (NDCG)

The key to our approach lies in employing a loss function based on the Discounted Cumulative Gain (DCG) ranking metric (Järvelin and Kekäläinen, 2002) as $\mathcal{L}(\mathit{XW},\mathit{Y})$ in Equation (1). Given the predicted ranking vector $\mathit{f}\in {ℝ}^{\mathit{m}}$ and the true drug response vector $\mathit{y}\in {ℝ}^{\mathit{m}}$, DCG@k evaluates how well the order of the top k recommendations in $\mathit{f}$ agrees with the order of the most effective drugs in $\mathit{y}$:

$$\text{DCG}@\mathit{k}(\mathit{f},\mathit{y})=\sum _{\mathit{i}=1}^{\mathit{k}}\frac{2^{{\mathit{y}}_{{\mathit{\pi }}_{\mathit{i}}}}-1}{\hspace{0.17em}{\text{log}}_2(1+\mathit{i})}$$ (2)

where $\mathit{\pi }$ sorts $\mathit{f}$ in decreasing order. DCG@k can be intuitively interpreted as follows: the numerator gives rewards proportional to the true responses of the k recommended drugs, while the denominator penalizes the incorrect ordering of these k recommendations. The gains are maximized when the most effective k drugs are the top k recommended drugs, ranked in the correct order.

The Normalized DCG (NDCG) is more practical:

$$\text{NDCG}@\mathit{k}(\mathit{f},\mathit{y})=\frac{\text{DCG}@\mathit{k}(\mathit{\pi },\mathit{y})}{\text{DCG}@\mathit{k}(\mathit{\sigma },\mathit{y})}$$ (3)

where $\mathit{\pi } \text{and} \mathit{\sigma } \text{sort} \mathit{f} \text{and} \mathit{y}$ in decreasing order, respectively. Hence, NDCG@k ranges from $0 \text{to} 1$ and is maximized (perfect recommendation) when ${\mathit{\pi }}_{\mathit{i}}={\mathit{\sigma }}_{\mathit{i}},1\le \mathit{i}\le \mathit{k}$.

Finally, we convert NDCG@k, a gain function, into a loss function by taking $1-\text{NDCG}@\mathit{k}(\mathit{f},\mathit{y})$, which allows us to rewrite Equation (1) and state the drug recommendation problem formally:

$$\underset{\mathit{W}}{\mathit{min}}{\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}(1-\text{NDCG}@\mathit{k}(}{\mathit{X}}_{\mathit{i}}\mathit{W},{\mathit{Y}}_{\mathit{i}}))+\mathit{\lambda }\left|\right|\mathit{W}|{|}_{\mathit{F}\mathit{r}\mathit{o}\mathit{b}}^2$$ (4)

where ${\mathit{X}}_{\mathit{i}}$ (the i-th row of $\mathit{X}$) is the molecular profile of the i-th cell line and ${\mathit{Y}}_{\mathit{i}}$ (the i-th row of $\mathit{Y}$) is the true response vector of the i-th cell line to the m drugs. $\left|\right|\mathit{W}|{|}_{\mathit{F}\mathit{r}\mathit{o}\mathit{b}}^2$ is the squared Frobenius norm of $\mathit{W}$ for the purpose of regularization.

3 Materials and methods

We stated the drug recommendation as minimization of $1-\text{NDCG}@\mathit{k}$. Unfortunately, it turns out that $1-\text{NDCG}@\mathit{k}$ is a highly non-convex and non-smooth function which makes its direct optimization difficult. Therefore, we minimize its convex upper bound derived by Weimer et al. (2007) instead and extend the Bundle Method for regularized Risk Minimization (BMRM) proposed by Teo et al. (2010) for the joint optimization of $\mathit{W}$ across all drugs. Finally, Equation (4) employs a linear predictor (${\mathit{X}}_{\mathit{i}}\mathit{W}$), which does not take feature interactions into account. To boost prediction performance by introducing non-linearity, we apply the well-known kernel trick (Cortes and Vapnik, 1995). We thus refer to our approach as Kernelized Rank Learning (KRL).

3.1 Convex upper bound of the loss function

Based on the work by Tsochantaridis et al. (2005), which describes how to find convex upper bounds of non-convex optimization problems, Weimer et al. (2007) showed that the following loss function is a convex upper bound of $1-\text{NDCG}@\mathit{k}(\mathit{f},\mathit{y})$:

$$\mathcal{\ell }(\mathit{f},\mathit{y})=\underset{\mathit{\pi }}{\mathit{max}}[1-\text{NDCG}@\mathit{k}(\mathit{f},\mathit{y})+\langle \mathit{c},{\mathit{f}}_{\mathit{\pi }}-\mathit{f}\rangle ]$$ (5)

where $\mathit{c}\in {ℝ}^{\mathit{m}}$ is a decreasing sequence, e.g. ${\mathit{c}}_{\mathit{i}}={(\mathit{i}+1)}^{-0.25}$ as suggested by the authors. Finding the permutation $\mathit{\pi }$ is a linear assignment problem which can be solved with the Hungarian Marriage algorithm (Kuhn, 1955).

3.2 Kernelized rank learning (KRL)

Non-linear kernel methods have shown good performance in a drug sensitivity collaborative competition (Costello et al., 2014). Therefore, we decided to kernelize the objective function defined in Equation (4).

Let $\mathit{W}={\mathit{X}}^{\mathit{T}}\mathit{U}$, where $\mathit{U}\in {ℝ}^{\mathit{n}\times \mathit{m}}$, the objective is rewritten as:

$$\underset{\mathit{U}}{\mathit{min}}{\displaystyle \sum _{\mathit{i}}^{\mathit{n}}\mathcal{\ell }}({\mathit{X}}_{\mathit{i}}{\mathit{X}}_{\mathit{i}}^{\mathit{T}}\mathit{U},{\mathit{Y}}_{\mathit{i}})+\mathit{\lambda }\text{Tr}\left({\mathit{U}}^{\mathit{T}}\mathit{X}{\mathit{X}}^{\mathit{T}}\mathit{U}\right)$$ (6)

where $\ell$ is the loss function defined in Equation (5), and $\text{Tr}$ is the trace of a square matrix. By replacing $\mathit{X}{\mathit{X}}^{\mathit{T}}$ with a kernel matrix $\mathit{K} \text{on} \mathit{X}$, we get the KRL's kernelized objective function:

$$\underset{\mathit{U}}{\mathit{min}}{\displaystyle \sum _{\mathit{i}}^{\mathit{n}}\mathcal{\ell }}({\mathit{K}}_{\mathit{i}}\mathit{U},{\mathit{Y}}_{\mathit{i}})+\mathit{\lambda }\text{Tr}\left({\mathit{U}}^{\mathit{T}}\mathit{KU}\right)$$ (7)

The time complexity of evaluating KRL's objective function comes down to the complexity of the linear assignment algorithm, which is $\mathit{O}\left({\tilde{\mathit{m}}}^3\right)$, where $\tilde{\mathit{m}}$ is the number of non-missing drug response measurements for the given sample, which is typically only a few. Moreover, the KRL loss function can be decomposed and evaluated in parallel across all samples.

Finally, to optimize Equation (7), we need the subgradient of the loss function $\mathcal{L}(\mathit{KU},\mathit{Y})={\sum }_{\mathit{i}}^{\mathit{n}}\ell ({\mathit{K}}_{\mathit{i}}\mathit{U},{\mathit{Y}}_{\mathit{i}})$ with regards to $\mathit{U}$:

$${\partial }_{\mathit{U}}\mathcal{L}(\mathit{KU},\mathit{Y})=\mathit{K}{\partial }_{\mathit{F}}\mathcal{L}$$ (8)

where $\mathit{F}=\mathit{KU} \text{and} {\left({\partial }_{\mathit{F}}\mathcal{L}\right)}_{\mathit{i}}={\partial }_{{\mathit{F}}_{\mathit{i}}}\ell ({\mathit{F}}_{\mathit{i}},{\mathit{Y}}_{\mathit{i}})={\mathit{c}}_{{\overline{\mathit{\pi }}}^{-1}}-\mathit{c} \text{where} \overline{\mathit{\pi }}$ is the permutation that maximizes $\ell (\mathit{f},\mathit{y}),\hspace{0.17em}{\overline{\mathit{\pi }}}^{-1}$ is the inverse permutation of $\overline{\mathit{\pi }}$, i.e. ${\left({\mathit{f}}_{\overline{\mathit{\pi }}}\right)}_{{\overline{\mathit{\pi }}}^{-1}}=\mathit{f}$, and $\mathit{c}$ is defined as in Equation (5). Supplementary Algorithm S1 details how to calculate the subgradient ${\partial }_{\mathit{U}}\mathcal{L}$.

3.3 KRL optimization

The objective function in Equation (7) is convex but due to the maximization problem in $\ell$ expensive to evaluate. The BMRM algorithm proposed by Teo et al. (2010) has been shown to work well on such problems. However, the authors introduced only a single-task version of BMRM, which means it cannot be directly applied to solve Equation (7). Therefore, we extended BMRM for KRL to allow for the following differences when compared to the single-task BMRM: (i) $\mathit{U}$ is a matrix rather than a vector and (ii) the objective function includes regularization on a positive definite kernel matrix, $\text{Tr}\left({\mathit{U}}^{\mathit{T}}\mathit{KU}\right)$, rather than an L² norm of a weight vector.

Algorithm 1. BMRM for Kernelized Rank Learning

 Data: $\mathit{U}[0],\hspace{0.17em}\mathit{K},\hspace{0.17em}\mathit{Y},\hspace{0.17em}\lambda ,\hspace{0.17em}\mathrm{ϵ}>0,\hspace{0.17em}\mathit{t}=0$

 Result: $\mathit{U}[\mathit{t}]$

1 repeat

2   $\mathit{t}=\mathit{t}+1$;

3   $\mathit{A}[\mathit{t}]={\partial }_{\mathit{U}}\mathcal{L}(\mathit{KU}[\mathit{t}-1],\mathit{Y})$;

4   $\mathit{B}[\mathit{t}]=\mathcal{L}(\mathit{KU}[\mathit{t}-1],\mathit{Y})-\langle \mathit{U}[\mathit{t}-1],\mathit{A}[\mathit{t}]\rangle$;

5   $\mathcal{J}(\mathit{U})=\mathit{\lambda }\text{Tr}({\mathit{U}}^{\mathit{T}}\mathit{KU})+\underset{{}_{1<\mathit{i}\le \mathit{t}}}{\mathit{max}}(\langle \mathit{U},\mathit{A}[\mathit{i}]\rangle +\mathit{B}[\mathit{i}])$;

6   $\mathit{U}[\mathit{t}]=\underset{{}_{\mathit{U}}}{\mathit{min}}\mathcal{J}(\mathit{U})$;

7   $\mathrm{ϵ}[\mathit{t}]=\underset{{}_{0\le \mathit{i}\le \mathit{t}}}{\mathit{min}}\mathcal{L}(\mathit{KU}[\mathit{i}],\mathit{Y})+\mathit{\lambda }\text{Tr}(\mathit{U}{[\mathit{i}]}^{\mathit{T}}\mathit{KU}[\mathit{i}])-\mathcal{J}(\mathit{U}[\mathit{t}])$;

8 until $\mathrm{ϵ}[\mathit{t}]\le \mathrm{ϵ}$;

Algorithm 1 describes BMRM for KRL. The general idea of the BMRM algorithm is to improve the lower bound of the objective function by its linearization (the first-order Taylor approximation) at the subgradient ${\partial }_{\mathit{U}}\mathcal{L}$ in different iterations. Lines 5 and 6 of Algorithm 1 require finding $\mathit{U}$ that minimizes the lower bound function $\mathcal{J}\left(\mathit{U}\right)$ of the objective function defined in Equation (7). The primal problem involves a maximization sub-problem, which is difficult to solve. The original BMRM algorithm solves the primal problem in its dual form, which is a quadratic program. In the following we show that also in the case of KRL, with $\mathit{U}$ being a matrix and regularization on a kernel, the problem can be solved in its dual form.

Firstly, $\mathit{U}$ is decomposed into m column vectors, and the objective function is rewritten as:

$$\underset{\mathit{U}}{\mathit{min}}\mathcal{L}(\mathit{KU},\mathit{Y})+{\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}\mathit{\lambda }}{\left({\mathit{U}}^{\mathit{i}}\right)}^{\mathit{T}}\mathit{K}{\mathit{U}}^{\mathit{i}}$$ (9)

where ${\mathit{U}}^{\mathit{i}}$ is the i-th column of $\mathit{U}$. Next, after introducing non-negative Lagrange multipliers α, the dual function is also decomposed by column:

$${\mathit{U}}^{\mathit{i}}\left[\mathit{t}\right]=-{\mathit{K}}^{-1}{\mathit{A}}^{\mathit{i}}\alpha \left[\mathit{t}\right]/\lambda$$ (10)

$$\begin{array}{l}\mathit{\alpha }\left[\mathit{t}\right]=\underset{\mathit{\alpha }\in {\mathit{ℝ}}^{\mathit{t}}}{\mathit{max}}-\frac{1}{2\mathit{\lambda }}{\mathit{\alpha }}^{\mathit{T}}\left({\displaystyle \sum _{\mathit{i}=1}^{\mathit{m}}{\left({\mathit{A}}^{\mathit{i}}\right)}^{\mathit{T}}}{\mathit{K}}^{-1}{\mathit{A}}^{\mathit{i}}\right)\mathit{\alpha }+{\mathit{\alpha }}^{\mathit{T}}\mathit{B}\hfill \\ \text{subject to }\mathit{\alpha }\ge 0\text{ and }\left|\right|\mathit{\alpha }|{|}_1=1\hfill \end{array}$$ (11)

where ${\mathit{A}}^{\mathit{i}}=\left[{\mathit{A}}^{\mathit{i}}\right[1],\dots ,{\mathit{A}}^{\mathit{i}}[\mathit{t}\left]\right],\hspace{0.17em}\mathit{B}=\left[\mathit{B}\right[1],\dots ,\mathit{B}[\mathit{t}\left]\right]$, and $\alpha \left[\mathit{t}\right],\hspace{0.17em}{\mathit{U}}^{\mathit{i}}\left[\mathit{t}\right],\hspace{0.17em}{\mathit{A}}^{\mathit{i}}\left[\mathit{t}\right]$, and $\mathit{B}\left[\mathit{t}\right] \text{represent} \alpha ,\hspace{0.17em}{\mathit{U}}^{\mathit{i}},\hspace{0.17em}{\mathit{A}}^{\mathit{i}}$, and $\mathit{B}$ in iteration t, respectively. This results in a quadratic program problem.

3.4 Datasets

3.4.1 Cancer cell lines

We designed, evaluated and trained our method using the Genomics of Drug Sensitivity in Cancer (GDSC) release 6 dataset with drug sensitivity measurements of 1 001 cancer cell lines (ranging 31 cancer types) to 265 pharmacological compounds (Iorio et al., 2016). Majority of the cell lines were characterized using gene expression, whole-exome sequencing, copy number variation and DNA methylation. We evaluated our method with all four data types individually, however, we focused our analysis on the predictions based on gene expression since it has been shown previously as the most predictive data type (Costello et al., 2014). To this end, we encoded each of the 962 profiled cell lines with the RMA-normalized (robust multi-array average) basal expression of 17 737 genes. Supplementary Table S1 lists the statistics regarding the number of profiled cell lines, features and missing values for all four data types.

Genomics of Drug Sensitivity in Cancer reports the drug sensitivity as the logarithm of half maximal inhibitory concentration ($\text{log}\hspace{0.17em}{\text{IC}}_{50}$), which denotes the concentration of the compound required to inhibit the cell growth at 50%. The measured ${\text{IC}}_{50}$ values are not, however, comparable between different compounds. Therefore, Iorio et al. (2016) calculated drug-specific sensitivity (binarization) thresholds for each of the 265 tested drugs. These thresholds were determined using a heuristic outlier procedure (Knijnenburg et al., 2016) following a previous observation that the majority of cell lines are typically resistant to a given drug (Garnett et al., 2012).

We used these drug-specific sensitivity thresholds to normalize the dataset. Furthermore, for compatibility with the ranking metric (NDCG@k), we scaled the normalized dataset into the range of $[0,\mathit{v}]$, where $\mathit{v}\in {ℝ}^{+}$ represents the strongest drug response in the dataset. Thus, the sensitivity scores used in this work were equal to $-\text{log}\hspace{0.17em}\frac{{\text{IC}}_{50}}{\mathit{t}\mathit{h}{\mathit{r}}_{\mathit{d}}}+\mathit{a}$, where thr_d is the sensitivity threshold of the given drug and a is the maximum normalized $\text{log}\hspace{0.17em}{\text{IC}}_{50}$ score across all drugs.

3.4.2 Clinical trials

Recently, Geeleher et al. (2014) showed that ridge regression models trained on in vitro cell line models can predict drug response in vivo. Their approach was particularly successful for the docetaxel breast cancer (Chang et al., 2003) and bortezomib multiple myleoma (Mulligan et al., 2007) clinical trials, yielding the area under the receiver operating characteristic curve (AUROC) scores of 0.81 and 0.71, respectively. The AUROC can be interpreted as the probability that for a randomly selected responder and non-responder, the responder was predicted to respond better to the given therapy than the non-responder. In Geeleher et al. (2014), the ridge regression models were trained using the GDSC release 2 dataset, which comprised responses of 482 and 280 cell lines for docetaxel and bortezomib, respectively. After re-running their analysis pipeline using the GDSC release 6 containing 833 and 391 cell lines for docetaxel and bortezomib, respectively, we found that while the performance for bortezomib (AUROC of 0.70) was comparable to the GDSC release 2 results, the docetaxel model resulted in a random performance (AUROC of 0.49). We conjecture that this could be attributed to experimental errors or unsuccessful homogenization of the expression profiles for some of the GDSC release 6 cell lines. Therefore, to avoid these potential outliers during training, we used the cell lines in the intersection of the GDSC release 2 and release 6. This approach resulted in a reasonable performance for both docetaxel (394 cell lines) and bortezomib (253 cell lines) with AUROCs of 0.74 and 0.71, respectively.

We used the docetaxel (24 patients) and bortezomib (169 patients) clinical trials to test if KRL's recommendations can generalize to cancer patients. To this end, KRL was trained using the 394 (docetaxel) and 253 (bortezomib) GDSC release 6 cell lines as explained above. We used the pipeline provided by Geeleher et al. (2014) to download the clinical trials datasets and homogenize the gene expression profiles of the cell lines, measured with Affymetrix HG-U219 and tumor biopsies, measured with Affymetrix HG-U95-v2 (docetaxel trial) and Affymetrix HG-U133B (bortezomib trial). The homogenization was implemented using the ComBat method (Johnson et al., 2007; Leek and Storey, 2007).

3.4.3 Breast cancer patients

We employed The Cancer Genome Atlas (TCGA) breast cancer cohort (BRCA, 1098 patients) to further evaluate how well KRL's predictions generalize to cancer patients (The Cancer Genome Atlas Network, 2012). We downloaded the Level 1 clinical annotations and Level 3 reverse phase protein array (RPPA) data from the Broad Institute TCGA Genome Data Analysis Center (2016), Firehose data run 2016_01_28 (https://doi.org/10.7908/C11G0KM9). We used the immunohistochemistry annotations to identify HER2-overexpressed (HER2⁺, 164 patients) and triple-negative breast cancers (TNBCs, 116 patients), and RPPA z-scores to identify patients with normal-to-high expression of JAK2 (JAK2⁺, z-score $\ge$ 0, 421 patients). Furthermore, we defined the BRCA1/2-mutant (mBRCA) patients using the list of 37 patients carrying germline loss-of-function BRCA1/2 mutations (Maxwell et al., 2017). Finally, we used the pipeline proposed by Geeleher et al. (2017) to download and homogenize the Level 3 Illumina HiSeq RNA-seq v2 data (1 080 patients) from the Firehose data run 2015_08_21. The homogenization approach was in part based on the Remove Unwanted Variation (RUV) method (Risso et al., 2014).

3.5 Evaluation

To get an unbiased estimate of KRL's prediction performance using the GDSC cell lines dataset, we employed three-fold cross-validation, where each fold was used once for testing while the other two folds were merged for training. Finally, we reported the mean performance across the three test folds. For the experiments with subsampled training datasets, we repeated the subsampling procedure 10 times, calculated standard deviations, and estimated statistical significance of our results using paired Student t-test. For the experiments with the full training dataset, standard deviations and statistical significance were estimated from the three cross-validation folds.

To evaluate the accuracy of our approach, we quantified if the top recommendations in $\mathit{f}\in {ℝ}^{\mathit{m}}$ agree with the most effective drugs in $\mathit{y}\in {ℝ}^{\mathit{m}}$, where $\mathit{f} \text{and} \mathit{y}$ are the predicted ranking vector and the true drug response vector, respectively. To this end, we used two different ranking metrics: Precision@k and NDCG@k. NDCG@k was defined in Equation (3), Section 2.1. The main shortcoming of NDCG@k is that there is no intuitive explanation of its values. Therefore, we used also Precision@k, which measures precision between the k highest-ranked recommendations in $\mathit{f}$ and the k most effective drugs in $\mathit{y}$:

$$\text{Precision}@\mathit{k}(\mathit{f},\mathit{y})=\frac{1}{\mathit{k}}\sum _{\mathit{i}=1}^{\mathit{k}}\sum _{\mathit{j}=1}^{\mathit{k}}\delta ({\mathit{\pi }}_{\mathit{i}},{\mathit{\sigma }}_{\mathit{j}})$$ (12)

where $\mathit{\pi } \text{and} \mathit{\sigma } \text{sort} \mathit{f} \text{and} \mathit{y}$ in decreasing order, respectively, and $\delta (\mathit{a},\mathit{b})=1 \text{if} \mathit{a}=\mathit{b} \text{and} 0$ otherwise. The interpretation of Precision@k is straightforward: $\text{Precision}@5=0.4$ means that out of five most effective drugs in $\mathit{y}$, two were among the top five recommendations in $\mathit{f}$.

3.6 Baselines and related work

We compared the method proposed here, Kernelized Rank Learning (KRL), with several state-of-the-art approaches for drug sensitivity prediction including the Elastic Net (EN), Kernel Ridge Regression (KRR), Random Forest (RF) regression and Kernelized Bayesian Multi-Task Learning (KBMTL). EN (Zou and Hastie, 2005) and KRR (Murphy, 2012) have been recommended as one of the best-performing algorithms in a systematic survey (Jang et al., 2014). Another survey identified KBMTL (Gönen and Margolin, 2014) and RF (Breiman, 2001) as the two best-performing algorithms in a challenge-based competition on a breast cancer dataset (Costello et al., 2014). KBMTL is a multi-task approach, thus instead of training a model for each task (drug) separately as done by EN, KRR and RF, it learns the relationship between different drugs during training. While there is an extension of the KBMTL method, which employs multiple kernel learning (MKL) to allow for the integration of different molecular data types, we focused on prediction using a single data type to facilitate a fair comparison of all compared methods. Finally, we compared two implementations of the proposed method: with linear and Radial Basis Function (RBF) kernels (LKRL and KRL, respectively).

We used the implementation of EN, KRR and RF from the Python scikit-learn package (Pedregosa et al., 2011). For KBMTL, we used the MATLAB implementation provided by the authors (https://github.com/mehmetgonen/bmtmkl).

3.7 Hyper-parameter optimization

For each of the compared methods, we tuned the relevant hyper-parameters with a grid search using nested three-fold cross-validation on the training set (Supplementary Table S2). That is, we split the two training folds of the ‘outer’ cross-validation procedure into three folds for hyper-parameter optimization. To simplify the hyper-parameter optimization for the evaluation of KRL on the clinical trials and TCGA-BRCA datasets, we heuristically determined the RBF kernel width (γ) using the ‘median trick’ which sets γ to the inverse of the median squared Euclidean distance of all training samples pairs. Then, we tuned the regularization parameter λ with a line search, $\lambda \in \{1.0,0.1,\dots ,1\times {10}^{-6}\}$.

4 Results

As described in Section 1, our method (KRL) is motivated by the clinically relevant scenario where (i) the training dataset in the form of a medical records knowledge bank is much sparser than a typical drug sensitivity screen of cultured cell lines, (ii) therapies recorded in the knowledge bank were prescribed by experienced doctors based on their expert judgment and (iii) only a few, accurate, recommendations are needed (as opposed to predicting the exact values of patient's sensitivity to all drugs on the market). To show how KRL performs under these three requirements, we conducted the following experiments. First, for the sake of completeness, we evaluated KRL on the full GDSC dataset. Second, to address (i), we randomly subsampled the number of drugs a cell line was treated with to make the training dataset sparse. Third, to address (ii), we extended the subsampling procedure to account for doctor's expert judgment by sampling from a predefined proportion of the most effective drugs. To address (iii) across all of the experiments, we evaluated our method with NDCG@k and Precision@k ranking metrics for different values of k, where k defines the number of top recommendations considered in the evaluation. We performed all experiments using the gene expression dataset (as it proved to be the most predictive data type) and then employed the other data types in the final analysis using the most realistic subsampling strategy where, for each cell line, only a few drugs were used for training. Finally, we evaluated how well KRL models trained on cell lines generalize to patient data using docetaxel and bortezomib clinical trials and TCGA breast cancer cohort.

4.1 Prediction using the full training dataset

We used the full GDSC dataset, which due to missing values included 82% of the drug sensitivity measurements, to compare the performance of KRL with related work using different evaluation ranking criteria. Figure 1 and Supplementary Figure S1 show the comparison for Precision@k and NDCG@k, respectively, with $\mathit{k}\in \{1,3,5,10,15,20\}$. KRL yielded comparable drug recommendations (paired Student t-test, $\mathit{P}>0.05$) to the second best method, KBMTL. Comparing KRL, which employs the RBF kernel, with the linear kernel implementation of our method (LKRL), KRL either outperformed ($\mathit{P}<0.05$, Precision@$\mathit{k} \text{for} \mathit{k}\in \{1,5,15,20\}$) or performed comparably to LKRL. Overall, KRL's performance was in the range of 23–36% for Precision@k and 47–58% for NDCG@k.

Fig. 1.

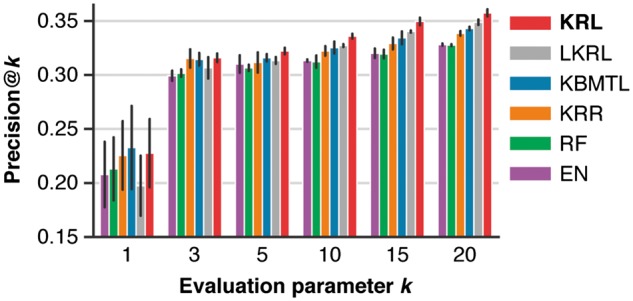
Comparison of KRL with related work (see Section 3.6 for details) in terms of Precision@k using the full training dataset for different values of the evaluation parameter k, which controls the number of predicted recommendations that are compared with the true drug ranking. The error bars show standard deviations from three cross-validation folds

4.2 Prediction using sparse training datasets

To evaluate the compared methods in a more clinically relevant scenario, in which only a few therapies can be recorded for each patient, we subsampled the training dataset (training folds) at sampling rates of 50%, 20% and 10%. At the same time, we kept the test set (test folds) unchanged. In the case of 10% sampling, this strategy resulted in training on 22 drug responses per cell line on average.

Figure 2 and Supplementary Figure S2 show Precision@5 and NDCG@5 as a function of the relative training dataset size, respectively. As expected, the performance of all compared methods decreased as the training dataset became sparser. Nonetheless, the Precision@5 improvements of KRL compared to the second method, KBMTL, were 1.1% ($\mathit{P}=8.3\times {10}^{-6}$), 2.1% ($\mathit{P}=2.5\times {10}^{-8}$) and 1.7% ($\mathit{P}=5.2\times {10}^{-7}$) for the sampling rates of 50%, 20% and 10%, respectively, compared to 0.6% ($\mathit{P}=0.138$) for the full training dataset. Thus, KRL appears to be more robust to sparse data than the regression approach. The same trend could also be observed for NDCG@5. The Precision@5 improvements of KRL compared to the other three methods using only 10% of the training dataset were 2.7% ($\mathit{P}=2.5\times {10}^{-7}$), 1.9% ($\mathit{P}=2.4\times {10}^{-7}$), 2.7% ($\mathit{P}=4.9\times {10}^{-8}$) and 5.5% ($\mathit{P}=1.6\times {10}^{-9}$) for LKRL, KRR, RF and EN, respectively.

Fig. 2.

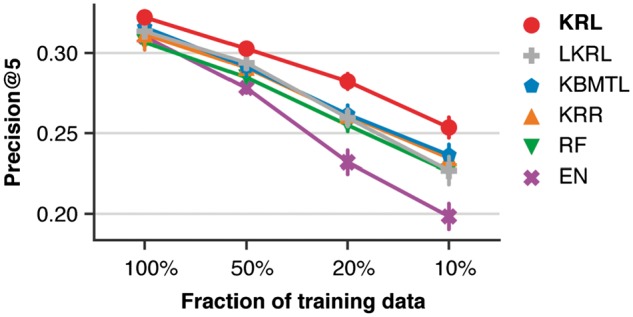
Comparison of KRL with related work (see Section 3.6 for details) in terms of Precision@5 using the subsampled training datasets. The error bars show standard deviations from 10 randomly subsampled training datasets

4.3 Prediction using sparse training datasets biased towards effective therapies

As discussed in the previous section, KRL appears to be more robust to missing data than related work. This is shown in Figure 2 where random subsampling of the training dataset was used to induce sparsity. Nonetheless, it can be argued that choosing a subset of drugs for each cell line randomly does not simulate medical records knowledge banks realistically. This is because clinicians do not prescribe therapies randomly but rather based on their expert judgment. Thus we employed another subsampling strategy: first, we selected a predefined proportion r of the most effective drugs per cell line and second, we randomly sampled q drugs per cell line from this selection. After this procedure, there might not be enough training data left for some of the drugs, therefore, after subsampling, we removed drugs with < 6 cell lines. We evaluated KRL and related work using training datasets generated with $\mathit{q}\in \{3,5,10\}$ (yielding datasets with 143–199, 202–246, and 239–265 drugs in total, respectively) and $\mathit{r}\in \{100\%,50\%,20\%,10\%\}$ (where $\mathit{r}=100\%$ is equivalent to sampling q drugs randomly). Here we analyze results with $\mathit{q}=5$ for brevity. Results for $\mathit{q}=3 \text{and} \mathit{q}=10$ showed a similar trend and are summarized in Supplementary Figures S3 and S4.

Figure 3 and Supplementary Figure S3a show Precision@5 and NDCG@5, respectively, as a function of the fraction of the most effective drugs (r) used for sampling five drugs (q) per cell line. We found that as the training dataset was composed of more effective drugs, the improvement of KRL compared to the second best method, KBMTL, was gradually increasing from 0.7% to 6.2% (Precision@5) and from 0.3% to 10.4% (NDCG@5).

Fig. 3.

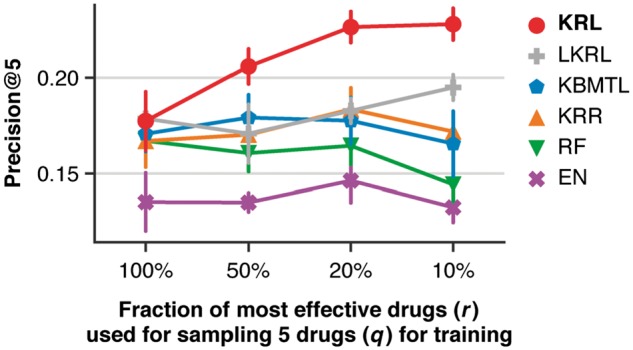
Comparison of KRL with related work (see Section 3.6 for details) in terms of Precision@5 using the subsampled training datasets, keeping five drugs (q) per cell line sampled from a predefined fraction (r) of the cell line's most effective drugs. The error bars show standard deviations from 10 randomly subsampled training datasets

Both Precision@k and NDCG@k improvements of KRL compared to related work were statistically significant ($\mathit{P}<$0.05) for $\mathit{r}\in \{50\%,20\%,10\%\}$ across a wide range of $\mathit{k}\in \{3,5,10,15,20\}$. KRL was also able to outperform LKRL ($\mathit{P}<0.05$) across all evaluated values of $\mathit{r} \text{and} \mathit{k}$ with the exception of $\mathit{r}=100$%, and $\mathit{r}=10$% for k = 1, in which case KRL and LKRL performed comparably. Figure 4 and Supplementary Figure S4a show Precision@k and NDCG@k as a function of the evaluation parameter k for the case of sampling five drugs from the 20% of the most effective drugs.

Fig. 4.

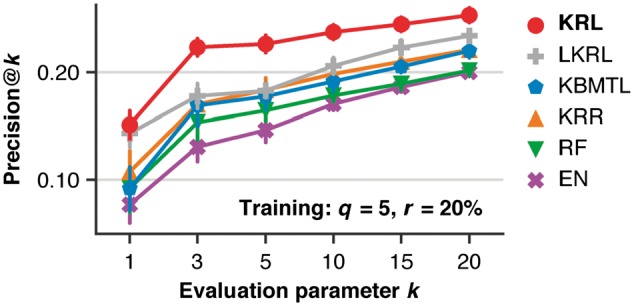
Comparison of KRL with related work (see Section 3.6 for details) in terms of Precision@k (for different values of the evaluation parameter k) using the subsampled training datasets, keeping five drugs (q) per cell line sampled from the 20% of the cell line's most effective drugs (r). The error bars show standard deviations from 10 randomly subsampled training datasets

4.4 Evaluation of the single top drug recommendations

We found that KRL outperformed related work in terms of both Precision@k and NDCG@k for a variety of settings. Arguably, the most clinically relevant setting was presented in the previous section where a few (q) drugs were sampled from a given proportion (r) of the most effective drugs. We analyzed this set of results further by looking at each cell line's single top recommendation (i.e. the drug with the highest predicted ranking score) and quantifying how close this recommendation was to the most effective drug (i.e. the ground truth). To this end, we looked at the distribution of percentile ranks of the recommended drugs.

We calculated a percentile rank of a recommended drug as the percentage of drugs to which the given cell line was less sensitive than it was to the recommended drug. For instance, a percentile rank of 90 means that the recommended drug was in the top 10% of the most effective drugs for the given cell line. Figure 5a–d compares histograms of percentile ranks for KRL and the second best method, KBMTL, when trained using five drugs (q) per cell line sampled from the 100%, 50%, 20% and 10% of the most effective drugs (r), respectively. The figure highlights that regardless of the sampling strategy, 49–56% of KRL's recommendations were within the top 10% of drugs to which the given cell line was most sensitive. While KRL and KBMTL performed comparably for sampling from the full dataset (Fig. 5a, $\mathit{P}=0.50$), the proportion of KRL's recommendations with percentile ranks $>90$ was higher by 4.5%, 18.6% and 24.4% for sampling from the 50%, 20% and 10% of the most effective drugs, respectively (Fig. 5b–d, $\mathit{P}=7.3\times {10}^{-5},\hspace{0.17em}7.2\times {10}^{-6}$ and $7.9\times {10}^{-8}$, respectively). Supplementary Figure S5 shows a similar trend for sampling three and 10 drugs per cell line.

Fig. 5.

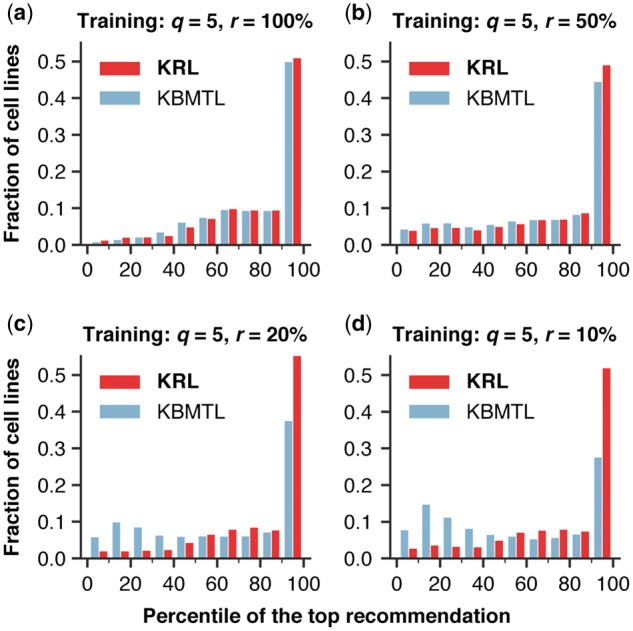
Histograms comparing the distributions of percentile ranks of drugs recommended by KRL and the second best method, KBMTL, using the subsampled training datasets, keeping five drugs (q) per cell line sampled from a predefined fraction (r) of the cell line's most effective drugs. The figure highlights that regardless of the sampling strategy, 49–56% of KRL's recommendations were within the top 10% of drugs to which the given cell line was most sensitive

4.5 Prediction with different data types

So far, all abovementioned results were based on representing a cell line with its gene expression profile. It is of interest to evaluate KRL and related work also for the other three available molecular profiles: whole-exome sequencing, copy number variation and DNA methylation (see Supplementary Table S1 for a summary of features derived from these data types). Figure 6 and Supplementary Figure S6 compare Precision@5 and NDCG@5, respectively, for the six compared methods across all four available data types. These results are based on sampling five drugs (q) from the 100%, 50%, 20% and 10% of the most effective drugs (r) per cell line (Fig. 6a–d, respectively). In agreement with the findings from a drug sensitivity collaborative competition (Costello et al., 2014), gene expression was the most predictive data type regardless of the employed method. Focusing on the other three data types, KRL yielded a comparable performance to KBMTL (the second best method) for $\mathit{r}=100\%$ and 50% and achieved Precision@5 improvements of 3–9% ($\mathit{P}<0.05$) for $\mathit{r}=20\%$ and 10%. NDCG@5 improvements were in the range of 7–15%.

Fig. 6.

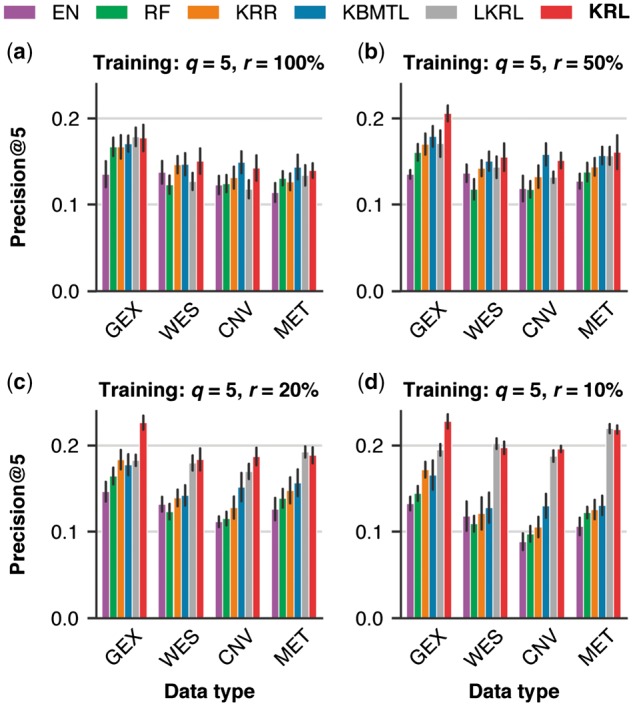
Comparison of KRL with related work (see Section 3.6 for details) across the four molecular data types: gene expression (GEX), whole-exome sequencing (WES), copy number variation (CNV) and DNA methylation (MET). The six compared methods were evaluated in terms of Precision@5 using the subsampled training datasets, keeping five drugs (q) per cell line sampled from a predefined fraction (r) of the cell line's most effective drugs. The error bars show standard deviations from 10 randomly subsampled training datasets

4.6 Clinical trials prediction with KRL

Recently, Geeleher et al. (2014) showed that ridge regression models trained on in vitro cell line models can predict drug response in vivo. We were interested if KRL models can also generalize to patient data. We used the pipeline provided by Geeleher et al. (2014) to download and homogenize docetaxel breast cancer (Chang et al., 2003) and bortezomib multiple myleoma (Mulligan et al., 2007) clinical trials datasets.

First, for docetaxel, there were 10 patients labeled as sensitive (S) and 14 as resistant (R). We used the predicted drug ranks to discriminate between the sensitive and resistant patients. We found that KRL had a tendency to rank docetaxel higher for the sensitive than the resistant patients (Wilcoxon rank sum test, $\mathit{P}=0.04$) with AUROC of 0.71 (Fig. 7a). Second, for bortezomib, there were 169 patients and their responses were classified as complete response (CR), partial response (PR), minimal response (MR), no change (NC), or progressive disease (PD). Comparably to the ridge regression approach (Geeleher et al., 2014), the medians of the predicted drug ranks were able to sort the five categorical responses in the correct order (Fig. 7b). The bortezomib trial defined also another classification which grouped 85 CR, PR and MR patients as responders and 84 NC and PD patients as non-responders. KRL was able to rank bortezomib higher for responders than for non-responders (Wilcoxon rank sum test, $\mathit{P}=2.4\times {10}^{-5}$) with AUROC of 0.68.

Fig. 7.

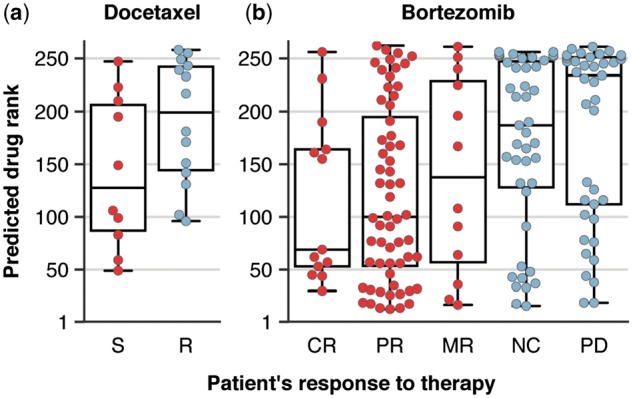
Predicted drug ranks for the docetaxel (a) and bortezomib (b) clinical trials. Docetaxel trial designated patients as sensitive (S) or resistant (R). Bortezomib trial classified the response into five categories: complete response (CR), partial response (PR), minimal response (MR), no change (NC) and progressive disease (PD). Moreover, the patients were grouped as responders (CR, PR and MR) and non-responders (NC and PD)

4.7 TCGA breast cancer cohort prediction with KRL

We showed that drug ranks predicted with KRL trained on cell lines correlate with patient response to treatment. However, the clinical trials datasets do not allow for evaluating how well KRL ranks two (or more) alternative drugs for a given patient. Therefore, we employed the TCGA-BRCA cohort (The Cancer Genome Atlas Network, 2012) and analyzed different molecular breast cancer subtypes to gauge if KRL's drug recommendations for patients are plausible.

Geeleher et al. (2017) showed how to homogenize gene expression profiles measured with RNA-seq (TCGA) and micro-arrays (GDSC), which in turn allowed them to train ridge regression models on the GDSC cell lines and use these models to ‘impute’ drug response of the TCGA patients. In their evaluation, they showed that HER2⁺ TCGA-BRCA patients were predicted to be more sensitive to lapatinib, a first-line therapy for HER2⁺ patients (Gomez et al., 2008), than patients without HER2 overexpression. Here we followed the idea of using molecular subtypes for evaluating KRL's recommendations and compared lapatinib to emerging targeted therapies for TNBCs (Kalimutho et al., 2015).

First, we compared lapatinib and four PARP1/2 inhibitors (PARPi), veliparib, olaparib, talazoparib and rucaparib, some of which have shown promising therapeutic response in BRCA1/2-mutant (mBRCA) tumors (Tutt et al., 2010). Consistent with our hypothesis, we found that lapatinib was ranked higher than all four PARPi for 149 of the 163 HER2⁺ patients (91%). In contrast, lapatinib was recommended over (ranked higher than) PARPi only for one out of nine mBRCA TNBCs (11%). We re-trained KRL 10 times with randomly selected 100 drugs to confirm that the results were statistically different from a random recommendation rate of 50% (unpaired Student t-test, $\mathit{P}=8.2\times {10}^{-14}$ for HER2⁺ and $1.7\times {10}^{-138}$ for mBRCA TNBCs). Table 1 details lapatinib recommendation rates for the individual PARPi. Upon randomly selecting 100 drugs, these results were also statistically different from random ($\mathit{P}\ll 0.05$) except for rucaparib ($\mathit{P}=0.15$), for which a recent clinical trial failed to report objective responses in breast cancer patients (Drew et al., 2016).

Table 1.

KRL’s recommendation rates for TCGA-BRCA molecular subtypes

Recommendation	HER2+	mBRCA TNBC	JAK2+ TNBC
	$n=163$	$n=9$	$n=56$
lapatinib > PARPi	0.91	0.11	—
lapatinib > veliparib	0.95	0.22	—
lapatinib > olapariba	0.94	0.38	—
lapatinib > talazoparib	0.92	0.22	—
lapatinib > rucaparib	0.94	0.44	—
lapatinib > ruxolitinib	0.86	—	0.29

Note: Recommendation rates shown here (lapatinib > alternative drug) are equal to the fractions of patients for which lapatinib was ranked higher than the alternative drug.

^aOlaparib was measured twice in the GDSC dataset but KRL performed comparably for both measurements, here we reported the mean recommendation rates.

Second, we considered ruxolitinib, a JAK1/2 inhibitor approved for the treatment of myelofibrosis, currently being investigated in several clinical trials as a treatment for TNBC (Kalimutho et al., 2015). As expected, we found that lapatinib was ranked higher than ruxolitinib for 140 of the 163 HER2⁺ patients (86%), whereas it was recommended over ruxolitinib only for 16 of the 56 TNBC patients (29%) with normal-to-high JAK2 expression (JAK2⁺). We re-trained KRL 10 times with randomly selected 100 drugs to confirm that these results were statistically different from random ($\mathit{P}=1.1\times {10}^{-11}$ for HER2⁺ and $7.7\times {10}^{-8}$ for JAK2⁺ TNBCs).

5 Conclusion and outlook

This work phrased personalized drug recommendation as a ranking problem of choosing the most effective drugs. This follows from the observation that in a clinical setting, we are interested in providing a recommendation of a few, most effective, drugs rather than predicting the exact response (sensitivity) to all drugs available on the market. To this end, we proposed KRL, which directly optimizes a ranking loss function.

In our empirical evaluation, we aimed to simulate a clinically relevant scenario, in which only a few therapies are prescribed for each patient, by subsampling the training cell lines dataset. We found that KRL outperforms state-of-the-art predictors in drug recommendation with the improvements being largest when the sampling was not random but biased towards effective therapies, thus simulating a medical records knowledge bank in which clinicians' prior knowledge is reflected.

In order to provide reliable and robust recommendations in a clinical setting, KRL needs to be re-trained on patient data and treatment outcomes. Unfortunately, there is currently no publicly available dataset of sufficient size to evaluate KRL in this setting directly. Nevertheless, we were able to show that even when trained on cell lines, KRL recommendations can generalize to patient data and provide plausible recommendations.

One potential direction for future work is extending KRL to learn treatment histories, interdependence and combinations of prescribed therapeutics. We envision that medical records knowledge banks which are currently being gathered by various research consortia will provide the opportunity to study these phenomena with a machine learning approach.

Funding

This work has been supported by the SNSF Starting Grant ‘Significant Pattern Mining’.

Conflict of Interest: none declared.