The latent geometry of the human protein interaction network

Abstract

Motivation

A series of recently introduced algorithms and models advocates for the existence of a hyperbolic geometry underlying the network representation of complex systems. Since the human protein interaction network (hPIN) has a complex architecture, we hypothesized that uncovering its latent geometry could ease challenging problems in systems biology, translating them into measuring distances between proteins.

Results

We embedded the hPIN to hyperbolic space and found that the inferred coordinates of nodes capture biologically relevant features, like protein age, function and cellular localization. This means that the representation of the hPIN in the two-dimensional hyperbolic plane offers a novel and informative way to visualize proteins and their interactions. We then used these coordinates to compute hyperbolic distances between proteins, which served as likelihood scores for the prediction of plausible protein interactions. Finally, we observed that proteins can efficiently communicate with each other via a greedy routing process, guided by the latent geometry of the hPIN. We show that these efficient communication channels can be used to determine the core members of signal transduction pathways and to study how system perturbations impact their efficiency.

Availability and implementation

An R implementation of our network embedder is available at https://github.com/galanisl/NetHypGeom. Also, a web tool for the geometric analysis of the hPIN accompanies this text at http://cbdm-01.zdv.uni-mainz.de/~galanisl/gapi.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Proteins are very complex machines in and of themselves, but their interactions with other proteins foster the formation of a very intricate molecular system. This level of complexity has propelled the development of methods to facilitate the analysis of protein interaction networks (Alanis-Lobato, 2015) and has led to notable advances in biology and medicine (Barabási et al., 2011; Huttlin et al., 2017; Luck et al., 2017; Taylor and Wrana, 2012; Vidal et al., 2011).

Of special interest are a series of algorithms and models that advocate for the existence of a geometry underlying the structure of complex networks, shaping their topology (Boguñá et al., 2009; Cannistraci et al., 2013b; Krioukov et al., 2010; Kuchaiev et al., 2009; Papadopoulos et al., 2012; Pržulj et al., 2004; Serrano et al., 2012; You et al., 2010) [see (Barthélemy, 2011) for an extensive review]. In particular, the Popularity-Similarity model (PSM) sustains that the emergence of strong clustering and scale invariance, properties common to most complex networks, is the result of certain trade-offs between node popularity and similarity (Papadopoulos et al., 2012). This model has a geometric interpretation in hyperbolic space (${\mathbb{H}}^2$), where distance-dependent connection probabilities lead to link formation, accurately describing the growth of complex systems (Alanis-Lobato and Andrade-Navarro, 2016; Boguñá et al., 2010; García-Pérez et al., 2016; Krioukov et al., 2010, 2012; Papadopoulos et al., 2012).

In the PSM, the N nodes comprising a network lie within a circle of radius $R\sim \ln N$, at polar coordinates $(r_i,{\theta }_i)$. The radial coordinate r_i represents the popularity or seniority status of a node i in the system. Nodes that joined the system first have had more time to accumulate links and are close to the circle’s centre, whereas younger nodes lie on the circle’s periphery and have only a few partners. The angular coordinate θ_i allows one to determine how similar a node i is to others. Finally, the hyperbolic distance between nodes, $d_{{\mathbb{H}}^2}(s,t)\approx r_s+r_t+2\ln ({\theta }_{st}/2)$, abstracts the optimization process mentioned above, in which a new node aims at forming a tie not only with the most popular system components but also with the ones that are most similar to it (Papadopoulos et al., 2012).

The PSM is markedly appealing to network biologists because the human protein interaction network (hPIN), the focus of this study, exhibits an approximately scale-free node degree distribution and has a strong clustering (see Supplementary Table S1). Furthermore, uncovering the hidden geometry of the hPIN could ease challenging problems in systems biology (Chuang et al., 2010), allowing us to address them from a geometric perspective. For example, the prediction of protein interactions would translate into the identification of disconnected protein pairs that are unexpectedly close to each other in the network’s latent space.

To investigate whether ${\mathbb{H}}^2$ represents a good host space for the hPIN, we developed an accurate and efficient algorithm for hyperbolic network embedding (Alanis-Lobato et al., 2016b) and explored whether the popularity and similarity dimensions inferred for each protein have a biological interpretation. Furthermore, we exploited the hyperbolic distance between proteins for link prediction and the reconstruction of signal transduction pathways.

2 Materials and methods

2.1 Protein interaction network construction

The hPIN used here represents a stringent subset of release 2.0 of the Human Integrated Protein-Protein Interaction rEference (HIPPIE) (Alanis-Lobato et al., 2017; Schaefer et al., 2012). HIPPIE retrieves interactions between human proteins from major expert-curated databases and calculates a score for each one, reflecting its combined experimental evidence. Only physical interactions that belong to the largest connected component (LCC) were considered. To test the validity of our findings under varying levels of noise, we constructed hPINs using confidence scores $\ge \{0.69,0.70,0.71,0.72,0.73\}$. The 0.72-network was preferred because it has the highest percentage of edges supported by more than one experiment. This network comprises N = 10 824 nodes and L = 66 154 edges. Structural information about all networks is listed in Supplementary Table S1. The networks themselves are provided in Supplementary Material S1.

2.2 Protein age determination

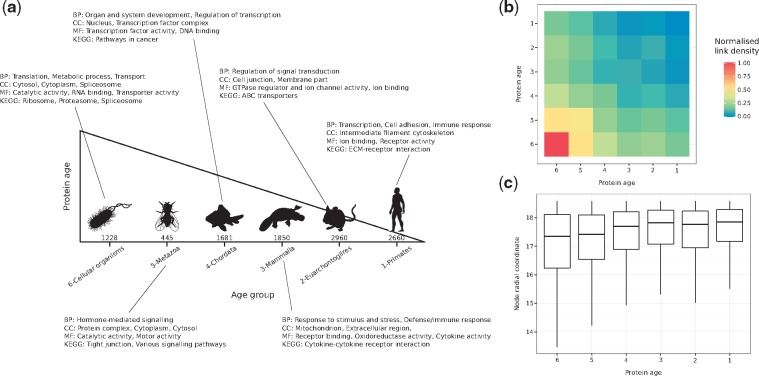
To determine the birth-time of hPIN nodes, we grouped proteins from SwissProt based on near full-length similarity and high threshold of sequence identity using FastaHerder2 (Mier and Andrade-Navarro, 2016). Briefly, age was assigned to human proteins according to the oldest common ancestor of its orthologs (sequences in different species that evolved from a common ancestor by speciation). For example, if a protein was found only in humans, it would have emerged recently, and it is considered a very young protein. If it had orthologs in all extant organisms, it is considerd an old protein. The resulting age groups, from oldest to youngest, were: 6-Cellular organisms, 5-Metazoa, 4-Chordata, 3-Mammalia, 2-Euarchontoglires and 1-Primates.

2.3 Identification of proteins classes

We integrated information from several resources to identify proteins with transcription factor (TF), receptor, transporter or RNA-binding activity; as well as constituents of the cytoskeleton, proteins involved in ubiquitination/proteolysis and cancer proteins. TFs were retrieved from the Animal Transcription Factor Database 2.0 (Zhang et al., 2015a), the census of human TFs (Vaquerizas et al., 2009) and the Human Protein Atlas (Uhlen et al., 2015). From the latter we also retrieved constituents of the cytoskeleton, proteolysis- and cancer-related proteins, receptors, transporters and RNA-binding proteins (RBPs). Additional receptors and transporters were taken from the Guide to Pharmacology (Southan et al., 2015). We also took into account RBPs from the RBP census (Gerstberger et al., 2014). Protein class membership is reported in Supplementary Material S2.

2.4 Mapping the human protein interactome to hyperbolic space

We embedded the hPIN to ${\mathbb{H}}^2$ using LaBNE + HM (Alanis-Lobato et al., 2016b), an approach that combines manifold learning (Alanis-Lobato et al., 2016a) and maximum likelihood estimation (Papadopoulos et al., 2015) to uncover the hidden geometry of complex networks. LaBNE + HM expects a connected network as input, typically the LCC. The other components cannot be mapped due to the lack of adjacency information relative to the LCC. The Laplacian-based Network Embedding (LaBNE), in charge of the manifold learning part of the algorithm, generates a first geometric configuration of a network in ${\mathbb{H}}^2$. This intermediate mapping is then passed on to HyperMap (HM), a maximum likelihood estimation method that searches the space of PSMs for the one that best fits the input network (Papadopoulos et al., 2015). See Supplementary Table S1 for parameter values used in the mapping of all analyzed networks and Supplementary Figure S1 for embedding quality tests.

2.5 Link density computation

We define link density as the observed number of links l between n nodes, divided by the number of possible links that can occur, i.e. $n(n-1)/2$. Since l varies greatly depending on the nodes being considered, we min-max normalized the link density to more easily visualize the difference between node groups. Link densities within and between age groups were compared with distributions of densities resulting from 100 random age assignments via a z-test.

2.6 Functional enrichment analyses

Gene Ontology (GO) (Ashburner et al., 2000) and KEGG pathway (Kanehisa and Goto, 2000) enrichment analyses were carried out with the Database for Annotation, Visualization and Integrated Discovery (DAVID) (Huang et al., 2009). Only GO terms and KEGG pathways enriched at the 0.05 significance level after Benjamini-Hochberg correction were considered.

2.7 Clustering in the similarity dimension

We computed the difference between consecutive inferred angles to identify big gaps separating groups of proteins in the similarity dimension (see Supplementary Fig. S3a). We chose the gap size g, such that the sectors flanked by two gaps contained at least 10 proteins (g = 0.0132, Supplementary Fig. S3b). Neighbouring clusters with similar biological functions and cellular localizations were merged to avoid redundancy.

We checked if protein classes agglomerate non-randomly within their corresponding similarity-based clusters by carrying out a Fisher’s exact test. For this, we compared the proportion of proteins in class $c=\{TF,receptor,transporter,RBP,cytoskeleton,ubiquitination/proteolysis\}$ that fall within a related similarity cluster against the proportion of proteins of the same class in the remaining clusters. The protein classes and their related cluster identifiers are: TF, 8; receptor, 12; transporter, 4, 5, 9 and 13; RBP, 7 and 14; cytoskeleton, 3; ubiquitination/proteolysis, 1, 2 and 15. The resulting P-values were adjusted with the Benjamini-Hochberg method.

2.8 Protein interaction prediction

Link prediction methods assign likelihood scores of interaction to all the disconnected node pairs of a network. We ranked these candidate interactions by hyperbolic distance and compared the top-100 with the best candidates from different classes of prediction methods: the neighbourhood-based link predictors Common Neighbours (CN) (Newman, 2001), Adamic & Adar (AA) (Adamic and Adar, 2003) and Preferential Attachment (PA) (Newman, 2001); the Cannistraci-Alanis-Ravasi index (CAR) and the CAR-based AA (CAA) and PA (CPA) (Cannistraci et al., 2013a); the embedding-based link predictors ISOMAP (Kuchaiev et al., 2009; Tenenbaum, 2000; You et al., 2010) and non-centred Minimum Curvilinear Embedding (ncMCE) (Cannistraci et al., 2013b); and the recently proposed Structural Perturbation Method (SPM) (Lü et al., 2015). See (Lü et al., 2015; Martínez et al., 2016) for more details and predictor formulations.

The discrimination between good and bad candidates was based on the Guilt-by-association Principle, which states that if two proteins are involved in similar biological processes or are located in the same cellular compartment, they are more likely to interact (Oliver, 2000). Thus, good candidate interactions correspond to top-ranked pairs of proteins that play a role in at least one common pathway (functional homogeneity) or locate to the same subcellular structure (localization coherence). This link prediction evaluation framework is extensively used in network biology (Alanis-Lobato et al., 2013, 2016a; Chen et al., 2006; Saito, 2002; Saito et al., 2003). Pathway memberships were determined via KEGG pathways (Kanehisa and Goto, 2000) and cellular localizations via the Cellular Compartment aspect of the GO (Ashburner et al., 2000) and the Cell Atlas (Thul et al., 2017). The top-100 candidate interactions of each link predictor are provided in Supplementary Material S6.

2.9 Greedy routing and pathway reconstruction

In greedy routing, the inferred hyperbolic coordinates of nodes are used as addresses to send signals between nodes. The process starts with the source checking which one of its direct neighbours is hyperbolically closest to the target and sends the signal there. The recipient checks amongst its direct partners for the one closest to the target, and so on, until the destination is reached (successful delivery). If, in the delivery process, a node sends the signal to the previously visited protein, i.e. it falls into a loop, the signal is dropped and the delivery flagged as unsuccessful (Krioukov et al., 2010).

We performed 100 routing experiments, each with 1000 source-target pairs. These pairs were selected at random or from a pool of TFs, receptors or cancer-related proteins. Since the number of proteins in each one of these classes differs, the pools were formed by 500 randomly-selected members of each one. Routing efficiencies (percentage of the 1000 source-target pairs in which greedy routing was successful) were averaged across the 100 experiments. Mann-Whitney U tests were used to compare efficiency distributions.

For pathway reconstruction, we computed greedy and shortest paths from sources to targets of the 24 signal transduction pathways listed in KEGG (Kanehisa and Goto, 2000) and their equivalents in Reactome (Fabregat et al., 2016) and WikiPathways (Kutmon et al., 2016). These starting- and end-points were determined based on KEGG itself and the literature (Berg et al., 2002; Cooper, 2000) and represent canonical transduction initiators and transcriptional regulators, respectively. We computed the fraction of reported pathway members forming the greedy or shortest paths. For some pathways, we compiled more than one source-target pair and computed the average fraction instead. All these pairs and their corresponding pathways are reported in Supplementary Material S7. Pathway membership was determined by integrating data from KEGG, Reactome and WikiPathways.

3 Results

3.1 The latent geometry of the human protein interactome

We constructed a protein network with high-quality interactions from the HIPPIE database (Alanis-Lobato et al., 2017; Schaefer et al., 2012) (see Section 2 and Supplementary Material S1). The resulting network was embedded to the two-dimensional hyperbolic plane ${\mathbb{H}}^2$ using LaBNE + HM (Alanis-Lobato et al., 2016a,b; Papadopoulos et al., 2015), a method to uncover the hidden geometry of complex networks (see Section 2). Once the hyperbolic coordinates of each protein in the network were inferred (see Supplementary Material S2), we proceeded to analyze whether these coordinates are meaningful or not from a biological point of view.

3.2 Radial coordinates and protein evolution

The popularity component of the PSM (radial coordinates of nodes in ${\mathbb{H}}^2$) is associated with the seniority status of network nodes. To verify if our mapping reflects this property, we assigned proteins to six different age groups according to the existence of evolutionarily-related counterparts in other organisms (see Fig. 1a, Section 2 and Supplementary Material S2).

Fig. 1.

(a) Proteins in the constructed hPIN were clustered into six different age groups (the number of proteins in each one is indicated). Over-represented biological functions and compartments in each group were determined via GO and KEGG pathway enrichment analyses (BP: Biological Process, CC: Cellular Compartment, MF: Molecular Function). (b) Normalized link density within and between age groups. (c) Distribution of inferred radial coordinates for the proteins in each age group

While old nodes have high degrees and are involved in essential functions, like metabolic processes or protein translation, younger nodes have only a few direct partners and are in charge of more specialized processes, like organ development and immune response (see Fig. 1a, Supplementary Fig. S2a and Supplementary Material S3). Moreover, there is a strong link density within and between old age groups, which is reduced within and between the young ones (see Fig. 1b and Section 2). This is in agreement with previous observations that there is a core of old highly interconnected proteins, surrounded by younger proteins with no interactions between them but dependent on the old core (Beltrao and Serrano, 2007; Zhang et al., 2015b). All these results cannot be replicated if proteins are randomly assigned to the six different age groups (see Supplementary Fig. S2b, c).

Finally, we checked the inferred radial coordinates of the proteins in each group and, consistent with the PSM, old proteins are closer to the centre of the hyperbolic circle compared to younger ones (see Fig. 1c). The observed trend is an indication that the radial positions of proteins in ${\mathbb{H}}^2$ encode information about their evolutionary origin.

3.3 Angular coordinates and protein function

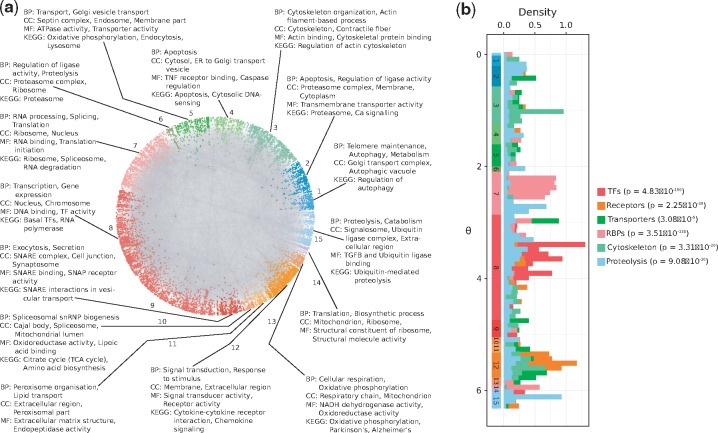
The similarity component of the PSM (angular coordinates of nodes in ${\mathbb{H}}^2$) abstracts the characteristics that make a node similar to others. To investigate the biological meaning of inferred angles, we identified protein agglomerations in the angular dimension of ${\mathbb{H}}^2$ (see Supplementary Fig. S3 and Section 2). As shown in Figure 2a, angles capture the functional and spatial organization of the cell, and this is supported by the three aspects of the GO and by KEGG (see Supplementary Material S4 and Supplementary Fig. S4). For example, the over-represented biological process of cluster 8 is transcription. The cellular compartment where this process takes place, the nucleus, is also enriched, as well as the molecular functions DNA binding and transcription factor activity together with the basal transcription factors pathway.

Fig. 2.

(a) Protein clusters identified by big gaps separating groups of proteins in the angular dimension of ${\mathbb{H}}^2$. The over-represented biological functions and compartments in each cluster were determined via GO and KEGG pathway enrichment analyses (BP: Biological Process, CC: Cellular Compartment, MF: Molecular Function). Each cluster was assigned a numeric identifier (1–15). (b) Distribution of inferred angular coordinates for proteins with specific molecular functions (TFs: Transcription Factors, RBPs: RNA-binding proteins). P-values highlight that these protein classes agglomerate non-randomly within their corresponding similarity-based cluster from a. The start and end of these clusters are indicated across the $[0,2\pi ]$ range, below the histograms

Figure 2b shows the distribution of inferred angles for different protein classes and highlights how they agglomerate in the similarity-based clusters enriched for their particular activity, in numbers that are significantly higher than expected by chance (see Section 2 and Supplementary Material S2). For example, RBPs accumulate in cluster 7, which, as expected, is enriched for RNA processing and protein translation. Also, nodes involved in marking proteins with ubiquitin for their degradation via the proteasome, though more dispersed across the full angular dimension, are more common in the clusters enriched for ubiquitination and proteolysis (1, 2 and 15).

To study whether the clusters suggested by the angular coordinates of proteins could have been detected with a traditional community detection method, we applied the Louvain algorithm to the hPIN (Blondel et al., 2008). This method identified communities that do not correspond with the obtained similarity-based clusters (see Supplementary Fig. S5a–d). The Louvain-based communities are either enriched for very specific biological processes or not enriched for any process in particular (see Supplementary Material S5). This outcome suggests that they represent protein complexes or groups of a few proteins that, together, play roles in very specific functions (see Supplementary Fig. S5d). In contrast, the angular clusters are formed by proteins with roles in more general pathways (see Supplementary Material S4) that can be analyzed in more detail if smaller gaps between angles are considered (see Supplementary Figs S3, S5c and Section 2).

The results presented so far correspond to an hPIN formed by interactions with HIPPIE confidence scores ≥ 0.72 (see Section 2), which means that they are well-supported by experimental evidence. However, this also means that the considered interactome is vastly incomplete. To test if our findings are robust to network topology changes (e.g. higher presence of false negatives if a more stringent score is used or more false positives if the score is less conservative), we constructed hPINs with varying quality levels (see Supplementary Table S1). Supplementary Figure S6 shows that regardless of the assessed confidence score, the inferred protein coordinates lead to the same conclusions: old proteins tend to be closer to the centre of ${\mathbb{H}}^2$ than young ones and proteins with specific molecular functions cluster together in the angular dimension. We expect these observations to hold true, or even improve, as hPIN charting efforts enhance network coverage and reliability (Huttlin et al., 2017; Luck et al., 2017).

3.4 Hyperbolic distances and protein interactions

Now that the two dimensions of the PSM have been interpreted in a biological context, we can use them to compute hyperbolic distances between proteins. Figure 3a shows connection probabilities (fraction of connected node pairs, amongst all pairs separated by a certain distance) as a function of the hyperbolic separation between proteins. In concordance with what the PSM predicts for a network with the same structural characteristics as the hPIN, we can see that, according to the coordinates inferred with LaBNE + HM, if two proteins are very close to each other, they most certainly interact. On the other hand, if proteins are far apart, their probability of interaction is very low. Additionally, protein interactions with high HIPPIE confidence scores are closer to each other than proteins with low scores (see Supplementary Fig. S7).

Fig. 3.

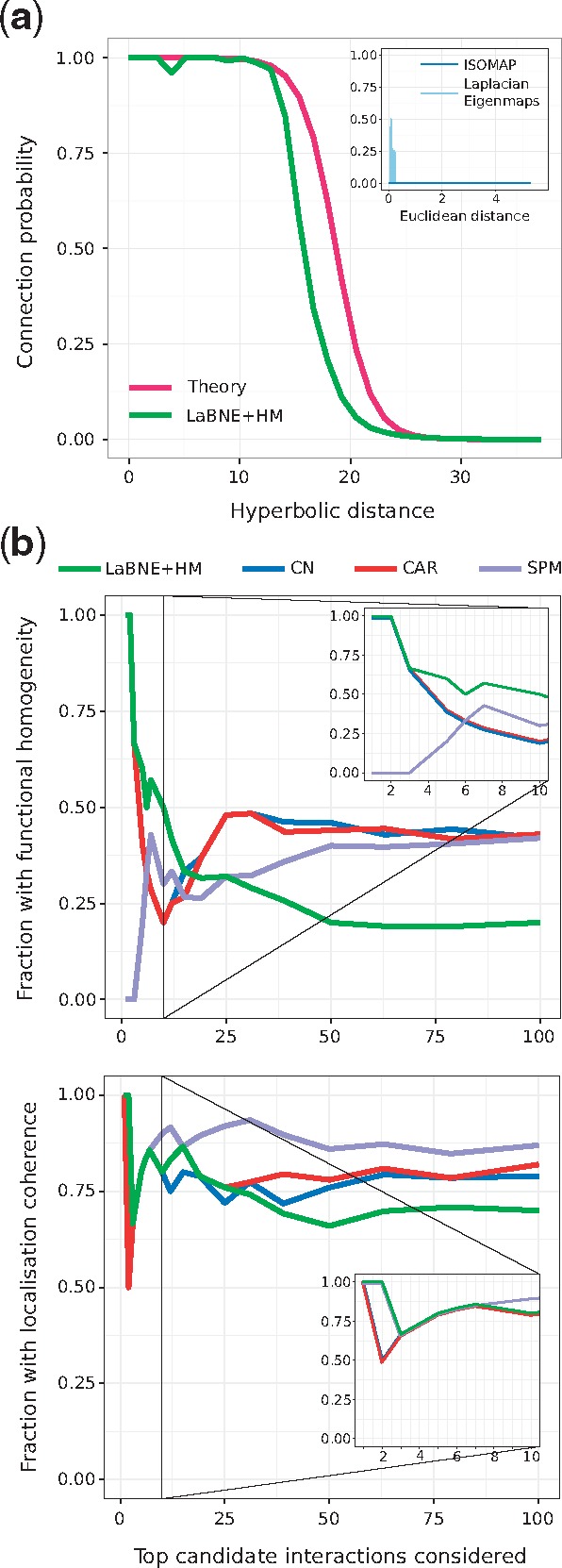
(a) Connection probability as a function of the hyperbolic or Euclidean (inset) separation between protein pairs. The probabilities predicted by the PSM (Theory) and the ones obtained by mapping the network to a geometric space with LaBNE + HM, ISOMAP and Laplacian Eigenmaps are shown. (b) We compared the top-100 disconnected proteins that are closest to each other in ${\mathbb{H}}^2$ (LaBNE + HM) with candidate protein interactions from representative link predictors of different classes (see Supplementary Fig. S8 for the complete analysis). The plot shows how the fraction of potential interactions with functional homogeneity and localization coherence changes as more protein pairs are assessed. Insets focus on the top-10 candidate pairs. CN: Common Neighbours, CAR: Cannistraci-Alanis-Ravasi index, SPM: Structural Perturbation Method

We tried to replicate the above findings by embedding the hPIN into the two-dimensional Euclidean space, using two different techniques (Belkin and Niyogi, 2001; Tenenbaum, 2000) [we refer the reader to (Cannistraci et al., 2013b; Kuchaiev et al., 2009; You et al., 2010) for details on how these network embeddings are performed]. The resulting connection probabilities are far from what the mapping to ${\mathbb{H}}^2$ achieves (see inset in Fig. 3a), further endorsing the suitability of this space to describe complex networks like the hPIN.

These results encouraged us to check whether the 100 hyperbolically-closest disconnected protein pairs represent plausible protein interactions. Figure 3b shows that LaBNE + HM’s predictions are more biologically meaningful than those from representatives of different link prediction classes (Lü et al., 2015; Martínez et al., 2016) (see Supplementary Fig. S8 for the complete analysis, as well as the Section 2 and Supplementary Material S6), especially if we focus on the top-10 candidates: non-adjacent proteins that are close in ${\mathbb{H}}^2$ play roles in at least one common pathway (functional homogeneity) and localize to the same cellular compartments (localization coherence).

Our top prediction, for example, involves proteins SUMO2 and p65 and is supported by recent studies in mouse and human. After observing that over-expression of SUMO2 derives in the lack of nuclear p65, a group working with mouse dendritic cells proposed that SUMO2 traps p65 in the cytoplasm and avoids its translocation to the nucleus (Kim et al., 2011). Further supporting this hypothesis, Liu and colleagues observed that the transfection of human hepatocarcinoma with increasing doses of SUMO2 gradually increases cytoplasmic p65 levels, whereas knock-down of SUMO2 decreases them (Liu et al., 2015).

Although the other link predictors improve as more candidates are evaluated, we cannot discard that some of LaBNE + HM’s predictions are actually part of the same pathway or organelle, as pathway membership and protein localization references are still incomplete. A sign of this lack of annotations is that only ∼20% of the top-100 potential interactions identified by each prediction method are reported in HIPPIE v2.0 (see Supplementary Fig. S9a) and a maximum of three were confirmed by two recent large-scale network charting efforts (Huttlin et al., 2017; Luck et al., 2017) (see Supplementary Fig. S9b, c). This means that there is no experimental evidence for the interaction of most of these protein pairs, a problem that proteome-scale and unbiased protein network mapping endeavours are addressing (Luck et al., 2017).

3.5 Greedy routing and signal transduction

Hyperbolic distances can also be used to study signal transduction pathways, the way in which cells communicate with each other and respond to environmental changes (Berg et al., 2002). These pathways normally start with a signal stimulating a cell membrane receptor, which leads to the activation of a series of proteins, until the signal reaches the nucleus, where a TF binds DNA and regulates target genes (Cooper, 2000). Interestingly, signals travel from source to target with the former not having knowledge of the global protein network structure (Boguñá et al., 2009; Krioukov et al., 2010). Proteins can only activate or repress their direct neighbours in the hPIN, and these stimuli cascade through the network in the same way, until the end of the pathway (Cooper, 2000). This prompted us to investigate whether a signal can effectively reach its target, using the shortest possible path, via greedy routing (see Section 2).

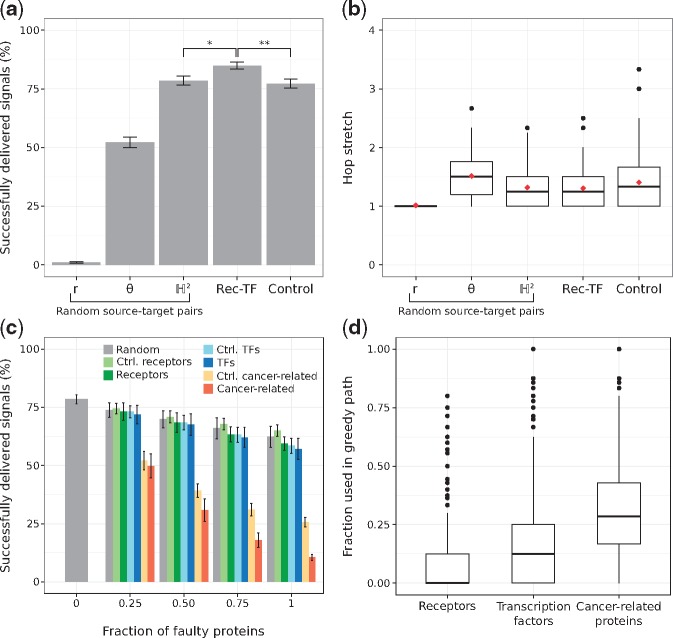
Figure 4a shows the average routing efficiencies. Note that if signals travel to the neighbour that is radially or angularly closest to the target, greedy routing is not as efficient as when the hyperbolic distances are used, underlining the importance of both dimensions for the proper navigation of the hPIN (Alanis-Lobato et al., 2016b; Krioukov et al., 2010). Moreover, the hop stretch (greedy path length divided by shortest path length) is close to 1 (see Fig. 4b), which means that greedy paths, guided by the network’s latent geometry, are very often shortest paths.

Fig. 4.

(a) Percentage of successfully greedy-routed signals for randomly chosen source-target proteins (using the neighbour radially r, angularly θ or hyperbolically ${\mathbb{H}}^2$ closest to the target), from receptors to transcription factors (Rec-TF) or from proteins that are neither receptors nor transcription factors, but have degrees similar to their counterparts (Control). *P=1.898 × 10^-34, ** P=1.233 × 10^-34, Mann-Whitney U test. (b) Hop stretches for all the cases presented in (a). Average hop stretches are reported with red diamonds. (c) Percentage of successfully delivered signals when increasing levels of faulty proteins are introduced. Faulty proteins are chosen at random or from a pool with the same number of receptors, TFs, cancer-related proteins, control receptors (Ctrl. receptors), control TFs (Ctrl. TFs) or control cancer-related proteins (Ctrl. cancer-related). (d) Distribution of the fraction of receptors, TFs and cancer-related proteins used in 1000 different greedy paths. Error bars correspond to standard deviations

Given the biological importance of signal transduction, we hypothesized that it should be more efficient to send signals from receptors (Recs) to TFs, and that is indeed the case ($P=1.898\times {10}^{-34}$, see Fig. 4a). The Rec-TF efficiency is also significantly larger than the one achieved through the use of proteins that are neither Recs nor TFs, but that have degrees similar to their counterparts ($P=1.233\times {10}^{-34}$, see Fig. 4a and Supplementary Fig. S10a, b). Here, we refer to them as control Recs and control TFs, respectively.

We also explored the effects of defective proteins in greedy routing efficiency. If a greedy path passes through a faulty protein, signal transduction is interrupted, making routing unsuccessful. From a biological perspective, this experiment could be modelling the effects caused by mutations or insufficient protein levels. In some situations, these defects manifest as disease phenotypes.

As depicted in Figure 4c, the increasing introduction of defective receptors or TFs impacts greedy routing efficiency more than the introduction of faulty proteins at random or from the pool of control receptors or control TFs. We tested these using pools with the same amount of receptors and TFs to make sure that the observed effects were not due to different abundances of these protein types in the hPIN. Interestingly, faulty nodes from a pool of cancer-related proteins (see Section 2) severely affect network navigability compared to TFs, receptors and even control cancer proteins (see Fig. 4c and Supplementary Fig. S10c). This result cannot be attributed to cancer proteins having more connections, as their degree distribution is similar to that of TFs and receptors (see Supplementary Fig. S10). Rather, it could be explained by how often cancer-related proteins are part of greedy paths (see Fig. 4d) and motivates a deeper investigation of the relationship between network navigation, function and disease, which is outside the scope of this work.

One of the major challenges in systems biology is the determination of the chain of reactions that guides signals from receptors in the cell membrane to TFs in the nucleus (Ritz et al., 2016). Although current experimental technologies enable the identification of the proteins in charge of sensing the cell’s environment and the deduction of the downstream effects of these sensory inputs, building the complete set of interactions that are part of signalling pathways still requires extensive and time-consuming manual curation efforts (Gitter et al., 2011; Ritz et al., 2016). As a result, the development of automatic pathway reconstruction methods is a field of active research (Gitter et al., 2011; Ritz et al., 2016; Supper et al., 2009; Yosef et al., 2009). Such methods aim at establishing pathway members and their interactions, given only two anchoring points: the receptor or source of the pathway and the target transcriptional regulator (Ritz et al., 2016).

We explored the extent to which well-established signal transduction pathways can be recapitulated by navigating the latent geometry of the hPIN with greedy routing. Note that our goal was not the full reconstruction of pathways, with all their diversions, loops and buffering controls. Rather, our objective was to study whether the inferred network geometry can guide signals through the core pathway members.

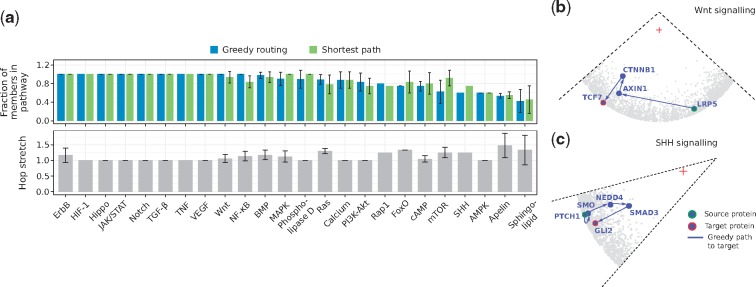
Using greedy routing and traditional shortest paths, we sent signals from canonical sources to canonical transcriptional regulators of the 24 signal transduction pathways listed in KEGG (Kanehisa and Goto, 2000) (see Supplementary Material S7). Then, we computed the fraction of proteins that are part of the resulting greedy/shortest paths and that are reported pathway members (see Section 2). Figure 5a and Supplementary Figure S11 show that, in 70% of the cases, greedy paths are as good as or better than shortest paths because they contain more proteins that are in fact part of the analyzed pathway. Along with this, hop stretches fluctuate around 1, indicating that the navigated greedy paths, found using local information only, are often shortest paths.

Fig. 5.

(a) Signals were routed from receptors to transcriptional regulators of the 24 signal transduction pathways listed in KEGG. Greedy routing and shortest-paths were employed. The fraction of greedy path and shortest path members that are part of each pathway is reported, together with the hop stretch (greedy path length divided by shortest path length). When more than one source or target was considered, the average fraction is reported. Error bars correspond to standard deviations. Reconstruction of the (b) Wnt and (c) SHH signal transduction pathways by navigation of the latent geometry of the hPIN with greedy routing. A red cross indicates the centre of the hyperbolic circle containing the hPIN

For example, Wnt signalling, a well-characterized pathway with an important role in embryonic development (Atsushi et al., 2004), can be recapitulated with greedy routing (see Fig. 5b). In its canonical form, this pathway is activated when a Wnt signal stimulates the LRP membrane receptors (LRP5 and LRP6), leading to their association with a multiprotein complex containing AXIN1. This event stabilizes the β-catenin protein (CTNNB1), which translocates to the nucleus, and binds TCF7 (Atsushi et al., 2004; Niehrs, 2006).

Longer greedy paths with just a small fraction of reported pathway members are also interesting, as they may contain new pieces of the signal transduction machinery. In Figure 5a we can see that only $60\%$ of the greedy path members for the SHH pathway is reported in our integrated dataset. It is known that the cellular response to an SHH signal is controlled by the transmembrane proteins PTCH1 and Smoothened (SMO), but the way in which SMO connects to the target TFs GLI1, GLI2 or GLI3 is still under discussion (Dennler et al., 2007; Luo et al., 2012). The geometric-based reconstruction of this pathway suggests that the proteins in charge of GLI2 activation are NEDD4 and SMAD3 (see Fig. 5c) and we found experimental evidence for this scenario. First, Luo and colleagues measured the interaction between SMO and NEDD4 and, by means of over-expression and knock-down experiments, identified the positive regulation of the SHH pathway by the latter (Luo et al., 2012). Secondly, Dennler et al. showed that the activation of GLI2 by SMAD3 is possible in vitro and in vivo (Dennler et al., 2007). Third, there is accumulating evidence placing the NEDD4 family of E3 ubiquitin ligases as key regulators of GLI (Chen et al., 2014; Di Marcotullio et al., 2011; Yue et al., 2014). This information supports what the geometry of the hPIN put forward and encourages further exploration of the involvement of NEDD4 and SMAD3 in SHH signal transduction.

4 Conclusion

We used manifold learning and maximum likelihood estimation to embed the human protein interactome into the two-dimensional hyperbolic plane (Alanis-Lobato et al., 2016b). Our results highlight that the latent geometry of the hPIN accurately reflects its structure and dynamics and represents a powerful tool to gain insights into the intricacies underlying this complex molecular machine.

On the one hand, the radial positioning of nodes (i.e. the geometric abstraction of their popularity or seniority status in the network) encapsulates information about the conservation and evolution of proteins. On the other, their angular positioning (abstracting the similarity between system components) captures the functional and spatial organization of the cell. Together, the inferred radial and angular coordinates of nodes can be used to compute hyperbolic distances and assess whether two proteins are likely to interact. In addition, hyperbolic coordinates and distances can be used to simulate cell signalling events, reconstruct signal transduction pathways and study the effects of perturbations in such protein communication channels.

It is important to stress that the hPIN used throughout this article is an aggregate of protein interactions that take place under different time scales, conditions and tissues. Consequently, the results obtained by means of the latent geometry of the hPIN must be interpreted in the right biological context in order to reach sound conclusions. Notwithstanding this caveat, the use of this mapping not only reduces the universe of possibilities to test in the laboratory but can also lead to a better understanding of the mechanisms underlying the onset and development of complex human disorders. To support this endeavour, we have developed a web tool for the geometric analysis of the hPIN (http://cbdm-01.zdv.uni-mainz.de/~galanisl/gapi). With it, users can easily relate the position of proteins of interest with that of age or functional clusters and can simulate signalling events utilising greedy routing.