Rotating Bacteria on Solid Surfaces without Tethering

Abstract

Bacterial motion is strongly affected by the presence of a surface. One of the hallmarks of swimming near a surface is a defined curvature of bacterial trajectories, underlining the importance of counter rotations of the cell body and flagellum for locomotion of the microorganism. We find that there is another mode of bacterial motion on solid surfaces, i.e., self trapping due to fluid flows created by a rotating flagellum perpendicular to the surface. For a rod-like bacterium, such as Escherichia coli, this creates a peculiar situation in that the bacterium appears to swim along a minor axis of the cell body and is pressed against the surface. Although a full hydrodynamic theory is still lacking to explain the self-trapping phenomenon, the effect is intriguing and can be exploited to study a variety of biophysical phenomena of swimming bacteria. In particular, we showed that self-trapped E. coli cells display a chemotaxis response that is identical to the classical rotation assay in which antibodies are used to physically “glue” a flagellum to the surface.

Introduction

A swimming bacterium is hydrodynamically attracted to a solid surface because of its own image (1). The effect is noticeable, as the concentration of bacteria near a surface is markedly higher than away from it. This attractive force is the reason that many cells swim close to a surface (2), and some of them eventually become immobile. Surface localization is a first step for bacteria to change lifestyles from planktonic to forming colonies. This switch provides bacteria with many advantages, such as being close to a nutrient source where organic materials are deposited (3) or spatial refuge where bacteria are protected by a heterogeneous environment (4). A fascinating example is Caulobacter crescentus, which oscillates between stalked and motile cell phenotypes and is able to adapt to both aqueous and surface environments.

Herein, we report behaviors of a subpopulation of surface-bound Escherichia coli bacteria that appear in an optical microscope as rotating cells akin to tethered cells using anti-flagellin antibodies, which we term classical rotation assay (5). Our investigation shows that these are normal swimming bacteria, and they are trapped by the fluid flow created by their own thrust force. Specifically, unlike a free-swimming bacterium for which the flagellar bundle is organized along the major axis of the body, a surface-bound rotating bacterium has its flagellar bundle perpendicular to the cell-body major axis and is aligned with the surface norm, indicating that flagellar bundle formation is strongly influenced by the symmetry of the cell as well as a bounding surface. Our observation showed that tumbling of the cell causes a disruption in the cell-body rotation speed but does not always destabilize self trapping. Video recording of these “trapped” cells reveals that the angular velocity Ω of individual bacteria fluctuates widely but is distributed in a bimodal fashion, indicating the existence of two rotation states for a bacterium (Videos S1, S2, and S3). This allows a time trace Ω (t), constructed for each cell, to be analyzed for its steady-state fluctuations as well as its responses to external stimuli. Remarkably, we found that the response to an impulsive chemical stimulation is biphasic, similar to results obtained by the classical assay (6, 7). A physical mechanism of self trapping is postulated, but a full explanation requires more theoretical analysis.

Video S1. Flow in the Neighborhood of a Flagellar Bundle

A nonmotile cell interacts hydrodynamically with the flagellar bundle of a rotating cell. The self-trapped cell, which is slightly out of focus, is rotating in the CW direction, whereas the nonmotile cell is pulled CCW about the rotation axis.

Video S2. Flagella Staining of a Trapped RP437 Cell

The video is a stitch of two videos: the first showing the rotating cell just before staining, and the second showing the result after staining. Multiple flagella can be seen extending from the cell body in random directions.

Video S3. Flagella Staining of a Trapped Smooth-Swimming Cell RP5232

The video is a stitch of two videos: the first shows two trapped cells rotating before the stain is applied, and the second shows the results of the staining. Both cells can be seen to have a single flagellar bundle extending away from the cell body normal to the glass surface.

Methods

Cell strains, plasmids, and growth conditions

To compare our observation with tethered cells, bacteriophage P1 transduction was carried out to delete the fliC gene in the wild-type (WT) E. coli strain RP437 using the donor strain JA11 (8). The resulting strain, XLWU100, was transformed to carry the plasmid pFD313 encoding a mutant FliC that displays a strong affinity to glass (9). This strain therefore can be used to study bacterial cell-body rotation using single-motor tethering, as in the classical rotation assay. Another mutant used in our experiment is RP5232, which is derived from RP437 by deleting cheY and is smooth swimming (10).

All bacteria (RP437, XLWU100, and RP5232) were grown according to the standard protocol, i.e., overnight cultures were grown in tryptone broth (1% tryptone powder, 0.5% NaCl) from single colonies, incubated at 33°C, and vigorously shaken at 200 rotations per minute by a rotary shaker. The overnight cultures were used to inoculate fresh tryptone broth medium at 1:100 and incubated for 4 hr at the same temperature with shaking (11). The bacteria were washed twice in a motility buffer (10 mM KPO₄, 0.1 mM ethylenediaminetetraacetic acid, 1 μM L-methionine, 67 mM NaCl, 10 mM sodium lactate) before being introduced to an observation chamber (12). When needed, the bacteria were sheared to different degrees, following the procedure described in (6). Briefly, the freshly grown bacteria were passed repeatedly through two 21-gauge syringe needles connected by a Tygon tube (Saint-Gobain, Malvern, PA) ∼5 cm long. The sheared cells were washed once more before observation.

Data collection and analysis

Our measurements were carried out on an inverted microscope (TE300; Nikon Instruments, Melville, NY) using a phase contrast and fluorescence mode. The homemade observation chamber, which consists of a stainless-steel frame and a 25 mm round cover glass (#0) that serves as the floor of the chamber, is depicted in Fig. 1. The top of the chamber is open to air, allowing rapid exchange of the buffer and stimulation of a bacterium by means of chemical or temperature. For chemical stimulation, a micropipette connected to a Picospritzer (Parker Instruments, Cleveland, OH) was used. The micropipettes were pulled from standard borosilicate glass capillaries (1.5–1.8 mm OD) using a microelectrode puller (PP-830; Narishige, Amityville, NY). For temperature stimulation, we used a fiber-coupled infrared (IR) solid-state laser (λ = 1440 nm). The free end of the fiber (∼50 μm in diameter) or the tip of the micropipette can be positioned precisely above a preselected bacterium by a three-axis micromanipulator (Siskiyou, Grant Pass, OR).

Figure 1.

Experimental setup. The observation chamber is open to air and filled with the motility buffer ∼3 mm in depth. The bottom of the chamber consists of a round cover glass and is sealed by compression using a silicon gasket and a delrin ring. The assembly is housed in a stainless-steel holder that fits onto the stage of our microscope. A surface-bound, rotating bacterium can be stimulated from above the chamber either using a micropipette or an IR laser (not shown). Cell-body rotation is measured using a 100× oil immersion objective. To see this figure in color, go online.

Video images were acquired by a Hamamatsu CCD camera (Model C9100-12; Hamamatsu, Japan) and transferred to a PC using Hamamatsu software. We recorded cell-body rotation for all strains at 50 fps using the CCD camera with phase contrast imaging. The images were processed by a custom MATLAB script (MathWorks, Natick, MA). To find the angular velocity Ω of cell-body rotation, an orientation vector of the cell was determined frame by frame using the cell’s long axis and center of mass, resulting in a time series Ω (t). All traces for an individual cell were then used to create a probability density function (PDF) of Ω, P(Ω). We found that this PDF could be fitted by a sum of two Gaussian functions, P(Ω) = P_t(Ω) + P_r(Ω), for both trapped and tethered cells, suggesting the existence of two rotation states of the body. Here, the subscripts t and r correspond to the tumble and the run states, respectively. To specify the state of cell-body rotation at a given time for trapped WT RP437 cells, we defined two thresholds Ω_t and Ω_r; for Ω < Ω_t, the cell is tumbling, and for Ω > Ω_r, the cell is running, where the lower and upper thresholds are set by the criteria P_t(Ω_t)/P(Ω_t) = 0.75 and P_r(Ω_r)/P(Ω_r) = 0.75 (see Fig. 3, A–C for its implementation). A transition from one state to the other takes place if and only if Ω (t) crosses both thresholds (13). For tethered XLWU100 bacteria, a simpler algorithm was used such that Ω (t) < 0 corresponds to a “run” state and Ω (t) > 0 corresponds to a “tumble” state (see Fig. 3, G–I for the implimentation). Using these algorithms, we calculate the time-dependent bias Φ(t), or the probability of a cell to be in a run state, by averaging the time traces aligned according to the stimulation pulses.

Figure 3.

Examples of rotation angular velocity PDFs for RP437 (top panels), RP5232 (middle panels), and XLWU100 (bottom panels). Each panel represents measurements from a single bacterium, and three panels for each cell type show typical cell-to-cell variations. We define Ω > 0 (Ω < 0) to be CW (CCW) cell-body rotation. The experimental data (black dots) are fitted with a sum of two Gaussians (P = P_t + P_r) for RP437 and XLWU100 and to a single Gaussian (P_r) for RP5232. (A)–(C) The dotted vertical lines, indicated by Ω_t and Ω_r, mark the boundary for the two (tumble, run) rotation states. These boundaries are determined according to the criterion P_i(Ω_i)/P(Ω_i) = 75%, where i = t or r. (D)–(F) The rotation speed of smooth-swimming mutant RP5232 can be fitted well by a single Gaussian. (G)–(I) The cell-body rotation of XLWU100 (ΔfliC) is expected to be similar to what is seen in the classical rotation assay because flagellar filaments of XLWU100 are sticky to glass. P(Ω) for this mutant is bimodal, similar to RP437; however, the two Gaussian peaks are well separated and are about equal in height. Note that for this mutant, CW motor rotation corresponds to Ω > 0 by our definition. Despite cell-to-cell variations, almost all cells (∼10²) examined for each strain have similar characteristics as displayed. To see this figure in color, go online.

Flagellar staining

To visualize flagella of a bacterium, a new (to our knowledge) real-time staining technique was implemented. In this technique, a micropipette, similar to the one used for chemical stimulation, was filled with Ryu Flagella Stain (Remel/Fisher Scientific, Pittsburgh, PA) and positioned several microns away from a surface-bound bacterium that rotated in a specific direction. The chemical was then gently released by applying a small positive pressure. To prevent clogging of the micropipette tip, Ryu Flagella Stain was first diluted by a factor of 10 using distilled and deionized water and then filtered through a 0.2 μm syringe filter.

A rotation assay without tethering

A significant part of this work is to demonstrate that the self-trapping phenomenon can be exploited to become a useful assay for studying bacterial response to external stimuli. In our rotation assay, we only considered cells meeting the following criteria: 1) a candidate cell rotates freely without periodic stops, 2) the pitch of the cell body with respect to the glass surface should not noticeably change during rotation, and 3) the average speed of the cell body in the clockwise direction is above a threshold, which we set to be 2 Hz. Single cells meeting these criteria were recorded for 10 s, and a single short pulse of chemoattractant or heat was applied to the cell 1 s after initiation of recording. For the chemical stimulation, a micropipette was filled with 1 μM chemoattractant L-serine and placed in a holder for use with the Picospritzer (Parker Instruments). The tip of the micropipette was placed slightly away from the bacterium to minimize mechanical disturbances due to pressure pulses of stimulation. Due to the finite distance between the tip and the targeted bacterium, the chemical concentration at the target site is less than inside the micropipette. This dilution factor was calibrated using a fluorescent dye and was found to be ∼15. As for the temperature stimulation, we measured local temperature rise ΔT as a function of the laser power using fluorescein. This calibration procedure yielded a linear relationship between ΔT and the laser power as is expected based on energy conservation (see the Supporting Material).

Results and Discussion

Self trapping of surface-bound E. coli bacteria

When WT E. coli RP437 were introduced into the observation chamber, there was an excess of bacteria swimming near the glass surface. Viewing under our inverted microscope or via the video system shows that most of these bacterial trajectories are smooth and arc in the clockwise (CW) direction. When observing from above the solid surface, CW turning trajectories are expected with E. coli (14, 15, 16) and are a result of flagellar bundles being left-handed helices and turning in the counterclockwise (CCW) direction during a run interval. This intrinsic turning direction of bacterial swimming trajectories allows us to establish the image orientation of our microscope, i.e., the trajectories seen by the camera are as if they were viewed from above the glass surface. This conclusion is confirmed by using a calibration ruler engraved with symbols that are not mirror symmetric.

In addition to swimming bacteria near the surface, we also observed bacteria that rotated in place about a fixed axis as if they were driven directly by a flagellar motor, as depicted in Fig. 2 A (5, 17). If this were the case, one expects that its body would rotate in the CCW direction most of the time, corresponding to a “run,” and in the CW direction occasionally, corresponding to a “tumble.” However, rotating WT cells in our experiment were overwhelmingly biased in the CW direction; i.e., most of them are in the CW state ∼90% of the time (see Fig. S1), which is exactly opposite to one’s expectations.

Figure 2.

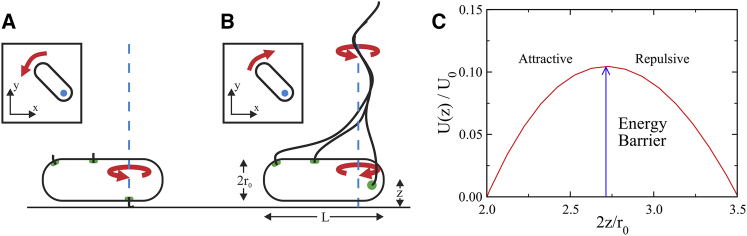
Rotating E. coli cells on surfaces. (A) In the standard tethering assay, the bacterial flagella are mechanically sheared off, and a single flagellar stub is “glued” to the surface. For left-handed flagellated bacteria, such as E. coli, CCW motor rotation causes the cell to swim forward. Thus, a tethered flagellar motor causes the cell body to rotate CCW when viewed from above, as indicated by the arrow in the insert. This sense of rotation is confirmed using XLWU100, which expresses a sticky flagellum. The vertical dashed line denotes the rotation axis (shown as a dot in the insert). (B) WT E. coli cells, without any special treatment to their flagella or to the glass, were observed to rotate their cell bodies predominantly in the CW direction when viewed from above, as indicated in the insert. A real-time staining technique revealed that these cells have flagella that stand perpendicular to the glass surface as shown. These flagella form a CCW rotating bundle that drives the CW rotation of the cell body. (C) The effective surface potential U(z) of a swimming bacterium is shown. Here, $U_0\simeq {10}^{-6}\text{erg}$ sets the scale of energy barrier at z/r₀ = e/2, and z/r₀ is a dimensionless measure of cell body to surface distance as delineated in (B). The force on a swimming bacterium is attractive to the surface for small z/r₀ or to the left of the energy barrier but repulsive for large z/r₀ (see main text). To see this figure in color, go online.

To ascertain what we have observed for RP437 is genuine to the WT behavior of E. coli and not due to some uncontrolled effects in our system, the following two experiments were carried out: in the first experiment, we repeated the same observation using the smooth-swimming mutant RP5232. We found that an overwhelming number of the surface-bound spinning bacteria (>95%) rotated their cell body exclusively in the CW direction, and the remaining rotated exclusively in the CCW direction. The major difference between RP437 and RP5232 is the temporal fluctuations of the cell-body rotation velocity Ω(t). For WT bacteria, Ω(t) varies widely over time, and its PDF P(Ω) is bimodal, as shown in Fig. 3, A–C. On the other hand, Ω(t) for RP5232 fluctuates less, and P(Ω) is unimodal, as displayed in Fig. 3, D–F. In the second experiment, P(Ω) was measured for XLWU100 with sticky flagella. As shown by Fig. 3, G–I, the rotation velocity of this bacterium also obeys a bimodal distribution, similar to WT RP437. However, there are two important differences for this mutant: first, the two peaks are well separated, and the peak heights are similar, indicating that for single motor tethering, the two rotation states have approximately equal probability. Upon stimulation with serine, we found that the probability of CW rotation is enhanced for RP437, but the opposite is true for XLWU100. These observations together leave us with little doubt that the two peaks seen for RP437 correspond to the run and tumble states of the bacteria, and the cell-body rotation direction in the run state is opposite to those cells having a sticky flagellum, indicating a different driving mechanism for cell-body rotation. Because both RP437 and RP5232 bacteria were occasionally seen to escape from the surface, but XLWU100 was not, we concluded that they were not physically tethered to the surface like their sticky counterpart.

What drives the cell-body rotation for surface-bound WT E. coli bacteria? To address this question, we modified the classical Ryu staining technique (see Methods) so that it can be applied to directly visualize flagella of a preselected bacterium with a defined rotation direction. Ryu stain forms a precipitate on the cell body and flagella, immobilizing the cell in the process (18). We found that surface-rotating RP5232 cells had flagella just like WT cells, but instead of forming a bundle along the cell-body axis, the flagella point away from the glass surface, as depicted in Fig. 4 A. For the cell body to rotate in the CW direction, the flagella must rotate in the CCW direction, indicating that the sense of flagellar rotation is identical to a free-swimming cell (see Fig. 2 B). For several CW rotating cells examined, we did not observe flagella attached to the glass surface, which suggests that the cell body is pushed by the thrust force generated by the flagellar bundle normal to the surface. In essence, these are normal swimming bacteria, but because they are pushed against the wall, their cell bodies rotate but cannot translate. The same staining technique when applied to WT cells typically shows multiple flagella that extend in random directions (Fig. 4 B). We believe that the stain may be a chemorepellent, resulting in an increased probability of cells being captured in a tumble state.

Figure 4.

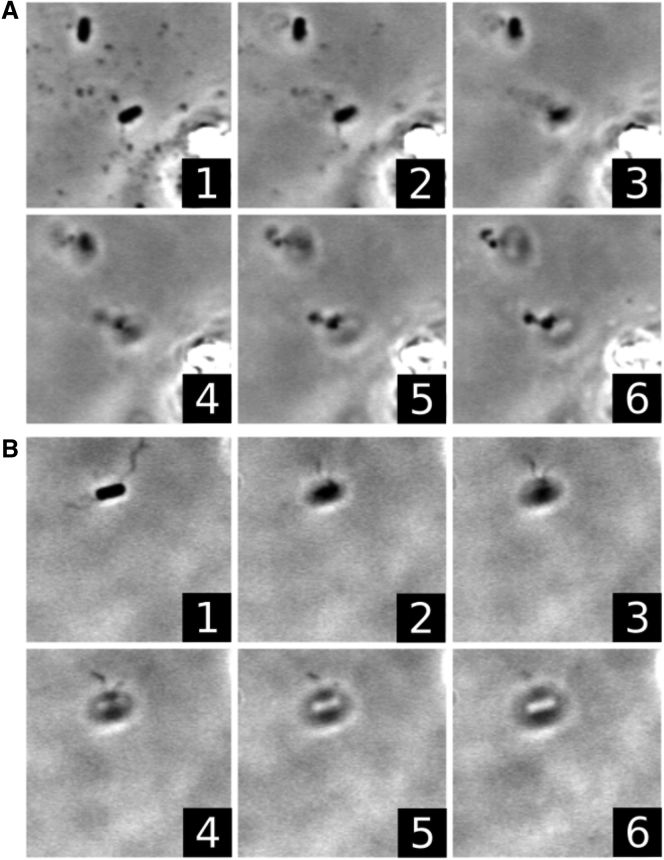
Z-stacked images of flagella staining. (A) The sequence shows images at increasing height above two typical RP5232 cells after flagella staining. The increment between images is Δz ∼ 1 μm. Both cells were rotating at the surface before staining, and both can be seen with a single flagella bundle extending away from the surface. (B) An analogous image sequence showing a typical result of WT RP437 staining is given. In this case, multiple flagella are visible extending in various directions from the cell. Both sequences are taken from videos that can be viewed online (see Videos S2 and S3).

A small minority of WT cells were found to change cell-body rotation directions readily, and our staining technique revealed that these cells possess only one and occasionally one dominant and one short flagellum. This suggests that even a single flagellum is sufficient to drive cell-body rotation, which is consistent with a previous observation that a single flagellum produces nearly as much torque as a multiflagella bundle does (19). It is interesting to note that even when a motor is CW rotating, corresponding to a tumble, the bacterium remains trapped with the same rotation axis. This is possible if the flagellum undergoes a polymorphic transformation, turning it into a right-handed helix (20). As a result of the polymorphic transitions a downward thrust is generated for both CW and CCW motor rotations. Such a scenario has been reported for certain Salmonella mutants that have extended CW intervals, which are sufficient to turn all flagella to a right-handed helical form, resulting in unusual inverted chemotaxis (21).

More evidence that a flagellar bundle normal to the glass surface is driving the cell-body rotation was found by observing the interactions of particles with the flagella of RP5232 cells. Polystyrene beads (1 μm in diameter) introduced into the sample were observed to wrap around the rotation axis of surface-bound rotating cells in the CCW direction. In addition, nonmotile cells that happened to be in the vicinity of these cells were often drawn toward and made to rotate CCW about the axis (see Video S1).

The hydrodynamic stability problem of bacterial self trapping on surfaces is quite complex. The difficulty stems from the fact that 1) the cell body is very close to a surface, 2) the body is nonspherical, and 3) rotation typically is off center of the long axis of the cell body. Although these difficult issues need to be addressed in a future analysis, here we point out that under a certain approximation, trapping by the flow created by a swimmer itself may indeed be possible. Suppose that the bacterial cell body is sufficiently long compared to its width, $L\gg 2r_0$, so that it can be treated as a slender body. The mobilities M_i = V_i/F_i of such a body laying parallel and a distance h from the surface has been studied by Katz et al. (22). Here, V_i and F_i are velocity and force components with $i=\parallel \text{and}\perp$, indicating, respectively, motions along and perpendicular to the cell body on the surface, and i = z, indicating motion away from the surface, which is relevant to our stability problem. To the leading order of slenderness $L\gg 2r_0$ and $h\gg r_0$, these investigators found $M_{\parallel }=2\pi \eta /\text{ln}\left(2h/r_0\right)$, $M_{\perp }=2M_{\parallel }$, and M_z = 4πη/[ln(2h/r₀) − 1], where η is the fluid viscosity. We note that there is a range of h, 1 ≤ h/r₀ ≤ e/2, in which M_z is negative, suggesting that the drag force F_z is opposite to the motion direction. This produces a restoring force, and motion of the cell body is subject to an effective potential,

$$U(z)\equiv -V_z\underset{r_0}{\overset{z}{\int }}{M}_z^{-1}\left(h^{\prime }\right)d{h}^{\prime }=-U_0\left[\left(\frac{2z}{r_0}\right)\left(\text{ln}\left(\frac{2z}{r_0}\right)-2\right)-2\left(\ln 2-2\right)\right].$$ (1)

For V_z being the velocity in the z direction, U₀ = r₀V_z/(8πη) sets the scale of the energy barrier for trapping. As shown in Fig. 2 C, the attractive force—the negative gradient of U(z)—is the strongest near the wall at z = r₀ and weakens away from it. On the right side of the energy barrier, the force becomes repulsive. We note that the depth of the potential is considerable $\left(U_0\simeq {10}^{-6}\text{erg}\right)$ if the escaping speed is assumed to be the typical swimming speed of E. coli, $V_z\simeq 25\mu \text{m}/\text{s}$. A back-of-the-envelope calculation shows that U₀ is orders of magnitude greater than the kinetic energy of bacterial swimming, and it might explain the reason that once a bacterium becomes trapped, as depicted in Fig. 2 B, it can hardly escape. Although the above description appears to capture the essential feature of self trapping, the mathematics is not rigorous because of the fact that the dimensionless parameter r₀/z is not sufficiently small, which is required for expansion using singularities in (22). It remains to be seen that calculations to higher orders do not invalidate the above simple picture. Experimentally, however, we do notice that most of the surface-bound rotating cells are relatively long, and shorter cells escape more frequently from a surface than long ones.

A rotation assay using self-trapped bacteria

Based on our observations, it seems feasible that self-trapped cells can be used, in a similar fashion as the classical rotation assay, to study bacterial swimming and responses to external stimuli. In addition to being simple experimentally, the advantage of our technique is that one can use intact cells directly without chemical and biological modifications. Consequently, the conditions a cell experiences in our assay are less contrived, i.e., cells have a functional flagellar bundle and the motors are under near-physiological load. To test this idea, two separate experiments were conducted using chemical and temperature stimulation.

Chemical stimulation by serine

For the sake of comparison, we used both RP437 and XLWU100 bacteria in this measurement. Both bacteria were impulsively stimulated using 1 μM of serine delivered by a micropipette. The pulse duration, controlled by the Picospritzer (Parker Instruments), was 25 ms, which is shorter than the bacterial response time of ∼1 s. Individual cells meeting the criteria explained in the Methods were found and recorded 20 times for 10 s each during which a single pulse was delivered at t = 1 s. To calculate the CCW bias Φ of the bacterial flagellar bundle for WT cells, we adapted a two-threshold crossing algorithm used by Yuan et al. (13), which is described in Methods. However, little is changed if a single threshold algorithm was used in the data analysis.

We found that there is a noticeable difference in the steady-state bias Φ₀ for RP437 and XLWU100, ∼0.7 for the former and ∼0.5 for the latter. However, upon stimulation, Φ (t) changes in a time-dependent manner, and the responses of the two bacteria appear similar, as delineated in Fig. 5. Here, the changes in the bias $\mathit{\Delta \Phi }\left(t\right)\equiv \mathit{\Phi }\left(t\right)-{\mathit{\Phi }}_0$, normalized by their maximal values $\mathit{\Delta }{\mathit{\Phi }}_{Max}$, are plotted as a function of time. It is seen that immediately after the application of chemical stimulation, $\mathit{\Delta \Phi }\left(t\right)/\mathit{\Delta }{\mathit{\Phi }}_{Max}$ increases and plateaus for about 1 s before decaying. The persistent time for XLWU100 is slightly longer than WT RP437, which is possibly due to the fact that a flagellar motor in XLWU100 experiences a heavier load than that of RP437. This is consistent with (13), which shows that under a high load, the motor increases its dwell times for both CW and CCW intervals but more so for CW than CCW. Our measurements therefore support the notion that a cell’s response to a chemical stimulus is not entirely determined by the chemotaxis network; the load on the motor contributes as well. Aside from this difference, we found that there is general agreement between measurements using the two strains, e.g., 1) ΔΦ(t) are biphasic, displaying a large positive response followed by a slow negative response, and 2) ΔΦ(t) recovers the prestimulation level in long times for both cases. These measurements demonstrate that self-trapped rotating cells can be used to measure response functions of bacteria to external stimuli. In our, to our knowledge, new assay, the cell-body rotation is driven by multiple flagella with a reduced load on individual motors, and hence the chemotactic behavior is expected to be closer to a free-swimming state. The measurements are somewhat noisier for the trapped RP437 than for tethered XLWU100, but such noise can be reduced if more cells are included in the average.

Figure 5.

Bacterial responses to external stimulation. The main figure shows the responses: the change in CCW bias of a flagellar bundle normalized by the maximal response $\left(\mathit{\Delta \Phi }\left(t\right)/\mathit{\Delta }{\mathit{\Phi }}_{Max}\right)$ of WT E. coli RP437 (circles) and fliC mutant XLWU100 (triangles) to impulsive simulations using 1 μM serine delivered at t = 1 s (solid line). Each data set is the average of 10 cells subjected to 20 pulses each. The pressure pulses were 25 ms long, but the concentration of serine near the cell relaxed more slowly, as displayed by the solid line (see Methods). For both RP437 and XLWU100, the response is biphasic and appears to be adaptive in long times. The inset is the response of RP437 to impulsive thermal stimulation. Surface-bound bacteria were stimulated at t = 1 s by a 50 ms heat pulse using an IR laser, which causes a local temperature change of $\mathit{\Delta }T\simeq 5{}^{\mathrm{o}}\text{C}$. As shown by the solid line, the thermal relaxation time is much faster than the chemical stimulation displayed in the main figure. The response curve (circles) is a result of averaging over ∼100 pulses on 10 cells. To see this figure in color, go online.

Temperature stimulation by an IR laser

Finally, we demonstrated that our assay can also be used to study the thermal response of RP437. In this case, repetitive short heat pulses, 50 ms in duration, were delivered to surface-bound rotating bacteria using an IR laser (see Methods). Each pulse causes a transient temperature change of $\mathit{\Delta }T\simeq 5{}^{\mathrm{o}}\text{C}$, which relaxes very rapidly due to localized heating by a small optical fiber tip and the large thermal diffusivity of water (D_T = 1.46 × 10⁵ μm²/s) at room temperature. Despite a much faster thermal relaxation time, which is delineated by the solid line in the inset of Fig. 5, the response function nevertheless appears very similar to when the same RP437 bacteria were stimulated by serine.

The precise timing employed in this measurement also reveals a clear delay in bacterial response and the applied pulses. Inspection of Fig. 5 shows that the delay is not restricted to temperature but to chemical stimulation as well. Interestingly, we found that the delay time of 130 ± 10 ms is about the same for both cases. Because the thermal diffusivity of water D_T is more than two orders of magnitude greater than the diffusion constant of serine $\left(D_s\simeq 430\mu {\text{m}}^2/\text{s}\right)$, our observation rules out the possibility that the delay is a result of diffusion of stimulants. Our observation, however, is consistent with the diffusion of regulator protein CheY-p, which, according to a previous in vivo measurement, was $D_{cheY}\simeq 4.6\mu {\text{m}}^2/\text{s}$ in RP437 (23). For a typical bacterium of size $L\simeq 3\mu \text{m}$, the diffusion time, estimated according to $\tau ={\left(L/2\right)}^2/2D_{CheY}$, is about 250 ms and is order-of-magnitude consistent with our observation.

Conclusions

We report what is to our knowledge a new state of bacterial motion near solid surfaces, which we termed self trapping. When free swimming, E. coli flagella form a bundle along the cell-body axis propelling the cell forward. We found that because of the planar geometry, surface-swimming bacteria can be trapped by their own swimming force; in this case, the flagella bundle is organized perpendicular to the cell-body major axis but normal to the surface. Compared to a cell in the classical rotation assay when a filament is tethered to the surface via antibodies or other chemical means (24), a self-trapped cell has the following distinctive attributes: 1) its body rotates in the opposite direction; 2) the rotation speed is generally slower; 3) CW cell-body bias (or equivalently CCW motor bias) is higher; and 4) the response to external stimuli is subtler because the cell body often does not completely reverse its rotation direction as displayed in Fig. 3, A–C. Importantly, we found that the cell-body rotation speed Ω(t) of a trapped cell obeys a bimodal distribution and can be mapped reliably to the swimming state, i.e., run or tumble, of the cell.

Based on this new understanding, we posit that a surface-bound rotating cell can be used to study a variety of phenomena such as bacterial propulsion, flagellar bundle formation, motor switch, and response to external stimulus. For certain investigations, it is a viable alternative to the standard tethering method. In our opinion, however, the strength of our technique is the possibility that it can be used to study microorganisms for which the standard methods, e.g., using antibodies, are unavailable or too costly to develop.

Finally, we would like to point out that the phenomenon reported here is likely not isolated to E. coli bacterium. Because it is a hydrodynamic effect assisted by the planar symmetry of the boundary, we believe that bacterial self trapping should be a general phenomenon. Indeed, spinning giant bacteria T. majus were seen to form two-dimensional crystals on a glass surface (25), and so was the surface localization of spinning V. alginolyticus (26). On the theoretical side, we still do not understand how the transition from free surface swimming to trapping takes places, and the same can be said about the stability of the trapping state. A careful analysis taking into account bacterial swimming in close proximity to a solid surface is urgently called for.

Author Contributions

C.N.D. and X.-L.W. designed research, performed research, analyzed data, and wrote the manuscript.

Editor: Dennis Bray.