The Persistent Homology Mathematical Framework Provides Enhanced Genotype-to-Phenotype Associations for Plant Morphology^,

Persistent homology offers a mathematical framework to quantify diverse plant morphologies and significantly increases the ability to capture phenotypic variation caused by genetic introgressions.

Abstract

Efforts to understand the genetic and environmental conditioning of plant morphology are hindered by the lack of flexible and effective tools for quantifying morphology. Here, we demonstrate that persistent-homology-based topological methods can improve measurement of variation in leaf shape, serrations, and root architecture. We apply these methods to 2D images of leaves and root systems in field-grown plants of a domesticated introgression line population of tomato (Solanum pennellii). We find that compared with some commonly used conventional traits, (1) persistent-homology-based methods can more comprehensively capture morphological variation; (2) these techniques discriminate between genotypes with a larger normalized effect size and detect a greater number of unique quantitative trait loci (QTLs); (3) multivariate traits, whether statistically derived from univariate or persistent-homology-based traits, improve our ability to understand the genetic basis of phenotype; and (4) persistent-homology-based techniques detect unique QTLs compared to conventional traits or their multivariate derivatives, indicating that previously unmeasured aspects of morphology are now detectable. The QTL results further imply that genetic contributions to morphology can affect both the shoot and root, revealing a pleiotropic basis to natural variation in tomato. Persistent homology is a versatile framework to quantify plant morphology and developmental processes that complements and extends existing methods.

Our current understanding of plant morphology arises from an exquisite, descriptive, anatomical-based understanding of comparative development (Esau, 1960; Steeves and Sussex, 1989; Kaplan, 2001). Although the trained eyes and minds of botanists, taxonomists, and developmental biologists amass significant morphological information at a glance, the ability to quantitatively capture and interpret this information so that it can be disseminated beyond the understanding of a trained individual remains in its infancy. Single-value measurements of plant morphology are used for very specific plant features (e.g. leaf width and length) and are the simplest means for capturing and summarizing the morphological information we discern. Several morphometric techniques quantify plant morphology more comprehensively. Landmarks (Weight et al., 2008; Chitwood et al., 2016) and pseudolandmarks (Langlade et al., 2005) rely on homologous points that collectively represent shapes. Elliptical Fourier descriptors (Kuhl and Giardina, 1982; Chitwood, 2014a) are a continuous representation of a closed contour that treats outlines as a wave and approximates their features as a harmonic decomposition. Each of these conventional phenotypic measures—both univariate and multivariate—capture partial aspects of morphology or can only be applied under limited circumstances (e.g. when there are homologous features between samples), thus limiting our ability to comprehensively quantify and compare the plant morphologies we observe.

The problem of capturing plant morphology is even more difficult for roots, which are highly branched structures that are rarely fully quantified and which lack a morphological framework like shoots (e.g. nodes). The current state of the art in root phenotyping is to measure as many features as possible, including simple measurements that could be made manually—like total area and root diameters—or somewhat less-intuitive measurements like center of mass and accumulated distributions of widths as a function of depth. For example, digital imaging of root traits (DIRT) outputs approximately 80 features that describe various aspects of 2D root shape from field-excavated samples (Bucksch et al., 2014; Das et al., 2015). These many univariate measurements can be considered separately or together. Previous work on rice roots demonstrated that multivariate approaches aggregating the total variation captured by many univariate features in one model could identify large-effect quantitative trait loci (QTLs) that were not identified by any univariate trait alone (Topp et al., 2013), suggesting that simpler traits only captured part of the true variation. To what extent such a priori assumptions in how we measure plant morphology limit our ability to understand its genetic basis is an open question (Chitwood and Topp, 2015; Topp et al., 2016). The answer has wide-ranging implications from our fundamental understanding of plant biology to advanced plant breeding techniques, such as genomic selection.

Here, we demonstrate the use of persistent homology (PH)—a topological data analysis method—as a mathematical framework to quantify diverse plant morphologies. There are two key features of a PH-based approach to quantifying the plant form: (1) PH-based traits integrate seemingly disparate morphological properties of plants into a single (type of) descriptor, which is more comprehensive than measuring univariate traits, and (2) no particular morphological characters are selected a priori. Our approach is completely exploratory, and we learn the most relevant traits through the analysis. Furthermore, PH can be implemented in a way that is robust against noise, is orientation invariant, and accommodates the diverse scales found in plant structures. We describe mapping the genetic basis of disparate morphological features—leaf shape, leaflet serrations, and root architecture—in individual, field-grown tomato plants from the Solanum pennellii introgression line (IL) population (Eshed and Zamir, 1995). Compared with conventional univariate or multivariate approaches, we find that PH-based phenotyping can significantly increase the ability to capture phenotypic variation caused by genetic introgressions, as evidenced by a greater normalized effect size and the detection of unique QTLs. We also found that the most substantial morphological differences between ILs and the parent background (cv M82) are typically in roots and leaf macro- and microstructures. By measuring plant morphology in both the shoot and root using a PH approach, we uncovered information that would have been missed using conventional techniques, and also the concerted genetic effects globally impacting plant architecture.

RESULTS

A Persistent-Homology Primer

PH is a topological data analysis method that can be used to quantify complex phenomena and construct informative summaries of data (Verri et al., 1993; Carlsson, 2009; Edelsbrunner and Harer, 2010). In our application, it can be used as a general approach to quantify shapes at any scale or complexity, without the use of ad hoc- and a priori-defined descriptors. Therefore, it represents a flexible and comprehensive framework for quantifying the entirety of the plant form. To implement PH, phenomena must be considered from a topological perspective and features examined across scale. The major idea behind PH is (1) for a given topological feature, (2) measure the persistence of components of the feature across the scales of a filtration set to (3) create a persistence barcode that can be used to compare the overall topological similarity between objects. In the primer below, we introduce each of these concepts, in turn.

(1) Topological features are homology groups. In biology “homology” refers to corresponding features in organisms related by descent from a common ancestor. We stress that the biological and topological uses of the word “homology” are not the same. In topology, homology groups record connectivity information. For example, 0-homology (H₀) represents path-connected components (like “islands”); 1-homology (H₁) describes one-dimensional holes (Hatcher, 2002; Supplemental Fig. S1A). H₀ path-connected components can simply be distinct, contiguous objects that are not touching each other, and H₁ holes are just holes in a 2D object. A single object can have both H₀ (path-connected components) and H₁ (holes) features (Supplemental Fig. S1A). We can measure one or both these topological features for each shape, using different functions that are appropriate for the shape.

(2) PH measures the persistence of topological features across scale. This is best illustrated by examples. Imagine increasing the radii of points distributed in a 2D plane (Supplemental Fig. S2). At each level of the function:radius, we keep track as points merge with each other, and eventually many distinct H₀ components become a single H₀ component. Or, imagine a complicated 2D lattice with many holes. We could dilate the width of the lattice itself, and at each level of the function:width, we record how many distinct H₁ components (holes) persist. By doing so, we are using a tailored mathematical function to monitor the persistence of topological features (the individual “birth” and “death” of components) using a filtration, which is a nested sequence of expanding shapes. In this manuscript, we illustrate filtration sets by color (e.g. from red to blue) on the object of study itself (Supplemental Fig. S1B).

(3) Finally, the “birth” and “death” of topological components across a filtration set are recorded as a persistence barcode (Supplemental Fig. S2F). Each topological component is assigned a distinct bar, where the base of the bar records the “birth” of the component and the end of the bar its “death.” Persistence barcodes capture the topological information of an object across scale. A distance matrix of persistence barcodes can be calculated, providing a convenient means to compare morphological similarity between objects. We can then apply statistical methods such as multidimensional scaling (MDS), principal component analysis (PCA), and canonical variant analysis (CVA) to turn the barcode information into a single value that describes shape.

Below, we employ a combined PH and statistical framework to diverse morphologies in the same tomato plants of a near-isogenic S. pennellii introgression line population (Eshed and Zamir, 1995), measuring leaf shape, leaflet serrations, and root architecture, to demonstrate the versatility of this approach.

Persistent Homology and Leaf Shape

Motivation

(1) To be able to robustly quantify diverse shapes (e.g. simple leaves, compound leaves, and leaves with holes), we developed a method that describes morphology without a priori feature selection. (2) Arbitrarily subsetting topological features makes the subsequent statistical discrimination of shapes more efficient. We subset shapes into a series of annuli. The annuli are orientation invariant so that the analysis is blind to rotation (i.e. there is no need to orient a leaf tip-to-base), substantially streamlining the workflow and generalizing the method to data sets that were not collected with orientation in mind (herbarium specimens, for example). Other approaches can be used instead of annuli, such as a disk emanating from the leaf’s barycenter, but we used annuli rather than disks because if the shapes are of vascular type, such as veins, using the disk makes everything connect artificially (Supplemental Fig. S3).

Method

We quantify tomato leaflet shape (Fig. 1A) by studying the leaflet contour (Fig. 1B), which is a 2D point cloud comprised of contour pixels. To focus only on shape, not size, we center and normalize the leaflet contour (so that the square root of the average squared distances of all the points to the leaflet center is 1). Since the images may be noisy and leaflets possess an orientation, we chose a method that is robust to noise and blind to orientation. To robustly represent the leaf contour, we used a Gaussian kernel density estimator (Fig. 1C), which can estimate the density directly from the data (Hwang et al., 1994). The density estimator is a smooth function that estimates the density of pixels surrounding each pixel, so that higher values are achieved around regions with high pixel density (such as the tip of the leaflet, serrations, and lobes). Noise (e.g. errant pixels that are processing artifacts) is usually very sparse, such that the function has smaller values around noise, thus making the function robust. To make the analysis rotation invariant, we study shapes falling in an annulus centered around the centroid of the leaflet contour (Fig. 1D).

Figure 1.

Persistent homology and leaf shape. A, A binary tomato leaflet image. B, Point cloud representing the contour of the leaflet and sampling of the 16 annuli used to subset data in analysis. The green ring (“10”) is used as an example subsequently. C, A color map of a Gaussian density estimator applied to the contour point cloud. The density estimator is robust to noise. Red indicates a larger density of contour points (e.g. near serrations); blue, a smaller density of contour points (e.g. straighter edges). D, An annulus kernel. A smooth function highlights the ring to localize and smoothen the isolation of density data. E, The multiplication of the density estimator (C) with the annulus kernel (D) emphasizes leaflet density features falling within the green ring indicated in B. F, Side view of E showing the distribution of density features within the annulus. G, A persistence barcode. Each bar (vertical axis) represents the “birth” and “death” of a connected component. Connected components are “born” as different scales of the density features are traversed (horizontal axis) and “die” as they merge with other components. Eventually only a single component persists. The traversal of scales across density features is visually depicted (bottom), with magenta dotted lines indicating the relevant position in the persistence barcode (top).

Subsetting of shapes (Fig. 1E) is achieved by multiplying the density estimator (Fig. 1C) with the annulus kernel (a function that highlights and smoothens the annulus; Fig. 1D). If we depict the function value as height, then the function is intuitively visualized as a set of ridges (Fig. 1F). As a plane moves from the highest function values to the lowest (red to blue; Fig. 1F), we study the function values as superlevel sets (that is, the shape above the plane). The plane sometimes touches the peak of a new ridge so that it generates a new connected component; alternatively, sometimes the ridges merge so that one connected component disappears. We use a persistence barcode (Fig. 1G) to record these changes: a bar, recording the scale at which the component is “born” and “dies,” represents each H₀-connected component (Supplemental Fig. S2F). For each leaflet contour, we compute 16 such persistence barcodes corresponding to 16 expanding annuli (Fig. 1B) to represent the shape of each leaflet. Note that 16 is a practical recommended parameter (16 annuli can cover the normalized leaflet contour, with the annuli width 0.1). Using a similar number with adjusted width of annuli (e.g. 15 or 17) does not change the result much, provided the number is consistently chosen for all the data. However, using too few annuli can lead to missing of many details, while too many may cost much more computational time without added benefit. Furthermore, although we do not choose particular morphological features a priori, we note that other PH functions may capture other aspects of the overall phenotypic variation that annuli do not.

Persistent Homology and Leaflet Serrations

Motivation

Although leaf shape contains some shape information about serrations, PH functions can be crafted to focus specifically on leaf serrations. The serrations can be treated as the difference between the leaflet contour and a coarse approximation. This difference can be used to more directly quantify serrations.

Method

To coarsely approximate the leaflet contour (Fig. 2A), we used elliptical Fourier descriptors (EFDs; Kuhl and Giardina, 1982; Iwata et al., 1998; Iwata and Ukai, 2002). Such descriptors decompose the contour into a weighted sum of wave functions with different frequencies. Summing the higher frequency waves in the series, we describe finer details of the contour and achieve a closer approximation of leaflet shape. In contrast, if we use EFDs of the five lowest frequencies, we capture only coarse shape information (Fig. 2B; Supplemental Fig. S4). We then compute a distance function from the leaf contour to the EFD approximation. We assign a negative sign to the distance value from the contour (blue) if the data point is inside the approximated outline and a positive sign distance value (red) if a data point falls outside. This function is a signed distance function (Fig. 2C). Given a threshold (a number), the sublevel set is the set of points on the contour that have smaller values than the threshold. Changing the threshold continuously from small to large, we get the sublevel set filtration. Such sets can be roughly interpreted as the intersection between the actual contour with a coarse shape of different sizes (dark magenta on contour in Fig. 2D). We use a Euler characteristic (the number of connected components minus the number of loops) curve (Fig. 2D) of the signed distance function between the leaflet contour and the EFD approximation to quantify leaflet serrations. Here, we note that the proper parameter to use in the EFD approximation might differ among species (Supplemental Fig. S4). For example, what we used for tomato leaves in this study may not be the best fit for grape leaves.

Figure 2.

Persistent homology and leaf serrations. A, Point cloud representing the contour of a leaflet. B, A coarse approximation (in black) of the contour (in gray) using an elliptical Fourier transform. C, A color map of a signed distance function from the contour to the Fourier approximation, positive sign for points outside the contour (more red), negative sign for points inside the contour (more blue). D, The Euler characteristic (the number of connected components minus the number of holes) curve. The Euler characteristic is plotted against traversal of the signed distance function. Shown are example leaves depicting the number of connected components (dark magenta) at the indicated positions in the curve (magenta dotted lines).

Persistent Homology and Root Architecture

Motivation

We have previously described the use of PH for quantifying the 3D branching topologies of root and shoot structures (Li et al., 2017). However, root architectures are vastly more typically measured using a “shovel-omics” (Trachsel et al., 2011) or similar approach, in which roots of field-grown plants are dug up, washed, and imaged as a two-dimensional projection (Bucksch et al., 2014; Das et al., 2015; Fig. 3A). The overall architectural complexity of a root is partly captured by the crossing of branches in the projection, which in these air-dried samples are essentially fixed. Whereas traditional branching metrics (e.g. number of the branches) are confounded by such crossings, we take advantage of them to quantify the complexity of the root system, which incorporates aspects of branch numbers, lengths, angles, tortuosities, and distributions.

Figure 3.

Persistent homology and root architecture. A, A binary image of root architecture as a 2D projection. B, A color map of a distance function of pixels to the root. Blue pixels are closer to the root, red pixels farther. C, A β₁ curve plotting the number of loops/holes as a function of the distance function (similar to dilating the root) to quantify the complexity of root architecture. Shown are example root images (bottom) at indicated positions in the curve (magenta dotted lines).

Method

When branches cross in a 2D image, they form loops, which is 1-homology (H₁). We assign each pixel a value based on the distance to the root (blue if closer to the root and red if farther from it; Fig. 3B). Given a threshold (a distance value), we study the shape consisting of the pixels that have smaller values than this threshold. We record the number of loops (β₁) formed by this shape. As we continuously vary this threshold, the number of loops also varies and becomes a β₁ curve (Fig. 3C). The number of loops and the slope of this curve can indicate the size, shape, and the density of the holes formed by the branches. This can indirectly quantify the complexity of the branching pattern of 2D root projections. Although the trait does not directly measure the roots, it captures the existing system architecture after destructive harvesting and projection onto a 2D plane.

Persistent Homology Can Detect Global, Genetic Changes to Shoot and Root Architectures in a Single Metric

As described above, a PH framework, combined with tailored functions, can describe morphologies as diverse as the shape of leaves (Fig. 1), serrations (Fig. 2), and root architecture (Fig. 3). By measuring these features in the same plants across a morphologically diverse population, we can determine the extent to which genetic differences influence plant architecture globally or locally. To do so, we leverage the near-isogenic S. pennellii tomato ILs (Eshed and Zamir, 1995). These lines each harbor a single, relatively small introgressed region from the wild desert tomato S. pennellii in an otherwise domesticated tomato background of the cultivar M82. Detecting a significant phenotypic difference between an IL and the cv M82 parent delimits the underlying genetic cause to the introgressed region (Chitwood et al., 2013); in other words, it defines a QTL. As we describe below, the ability to compare each IL against the cv M82 parent provides a convenient means to reduce PH-based data describing global features of complex morphologies into single discriminant values. We emphasize that these single values represent highly multivariate features of the shapes and so are not necessarily intuitive the way univariate traits such as length, width, and density are. Nonetheless, they capture more information than any single trait and do not rely on a priori assumptions about the most important features of the data. Furthermore, the discriminant values can be correlated with each other to test hypotheses of how the overall morphology of different organs change in a concerted fashion or independently from each other in the presence of different introgressed regions.

In the examples below, we compare the introgression line IL4-3, which has large, previously documented changes in leaf shape and serrations (Chitwood et al., 2013, 2014b), to the cv M82 parent. In order to translate persistence barcodes to quantitative comparisons, we employed the following statistical approaches. First, we use 16 persistence barcodes, derived from 16 rings (a practical recommended parameter, described above; Fig. 1), to quantify each leaf shape. For each pair of leaf shapes, we compute the bottleneck 2-distance (i.e. compute the bottleneck distance for each ring, then take the square root of the sum of these 16 bottleneck distances squared) between them. From all pairwise distances, we employ MDS to project the data into a reduced dimensional (7-dimensional, explaining more than 50% of variation) Euclidean space, to preserve the pairwise distances as much as possible. We then perform a CVA to the reduced dimensional projection to determine the discriminant features for two groups, which in this case is each individual IL compared to the cv M82 parent. Because there are only two groups (IL versus cv M82), there is only one canonical variate value (CV1). For example, CV1 values separating IL4-3 and cv M82 is a composite of PH features discriminating these two groups (Fig. 4A). We then randomly permute the samples 10,000 times and count how many times the distance between the group means are larger than the nonpermuted means and use this ratio as a P value. This bootstrap test demonstrates that the detected difference between the mean CV1 scores of these two groups has high statistical significance (P < 0.0001; Fig. 4). To interpret the morphological differences between lines, we can compute the weight of each annulus to the shape difference by performing a linear discriminant analysis. For each ring, we compute the ratio of between-class scatter to within-class scatter to measure the contribution of each ring. Then we normalize the values so that the sum of all contributions is equal to 1. For the comparison between IL4-3 and cv M82, we see that the 16th ring contributes the most discrimination between these genotypes (Fig. 4A). From the illustration (Fig. 4A), we can see that the difference is mainly derived from leaf length. The sixth and tenth rings contribute to the discrimination of the IL4-3 phenotype as well, and we can see that these differences mainly result from leaf width and lobing. The length and width of IL4-3 leaves has been previously shown to be some of the most discriminating features of this introgression line (Chitwood et al., 2013, 2014b). However, persistent homology captures these features, their covariances, and other less-linear information such as lobing, in a single function.

Figure 4.

Comparing results of persistent homology between IL4-3 and the parent cv M82. A, Analysis of leaf shape. Left, A box plot of the canonical variate scores (CV1) between IL4-3 (red) and cv M82 (blue), representing the discrimination of these two genotypes by 16 persistence barcodes. On each box, “+” indicates an outlier if it is more than 1.5 interquartile ranges above the upper quartile or below the lower quartile; the central line indicates the median; the top and bottom edges of the box indicate the 25th and 75th percentiles; and the whiskers extend to the most extreme nonoutlier data. Middle, Example leaflets from each genotype and the superimposition of annuli used for analysis. Right, The weight of each ring to discriminating leaf shape between IL4-3 and cv M82. B, Analysis of serrations. Left, The box plot of CV1 scores. Middle, The Euler characteristic curves across signed distance function from contour to its approximation for all replications of IL4_3 (red) and cv M82 (blue). Right, The weight at each signed distance level to discrimination of serration differences between the genotypes. C, Analysis of root architecture. Left, The box plot of CV1 scores. Middle, β₁ curves depicting the number of loops across distance function from pixels to root for all replications of IL4-3 (red) and cv M82 (blue) and example root data. Right, The weight at each distance level to discriminating IL4-3 and cv M82 root architecture.

Another previously described feature of IL4-3 leaves is less serration than in cv M82, as quantified using circularity (a ratio of area to perimeter; Chitwood et al., 2013, 2014b). The Euler characteristic (EC) curves for all IL4-3 and cv M82 replicates clearly indicate quantitative differences in leaflet serration as detected using the PH-based method. Note that the Euler characteristic rises earlier and more quickly for cv M82 (blue) than for IL4-3 (red), indicating more numerous and deeper serrations (Fig. 4B). The EC curve for each leaflet is discretized into a 110-dimensional vector and then reduced in its dimensionality by performing a PCA. As done for leaf shape, we then apply a CVA and compute the CV1 score discriminating the genotypes by serration. Multiplying the PCA loadings by CVA loadings, we can measure the weight at each signed distance level to the morphological differences between IL4-3 and cv M82 (Fig. 4B).

Although root architecture traits in mature plants have not been previously described for the S. pennellii introgression lines, the first-order Betti number (β₁) curves (the number of loops) for all replicates of IL4-3 and cv M82 reveal clear differences in root architecture between these genotypes (Fig. 4C). We discretize each curve into an 80-dimensional vector and reduce the dimensionality by PCA to compute CV1 scores (Fig. 4C). Similar to our analysis for differences in leaf serration, we computed the weight at each distance level to the root architecture differences by multiplying the PCA loadings by CVA loadings. Examination of the β₁ curves shows that cv M82 has greater root architecture complexity than IL4-3. We show in the subsequent analyses that some of this complexity can be accounted for by simple traits like root area and estimated numbers of root tips but that the β₁ curves capture a significant amount of additional information.

After the comparisons of IL4-3 and cv M82, we compare the other 75 ILs with cv M82 (Fig. 5; Supplemental Data Set 1). PH can detect a wide range of morphological and architectural differences in a highly multivariate space. Thus, comparing each IL to cv M82 with a discriminant analysis provides an indicator of global morphological differences for each IL as a single magnitude value (CV1; Fig. 5), rather than an ad hoc list of traits developed separately for roots and macro- and microleaf shapes that would covary differently for each IL. In other words, overall differences in leaf shape (Fig. 5A), leaf serrations (Fig. 5B), and root architecture (Fig. 5C) can be directly compared and represented, regardless of the myriad potential ways such morphological differences manifest, and with fewer a priori assumptions about how to quantify them than current methods.

Figure 5.

Overall morphological differences between near-isogenic introgression lines and the parent cv M82. Normalized canonical variate scores (CV1) measuring global, discriminating differences between introgression lines (ILs) and cv M82 plotted against IL identity, ranked by median CV1 value. On each box, “+” indicates an outlier if it is more than 1.5 interquartile ranges above the upper quartile or below the lower quartile; the central line indicates the median; the top and bottom edges of the box represent the 25th and 75th percentiles; and the whiskers extend to the most extreme nonoutlier data. The solid gray line across all ILs shows the median CV1 value of cv M82. The color of each box indicates P values calculated using a bootstrap test. Shown are CV1 scores for leaf shape (A), leaf serrations (B), and root architecture (C).

Persistent Homology Can Discriminate between Genotypes with Larger Effect Sizes Than Conventional Univariate Traits and Shows Heritability Results Similar to Those Obtained by Conventional Multivariate Approaches

PH captures morphological information more comprehensively than conventional univariate traits. We wanted to determine if that information helps to better discriminate between different genotypes and better understand the genetic basis of plant shape. Therefore, we calculated effect sizes using a normalized metric, Cohen’s d, which is the difference of the means between each IL and cv M82 divided by the standard deviation (Fig. 6). We compared the canonical variate values of the leaf shape and serration PH traits with four conventional leaf traits that are the most commonly used indicators of serration and lobing (circularity and solidity) and length-to-width ratio (aspect ratio and roundness). We also compared the canonical variate values of the root PH trait with the four most heritable conventional root traits derived from DIRT (Bucksch et al., 2014; Das et al., 2015): number of root tip paths, projected root area, number of root tips emerging from the taproot, and estimated number of basal roots (Supplemental Fig. S5). In both cases, PH has a larger effect size than the conventional traits (Fig. 6, A and B).

Figure 6.

Effect size of persistent homology versus conventional traits. A, Effect size, as measured using Cohen’s d, for leaf shape and serration persistent-homology (PH) traits and circularity, aspect ratio, roundness, solidity, canonical variate score (CV1), and first two PC scores with the percentage of variance they explained on the four conventional leaf traits, as well as the root PH trait, the top four heritable digital imaging for root traits (DIRT) traits number of root tips (Nr._of_RTPS), projected root area (projected_root_area), number of root tips emerging from the taproot (rootsSeg2), estimated number of basal roots (X_.Basal_roots), CV1 and first seven PC scores with the percentage of variance they explained on 80 DIRT traits. White/yellow indicates high effect size, and black/red indicates low effect size. Green boxes with cross marks indicate those ILs for which PH traits, but not conventional traits, can detect QTL. B, Summation of the overall effect size for the 76 ILs for different traits (PH traits in red, conventional univariate traits in blue, and multivariate traits in green). C to E, Venn diagrams for leaf QTL (C), root architecture QTL (D), and QTL common to leaves and roots (E). For each are diagrams comparing shared and unique QTL for conventional univariate traits (blue) and PH traits (red; top) and multivariate conventional traits (green) and PH traits (red; bottom).

Because analysis of univariate traits in multivariate space can also reveal otherwise hidden influences on effect size, we performed a multivariate analysis (CVA) on the four conventional leaf traits, PCA on the four conventional leaf traits, CVA on four DIRT traits, and PCA on all 80 DIRT traits for root architecture. PH traits had very similar effect sizes as the multivariate traits computed from conventional traits (Fig. 6, A and B), reinforcing the general power of multivariate approaches for genotypic discrimination of complex traits. We then compared heritabilities to discern the relative proportion of phenotypic variance due to genotype for each type of trait. As expected, the simplest measures for the simplest shapes were highly heritable: 0.445 to 0.603 for the univariate leaf traits and 0.189 to 0.357 for the top univariate root traits (Supplemental Fig. S5); however, they explained the least amount of phenotypic variation (Fig. 6). The top PH traits for roots (0.291), leaf shape (0.527), and serrations (0.446) were also very heritable, similar to the principle components computed from conventional descriptors (highest root value = 0.135; highest leaf value = 0.593). These results highlight that PH can be a powerful approach to capturing large-effect heritable traits that describe complex shapes.

Persistent Homology Reveals Novel QTLs Not Identified Using Conventional Univariate or Multivariate Traits

Multivariate analysis of complex phenotypes, including those of roots, has been shown to identify latent genetic variation controlling large-effect QTLs (Topp et al., 2013; Mitteroecker et al., 2016). We conducted a QTL analysis, using pairwise t tests of the CV1 value for each IL versus cv M82 with P < 0.05 and a “large” effect size >1.2 as cutoffs (Fig. 5; Sawilowsky, 2009). PH traits for leaf shape, serration, and roots identified more QTLs than the conventional univariate traits alone. For the leaves, 15 QTLs are commonly detected with conventional traits, and 10 QTLs are uniquely detected by PH (Fig. 6C), whereas only 1 QTL was identified by conventional traits, but not PH. For the root QTLs, 36 QTLs are commonly detected with conventional traits, and 22 are uniquely detected by PH (Fig. 6D), with 7 conventional QTLs not detected using PH. Overall, the PH QTLs explained a relatively large amount of shape variation in our data set, with root QTLs explaining more variation (mean = 21.1%, max. = 44.6%, min. = 7.59%) than the leaf shape (mean = 12.0%, max. = 40.3%, min. = 3.37%) and serrations (mean = 10.0%, max. = 27.4%, min. = 1.7%; Supplemental Data Set 1; see “Materials and Methods”).

We also calculated QTLs for the conventional multivariate traits (Fig. 6, C and D), so that the conventional traits in aggregate could be compared against PH. Multivariate analyses (whether with conventional traits or PH) always outperform univariate traits. For leaf shape, four univariate traits together can identify 16 QTLs, while the multivariate trait can detect 27 QTLs. For root architecture, four univariate traits together can identify 43 QTLs, while the multivariate trait can detect 57 QTLs. Ten QTLs common between leaves and roots can be detected by univariate traits together, but 20 common QTLs can be identified using the multivariate trait (Fig. 6E). This confirms that aggregating conventional traits into a multivariate trait can increase the ability to discriminate genetic determinants of plant morphology and that PH-based approaches can detect more unique QTLs, thus further expanding our understanding of genotype-phenotype relationships.

Persistent Homology Detects Concerted Changes in Shoot and Root Architecture

Applying a PH framework to and performing statistical data analysis for the S. pennellii ILs allows a single value (CV1) encapsulating the global morphological features of different plant organs—leaf shape, serrations, and root architecture—to be calculated across genotypes. Such comprehensive traits differ from univariate traits that dramatically changed during domestication, such as fruit weight (Frary et al., 2000), for which a large amount of phenotypic variance is attributable to a single locus. Rather, PH traits more closely resemble other multivariate traits, such as was used to identify QTLs controlling 3D rice-root architecture (Topp et al., 2013) or the Fourier decomposition of leaf shape (Chitwood et al., 2013, 2014b), which are highly heritable but extremely polygenic. By reducing the myriad possible shapes of roots and leaves to a single value reflecting magnitude through discriminant analyses between ILs and cv M82, we ask and partially begin to answer fundamental questions in plant biology: Do genetic alterations affecting one part of the plant affect others? Generally, are genetic changes in shoot architecture accompanied by changes in the root (and vice versa), or are these organ systems under separate genetic controls?

Comparison of CV1 values normalized to cv M82 across traits shows that ILs with the largest differences from cv M82 for one trait tend to also be the most different for others (Fig. 7A). Eight ILs (IL3-2, IL4-2, IL4-3, IL6-2-2, IL7-2, IL8-1, IL8-1-1, and IL8-1-5) are among the strongly altered ILs for leaf shape (in the top 12), leaf serrations (in the top 15), and root architecture (in the top 27). Furthermore, the median values of the normalized CV1 values for each trait are significantly correlated with each other (Fig. 7B), although leaf shape and serrations are more highly correlated with each other than with root architecture. At the QTL level, PH showed a higher percentage overlap of root and shoot QTLs (28.9%) than univariate (17%) or multivariate (23.8%) traits (Fig. 6).

Figure 7.

Concerted changes in leaf and root architecture underlie morphological diversity in tomato introgression lines. A, The most extreme ILs for each trait ranked by median of normalized canonical variate value (CV1). Left, leaf shape; middle, serrations; right, root architecture. On each box, “+” indicates an outlier if it is more than 1.5 interquartile ranges above the upper quartile or below the lower quartile; the central line indicates the median; the top and bottom edges of the box represent the 25th and 75th percentiles; and the whiskers extend to the most extreme nonoutlier data. The solid gray line across shows the median CV1 value of cv M82. The color of each box indicates P values calculated using a bootstrap test. B, Scatter plots of median CV1 values for leaf shape versus serrations (left), leaf shape versus root architecture (middle), and root architecture versus serrations (right). The P value and Spearman’s rho value are shown in the upper left corner on each plot. The ILs most morphologically different from cv M82 are consistently so across traits. The most extreme ILs are similarly colored across all plots. Black indicates cv M82.

Our results indicate that shoot and root architectures, when analyzed with a metric capable of quantifying multivariate features across scales, are under concerted genetic control. We emphasize that these differences only represent the magnitude of architectural changes, implying that changes in shoot morphology are simply accompanied by alterations in root architecture (and vice versa), but that nothing is implied about the direction of the phenotypic changes within the multivariate space. To what extent such global changes are affected by the same loci, rather than a product of genetic linkage, remains to be determined.

DISCUSSION

PH is a framework for analyzing topological structure in different types of data at different resolutions, and as such bypasses major obstacles that currently confound the analysis of discretized shoot and root architectures. It can be applied in an orientation-independent fashion, is robust to noise, and accommodates features at multiple scales. The most versatile feature of a PH framework is that any number of continuous functions, specific to the task at hand, can be analyzed. The examples of leaf shape, serrations, and root architecture in this study exemplify the utility of such an approach in the global analysis of plant morphology. Density functions applied through growing annuli originating from leaf centroids measure shape (Fig. 1); level sets emanating from a Fourier transform approximation of leaf shape measure serrations (Fig. 2), and dilation of root architectures can detect first-order Betti number (β₁) loops that approximate overall complexity (Fig. 3). The metaphor of topology used across varying resolutions is an adaptable one, and when applied to different features throughout the same plants, can determine the genetic basis of global morphology (Figs. 4–6), detect more overall changes in morphology between genotypes with a greater effect size than conventional traits (Fig. 6), and reveal concerted changes in root and shoot architectures (Fig. 7).

By applying functions over a range of resolutions and combined with statistical methods presented here, PH can measure local features in a global manner, and this is where its versatility and power lies. The multivariate representations of PH do not result from a priori assumptions about the sources of phenotypic variation; rather, the approach is completely exploratory, and we learn the most relevant traits through the analysis. This characteristic is fundamentally different from other multivariate analyses, such as PCA and multivariate ANOVA, where the most salient features of the data are derived from statistical covariances of existing features. Machine-learning analyses published to date have been performed in a similar way: to maximize the discrimination of a defined set of input traits. For example, support vector machine (Iyer-Pascuzzi et al., 2010) and logistic regression (Zurek et al., 2015) were used to determine the combinations of root traits that best separated pairs of genotypes. Recent deep-learning approaches have been effectively used for object recognition from plant images, from which features of interest are subsequently defined by the human user. Pound et al. (2017) used convolutional neural networks (CNN) to detect the locations of root tips and aboveground plant features, but then derived a list of standard univariate traits from that information. They were able to show that their CNN model could detect most of the QTLs identified manually from the same traits (albeit rapidly and automatically, once they defined the traits of interest). It would be interesting to apply statistical multivariate analyses and PH to the outputs of CNN and other deep-learning computer vision approaches.

Just as in QTL approaches with any type of trait, univariate or multivariate, our goal is to eventually understand the molecular mechanisms underlying phenotypic differences by connecting genotype to phenotype. Significant progress has recently been made in multiscalar evaluations of leaf shapes (Armon et al., 2014; Biot et al., 2016) and shoot architectures (Boudon et al., 2014; Conn et al., 2017). These methods, including PH, allow the quantification of more variation than conventional means, especially for complex shapes. But PH can also be applied to any number of plant morphologies—shape (Carlsson et al., 2005; Gamble and Heo, 2010), branching patterns (Li et al., 2017), texture (such as in pollen grains; Mander et al., 2013), ecological distributions of plants (Mander et al., 2017), and more—permitting an unprecedented view of spatial patterns in plant biology across scales and subfields. It will be particularly useful for analyzing dynamic changes in plant morphology over time, a reflection of the ability to apply PH in n-dimensional spaces and of the requirement to analyze over ranges of resolutions (Li et al., 2017). Importantly, PH is also well suited to network analysis, and by reducing data sets (such as gene expression, proteomic, metabolite, and other molecular data) to topologies, it can be used to analyze disparate data types in a more integrated fashion (Horak et al., 2009). Developing such a unified system view of plant science will be critical as the increasingly automated acquisition of plant morphological and molecular data are outpacing our existing frameworks for analyzing it. With greater understanding of the true multivariate and multiscalar nature of genotype-to-phenotype relationships will come increased insight into the mechanistic and developmental underpinnings of plant form and function.

MATERIALS AND METHODS

Plant Material and Growth Conditions

Solanum pennellii ILs (LA4028-LA4103; Eshed and Zamir, 1995) and cv M82 seeds were treated with 50% bleach for 1 min, rinsed with water, and germinated in phytatrays lined with moist paper towels. The seeds were left in the dark for 3 d, followed by 3 d in light, and transferred to greenhouse conditions in 50-plug trays. At this point, the plants were randomized according to a block design at a replication of 15. Plants were hardened by moving them outside for 10 d (5/10/2014). Hardened plants were transplanted to field conditions (5/21/2014, Bradford Research Station, Columbia, MO) with 10 feet between rows and 4-foot spacing between plants within rows. The final design had 15 blocks, each consisting of 4 rows with 20 plants per row (15 plants per line). Each of the 76 ILs and 2 experimental cv M82 plants were randomized within each block. After flowering (the week of 7/21/2014), four fully expanded adult leaves were harvested from each plant, and the adaxial surfaces of the left distal leaflets were scanned. The scans were processed using ImageJ macros to segment individual leaflets and to threshold and binarize each leaflet image. After fruit harvest, the roots of all plants were dug out manually, washed, and imaged using a camera setup, as detailed in Das et al. (2015).

Persistent Homology

PH (Verri et al., 1993; Carlsson, 2009; Edelsbrunner and Harer, 2010) is a topological data analysis tool that is well suited for the study of plant morphological data. This tool captures morphological information by integrating topological signatures, described by a function, across sublevel or superlevel sets into a persistence barcode. The data analyzed in this paper consists of 2D point clouds of leaves and roots extracted from images that are converted into functions that encode local-to-global morphological properties, such as leaf shape, serrations, and root architecture.

Our pipeline for converting 2D plant imaging data into persistence barcodes involves four main steps: extracting point clouds from images, converting point clouds to functions, forming filtrations, and computing persistent homology (Supplemental Fig. S1B).

Extracting Point Clouds from Images

From binary images, we extracted 2D point clouds representing leaf contours or 2D projections of roots, where a pixel is converted into a point via its coordinates.

Converting Point Clouds to Functions

From point cloud data, we constructed various functions that carry local and global information about leaf shape, leaflet serrations, or root architecture. Functions that effectively capture shape properties at the local, regional, and global levels are described below for leaf shape, leaflet serrations, and root architecture.

Leaf Shape.

Topological features more effectively discriminate objects using spatial localization. We begin with a Gaussian density estimator for the entire contour of the leaf, defined as , where are the data points on the contour and h is a bandwidth parameter (all parameter values are practical values that are shown in the code); see Figure 1C. We then modulate this function by multiplying it by a “bump” function K, which localizes it to a particular region. In our analyses, we use localization to concentric rings about the centroid of a leaf. The annular domains ensure that the resulting topological features are independent of orientation, as shown in Figures 1D to 1F. More precisely, we use modulation by kernels of the form , where y is the center of the annulus, its radius, and the parameter σ its width (all parameter values are practical values that are shown in the code). We refer to PH derived from such localized functions as local persistent homology.

Leaf Serrations.

EFDs decompose a contour into a weighted sum of wave functions with different frequencies. Summing only over a finite number of harmonics gives a smooth approximation of the contour. This smoothing effect leads to loss in such details as serrations. We take advantage of this and quantify serrations by looking at residuals, i.e. the difference between the original contour and the smooth approximation. Our experiments indicated that EFDs for the first five lowest frequencies yield smooth approximations suitable for serration analysis. Let C denote the original leaf contour and T the smooth approximation. We computed the distance from each point on C to T with the convention that if the point on C is inside the contour T, then we assigned a negative sign to the distance. The distance is nonnegative otherwise. We analyzed serrations via the Euler characteristic function associated with the sublevel set filtration of this signed distance function.

Root Architecture.

From an image of a 2D root projection, we construct a distance function that computes the distance from a point to the nearest pixel on the root. Thus, all points on the root have the value 0. The farther the point is from the root, the larger the value of the function. If we increase the threshold value starting from 0, the sublevel set filtration gives progressively larger dilations of the root. Since root branching typically creates numerous crossings and loops in 2D projections, we use the curve associated with this distance function as a measure of the complexity of root architecture (e.g. the number of root axes, their tortuosity, and how often they cross over).

Forming Filtrations

Before constructing the filtration, we needed to make a connection among the points so that they were not just individual points. For the points on the leaf contour, we connected two points by an edge if they are neighbors. For the image of the 2D projection of roots, we treated each pixel as a point and connected it with its six neighbors in the south, north, east, west, northwest, and southeast directions. Then, we filled all the triangle hollows with triangle faces. For points on a full rectangle containing the data, we discretized the rectangle into grids in which the intersections are points and connect each point with its six neighbors in the south, north, east, west, northwest, and southeast directions. Then, we filled all the triangle hollows with triangle faces. A filtration of a domain D is an expanding sequence of subsets that eventually cover D. In applications, D may be a leaf contour, a 2D projection of a root, or a full rectangle containing such data. A function on D yields a filtration as follows: Given a threshold value r (a number), the set of points in D whose function values do not exceed the threshold is called the sublevel set for r, which can be mathematically described as . Similarly, the set consisting of points whose function values are not smaller than the threshold is called the superlevel set for r and determined by . If r₁ < r₂, then the sublevel set for r₁ is always included in the sublevel set for r₂. As we reached the maximum value of the function, its sublevel set comprised the entire domain. Thus, we obtained a filtration called the sublevel set filtration. A similar construction applies to superlevel sets. Figure 1G provides an example of a superlevel set filtration, where the domain D is a square containing a leaf. Figure 2D depicts a filtration of the contour of a leaf in which sublevel sets correspond to intersections of the growing pink regions with the leaf contour. In Figure 3C, the sublevel sets correspond to different dilations of a root.

Computing Persistent Homology

From a filtration, as described above, we constructed barcodes that summarizeed the topology of the various stages of the filtration; more specifically, their 0-dimensional and 1-dimensional homology. Here, homology refers to a mathematical descriptor of the shape of the filtration, distinct from the concept of homology by descent from a common ancestor in biology. The rank of the 0-homology captures the number of connected components (the number of islands) at each stage of the filtration. This number is known as the 0-th Betti number and is denoted as . For example, in Figure 2D, we see three connected components at the first stage, then six, and so on. The full evolution as components are created or merge along the filtration can be encoded in a single barcode (Carlsson et al., 2005), as illustrated in Figure 1G. A bar in a barcode starting at a value b (birth) and ending at d (death) indicates a connected component newly generated at the level b that merges with others at level d. Thus, more than just tracking the evolution of , a persistence barcode contains information about how components coalesce at different stages of the filtration. Similarly, the rank of the 1-homology is about the number of essential loops (holes), known as the first Betti number, leading to a barcode for the 1-homology of a filtration. There are higher dimensional analogs; however, they do not play a role in our analyses because our data are two-dimensional. We used the software package JavaPlex (Adams et al., 2014) to compute barcodes. Some useful reductions of persistence barcodes that are simpler to compute are the 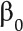curve, the curve, and the Euler characteristic curve, which are described next. As we varied the threshold r continuously, also changed, producing a 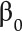curve that described how the 0-th Betti number evolves with the threshold. Similarly, we obtained a curve, as exemplified in Figure 3C (to measure complexity of root architecture). For 2D domains, the EC was given by 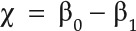, also viewed as a curve, as in Figure 2D (to measure serrations). The EC is the easiest to compute since it may be calculated directly from the following formula: the number of vertices (V) minus the number of edges (E) plus the number of faces (F) (χ = V − E + F). Strictly speaking, an EC curve or Betti curve should belong to topological data analysis rather than PH. Since it is the reduced information of persistence barcode, we categorized it as PH framework.

Statistical Analysis

Bottleneck distance is a robust metric for calculating similarity between persistence barcodes (Cohen-Steiner et al., 2007). In brief, bottleneck distance calculates the minimal cost to move bars from one persistence barcode to resemble another (Li et al., 2017). Output pairwise bottleneck distances and EC curves can be used with standard statistical techniques such as PCA, MDS, and CVA. PCA, MDS, and CVA were calculated using the Matlab functions princomp(), cmdscale(), and implemented function lda(). All Matlab functions necessary to calculate persistence barcodes, bottleneck distances for leaf shape, Euler characteristic curves for leaf serrations, and curves for root architecture used in this manuscript can be found at the following GitHub repository: https://github.com/maoli0923/Persistent-Homology-Tomato-Leaf-Root. Using a standard personal computer, PH for leaf serrations and root architecture can be calculated within a day, and leaf shape in 2 to 3 d.

Heritability was calculated using mixed-effects linear-model packages lme4 (Bates et al., 2014) and lmerTest (Kuznetsova et al., 2015) in R with M82 as an intercept, the IL genotype as a fixed effect, and field position attributes (block and column) as random effects.

We calculate the shape variation explained by each IL as follows: For a given IL, and cv M82, we calculate the CV1 values and the projection axis to find the best separation between these two genotypes. Then we map all the remaining ILs to the same projection axis to obtain their CV1 scores. The shape variation is calculated as the difference between the means of this given IL and cv M82 divided by the entire range of the CV1 scores of the entire data set. The information of the shape variation is reported in columns H, N, and U of Supplemental Data Set 1. Raw data can be found at https://www.danforthcenter.org/scientists-research/principal-investigators/chris-topp/resources.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Examples of homology groups and pipeline of persistent-homology framework.

• Supplemental Figure S2. Example of persistent homology applied to point cloud data set.

• Supplemental Figure S3. An example to show why we chose annulus rather than disk.

• Supplemental Figure S4. Elliptical Fourier transform with different parameters k to approximate a leaflet contour.

• Supplemental Figure S5. Heritability of traits.

• Supplemental Data Set 1. Distribution information for normalized canonical variate scores (CV1) shown in Figure 5.

Dive Curated Terms

The following phenotypic, genotypic, and functional terms are of significance to the work described in this paper:

• leaf AmiGo: PO:0025034

• leaf shape Planteome: TO:0000492

• leaf width Planteome: TO:0000370

• root AmiGo: PO:0009005