Beyond the RfD: Broad Application of a Probabilistic Approach to Improve Chemical Dose–Response Assessments for Noncancer Effects

Abstract

Background:

The National Academies recommended risk assessments redefine the traditional noncancer Reference Dose (RfD) as a probabilistically derived risk-specific dose, a framework for which was recently developed by the World Health Organization (WHO).

Objectives:

Our aim was to assess the feasibility and implications of replacing traditional RfDs with probabilistic estimates of the human dose associated with an effect magnitude M and population incidence I (${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$).

Methods:

We created a comprehensive, curated database of RfDs derived from animal data and developed a standardized, automated, web-accessible probabilistic dose–response workflow implementing the WHO framework.

Results:

We identified 1,464 RfDs and associated endpoints, representing 608 chemicals across many types of effects. Applying our standardized workflow resulted in 1,522 ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ values. Traditional RfDs are generally within an order of magnitude of the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ lower confidence bound for $\mathrm{I}=1\%$ and M values commonly used for benchmark doses. The greatest contributor to uncertainty was lack of benchmark dose estimates, followed by uncertainty in the extent of human variability. Exposure at the traditional RfD frequently implies an upper 95% confidence bound of several percent of the population affected. Whether such incidences are considered acceptable is likely to vary by chemical and risk context, especially given the wide range of severity of the associated effects, from clinical chemistry to mortality.

Conclusions:

Overall, replacing RfDs with ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ estimates can provide a more consistent, scientifically rigorous, and transparent basis for risk management decisions, as well as support additional decision contexts such as economic benefit–cost analysis, risk–risk tradeoffs, life-cycle impact analysis, and emergency response. https://doi.org/10.1289/EHP3368

Introduction

The Reference Dose (RfD) and its variants, such as the acceptable daily intake (ADI) and minimal risk level (MRL), are workhorses of chemical risk assessment, having been routinely used in a wide range of risk management decisions. As exemplified by the definition of the RfD by the U.S. Environmental Protection Agency (EPA), these toxicity values are intended to define an exposure level (oral dose or air concentration) that is considered, in the colloquial sense, safe (Dourson and Stara 1983). Thus, risk is typically characterized through a Hazard Quotient (HQ) defined as the estimated exposure divided by the RfD, so that $\text{HQ}\le 1$ indicates an acceptable risk and $\text{HQ}>1$ indicates a possible risk of concern (U.S. EPA 1989). In practice, therefore, the RfD is treated as a bright line below which potential public health impacts of exposure are no longer a concern (NAS 2009).

Toxicity values such as the RfD are typically derived by first identifying a Point of Departure (POD) from an experimental animal toxicology or human epidemiologic study, and then dividing this value by a number of uncertainty (or safety) factors (U.S. EPA 2002). The POD has traditionally been a No Observed Adverse Effect Level (NOAEL) or Lowest Observed Adverse Effect Level (LOAEL), although use of a statistically derived benchmark dose lower confidence limit (BMDL) is generally preferred (U.S. EPA 1995, 2012). The most commonly applied uncertainty factors are a factor of 10 to address differences between experimental animals and humans (${\text{UF}}_{\mathrm{A}}$) and a second factor of 10 to address variability among humans (${\text{UF}}_{\mathrm{H}}$). This concept of dividing a NOAEL by 100 dates back to 1950s in the context of FDA regulation of food additives (Lehman and Fitzhugh 1954). This factor has been refined over the years, first by subdividing the original 100 into two separate factors of ${\text{UF}}_{\mathrm{A}}=10$ and ${\text{UF}}_{\mathrm{H}}=10$, and then further subdividing each factor of 10 into toxicokinetic (TK) and toxicodynamic (TD) portions. More recently, the option has been introduced to replace default uncertainty factors with chemical-specific adjustment factors (CSAFs) based on available chemical-specific data on interspecies differences or human variability in TK or TD (WHO/IPCS 2005). Additionally, the EPA recommends, when possible, to first apply a dosimetric adjustment factor to account for physiological differences (e.g., using allometric scaling by body weight to the ¾ power) followed by a smaller a 3-fold ${\text{UF}}_{\mathrm{A}}$ (U.S. EPA 1994, 2011c). Furthermore, other uncertainty factors are commonly employed to address other limitations, including factors to adjust from a LOAEL to a NOAEL, to address lack of availability of a chronic study, and to take into account inadequacies in the toxicity database. Overall, however, the fundamental approach of a NOAEL divided by fixed factors has undergone little essential change in the last half-century.

A number of limitations of the RfD have been recognized. First, each of these components—the NOAEL, ${\text{UF}}_{\mathrm{A}}$, and ${\text{UF}}_{\mathrm{H}}$—is assumed to be conservative in the sense of erring on the side of protecting public health, but without much specificity as to how conservative they actually are (WHO/IPCS 2014). For instance, with respect to the NOAEL, it is assumed that the degree, severity, and/or probability of effects at this exposure level are negligible, but the extent to which this assumption is true depends on the endpoint examined and the statistical power of the study (Crump 1984; U.S. EPA 2012). For ${\text{UF}}_{\mathrm{A}}$, it is assumed that 10 is sufficient to address interspecies differences for most chemicals— i.e., that in most cases humans are no more than 10-fold more sensitive than the experimental animal species. However, it is not specified the actual proportion of cases (90%, 95%, 99%?) for which this assumption is presumed to be true. Similarly, for ${\text{UF}}_{\mathrm{H}}$, it is assumed that individuals more susceptible to toxicity are no more than 10-fold more sensitive than more typical individuals. Here, there are two ambiguities: first, like ${\text{UF}}_{\mathrm{A}}$, the proportion of cases for which it is assumed that 10-fold is sufficient, and second, what it means to be susceptible in terms of the more sensitive tail of the population distribution (e.g., 5%, 1%, 1 in a million?).

Taken together, RfDs characterize neither the likelihood that harm may occur, nor the degree or severity of such harm if it should occur, nor the fraction of the population that might be affected (NAS 2009; WHO/IPCS 2014). Although the EPA’s definition of the RfD includes a statement that it is an “estimate (with uncertainty spanning perhaps an order of magnitude),” the actual degree of uncertainty in the RfD is not known or quantified. Thus, the resulting HQs used for noncancer risk characterization provide no quantitative information about public health impacts in terms of likelihood, degree, or incidence of harm or their uncertainty – they merely denote a level below which such impacts are presumed to be acceptably small, and above which public health impacts cannot be ruled out (NAS 2009). The result is that different risk characterizations with the same HQ may imply vastly different levels of risk. Additionally, this lack of risk quantification limits the ability to assess changes in risk, to compare risks, or to weigh benefits of risk management options versus costs (McGartland et al. 2017; WHO/IPCS 2014). By contrast, toxicity values for cancer effects typically take the form of a slope factor or unit risk, which is an (upper bound) estimate of the incremental risk to the population per unit exposure (U.S. EPA 2005). Thus, unlike the HQ used for noncancer effects, the results of cancer risk assessments provide a characterization of the incidence in the population of cancer at different exposure levels.

These limitations in noncancer risk assessment have led to calls for moving to a probabilistic approach to better quantify the predicted noncancer impacts of chemical exposures, along with the uncertainties and variability of these impacts (Baird et al. 1996; Chiu and Slob 2015; Evans et al. 2001; Hattis et al. 2002; NAS 1994, 2009; Slob and Pieters 1998; Swartout et al. 1998; WHO/IPCS 2014). The National Academy of Sciences (NAS) in particular recommended that the RfD be redefined as a “risk-specific dose” (NAS 2009), resulting in predictions of the risk associated with different exposure levels. The WHO/IPCS followed by developing a comprehensive framework to implement such a redefinition (WHO/IPCS 2014) (Chiu and Slob 2015), fulfilling the NAS (2009) recommendation to disaggregate risk into the distinct concepts of uncertainty (likelihood of harm), magnitude of effect (degree of harm), and incidence of effect (fraction of the population affected), resulting in a more complete characterization of the public health impact of chemical exposures (NAS 2009).

The key concepts underlying the WHO/IPCS approach were previously reported in Chiu and Slob (2015). The most essential elements are shown in Figure 1. First, as shown on the lower left, individual dose–response curves can differ across the population due to intrinsic human variability. Second, this population of dose-responses can be expressed in terms of the concept of the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ – the human dose (HD) associated with an effect of magnitude M, and population incidence I. Third, the traditional RfD can be replaced with a probabilistic RfD, represented by the lower 95% confidence bound of the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$. Moreover, the calculation of the probabilistic RfD is similar to that of the traditional RfD but with more precisely defined uncertainty factors, treated as probabilistic distributions instead of fixed values. Specifically, the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ and associated probabilistic RfD can be thought of as a more precisely defined version of the traditional RfD, with the somewhat ambiguous aspects of the RfD definition replaced with quantitatively specified definitions as follows: (a) the concept of “deleterious effects” is replaced by a specific magnitude of effect in terms of degree of harm (e.g., a 5% change in hematocrit) (Figure 1, italic underline, in green), (b) the “estimate” of the dose “likely” to be without these effects is replaced by a specific statistical confidence bound (e.g., 95% lower confidence bound) (Figure 1, italic bold, in purple), and (c) the idea of protecting “sensitive subpopulations” is replaced by a specific population incidence level (e.g., 1% of the population) (Figure 1, italic bold underline, in red).

Figure 1.

Comparison of traditional and probabilistic definitions of the Reference Dose (RfD), along with definition of the output of probabilistic dose–response framework, ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$. Top: the definitions of the traditional and probabilistic RfDs are compared in terms of the equations used to derive them and the textual definition. The arrows show how the probabilistic RfD is more precisely defined quantitative by replacing: “deleterious effects” with a specific magnitude of effect in terms of degree of harm (italic underline, in green), the “estimate” of the dose “likely” to be without these effects with a specific statistical confidence bound (bold italic, in purple), and protecting “sensitive subpopulations” by a specific population incidence level (bold italic underline, in red). Additionally, the conceptual basis of the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ is displayed graphically as being based on individual dose-response curves for different percentiles of the population (lower left), along with its definition as the “Human dose associated with an effect of magnitude M and population incidence I” (lower right). Note: NOAEL, No Observed Adverse Effect Level; ${\text{UF}}_{\mathrm{A}}$, traditional uncertainty factor for animal-to-human extrapolation; ${\text{UF}}_{\mathrm{H}}$, traditional uncertainty factor for human variability; ${\text{BMD}}_{\mathrm{M}}$, benchmark dose for a magnitude of effect M; ${\text{UF}}_{\mathrm{A,BW}}$, probabilistic factor for interspecies body weight (BW) scaling (Figure 4); ${\text{UF}}_{\mathrm{A,BW}}$, probabilistic factor for interspecies toxicokinetic (TK) and toxicodynamic (TD) differences (after BW scaling); ${\text{UF}}_{\mathrm{A,BW}}$, probabilistic factor for human variability in sensitivity for a population incidence I. Adapted from WHO/IPCS (2014).

Although WHO/IPCS (2014) and Chiu and Slob (2015) presented some case examples of how the RfD could be replaced by a probabilistic version, broad application of a probabilistic approach has not yet been demonstrated. Because of the limited number of case examples, it is difficult to estimate the feasibility or the potential implications of moving away from an approach to deriving toxicity values that has been applied for over half a century. To fill this gap, we endeavored to apply the WHO/IPCS framework to a large database of existing RfD values, with the goal of developing and demonstrating an automated workflow that enables routine use of the probabilistic approach. We applied our workflow to over 1,400 endpoints for over 600 chemicals, generating over 1,500 probabilistic RfDs and associated ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ estimates. Moreover, this large number of endpoints and chemicals enabled us to draw general conclusions as to the level of protection implied by current RfDs, extending previous work by Castorina and Woodruff (2003), the extent that exposure limits based on a probabilistic RfD are likely to differ from current RfDs, and what additional data or analyses could reduce uncertainty in the predicted risks. Finally, we deployed the workflow in two online tools: a standalone web app titled APROBAweb at https://wchiu.shinyapps.io/APROBAweb/ (Chiu 2018a) and an implementation that could be integrated with Bayesian benchmark dose modeling at https://benchmarkdose.org (Shao and Shapiro 2018).

Methods

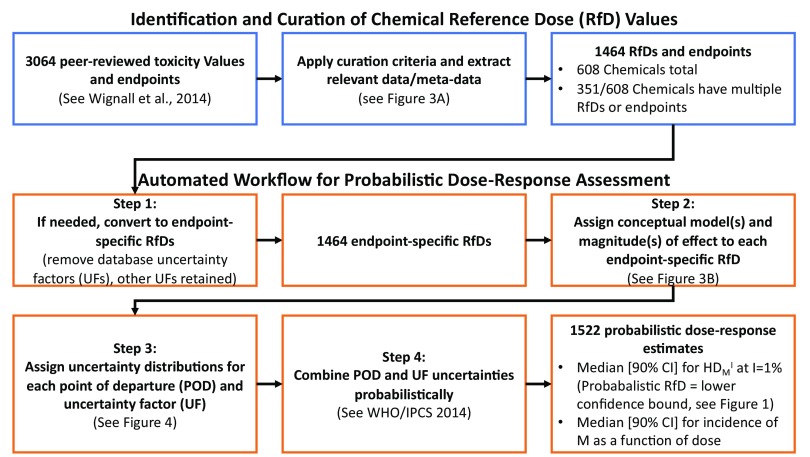
Figure 2 provides an overview of our approach to apply an automated probabilistic dose–response workflow to a large number of chemicals and endpoints. Additional details follow, with the data and code available on github (https://github.com/wachiuphd/Probabilistic-RfD) (Chiu 2018b).

Figure 2.

Overview of curation of toxicity values and probabilistic dose–response workflow. Blue boxes relate to the identification, curation, and extraction of chemical reference doses (RfDs); orange boxes relate to the automated workflow for replacing RfDs with probabilistic dose-response estimates. Note: The number of probabilistic dose-response estimates (1,522) exceeds the number of endpoints-specific RfDs (1,464) because some RfDs did not specific whether a continuous or dichotomous endpoint was used, so both possibilities were evaluated in the probabilistic approach (see Figure 3B). CI, Confidence Interval; POD, Point of Departure; UF, Uncertainty factor; ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$, Human dose associated with an effect of magnitude M and population incidence I.

Identification and Curation of Chemical Reference Doses

As part of previously published work (Wignall et al. 2014), we compiled a database of 3,064 publicly available, peer-reviewed human health toxicity values as of June 2011 from U.S. EPA (Integrated Risk Information System [IRIS], Office of Pesticide Programs [OPP], Superfund Regional Screening Levels [RSLs]), or California EPA (Office of Environmental Health Hazard Assessment). Superfund RSLs included data from the above sources as well as the Centers for Disease Control and Prevention (CDC) Agency for Toxic Substances and Disease Registry (ATSDR) Toxicological Profiles, EPA Provisional Peer Reviewed Toxicity Values (PPRTV), EPA Health Effects Assessment Summary Tables (HEAST), and the EPA Office of Water Environmental Criteria and Assessment Office. Curation and data extraction, summarized in Figure 3A, were performed to enable application of our automated probabilistic dose–response workflow. The focus here is on noncancer toxicity values from oral exposure, with other routes of exposure left for future work. Toxicity values based on human data were also excluded because such data are more heterogeneous than experimental animal data (clinical versus epidemiologic, different subpopulations, summary versus individual data) and require case-by-case consideration of uncertainties. In a similar vein, toxicity values using chemical-specific adjustment factors were excluded, again because they require case-by-case uncertainty evaluation. Toxicity values from different organizations were considered unique even if they used the same endpoint and had the same value, in order to be able to examine results by organization. Additional details are shown in Figure 3A. The database is available through github or the APROBAweb portal (Chiu 2018a, b).

Figure 3.

Details of (A) toxicity value curation and data extraction and (B) assignment of conceptual model based on type of effect. Note: BMD, Benchmark Dose; BMDL, Benchmark Dose Lower Confidence Limit; BMR, Benchmark Response; CASRN, Chemical Abstracts Service Registry Number; ED50, Effective Dose for a 50% response; LOAEL, Lowest Observed Adverse Effect Level; MRL, Minimal Risk Level; NOAEL, No Observed Adverse Effect Level; POD, Point of Departure; RfD, Reference Dose; SD, Standard Deviation; SE, Standard Error; UF, Uncertainty factor. See WHO/IPCS (2014) and Chiu and Slob (2015) for detailed definitions and descriptions of each conceptual model.

To assess the diversity of chemicals, effects, and toxicity values represented in our analysis, we examined the resulting curated database in terms of (a) types of effects covered; (b) types of PODs; (c) value of composite UF; (d) comparisons of RfDs from different sources (e.g., IRIS vs. ATSDR vs. OPP); and (e) range of chemical properties in comparison with a larger space of environmental chemicals. For assessing the diversity of chemicals, we used the open-source Chemistry Development Kit (CDK), as implemented in the R (version 3.3.2; R Core Team) package rcdk (Guha 2007), to generate molecular descriptors for each RfD compound based on each compound’s simplified molecular-input line-entry system (SMILES). Molecular descriptors include a variety of physicochemical properties, such as Octanol:Water Partition Coefficient, Molecular Weight, and Topological Polar Surface Area, in addition to properties related to the number and configuration of atoms in a molecule, such as the number of aromatic atoms. Specifically, CDK descriptor categories we used were: topological, constitutional, geometric, electronic, and hybrid. “Fingerprint” representations were not used. Descriptors that could be calculated for any RfD compound were included. For comparison, CDK descriptors also were generated for the 32,464 structures in the Collaborative Estrogen Receptor Activity Prediction Project (CERAPP) “prediction” dataset (Mansouri et al. 2016). The CERAPP set of chemicals was chosen to represent the compendium of chemicals to which humans may be exposed. To provide an overview of the diversity of the structures and the overall chemical space, the chemical structures in each list were first analyzed using principal component analysis to account for correlations across descriptors. Additionally, structures were compared using the easily interpretable descriptors Octanol:Water Partition Coefficient, Molecular Weight, and Topological Polar Surface Area.

Automated Workflow for Probabilistic Dose–Response Assessment

Our automated workflow for probabilistic dose–response assessment, illustrated in Figure 2, consisted of four steps:

1. Each RfD and associated endpoint was converted to an endpoint-specific RfD, meaning that any database UF is removed (317 out of 1464 RfDs). This step was necessary because the probabilistic dose–response framework aims to make predictions related to the specific effects associated with the POD, as shown in Figure 1, rather than a general statement about lack of “deleterious effects.” Because the database factor is meant to cover the case where a different effect might be observed in an as-yet-unperformed study, it is not meaningful to include in deriving the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$. All other UFs were retained because steps 3 and 4, below, will replace each of these fixed UFs with an appropriate uncertainty distribution, and thereby derive the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ as a human equivalent dose (Figure 1).

2. For each RfD-endpoint combination, a conceptual model was assigned based on the type of effect (continuous or dichotomous, reflecting a stochastic process or not) associated with the POD (see Figure 3B). Effect categories were standardized during curation (Figure 3A) so assigning conceptual models could be automated. The conceptual model, along with the benchmark response (BMR) for PODs that are BMDLs, determined the magnitude of effect (M) being carried through the framework. In some cases, such as when a NOAEL was reported for a general category of “reproductive” effects that might include both continuous and quantal endpoints, multiple conceptual models were assigned, resulting in multiple ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ estimates for a single RfD-endpoint combination.

3. Uncertainty distributions were generated for the POD and each UF, based on the approaches and default distributions outlined in WHO/IPCS (2014) and Chiu and Slob (2015), summarized in Figure 4. Of note is that if the POD was a LOAEL, there were two adjustments―one based on how much lower the NOAEL might be, and a second one based on what the BMD might be for a given NOAEL. Both of these adjustments incorporated uncertainties.

4. The uncertainties were combined probabilistically, using the approximation described in WHO/IPCS (2014) that assumes lognormal distributions for each factor. This approximation was previously implemented in a spreadsheet tool titled APROBA, which is available from the WHO/IPCS web page (http://www.who.int/ipcs/methods/harmonization/areas/hazard_assessment/en/) (WHO/IPCS 2017). The accuracy of the approximation was previously evaluated in WHO/IPCS (2014) but was confirmed in the specific calculations in the present analysis by Monte Carlo simulation using ${10}^7$ independent random samples from each underlying probability distribution.

Figure 4.

Details of uncertainty factor probability distributions assigned. Note: BMD, Benchmark Dose; BMDL, Benchmark Dose Lower Confidence Limit; BMDU, Benchmark Dose Upper Confidence Limit; BW, Body Weight; ED50, Effective Dose for a 50% response; LOAEL, Lowest Observed Adverse Effect Level; NOAEL, No Observed Adverse Effect Level; POD, Point of Departure; P50, median of the distribution = Geometric mean of lognormal distribution; P95/P50, ratio between the 95th percentile and the median of the distribution = (Geometric standard deviation of lognormal distribution)^1.6449; RfD, Reference Dose; SD, Standard Deviation; TD, Toxicodynamic; TK, Toxicokinetic; ${\text{UF}}_{\mathrm{L}}$, Uncertainty Factor for LOAEL-to-NOAEL.

The results of this workflow were expressed in multiple ways. First, an estimate of the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ for a specific incidence in the relevant population was generated. Based on limited previously published examples of probabilistic analyses, we used an incidence of 1% as a nominal value (U.S. EPA 2011a, b). One additional reason for choosing 1% was that values much less than 1% become increasingly sensitive to the choice of distribution for human variability (Crump et al. 2010). In keeping with the conventions used for benchmark dose analyses, we reported the median estimate along with the 90% two-sided confidence interval (CI), so that the probabilistic RfD is defined as the lower one-tailed 95% confidence bound (see Figure 1). Additionally, it is important to understand what the most important sources of uncertainty are. Therefore, we also investigated the fraction of the overall variance that is contributed by each of the factors in Figure 4. Given that one of the main motivations for this approach was the ability to better quantify the dose–response relationship, ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ for varying levels of incidence (I) were also estimated, resulting in the estimated incidence as a function of dose.

Comparisons to Traditional RfDs

We made several comparisons to traditional RfDs to estimate the risks associated with traditional risk assessment practices. First, a direct comparison was made between the traditional RfDs and the probabilistic RfD for $\mathrm{I}=1\%$ at 95% confidence to benchmark the traditional RfD in comparison to a probabilistic RfD associated with a nominally selected value for I. Additionally, the level of conservativeness of the traditional RfD was assessed by estimating its percent confidence in context of the uncertainty distribution for the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ at the $\mathrm{I}=1\%$ nominal value described above. Furthermore, the (residual) risk at the traditional RfD was estimated in terms of which incidence of effect (including CIs) was predicted for exposures at that level. Finally, the predicted incidence I as a function of the traditional hazard quotient ($\text{HQ}=\text{Exposure}/\text{traditional}\text{RfD}$) was also compared across chemicals and endpoints to evaluate how consistently the HQ characterized risk (e.g., whether a $\text{HQ}=10$ implied the same level of risk for different chemicals and endpoints).

Results

Identification and Curation of Chemical Reference Doses

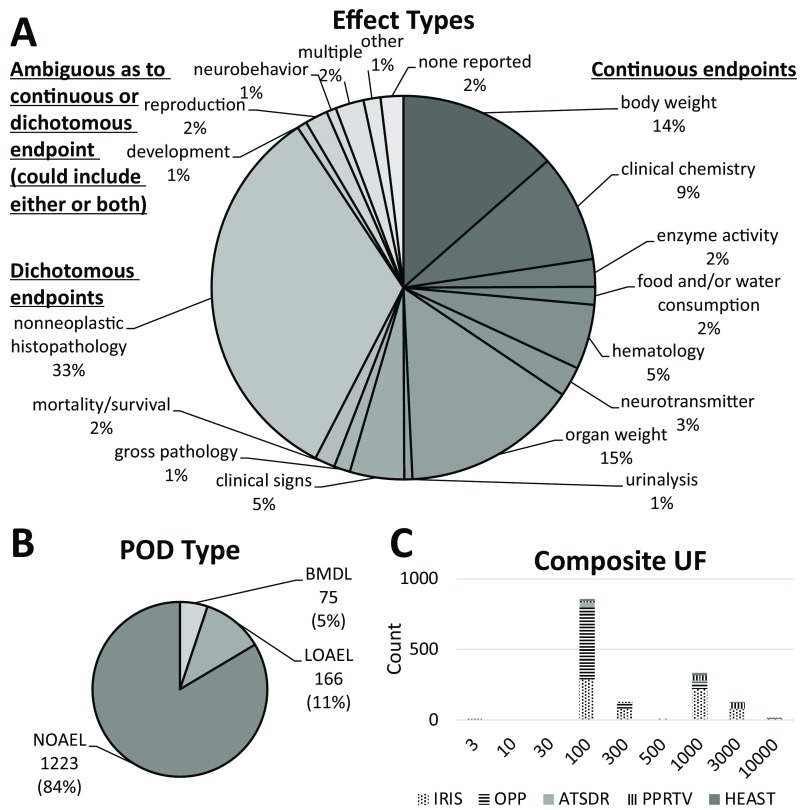
After curation and data extraction, the database consisted of 1,464 RfD-endpoint combinations, comprising 608 unique chemicals, 351 of which had multiple RfD-endpoint combinations. Characteristics of the database are summarized in Figure 5. Briefly, a wide range of endpoints were covered, with nonneoplastic histopathology (33%), organ weight (15%), and body weight (14%) being the most common. The clear majority of PODs were NOAELs (84%), followed by LOAELs (11%), with only 5% being BMDLs. The most common value for the composite UF was 100 (more than half), followed by 1,000, 300, and 3,000. For the same chemical, RfDs or PODs are largely consistent across organizations, with values from different sources being in almost all cases within 10-fold of each other (Figure S1).

Figure 5.

Characteristics of the database of references doses (RfDs). (A) Distribution of toxicological effects, including continuous endpoints, dichotomous endpoints, and endpoints that could be either continuous or dichotomous. (B) Distribution of types of points of departure (POD), including NOAEL (no observed adverse effect level), LOAEL (lowest observed adverse effect level), and BMDL (benchmark dose lower confidence limit). (C) Distribution of composite uncertainty factors (UFs) applied across RfDs, depending on source (IRIS, Integrated Risk Information System; OPP, Office of Pesticide Programs; ATSDR, Agency for Toxic Substances and Disease Registry; PPRTV, Provisional Peer-reviewed Toxic Values; HEAST, Health Effects Assessment Summary Tables).

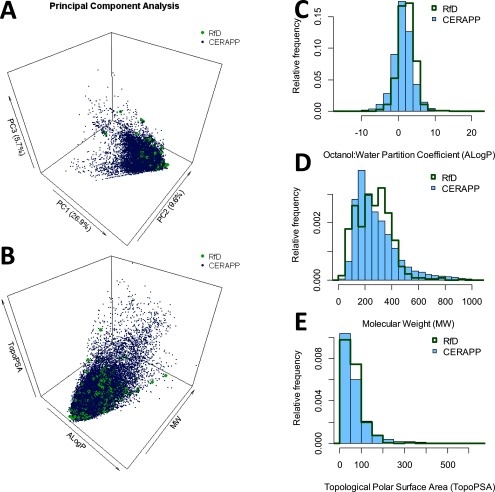
Results of comparison of CDK molecular descriptor space to CERAPP compounds using principal component analysis are shown in Figure 6A. Additionally, comparisons were made with selected physicochemical properties frequently used in the pharmaceutical industry to triage compounds (Lipinski 2016), considered together (Figure 6B) or independently (Figure 6C–E). Together, these comparisons show substantial overlap between RfD and CERAPP compounds.

Figure 6.

Chemical space coverage of reference doses (RfDs). The chemical properties of chemicals from the database of RfDs was compared to 32,464 structures in the Collaborative Estrogen Receptor Activity Prediction Project (CERAPP) “prediction” dataset from Mansouri et al. (2016), based on chemical descriptors generated from chemistry development kit (CDK) (Guha 2007). (A) 3-D plot of coverage based on first three principal components; (B)–(E) Coverage comparisons based on easily interpretable descriptors Octanol:Water Partition Coefficient (ALogP), Molecular Weight (MW) in Daltons, and Topological Polar Surface Area (TopoPSA) in angstroms squared. (B) is a 3D plot, and (C)–(E) are histograms comparing the distributions of compounds for each descriptor.

Automated Workflow for Probabilistic Dose–Response Assessment

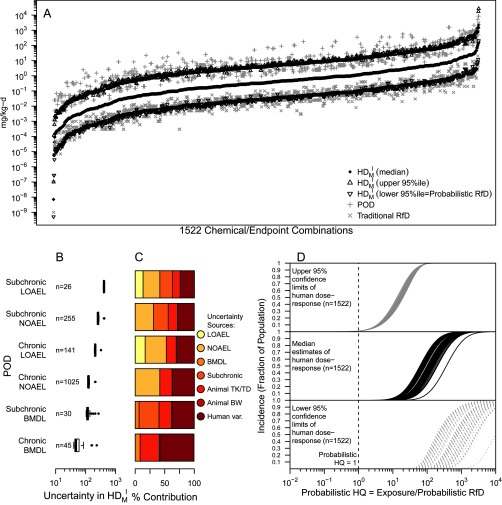
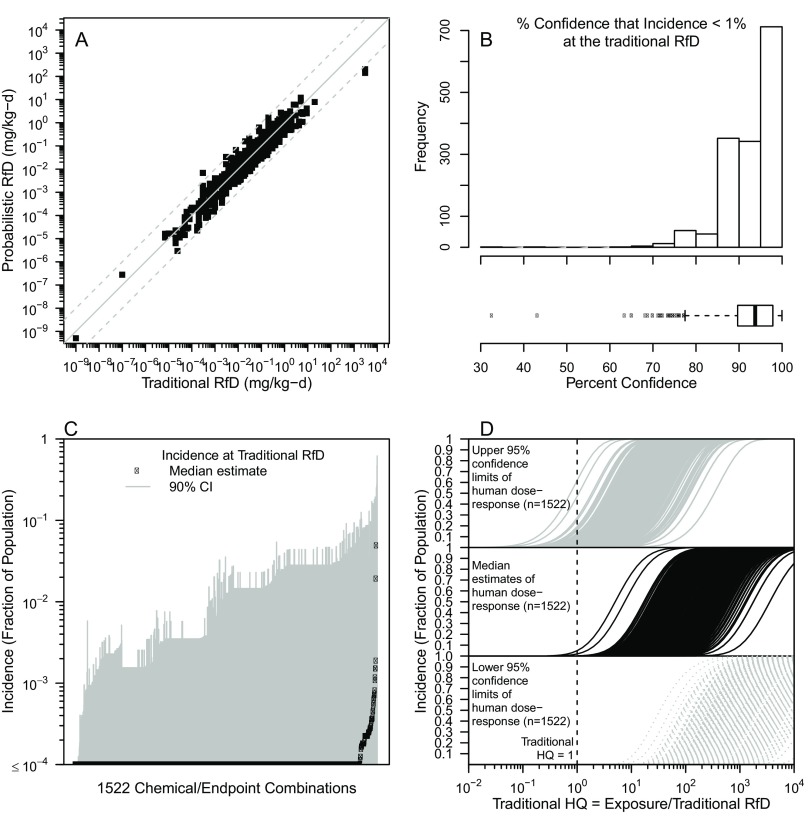
The results of applying our automated workflow are summarized in Figure 7. First, using the definition illustrated in Figure 1, we derived estimates for the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ for a population incidence of $\mathrm{I}=1\%$, where the probabilistic RfD is defined as the lower (one-tail) 95% confidence bound (Figure 7A). The traditional RfDs tends to correlate with the probabilistic RfDs (see also Figure 8A, below). Additionally, the PODs tend to track with the upper (one-tail) 95% confidence bounds on the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ (Figure 7A).

Figure 7.

Results of automated probabilistic dose-response workflow applied to 1,522 chemicals and endpoints. (A) Comparison of traditional and probabilistic values: traditional POD ($\text{grey}+$), traditional RfD ($\text{grey}\times$); ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ median (black diamond); ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ upper 95% confidence (black open triangle); ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ lower 95% $\text{confidence}=\text{probabilistic}$ (black open downward triangle). (B) Boxplots of degree of uncertainty in ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ (ratio between upper-tail 95% confidence bound and lower-tail 95% confidence bound), for different types of PODs (number “n” of PODs of each type is also shown). Each boxplot includes the interquartile range (box), median (line in box), 95% confidence interval (whiskers), and values outside 95% confidence interval (black dots). (C) Contribution to overall uncertainty from each potential source of uncertainty, for the types of PODs. (D) Dose-response functions, derived by estimates of ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ at varying levels of incidence I, with exposure converted to a probabilistic hazard quotient through division by the probabilistic RfD. LOAEL, Lowest Observed Adverse Effect Level; NOAEL, No Observed Adverse Effect Level; BMDL, Benchmark Dose Lower Confidence Limit; TK/TD, Toxicokinetic and Toxicodynamic; BW, Body Weight scaling; POD, Point of Departure; UF, Uncertainty Factor; ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$, Human dose associated with an effect of magnitude M and population incidence I; RfD, Reference Dose; HQ, Hazard Quotient.

Figure 8.

Comparison of results of traditional and probabilistic dose-response assessment. (A) Scatterplot of traditional RfD versus probabilistic RfD, defined as shown in Figure 1 for $\mathrm{I}=1\%$. Grey solid line denotes equality, and grey dashed lines denote 10 times greater or less. (B) Comparison of traditional RfD in terms of the uncertainty distribution of ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$, expressed as the percent confidence that $\mathrm{I}<1\%$ at exposures equal to the traditional RfD, shown as a frequency histogram and a boxplot. The boxplot displays the interquartile range (box), median (line in box), 95% CI (whiskers), and values outside 95% confidence interval (black dots). (C) Predicted incidence at the traditional RfD ($\text{median}=\text{black}\text{dots}$, 90% $\text{CI}=\text{vertical}\text{grey}\text{lines}$). (D) Dose-response functions, derived by estimates of ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ at varying levels of incidence I, with exposure converted to a traditional hazard quotient through division by the traditional RfD. CI, Confidence Interval; HQ, Hazard Quotient; RfD, Reference Dose.

The degree of uncertainty associated with the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ (i.e., ratio between the upper confidence and lower confidence bounds) expresses how much greater the actual value of ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ might be in comparison with the Probabilistic RfD (i.e., the lower 95% confidence bound). As shown in Figure 7B, the degree of uncertainty depends strongly on the type of POD available for each chemical and endpoint. For instance, using PODs consisting of LOAELs from subchronic studies results in the greatest uncertainty (around 400-fold), whereas using PODs consisting of BMDLs from chronic studies results in the least uncertainty (mostly around 50-fold). The most common type of POD, NOAELs from chronic studies, lead to uncertainties of around 100-fold.

The greatest source of uncertainty, shown as a percentage of the variance in the bar graphs in Figure 7C, tends to be related to using LOAELs and NOAELs, which are imprecise estimates of the dose associated with a specific magnitude of effect. Uncertainty in the degree of human variability is the next greatest contributor overall, followed by uncertainty due to use of subchronic studies in place of chronic studies, and then uncertainty in animal-to-human extrapolation due to unknown chemical-specific TK or TD differences. Uncertainty in the BMD and uncertainty in the allometric interspecies scaling relationship are small contributors overall.

In addition to estimating a more precise, probabilistically defined RfD, the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ can be derived at multiple values of incidence I, leading to a population dose–response function rather than a point estimate. Figure 7D illustrates the results of this calculation, showing estimates of the fraction of the population affected as exposure increases. In analogy to traditional risk assessment practices, exposure can be re-expressed as a probabilistic hazard quotient (HQ) defined as the ratio between exposure and the probabilistic RfD. By anchoring exposure to the probabilistic RfD, which is the lower confidence bound on the dose leading to a 1% incidence, the probabilistic HQ leads to a consistent relationship across compounds and endpoints between exposure and the upper confidence bound on incidence. In other words, by definition, a probabilistic $\text{HQ}=1$ in this analysis always means the upper 95% confidence bound on $\mathrm{I}=1\%$; but as the probabilistic HQ increases, the upper confidence bound on I is similar across compounds and endpoints. For instance, an HQ of 3 is associated with an upper confidence bound on I ranging from 6% to 9% (interquartile range (IQR) 7.4–7.8%). Similarly consistent are estimates at HQ of 10, with the upper confidence bound on I ranging from 26–39% (IQR 32–34%). Thus, the upper bound on risk associated with exposures above the probabilistic RfD is fairly consistent across chemicals and endpoints.

The accuracy of the approximate approach used in the automated workflow was confirmed, as the results for the both the confidence bounds and the median of the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ were all within 20–30% of the results of using Monte Carlo simulation (Figure S2).

Comparisons with Traditional RfDs

The comparisons between the results of our probabilistic dose–response workflow and traditional risk assessment results are summarized in Figure 8. First, as shown in Figure 8A, the traditional RfD is generally within an order of magnitude of the probabilistic RfD for $\mathrm{I}=1\%$. We examined whether this correlation depended on the type of endpoint, type of POD, and decade of publication of the traditional RfD, but we could find no discernable pattern (Figures S3-S5). The comparison between the traditional and probabilistic RfDs can be re-expressed as the percent confidence that $\mathrm{I}<1\%$ at the traditional RfD, summarized in Figure 8B. The IQR across the 1,522 chemicals and endpoints for the percent confidence that $\mathrm{I}<1\%$ is 90–98% confidence, with a range of 33–99.98% confidence. Thus, almost all traditional RfDs are conservative in the sense that they are protective at $>50\%$ confidence of no more than 1% population incidence of effects, though a substantial fraction falls short of the 95% confidence that is often used as a threshold, as with the BMDL.

Also of interest is the estimate of risk for exposures equal to the traditional RfD, which is left unspecified in traditional risk assessment. As illustrated in Figure 8C, the median estimate of the residual risk at the traditional RfD is $\mathrm{I}<0.01\%$ in the clear majority of cases. The upper 95% confidence bounds on I at the traditional RfD range from $\mathrm{I}<0.01\%$ to $\mathrm{I}=62\%$, with an IQR of $\mathrm{I}=0.3\%$ to 3%. Thus, the traditional RfD is predicted to have an upper bound population incidence around a few percent, although as with the percent confidence, exceptions in either direction are not uncommon.

Finally, a common issue in risk assessment is determining the level of concern associated with exposure above the traditional RfD, corresponding the traditional $\text{HQs}>1$. As illustrated in Figure 8D, $\text{HQs}>1$ may correspond to a wide range of possible population incidence values. For instance, an HQ of 3 is associated with an upper confidence bound on I ranging from $<0.01\%$ to 96% (IQR 3–15%). The results are even more variable at HQ of 10, with the upper confidence bound on I ranging from $<0.2\%$ to $>99\%$ (IQR 17–54%).

Discussion

The first objective of this study was to demonstrate the feasibility of broadly applying the probabilistic framework developed by the WHO/IPCS (2014) across diverse compounds. Our database of existing RfD values appear representative of the larger universe of the chemicals in the environment and/or on various chemical inventories, as evidenced by the comparison of molecular properties, particularly using principal component analysis (Figure 6). We then developed an automated workflow with standardized decision rules for assigning conceptual models and magnitudes of effect, default uncertainty distributions based largely on the WHO/IPCS (2014) review, and a simplified calculation approach using lognormal distributions that has been validated for accuracy. Use of this workflow to implement probabilistic dose–response assessment successfully for over 1,400 endpoints using laboratory animal data across over 600 chemicals shows that going “beyond the RfD” to estimate the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ is both practical and practicable on a broad scale, presenting few challenges beyond those associated with traditional deterministic risk assessment procedures. Thus, because of the work previously done by the WHO/IPCS to develop default distributions and simplified computational approaches, the additional cost and effort to replace the traditional RfD with a probabilistic RfD is minimal.

Moreover, with the minimal added cost and effort come great benefits in terms of scientific rigor, transparency, and consistency. In terms of scientific rigor, the individual uncertainties being addressed have a stronger underpinning than the current deterministic uncertainty factors, being based on historical data on chemical toxicity as opposed to being based on more or less arbitrary factors of 10 (often justified post hoc). As was noted in WHO/IPCS (2014), current default factors of 10 are not necessarily conservative at the 95% confidence level when compared with historical data, so analyses that assume that the current default factors are 95% upper bounds will be misleading and underestimate potential risk (e.g., Simon et al. 2016). Of course, as recommended by the WHO/IPCS (2014), these distributions can be further improved through systematic reviews and/or chemical-specific data. Additionally, the combining of uncertainties properly accounts for their probabilistic nature, avoiding the potential for compounding of conservatism that can occur when traditional uncertainty factors are multiplied together (Cullen 1994). As it turns out, our analysis has shown that, by coincidence, these two issues of (a) current deterministic factors covering fewer than 95% of cases and (b) the compounding conservatism of multiplying upper bounds together roughly cancel out for a population incidence of around 1% for most chemicals. Whereas the EPA definition of the RfD suggests “uncertainty spanning perhaps an order of magnitude,” we find that the ratio between the traditional and probabilistic RfD spans about two orders of magnitude. Thus, a traditional RfD can be treated as an estimate of the probabilistic RfD with an uncertainty of about 10-fold in either direction. Additionally, the uncertainty in the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ itself (i.e., its 90% CI) spans at least two orders of magnitude, except in the case of a chronic study with a BMDL as the POD, in which the uncertainty generally spans about 40-fold.

In terms of transparency, the traditional RfD and uncertainty factors are vague as to the degree of health protection intended and the associated confidence level, whereas the probabilistic approach is, by definition, explicit as to both the degree of health protection (degree, severity, and incidence of effect) as well as the level of confidence to which the estimated human dose is protective (see Figure 1). Based on our analysis, in any particular case, the upper bound on risk associated with exposures above the traditional RfD is highly uncertain (Figure 8C), whereas for the probabilistic RfD, it is prespecified (e.g., 1% incidence). A corollary of the greater transparency of a probabilistic RfD is the ability to be consistent across endpoints and chemicals, ensuring that the same procedure for deriving an exposure guideline yields the same degree of health protection and level of confidence. In our current analysis, this consistency is hampered by the fact that the severity of endpoint that is to be protected against is inconsistent across RfD, ranging from mild clinical chemistry changes to increased mortality. Nonetheless, the ability, in principle, to have consistency in the probabilistic RfD across chemicals and endpoints is particularly useful for priority-setting, where the unspecified precision of current RfDs makes it difficult, if not impossible, to rank risks even for the same endpoint.

An additional benefit of the probabilistic approach is that it reveals the relative contributions of each source of uncertainty to the overall uncertainty. As mentioned previously, typical uncertainties in the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ have a 90% CI spanning at least 100-fold (Figure 7B), and understanding what contributes to this uncertainty can provide quantitative guidance as to the value of information of additional studies in terms of reducing uncertainty. This approach differs from comparing the traditional UFs with the composite UF for several reasons. First, in the probabilistic approach, each extrapolation is assumed to be independent, as opposed to being directly multiplicative in the deterministic approach. Second, the traditional UFs are almost always either 1, 3, or 10 and thus are a crude measure of uncertainty poorly supported by data. Third, the individual uncertainties themselves are based on historical data in the probabilistic approach and so provide a better representation of their contribution. Finally, the traditional RfD does not address the uncertainty introduced by using a NOAEL instead of a BMD, instead treating them as equivalent.

As shown in Figure 7C, our analysis across a large database of chemicals and endpoints reveals that the single largest source of uncertainty is when a NOAEL is used instead of a BMD(L) as the POD. The limitations of the NOAEL as a starting point for toxicological risk assessment have been recognized for decades, and it is generally accepted that the BMD, introduced by Crump (1984), is more scientifically appropriate (e.g., EFSA 2009; NAS 2001; U.S. EPA 1995, 2012; WHO/IPCS 2009). Three-quarters of the RfDs using BMDs were developed since 2007, but BMDs still comprise only about 20% of the PODs in that time period. Our results argue strongly for broader application of BMD modeling in regulatory risk assessment, which can be facilitated by use of automated workflows and decision rules exemplified by previous work by Wignall et al. (2014).

The second largest source of uncertainty is due to lack of knowledge as to the extent of human variability. This finding suggests that use of novel in vivo, in vitro, and in silico approaches to model the chemical-specific variation in toxicokinetics and/or toxicodynamics across the human population should be greatly expanded. Chiu and Rusyn (2018) recently reviewed the available approaches, which include population physiologically based pharmacokinetic (PBPK) modeling for addressing toxicokinetics (Chiu et al. 2014; Ring et al. 2017) and population-based in vitro systems for addressing toxicodynamics (Abdo et al. 2015; Chiu et al. 2017). By contrast, based on our analysis using the default uncertainty distributions from the WHO/IPCS (2014), uncertainty in animal-to-human extrapolation and in BMD uncertainty (when BMD modeling is used) contributed the least to overall uncertainty. This result suggests that once human relevance is established qualitatively, better quantifying the degree of interspecies differences may warrant less emphasis from a value of information perspective in comparison with better quantifying human variability.

The final major benefit of the probabilistic approach is that it provides quantitative predictions as to the full dose–response relationship (see Figure 7D), rather than only a single point value, as is the case for traditional RfDs. By contrast, in current practice of noncancer risk assessment, such predictions are available only when there are extensive exposure–response data from human epidemiology. Indeed, the ability to provide information on the incremental change in response as a function of dose, such as what is required to conduct economic benefits analysis, was one of the major motivations described by the NAS in recommending replacement of the traditional RfD with a “risk-specific dose” (NAS 2009). Moreover, the probabilistic RfD is a consistent anchor point for the risk-specific dose, in the sense that the same HQ for different chemicals and endpoints, when based on the probabilistic RfD, gives similar estimates for the population incidence. For instance, an upper bound incidence of 50% is predicted at a probabilistic HQ between 13 and 20 for all 1,522 chemicals and endpoints in our database. On the other hand, an upper bound incidence of ${10}^{-4}$ (0.01%) corresponds to a probabilistic HQ between 0.12 and 0.17. Thus, using the probabilistic approach, risk managers could approach noncancer risk assessment in a manner more similar to that of cancer risk assessment. For instance, based on the above results, choosing a protection level of 0.01% incidence would lead to a human dose estimate between 6 and 8 times lower than those based on the nominal incidence of 1%. However, it should be noted that this nonlinearity is driven by the use of a lognormal distribution for human variability, an approximation whose uncertainty increases substantially at levels of incidence much below 1% (Crump et al. 2010). Nonetheless, the probabilistic outputs allow for the determination of safety or acceptability to be drawn from science policy considerations and the discretion of the risk manager. Such discretion is even more important for noncancer effects, because the endpoints tend to be more heterogeneous in their severity than cancer effects.

There are several additional risk management contexts where probabilistic approaches can be more informative than traditional deterministic approaches. Life-cycle impact assessment, like economic benefit analysis, also requires estimates of the incremental risk predicted to result from incremental exposure (Rosenbaum et al. 2007), for which traditional RfDs are uninformative. Analyses of risk–risk tradeoffs can benefit from being able to compare both the central estimates as well as the CIs of different choices. Emergency response situations, for example, may be more interested in expected values of risk rather than conservative estimates, given the priority of protecting emergency responders and the public from imminent and acute hazards.

The second major objective of this study was to compare the results of applying a probabilistic approach with the traditional RfD. As illustrated in Figure 1, the traditional RfD can be viewed as an approximation of the probabilistic RfD, due to its having a less precise definition. Interestingly, as shown in Figure 8A, across our database of chemicals and endpoints, the traditional RfD is almost always within a factor of 10 of the probabilistic RfD for a 1% incidence at magnitudes of effect typically used in BMD modeling. One implication is that exposures more than a factor of 10 below the traditional RfD will almost always be below the probabilistic RfD for $\mathrm{I}=1\%$. The only exception in our database was for PPRTV based on a dog NOAEL in which the only UF applied in the traditional RfD was a partial ${\text{UF}}_{\mathrm{H}}=3$. For exposures at the traditional RfD, as illustrated in Figures 8B–8C, in about half the cases, an incidence of 1% could be ruled out with 95% confidence, but in the other half of cases, it could not. Additionally, for exposure above the traditional RfD, the upper confidence bound on incidence increases rapidly, as shown in Figure 8D.

A key limitation of our automated workflow is that the magnitude of effect is standardized only with regard to the type or category of endpoint supporting the original traditional RfD, without any further consideration of the endpoint’s severity. The variation in severity is particularly great with so-called deterministic quantal endpoints–endpoints reported as incidence, but which actually reflect an underlying continuum. Some of the less severe endpoints reported include “mild lesions” or “cytomegaly” in an organ and “mild irritation,” whereas some of the more severe endpoints include “atrophy” of the testes, “hemorrhage,” or even “increased mortality.” In all cases, the calculated ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ refers to an estimated human dose at which a 1% incidence occurs, but clearly a 1% incidence of “mild irritation” has a very different severity than a 1% incidence of “increased mortality.” This lack of standardization of endpoint severity also occurs with traditional RfDs but is less transparent. However, the advantage of the probabilistic approach is that these differences in severity can be accommodated by specifying different levels of the target incidence on a case-by-case basis. For instance, for mortality, a value $\mathrm{I}=0.01\%$ could be used, similar to what is regarded as the highest acceptable upper-bound risk for cancer. Moreover, with BMD modeling, the magnitude of effect M could also be specified on case-by-case basis.

Our demonstration has some additional limitations. First, it explicitly excluded RfDs that utilized chemical-specific approaches such as PBPK modeling. Thus, our conclusions would not necessarily generalize to those cases where such approaches are available. It should be noted, however, that to date, most PBPK modeling or other chemical-specific approaches have not incorporated quantitative uncertainty estimates, so use of these approaches in the WHO/IPCS (2014) framework, although feasible, would need to address that gap. Additionally, as described in Methods, our endpoint-specific RfD values removed the database factors accounting for uncertainty due to an incomplete database, which was applied in the original RfDs in 317 of the 1,464 cases. In these cases, the original RfD values that included the database factor may be more protective than indicated by our analysis, but it is difficult to make a definitive conclusion in the absence of quantifying the extent of database uncertainty itself.

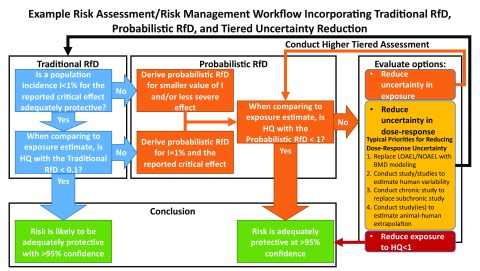
Despite these limitations, the results of and lessons learned from our analysis suggest that a probabilistic dose–response workflow can be incorporated into an overall risk assessment/risk management workflow, such as the one illustrated in Figure 9.

Figure 9.

Example risk assessment/risk management workflow integrating traditional and probabilistic dose–response approaches with tiered uncertainty reduction. Note: LOAEL, Lowest Observed Adverse Effect Level; NOAEL, No Observed Adverse Effect Level; BMD, Benchmark Dose; HQ, Hazard Quotient; RfD, Reference Dose; I, Population Incidence.

• The first step is to consider the severity of the critical effect and the degree to which it is occurring, and whether a 1% population incidence would be adequately protective. This step thus involves risk management considerations, showing that increased transparency also requires the involvement of risk managers at early points in the process, a point emphasized in the NAS Science and Decisions (2009) report and the EPA Framework for Human Health Risk Assessment to Inform Decision Making (U.S. EPA 2014).

• Given comparisons between the traditional and probabilistic RfD shown in Figure 8, only in the case that the 1% incidence is acceptable and the HQ is less than 0.1 can one be assured that the level of risk with a traditional RfD is acceptable at 95% confidence.

• If either of these criteria is not met, then implementing a chemical-specific probabilistic workflow would be needed to provide assurance of adequate health protection for an $\text{HQ}<1$.

• If the risk management protection goals are not met, then both risk assessment and risk management options can be evaluated. The typical contributions to uncertainty in dose–response shown in Figure 7C can then be used to prioritize how to refine the probabilistic RfD estimates to reduce uncertainty.

Overall, this example workflow shows how probabilistic dose–response assessment can be integrated into a tiered risk assessment/risk management framework. More sophisticated frameworks could incorporate probabilistic exposure estimates, such as through the Integrated Probabilistic Risk Assessment approach of van der Voet and Slob (2007).

To further facilitate uptake and use of probabilistic dose–response approaches, we have developed two web-based tools that implement these approaches. First, we implemented the approximate probabilistic approach in an R Shiny web application titled APROBAweb, which essentially converts the WHO/IPCS (2014) Excel^® spreadsheet tool APROBA into a web application. APROBAweb is appropriate for users new to probabilistic dose-response assessment, and mirrors the implementation of the automated workflow described above.

Second, for more advanced users, a Monte Carlo simulation-based implementation of the approach described above has been built in the online Bayesian benchmark dose (BBMD) system available at https://benchmarkdose.org (Shao and Shapiro 2018). The primary feature of the system is that it allows a user to utilize the posterior sample of BMD estimates generated in BBMD as an input for computing probabilistic RfD and other quantities of interest. The Monte Carlo approach implements the methods described in Chiu and Slob (2015) and replaces two simplifying assumptions of the approximate probabilistic approach implemented in the WHO/IPCS spreadsheet tool APROBA, the APROBAweb tool, in the automated workflow described in Methods. Specifically, whereas the approximate approach assumes the BMD is distributed lognormally, BBMD utilizes Bayesian posterior samples of the BMD, providing a more accurate estimate of uncertainty distribution. Second, for human variability, the approximate approach assumes the uncertainty in the ratio between median and the I% of the population is lognormally distributed, whereas the available human variability data suggest that the log-transformed standard deviation is lognormally distributed. Thus, the calculations in the BBMD system are more accurate, especially with respect to the shape of the distribution, in comparison with the approximate approach. The main benefit, though, of the BBMD system is that it automatically integrates with BMD modeling, the lack of which appears to be a major contributor to uncertainty in the probabilistic RfDs calculated using our automated workflow.

Conclusions

We have demonstrated the feasibility of routinely applying probabilistic dose–response approaches in noncancer risk assessment, applying the probabilistic framework developed by WHO/IPCS (2014) to over 1,400 endpoints for over 600 chemicals. The application of this framework fulfills a key recommendation of the NAS to use probabilistic methods to address uncertainty as well as to replace the traditional RfD with a risk-specific dose (NAS 1994, 2009). Specifically, in the WHO/IPCS (2014) framework, the RfD is replaced by ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$, an estimated human dose associated with a population incidence I (e.g., 1%) of a specified magnitude of effect M, along with a statistically derived confidence interval. A probabilistic RfD, defined as the lower confidence bound of the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$, thereby provides assurance at 95% confidence that no more than I% of the population experiences the critical effect defined by M.

Key conclusions of our analysis include the following:

• Uncertainties in the ${{\text{HD}}_{\mathrm{M}}}^{\mathrm{I}}$ are typically around 100-fold, meaning that the upper and lower 95% confidence bounds differ by a factor of 100, so that there is 90% confidence that the true value is within this range.

• The greatest contributions to uncertainty are use of a LOAEL or NOAEL instead of a BMD, and the uncertain degree of human variability, so reducing these uncertainties would provide the greatest value of information in refining probabilistic RfDs.

• Traditional RfDs are generally within a factor of 10 greater or less than the probabilistic RfD for $\mathrm{I}=1\%$, suggesting that in the absence of a probabilistic RfD, only $\text{HQ}<0.1$ can provide assurance of an upper 95% confidence bound on the population incidence of less than 1%.

• Traditional RfDs do appear protective at 95% confidence for population incidences of a few percent, but the severity of the associated effects ranges widely, from changes in clinical chemistry to increased mortality.

These conclusions suggest the possibility of an integrated risk assessment/risk management framework that incorporates both the traditional and probabilistic RfD along with a tiered approach to reducing uncertainty, as illustrated in Figure 9.

Overall, implementation of the probabilistic dose–response framework developed by the WHO/IPCS (2014) provides a more consistent, scientifically rigorous, and transparent basis for risk management decisions than traditional approaches. We have demonstrated the feasibility of the approach with an automated probabilistic workflow, made available in multiple open-source tools, as well as provided an example of how it could be part of an integrated risk assessment/risk management workflow in the context of HQ-based risk characterization. Future work can focus on refinements and extensions, such as integrating automated benchmark dose modeling, use of chemical-specific data and models to reduce uncertainty, and application to broader risk management contexts, such as economic benefit–cost analysis, life-cycle assessment, risk–risk tradeoffs, and emergency response. Such work can pave the path for further progress in implementing the overall vision of the NAS of risk-based decision-making.