Abstract
Once Aedes aegypti and Aedes albopictus mosquitoes that spread Chikungunya virus, dengue virus, and Zika virus are infected with Wolbachia, they have reduced egg laying rates, reduced transmission abilities, and shorter lifespans. Since most infected mosquitoes are only infectious in the last few days of their lives, shortening a mosquito’s lifespan by a day or two can greatly reduce their abilities to spread mosquito-borne viral diseases, such as Chikungunya, dengue fever, and Zika. We developed a mathematical model to compare the effectiveness of the wMel and wAlbB strains of Wolbachia for controlling the spread of these viruses. The differences among the diseases, mosquitoes, and Wolbachia strains are captured by the model parameters for the mosquito-human transmission cycle. Moreover, the model accounts for the behavior changes of infectious population created by differences in the malaise caused by these viruses. We derived the effective and basic reproduction numbers for the model that are used to estimate the number of secondary infections from the infectious populations. In the same density of Wolbachia-free Aedes aegypti or Aedes albopictus mosquitoes, we observed that wMel and wAlbB strains of Wolbachia can reduce the transmission rates of these diseases effectively.
Author summary
Mosquitoes infected with Wolbachia bacteria are less capable of transmitting dengue virus, Chikungunya virus, and Zika virus. We use a mathematical model to quantify the impact of infecting wild Aedes aegypti and Aedes albopictus mosquitoes with wAlbB and wMel strains of Wolbachia in reducing the transmission of these viruses. The model is a system of ordinary differential equations that accounts for reduced fitness of the Wolbachia-infected mosquitoes, reduced transmissibility of an infection, and the behavior changes of infected individuals caused by the infection. We derived an explicit formula for the effective reproduction number for when the host population are partially immune to new infections, as occurs in seasonal outbreaks. We compared the effectiveness of different species of mosquitoes, different strains of Wolbachia, and different diseases. Our model is a general model that can produce outputs for a specific location, once the data for the location are available to parameterize the model. The spatial heterogeneity of the populations must be considered before using this model to help guide policy decisions.
Introduction
The current pandemics of Chikungunya caused by Chikungunya virus (CHIKV), dengue fever caused by dengue virus (DENV), and Zika resulted from Zika virus (ZIKV) infect over one hundred million people each year [1]. In the past decade, CHIKV has spread around the world [2, 3] and recently over a million cases occurred in the Caribbean and Latin America. Symptoms of infection with CHIKV include high fever and headache, with arthritis affecting joints, and may sustain for weeks or months [4]. Dengue fever has spread around the world and is endemic in South America and Asia [1]. People infected with DENV have symptoms ranging from mild headaches, severe headaches and joint pains to hemorrhagic or shock syndrome fever. Recently, ZIKV has spread through the Americas, starting with a 2015 explosive outbreak in Brazil. Although most people infected with ZIKV have mild symptoms, there is a correlation between infections in pregnant women and their children born with microcephaly (an abnormally small brain). Currently no vaccines are commercially available for Zika and Chikungunya. The first dengue vaccine, Dengvaxia (CYD-TDV), registered in Mexico in December, 2015 is not effective for the younger ones and for the seronegative population due to ethical concern of non-maleficence [5].
Although both Aedes aegypti (Ae. aegypti) and Aedes albopictus (Ae. albopictus) mosquitoes can transmit these viruses, Ae. aegypti mosquitoes are more abundant in urban areas and are the primary vectors. Current prophylactic measures include individual protection from mosquito bites, such as applying mosquito repellent and avoiding exposure to mosquitoes. Limited control options focus on reducing the mosquito populations, including spraying insecticides, treatments, and removal of mosquito breeding sites. These control strategies are hard to sustain because of the vigilance needed to eradicate the breeding sites, the expense of repeated spraying, and the mosquitoes developing resistance to the insecticides.
The cost and difficulty of eliminating the mosquitoes motivate the need of developing more efficient strategies to mitigate and control the transmission of these viruses. Wolbachia is a genus of bacteria that can infect 25-75% of all insects [6] and recent studies have shown that some strains of Wolbachia can increase the resistance of mosquitoes being infected with these viruses [7]. Recent experiments have shown that wMel strain of Wolbachia infection in Ae. albopictus inhibits the growth of CHIKV [8]. Moreover, Wolbachia infection in mosquitoes reduces egg laying rates, reduces their ability of transmitting viral infections, and shortens their lifespans by a few days. Since many mosquitoes infected with DENV, ZIKV, or CHIKV are infectious for only a few days at the end of their lifespans, the shortened lifespans of Wolbachia-infected mosquitoes result in more mosquitoes dying before they can transmit the infection. This implies that Wolbachia-infected mosquitoes sustaining in a wild mosquito population will be less likely to transmit these viral diseases.
Infected females can pass the bacteria to their offsprings and spread Wolbachia vertically from one generation to the next. Wolbachia disrupts the reproductive cycle of hosts through a cytoplasmic incompatibility between the sperms and eggs. Cytoplasmic incompatibility occurs when Wolbachia-infected male mosquitoes mate with Wolbachia-free female mosquitoes, and causes the Wolbachia-free females to produce fewer progeny [9, 10]. These effects provide the Wolbachia a vertical transmission advantage. However, this is offset by a reduced lifespan and reduced number of eggs hatched by a Wolbachia-infected mosquito.
When Wolbachia-infected mosquitoes are introduced in a wild population of uninfected mosquitoes, the infection is quickly wiped out unless the fraction of infected mosquitoes exceeds a threshold θ of the total population. Recent mathematical models have established these threshold conditions as θ = 0.15, 0.24, and 0.6 for wAlbB-, wMel-, and wMelPop-infected mosquitoes to establish a stable population, respectively [11]. Note that these threshold estimates are for an ideally controlled situation where mosquitoes do not mix with surrounding uninfected mosquitoes. The thresholds could be much higher for a release in the wild. Recent studies have found that maintaining a sustained wMelPop-infection requires continually introducing new wMelPop-infected mosquitoes into the wild population [12]. A recent research has reported that large-scale releases of Wolbachia-infected Ae. aegypti in the city of Cairns, Australia, invaded and spread through the populations, while Wolbachia infection at a smaller release site collapsed due to the immigration of Wolbachia-free mosquitoes from surrounding areas [13]. Population cage experiments indicated that the wAlbB strain can be successfully introduced into populations, and subsequently persist and spread [14]. Ndii et al. analyzed a first-order differential equation and found that a significant reduction in human dengue cases can be obtained by releasing wMel-infected mosquitoes, instead of wMelPop-infected mosquitoes due to the greatly reduced lifespans [15]. Ferguson et al. developed a mathematical model of DENV transmission incorporating the dynamics of viral infection in humans and mosquitoes, and predicted that wMel-infected Ae. aegypti mosquitoes have a substantial effect on transmission [16]. Ross et al. found that, in most situations, it was easier to establish wMel than wAlbB in mosquito populations, except when the conditions were particularly hot [17]. They also observed that the wMel infected larvae survived better than wAlbB infected larvae under starvation conditions [18].
Many mathematical models have been developed to explore conditions under which Wolbachia can be used to fight against the spread of viruses effectively. The analysis of a compartmental mathematical model showed that a significant reduction in human dengue cases can be obtained provided that Wolbachia-infected mosquitoes persist when competing with Wolbachia-free mosquitoes [15]. Zhang et al. developed an ordinary differential equation (ODE) model to assess how best to replace DENV vectors with Wolbachia-infected mosquito populations and the results showed that successful population replacement will rely on the selection of suitable strains of Wolbachia and careful design of augmentation methods [19]. The analysis for an impulsive model for Wolbachia infection control of mosquito-borne diseases with general birth and death rates showed that strategies may be different due to different birth and death rate functions, the type of Wolbachia strains, and the initial number of Wolbachia-infected mosquitoes [20]. Xue et al. [21] created a two-sex model that included an egg/aquatic stage for the mosquito lifecycle and observed that an endemic Wolbachia infection can be established only if a sufficient number of infected mosquitoes are released. Recently, this model was extended by Qu et al. [22] to better account for the cytoplasmic incompatibility by considering the fact that most female mosquitoes only mate once. They used the model to investigate the effectiveness of multiple releases of infected mosquitoes in sustaining an endemic Wolbachia infection.
Manore et al. [23] used a mathematical model to compare the spread of DENV and CHIKV in Ae. aegypti and Ae. albopictus mosquitoes that are not infected with Wolbachia. Our study is based on extending these results to evaluate the effectiveness of infecting these mosquitoes with different strains of Wolbachia to show their different roles in controlling different vector-borne diseases. In our model, we assume that lifespans of the infected adult mosquitoes are slightly shorter than those of uninfected mosquitoes (reducing transmission), and the larval survival rates of wAlbB-infected mosquitoes are less than those of wMel-infected mosquitoes (making invasion somewhat potentially harder for wAlbB). We evaluated the effectiveness of infecting these mosquitoes with wMel and wAlbB strains of Wolbachia to show their different roles in controlling the transmission of DENV, ZIKV, and CHIKV. Since transmission of ZIKV is estimated to be similar to transmission of DENV but exact values of parameters are not available [24], we assume that the parameter values for ZIKV are the same as those for DENV except the fraction of infectious humans exposed to mosquito bites. Our simulation results show that the differences between the spread of DENV and ZIKV lie in different behaviors of infectious humans, and wMel is more effective than wAlbB strain of Wolbachia in simulations with the available baseline parameters.
Methods
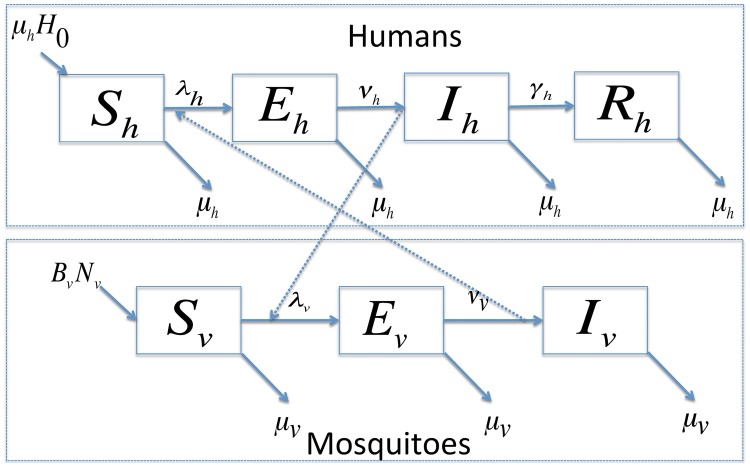
Our compartmental model (Fig 1) divides the human population into four classes: susceptible, Sh, exposed (infected but not infectious), Eh, infectious, Ih, and recovered (immune), Rh, and splits the mosquitoes into three classes: susceptible, Sv, exposed, Ev, and infectious, Iv. We assume that humans advance from the infectious state to the recovered state, while mosquitoes do not. Model parameters are defined in Table 1, and the ODEs are:
| (1) |
The equations are homogenous with respect to the populations of humans and mosquitoes. The solution is invariant as long as both populations are scaled by the same factors and the ratio ρvh = V0/H0 is kept fixed. That is, all the results in this study hold for other populations with the same vector-to-human ratio, ρvh.
Fig 1. The schematic diagram for Model (1).
Susceptible humans can be infected from bites of an infectious mosquito, and susceptible mosquitoes can be infected from blood meals on an infectious person. The forces of infection, λ*, are defined in Eq (4). After being infected, the susceptible individuals progress through the infectious states. Humans advance from the infectious state to the recovered state, while we assume that mosquitoes do not recover from an infection before dying.
Table 1. Parameters for the Model (1).
| Parameter | Description | Unit |
|---|---|---|
| Sh(t) | The number of susceptible humans at time t | Number |
| Eh(t) | The number of exposed humans at time t | Number |
| Ih(t) | The number of infectious humans at time t | Number |
| Rh(t) | The number of recovered humans at time t | Number |
| Sv(t) | The number of susceptible mosquitoes at time t | Number |
| Ev(t) | The number of exposed mosquitoes at time t | Number |
| Iv(t) | The number of infectious mosquitoes at time t | Number |
| H0 | The steady-state human population | Number |
| b(t) | The total number of bites per day | Bites Day−1 |
| biv(t) | The average number of bites per day for an infectious mosquito | Bites Day−1 |
| bih(t) | The total number of bites per day for an infected human | Bites Day−1 |
| Rhv(t) | The effective reproduction number for transmission from mosquitoes to humans | Dimensionless |
| Rvh(t) | The effective reproduction number for transmission from humans to mosquitoes | Dimensionless |
| ψv | Per capita birth rate of mosquitoes | Number Day−1 |
| σv | Average number of times one mosquito bites a human per day | Bites Day−1 |
| σh | The maximum number of mosquito bites a human tolerates per unit time | Bites Day−1 |
| βhv | Probability of pathogen transmission from an infectious mosquito to a susceptible human per bite | Dimensionless |
| βvh | Probability of pathogen transmission from an infectious human to a susceptible mosquito per bite | Dimensionless |
| νh | Average incubation rate for humans | Day−1 |
| νv | Average incubation rate for mosquitoes | Day−1 |
| γh | Per capita recovery rate for humans from the infectious state to the recovered state | Day−1 |
| μh | Per capita recruitment / death / emigration rate for humans | Day−1 |
| μv | Death rate for mosquitoes | Day−1 |
| Kv | Mosquito carrying capacity and steady-state | Number |
| ϕψ | Factor for decreased birth rate: | Dimensionless |
| ϕμ | Factor for increased death rate: | Dimensionless |
| ϕb | Factor for decreased biting rate: | Dimensionless |
| ϕβ | Factor for decreased transmissibility: | Dimensionless |
Humans and mosquitoes leave the population through combined per capita recruitment / death / emigration rates, μh and μv, respectively. Although the model equations can accommodate variations in the human and mosquito populations, we assume a constant size of human population in simulations. Susceptible humans enter the population at a fixed rate of μhH0 per day to maintain a steady at-risk human population of H0. In our simulations, we assume that 1/μh = 20 years, where about 5% of the population turns over each year to account for individuals moving in and out of the population. Note that μh depends on the particular region being modeled and will be larger in regions where there are migrant workers, or smaller in isolated villages.
Mosquitoes are born into the population at the rate of Bv(Nv)Nv per day, where the mosquito birth and population saturation function Bv is given by [23]
Here ψv is the mosquito birth rate when there are abundant resources for the eggs and larvae, and V0 is the carrying capacity and steady state for the mosquitoes.
The viruses can be transmitted from infectious mosquitoes to susceptible humans, and from infectious humans to susceptible mosquitoes through blood meals. We formulate the viral transmission in terms of the rate at which infectious mosquitoes or infectious humans infect others, rather than the traditional formulation in terms of the rate at which the susceptible individuals are being infected as in [23]. The notation in this infectious viewpoint emphasizes that the infectious population drive the epidemic and clarifies the derivation for effective reproduction number.
The force from infection for humans, αv(t), and force from infection for mosquitoes, αh(t), are the rates at which infectious individuals infect others and are equal to the product
where * = v or h. That is,
| (2) |
Here βhv is the probability that an infectious mosquito will infect a susceptible human in one bite. Similarly, βvh is the probability that an infectious human will infect a susceptible mosquito in one bite.
The parameter biv is the average number of times an infectious mosquito bites a susceptible human per day. Similarly, bih is the average number of times that an infectious human is bitten by a susceptible mosquito per day. We assume that the biting rates for the mosquitoes do not change after they become infected.
We assume that infectious people, especially those with symptoms may avoid exposure to mosquito bites. Around 20–93% individuals infected with DENV are asymptomatic [25, 26], and asymptomatic prevalence of Chikungunya was estimated in the range 16.7–27.7% during some recorded outbreaks [27, 28], while only around 20% of people infectious with ZIKV have significant symptoms [29–31]. The biting rate accounts for a fraction, π, of infectious humans do not change their behaviors due to the illnesses and continue being bitten by mosquitoes at the same rate as the susceptible population. In our model, we assume π = 0.75 for DENV, π = 0.3 for CHIKV, and π = 0.8 for ZIKV. The remaining fraction (1 − π) avoid being bitten by mosquitoes. This behavior change has a significant impact on the force of infection from humans to mosquitoes and is an important aspect of any vector-borne transmission model.
We define σv as the maximum rate at which a typical mosquito will bite humans per day, and σh is the maximum number of bites that a susceptible human will tolerate being bitten per day. We define Nv = Sv + Ev + Iv as the number of mosquitoes that bite humans. Similarly, we define Nh = Sh + Eh + πIh + Rh as the number of humans being bitten by mosquitoes. Recall that the at-risk population, Nh, is only a fraction of the total human population since some infectious people are not being bitten by mosquitoes. One of the most difficult parameters to estimate when applying any vector-borne epidemic models to a particular situation is the fraction of the population at risk of an infection. Using these definitions, σvNv is the maximum number of bites a mosquito seeks per day, while the maximum number of available human bites per day is σhNh.
The total number of times that all the mosquitoes bite humans must equal to the total number of times that humans are bitten by mosquitoes. To enforce this balance condition, we extend the harmonic average described in [23, 32] and define the total number of bites per day (total biting rate) as
| (3) |
This biting rate allows a wide range of vector-to-host ratios, as opposed to the more standard frequency-dependent contact rates that are applicable only over a limited range of vector-to-host ratios [33].
The total number of bites from mosquitoes is b(t) = bvNv, where bv is the average number of bites per mosquito per day (the biting rate). Because we assume that the infection does not affect the biting rate, the average number of bites per day for an infectious mosquito is also biv = bv = b(t)/Nv. To satisfy the balance condition, the total number of bites on humans is also b(t) = bh Nh, where bh is the average number of times an infectious human being bitten per day. Because (1 − π) of infectious humans have changed their behaviors and are not being bitten, the average number of times an infectious human being bitten per day is bih = πbh = πb(t)/Nh.
We define Psh(t) as the probability that an infectious mosquito bites a susceptible human. If we assume that the bites on humans are randomly distributed, then Psh(t) = Sh(t)/Nh(t). Similarly, Psv(t) is the probability that when an infectious human is bitten, the bite is from a susceptible mosquito. Hence, Psv(t) = Sv(t)/Nv(t).
The ODES in Model (1) are formulated from the viewpoint of infectious population where the transmission parameter, α, is the force from infection. This is equivalent to the usual way of formulating the equations for force of infection from the susceptible viewpoint [23]. From the susceptible viewpoint, the ODEs for the susceptible humans and vectors have the form:
Here λ is force of infection and is related to α by
| (4) |
where the factors for λ* are all from the viewpoint of the susceptible population, instead of the viewpoint of the infectious population in Eq (2). Pih(t) = πIh(t)/Nh(t) is the probability that when a susceptible mosquito bites a human, the human is infectious; bsh = b(t)/Nh is the rate at which susceptible humans are bitten; Piv(t) = Iv(t)/Nv(t) is the probability that when a susceptible human is bitten, the mosquito is infectious; and bsv = b(t)/Nv is the rate at which susceptible mosquitoes bite humans.
The effective reproduction number
The basic reproduction number, , is defined as the number of new infections produced by one infected individual in a completely susceptible population. When the population is not fully susceptible, or more than one person is infected, then the effective reproduction number, , estimates the number of secondary cases produced by a typical infected individual at any time during the epidemic. We derived the effective reproduction number from infectious point of view for DENV, ZIKV, and CHIKV to estimate the reproduction rate of an epidemic at any stage.
Because this is a bipartite transmission cycle, mosquitoes only infect humans and humans only infect mosquitoes, we have different effective reproduction numbers for each part of the cycle. We define as the effective reproduction number for transmission from mosquitoes to humans, and is the average number of humans infected by one infectious mosquito. Similarly, defined as the effective reproduction number for transmission from humans to mosquitoes, is the average number of mosquitoes infected by one infectious human. These dimensionless numbers are defined by
| (5) |
| (6) |
Here, in Eq (5), Pv = νv/(νv + μv) is the probability that an infected mosquito survives through the incubation period and becomes infectious, αv(t) is the average number of susceptible people infected by an infectious mosquito per day, and τiv = 1/μv is the average life span of a mosquito. Similarly for Eq (6), Ph = νh/(νh + μh) is the probability that an infected human becomes infectious, αh(t) is the average number of susceptible mosquitoes infected by an infectious person per day, and τih = 1/(γh + μh) is the average time that a human remains infectious.
The explicit expressions of and are:
Because a full transmission cycle is consisted of two stages, and measures the average effective reproduction number over one cycle. We take the geometric average of these two reproductive numbers to define:
We denote as the population of susceptible people at the endemic equilibrium (EE) for Model (1). We define the fraction of humans susceptible at the EE, of the population has never been infected, as susceptibility of humans at EE,
To quantify the differences in impact of different strains of Wolbachia on an epidemic, we define the coefficient for effectiveness [15] as the relative decrease in the number of people predicted to be infected if the mosquitoes are infected with Wolbachia, HW, compared with the predicted number of people who will be infected if the mosquitoes are Wolbachia-free, HF;
| (7) |
If κ = 1, then Wolbachia is predicted to be effective in stopping all the infections, while if κ = 0, then it is predicted to have no effects on the epidemic.
The basic reproduction number
The basic reproduction number is the effective reproduction number at the disease free equilibrium where Sv(0) = V0 and Sh(0) = H0, and all other states are zero:
and are the effective reproduction numbers for the vectors and humans at the disease free equilibrium:
The biting rates at the disease free equilibrium are biv(0) = b(0)/V0 and bih(0) = πb(0)/H0, where
The basic reproduction number derived in this way is consistent with the computed using the next generation matrix approach in [23].
After an epidemic has run its course and the infection has died out, then the previously infectious people are immune to new infections. is the average number of new infectious individuals produced in one cycle when an infectious human or mosquito is introduced into the population where some of the population is immune to infection. We define ph = Rh(0)/H0 as the fraction of people who are immune to the infection, such as those who have already had the disease or have been immunized. If we reinitialize our model at t = 0 with an infection-free equilibrium, such as the beginning of a seasonal outbreak, where ph of the humans are immune to the infection, Rh(0) ≠ 0, and Sh(0) + Rh(0) = H0. For this case, the effective reproduction number for human-to-mosquito transmission, , is unchanged, while the effective reproduction number for mosquito-to-human transmission is reduced to . Therefore, the effective reproduction number for Model (1) with ph people immune to infection becomes
Note that, unlike human-to-human transmitted disease where the is reduced by (1 − ph) when ph of the population is immune, is only reduced by in this bipartite epidemic.
Model parameters
In the simulations, the parameters are set to the baseline values in Table 2, unless specifically stated otherwise. Most of the parameter values used in this study were derived, or extensively referenced, by Manore et al. [23] for disease transmission in Wolbachia-free mosquitoes. Manore et al. provided a comprehensive sensitivity analysis on how the model predictions change with respect to variations in the key parameters [23]. Although these baseline values are our best estimates for the parameters, they are scalar estimates from a distribution of possible values. To help quantify the uncertainty in the parameters, we will investigate the behavior of the model over a wide range of feasible parameters. The model predictions for a specific value of the basic reproduction number or the fraction of the population infected at the endemic equilibrium depend on the specific values used in the simulations. Although these specific values for these predictions are sensitive to the parameter values, we find that the qualitative differences between different diseases and strains of Wolbachia are fairly insensitive over the feasible ranges of parameters.
Table 2. The parameters for Model (1) with baseline values, range, and references.
The behavior change parameter π = 0.75 for DENV, π = 0.3 for CHIKV, and π = 0.8 for ZIKV [25–31]. Time is in days, and the default baseline populations are H0 = 10,000 and V0 = 200,000 with 20 mosquitoes per human, ρvh = V0/H0 = 20. The model predictions scale to other populations with the same ρvh.
| Par | Baseline | Range | Reference | Par | Baseline | Range | Reference |
|---|---|---|---|---|---|---|---|
| DENV and ZIKV | CHIKV | ||||||
| Human | Human | ||||||
| σh | 19 | 0.1 − 50 | [38] | σh | 19 | 0.1 − 50 | [38] |
| 1/νh | 5 | 4 − 7 | [39, 40] | 1/νh | 3 | 2 − 4 | [4, 41–43] |
| 1/γh | 6 | 4 − 12 | [44, 45] | 1/γh | 6 | 3 − 7 | [43, 46] |
| 1/μh | 20 × 365 | (15 − 25) × 365 | Assume | 1/μh | 20 × 365 | (15 − 25) × 365 | Assume |
| DENV and ZIKV (Ae. aegypti) | CHIKV (Ae. aegypti) | ||||||
| βhv | 0.33 | 0.10 − 0.75 | [47, 48] | βhv | 0.24 | 0.001 − 0.35 | [4, 49, 50] |
| βvh | 0.33ϕβ | (0.10 − 0.75)ϕβ | [47, 48] | βvh | 0.24ϕβ | (0.005 − 0.35)ϕβ | [4, 49, 50] |
| ψv | 0.30ϕψ | (0.28 − 0.32)ϕψ | [38, 51, 52] | ψv | 0.30ϕψ | (0.28 − 0.32)ϕψ | [38, 51, 52] |
| σv | 0.5ϕb | (0.33 − 1)ϕb | [53, 54] | σv | 0.5ϕb | (0.33 − 1)ϕb | [53, 54] |
| 1/νv | 10 | 7 − 14 | [39, 55] | 1/νv | 11 | 7 − 15 | [49] |
| 1/μv | 14/ϕμ | (8 − 42)/ϕμ | [53, 56, 57] | 1/μv | 14/ϕμ | (8 − 42)/ϕμ | [53, 56, 57] |
| DENV and ZIKV (Ae. albopictus) | CHIKV (Ae. albopictus) | ||||||
| βhv | 0.31 | 0.1 − 0.5 | [48, 58] | βhv | 0.33 | 0.001 − 0.54 | [41, 50, 59] |
| βvh | 0.31ϕβ | (0.1 − 0.5)ϕβ | [48, 58] | βvh | 0.33ϕβ | (0.3 − 0.9)ϕβ | [49, 50, 59, 60] |
| ψv | 0.24ϕψ | (0.22 − 0.26)ϕψ | [38, 51, 61] | ψv | 0.24ϕψ | (0.22 − 0.26)ϕψ | [38, 51, 61] |
| σv | 0.26ϕb | (0.19 − 0.39)ϕb | [62, 63] | σv | 0.26ϕb | (0.19 − 0.39)ϕb | [62, 63] |
| 1/νv | 10 | 7 − 14 | [51] | 1/νv | 3.5 | 2 − 6 | [41, 46, 64–66] |
| 1/μv | 21/ϕμ | (14 − 42)/ϕμ | [41, 42, 51] | 1/μv | 21/ϕμ | (14 − 42)/ϕμ | [41–43, 46] |
We assume that the probability of transmission per bite from a mosquito to a human is related to the viral load in the mosquito. Recent experimental comparisons of the growth of DENV, ZIKV, and CHIKV in mosquitoes indicate that the viral loads and the extrinsic incubation period (EIP) for an infected mosquito to become infectious are comparable [34]. Because there are no experimental estimates for the infectivity of ZIKV-infected mosquitoes, we assume that the parameter values for infectivity of ZIKV are the same as those of DENV in our simulations. Note that, although we assume that the probability of transmission per mosquito bite is assumed to be the same for ZIKV- and DENV- infected mosquitoes. The behavior changes of humans infectious with ZIKV and DENV are different, leading to very different epidemics. That is, one must be very careful in extrapolating findings between ZIKV and DENV epidemics [24].
Duong et al. [26] showed that asymptomatic individuals infected with DENV may be infectious before the onset of symptoms and continue infecting mosquitoes as they visit multiple locations during the day. They also noted that sick people who are hospitalized or stay at home are only exposed to their residential mosquitoes. Grange et al. [25] summarized data from a large number of studies, showing that often 20–93% of DENV infected individuals are asymptomatic. In our simulations, we assume that 75% of DENV-infectious people continue exposing to mosquitoes (π = 0.75).
Bloch et al. [27] concluded that about 62.5% CHIKV infections are symptomatic through extensive statistical analysis. They observed that about one-third of CHIKV-infected participants are asymptomatic, which is consistent with estimates of 3–39% asymptomatic cases in past outbreaks. Robinson et al. [28] also noted that 16.7–27.7% of the infections in Chikungunya outbreaks are asymptomatic. In our simulations, we assume that 30% of infectious people with CHIKV continue exposing to mosquitoes (π = 0.30).
ZIKV infection is a self-limiting illness that is mostly asymptomatic. Lazear et al. [29] noted that approximately 20% of the individuals infected with ZIKV progress to a clinically apparent febrile illness, although rarely hospitalized. Rajah et al. [30] also observed that 20% of the people infected with ZIKV present mild symptoms. In our simulations, we assume that 80% of ZIKV-infectious people continue exposing to mosquitoes (π = 0.80).
The Wolbachia infection changes the mosquito’s birth, death, biting rates, and the transmissibility of an infection. We account for the change in these parameters by including a scaling factor, ϕ*. We identify the rates of Wolbachia-free mosquitoes by a tilde, , and define the factors for Wolbachia-infected mosquitoes as:
ϕψ—factor for decreased birth rate:
ϕμ—factor for increased death rate:
ϕβ—factor for decreased transmissibility:
ϕb—factor for decreased biting rate:
The values for the factors ϕ* in Table 3 are used in Table 2 for the baseline parameter values used for this study. These factors coincide with the factors applied by [35] for comparing the effects of different strains of Wolbachia. The ranges of the lifespans for wMel-infected, wAlbB-infected, and Wolbachia-free mosquitoes in Table 2 coincide with the plot for longevity of wAlbB- and wMel- infected mosquitoes plotted by Joubert et al. [36].
Table 3. The scaling factors for the Wolbachia-free model parameters to convert some parameters to their appropriate values for Wolbachia-infected mosquitoes.
ϕψ—factor for decreased birth rate: , ϕμ—factor for increased death rate: , ϕβ—factor for decreased transmissibility: , ϕb—factor for decreased biting rate: .
Results
We compare the differences in the spread of DENV, ZIKV, and CHIKV in wMel- and wAlbB-infected Ae. aegypti and Ae. albopictus mosquitoes with the spread in Wolbachia-free mosquitoes. In the simulations, the parameters are set to the baseline values in Table 2, unless specifically stated otherwise. The baseline values are the best estimates available for these parameter values. Since parameter uncertainty exists, it is important to investigate the behavior of the model over the wide range of feasible parameters. By investigating the model over the full range of parameters, we have focused on the qualitative differences between different infections and strains of Wolbachia.
Cumulative number of infectious humans
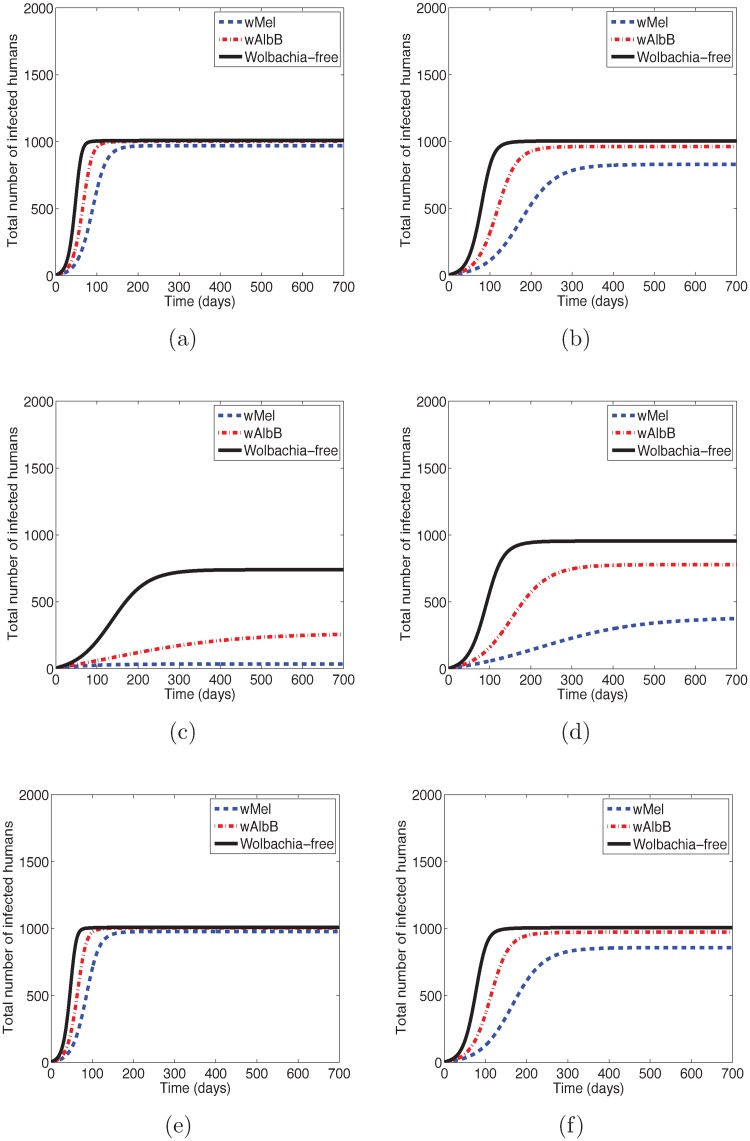
Fig 2 shows the cumulative number of infectious humans up to time t = 700 when 0.1% of humans are infected at t = 0. The figure illustrates that the wMel-infected mosquitoes are more effective in slowing disease transmission than wAlbB-infected mosquitoes. For DENV and ZIKV, the number of people infected by Ae. aegypti mosquitoes is greater than the number of humans infected by Ae. albopictus mosquitoes carrying the same strain of Wolbachia. The opposite is true for CHIKV where the number of people infected by Ae. albopictus mosquitoes is greater than the number of people infected by Ae. aegypti mosquitoes carrying the same strain of Wolbachia. Note that in these simulations we assume the same mosquito populations for both genera. Typically the density of Ae. aegypti mosquitoes is much greater than the density for Ae. albopictus in urban areas, while the opposite is true in wooded rural areas. In this study, we only considered one mosquito genus at a time. When both mosquitoes are present, then the predictions will depend on the total mosquito population. As a first order approximation, the results are interpolated based on the fraction of each mosquito genus.
Fig 2. The total number of infectious humans produced by infectious Ae. aegypti and Ae. albopictus for the baseline parameters in Table 2.
The model predicts that the wMel-infected mosquitoes are more effective than wAlbB-infected mosquitoes in reducing the number of people infectious with the diseases. We find that for the same mosquito densities, Ae. aegypti is more effective than Ae. albopictus in transmitting DENV and ZIKV, while the opposite is true for CHIKV. (a) DENV infection transmitted by Ae. aegypti. (b) DENV infection transmitted by Ae. albopictus. (c) CHIKV infection transmitted by Ae. aegypti. (d) CHIKV infection transmitted by Ae. albopictus. (e) ZIKV infection transmitted by Ae. aegypti. (f) ZIKV infection transmitted by Ae. albopictus.
The reproduction numbers
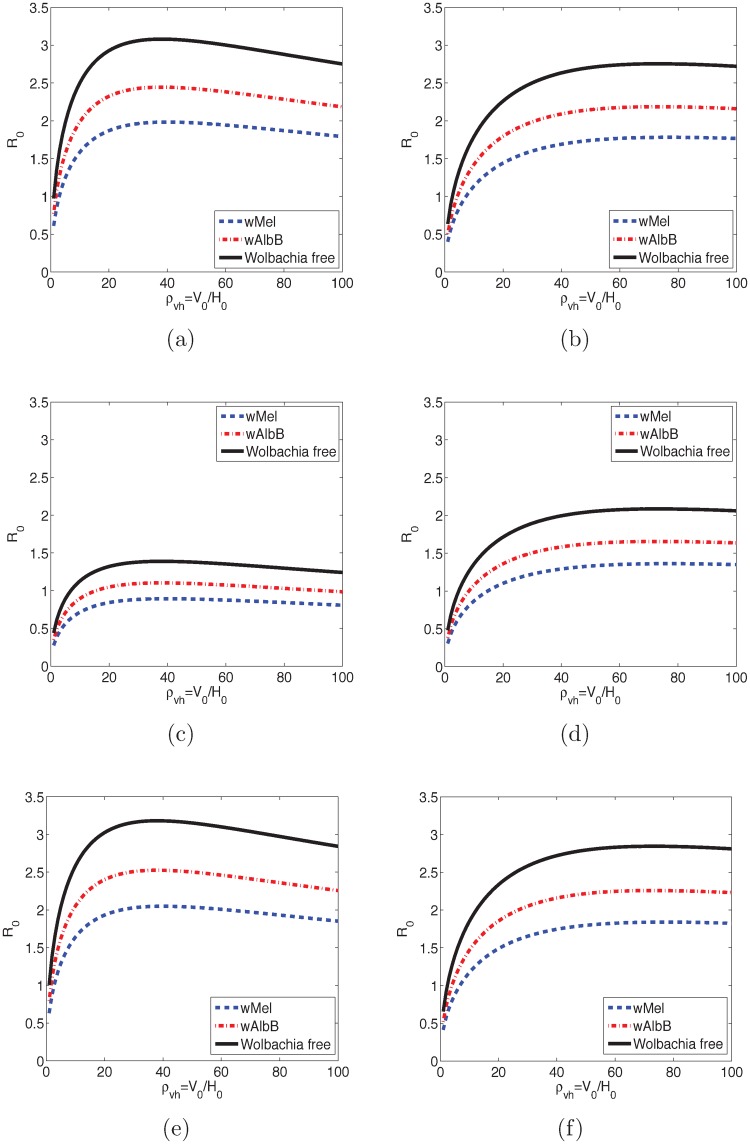
The reproduction numbers depend on the ratio of mosquitoes to humans. The model predictions are scaled for all populations with the same ρvh = V0/H0, V0 is the initial total number of mosquitoes, and V0 = Kv. In Fig 3, the reproduction numbers are plotted as ρvh varies from a ratio of ρvh = 1, with an equal number of mosquitoes as humans, to ρvh = 100, with 100 times more mosquitoes than humans. Infecting mosquitoes with Wolbachia can reduce over the full range of mosquito to human ratios.
Fig 3. changes with the increase of initial number of mosquitoes per person.
increases when few mosquitoes bite a person, and eventually decreases when there are many more mosquitoes than humans, ρvh > 40. In all cases, for infection transmitted by Wolbachia-free mosquitoes is the largest, followed by for infection transmitted by wAlbB-infected mosquitoes, and for infection transmitted by wMel-infected mosquitoes is the smallest. (a) for DENV transmitted by Ae. aegypti mosquitoes. (b) for DENV transmitted by Ae. albopitus mosquitoes. (c) for CHIKV transmitted by Ae. aegypti mosquitoes. (d) for CHIKV transmitted by Ae. albopictus mosquitoes. (e) for ZIKV transmitted by Ae. aegypti mosquitoes. (f) for ZIKV transmitted by Ae. albopictus mosquitoes.
When only few mosquitoes are present, then for all the diseases. As expected, increases as the number of mosquitoes increases, as more and more mosquitoes transmit the infection. When there are about 20 to 30 mosquitoes per human, then slowly decreases as the biting rate for the mosquitoes decreases. The rate of decrease depends upon the specific biting Eq (3) being used in the model.
Table 4 lists the basic reproduction number computed with the baseline parameters. For this case, the of DENV (ZIKV, or CHIKV) transmitted by Wolbachia-free mosquitoes is the highest, followed by of DENV (ZIKV, or CHIKV) transmitted by mosquitoes infected with wAlbB strain of Wolbachia, and for mosquitoes carrying wMel strain is the smallest. The basic reproduction number for ZIKV is the largest in all cases. The basic reproduction number of DENV is greater than the basic reproduction number of CHIKV for mosquitoes carrying the same strain of Wolbachia or Wolbachia-free mosquitoes.
Table 4. The basic reproduction number for the parameter values in Table 2.
for ZIKV is the largest. For any strains of Wolbachia, for ZIKV is still greater than one. For the same virus, is the largest for Wolbachia-free mosquitoes, and second largest for wAlbB-infected mosquitoes.
| Wolbachia | Ae. aegypti | Ae. albopictus | ||||
|---|---|---|---|---|---|---|
| DENV | ZIKV | CHIKV | DENV | ZIKV | CHIKV | |
| wMel | 1.87 | 1.93 | 0.84 | 1.44 | 1.49 | 1.10 |
| wAlbB | 2.32 | 2.40 | 1.05 | 1.80 | 1.85 | 1.36 |
| Wolbachia-free | 2.93 | 3.02 | 1.32 | 2.26 | 2.34 | 1.71 |
The basic reproduction number is a function of the baseline parameters. Others may come up with different baseline values for different outbreaks. The readers can estimate the model response to different baseline values of a parameter using the sensitivity indices in Table 5. The relative sensitivity index of the quality of interest, q, with respect to the parameter of interest, p is
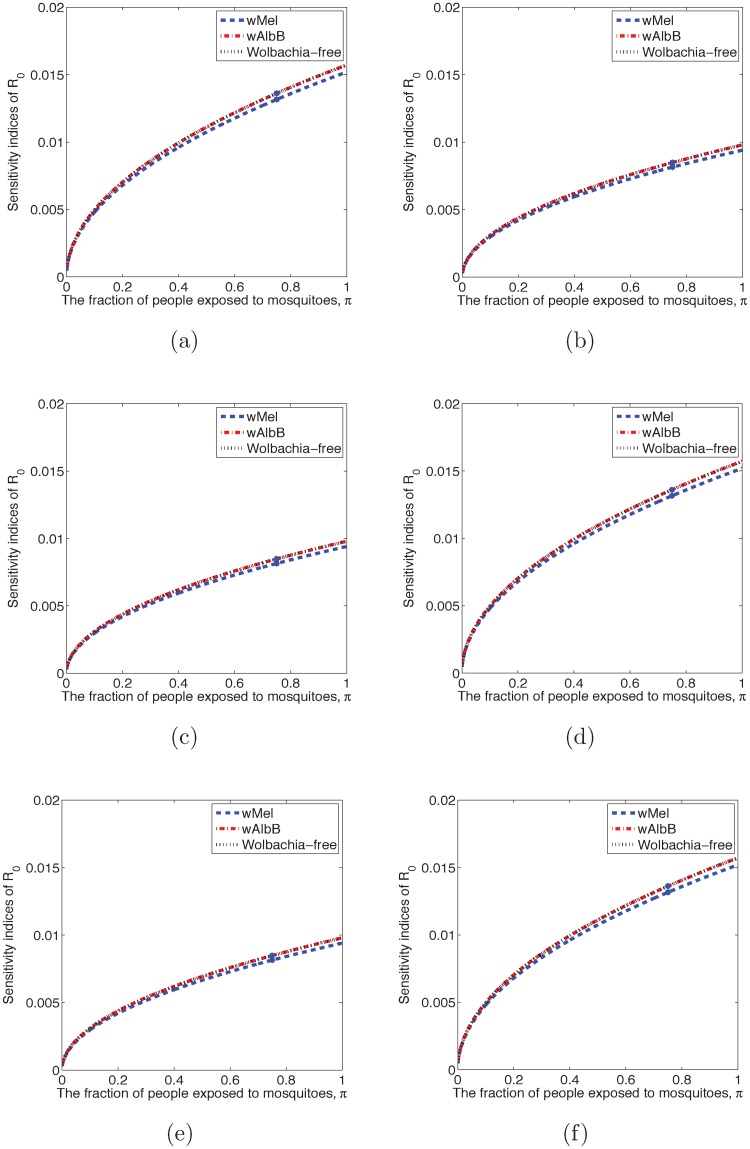
as described in [23], where the notation p* indicates that a variable is evaluated at the model baseline values. For example, for DENV transmitted by wAlbB-infected Ae. aegypti mosquitoes, if we reduce π, by 10%, then will be reduced by 0.00136, since −0.1 × 0.0136 = −0.00136. Sensitivity indices of varying with the fraction of people exposed to mosquitoes are shown in Fig 4.
Table 5. Sensitivity indices of for the Model (1) at the baseline parameter values in Tables 2 and 3.
As can be seen from the table, for Ae. aegypti mosquitoes, the most sensitive parameter is the mosquito death rate, μv. However, for Ae. albopictus mosquitoes, the most sensitive parameter is the mosquito biting rate, σv, and the least sensitive parameter is the incubation rate for humans, νh.
| Parameter | DENV | DENV | ZIKV | ZIKV | CHIKV | CHIKV | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ae. aegypti | Ae. albopictus | Ae. aegypti | Ae. albopictus | Ae. aegypti | Ae. albopictus | |||||||
| wAlbB | wMel | wAlbB | wMel | wAlbB | wMel | wAlbB | wMel | wAlbB | wMel | wAlbB | wMel | |
| σv | +0.66 | +0.67 | +0.79 | +0.79 | +0.66 | +0.67 | +0.79 | +0.79 | +0.66 | +0.67 | +0.79 | +0.79 |
| μv | -0.71 | -0.72 | -0.66 | -0.67 | -0.71 | -0.72 | -0.66 | -0.67 | -0.72 | -0.73 | -0.57 | -0.58 |
| βhv | +0.50 | +0.50 | +0.50 | +0.50 | +0.48 | +0.48 | +0.48 | +0.48 | +0.79 | +0.79 | +0.79 | +0.79 |
| βvh | +0.50 | +0.50 | +0.50 | +0.50 | +0.48 | +0.48 | +0.48 | +0.48 | +0.79 | +0.79 | +0.79 | +0.79 |
| γh | -0.50 | -0.50 | -0.50 | -0.50 | -0.48 | -0.48 | -0.48 | -0.48 | -0.79 | -0.79 | -0.79 | -0.79 |
| σh | +0.34 | +0.33 | +0.21 | +0.21 | +0.33 | +0.32 | +0.21 | +0.20 | +0.55 | +0.53 | +0.34 | +0.33 |
| νv | +0.21 | +0.22 | +0.16 | +0.17 | +0.20 | +0.21 | +0.16 | +0.17 | +0.35 | +0.37 | +0.11 | +0.12 |
| H0 | -0.16 | -0.17 | -0.29 | -0.29 | -0.15 | -0.16 | -0.28 | -0.28 | -0.25 | -0.26 | -0.45 | -0.46 |
| V0 | +0.16 | +0.17 | +0.29 | +0.29 | +0.15 | +0.16 | +0.28 | +0.28 | +0.25 | +0.26 | +0.45 | +0.46 |
| π | +0.0136 | +0.0132 | +0.0085 | +0.0081 | +0.0141 | +0.0136 | +0.0088 | +0.0084 | +0.0086 | +0.0083 | +0.0054 | +0.0052 |
| μh | -0.0007 | -0.0007 | -0.0007 | -0.0007 | -0.0007 | -0.0007 | -0.0007 | -0.0007 | -0.0010 | -0.0010 | -0.0010 | -0.0010 |
| νh | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 | +0.0003 |
Fig 4. Sensitivity indices of changing with the fraction of people exposed to mosquitoes, π, ranging from 0 to 1.
(a) Sensitivity indices of for DENV transmitted by Ae. aegypti mosquitoes. (b) Sensitivity indices of for DENV transmitted by Ae. albopitus mosquitoes. (c) Sensitivity indices of for CHIKV transmitted by Ae. aegypti mosquitoes. (d) Sensitivity indices of for CHIKV transmitted by Ae. albopictus mosquitoes. (e) Sensitivity indices of for ZIKV transmitted by Ae. aegypti mosquitoes. (f) Sensitivity indices of for ZIKV transmitted by Ae. albopictus mosquitoes.
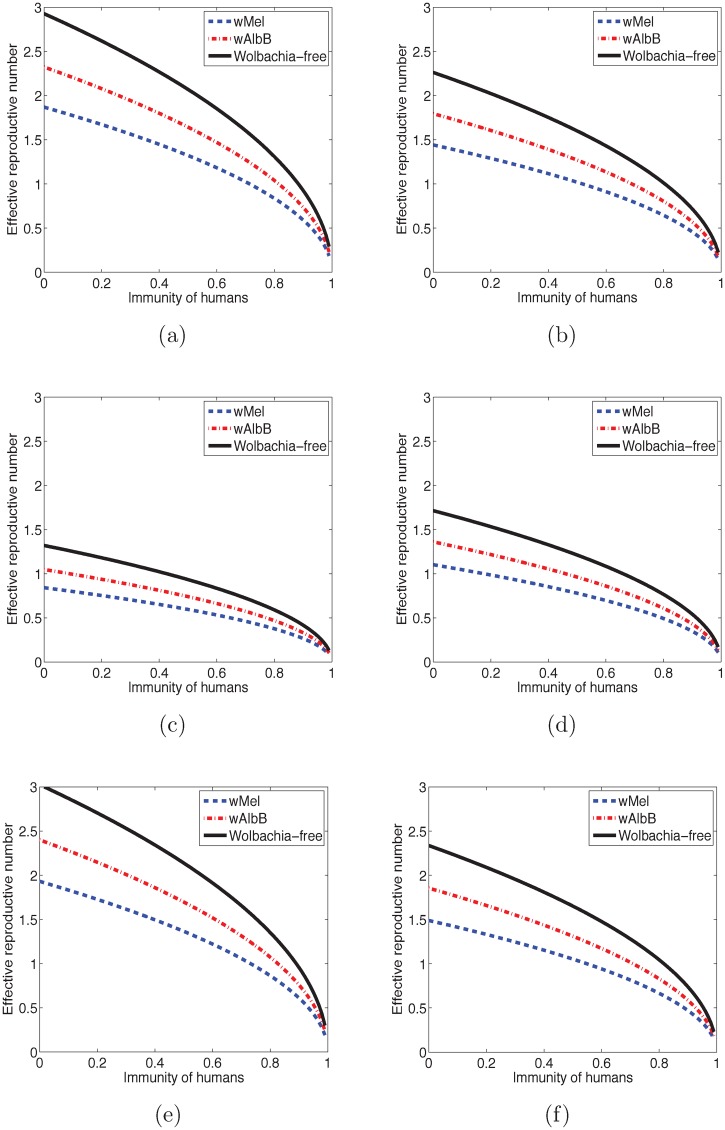
The effective reproduction number depends on the fraction of humans who are immune to the infection. Fig 5 shows the effective reproduction number varying with the immunity of humans, assuming that all mosquitoes are susceptible and the initial total mosquito population is V0. The effective reproduction number decreases with the increase of the immunity of humans. When all humans are immune to the disease, then the effective reproduction number is the same as the basic reproduction number.
Fig 5. Initial effective reproduction number, changing with immunity in humans.
The decreases as the immunity in humans increases and Ae. aegypti are infected with Wolbachia. This indicates that even though infecting the mosquitoes with Wolbachia might not reduce the initial to be less than one, it could be an effective strategy in future seasonal outbreaks to bring to be less than one when part of the population is immune. (a) for DENV transmitted by Ae. aegypti mosquitoes. (b) for DENV transmitted by Ae. albopictus mosquitoes. (c) for CHIKV transmitted by Ae. aegypti mosquitoes. (d) for CHIKV transmitted by Ae. albopictus mosquitoes. (e) for ZIKV transmitted by Ae. aegypti mosquitoes. (f) for ZIKV transmitted by Ae. albopictus mosquitoes.
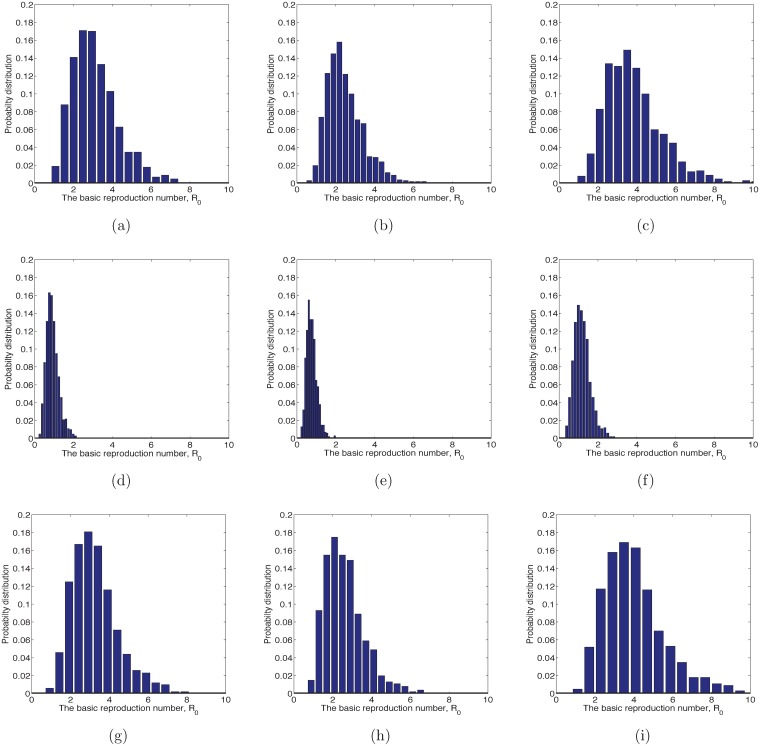
Previous examples kept most of the parameters at their baseline values. If we allow all the parameters to vary over the entire feasible sampling space, we will obtain a distribution for . The distribution for is a function of the distributions for the model parameters as they vary within their allowed ranges. We assumed a triangular distribution that vanishes at the endpoints of the feasible region and has the mode at the baseline values in Table 2. If we had assumed that the distribution was uniform over the range, where the parameter was just as likely to be at the upper or lower bound as our best guess (the baseline case), then the ranges for the reproduction numbers in Fig 6 will not change, but the distributions will have fatter tails.
Fig 6. Histogram for .
Histograms from 1000 realizations of for DENV, ZIKV and CHIKV when Wolbachia-infected and Wolbachia-free Ae. aegypti mosquitoes. The baseline parameters in Table 2 were sampled from a triangular distribution having the mode at the baseline values and vanishing at the edges of the feasibility region. The mean and median of Zika are the largest. (a) When DENV is transmitted by wAlbB-infected mosquitoes, median and mean of are 2.94 and 3.13, respectively. (b) When DENV is transmitted by wMel-infected mosquitoes, median and mean of are 2.30 and 2.48, respectively. (c) When DENV is transmitted by Wolbachia-free mosquitoes, median and mean of are 3.65 and 3.84, respectively. (d) When CHIKV is transmitted by wAlbB-infected mosquitoes, median and mean of are 0.88 and 0.92, respectively. (e) When CHIKV is transmitted by wMel-infected mosquitoes, median and mean of are 0.73 and 0.76, respectively. (f) CHIKV transmitted by Wolbachia-free mosquitoes, median and mean of are 1.14 and 1.19, respectively. (g) When ZIKV is transmitted by wAlbB-infected mosquitoes, median and mean of are 3.10 and 3.28, respectively. (h) When ZIKV is transmitted by wMel-infected mosquitoes, median and mean of are 2.45 and 2.62, respectively. (i) When ZIKV is transmitted by Wolbachia-free mosquitoes, median and mean of are 3.79 and 4.03, respectively.
The histograms of the distribution for for DENV, ZIKV, and CHIKV transmitted by Ae. aegypti are shown in Fig 6. The means and medians of for wMel-infected mosquitoes are the smallest. for ZIKV is the largest, followed by DENV, and then CHIKV. In a similar analysis for Ae. albopictus, is the largest for ZIKV, followed by CHIKV, and the least is DENV. This is in agreement with the analysis where we varied the parameters one at a time over their feasible ranges.
Endemic equilibrium analysis
If Wolbachia is successful in reducing the spread of the viruses, then there will be more people uninfected at the EE. In Table 6, the fraction of humans still susceptible at the EE for wMel-infected mosquitoes is the largest, while the susceptibility of Wolbachia-free mosquitoes is the smallest when a certain disease is transmitted by a certain genus of mosquitoes. For Ae. aegypti infected with the same strain of Wolbachia, the percentage of humans susceptible to CHIKV is higher than the percentage of humans susceptible to DENV or Zika. For Ae. albopictus infected with the same strain of Wolbachia, the percentages of humans susceptible to DENV and ZIKV are higher than the percentage of humans susceptible to CHIKV. Although the wMelPop-infected mosquitoes are the most effective in stopping an epidemic, it is unrealistic to consider a fully infected wild population of wMelPop-infected mosquitoes. Hence, we did not include the analysis for wMelPop strain of Wolbachia. This coefficient for effectiveness computed using Eq (7) listed in Table 7 shows that wMel is significantly more effective than wAlbB in reducing the number of infections in simulations with the baseline parameters in Table 2.
Table 6. The fraction of susceptible humans at the endemic equilibrium.
A larger susceptibility means fewer people are infected at the endemic equilibrium.
| Wolbachia | Ae. aegypti | Ae. albopictus | ||||
|---|---|---|---|---|---|---|
| DENV | ZIKV | CHIKV | DENV | ZIKV | CHIKV | |
| wMel | 0.21 | 0.21 | 0.42 | 0.36 | 0.36 | 0.25 |
| wAlbB | 0.14 | 0.14 | 0.27 | 0.23 | 0.23 | 0.16 |
| Wolbachia-free | 0.09 | 0.09 | 0.17 | 0.15 | 0.15 | 0.10 |
Table 7. The coefficient for effectiveness, κ.
This coefficient measures the relative reduction in the total number of humans infected with DENV, ZIKV, or CHIKV transmitted by wMel- and wAlbB-infected mosquitoes, with respect to the number of humans infected with Wolbachia-free mosquitoes, by t = 700. Note that wMel is more effective than wAlbB in each case.
| Wolbachia | Ae. aegypti | Ae. albopictus | ||||
|---|---|---|---|---|---|---|
| DENV | ZIKV | CHIKV | DENV | ZIKV | CHIKV | |
| wMel | 0.04 | 0.03 | 0.95 | 0.17 | 0.15 | 0.61 |
| wAlbB | 0.01 | 0.01 | 0.65 | 0.04 | 0.03 | 0.18 |
Discussion
A mosquito infected with the Wolbachia bacteria is less capable of transmitting DENV, ZIKV, and CHIKV, and one of the leading new mitigation strategies is to fight the spread of these viral infections by releasing Wolbachia-infected mosquitoes. We quantified the impact of wAlbB, wMel, and wMelPop strains of Wolbachia in reducing the transmission of CHIKV, DENV, and ZIKV. The model accounts for reduced fitness of the Wolbachia-infected mosquitoes, reduced ability of transmitting viruses, and the behavior changes of infected individuals caused by the infection. Because people infectious with DENV and CHIKV are more likely to have serious symptoms, we assumed that the people infectious with these viruses were less likely to be bitten by mosquitoes than the people infectious with ZIKV. The behavior changes of humans have significant impacts on the model predictions and, unfortunately, is often let out of most vector-borne disease models.
The baseline model parameters are estimates for the general population and our best guess from the literature. The relative sensitivity indices for these parameters (Table 5) can be used to predict how slightly different assumptions about these input parameters will change the basic reproduction number. The relative sensitivity analysis quantified the relative importance of the model parameters on the model predictions and can be used to quantify the importance of obtaining more accurate data to reduce the parameter uncertainty and improve the model’s predictability.
Over the entire range of parameter values, our simulation results show that the for wMel-infected mosquitoes is the smallest. For Ae. aegypti, for ZIKV is the largest, followed by DENV, then CHIKV. In a similar analysis for Ae. albopictus, is the largest for ZIKV, followed by DENV, then CHIKV. This is in agreement with the analysis where we varied the parameters one at a time over their feasible range. Our simulation results show that the wMel strain is more effective in controlling these viruses than wAlbB strain in all of the situations we tested. We find that for the same mosquito densities, Ae. aegypti is more effective than Ae. albopictus in transmitting DENV and ZIKV, while the opposite is true for CHIKV.
The results are based on the simulations with the parameter values available in current literature, which may vary for different locations at different times. Our model is a general model that can produce outputs for a specific location, once the data for the location are available to parameterize the model.
Comparisons of the model predictions for Ae. aegypti versus Ae. albopictus must take into account the ratio of mosquitoes to humans. is sensitive to this ratio and the density of Ae. aegypti mosquitoes is typically higher in urban areas than in rural areas, while the opposite is true for Ae. albopictus mosquitoes [37]. When there are few mosquitoes per human, then . As the number of mosquitoes increases, then quickly increases to be greater than one. As the number of mosquitoes per human becomes very large, eventually decreases in our model where the number of times that humans allow themselves to be bitten is limited to a maximum number of times per day. The rate of decrease depends upon the specific biting rate in Eq (3) being used in the model.
Although wMelPop-infected mosquitoes do not transmit these viruses, the increased death rate of wMelPop-infection has a high fitness cost. It is difficult for wMelPop-infected mosquitoes to survive in the wild mosquito populations because a much larger number of wMelPop-infected mosquitoes needs to be released in order to sustain in the wild mosquito population.
The analysis of the basic reproduction number assumes that when the infections first enter a population, then everyone is fully susceptible to the infection. We derived the effective reproduction number for when the host population is partially immune to new infections, perhaps due to a previous epidemic. The effective reproduction number increases with the susceptibility of humans. When more people are immune to DENV and CHIKV than ZIKV, as happened in the 2015 Zika epidemic, then the numbers of dengue and Chikungunya cases tend to be stable, while the number of Zika cases exploded. Hence, the susceptibility of the human population must be taken into account in future seasonal outbreaks. Our analysis quantified how depends upon a fraction of the population being immune to the infection in a vector-host transmission model.
There are ongoing efforts for releasing Wolbachia-infected mosquitoes in the wild to fight against the spread of these viral infections. Wolbachia-infected mosquitoes could contribute to the reduction of transmission instead of elimination. Besides, the number of Wolbachia-infected mosquitoes released has to exceed the threshold and continual introductions are required. The real-world thresholds for sustaining an epidemic will be greater than the threshold estimates derived for ideal conditions where there is a homogenous population of infected and uninfected mosquitoes.
These field tests suggest that the spatial heterogeneity of the populations must be considered before this model will be appropriate to help guide policy decisions. Also, our simulations are based on an environment of Wolbachia-infected mosquitoes where most of the wild mosquitoes are infected with Wolbachia. When introducing the wMel or wAlbB strains of Wolbachia into a wild mosquito population, it may take several weeks or months for it to reach the equilibrium level and may require several introductions [22]. Furthermore, the model parameter values are based on average estimates from the literature, and not the parameters for a specific location. Before this model can be applied to a specific location, then model parameters, such as the average number of mosquitoes per person, must be estimated for this location.
In future studies, we will couple the model for the spread of Wolbachia [22] with the disease transmission model [23] to evaluate effectiveness of this approach for the situations where the mosquito population is only partially infected with Wolbachia and consider new human arrivals including people who are immune and infectious.
Data Availability
Data are all contained within the paper.
Funding Statement
This work is funded by National Natural Science Foundation of China 11501145, the Fundamental Research funds for the Central Universities of China HEUCFM181101, the endowment for the Evelyn and John G. Phillips Distinguished Chair in Mathematics at Tulane University, the National Science Foundation awards MPS-DMS-1122666, MPS-DMS-156353, DEB-RAPID 1641130, and the NIH/NIGMS program for Models of Infectious Disease Agent Study award U01GM097661. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Gubler DJ. Epidemic dengue/dengue hemorrhagic fever as a public health, social and economic problem in the 21st century. Trends Microbiol. 2002;10(2):100–103. 10.1016/S0966-842X(01)02288-0 [DOI] [PubMed] [Google Scholar]
- 2. Burt FJ, Rolph MS, Rulli NE, Mahalingam S, Heise MT. Chikungunya: a re-emerging virus. The Lancet. 2012;379(9816):662–671. 10.1016/S0140-6736(11)60281-X [DOI] [PubMed] [Google Scholar]
- 3. Hancock PA, Sinkins SP, Godfray HCJ. Strategies for introducing Wolbachia to reduce transmission of mosquito-borne diseases. PLoS Negl Trop Dis. 2011;5(4):e1024 10.1371/journal.pntd.0001024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Pialoux G, Gaüzère BA, Jauréguiberry S, Strobel M. Chikungunya, an epidemic arbovirosis. Lancet Infect Dis. 2007;7(5):319–327. 10.1016/S1473-3099(07)70107-X [DOI] [PubMed] [Google Scholar]
- 5. Gupta D. Dengvaxia: Prayers answered or NOT? Indian J Community Health. 2016;28(4):398–399. [Google Scholar]
- 6. Kozek WJ, Rao RU. The discovery of Wolbachia in arthropods and nematodes—A historical perspective In: Wolbachia: a bug’s life in another bug. vol. 5 Karger Publishers; 2007. p. 1–14. [Google Scholar]
- 7. Hedges LM, Brownlie JC, O’Neill SL, Johnson KN. Wolbachia and virus protection in insects. Science. 2008;322(5902):702–702. 10.1126/science.1162418 [DOI] [PubMed] [Google Scholar]
- 8. Blagrove MSC, Arias-Goeta C, Genua CD, Failloux AB. A Wolbachia wMel transinfection in Aedes albopictus is not detrimental to host fitness and inhibits Chikungunya virus. PLoS Negl Trop Dis. 2013;7(3):e2152 10.1371/journal.pntd.0002152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Werren JH. Biology of Wolbachia. Annu Rev Entomol. 1997;42(1):587 10.1146/annurev.ento.42.1.587 [DOI] [PubMed] [Google Scholar]
- 10. Weeks AR, Turelli M, Harcombe WR, Reynolds KT, Hoffmann AA. From parasite to mutualist: rapid evolution of Wolbachia in natural populations of Drosophila. PLoS Biol. 2007;5(5):e114 10.1371/journal.pbio.0050114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Hughes H, Britton NF. Modelling the use of Wolbachia to control dengue fever transmission. Bull Math Biol. 2013;75(5):796–818. 10.1007/s11538-013-9835-4 [DOI] [PubMed] [Google Scholar]
- 12. Nguyen TH, Le Nguyen H, Nguyen TY, Vu SN, Tran ND, Le T, et al. Field evaluation of the establishment potential of wMelPop Wolbachia in Australia and Vietnam for dengue control. Parasit Vectors. 2015;8(1):563 10.1186/s13071-015-1174-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Jiggins FM. The spread of Wolbachia through mosquito populations. PLoS Biol. 2017;15(6):e2002780 10.1371/journal.pbio.2002780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Axford JK, Ross PA, Yeap HL, Callahan AG, Hoffmann AA. Fitness of wAlbB Wolbachia infection in Aedes aegypti: parameter estimates in an outcrossed background and potential for population invasion. Am J Trop Med Hyg. 2016;94(3):507–516. 10.4269/ajtmh.15-0608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Ndii MZ, Hickson R, Allingham D, Mercer G. Modelling the transmission dynamics of dengue in the presence of Wolbachia. Math Biosci. 2015;262:157–166. 10.1016/j.mbs.2014.12.011 [DOI] [PubMed] [Google Scholar]
- 16. Ferguson NM, Kien DTH, Clapham H, Aguas R, Trung VT, Chau TNB, et al. Modeling the impact on virus transmission of Wolbachia-mediated blocking of dengue virus infection of Aedes aegypti. Sci Transl Med. 2015;7(279):279ra37–279ra37. 10.1126/scitranslmed.3010370 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ross PA, Wiwatanaratanabutr I, Axford JK, White VL, Endersbyharshman NM, Hoffmann AA. Wolbachia infections in Aedes aegypti differ markedly in their response to cyclical heat stress. PLoS Pathog. 2017;13(1):e1006006 10.1371/journal.ppat.1006006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ross PA, Endersby NM, Hoffmann AA. Costs of three Wolbachia infections on the survival of Aedes aegypti larvae under starvation conditions. PLoS Negl Trop Dis. 2016;10(1):e0004320 10.1371/journal.pntd.0004320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Zhang X, Tang S, Cheke RA. Models to assess how best to replace dengue virus vectors with Wolbachia-infected mosquito populations. Math Biosci. 2015;269:164–177. 10.1016/j.mbs.2015.09.004 [DOI] [PubMed] [Google Scholar]
- 20. Li Y, Liu X. An impulsive model for Wolbachia infection control of mosquito-borne diseases with general birth and death rate functions. Nonlinear Anal Real World Appl. 2017;37:412–432. 10.1016/j.nonrwa.2017.03.003 [DOI] [Google Scholar]
- 21. Xue L, Manore CA, Thongsripong P, Hyman JM. Two-sex mosquito model for the persistence of Wolbachia. J Biol Dyn. 2017; 11(sup1): 216–237. [DOI] [PubMed] [Google Scholar]
- 22. Qu Z, Xue L, Hymans JM. Modeling the transmission of Wolbachia in mosquitoes for controlling mosquito-borne diseases. SIAM J Appl Math. 2018; 78(2): 826–852. [Google Scholar]
- 23. Manore CA, Hickmann KS, Xu S, Wearing HJ, Hyman JM. Comparing dengue and Chikungunya emergence and endemic transmission in Ae. aegypti and Ae. albopictus. J Theor Biol. 2014;356:174–191. 10.1016/j.jtbi.2014.04.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Funk S, Kucharski AJ, Camacho A, Eggo RM, Yakob L, Murray LM, et al. Comparative analysis of dengue and Zika outbreaks reveals differences by setting and virus. PLoS Negl Trop Dis. 2016;10(12):e0005173 10.1371/journal.pntd.0005173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Grange L, Simon-Loriere E, Sakuntabhai A, Gresh L, Paul R, Harris E. Epidemiological risk factors associated with high global frequency of inapparent dengue virus infections. Front Immunol. 2014;5:280 10.3389/fimmu.2014.00280 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Duong V, Lambrechts L, Paul RE, Ly S, Lay RS, Long KC, et al. Asymptomatic humans transmit dengue virus to mosquitoes. P Natl Acad Sci USA. 2015;112(47):14688–93. 10.1073/pnas.1508114112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Bloch D, Roth NM, Caraballo EV, Munozjordan J, Hunsperger E, Rivera A, et al. Use of household cluster investigations to identify factors associated with Chikungunya virus infection and frequency of case reporting in Puerto Rico. PLoS Negl Trop Dis. 2016;10(10):e0005075 10.1371/journal.pntd.0005075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Robinson M, Conan A, Duong V, Ly S, Ngan C, Buchy P, et al. A model for a Chikungunya outbreak in a rural cambodian setting: Implications for disease control in uninfected areas. PLoS Negl Trop Dis. 2014;8(9):e3120 10.1371/journal.pntd.0003120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Lazear HM, Diamond MS. Zika virus: New clinical syndromes and its emergence in the western hemisphere. J Virol. 2016;90(10):4864–4875. 10.1128/JVI.00252-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rajah MM, Pardy RD, Condotta SA, Richer MJ, Sagan SM. Zika virus: Emergence, phylogenetics, challenges, and opportunities. Acs Infect Dis. 2016;2(11):763 10.1021/acsinfecdis.6b00161 [DOI] [PubMed] [Google Scholar]
- 31. Duffy MR, Chen TH, Hancock WT, Powers AM, Kool JL, Lanciotti RS, et al. Zika virus outbreak on Yap Island, Federated States of Micronesia. N Engl J Med. 2009;360(24):2536 10.1056/NEJMoa0805715 [DOI] [PubMed] [Google Scholar]
- 32. Chitnis N, Cushing JM, Hyman J. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J Appl Math. 2006;67(1):24–45. 10.1137/050638941 [DOI] [Google Scholar]
- 33. Wonham MJ, Lewis MA, Rencławowicz J, Van den Driessche P. Transmission assumptions generate conflicting predictions in host—vector disease models: a case study in West Nile virus. Ecol Lett. 2006;9(6):706–725. 10.1111/j.1461-0248.2006.00912.x [DOI] [PubMed] [Google Scholar]
- 34. Rückert C, Weger-Lucarelli J, Garcia-Luna SM, Young MC, Byas AD, Murrieta RA, et al. Impact of simultaneous exposure to arboviruses on infection and transmission by Aedes aegypti mosquitoes. Nat Commun. 2017;8 10.1038/ncomms15412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Zhang X, Tang S, Cheke RA, Zhu H. Modeling the effects of augmentation strategies on the control of dengue fever with an impulsive differential equation. Bull Math Biol. 2016;78(10):1968–2010. 10.1007/s11538-016-0208-7 [DOI] [PubMed] [Google Scholar]
- 36. Joubert DA, Walker T, Carrington LB, De Bruyne JT, Kien DHT, Hoang NLT, et al. Establishment of a Wolbachia superinfection in Aedes aegypti mosquitoes as a potential approach for future resistance management. PLoS Pathog. 2016;12(2):e1005434 10.1371/journal.ppat.1005434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Tsuda Y, Suwonkerd W, Chawprom S, Prajakwong S, Takagi M. Different spatial distribution of Aedes aegypti and Aedes albopictus along an urban—rural gradient and the relating environmental factors examined in three villages in northern Thailand. J Am Mosq Control Assoc. 2006;22(2):222–228. 10.2987/8756-971X(2006)22[222:DSDOAA]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- 38. Chitnis N, Hyman JM, Cushing JM. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull Math Biol. 2008;70(5):1272–1296. 10.1007/s11538-008-9299-0 [DOI] [PubMed] [Google Scholar]
- 39. Siler JF, Hall MW, Hitchens AP. Dengue: the history, epidemiology, mechanism of transmission etiology, clinical manifestations, immunity, and prevention. Philipp J Sci. 1926;29:1–304. [Google Scholar]
- 40. Sabin SB. Research on dengue during World War II. Am J Trop Med Hyg. 1952;1:30–50. 10.4269/ajtmh.1952.1.30 [DOI] [PubMed] [Google Scholar]
- 41. Dumont Y, Chiroleu F. Vector control for the Chikungunya disease. Math Biosci Eng. 2010;7(2):315–348. [DOI] [PubMed] [Google Scholar]
- 42. Lahariya C, Pradhan SK. Emergence of Chikungunya virus in Indian subcontinent after 32 years: a review. J Vector Borne Dis. 2006;43(4):151 [PubMed] [Google Scholar]
- 43. Schwartz O, Albert ML. Biology and pathogenesis of Chikungunya virus. Nat Rev Microbiol. 2010;8(7):491–500. 10.1038/nrmicro2368 [DOI] [PubMed] [Google Scholar]
- 44. Gubler DJ, Suharyono W, Tan R, Abidin M, Sie A. Viraemia in patients with naturally acquired dengue infection. Bull World Health Organ. 1981;59:623–630. [PMC free article] [PubMed] [Google Scholar]
- 45. Vaughn DW, Green S, Kalayanarooj S, Innis BL, Nimmannitya S, Suntayakorn S, et al. Dengue viremia titer, antibody response pattern, and virus serotype correlate with disease severity. J Infect Dis. 2000;181:2–9. 10.1086/315215 [DOI] [PubMed] [Google Scholar]
- 46. Moulay D, Aziz-Alaoui M, Cadivel M. The Chikungunya disease: modeling, vector and transmission global dynamics. Math Biosci. 2011;229(1):50–63. 10.1016/j.mbs.2010.10.008 [DOI] [PubMed] [Google Scholar]
- 47. Newton EAC, Reiter P. A model of the transmission of dengue fever with an evaluation of the impact of ultra-low volume (ULV) insecticide applications on dengue epidemics. Am J Trop Med Hyg. 1992;47:709–720. 10.4269/ajtmh.1992.47.709 [DOI] [PubMed] [Google Scholar]
- 48. Paupy C, Ollomo B, Kamgang B, Moutailler S, Rousset D, Demanou M, et al. Comparative role of Aedes albopictus and Aedes aegypti in the emergence of dengue and Chikungunya in central Africa. Vector Borne Zoonotic Dis. 2010;10(3):259–266. 10.1089/vbz.2009.0005 [DOI] [PubMed] [Google Scholar]
- 49. Massad E, Ma S, Burattini MN, Tun Y, Coutinho FAB, Ang LW. The risk of Chikungunya fever in a dengue-endemic area. J Travel Med. 2008;15(3):147–155. 10.1111/j.1708-8305.2008.00186.x [DOI] [PubMed] [Google Scholar]
- 50. Turell MJ, Beaman JR, Tammariello RF. Susceptibility of selected strains of Aedes aegypti and Aedes albopictus (Diptera: Culicidae) to Chikungunya virus. J Med Entomol. 1992;29(1):49–53. 10.1093/jmedent/29.1.49 [DOI] [PubMed] [Google Scholar]
- 51. Nur AH, Abu HA, Nurita AT, Che SM, Norasmah B. Population analysis of Aedes albopictus (Skuse) (Diptera:Culicidae) under uncontrolled laboratory conditions. Trop Biomed. 2008;25(2):117. [PubMed] [Google Scholar]
- 52. Costero A, Edman JD, Clark GG, Scott TW. Life table study of Aedes aegypti (Diptera: Culicidae) in Puerto Rico fed only human blood versus blood plus sugar. J Med Entomol. 1998;35(5):809–813. 10.1093/jmedent/35.5.809 [DOI] [PubMed] [Google Scholar]
- 53. Trpis M, Haussermann W. Dispersal and other population parameters of Aedes aegypti in an African village and their possible significance in epidemiology of vector-borne diseases. Am J Trop Med Hyg. 1986;35:1263–1279. 10.4269/ajtmh.1986.35.1263 [DOI] [PubMed] [Google Scholar]
- 54. Putnam JL, Scott TW. Blood feeding behavior of dengue-2 virus-infected Aedes aegypti. Am J Trop Med Hyg. 1995;55:225–227. 10.4269/ajtmh.1995.52.225 [DOI] [PubMed] [Google Scholar]
- 55. Watts DM, Burke DS, Harrison BA, Whitmore RE, Nisalak A. Effect of temperature on the vector efficiency of Aedes aegypti for dengue 2 virus. Am J Trop Med Hyg. 1987;36:143–152. 10.4269/ajtmh.1987.36.143 [DOI] [PubMed] [Google Scholar]
- 56. Sheppard PM, Macdonald WW, Tonn RJ, Grab B. The dynamics of an adult population of Aedes aegypti in relation to dengue haemorrhagic fever in Bangkok. J Anim Ecol. 1969;38(3):661–702. 10.2307/3042 [DOI] [Google Scholar]
- 57. Trpis M, Haussermann W, Craig GB. Estimates of population size, dispersal, and longevity of domestic Aedes aegypti by mark-release-recapture in the village of Shauri Moyo in eastern Kenya. J Med Entomol. 1995;32:27–33. 10.1093/jmedent/32.1.27 [DOI] [PubMed] [Google Scholar]
- 58. Lambrechts L, Scott TW, Gubler DJ. Consequences of the expanding global distribution of Aedes albopictus for dengue virus transmission. PLoS Negl Trop Dis. 2010;4(5):e646 10.1371/journal.pntd.0000646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Dumont Y, Chiroleu F, Domerg C. On a temporal model for the Chikungunya disease: modeling, theory and numerics. Math Biosci. 2008;213(1):80–91. 10.1016/j.mbs.2008.02.008 [DOI] [PubMed] [Google Scholar]
- 60. Pesko K, Westbrook CJ, Mores CN, Lounibos LP, Reiskind MH. Effects of infectious virus dose and bloodmeal delivery method on susceptibility of Aedes aegypti and Aedes albopictus to Chikungunya virus. J Med Entomol. 2009;46(2):395 10.1603/033.046.0228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Costanzo KS, Mormann K, Juliano SA. Asymmetrical competition and patterns of abundance of Aedes albopictus and Culex pipiens (Diptera: Culicidae). J Med Entomol. 2005;42(4):559–70. 10.1093/jmedent/42.4.559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sivanathan MM. The ecology and biology of Aedes Aegypti (L.) and Aedes Albopictus (Skuse)(Diptera: Culicidae) and the resistance status of Aedes Albopictus (Field Strain) against organophosphates in Penang, Malaysia [QL536. M266 2006 f rb]. Universiti Sains Malaysia; 2006.
- 63. Delatte H, Gimonneau G, Triboire A, Fontenille D. Influence of temperature on immature development, survival, longevity, fecundity, and gonotrophic cycles of Aedes albopictus, vector of Chikungunya and dengue in the Indian Ocean. J Med Entomol. 2009;46(1):33–41. 10.1603/033.046.0105 [DOI] [PubMed] [Google Scholar]
- 64. Vazeille M, Moutailler S, Coudrier D, Rousseaux C, Khun H, Huerre M, et al. Two Chikungunya isolates from the outbreak of La Reunion (Indian Ocean) exhibit different patterns of infection in the mosquito, Aedes albopictus. PLoS One. 2007;2(11). 10.1371/journal.pone.0001168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Dubrulle M, Mousson L, Moutailler S, Vazeille M, Failloux AB. Chikungunya virus and Aedes mosquitoes: saliva is infectious as soon as two days after oral infection. PLoS One. 2009;4(6):e5895 10.1371/journal.pone.0005895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Sebastian MR, Lodha R, Kabra S. Chikungunya infection in children. Indian J Pediatr. 2009;76(2):185–189. 10.1007/s12098-009-0049-6 [DOI] [PubMed] [Google Scholar]
- 67. Xi Z, Khoo CC, Dobson SL. Wolbachia establishment and invasion in an Aedes aegypti laboratory population. Science. 2005;310(5746):326 10.1126/science.1117607 [DOI] [PubMed] [Google Scholar]
- 68. Bian G, Xu Y, Lu P, Xie Y, Xi Z. The endosymbiotic bacterium Wolbachia induces resistance to dengue virus in Aedes aegypti. PLoS Pathog. 2010;6(4):e1000833 10.1371/journal.ppat.1000833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Hoffmann A, Montgomery B, Popovici J, Iturbe-Ormaetxe I, Johnson P, Muzzi F, et al. Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature. 2011;476(7361):454–457. 10.1038/nature10356 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data are all contained within the paper.