Abstract
A good data sampling scheme is important for diffusion MRI acquisition and reconstruction. Diffusion Weighted Imaging (DWI) data is normally acquired on single or multiple shells in q-space. The samples in different shells are typically distributed uniformly, because they should be invariant to the orientation of structures within tissue, or the laboratory coordinate frame. The Electrostatic Energy Minimization (EEM) method, originally proposed for single shell sampling scheme in dMRI by Jones et al., was recently generalized to the multi-shell case, called generalized EEM (GEEM). GEEM has been successfully used in the Human Connectome Project (HCP). Recently, the Spherical Code (SC) concept was proposed to maximize the minimal angle between different samples in single or multiple shells, producing a larger angular separation and better rotational invariance than the GEEM method. In this paper, we propose two novel algorithms based on the SC concept: 1) an efficient incremental constructive method, called Iterative Maximum Overlap Construction (IMOC), to generate a sampling scheme on a discretized sphere; 2) a constrained non-linear optimization (CNLO) method to update a given initial scheme on the continuous sphere. Compared to existing incremental estimation methods, IMOC obtains schemes with much larger separation angles between samples, which are very close to the best known solutions in single shell case. Compared to the existing Riemannian gradient descent method, CNLO is more robust and stable. Experiments demonstrated that the two proposed methods provide larger separation angles and better rotational invariance than the state-of-the-art GEEM and methods based on the SC concept.
1 Introduction
Diffusion MRI (dMRI) is a unique imaging technique to explore microstructure properties of white matter in the human brain by mapping local diffusion of water molecules. In dMRI, one obtains a limited number of samples of the 3D diffusion signal attenuation E(q) in q-space. Reconstruction in dMRI is to recover the continuous E(q) from these scanned measurements and to estimate some meaningful quantities including the diffusion tensor, the Ensemble Average Propagator (EAP), etc. An appropriate sampling scheme in q-space is important for all dMRI acquisition and reconstruction applications in order to recover as much information as possible using a minimal number of measurements. It is infeasible to develop a general optimal sampling scheme that works best for all signal types and all reconstruction methods. However, a necessary property for an optimal sampling scheme is that the samples should be spherically uniformly distributed with no directional preference, such that the sampling scheme is invariant to the orientation of tissue structures, or the laboratory coordinate frame of scanner.
Uniform single shell sampling schemes are widely used in dMRI, where samples in q-space are uniformly distributed in a sphere with a fixed b-value. The Electrostatic Energy Minimization (EEM) method proposed in dMRI by Jones et al., [1] is the most popular way to generate a general single shell sampling scheme with an arbitrary number of samples. EEM considers the samples as electrons in sphere, and estimates the sample configuration by minimizing the electrostatic repulsive force based on the Coulomb's law, i.e., , where antipodal symmetry is considered because antipodal symmetric samples have the same role in dMRI data reconstruction. Some solutions to the EEM problem with different number K have been collected in CAMINO [2]. Recently [4] generalized EEM from single shell to multiple shell, called generalized EEM (GEEM), by considering the electrostatic energies both in each individual shell and in the combined shell with all samples. The obtained multi-shell schemes have been successfully used in the Human Connectome Project (HCP). Although EEM and GEEM are widely used, the electrostatic energy formulation does not directly maximize the angular separation between measurements. There is no study to validate how the electrostatic energy is related with dMRI data reconstruction.
The Spherical Code (SC)1 was recently proposed to design single and multiple shell sampling schemes [5]. The SC formulation directly maximizes the separation angles between samples in each shell and in the combined shell for all samples, which is more natural than the electrostatic energy formulation. In [5] three algorithms were proposed based on the SC formulation. Although these three methods have larger separation angles compared to GEEM, they have limitations which will be discussed later.
In this paper, we propose two novel methods based on the SC concept to design single and multi-shell schemes. We propose a very efficient method, called Iterative Maximum Overlap Construction (IMOC), to incrementally generate samples from a given fine uniform sampling scheme. Although IMOC is a greedy method, it obtains globally optimal solutions in 𝕊1 for the 2D case and approximately globally optimal solutions in 𝕊2 for single shell scheme design in dMRI. The separation angles by IMOC are much larger than EEM, GEEM and the incremental SC (ISC) in [5]. We also propose Constrained Non-Linear Optimization (CNLO) to produce a local optimal solution from a given initialization. CNLO is more stable and generates larger separation angles than Riemannian gradient descent (RGD) in [5]. Experimental results demonstrate that the proposed methods yield larger separation angles and better rotational invariance than the state-of-the-art GEEM used in the HCP [4], and existing methods based on SC [5].
2 Methods
2.1 Spherical Code (SC) Formulation: Maximize the Minimal Separation Angle
The covering radius of a given sampling scheme is the minimal angular distance between samples, i.e.,
| (1) |
where the absolute value operator is used because the antipodal symmetric samples have the same role in dMRI data reconstruction. The SC formulation on a single shell is to find K samples such that the covering radius is maximized [5], i.e.,
| (2) |
The SC formulation is also called as Tammes problem2, which is well studied in the mathematics literature. [6] proposed to iteratively optimize a continuous cost function that approximates the original discontinuous cost function in Eq. (2), and the authors also released a collection of best known solutions to the SC problem in 𝕊2 [6]3.
[5] generalized SC problem from single shell case in mathematics to multiple shell case in dMRI field by solving
| (3) |
where S is the number of shells, Ks is the number of points on the s-th shell, us,i is the i-th point on the s-th shell, and w is a weighting factor between the mean covering radius of the S shells and the covering radius of the combined shell containing all points from the S shells. It is normally set as 0.5. [5] proposed three algorithms to solve the SC problem in Eq. (2) and Eq. (3), i.e., a greedy method called Incremental SC (ISC), a Mixed Integer Linear Programming (MILP) method, a Riemannian Gradient Descent (RGD) method. MILP selects globally optimal one or multiple subsets of points from a given full set of points. However, MILP is known to be NP hard, thus it is impractical to select samples from a very fine uniform sample set, and [5] obtains an acceptable scheme by MILP within 10 minutes from 321 uniform samples generated by sphere tessellation. RGD updates a given sampling scheme to a better local optimal solution. However the cost functions in Eq. (2) and Eq. (3) are not continuous, and the gradients of the cost functions which are determined by the sample pairs that have the minimal separation angle are not continuous neither. Moreover, the implementation of RGD needs a threshold to determine the sample pairs that can be considered to be equal to the minimal separation angle, and a little change of the threshold can significantly change the final results, which makes RGD unstable.
2.2 Constrained Non-Linear Optimization (CNLO)
Since RGD is not stable due to the reasons we discussed above, we propose a stable method, called Constrained Non-Linear Optimization (CNLO), to obtain a local minimum. SC problem in Eq. (2) can be solved using CNLO in Eq. (4a), where Eq. (4b) means all separation angles are larger than θ.
| (4a) |
| (4b) |
| (4c) |
Note that both cost function and constraints are continuous, considering . CNLO does not need to determine the sample sets with the minimal separation angle, which is more robust and avoids the threshold in RGD.
Multi-shell SC problem in Eq. (3) can be solved using CNLO in Eq. (5a):
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
Eq. (5b) means that the separation angles of samples in the s-th shell are larger than its corresponding covering radius θs. Eq. (5c) means that the separation angles of samples in two different shells are larger than the covering radius θ0 for the combined shell with all samples. Eq. (5d) means that the covering radii for all single shells are always larger than the covering radius for the combined shell. In other words, Eq. (5d) means that the separation angles of samples in the same shell are larger than θ0, because of Eq. (5b).
CNLO in Eq. (4a) and Eq. (5a) are continuous non-convex constrained optimization problems. We use sequential quadratic programming (SQP) to solve them. In each step, SQP solves a quadratic programming problem which locally approximates the original optimization problem. In practice, we use the SQP solver in NLOPT library [7]. CNLO obtains a locally optimal solution with a given initialization. The initialization can be set as a set of random samples, or the schemes provided by other methods.
2.3 Iterative Maximum Overlap Construction (IMOC)
Incremental sampling scheme design methods, i.e., incremental EEM [3], incremental GEEM (IGEEM) [4], and incremental SC (ISC) [5], were proposed to obtain reasonable uniform coverage when the acquisition is terminated and only a subset of the first several samples is used. These incremental scheme design methods are all greedy methods. In each step, they select the best sample from a fine uniform sample set based on the chosen samples in previous steps. They have the same limitations. 1) Since they are devised to work reasonably well for any subset with first several samples, the electrostatic energy or covering radius of the full sample set is not good, compared to optimization based methods. 2) If a finer uniform sample set is used, the electrostatic energy or covering radius of the obtained sampling scheme may not improve, which is beyond our expectation.
Here we propose Iterative Maximum Overlap Construction (IMOC) to overcome the above two limitations. See the IMOC algorithm in Alg. 1 for designing multi-shell schemes, whose simplified version with S = 1 is for single shell case. IMOC uses MOC in Alg. 2 to verify whether a candidate covering radius set (θ0, θ1, …, θS) is able to construct an acceptable scheme with (K1, …, Ks) samples for S shells. We define the coverage set of a point x as C(x, θ) = {y | arccos(|yTx|) < θ}. With a given candidate (θ0, θ1, …, θS), MOC constructs samples one by one. In the i-th step,
|
|
| Algorithm 1. IMOC for Multiple shell Scheme Design: |
|
|
| Input: number of samples for S shells: |
| Output: . |
| // binary search {θs} from {(0, )}. are the upper bounds of the covering radii; |
| , , ∀s = 0, 1, …, S; |
| repeat |
| , ∀s = 0, 1, …, S; |
| if IsSatisfied then , ∀s = 0, 1, …, S; |
| else , ∀s = 0, 1, …, S; |
| until θs does not change, ∀s = 0, 1, …, S; |
|
|
| Algorithm 2. MOC for Multiple shell Scheme Design: |
|
|
| Input: , |
| Output: IsSatisfied, . |
| Initialize coverage sets as S + 1 empty sets, and initialize Ns = 0, ∀s ∈ [1, S]; |
| for n = 1 to do |
| if n == 1 then choose any point as u1,1, s ← 1, i ← 1; |
| if 1 < n ≤ S then s ← n, i ← 1, choose us,i in (𝕊2 – CS0) such that the set |
| C(us,i, θ0) ⋂ CS0 has the largest area ; |
| if n > S then |
| Set V as an empty set; |
| for s′ = 1 to S do |
| if Ns′, < Ks′, and (𝕊2 – (CSs′ ⋃ CS0)) is not empty then |
| choose vs′ in (𝕊2 – (CSs′ ⋃ CS0)) such that the overlap set |
| C(vs′,, θs′) ⋂ (CSs′ ⋃ CS0) has the largest area denoted as As′; |
| V ← V ⋃ {vs′}; |
| end |
| end |
| if V is empty then |
| IsSatisfied = False; return |
| else |
| choose s and vs ∈ V such that their corresponding area As is the largest one among ; |
| i ← Ns + 1, us,i ← vs; |
| end |
| end |
| CSs ← CSs ⋃ C(us,i, θs); CS0 ← CS0 ⋃ C(us,i, θ0); Ns ← Ns + 1; |
| end |
| IsSatisfied=True; return; |
MOC searches the best point us,i for the s-th shell such that its coverage C(us,i, θs) has the largest overlap with the existing total coverage set CSs ⋃ CS0 among all possible samples and possible shells, and then adds C(ui,s, θs) into CSs, C(ui,s, θ0) into CS0. IMOC performs a binary search of the covering radii along the line segment determined by , where is a upper bound of the covering radius with Ks symmetric points [5,8]. The one dimension search provides good results in compromise for both individual shells and the combined shell.
Note that for single shell case, it is easy to see that IMOC yields the globally optimal solution for K samples in 𝕊1 in the 2D case, while ISC and IGEEM cannot. Similarly with ISC, IMOC can analytically select the best point in each iteration in 2D case from all points in 𝕊1. However for 𝕊2 IMOC requires a fine uniform discretization of the sphere to find the best point in each step with the largest overlap area by counting the number of points in overlap sets. We consider several issues for efficient implementation of IMOC. 1) KD-tree is used for efficient nearest neighbor search. 2) In the (i + 1)-th step, the overlap area As(x) is different from the i-th step and needs to be re-calculated only if the determined point us′,i in the i-th step satisfies arccos(|xTus′,i|) < θ0, if s ≠ s′, or arccos(|xTus′,i|) < θs, if s = s′. 3) In MOC, the candidate points can be selected from a small “outside surface” of CS, i.e., {x | x ∉ CS, ∃y ∈ CS, s.t. arccos(|xTy|) ≤ δ}, instead of the whole complementary set (𝕊2 – CS). δ is set as twice of the covering radius of the fine uniform sampling set used in IMOC. This modification does not change the results by IMOC in our experiments, although we currently have no proof for this phenomenon. These three issues significantly speed up MOC, because they reduce the time for each neighborhood search, and reduce the number of neighborhood search. In our implementation, IMOC only requires a few seconds on an ordinary laptop.
3 Experiments
Effect of Discretization in Incremental Methods
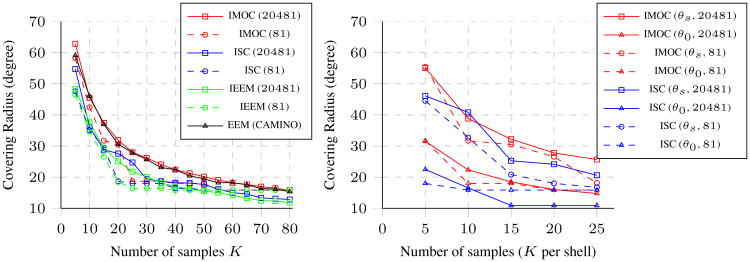
These incremental methods, i.e., Incremental EEM (IEEM) [3], IGEEM [4], ISC [5], and IMOC, all require a uniform sample set as a discretization of 𝕊2 to determine the best sample in each step. We would like to test whether a finer discretization in 𝕊2 can obtain better schemes with larger separation angles. Two uniform sample sets respectively with 81 samples and 20482 samples from sphere tessellation were used for comparison. With these two uniform sets, IEEM, ISC, and IMOC were performed to generate single shell schemes with K ∈ [5, 80]. The left subfigure of Fig. 1 shows the covering radii of schemes obtained by different methods using two uniform discretization. It also shows the best known single shell schemes using EEM in CAMINO [2]. Note that when K ∈ [50, 80] is close to 81, covering radii by IEEM and ISC using finer discretization are actually smaller than using coarse discretization, and only when K < 50 is far from 81, IEEM and ISC obtain larger covering radii using finer discretization. When using finer discretization, covering radii by IMOC are always improved, and are even larger than the well optimized schemes by EEM in CAMINO. ISC and IMOC were performed to generate schemes with 3 shells, K ∈ [5, 25] per shell. The right subfigure of Fig. 1 shows mean of covering radii of three shells (θs) and the covering radii of the combined shell (θ0). It also demonstrates that when K × 3 is close to 81, covering radius of the combined shell by ISC is not improved using the finer discretization, while IMOC has no such issue.
Fig. 1. Effect of discretization.
Covering radii of sampling schemes (K in left side, K × 3 in right side) by different methods with two uniform discretization (81 samples and 20481 samples).
Covering Radii in Sampling Schemes
We evaluated the proposed method by generating a multi-shell scheme with 28 × 3 samples, which was also used for evaluation in [5] and [4]. Table 1 shows the covering radii of the schemes obtained by different methods, where MILP+RGD means RGD using the result by MILP as the initialization, IMOC+CNLO means CNLO using the result by IMOC as the initialization. The results by GEEM, IGEEM in [4], and ISC, MILP, MILP+RGD in [5] were directly extracted from the papers. The single shell schemes with 28 and 28 × 3 samples using EEM from CAMINO [2] were also listed as references. IMOC obtains better covering radii than existing incremental methods, and even better than MILP. IMOC+CNLO obtains largest covering radii in both 3 individual shells and the combined shell, and the covering radii by IMOC+CNLO in these 3 shells are even better than best known scheme collected in CAMINO using EEM [1, 2], similarly with Fig. 1.
Table 1.
Covering radii of multi-shell sampling schemes with 28×3 samples generated by various methods. The best known schemes by EEM are individually for each single shell.
| Shell 1 (28) | Shell 2 (28) | Shell 3 (28) | Combined (28 × 3) | |
|---|---|---|---|---|
|
| ||||
| GEEM [4] | 22.2° | 22.2° | 22.0° | 13.2° |
| IGEEM [4] | 19.2° | 19.7° | 19.3° | 4.7° |
| ISC (N = 20481) [5] | 21.3° | 19.3° | 21.1° | 10.5° |
| MILP (N = 321) [5] | 23.8° | 23.8° | 24.3° | 13.3° |
| MILP + RGD [5] | 25.7° | 25.7° | 25.4° | 13.6° |
| IMOC (N = 20481) | 24.3° | 24.3° | 24.3° | 14.0° |
| IMOC + CNLO | 26.3° | 25.9° | 26.6° | 14.6° |
|
| ||||
| EEM (CAMINO) [1,2] | 25.7° | 25.7° | 25.7° | 15.6° |
Rotational Invariance in Reconstruction
We would like to test rotational invariance of the schemes with 28 × 3 samples by different methods in Table 1. We generated synthetic diffusion signals from a mixture tensor model E(qu) = 0.5 exp(−q2uTD1u) + 0.5 exp(−q2uTD2u), where b = q2 = 1000, 2000, 3000 s/mm2, and these two tensors have the same eigenvalues [1.7, 0.2, 0.2] × 10−3 mm2/s with a crossing angle of 55°. With each tested scheme, we rotated the model and generated signals 20481 times with the rotation angles determined by the uniform sample set with 20481 samples. Then we performed Spherical Polar Fourier Imaging with spherical order 6 and radial order 2 [9] to estimate the EAP profiles with radius of 15μm, detected the peaks of the EAP profiles, and calculated the mean angular differences by comparing the detected peaks with the ground-truth fiber directions in these 20481 tests. Table 2 lists the mean and standard deviation of angular differences obtained by different schemes. IMOC+CNLO yields the significantly lowest angular differences (paired t-test, p < 0.001) with the lowest deviation, and IMOC has the lower mean and deviation than other incremental methods.
Table 2.
Angular differences between estimated directions and ground-truth fiber directions using different schemes by various methods.
4 Conclusion
We propose IMOC and CNLO based on the SC concept to design single and multiple shell uniform sampling schemes. IMOC is a very efficient incremental method which obtains globally optimal solutions in the 2D case. For the 3D case in dMRI, covering radii of IMOC schemes are even larger than EEM in CAMINO. IMOC obtains better schemes when using a finer discretization, while existing incremental methods (IEEM [3], IGEEM [4], ISC [5]) may have a worse result when using finer discretization. CNLO is a local optimization method which has better theoretical properties than RGD in [5]. The multi-shell scheme by CNLO using IMOC as initialization obtains larger covering radii and better rotational invariance than existing methods [4, 5] based on electrostatic energy and the SC formulation. The codes and best known schemes will be released in DMRITool package (https://github.com/DiffusionMRITool).
Acknowledgments
This work is supported in part by NICHD and NIBIB Intramural Research Programs, a UNC BRIC-Radiology start-up fund, and NIH grants (EB006733, EB009634, AG041721, MH100217, and 1UL1TR001111).
Footnotes
References
- 1.Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine. 1999 [PubMed] [Google Scholar]
- 2.Cook P, Bai Y, Nedjati-Gilani S, Seunarine K, Hall M, Parker G, Alexander D. Camino: Open-source diffusion-MRI reconstruction and processing. ISMRM. 2006 [Google Scholar]
- 3.Deriche R, Calder J, Descoteaux M. Optimal real-time q-ball imaging using regularized kalman filtering with incremental orientation sets. Medical Image Analysis. 2009;13(4) doi: 10.1016/j.media.2009.05.008. [DOI] [PubMed] [Google Scholar]
- 4.Caruyer E, Lenglet C, Sapiro G, Deriche R. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magnetic Resonance in Medicine. 2013 doi: 10.1002/mrm.24736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cheng J, Shen D, Yap PT. Designing single- and multiple-shell sampling schemes for diffusion MRI using spherical code. In: Golland P, Hata N, Barillot C, Hornegger J, Howe R, editors. MICCAI2014, Part III LNCS. Vol. 8675. Springer; Heidelberg: 2014. pp. 281–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Conway JH, Hardin RH, Sloane NJ. Packing lines, planes, etc.: Packings in Grassmannian spaces. Experimental Mathematics. 1996;5(2):139–159. [Google Scholar]
- 7.Johnson SG. The nlopt nonlinear-optimization package. http://ab-initio.mit.edu/nlopt.
- 8.Tóth LF. On the densest packing of spherical caps. The American Mathematical Monthly. 1949;56(5):330–331. [Google Scholar]
- 9.Cheng J, Ghosh A, Jiang T, Deriche R. Model-Free and Analytical EAP Reconstruction via Spherical Polar Fourier Diffusion MRI. In: Jiang T, Navab N, Pluim JPW, Viergever MA, editors. MICCAI 2010, Part I LNCS. Vol. 6361. Springer; Heidelberg: 2010. pp. 590–597. [DOI] [PubMed] [Google Scholar]