Controlling T2 Blurring in 3D RARE Arterial Spin Labeling Acquisition through Optimal Combination of Variable Flip Angles and k-space Filtering

Abstract

Purpose

To improve the SNR efficiency and reduce the T2 blurring of 3D RARE stack-of-spiral arterial spin labeling (ASL) imaging by using variable refocusing flip angles and k-space filtering.

Methods

An algorithm for determining the optimal combination of variable flip angles and filtering correction is proposed. The flip angles are designed using extended phase graph physical simulations in an analytical and global optimization framework, with an optional constraint on deposited power. Optimal designs for correcting to Hann and Fermi window functions were compared to conventional constant amplitude or variable flip angle only designs on six volunteers.

Results

With the Fermi window correction, the proposed optimal designs provided 39.8% and 27.3% higher SNR (p<0.05) than conventional constant amplitude and variable flip angle designs. Even when power deposition was limited to 50% of the constant amplitude design, the proposed method outperformed the SNR (p<0.05) of the above two conventional approaches by 32.5% and 20.7%. The sharpness and the contrast between gray and white matter were improved with the k-space filtering correction for all the flip angle designs. The improvements were moderate for the Hann window correction.

Conclusion

This work demonstrates that variable flip angles can be derived as the output of an optimization problem. The combined design of variable flip angle and k-space filtering provided superior SNR to designs primarily emphasizing either approach singly.

Introduction

Arterial spin labeling (ASL) (1) provides clinically important perfusion information without a contrast agent. However, ASL is limited by its inherently low signal-to-noise ratio (SNR). To improve image quality, ASL is typically acquired with 3D readouts, such as stack-of-spiral (2) and GRASE (3), in which spiral or echo-planar (EPI) readouts are inserted between the refocusing pulses of RARE (4) (Fast Spin Echo, FSE or Turbo Spin Echo, TSE) sequences. 3D ASL with stack-of-spiral (5–8) or GRASE (9–12) has been demonstrated in a wide arrange of studies, and has been recommended by the ISMRM Perfusion Study Group (13). These 3D fast acquisitions are compatible with high-efficiency background suppression because they use only one excitation pulse. Background suppression is desirable because it reduces the motion artifacts and physiological noise in the ASL acquisition (8). Despite these benefits, such 3D RARE sequences do have some limitations.

A disadvantage of 3D RARE acquisitions is that they can result in blurred ASL images. This blurring is a direct result of the T2 decay of the ASL signal along the RARE echo train. This acts as an exponential filter, or window, in k-space along the direction encoded during the echo train. Depending on the k-space acquisition order, a variety of distorted point spread functions (PSF) in the image can occur. Because T2 weighting of ASL acquisitions could affect quantitative accuracy and SNR, RARE sequences used for ASL acquisition are typically implemented with centric phase encoding. For centric ordering, T2 decay primarily blurs the PSF (14,15), especially for echo trains longer than π/2*T2 (16). In 3D stack-of-spiral or GRASE ASL applications, however, the total length of the readout commonly exceeds 300ms, which is much larger than π/2*T2 of brain tissue and will result in seriously blurred images if not corrected. This places 3D ASL among the RARE applications most seriously affected by T2 blurring.

The presence of T2 blurring can make ASL imaging less useful and powerful. Blurring reduces the detectability of small lesions, short T2 structures and key features used for clinical diagnoses (17). Since blurring is typically largest in the superior/inferior direction because of the selected acquisition order, important regions with detailed structure along this direction, such as the medial temporal lobes, will be particularly degraded. T2 blurring will also produce a PSF with poorly controlled wings that can sum across voxels to produce anomalous signals, such as erroneously high flow in white matter. Furthermore, blurring undermines advanced image processing techniques such as 3D registration, segmentation, and partial volume correction. Methods to minimize T2 blurring could increase the diagnostic and research impact of ASL.

One approach to minimize T2 blurring in ASL is to avoid RARE and especially 3D RARE based acquisitions. 3D magnetization prepared fast gradient echo acquisitions have been proposed for ASL. For example, a 3D gradient echo based spiral was proposed with optimal SNR (18). Unbalanced gradient echo sequences generally suffer from lower SNR efficiency than RARE sequences, however. Balanced steady-state free precession (SSFP) acquisitions have the potential for competitive SNR efficiency but they can suffer from magnetic field inhomogeneity artifacts and T2 decay (19). Another widely used approach is 2D echo-planar acquisition. The recent addition of simultaneous multi-slice echo-planar capabilities for ASL (20) make it possible to acquire the whole brain at improved resolution in the slice direction. However, background suppression is less effective in the 2D gradient echo acquisitions, because groups of slices are acquired at different times. For example, Shao et al (21) improved the background suppression in multi-slice ASL by achieving 5% background signal. In contrast, the 2D and 3D ASL acquired with RARE is commonly performed with less than 1% (22) or 0.3% (23) background signal. The benefits of background suppression to improve SNR by decreasing physiological noise in ASL have been a major driver for the use of 3D RARE based acquisitions (24).

A straightforward strategy for controlling T2 decay in 3D RARE is to reduce the echo train duration. With a shorter echo train, there is less time for T2 decay and consequently reduced modulation of k-space signals. Echo train shortening can be achieved by acquiring k-space over multiple excitations (25,26), acceleration with parallel imaging (27,28) or a combination of the two. Though these methods can contribute to solving the problem of blurring, limiting the acquisition to the period when T2 decay is small reduces SNR efficiency and can limit the temporal resolution of ASL.

T2 blurring in RARE can also be addressed by correction in reconstruction. The simplest approach is to scale the attenuated signal in later echoes by a multiplicative k-space factor, or k-space filtering (29). An alternative approach in image space is to estimate the PSF and correct the blurring by iterative deconvolution (25). Even more complex is the use of compressed sensing, which can potentially correct blurring even for a range of T2’s(30,31). These approaches can be effective at reducing blurring, but require longer and parameter dependent reconstructions and can rapidly increase image noise.

Finally, blurring can be reduced by varying the refocusing flip angles to reduce the signal decay during the RARE echo train. Reduced refocusing flip angles store some of the magnetization in the longitudinal direction where it decays with T1, typically much longer than T2. For long T2 tissues, ramp optimized flip angle trains have been proposed to achieve a stable, pseudosteady state signal (32–34) with negligible T2 decay. For shorter T2 tissues, variable flip angle can also be used to reduce the blurring by targeting a desired signal response such as a Hann or Fermi window function (35,36). The design of variable flip angle trains, however, is generally performed using heuristic rather than systematic methods. For example, variable flip angles schemes were proposed in an intuitive way by designing the maximum signal at the last echo (37) or attempting to maintain constant signal until the k-space center was covered and then increasing flip angles linearly (38,39). Such empirical designs are often targeted for very specific problems and may only provide suboptimal performance.

In this work, we propose an analytic framework for variable flip angle design and hypothesize that a combined optimization of variable flip angle and k-space scaling could provide more flexibility. The proposed method suggests the potential to achieve superior SNR performance for T2 blurring reduction in 3D RARE ASL. Its performance was evaluated with respect to SNR, through-plane blurring, and gray-white matter contrast in six healthy volunteers.

Materials and Methods

This study proceeded in two stages. First, we designed variable flip angle trains for RARE acquisitions using three different schemes: (1) achieving constant signal neglecting T2 decay by flip angle modulation, (2) achieving targeted signal response including T2 decay by flip angle modulation, and (3) achieving targeted signal response including T2 decay by a combination of flip angle modulation and k-space filtering. Second, we assessed the performance of the proposed designs with simulations and with in-vivo 3DASL images obtained in healthy volunteers.

Flip Angle Designs

Three flip angles schemes were designed for the parameters of a typical 3D ASL configuration. Echo train length was set to 32 and echo spacing was 10ms. Centric phase encoding was specified and the T2 and T1 of gray matter were assumed to be 100ms (40) and 1600ms (41). The extended phase graph algorithm (42) was used to calculate the signals for all of the designs.

Constant Amplitude Design Neglecting Decay

A flip angle train providing constant amplitude signal when T1 and T2 are neglected was designed targeting a 95° asymptotic flip angle (32,33). This asymptotic constant amplitude flip angle scheme has been commonly used in clinical and research studies and was used as a benchmark for this study. This method will be referred to as ‘Constant’ in the following.

Direct Decay Corrected Designs Using Only Variable Flip Angles

Two variable flip angle trains were designed, including T1 and T2 decay, which can directly achieve Hann or Fermi window shaped amplitudes across the echo train. Since the desired signal response cannot be achieved for an arbitrarily high amplitude, echo trains were iteratively calculated as the first echo amplitude was gradually increased from zero until the target shape of response could not be achieved. This method will be referred to as ‘Direct’ in the following.

For our study, the Fermi window is defined as

$$W_i=\frac{1}{1+exp\left(\frac{i-\chi N}{\kappa N}\right)}$$ [1]

where, i is the echo number (starting with 1). N=32 is the number of echoes. Other parameters are χ = 0.9 and κ = 0.046.

Decay Corrected Designs Using Both Variable Flip Angles and k-space Filtering

Using both variable flip angles and k-space filtering provides additional flexibility to optimize the SNR performance of the acquisition. Since k-space filtering can be used to convert the signals of any acquired echo train to a target response, a wide range of potential flip angle trains is able to provide acceptable signals. The corrected signal with optimal SNR performance was selected by minimizing the cost function below.

A mathematical expression for the SNR of an image was used for the optimization. Assuming the acquired RARE signal is S_i for the i^th echo and S₀ is the echo acquired at the center of k-space. Before applying the filter, the SNR can be defined as the ratio between signal amplitude and noise level (43):

$$\text{SNR}=c\frac{S_0}{\sigma }$$ [2]

where c is a calibration factor and σ is the standard deviation of the thermal noise.

When the k-space signal is filtered to match the target k-space window function (W_i) (e.g. Hann or Fermi window), each echo signal is multiplied by the scaling factor (W_i/S_i). The signal amplitude becomes W_i. The noise amplitude is also scaled by the factors of $\frac{W_i}{S_i}$ and the standard deviation of noise becomes $\sigma \sqrt{\sum {\left(\frac{W_i}{S_i}\right)}^2}$. The SNR of the resulting image can be expressed as:

$$\text{SNR}=c\frac{1}{\sigma }\frac{W_0}{\sqrt{\sum {\left(\frac{W_i}{S_i}\right)}^2}}$$ [3]

Since the SNR only depends on the signal (S_i ) in above equation, the maximum SNR can be achieved by minimizing the cost function:

$$\widehat{S}=argmin\sum {\left(\frac{W_i}{S_i}\right)}^2$$ [4]

The next step is to find the variable flip angle that can achieve the desired signal by minimizing the above cost function. Because the echo amplitude of RARE depends on the history of flip angles, the optimal flip angles can be calculated by minimizing the cost function for each flip angle sequentially (44). However, since the flip angles are not independent, this sequential solution may limit the performance of later flip angles and result in a local minimum solution that does not provide the best design (45). In our implementation, all flip angles, including the corresponding k-space scaling factors, were designed together with a global optimization algorithm (GlobalSearch) provided by MATLAB (46). The inputs of this implementation were the target k-space window (W), echo spacing, and relaxation rates (T1 and T2), and the outputs were variable flip angles and scaling factors used in k-space filtering.

In addition to maximizing SNR, reduction of deposited radiofrequency field (RF) power, or Specific Absorption Rate (SAR) is often another goal of the variable flip angle design (47). Limitation of SAR can be imposed with an additional constraint on the optimization, using the sum of squares of the flip angles θ:

$$\sum {\theta }_i^2<\mathit{SAR}$$ [5]

In this study, two flip angle schemes were designed for Hann and Fermi window corrections with maximum flip angle 150 degrees. This method will be referred to as ‘Optimal’ in the following. Two additional optimal flip angle schemes were designed for Hann and Fermi window corrections, with both maximum flip angle 150 degree and SAR limited to 50% of that in the benchmark ‘Constant’. This method will be referred to as ‘50%SAR’ in the following.

Assessment of Flip Angle Train Performance

Simulations

The echo signals of the above flip angle schemes were simulated with the extended phase graph algorithm. The performances of the proposed designs were quantified as follows.

The total signal of each design was calculated as the summation of all the echo amplitudes. The SNR of each flip angle train corrected to each target window was calculated using Eq. [3]. The results were normalized to the SNR of the constant amplitude method. The relative SAR of each flip angle scheme was calculated using Eq. [5] and normalized to that of the constant amplitude method.

The sensitivity of echo amplitudes to RF imperfections was also evaluated. RF miscalibration and especially spatial nonuniformity can be substantial at higher field strengths. Some variable flip angle designs could have increased sensitivity to RF variations, which might be a limitation to the performance of the proposed methods. The deviation of the echo signal was quantified as a normalized root of mean squared error (NRMSE) with Eq. [6]. Because, the deviation can be amplified by k-space scaling, the deviations were also calculated after the designed scaling factors were applied to the signals.

$$\sqrt{\frac{\mathit{mean}\left({\left(S-S_{\mathit{design}}\right)}^2\right)}{\mathit{mean}(S_{\mathit{design}}^2)}}$$ [6]

where, S_design were the echo signals of the designed flip angles and S were the signals generated when the rotating RF magnetic field, B1, increased or decreased by 15%.

In-vivo Assessments

Healthy volunteers were recruited following a protocol approved by our Institutional Review Board and written informed consent was obtained from all subjects.

The study was performed on a 3T GE MR750 scanner with the body transmit coil and a 32 channel head receiver coil. Anatomic images were first acquired with FSPGR BRAVO in about 5 minutes for each volunteer.

The proposed method was evaluated on six subjects with unbalanced pseudo continuous arterial spin labeling (PCASL) (6,48). The ASL was performed with labeling duration 1450ms and post labeling delay of 1525ms. Arterial blood was labeled by the unbalanced pCASL scheme (6). The duration of labeling Hann RF pulses was 500us. For the labeling, average B1 was 1.4uT, averaged gradient was 0.7mT/m and the selective gradient was 7mT/m. ASL images were acquired by interleaved 3D stack-of-spiral RARE. Each slice was fully sampled by spiral trajectory and different slices were phase encoded. The spiral trajectory consisted of eight arms, which provided 3.6mmx3.6mm in-plane resolution for a 240mm x 240mm FOV. The readout length of each spiral arm was 4.1ms. The same arm of the spiral was acquired for all echoes of an excitation while slice direction phase encoding was performed across echoes. The eight different spiral arms were acquired with eight different excitations. 32 slices were acquired with slice thickness of 4mm. Four pairs of control and label images were acquired in about 6 minutes. TR was 4.5s. Echo time (TE) and echo spacing were 10.5ms. A reference scan, which was used for CBF quantification, was also performed with the same readout parameters and flip angle scheme.

The proposed method was also examined on T1 weighted images, since the blurring measurement algorithm could be inaccurate when applied to the low SNR ASL images. To achieve an ‘ASL-like’ contrast, the T1 weighted images were prepared by four saturation pulses at the beginning of the sequence and three FOCI inversion pulses at 2980ms, 704ms and 112ms before the excitation pulse. This timing nulled cerebrospinal fluid signal and produced a much larger gray matter than white matter signal. The images were acquired with the same readout as the ASL sequence, with a longer, 6s, TR.

RF inhomogeneity was measured on one healthy volunteer with a double flip angle method (49). 3D images were acquired with the same readout as ASL. Scans were repeated with excitation flip angles of 90 degrees and 45 degrees the excitation pulses, while the same constant amplitude flip angles were used in the refocusing pulses of RARE. The images were smoothed by a 3D Gaussian filter with σ 5.6mm and actual flip angles were quantified. The effective flip angle was measured as the mean of the actual flip angle of the whole brain.

All ASL and T1 weighted images were reconstructed with MATLAB 2015a (The MathWorks Inc., Natick, MA, USA). To correct the T2 blurring, the acquired data were scaled by the ratio of Hann or Fermi window to the simulated echo signal of each flip angle scheme. The corrected k-space data were 1D Fourier transformed along the slice direction, then nonuniform Fourier transformed in the slice plane to reconstruct images with a nominal matrix size of 128x128.

Signals were evaluated using spatial masks derived from the T1 weighted, SPGR images. Gray and white matter masks were generated by segmenting the anatomic images with a probability map in SPM12 (Wellcome Trust Centre for Neuroimaging). The segmented gray matter mask was co-registered with the ASL images and the white matter mask was transformed accordingly.

Cerebral blood flow (CBF) maps were quantified by assuming that the post label delay was longer than the arterial transit time (50):

$$f=\frac{\mathit{\Delta }M}{M_0}\frac{\lambda }{2\alpha T_1}\frac{1}{exp\left(-\frac{w}{T_1}\right)-exp\left(-\frac{w+\tau }{T_1}\right)}$$ [5]

ΔM is the ASL difference signal between control and label scans; M is the signal of reference scan; f is the CBF; λ is the brain blood partition coefficient (assumed to be 0.9); α the labeling efficiency (0.8); T₁ is the longitudinal relaxation factor of tissue (1600ms); w is the post label delay (1525ms); τ is the labeling duration (1450ms). The perfusion was measured as the mean of the gray matter and white matter region for each subject. The standard deviation across subjects was also calculated.

The SNR was quantified on ASL images to enable comparison across the methods. The signal level was measured as the mean across all gray matter regions in the whole brain. The noise level is difficult to measure with ASL images, in which physiologic noise accounts for an essential proportion (51). Here, we calculated noise in two steps. First, the temporal differences between the first two and last two repetitions of ASL images were calculated (52). Second, the spatial standard deviation was calculated from a region outside the head on the temporal difference images. Contrast was calculated as the ratio between the mean signal of grey and white matter in the ASL images. The improvements of SNR and contrast were statistically evaluated between methods by a paired Wilcoxon signed rank test.

The reduction of blurring was evaluated using a non-reference method (53), which measured the difference of spatial variance before and after applying a low-pass filter. We performed the blurring measurement on the high SNR T1 weighted images to avoid the influence of the low SNR of ASL images. This non-reference blurring metric was modified to measure the blurring only in the slice direction. The blurring of the central 64 coronal slices was quantified and averaged. The blurring metric was scaled from 0 to 100, in which a larger value of the blurring metric indicates a more blurred image.

Results

Flip Angle Designs and Theoretical Performance

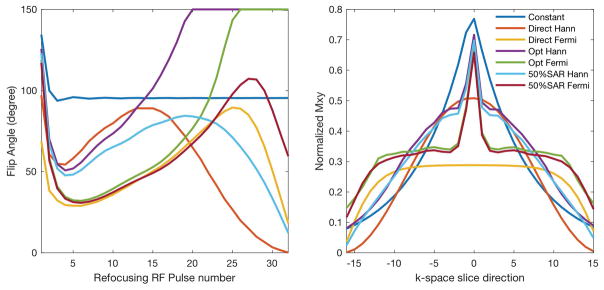
As shown in Figure 1, different flip angle design algorithms produced very different flip angles and echo train amplitudes. As expected, the ‘Constant’ resulted in high amplitude signal at the first echo, but the signal dropped quickly in the later echoes at a rate close to T2. In contrast, the ‘Direct’ with only variable flip angles employed lower flip angle pulses in the early part of the echo train in order to distribute the echo signal according to the correction windows. The proposed ‘Optimal’ employed larger flip angles at the first few and later RF pulses.

Figure 1.

The optimized flip angle trains (left) and resulting signal responses in k-space (right).

The performance of the designs is shown in Table 1. The SNR improvement of the proposed ‘Optimal’ method was moderate in the Hann window correction and about 50% higher in the Fermi window correction, compared to the conventional approaches. However, it also resulted in a 48% SAR increase. With the added SAR constraint, the proposed ‘50%SAR’ precisely achieved 50% SAR of the constant amplitude method and maintained the superior SNR performance. The ‘Direct’ resulted in the lowest SAR, but intermediate SNR.

Table 1.

Simulated signal level, SAR and expected SNR after k-space filtering correction.

	%	Total Signal	SAR	SNR
Hann	Constant	100	100	100
	Direct	86.0	42.4	84.5
	Optimal	104.5	148	111.4
	50%SAR	99.7	50.0	107.3
Fermi	Constant	100	100	100
	Direct	79.7	35.5	118
	Optimal	105.5	94.1	153
	50%SAR	102.4	50.0	149

As shown in Figure 1, the RF amplitude sensitivity of the proposed ‘Optimal’ was moderate. Before the k-space filtering, the signal profile of the ‘Optimal’ showed slightly more deviation than the constant amplitude method, which suggested more RF sensitivity, Table 2. With 15% RF reduction, the echo amplitude of the ‘Constant’ deviated 8.4%, while the proposed methods deviated 9.7% (10.5% when SAR was constrained) in the designs for Hann window correction. In contrast, the ‘Direct’ showed greater deviation (11.8%). After the correction with k-space scaling factors, the proposed ‘Optimal’ also displayed more sensitivity to RF amplitude than the constant amplitude design. The proposed ‘50%SAR’, however, maintained a similar B1 sensitivity as the constant amplitude flip angles.

Table 2.

RF amplitude sensitivity of the standard flip angle and proposed flip angle schemes. Left: the RF sensitivity of the echo amplitudes. Right: the RF sensitivity of the corrected images after k-space filtering.

		Acquired Signal		Corrected Signal
		+15% B1	−15% B1	+15% B1	−15% B1
Hann	Constant	5.9%	8.4%	8.4%	11.6%
	Direct	9.3%	11.8%	18.4%	23.2%
	Optimal	7.7%	9.7%	11.1%	15.2%
	50%SAR	7.1%	10.5%	11.0%	16.4%
Fermi	Constant	5.9%	8.4%	18.9%	19.1%
	Direct	13.1%	14.8%	45.8%	52.0%
	Optimal	8.6%	10.6%	19.8%	23.9%
	50%SAR	8.2%	10.5%	18.2%	24.3%

Theoretical blurring of the ‘constant’ echo trains and corrections with k-space filtering were calculated by the edge rise distance (10–90%) (54). The results are normalized to the case when k-space is corrected to a box function. The relative edge rise distances are 4.3, 1.8, and 1.1 for the uncorrected ‘constant‘, Hann and Fermi windows, respectively. It indicates reduced blurring in Hann and Fermi window corrections.

In-vivo Performance

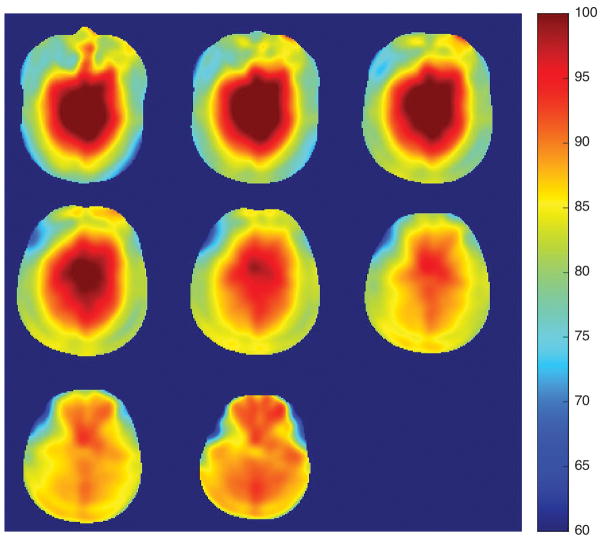
Figure 2 shows the measured RF inhomogeneity, which was appreciable in this study. The center of the brain had 15% higher RF amplitude than targeted and the edge of the brain had approximately 15% lower amplitude. The average flip angle across the whole brain was 86.7 degrees, close to the targeted flip angle, 90 degrees.

Figure 2.

RF inhomogeneity map for a targeted flip angle of 90 degrees. The colorbar scale is in degrees.

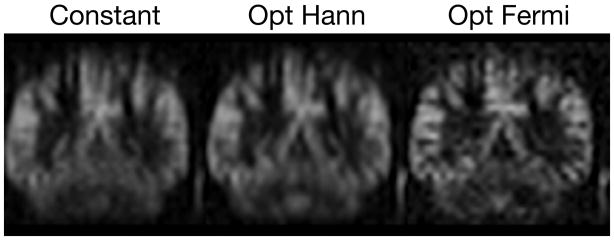
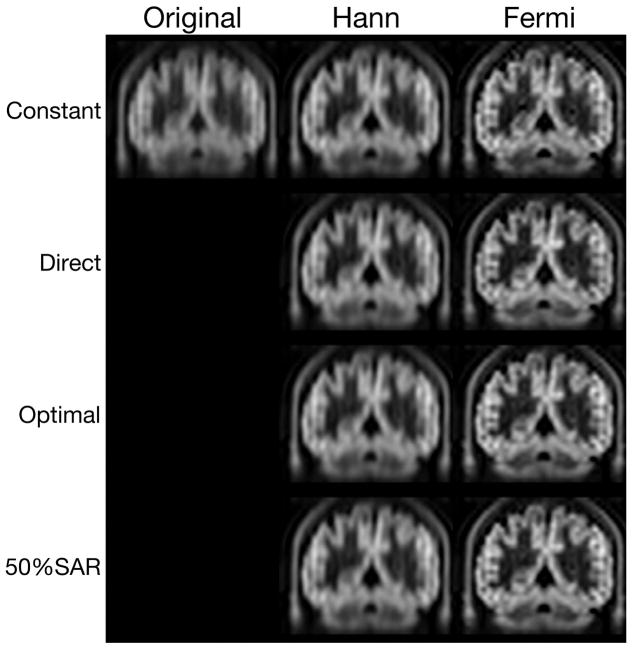
Figure 3 shows that the correction with k-space filtering improved the resolution of the ASL images. The proposed ‘Optimal’ with Hann and Fermi window correction showed improved resolution in the coronal plane, compared to the results of the ‘Constant’.

Figure 3.

ASL images acquired with the ‘Constant’ and the proposed ‘Optimal’ with Hann (Opt Hann) and Fermi (Opt Fermi) window corrections.

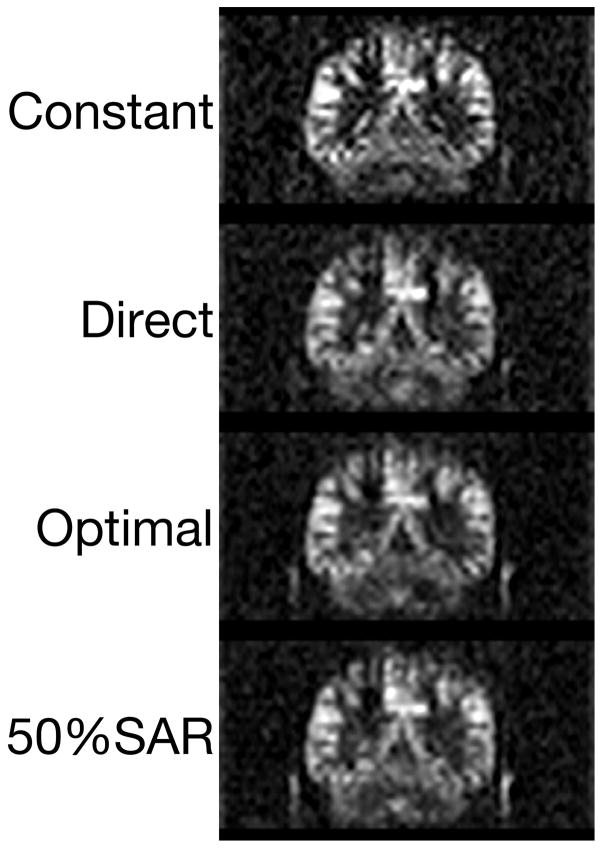
Figure 4 shows that the ‘Optimal’ method provided high SNR, when the images were corrected to Fermi window. The ‘Optimal’ and ‘50%SAR’ images showed visibly increased SNR compared to the ‘Constant’ and ‘Direct’. As expected, the sharpness of the corrected images was similar, due to the same targeted Fermi window in k-space.

Figure 4.

Comparison of Fermi window corrected images. A constant scale is used to enable visual assessment of SNR.

The correction of T2 blurring was expected to reduce the partial volume effect. As shown in Table 3, the mean perfusion of gray matter increased sequentially with improvement in resolution from the original ASL image, to the Hann window correction, and to the Fermi window corrections. The perfusion of white matter also decreased sequentially as partial volume of gray matter perfusion signal was reduced. This result indicates that the correction of T2 blurring provides better control of the PSF and reduces the overlap between gray and white matter signals.

Table 3.

Impact of the T2 blurring corrections on cerebral blood flow quantification.

	(ml/100g/min)	Gray Matter	White Matter
Original	Constant	66.5±10.1	33.6±6.6
Hann	Constant	69.9±10.7	30.7±6.6
	Direct	68.5±9.3	31.1±5.4
	Optimal	68.1±11.3	31.7±7.7
	50%SAR	68.6±12.5	32.5±8.1
Fermi	Constant	72.5±11.1	30.0±6.0
	Direct	70.2±9.8	29.2±4.8
	Optimal	70.1±13.4	29.6±8.3
	50%SAR	68.4±13.3	29.3±7.3

With the Hann and Fermi window corrections, the contrast between gray and white matter was also improved, in both the slice direction on the ASL, Figure 4, and T1 weighted images, Figure 5. Similar results can also be found in three-plane views of ASL images, Figure 6. The counterintuitive improvement in the axial plane likely is an indirect effect of reduced partial volume effect in the slice direction. Additional comparisons among different window corrections and flip angle designs were provided in the Supporting Figure S1.

Figure 5.

Reduced T2 blurring of 3D T1 weighted images acquired by the stack of spiral RARE in a representative subject.

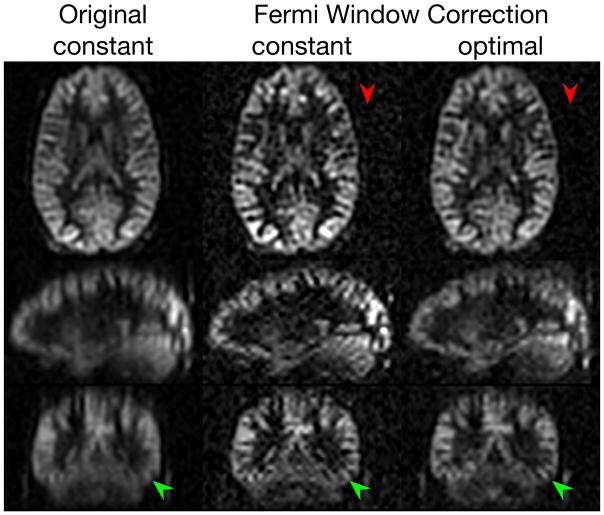
Figure 6.

Reduced T2 blurring and improved SNR of ASL images on one selected case. The three-plane views of the ASL were compared between the ‘constant’ and the ‘optimal’ with the Fermi window correction. The resolution improvement is highlighted by green arrows. The SNR improvement is apparent as reduced background noise as indicated by red arrows.

Table 4 shows the significantly improved SNR of the proposed method across subjects. The ‘Optimal’ and ‘50%SAR’ resulted in significant higher SNR than the ‘Direct’ for Hann window correction (p<0.05). With the Fermi window correction, the ‘Optimal’ showed 39.8% and 27.3% higher SNR (p<0.05) compared to ‘Constant’ and ‘Direct’, respectively. With reduced SAR, the ‘50%SAR’ maintained its good performance with 32.5% and 20.7% higher SNR (p<0.05) than ‘Constant’ and ‘Direct’. The magnitude of SNR improvement was consistent with the prediction of simulation. The contrast between gray and white matter and the sharpness in the slice direction also improved sequentially from Hann window to Fermi window.

Table 4.

The performance of the proposed method across seven subjects. The error bars are standard deviations.

		SNR	Blurring	Contrast
Original	Constant	19.9±3.5	16.0±0.9	1.7±0.1
Hann	Constant	17.4±3.1*	12.6±0.7	1.9±0.1
	Direct	14.2±2.3	12.4±0.7	1.8±0.1
	Optimal	18.1±3.6*	12.7±07	1.8±0.1
	50%SAR	17.7±3.9*	12.5±0.7	1.7±0.1
Fermi	Constant	7.5±1.3	8.7±0.5	2.1±0.1
	Direct	8.2±1.4	9.0±0.5	1.9±0.1
	Optimal	10.5±2.5*+	9.0±0.5	1.9±0.2
	50%SAR	9.9±2.7*+	8.9±0.6	1.9±0.2

^*indicates significantly higher SNR (p<0.05) compared with the ‘Direct’.

⁺indicates significantly higher SNR (p<0.05) compared with the corrected signal from the ‘Constant’.

Discussion

In this work, we proposed a systematic framework for variable flip angle design and demonstrated its advantages in a combined design of the flip angle and k-space filtering for control of T2 blurring in 3D ASL. This method outperformed the conventional methods by providing superior SNR. The performance was well maintained even when the SAR was constrained to 50% of the constant amplitude flip angle design. Relative to the direct design with only variable flip angle, the optimal designs are characterized by higher flip angles in the first few echoes. This likely improves the efficiency of the transition to the pseudosteady state (19). The flip angle trains also maintain higher flip angles at intermediate echo numbers. This appears more efficient than the rise of flip angle at the end of the echo train in the direct design with only variable flip angle.

The framework of variable flip angle design proposed in this work has several additional advantages. First, the SAR can be designed simultaneously and precisely with the variable flip angles. As demonstrated in the 50% SAR limitation design, the proposed method can include an arbitrary level of SAR requirement as a constraint in the design and achieve it precisely. It provides a general approach for SAR optimization in RARE applications. Second, the proposed framework also allows for constraints on both the maximum and minimum flip angle in the design. Maximum flip angle constraints can be useful for RF amplitude limited systems. Minimum flip angle constraints can help to control the sensitivity to motion and flow of low flip angle RARE designs (55). Third, in addition to PSF and SNR optimization, the proposed framework is capable of designing variable flip angles for a general cost function, with the potential for added terms to reduce the sensitivity to RF transmit inhomogeneity or to achieve a certain effective TE.

Though our optimized 3D ASL acquisition with variable flip angles was demonstrated to improve resolution in perfusion and anatomic images (Figures 4 and 5), the low flip angles used may suppress the signal from flowing blood in arteries (55). Such low flip angle signal attenuation would blur arterial signal. This would be a problem, for example, if a substantial fraction of the ASL signal is in arteries, as may occur at shorter post-labeling delays. Indeed, there is some indication of bright vascular signal in the Constant image of Figure 4 that is reduced in the other, low flip angle, images. Bright signal in arteries may be an artifact for some applications, but may also provide diagnostic information. Delayed signal in vessels in ischemic stroke may be an indicator of collateral flow (56) and bright signal can indicate shunted flow through Arteriovenous Malformations (AVM) (57) or Dural Arteriovenous Fistulas (58) selection of different minimum flip angle constraints in the optimizations for different applications may be appropriate.

Depending on the details of the imaging sequence employed for ASL, the number of echoes and time between echoes may differ from those we explored here. Generally, the total duration of the echo train is the primary driver of the flip angle modulation. Interpolation between optimized flip angles to create a larger number of echoes while preserving the duration of the echo train will produce a result very similar to a full optimization. We expect that echo trains very long compared to T2 will require lower flip angles and larger k-space filtering scaling factors for deblurring. Because deblurring has a larger impact on signal and noise for such long echo trains, they will benefit more from using an optimal correction. Our optimization strategy is general, however, and can be performed for any selected echo number and spacing.

The proposed method also has potential for correcting T2 blurring and optimizing the acquisition in general RARE applications, such as abdominal imaging, pediatric MR imaging and MR angiography. Future work should extend the method to enable flexible T2 weighting and optimize k-space ordering for such applications.

The proposed T2 blurring correction is anticipated to provide better performance in general RARE applications where T2 differences are present. ASL is a specific application where centric ordering is preferred to minimize T2 weighting. A generalization of our method would be required to design arbitrarily T2 weighted RARE sequences. Even in the ASL application, differences in T2 between gray matter, white matter, blood and potential lesions were not accounted for in our optimization. Still, the optimization appears to provide an excellent first order correction for blurring.

Although the proposed method demonstrated superior SNR, we should note a few limitations of the SNR definition used for optimization in this work. While our SNR definition was a reasonable initial approach, SNR using a better definition of the size, shape, and contrast of the feature being detected could produce different echo trains with potentially improved application, although the benefits of combined design of variable flip angles and k-space filtering will likely stay the same. A complement or alternative to specifying the target object would be to specify an optimal noise distribution. After correction with k-space filtering, the white Gaussian noise typical in MRI becomes spatial frequency varying, or colored, noise. In complex images with colored noise, the pixel SNR is known to be a poor measure of image quality (59) A number of studies have shown superior detection of natural image features when the spatial frequency distribution of noise rises with frequency(60,61). A weighting factor could be added to our definition of SNR to prioritize preferred spatial frequency distributions of noise.

Reduced flip angle echo trains can be vulnerable to errors in RF amplitude and our optimized echo trains were not unaffected. The echo amplitudes of the proposed optimized echo trains showed slightly more RF sensitivity than those of the constant amplitude method. In our measurements, the greatest RF amplitude variation was less than 15%, for which our simulations suggest about 10% deviation of signal in the proposed method, smaller than the direct decay correction with only variable flip angles. In our images, there was no sign of artifact from RF imperfections and we did not need to discard any echoes to achieve a steady signal.

Although the proposed methods were demonstrated on the Hann and Fermi window corrections, whether the Hann or Fermi window is preferable may depend on the application. The Hann window has a larger edge rise distance and a more visually blurred appearance but the Fermi window has higher power in side lobes far from its center. The Fermi window may be preferable for visual detection of boundaries while the Hann window may be preferred for some quantitative analyses.

Conclusion

This work demonstrates the SNR benefit of a combined optimization of variable flip angles and k-space filtering in the control of the T2 blurring in 3D ASL RARE acquisitions. The proposed framework of variable flip angle design can improve the quality of 3D ASL images and hold broader promise for the improvement of long echo train RARE images.

Supplementary Material

Supp info

Figure S1 Reduced T2 blurring of RARE with 3D stack-of-spiral on one additional case. Three-plane views of the ASL, CBF and T1 weighted images are compared across different methods. SNR improvement is apparent as reduced background noise as indicated by red arrows. Resolution improvements are highlighted by green arrows. The Grayscale for the CBF images is in units of ml/100g/min.