How Mechanical Forces Shape the Developing Eye

Abstract

In the vertebrate embryo, the eyes develop from optic vesicles that grow laterally outward from the brain tube and contact the overlying surface ectoderm. Within the region of contact, each optic vesicle and the surface ectoderm thicken to form placodes, which then invaginate to create the optic cup and lens pit, respectively. Eventually, the optic cup becomes the retina, while the lens pit closes to form the lens vesicle. Here, we review current hypotheses for the physical mechanisms that create these structures and present novel three-dimensional computer (finite-element) models to illustrate the plausibility and limitations of these hypotheses. Taken together, experimental and numerical results suggest that the driving forces for early eye morphogenesis are generated mainly by differential growth, actomyosin contraction, and regional apoptosis, with morphology mediated by physical constraints provided by adjacent tissues and extracellular matrix. While these studies offer new insight into the mechanics of eye development, future work is needed to better understand how these mechanisms are regulated to precisely control the shape of the eye.

1 Introduction

In the vertebrate embryo, eye development begins with a pair of optic vesicles (OVs) growing outward from the anterior end of the primitive brain tube.¹ As the OVs grow, they soon meet the surrounding surface ectoderm (SE) and are forced to bend. Next, within the region of contact, the OV and SE invaginate together to create the optic cup (OC, future retina) and lens vesicle (LV), respectively (Fig. 1). Whereas much is now known about the molecular signals involved in these processes, the physical mechanisms that construct the eyes have remained poorly understood.

Figure 1.

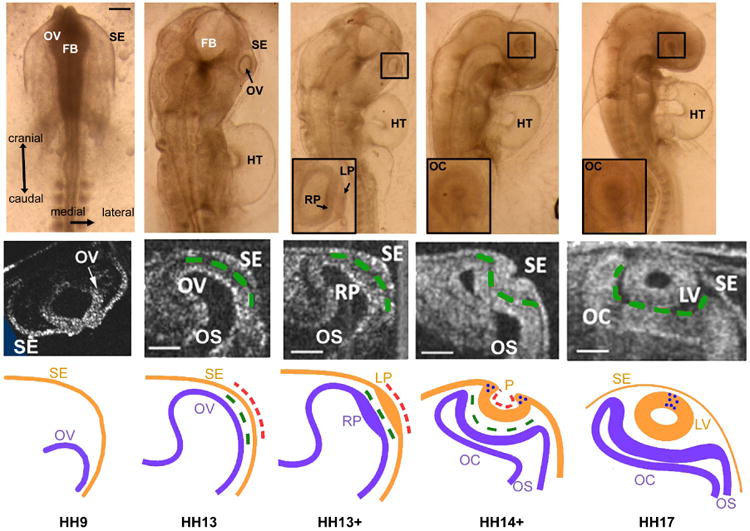
Morphology of eye formation in chick embryo (stages HH9 to HH17). Top row: Brightfield images of embryo at stages indicted along bottom. Inserts show expanded view of eye within black boxes. Scale bar = 150 μm. Middle row: Representative OCT images of eye cross sections for each stage (cranial view). Scale bars = 100 μm. Bottom row: Schematic diagrams of eye cross sections for each stage. FB = forebrain; HT = heart tube; LP = lens placode; LV = lens vesicle; P = lens pit; OV = optic vesicle; OC = optic cup; OS = optic stalk; RP = retinal placode; SE = surface ectoderm; dashed green lines = extracellular matrix; dashed red lines = actomyosin contraction; blue dots = apoptosis. Except for HH9 OCT image, middle and bottom rows are reprinted from Oltean & Taber (2017) with modifications.

This paper focuses on the mechanics of early eye development. The current state of knowledge is reviewed, and the physical plausibility and limitations of proposed morphogenetic mechanisms are examined using computational models. These models, which are based on the fundamental laws of solid mechanics, extend to three dimensions our recent two-dimensional models for OV, OC, and LV morphogenesis (Hosseini et al. 2014, Oltean et al. 2016, Oltean & Taber 2017). The results illustrate how relatively simple processes can produce the complex morphological changes observed in the embryonic eyes.

Most of the studies discussed here involve experiments with mice or birds, which share many common characteristics during eye development. Although fish also have furnished much useful information, some results suggest some distinct differences in the ways their eyes form. For example, cell migration seems to play a more significant role in fish than in mice and birds. For a review of eye development in fish, see Sinn & Wittbrodt (2013).

2 Methods

2.1 Experimental Methods

This paper focuses on eye development in the chick embryo during the second and third day of a 21-day incubation period. Developmental stages in the chick are based on the system of Hamburger & Hamilton (1951), with HHx denoting Hamburger-Hamilton stage x. For convenience, we define three morphogenetic processes from HH9 to HH17 (approximately 30–58 h): OV formation (HH9–13), OC formation (HH13–17) and LV formation (HH12–17) (see Table 2). Although there is some overlap and interdependence between these processes, here they are considered separately.

Table 2. Stages, approximate incubation times, and model times for chick embryo.

Stage	Inc Time (h)	Model Time (h)
HH9	30	0
HH10	33	3
HH11	40	10
HH12	47	17
HH13	50	20
HH14	51.5	21.5
HH15	53	23
HH16	55	25
HH17	58	28

Fertilized white Leghorn chicken eggs were incubated in a humidified, forced draft incubator at 38° C. Whole embryos were removed from the eggs and cultured using a filter paper method (Voronov & Taber 2002). Brightfield images were acquired using a Leica MZ8 microscope, and cross-sectional images were obtained using optical coherence tomography (OCT; Thorlabs, Newton, NJ).

2.2 Computational Methods

Computational models for OV, OC, and LV formation were developed using the commercial finite-element software ABAQUS (version 6.10, SIMULIA, Providence, RI). Constitutive relations (material properties) and morphogenetic processes were defined via the ABAQUS user subroutine UMAT, as described in Young et al. (2010).

2.2.1 Overview of Models

Model geometry is based roughly on images of the developing eye in chick embryos (Fig. 1). In the initial configuration (HH9), the OV is represented by a hemispherical shell (inner radius = 40 μm; outer radius = 55 μm), while the SE is modeled as a cylindrical shell with a hemispherical cap (inner radii = 205 μm; outer radii = 215 μm) (Fig. 2). The edges of both structures are fixed. Because of symmetry, the model includes only one OV and half the SE, with appropriate symmetry conditions enforced. Finally, to account for the influence of the brain tube, which is not included in the model, the OV is located slightly off the embryonic midline and toward the ventral side of the SE (Fig. 2).

Figure 2.

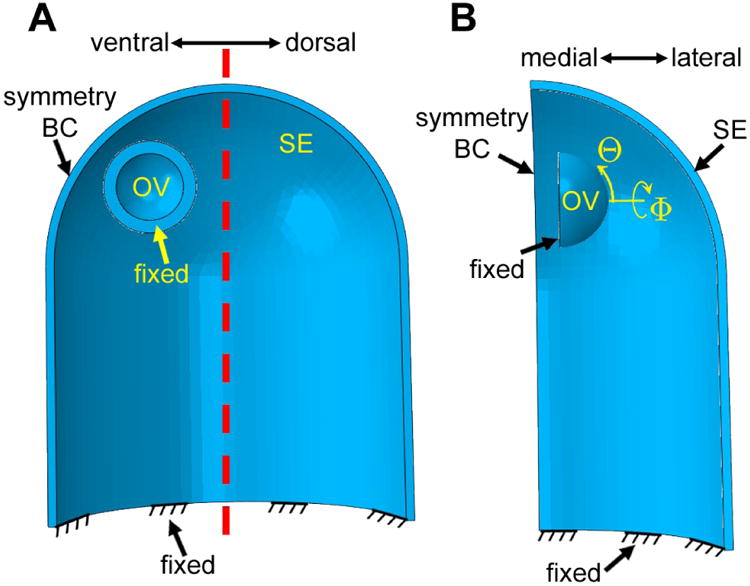
Computational model for optic vesicle (OV), optic cup (OC), and lens development (initial configuration, HH9). (A) Lateral view of cross section. The OV is a hemispherical shell offset ventrally relative to the surface ectoderm (SE), which is represented by a thin cylindrical shell with a hemispherical cap. Both structures are fixed at their bases. OS = optic stalk; dashed red line = axis of symmetry for SE. (B) Ventral view of section cut through symmetry axis. Spherical coordinates for OV are indicated. Because of bilateral symmetry, only one OV is modeled.

When we tried to integrate OV, OC, and LV formation into a single model, numerical convergence issues limited the simulation to only as far as the early stages of invagination (see Fig. S1, Movie 2). Moreover, in the embryo, the lens pit separates from the OV as it invaginates (Hendrix & Zwaan 1974). Thus, LV formation is simulated using a model that includes only the SE. On the other hand, we were able to use a single model to simulate both OV and OC formation, including the SE but without lens invagination.

The models contain no external loading. All forces are generated internally by growth and contraction, as described below. Tetrahedral elements (C3D4) are used for both the OV and SE, with the OV having a finer mesh. The full model is discretized into 227,000 elements with 57,000 nodes. Testing with finer meshes confirmed that the chosen mesh size is accurate enough for the present purposes.

2.2.2 Mechanical Theory for Morphogenesis

The simulation is based on the theory of Rodriguez et al. (1994) for large deformation and growth of soft tissue. Active contraction is simulated as negative growth along specified directions (Taber 2009). To a first approximation, the embryonic tissues are treated as pseudoelastic with viscous effects neglected (Fung 1993).

Briefly, the total deformation gradient tensor F, which maps material points from the initial configuration to the deformed configuration at a later time, is decomposed as

$$\mathbf{F}={\mathbf{F}}^{\ast }\cdot \mathbf{G},$$ (1)

where G and F* are the growth tensor and elastic deformation gradient tensor, respectively. As the tissue grows, G changes the zero-stress configuration for each material particle, and F* generates stress by enforcing geometric compatibility between particles.

In the initial configuration, separate spherical coordinate systems (R, Θ, Φ) are defined for the OV and SE (Figs. 2B and 7B). Relative to these coordinates, the growth tensor is taken in the orthotropic form

Figure 7.

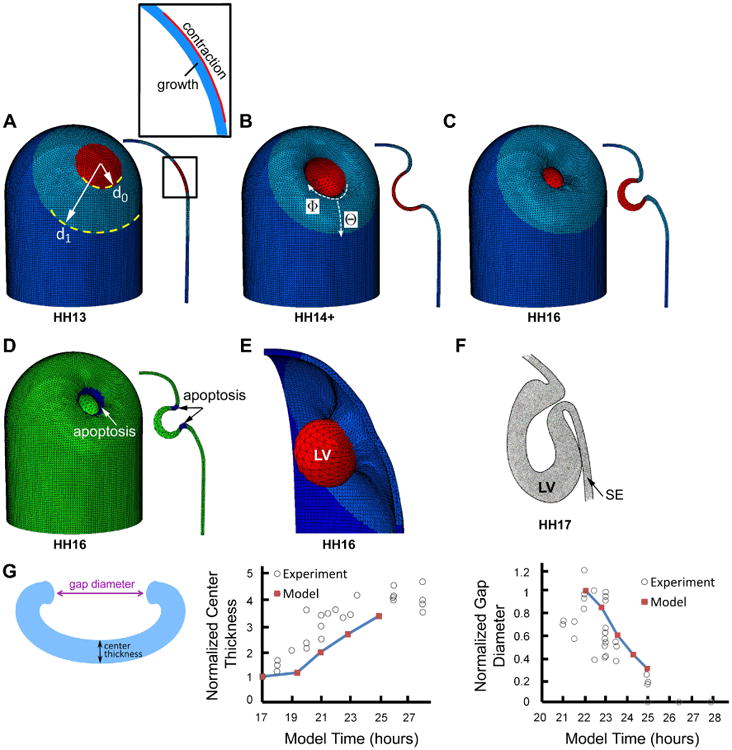
Computational model for lens vesicle (LV) formation. (A) Initial configuration of surface ectoderm (SE). Red, light blue, and dark blue colors, respectively, indicate invagination region, relatively soft surrounding annular region, and outer region with normal stiffness. Inset shows details of invaginating region (defined as circular region in contact with optic vesicle, see Fig. 6A), which consists of an inner growing layer (blue) and an outer contracting layer (red). (B, C) Model during (HH14+) and at end (HH16) of LV formation. (D) Model at HH16 with dark blue indicating region of apoptosis. Cross section is shown at right. (E) 3-D representation of lens vesicle in model at HH16. (F) Schematic diagram of forming chick lens at HH17. Reprinted with permission from Schook (1980a). (G) Comparison of numerical and experimental results for forming LV. Schematic shows measured quantities. Wall thickness at center of invaginating region (normalized by value at HH12) and average diameter of lens pit opening (normalized by value at HH14) are plotted versus time. Experimental data are from Oltean & Taber (2017).

$$\mathbf{G}=G_R{\mathrm{e}}_R{\mathrm{e}}_R+G_{\mathrm{\Theta }}{\mathrm{e}}_{\mathrm{\Theta }}{\mathrm{e}}_{\mathrm{\Theta }}+G_{\mathrm{\Phi }}{\mathrm{e}}_{\mathrm{\Phi }}{\mathrm{e}}_{\mathrm{\Phi }},$$ (2)

where the e_I are unit base vectors. Here, G_I = 1 for no growth, G_I > 1 for positive growth, and 0 < G_I < 1 for negative growth (apoptosis) or active contraction. Since contracting tissues stiffen (Zhou et al. 2009, Filas et al. 2012), contraction also is accompanied by a specified increase in material modulus.

Stress depends on the elastic part of the deformation. With the tissues assumed to be slightly compressible, the constitutive relation has the form (Taber 2004)

$$\mathbf{\sigma }=\frac{1}{J^{\ast }}{\mathbf{F}}^{\ast }\cdot \frac{\partial W}{\partial {\mathbf{E}}^{\ast }}\cdot {\mathbf{F}}^{\ast T},$$ (3)

which determines the Cauchy stress tensor σ from the strain-energy density function W(E*). In this equation, J* = det F* is the elastic volume ratio and E* = (F*^T · F* – I)/2 is the Lagrangian elastic strain tensor, with I being the identity tensor and T indicating the transpose. Based on data for the embryonic chick brain (Xu et al. 2010), the strain-energy density function is taken in the form

$$W=\frac{\mu }{2}({\overline{I}}_1-3)+\frac{1}{D}[\frac{1}{2}(J^{\ast 2}-1)-ln{J}^{\ast }],$$ (4)

where μ = 220 Pa is the shear modulus for the cells of the OV and SE, D = 0.001 Pa⁻¹ represents the volumetric compliance, and Ī₁ = J*^−2/3tr (I+2E*) is a modified strain invariant.

Details of the models and simulations for each process are described in the following sections. Specified distributions of growth, contraction, stiffness, etc., are based on previous 2-D models developed in our lab (Hosseini et al. 2014, Oltean et al. 2016, Oltean & Taber 2017). In some cases, however, aspects of the models have been modified somewhat to obtain better agreement with experimental data. Throughout the remainder of the paper, all times t are model times expressed relative to stage HH9 (see Table 2).

3 Optic Vesicle Formation

The OVs are spherical protrusions that evaginate laterally from the primitive forebrain (Fig. 1, HH9). Each OV is attached to the forebrain by the optic stalk (OS), an open tube that eventually becomes the optic nerve (Fig. 1, HH13, middle row). The OVs soon become pear-shaped, contact the SE, and bend in the dorsocaudal direction, thus completing the first phase of eye development (Fig. 1, HH13) (Schook 1980b).

3.1 Morphogenetic Mechanisms

Morphogenesis of the OVs has received relatively little attention from investigators. Studies have shown that OV evagination is caused by growth, mainly through cell proliferation in chickens and influx of cells from the brain tube in fish (Hilfer et al. 1981, Martinez-Morales & Wittbrodt 2009, Kwan et al. 2012, Rembold et al. 2006). In chick embryos, Hilfer et al. (1981) reported regional variations in OV growth, and we have found that contact with the SE has a major effect on OV shape (Hosseini et al. 2014). Taken together, these results suggest that the shape of the OV is determined by a combination of differential growth and constraining forces exerted by the SE.

Previously, we used 2-D models for OV cross sections to show that these mechanisms can produce realistic morphology (Hosseini et al. 2014). However, mechanisms that seem plausible in two dimensions do not always hold up in three dimensions. For example, as discussed later in section 5.1, hoop stress makes closing a circular hole in a spherical shell considerably more difficult than closing an opening in a cylindrical model for a cross section of the sphere. Thus, understanding the mechanics of closing the relatively spherical lens vesicle requires a 3-D model (Oltean & Taber 2017). Here, we present a 3-D model for OV morphogenesis.

3.2 3-D Model for OV Formation

The OV is represented by a hemispherical shell in the initial configuration (HH 9). In the model, we specify patterns of growth that are consistent with available geometric measurements and yield results that capture the most essential aspects of global morphology. Since the OV remains relatively axisymmetric until it encounters the SE, the initial growth rates are taken independent of Φ. In addition, for simplicity, the spatial patterns of growth are the same in the circumferential (Φ) and meridional (Θ) directions. However, since the OV takes a lightbulb-like shape by expanding more circumferentially than meridionally toward its distal tip, the growth rates increase toward the tip (Fig. 3A). Throughout the analysis, we set Ġ = 0, giving no change in wall thickness due to growth.

Figure 3.

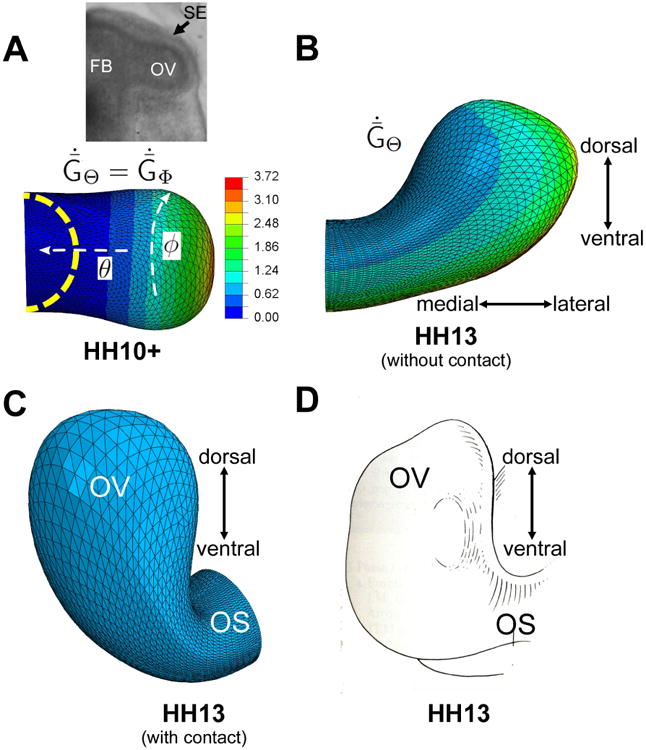
Computational model for optic vesicle (OV) formation. (A) Growth pattern prior to contact with SE at stage HH10⁺ (dorsal view). Dashed yellow curve indicates initial shape at HH9. Colors represent nondimensional growth rate ( ${\dot{\overline{G}}}_{\mathrm{\Theta }}={\dot{G}}_{\mathrm{\Theta }}/a_{1\mathrm{\Theta }}$, ${\dot{\overline{G}}}_{\mathrm{\Theta }}={\dot{G}}_{\mathrm{\Theta }}/a_{1\mathrm{\Theta }}$; see Eq. (5) in Appendix). Inset shows brightfield image of OV in HH10⁺ embryo. (B) Growth pattern fromHH10⁺ to HH13 ( ${\dot{\overline{G}}}_{\mathrm{\Phi }}={\dot{G}}_{\mathrm{\Phi }}/a_{2\mathrm{\Phi }}$; see Eq. (6) in Appendix). Model is shown at HH13 with SE omitted to show unconstrained bending of OV. (C) Reoriented cranial view of model at HH13 with SE included (but not shown). (D) Schematic diagram of OV at same stage (reprinted with permission from Schook (1980b). FB = forebrain; OV = optic vesicle; OS = optic stalk; SE= surface ectoderm. 24

After the OV encounters the SE, frictionless contact is enforced and the OV bends in both the caudal and dorsal directions. Most of the caudal bending is caused by constraining effects of the SE on deformation, but a considerable amount of dorsal bending is intrinsic to the OV (Hosseini et al. 2014). To capture the inherent bending, the circumferential growth rate (Ġ_Φ) remains axisymmetric after contact, but the meridional growth rate (Ġ_Θ) now depends also on Φ, with the highest rate occurring along the ventral side. In addition, experiments suggest that the SE is under tension caused, in part, by actomyosin contraction (Hosseini et al. 2014); thus, isotropic contraction (G_Θ = G_Φ < 1) is specified in the plane of the SE. This effectively increases SE stiffness and further enhances the amount of bending (Hosseini et al. 2014). Parameter values and mathematical details for the growth patterns are provided in the Appendix.

When the SE is removed from the model, the specified pattern of growth causes the OV to bend toward its dorsal side (Fig. 3B). If the SE is included, the contact force causes considerably more bending including a caudal component (Fig. 3C). The shape at stage HH13 agrees reasonably well with the actual shape of the OV (Fig. 3D).

To test the model, we use published experimental measurements of OV bending angle at stage HH13 with and without the presence of the SE (Hosseini et al. 2014). After dissection, the OV immediately loses much of its bending in both ventral and cranial views (Fig. 4). The predicted bending angles before and immediately following SE dissection agree relatively well with the data (Fig. 4C).

Figure 4.

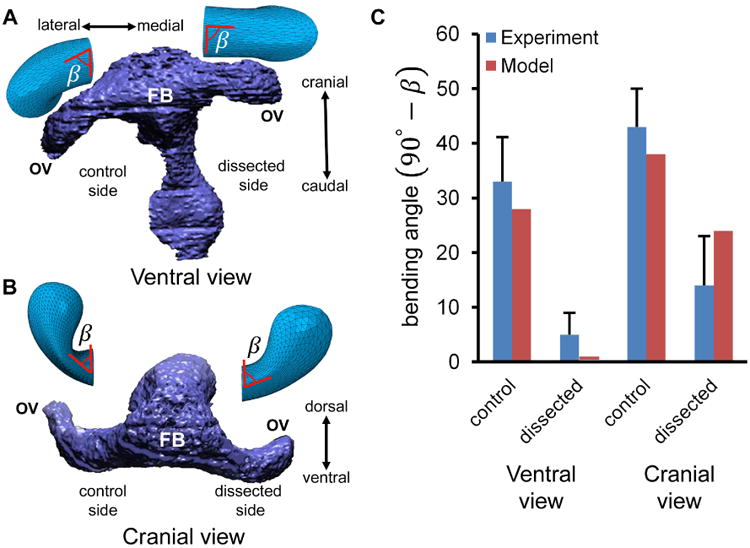
Comparison of numerical and experimental results following removal of surface ectoderm (SE) at HH13. (A) 3-D reconstruction of embryo (ventral view) with SE dissected from one optic vesicle (OV). Model results are shown above both OVs with angle β indicated. (B) Same embryo and model (cranial view). (C) Plots of control and dissected bending angle (90° – β; mean ± s.d.). Embryo reconstructions in A and B are reprinted with permission from Hosseini et al. (2014), which also is the source of the experimental data. FB = forebrain

4 Optic Cup Formation

As primary OV morphogenesis completes at about stage HH13, the OV and SE secrete extracellular matrix (ECM) that binds these layers together within their mutual region of contact (Fig. 1, HH13). By HH13⁺, the OV and SE thicken in this region to create the retinal placode and lens placode, respectively (Fig. 1, HH13⁺). Next, these placodes invaginate together to form the OC and lens pit (Fig. 1, HH14+). After invagination is complete, the OC resembles a bilayered cup with inner and outer layers becoming the prospective neural retina and pigmented retinal epithelium, respectively. During this process, the optic fissure (or choroid fissure) forms as a groove on the ventral side of the OC and extending into the optic stalk (Schook 1980b) (see Fig. 6C). The optic fissure, which eventually closes, provides a path for the formation of retinal blood vessels and axons.

Figure 6.

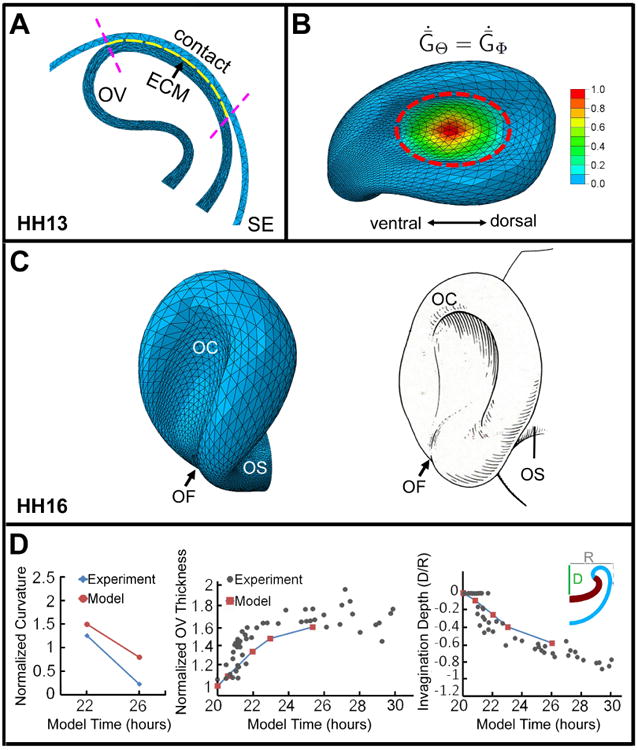
Computational model for optic cup (OC) formation. (A) Cross section of model at stage HH13. Region of contact between optic vesicle (OV) and surface ectoderm (SE) (between purple dashed lines) defines location of ECM layer (yellow). (B) Model at HH16 showing growth pattern in OV during invagination phase. Colors represent nondimensional growth rate ( ${\dot{\overline{G}}}_{\mathrm{\Theta }}={\dot{G}}_{\mathrm{\Theta }}/(b_1+b_2)$, ${\dot{\overline{G}}}_{\mathrm{\Phi }}={\dot{G}}_{\mathrm{\Phi }}/(b_1+b_2)$; see Eq. (7) in Appendix). (C) Comparison of model (left) and schematic of chick OV (right) at HH16. OS = optic stalk; OF = optic fissure. Schematic reprinted with permission from Schook (1980b). (D) Comparison of numerical and experimental results for OV geometry during invagination. Curvature, wall thickness, and invagination depth at the center of the forming OC are plotted versus time (normalized by their values at HH13). Experimental data are from Oltean et al. (2016)

4.1 Morphogenetic Mechanisms

Prior work implicates the ECM as a major player in OC morphogenesis. In chick embryos, Zwaan & Hendrix (1973) observed that the contact area between the OV and SE remains essentially constant during placode formation, although the cells continue to proliferate. These authors proposed that the matrix deposited between these layers inhibits lateral expansion of the SE, causing it to thicken into a placode. For this mechanism to be effective, the matrix must be considerably stiffer than the cells, as confirmed by microindentation tests (Oltean et al. 2016). Recently, Huang et al. (2011) found that this mechanism likely causes the formation of both the lens and retinal placodes in mice.

The ECM also apparently plays a major role in the invagination that creates the OC. In fish, studies suggest that invagination is driven by a combination of actomyosin-mediated contraction at the basal (outer) surface of the OV and growth caused by migration of cells from the brain tube into the OC (Martinez-Morales & Wittbrodt 2009, Heermann et al. 2015, Nicolas-Perez et al. 2016). The matrix likely helps regulate the movements of individual cells, while cell-matrix binding may strengthen contractile force and its supracellular transmission (Nicolas-Perez et al. 2016).

Basal constriction also is involved in shaping the brain tube in zebrafish (Gutzman et al. 2008). However, in the embryonic chick and mouse OV, actin is concentrated primarily at the apical (inner) surface (Martinez-Morales & Wittbrodt 2009, Borges et al. 2011), which is the wrong side to drive invagination. This observation suggests that contraction does not cause OV invagination in these embryos.

One possibility is that the lens placode pushes the OV inward as it invaginates. This idea is contradicted, however, by experiments of Hyer et al. (2003), who removed the SE at various stages of chick development. When the SE was ablated prior to lens placode formation at HH!3, OV invagination did not occur, but if removed after placode formation (after HH13⁺), invagination proceeded relatively normally. These results suggest two important conclusions. First, the forming LV is not necessary for OV invagination. Second, the presence of prospective lens tissue is needed until about HH13. To explain these results, Hyer et al. (2003) speculated that the SE is needed before HH13 to send a biochemical signal to the OV that induces invagination.

Recently, we suggested an alternative possibility which is a natural extension of the matrix-constrained growth mechanism that produces the retinal placode (Oltean et al. 2016). We postulated that continued growth forces the placode to bend with the matrix located at the inner curvature, similar to the behavior of a so-called bimetallic strip, which is a beam composed of two layers of different metals. When heated, the metals expand different amounts, forcing the beam to bend with the less expanded layer along the inner curvature. This idea is consistent with an early study by Yang & Hilfer (1982), who found that disrupting the matrix blocks OV invagination in the chick.

To explain the experiments of Hyer et al. (2003), we note that the ECM binding the OV and SE is secreted by both layers, but mostly by the SE. Moreover, experiments have shown that part of the matrix remains attached to the OV after the SE is dissected (Oltean et al. 2016). Accordingly, if the SE is removed before HH13, the amount of matrix between the layers may not yet be enough for invagination to occur. Conversely, if the SE removed after placode formation, enough matrix is present to cause invagination.

Previous experimental and numerical results from our lab support this hypothesis (Oltean et al. 2016). In one set of experiments, for example, we used collagenase to locally degrade the ECM at various stages of invagination after the SE was removed. Exposure during early stages caused most OVs to pop back out within several minutes, i.e., the concave curvature became convex. However, the fraction that popped out decreased with increasing age, with all OVs remaining invaginated following treatment after HH14. These results suggest that the matrix is necessary for OV invagination until the latest stages of OC formation.

Recently, Eiraku et al. (2011) found that mouse embryonic stem cells have the remarkable ability to self-organize into a vesicle that invaginates to create a structure resembling the OC. Using these model tissues to study the mechanics of OC morphogenesis, they proposed a process consisting of four phases (Fig. 5): (1) uniform contraction of the apical surface produces a spherical vesicle; (2) regional relaxation creates a placode; (3) apical constriction at the placode border causes local cell wedging and slight invagination; and (4) growth of the placode region deepens the invagination. They also constructed an axisymmetric computer model to demonstrate the feasibility of their hypothesis (Eiraku et al. 2011, 2012).

Figure 5.

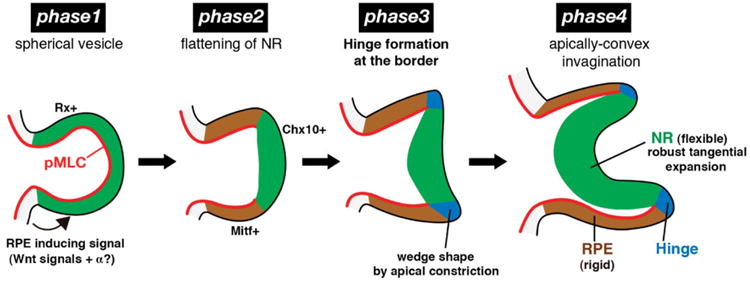
Alternative hypothesis for optic cup formation. Phase 1: Apical contraction (red) produces spherical optic vesicle. pMLC = phosphorylated myosin light chain. Phase 2: Relaxation in central region produces retinal placode (green). Phase 3: Apical contraction at placode border causes sharp bending (blue) and slight invagination. Phase 4: Growth of placode region deepens invagination. Republished with permission from Eiraku et al. (2012).

Notably, this model does not require the presence of an ECM layer. Therefore, the model cannot directly explain the results from ECM degradation experiments, and Sasai et al. (2012) recognized the possibility that OV invagination may occur by a different mechanism in vitro. On the other hand, it may be that these investigators have uncovered a redundant mechanism that has evolved to help minimize developmental defects. Additional studies are needed to further evaluate these possibilities.

Less is known about how the optic fissure forms, although studies have implicated increased cell proliferation and apoptosis (Calvente et al. 1988, Cuadros & Rios 1988, Ozeki et al. 2000, Francisco-Morcillo et al. 2014). As shown below, passive mechanical deformation also may play a role.

4.2 3-D Model for OC Formation

The simulation of OC formation begins at stage HH13 (t = 20 h), where the OV formation model ends, and is based on the axisymmetric model of Oltean et al. (2016). At HH13, two new facets enter the model. First, an ECM layer is included by changing the properties in the outer 10% of the OV wall where it contacts the SE (Fig. 6A). In this layer, growth is turned off and the modulus is gradually increased by 50 times, in agreement with previous measurements of material properties (Oltean et al. 2016).

Second, the growth pattern outside the ECM layer is altered to better reflect the actual growth in the OV. Consistent with the model of Oltean et al. (2016), tangential growth remains isotropic (Ġ_Θ = Ġ_Φ), and, in the region of contact, the growth rates increase and include a gradient with the highest rate occurring at the center (Fig. 6B). Due to convergence issues, the ECM thickness is half that in the model of Oltean et al. (2016), and, owing to the resulting reduced extensional stiffness of this layer, the model does not capture the extent of wall thickening that occurs in the retinal placode (Hilfer et al. 1981, Schook 1980a,b, Oltean et al. 2016). Thus, uniform radial growth (Ġ_R) is also specified in the model. Please see Appendix for additional details.

When these patterns of growth are turned on, the constraint provided by the stiffening ECM causes the OV to invaginate (Movie 1). At stage HH16, the shape of the OC agrees reasonably well with the shape of the OC in the chick embryo (Fig. 6C). Interestingly, a groove resembling the optic fissure also forms along the ventral side of the OC and eventually propagates into the optic stalk, in agreement with observations Schook (1980b). This feature is a consequence of an asymmetric structure, the bent OV, undergoing invagination. Since the specified growth is relatively symmetric in the invaginating region, there is no need for morphogens, cell proliferation, or cell death specifically designed to create the fissure.

To test the model further, we compared numerical results and experimental data of Oltean et al. (2016) for various geometric quantities as functions of time (Fig. 6D). At the center of the OC, model-predicted curvature, wall thickness, and invagination depth show reasonably good agreement with the data. Consistent with the measurement procedure of Oltean et al. (2016), curvature in the model was estimated by fitting a circle through five markers near the center of the OV along the basal surface. Numerical problems prevented the simulation from progressing to the end of the experimental time period.

5 Lens Vesicle Formation

After the lens placode forms, it invaginates concurrently with the retinal placode to create the lens pit, which later closes to form the fluid-filled LV (Fig. 1, HH14⁺, HH17). During this process, the forming LV separates from the OC and eventually also from the surrounding SE (Fig. 1, HH17). The cells in the LV later elongate and fill the lumen to create the primitive lens (Cvekl & Ashery-Padan 2014). Here, we consider how the LV is created.

5.1 Morphogenetic Mechanisms

Like the OV, actin is concentrated mainly on the apical side of the SE. Unlike the OV, however, the actin is on the appropriate side to drive invagination, i.e., the inner curvature of the lens pit. Indeed, studies have shown that apical constriction generated by actomyosin contraction causes the lens placode to invaginate (Medina-Martinez & Jamrich 2007, Plageman et al. 2010, Borges et al. 2011). For example, exposure of chick embryos to the myosin II inhibitor blebbistatin or mouse embryos to the rho-kinase inhibitor Y27632 prevents lens pit formation (Borges et al. 2011, Plageman et al. 2011).

On the other hand, the mechanism that closes the lens pit into a complete vesicle remains poorly understood. This problem is similar to closing a circular wound in an epithelium. In the embryo, an actomyosin ring forms around the wound margin and contracts to close the wound (Redd et al. 2004). Actin staining, however, reveals no such ring, and modeling suggests that apical contraction alone cannot generate enough force to overcome large circumferential compressive stresses that develop as the perimeter of the lens pit decreases toward zero (Oltean & Taber 2017).

Recently, our lab investigated the possibility that apoptosis, or programmed cell death, generates the additional force needed to complete LV closure (Oltean & Taber 2017). We speculated that apoptosis removes cells near the opening, thus decreasing its circumference. It has been known for decades that a ring of dying cells appears around the lens pit as it closes, and researchers have speculated that apoptosis helps trigger invagination, shape the LV, or detach the LV from the surrounding SE (Garcia-Porrero et al. 1979, Francisco-Morcillo et al. 2014). Some have suggested that this process may be involved in closing the LV (Bozanic et al. 2003, Yan et al. 2006), but how this may occur had not yet been studied.

The idea that apoptosis plays a role in LV closure is supported by experiments with chick embryos in which exposure to caspase (apoptosis) inhibitors prevented closure (Oltean & Taber 2017). Moreover, results from a finite-element model indicate that a ring of apoptosis could plausibly close the LV (Oltean & Taber 2017).

5.2 3-D Model for LV Formation

The present model extends the axisymmetric lens model of Oltean & Taber (2017) to 3-D. Previously, Hendrix et al. (1993) published a geometric model for the forming LV based on constrained growth and cell wedging, but their model does not include mechanical forces.

As discussed above, the present model for LV morphogenesis includes only the SE. The lens forming region is taken as a circular area of radius d₀ within the region of contact with the OV (Fig. 7A). Moreover, the model does not include detachment of the forming LV from the surrounding SE, which can impede closure. To roughly simulate detachment, however, a relatively soft ring of SE is defined around the invaginating region (Fig. 7A). Within this region, the modulus changes from 100 times smaller than the normal SE modulus at the edge of the invagination to 10 times smaller near its outer boundary. The added compliance allows the edges of the lens pit to move closer together during closure. To further relieve the stresses, we simulated viscoelastic stress relaxation by including a relatively small amount of negative circumferential growth and positive radial growth in this region.

The lens forming region includes a contractile layer comprising the outer 10% of the wall (Fig. 7A). The rest of the wall in this region grows isotropically in the local Θ and Φ directions at a rate that increases with distance from the center of the lens (Fig. 7B). Radially, it grows uniformly at a constant rate. As shown in the model of Oltean & Taber (2017), this pattern of growth yields a shape for the LV consistent with observations in the chick embryo. See Appendix for more details.

The simulation begins at HH12 (t = 17 h). As the opening in the lens pit begins to close at t = 22 h and its boundary moves radially inward, circumferential compressive stress builds near the boundary (Oltean & Taber 2017). These stresses resist closure, causing it to slow and eventually stop (Fig. 7C). Therefore, to facilitate closure and consistent with the model of Oltean & Taber (2017), removal of cells through apoptosis is simulated within a narrow ring near the edge by specifying Ġ_Φ < 0 and Ġ_Θ = 0 for t ≥ 25 h. This anisotropic pattern of cell death generates circumferential shortening with accompanying tension that further closes the LV (Fig. 7D). Convergence issues prevented the model from progressing to full closure.

Although the predicted shape of the LV is reasonably accurate (Fig. 7D,E), the model does not capture the extent of the asymmetry that occurs during invagination in the chick embryo (Fig. 7F). This discrepancy could indicate that apical contraction is not symmetric in the lens placode, or that stiffness or stress relaxation in the surrounding SE is asymmetric (see Fig. S2). Further investigation of this aspect is warranted. Otherwise, the numerical results agree relatively well with experimental measurements of temporal changes in wall thickness and diameter of the lens pit opening (Fig. 7G).

6 Conclusions

Perhaps more than any other organ, normal functioning of the eye depends intimately on its precise shape. Even relatively minor abnormalities can have major effects on vision. Developmental malformations also can lead to ocular defects including coloboma (missing part of eye, possibly caused by failure of the optic fissure to close), microphthalmia (abnormally small eye), congenital cataracts (opaque lens), microphakia (small lens), ectopia lentis (abnormal lens position), aniridia (absence of the iris), and aphakia (absence of the lens) (Mic et al. 2004, Khong 2015). Fully understanding the causes of these defects requires knowing how the eye is constructed.

Determining morphogenetic processes is challenging for many reasons. One of the more difficult complications is that multiple redundant mechanisms may have evolved to minimize developmental defects. Thus, if one process is downregulated, another may be upregulated with little or no apparent perturbation in morphology. During OC formation, for example, the invagination mechanism proposed by Eiraku et al. (2011, 2012) may be just as valid as the matrix constraint hypothesis. When one fails, the other takes over.

The results presented in this paper favor the mechanisms summarized in Fig 1 (third row). First, relatively stiff ECM locally constrains growth of the OV and SE to create the retinal and lens placodes, respectively. Next, continued constraint on growth causes the retinal placode to invaginate and form the OC, while apical contraction causes the lens plancode to invaginate and form the lens pit. Finally, apoptosis encircling the lens pit opening closes this structure to create the LV.

Other mechanisms may affect the ultimate size and shape of the eye. For example, growth of the eye during development is retarded by reduced intraocular fluid pressure (Coulombre 1956, Coulombre & Coulombre 1958). As in the brain tube (Garcia et al. 2016), pressure-induced wall stress may affect regional growth. In addition, gradients in growth, contraction, and stiffness may play a role in refining the shape of the eye (Oltean et al. 2016, Oltean & Taber 2017). Measuring spatiotemporal variations in morphogenetic processes such as proliferation and apoptosis, as well as mechanical properties, should be a focus of future research.

Morphogenesis is ultimately a tissue-level phenomenon driven by cell-level forces that are regulated by molecular signals. Fully understanding development requires integrating biochemical and biomechanical experiments and models across scales. Thus, much work remains to be done in determining how the eye is constructed.

Supplementary Material

1

Movie 1. Model for optic vesicle and optic cup formation.

2

Movie 2. Full model including optic vesicle formation and first phase of retinal and lens placode invagination.

3

Figure S1: Comprehensive model including optic vesicle (OV), optic cup (OC), and lens vesicle (LV) formation. Cross section is shown at the last time for which the solution converged (t = 21.6 h). OS = optic stalk

Figure S2: Effects of asymmetric growth in surrounding surface ectoderm (SE) on shape of invaginating lens pit (LP). Schematic of chick LP (left) and model results (right) are shown for stage HH14. Stress relaxation in SE (simulated by growth) occurs at a faster rate below than above the lens pit. Schematic is reprinted with permission from Schook (1980a).

Table 1. List of Abbreviations.

ECM	extracellular matrix
HH	Hamburger-Hamilton stage
LV	lens vesicle
OC	optic cup
OCT	optical coherence tomography
OV	optic vesicle
SE	surface ectoderm

Appendix.

This appendix lists the equations used to prescribe regional growth and contraction in the models. These patterns were modified slightly from those used in previous models (Hosseini et al. 2014, Oltean et al. 2016, Oltean & Taber 2017) to obtain improved agreement between numerical results and global morphology, as well as measured changes in local geometry in the chick embryo. The rate equations given below were integrated with G_R = G_Θ = G_Φ = 1 everywhere at t = 0, where (R, Θ, Φ) are spherical coordinates in the initial configuration (see Figs. 2B and 7B).

Optic Vesicle Formation (t = 0-20 h)

Prior to contact with the SE at HH10⁺ (t = 5 h), the initially hemispherical OV grows laterally outward from the forebrain and expands near its tip, while remaining approximately axisymmetric (Fig. 3A). With the tip located at Θ = 0, the growth rates are taken in the form

$$\begin{array}{c}{\dot{G}}_R=0\\ {\dot{G}}_{\mathrm{\Theta }}(\mathrm{\Theta })=a_{1\mathrm{\Theta }}{(\frac{\pi }{2}-\mathrm{\Theta })}^3\\ {\dot{G}}_{\mathrm{\Phi }}(\mathrm{\Theta })=a_{1\mathrm{\Phi }}{(\frac{\pi }{2}-\mathrm{\Theta })}^3,\end{array}$$ (5)

where dot denotes time differentiation and the rate constants are a_1Θ = 0.02 h⁻¹ and a_1Φ = 0.03 h⁻¹. The pattern defined by these equations is shown in Fig. 3A.

After the OV contacts the SE, the OVs bend in both the caudal and dorsal directions. Results from SE removal experiments show that most of the caudal bending is caused by constraining effects of the SE, but a significant portion of the dorsal bending is generated within the OV itself (Fig. 4). This intrinsic dorsal bending implies that the OV grows more longitudinally on its ventral side than the dorsal side. Consequently, for 5 < t ≤ 20 h, the growth rates are given by

$$\begin{array}{c}{\dot{G}}_R=0\\ {\dot{G}}_{\mathrm{\Theta }}(\mathrm{\Theta },\mathrm{\Phi })=a_{2\mathrm{\Theta }}{e}^{-2|\mathrm{\Phi }-\pi |}\\ {\dot{G}}_{\mathrm{\Phi }}(\mathrm{\Theta })=a_{2\mathrm{\Phi }}{(\frac{\pi }{2}-\mathrm{\Theta })}^3,\end{array}$$ (6)

where a_2Θ = 0.045 h⁻¹ and a_2Φ = 0.02 h⁻¹. The pattern for Ġ_Θ is shown on the deformed OV in Fig. 3B.

Finally, based on results in Hosseini et al. (2014), a relatively small amount of contraction is specified in the SE by setting Ġ_R = 0 and Ġ_Θ = Ġ_Φ = −0.0025 h⁻¹ in this layer. At HH13 (t = 20 h), this gives G_Θ = G_Φ = 0.95, which remain unchanged during subsequent OC and LV formation.

Optic Cup Formation (t = 20-28 h)

After HH13, the OV invaginates to create the OC. At this time, the accumulating ECM between the OV and SE is introduced by stiffening a relatively thin section of the outer part of the OV wall within the region of contact (see Fig. 6A). The shear modulus of this layer increases linearly with time by a factor of 50, beginning at the cell value μ = 220 Pa (Oltean et al. 2016).

We approximate the contact area between the OV and SE as an elliptical region centered at the origin of the newly defined spherical coordinates (R, Θ, Φ) shown in Fig. 3B. With (Θ₀, Φ₀) defining the ends of the ellipse semi-axes, the growth rates in this region are

$$\begin{array}{c}{\dot{G}}_R=b_0\\ {\dot{G}}_{\mathrm{\Theta }}={\dot{G}}_{\mathrm{\Phi }}=b_1+b_2\left[\frac{{\mathrm{\Theta }}_0-\mathrm{\Theta }}{{\mathrm{\Theta }}_0}\right]\left[\frac{{\mathrm{\Phi }}_0-\mathrm{\Phi }}{{\mathrm{\Phi }}_0}\right],\end{array}$$ (7)

where (b₀, b₁, b₂) = (0.05, 0.1, 0.4) h⁻¹. The value for b₁ is chosen so the tangential growth rates in the invaginating region are continuous with the uniform growth rates in the rest of the OV (Ġ_Θ = Ġ_Φ = b₁ + b₂ at Θ = Θ₀, Φ = Φ₀). These distributions approximate those in the axisymmetric model of Oltean et al. (2016), with the maximum growth rate occurring at the center of the invaginating region (Fig. 6B).

Lens Vesicle Formation (t = 17-25 h)

The lens forming region is defined as a circular region (radius d₀) of the SE in contact with the OV at HH12 (t = 17 h). In this region, the SE wall is divided into a thin outer contractile layer and an inner growing layer (Fig. 7A).

For LV formation, we define two phases: (1) invagination (t = 17-22 h) and (2) closure (t = 22-25 h). During Phase 1, the relatively thin outer layer of the lens forming region contracts while the inner layer grows. During Phase 2, these processes continue while apoptosis begins within a thin ring comprising the outer 15% of the invaginating region. These mechanisms are consistent with the model of Oltean & Taber (2017).

During Phase 1, the growth and contraction rates are constant with (Ġ_R, Ġ_Θ, Ġ_Φ) having values (0.1, 0.2, 0.2) h⁻¹ in the inner growing layer and (0, −0.1, −0.1) h⁻¹ in the outer contracting layer. During Phase 2, again following Oltean & Taber (2017), we assume that both growth and contraction increase slightly with distance d from the center of the lens forming region according to the relations

$$\begin{array}{c}{\dot{G}}_R=c_0\left(\frac{d}{d_0}\right)\\ {\dot{G}}_{\mathrm{\Theta }}={\dot{G}}_{\mathrm{\Phi }}=c_1\left(\frac{d}{d_0}\right),\end{array}$$ (8)

where (c₀, c₁) = (0.1, 0.2) h⁻¹ in the inner layer and (c₀, c₁) = (0, −0.1) h⁻¹ in the outer layer. Over the eight-hour invagination period beginning at t = 17 h, the latter set of numbers produces an isotropic contraction that peaks at 80%. Contraction is accompanied by a progressive increase in shear modulus (linear with time) to 85 times its initial value of 220 Pa. Due to convergence issues, the peak stiffness is slightly lower that that used in the model of Oltean & Taber (2017).

During Phase 2, apoptosis is simulated in the outer ring by setting (Ġ_R, Ġ_Θ, Ġ_Φ) = (0.0, 0.0, −0.6) h⁻¹, which produces negative growth tangent to the opening in the lens pit. Note that this procedure subtracts from the positive growth that occurs prior to this phase.

Finally, within the relatively soft annular region of SE surrounding the lens forming region (Fig. 7A), viscoelastic stress relaxation is simulated by setting the growth rates to 0.03 and -0.03 in the normal and tangential directions, respectively, relative to the invaginating region.