Generalized accelerated recurrence time model for multivariate recurrent event data with missing event type

Summary

Recurrent events data are frequently encountered in biomedical follow-up studies. The generalized accelerated recurrence time (GART) model (Sun et al., 2016), which formulates covariate effects on the time scale of the mean function of recurrent events (i.e. time to expected frequency), has arisen as a useful secondary analysis tool to provide meaningful physical interpretations. In this paper, we investigate the GART model in a multivariate recurrent events setting, where subjects may experience multiple types of recurrent events and some event types may be missing. We propose methods for the GART model that utilize the inverse probability weighting technique or the estimating equation projection strategy to handle event types that are missing at random. The new methods do not require imposing any parametric model for the missing mechanism, and thus are robust; moreover they enjoy easy and stable implementation. We establish the uniform consistency and weak convergence of the resulting estimators and develop appropriate inferential procedures. Extensive simulation studies and an application to a dataset from Cystic Fibrosis Foundation Patient Registry (CFFPR) illustrate the validity and practical utility of the proposed methods.

1. Introduction

Recurrent events data are frequently encountered in biomedical follow-up studies where subjects may experience events of interest repeatedly over time. A major analytic strategy for recurrent events data is to assess and model the mean or rate functions of recurrent events (Pepe and Cai, 1993; Lawless and Nadeau, 1995; Lin et al., 2000, among others) which are intuitive to interpret and implicate weak assumption on the within-subject dependency. While existing mean or rate function based approaches mostly attend to the frequency scale of the mean function, there are increasing interests in characterizing the progression of recurrent events by the time scale of the mean function for meaningful physical interpretations. For example, the classic accelerated failure time model (AFT) for recurrent events (Lin et al., 1998) specifies covariate effects as constant time scale changes of the mean function. To explicitly quantify the changes in the time scale of the mean function, Huang and Peng (2009) introduced the concept of time to expected frequency, defined as the inverse function of the mean function, and proposed the accelerated recurrence time model (ART) model. The ART model extends the AFT model by allowing for evolving covariate effects on time to expected frequency. More recently, Sun et al. (2016) derived the generalized accelerated recurrence time (GART) model from a counting process modeling perspective. The GART model is a strict extension of the ART model, permitting a more flexible transformation from the frequency scale to the time scale of the mean function. The inferential methods developed by Sun et al. (2016) accommodate recurrent events data subject to observation windows that take the form of general time interval(s).

However, the aforementioned methods are all oriented to the settings where recurrent events are of the same type. In practice, subjects may experience multiple recurrent events of different types and moreover the identification of the event type can be missing due to a variety of reasons. For example, Pseudomonas aeruginosa (Pa) is a major respiratory pathogen acquired in the early life of patients with cystic fibrosis (CF) and usually leads to chronic infections. The organism can also transition from a motile, virulent, nonmucoid type to a nonmotile, comparatively avirulent, mucoid type. The mucoid type is more likely to be drug-resistent and associated with more severe CF disease progression. In the past, the two were not always differentiated in clinics. Recently, it has become a common practice to classify Pa positive cultures into mucoid and nonmucoid types to aid in treatment decisions. However unknown or missing Pa infection types still occur. As shown by our simulations studies (see Section 5), ignoring this data complication can seriously bias the estimation of the recurrence pattern of Pa infections of each type. This can potentially misguide the CF disease management.

In this paper, we consider the problem of fitting the GART models to the multivariate recurrent events data with missing event types. Several authors have addressed such recurrent events data in other model settings. For example, Chen and Cook (2009) specified a multiplicative conditional Poisson model for the multivariate recurrent events data and derived an EM-algorithm to perform the maximum likelihood analysis in the presence of missing event types. Schaubel and Cai (2006a) and Schaubel and Cai (2006b) studied the semiparametric proportional rate model, using the multiple imputation technique and weighted estimating equations respectively to account for missing event types. Schaubel and Cai (2006a)’s weighted estimating equations were further adapted to the additive rate model (Ye, Zhao, Sun, and Xu, 2015) and the additive-multiplicative rate models (Ye, Sun, Zhao, and Xu, 2015). More recently, Lin et al. (2013) proposed a fully nonparametric estimator of the mean function in the one-sample case. While these methods shed useful insight for dealing with missing event types, they are not readily extendable to the GART model. This is because the GART model does not imply a likelihood, unlike a parametric model. In addition, the semiparametric rate models mentioned above only involve real valued coefficients, while the coefficients of the GART model, which accommodate varying covariate effects, take the form of functions.

To tackle the data complication caused by missing event types under the GART models, we consider two strategies. One is to apply the inverse probability weighting (IPW) technique to correct the bias only using the data with observed event types. The other one is to impute the missing event type by its estimated probability of being each specific event type in the estimating equation that assumes a complete observation of event types. The second strategy shares the same spirit as that of Schaubel and Cai (2006a), Schaubel and Cai (2006b), and Lin et al. (2013), and we shall refer it to as estimating equation projection (EEP) strategy hereafter. To carry out the IPW or EEP strategy, the key task is to estimate the conditional probability of event type being observed or the missing event type being a specific type given covariates and/or other observed data. To this end, we propose nonparametric Nadaraya-Watson type estimators to avoid additional parametric modeling. Like in Lin et al. (2013), the proposed conditional probability estimators can be justified from the local likelihood estimation perspective. Our estimators also have explicit closed forms despite the incorporation of covariates, which are not available in Lin et al. (2013)’s method. As another appealing feature, the two methods derived from the IPW and EEP strategies can be unified in an inferential framework that resembles Sun et al. (2016)’s method. This entails simple and stable implementations of the proposed methods. For example, we are able to obtain the proposed estimators via algorithms that only involve minimizations of a sequence of L₁-type convex functions, which can readily be solved by existing functions in R and S-PLUS. By our asymptotic studies, the two proposed estimators are shown to be asymptotically equivalent.

We organize the rest of the paper as follows. In Section 2, we present the generalized accelerated recurrence time (GART) model and propose the estimating methods derived from the IPW and EEP strategies. We establish the asymptotic properties of the proposed estimators, including the uniform consistency and weak convergence, in Section 3, and discuss the inference procedures in Section 4. The simulation studies that investigate the finite sample performance of the proposed estimators are reported in Section 5. We illustrate the proposed methods via an application to a dataset from the Cystic Fibrosis Foundation Patient Registry (CFFPR) in Section 6. Finally, we provide some concluding remarks in Section 7.

2. The Proposed Methods

2.1 Data and Model

Suppose that a subject may experience K types of recurrent events, and recurrent events are subject to an observation window that is an time interval, (L,R]. Let T^(j) denote the j-th recurrent event time, δ̄(t) ∈ {1, …, K} denote the type of the event that occurs at time t, and A(t) is a binary indicator which equals 1 if the event type is observed at time t and 0 otherwise. Define δ_k(t) = I{δ̄(t) = k}, where I(·) is the indicator function, and write ${\delta }_k^{(j)}\doteq {\delta }_k(T^{(j)})$ and A^(j) = A(T^(j)). Let X̃ be a (p − 1) × 1 covariate vector and X = (1, X̃).

For type-k events, the underlying counting process is given by $N_k^{\ast }(t)={\sum }_{j=1}^{\infty }I(T^{(j)}\le t,{\delta }_k^{(j)}=1)$, which represents the total number of type-k events that have occurred by time t. The observation of recurrent events is only available in the time interval, (L,R]. When all event types are known, $N_k(t)\doteq {\sum }_{j=1}^{\infty }I(L<T^{(j)}\le t^R,{\delta }_k^{(j)}=1)$ captures the total number of type-k events observed by time t. Accounting for the fact that some event types may be missing, we define ${\check{N}}_k(t)={\sum }_{j=1}^{\infty }I(L<T^{(j)}\le t^R,A^{(j)}=1,{\delta }_k^{(j)}=1\}$ to represent the total number of type-k events that are observed by time t and are known to be type-k. Finally, we define $N.(t)={\sum }_{k=1}^K{N}_k(t)$, which captures the total number of recurrent events (regardless their types) observed by time t. We assume that $N_k^{\ast }(·)$ is independent of L and R given X for each k, $d{N}_k^{\ast }(s)\in \{0,1\}$, and $d{N}_k^{\ast }(s)d{N}_l^{\ast }(s)=0$ for k ≠ l. This means, the observation window (L,R] is non-informative of the recurrent events, and only up to one type of event can occur at one time point.

For the multivariate recurrent events data considered in this paper, recurrent event times are always observed but the corresponding event types may be unkown/missing. That is, the observed data consist of n independent and identically distributed (i.i.d.) replicates of {N_·(t), Ň_k(t), L, R, dN_· (t)A(t), dN_· (t)A(t)δ_k(t), X; t > 0, k = 1, …, K}, denoted by ${\{N_{i·}(t),{\check{N}}_{ik}(t),L_i,R_i,d{N}_{i·}(t)A_i(t),d{N}_{i·}(t)A_i(t){\delta }_{ik}(t),{\mathbf{X}}_i;t>0,k=1,\dots ,K\}}_{i=1}^n$.

For type-k events, time to expected frequency u (Huang and Peng, 2009) is defined as

$${\tau }_{\mathbf{X},k}(u)=inf\{t\ge 0:{\mu }_{\mathbf{X},k}(t)\ge u\},$$

where ${\mu }_{\mathbf{X},k}(t)\doteq E\{N_{ik}^{\ast }(t)\mid \mathbf{X}\}$ is the conditional mean function of the type-k event given X. For each event type k, we assume the generalized accelerated recurrence time (GART) model (Sun et al., 2016):

$${\tau }_{\mathbf{X},k}\{G(u)\}=\text{exp}\{{\mathbf{X}}^{\top }{\mathit{\beta }}_{0k}(u)\},u\in (0,U],$$ (1)

where $G(u)={\int }_0^{u}g(s)ds$ with g being a known positive continuous function, β_0k(·) is a p×1 vector of unknown coefficient functions, and U is a positive constant. The non-intercept components of β_0k(u) represent covariate effects on the time to expected frequency G(u) of the type-k event. When they are all constant over u and g(·) = 1, model (1) becomes the AFT model for recurrent events. In the non-recurrent event setting (i.e. $T_i^{(j)}=\infty$ for all j > 1), model (1) with g(·) = 1 reduces to a standard quantile regression model for the type-k event time.

2.2 The Proposed Estimating Equations

By Sun et al. (2016), model (1) implies $E\left\{N_{ik}({\mathbf{e}}^{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_{0k}(u)})\mid {\mathbf{X}}_i\right\}=E\left\{{\int }_0^u{Y}_i({\mathbf{e}}^{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_{0k}(s)})g(s)ds\mid {\mathbf{X}}_i\right\}$, where Y_i(t) = I(L_i < t ≤ R_i) denotes the at-risk process for recurrent events. When the event types are always observed, we have N_ik(t) = Ň_ik(t). Thus we can apply Sun et al. (2016)’s method to estimate β_0k(u). That is, we solve the following estimating equation for β_k(·):

$$n^{-1/2}\sum _{i=1}^n{\mathbf{X}}_i\left\{{\check{N}}_{ik}(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(u)\})-{\int }_0^u{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(s)\})g(s)ds\right\}=0.$$ (2)

When some of event type information is missing, using equation (2) to estimate β_0k(u) corresponds to the so called complete–case (CC) analysis, which ignores the events of unknown type. In this case, Ň_ik(·) deviates from N_ik(·) if $A_i^{(j)}=0$ for some j. Consequently, the expectation of the left-hand side of estimating equation (2) with β_k(u) = β_0k(u) is generally away from zero, even when the event type is missing completely at random (MCAR) (Little and Rubin, 2002). This suggests that the CC analysis based on estimating equation (2) is problematic and can yield a biased estimator of β_0k(u).

To obtain an unbiased estimator of β_0k(u), our basic idea is to find an appropriate proxy of N_ik(t), denoted by N̂_ik(t), and then solve the following equation for β_k(·):

$$n^{-1/2}\sum _{i=1}^n{\mathbf{X}}_i\left\{{\check{N}}_{ik}(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(u)\})-{\int }_0^u{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(s)\})g(s)ds\right\}=0.$$ (3)

To attain consistent estimation of β₀(·), we shall properly design N̂_ik(t) so that the left-hand side of equation (3) (multiplied by n^−1/2) approaches zero as n →∞ when β_k(·) = β_0k(·).

To proceed, we assume a missing-at-random (MAR) mechanism (Little and Rubin, 2002) for event types that implies the conditional independence between A_i(t) and δ_ik(t) given dN_i·(t) and Z_i, where Z_i encompasses covariate X_i and possibly other observed time-independent data, such as L_i and R_i. Similar MAR assumptions for recurrent event type were adopted in previous work, such as Schaubel and Cai (2006a,b); Lin et al. (2013). With Z_i formulated as independent of time, our MAR assumption imposes an implicit constraint that the event type missing probability is only influenced by the observed data that are fixed over time. As shown in Sections 2.2.1 and 2.2.2, this MAR assumption facilitates the derivation of an appropriate inverse probability weight and the construction of the proposed EEP equation.

In the following subsections, we give two specific forms of N̂_ik(t) based on the inverse probability weighting (IPW) technique and the estimating equation projection (EEP) strategy respectively.

2.2.1 Inverse Probability Weighting (IPW) Method

Let π_k(t,z) = E{A_i(t)|dN_ik(t)} = 1,Z_i = z}, $A_i^{(j)}=A_i(T_i^{(j)})$, and ${\pi }_{ik}^{(j)}={\pi }_k(T_i^{(j)},{\mathbf{Z}}_i)$. Using the standard IPW arguments, we can show that $E\{d{N}_{ik}(t)\mid {\mathbf{Z}}_i\}=E\{\frac{1}{{\pi }_k(t,{\mathbf{Z}}_i)}d{\check{N}}_{ik}(t)\mid {\mathbf{Z}}_i\}$, and thus $E\{N_{ik}(t)\mid {\mathbf{Z}}_i\}=E\{{\int }_0^t\frac{1}{{\pi }_k(s,{\mathbf{Z}}_i)}d{\check{N}}_{ik}(s)\}$. Therefore, a special form of N̂_ik(t) is suggested as

$${\widehat{N}}_{ik}^{\text{IPW}}(t)={\int }_0^t\frac{1}{{\widehat{\pi }}_k(s,{\mathbf{Z}}_i)}d{\check{N}}_{ik}(s)\doteq \sum _{j=1}^{\infty }\frac{1}{{\widehat{\pi }}_{ik}^{(j)}}I(L_i<T_i^{(j)}\le t\wedge R_i,A_i^{(j)}=1,{\delta }_{ik}^{(j)}=1),$$

where π̂_k(t, z) (or ${\widehat{\pi }}_{ik}^{(j)}$) is a reasonable estimate for π_k(t, z) (or ${\pi }_{ik}^{(j)}$).

To derive π̂_k(t, z) (or ${\widehat{\pi }}_{ik}^{(j)}$), we first note that under the assumed MAR mechanism,

$${\pi }_k(t,\mathbf{z})=E\{A_i(t)\mid {\delta }_{ik}(t)=1,d{N}_{i·}(t)=1,{\mathbf{Z}}_i=\mathbf{z}\}=E\{A_i(t)\mid d{N}_{i·}(t)=1,{\mathbf{Z}}_i=\mathbf{z}\}.$$ (4)

This implies that π_k(t, z)’s are the same for all k ∈ {1, …, K}. Thus, we can drop the subscript k in π_k(t, z), ${\pi }_{ik}^{(j)}$, and ${\widehat{\pi }}_{ik}^{(j)}$, and use the notation π(t, z), ${\pi }_i^{(j)}$, and ${\widehat{\pi }}_i^{(j)}$ instead.

Intuitively, one may adopt a parametric regression model, such as a logistic regression model, for A_i(t) to obtain an estimate for π(t, z). However, such an estimator may be biased when the parametric model is misspecified. To avoid this issue, we propose a fully nonparametric method to estimate π(t, z). Specifically, we propose a Nadaraya-Watson type nonparametric estimator of π(t, z) that takes the form

$$\widehat{\pi }(t,\mathbf{z})=\frac{{\sum }_{i=1}^n{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}={\mathbf{z}}_2)\int K_h(s-t)A_i(s)d{N}_{i·}(s)}{{\sum }_{i=1}^n{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}={\mathbf{z}}_2)\int K_h(s-t)d{N}_{i·}(s)},$$ (5)

where K_h(u) = h⁻¹K(u/h), h is a bandwidth depending on n, ${\mathbf{K}}_h(\mathbf{u})={\mathrm{\Pi }}_{i=1}^d{K}_h(u_i)$ for u = (u₁, u₂, …, u_d) ∈ ℛ^d, z = (z₁, z₂), d is the number of the continuous elements in Z_i, and Z_1i and Z_2i are the continuous and discrete elements of Z_i respectively. Here K(u) is a rth order (r > d + 1) kernel function with compact support satisfying ∫K(u)du = 1, ∫u^mK(u)du = 0 for m = 1, 2, …, r − 1, ∫u^rK(u)du ≠ 0, and ∫K(u)²du < ∞. In the Supplementary Materials, we show that π̂(t, z) is the (kernel-based) local likelihood estimator of π(t, z) via a locally constant likelihood approximation. Similar types of estimators have been used in other methods that deal with missing data, for example, Zhou et al. (2008), Chen et al. (2015), and Qiu et al. (2017).

Plugging ${\widehat{N}}_{ik}^{\text{IPW}}(t)$ with ${\widehat{\pi }}_{ik}^{(j)}=\widehat{\pi }(T_i^{(j)},{\mathbf{Z}}_i)$ into (3), we obtain an IPW type estimating equation for β_0k(·):

$${\mathbf{S}}_{nk}^{\text{IPW}}({\mathit{\beta }}_k)\doteq n^{-1/2}\sum _{i=1}^n{\mathbf{X}}_i\left\{{\widehat{N}}_{ik}^{\text{IPW}}(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(u)\})-{\int }_0^u{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(s)\})g(s)ds\right\}=0.$$ (6)

The procedure to solve this estimating equation is elaborated in Section 2.3.

2.2.2 Estimating Equation Projection (EEP) Method

Following the EEP strategy exploited in literature (Schaubel and Cai, 2006a,b; Lin et al., 2013, among others), we write

$$N_{ik}(t)={\int }_0^t[A_i(s){\delta }_{ik}(s)+\{1-A_i(s)\}{\delta }_{ik}(s)]d{N}_{i·}(s)\doteq \sum _{j=1}^{\infty }\{A_i^{(j)}{\delta }_{ik}^{(j)}+(1-A_i^{(j)}){\delta }_{ik}^{(j)}\}I(L_i<T_i^{(j)}\le R_i\wedge t),$$

and propose to recover the missing component of N_ik(t) (i.e. {1− A_i(s)}δ_ik(s)) by imputing the δ_ik(s) with A_i(s) = 0 by its estimated expectation.

Specifically, define p_k(t, z) = E{δ_ik(t)|A_i(t) = 0, dN_i·(t) = 1,Z_i = z}. Under the assumed MAR mechanism, we have p_k(t, z) = Pr{δ_ik(t) = 1|A_i(t) = 1, dN_i·(t) = 1,Z_i = z}. We propose a Nadaraya–Watson type nonparametric estimator of p_k(t, z), given by

$${\widehat{p}}_k(t,\mathbf{z})=\frac{{\sum }_{i=1}^n{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}={\mathbf{z}}_2)\int K_h(s-t)A_i(s){\delta }_{ik}(s)d{N}_{i·}(s)}{{\sum }_{i=1}^n{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}={\mathbf{z}}_2)\int K_h(s-t)A_i(s)d{N}_{i·}(s)}.$$

Similar to the derivation of π̂(t, z), p̂_k(t, z) is a maximum local likelihood estimator when p_k(t, z) is approximated by a constant within a kernel band in t and z; more details can be found in the Supplementary Materials. Note that Lin et al. (2013) also adopted a similar local likelihood method to estimate the counterpart of p_k(t, z) in the one-sample case. They used a local polynomial with order q to approximate the imputed probability, and it is hard to generalize their estimator to account for covariates. Our idea of using a locally constant approximation circumvents such a difficulty. Moreover it enables a closed form for p̂_k(t, z), which facilitates the computation while not sacrificing the estimation efficiency.

A special form of N̂_ik(t) derived by the EEP strategy is given by

$$\begin{gathered} {\widehat{N}}_{ik}^{\text{EEP}}(t)={\int }_0^t[A_i(s){\delta }_i(s)+\{1-A_i(s)\}{\widehat{p}}_k(s,{\mathbf{Z}}_i)]d{N}_{i·}(s) \\ \doteq \sum _{j=1}^{\infty }\left[A_i^{(j)}{\delta }_{ik}^{(j)}+(1-A_i^{(j)}){\widehat{p}}_{ik}^{(j)}\right]I(L_i<T_i^{(j)}\le R_i\wedge t) \end{gathered}$$

where ${\widehat{p}}_{ik}^{(j)}={\widehat{p}}_k(T_i^{(j)},{\mathbf{Z}}_i)$. The resulting EEP type estimating equation takes the form,

$${\mathbf{S}}_{nk}^{\text{EEP}}({\mathit{\beta }}_k)\doteq n^{-1/2}\sum _{i=1}^n{\mathbf{X}}_i\left\{{\widehat{N}}_{ik}^{\text{EEP}}(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(u)\})-{\int }_0^u{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(s)\})g(s)ds\right\}=0.$$ (7)

2.3 Computation algorithm

We generally denote the proposed estimating equations by

$${\mathbf{S}}_{nk}^{\mathrm{L}}({\mathit{\beta }}_k)=n^{-1/2}\sum _{i=1}^n{\mathbf{X}}_i\left\{{\widehat{N}}_{ik}^{\mathrm{L}}(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(u)\})-{\int }_0^u{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(s)\})g(s)ds\right\}=0,$$ (8)

with L = IPW or EEP. The resulting estimators are denoted as ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(·)$. Following Peng and Huang (2008) and Sun et al. (2016), we adopt a grid-based algorithm to get ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(·)$ based on equations (8). Specifically, define a grid S_L(n) = {0 = u₀ < u₁ < ··· < u_L(n) = U}, and denote its size by ||S_L(n)|| = max_j=1,…,L(n) |u_j − u_j−1|. We define ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(·)$ as a right continuous piecewise-constant function that jumps only at the grid points of S_L(n). We set $\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(0)\}=0$ for every i since τ_X,k(0) = exp{X^⊤β_0k(0)} = 0. We obtain ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u_l)$, l = 1, 2, …, L(n) by sequentially solving the estimating equation,

$$n^{-1/2}\sum _{i=1}^n{\mathbf{X}}_i\left\{{\widehat{N}}_{ik}^{\mathrm{L}}(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(u_l)\})-\sum _{m=0}^{l-1}{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u_m)\}){\int }_{u_m}^{u_{m+1}}g(s)ds\right\}=0,$$ (9)

with L = IPW or EEP.

An exact solution that makes the equation (9) strictly hold may not exist owning to the fact that (9) is not continuous. Since equation (9) is monotone, ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u_l)$ is defined as a generalized solution to equation (9) and the set of generalized solutions is convex of diameter O(n⁻¹) An equivalent alternative approach to find a generalized solution to (9) is to locate the minimizer of the L₁-type convex function,

$$W_{l,k}^{\mathrm{L}}(\mathbf{h})=\sum _{i=1}^n\sum _{j=1}^{\infty }{\widehat{\omega }}_{i,j,k}^{\mathrm{L}}\left|log{T}_i^{(j)}-{\mathbf{X}}_i^{\top }\mathbf{h}\right|+\left|R^{\ast }-\left\{\sum _{i=1}^n\sum _{j=1}^{\infty }{\widehat{\omega }}_{i,j,k}^{\mathrm{L}}(-{\mathbf{X}}_i^{\top }\mathbf{h})\right\}\right|+\left|R^{\ast }-\left\{\sum _{i=1}^{n}2{\mathbf{X}}_i^{\top }\mathbf{h}\sum _{m=0}^{l-1}{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\beta }}_k^{\mathrm{L}}(u_m)\}){\int }_{u_m}^{u_{m+1}}g(s)ds\right\}\right|,$$

where L = IPW or EEP, ${\widehat{\omega }}_{\mathit{ijk}}^{\text{IPW}}=\frac{A_i^{(j)}}{{\widehat{\pi }}_i^{(j)}}{\delta }_{ik}^{(j)}I(L_i<T_i^{(j)}\le R_i),{\widehat{\omega }}_{\mathit{ijk}}^{\text{EEP}}=\left[A_i^{(j)}{\delta }_{ik}^{(j)}+(1-A_i^{(j)}){\widehat{p}}_{ik}^{(j)}\right]I(L_i<T_i^{(j)}\le R_i)$, and R^* is a large constant that bounds $\left|{\sum }_{i=1}^n{\sum }_{j=1}^{\infty }{\widehat{\omega }}_{i,j,k}^{\mathrm{L}}(-{\mathbf{X}}_i^{\top }\mathbf{h})\right|$ and $\left|{\sum }_{i=1}^{n}2{\mathbf{X}}_i^{\top }\mathbf{h}{\sum }_{m=0}^{l-1}{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u_m)\}){\int }_{u_m}^{u_{m+1}}g(s)ds\right|$ from the above.

We can show that $\partial W_{l,k}^{\mathrm{L}}(\mathit{\beta }(u_l))/\partial \mathit{\beta }(u_l)$ equals −2 times the estimating equation in (9) by following arguments similar to those in the Appendix of Peng and Fine (2009). This justifies the use of the minimizer of $W_{l,k}^{\mathrm{L}}(\mathbf{h})$ as a generalized solution to equation (9). We can solve the minimization of $W_{l,k}^{\mathrm{L}}(\mathbf{h})$ by using standard statistical software, for example the l1fit() function in S-PLUS or the rq() function in R package quantreg. More specifically, let m_i = N_i·(R_i), 1_mi denote a m_i × 1 vector with all components equal to 1, and ⊗ denote the Kronecker product. One may directly apply the l1fit() or rq() to solve a median regression problem with an augmented dataset, where the response vector is

$${(log(T_1^{(1)}),\dots ,log(T_1^{(m_1)}),\dots ,log(T_n^{(1)}),\dots ,log(T_n^{(m_n)}),R^{\ast },R^{\ast })}^{\top },$$

the covariate matrix is

$$({({\mathbf{1}}_{m_1}\otimes {\mathbf{X}}_1^{\top })}^{\top },\dots ,{({\mathbf{1}}_{m_n}\otimes {\mathbf{X}}_n^{\top })}^{\top },-\sum _{i=1}^n\sum _{j=1}^{\infty }{\widehat{\omega }}_{i,j,k}^{\mathrm{L}}{\mathbf{X}}_i,\sum _{i=1}^{n}2{\mathbf{X}}_i\sum _{m=0}^{l-1}{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u_m)\})·{\int }_{u_m}^{u_{m+1}}g(s)ds),$$

and the weight vector is ${({\widehat{\omega }}_{1,1,k}^{\mathrm{L}},\dots ,{\widehat{\omega }}_{1,m_1,k}^{\mathrm{L}},\dots ,{\widehat{\omega }}_{n,1,k}^{\mathrm{L}},\dots ,{\widehat{\omega }}_{n,m_n,k}^{\mathrm{L}},1,1)}^{\top }$.

3. Asymptotic Properties

In this Section, we establish the uniform consistency and weak convergence of the proposed estimator ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(·)$. Denote the density of Z by f(z). Define

$$N_{ik}^{\text{AIPW}}(t)=\sum _{j=1}^{\infty }\left[\frac{A_i^{(j)}}{{\pi }_i^{(j)}}{\delta }_{ik}^{(j)}+\left(1-\frac{A_i^{(j)}}{{\pi }_i^{(j)}}\right)p_{ik}^{(j)}\right]I(L_i<T_i^{(j)}\le R_i\wedge t),$$

μ̃_Z,k(t) = E{N_ik(t)|Z_i}, g_Z,k(t) = dμ̃_Z,k(t)/dt, $g_{\mathbf{Z}}(t)={\sum }_{k=1}^K{g}_{\mathbf{Z},k}(t)$, μ̃_X,k(x) = E{N_ik(x)|X_i}, g_X,k(x) = dμ̃_X,k(x)/dx, ${\mathbf{v}}_k(\mathbf{b})=E[{\mathbf{X}}_i{N}_{ik}\{\text{exp}({\mathbf{X}}_i^{\top }\mathbf{b})\}]$, and B_k(b) = dυ_k(b)/db^⊤. It follows from simple algebra that B_k(b) = E{X^⊗2e^X⊤bg_X,k(e^X⊤b)}, where v^⊗2 = vv^⊤ for any vector v. Let $f_{\mathbf{X}}^L(x)$ and $f_{\mathbf{X}}^R(x)$ be the conditional density functions of L and R given X respectively, $\stackrel{\sim }{\mathbf{v}}(\mathbf{b})=E[{\mathbf{X}}_i{Y}_i\{\text{exp}({\mathbf{X}}_i^{\top }\mathbf{b})\}]$, and J(b) = dυ̃(b)/db^⊤, we have $\mathbf{J}(\mathbf{b})=E[{\mathbf{X}}^{\otimes 2}{e}^{{\mathbf{X}}^{\top }\mathbf{b}}\{f_{\mathbf{X}}^L(e^{{\mathbf{X}}^{\top }\mathbf{b}})-f_{\mathbf{X}}^R(e^{{\mathbf{X}}^{\top }\mathbf{b}})\}]$. Denote ℬ_k(d) = {b ∈ R^p : inf_u∈(0,U]||υ_k(b) − υ_k{β_0k(τ)}|| ≤ d} as a neighborhood containing {β_0k(u), u ∈ (0, U]}, where ||·|| is the Euclidean norm.

We assume the following regularity conditions:

• C1X_i and N_ik(R_i) are bounded, E(X^⊗2) is positive definite.
• C2Each component of υ_k{β_0k(u)} is Lipschitz continuous for u ∈ (0, U], k = 1, …, K.
• C3For some d₀ > 0, g_X,k(exp(X^⊤b)) > 0 for any b ∈ ℬ_k(d₀) and X ∈ 𝒳.
• C4Each component of J(b)B_k(b)⁻¹ is uniformly bounded in b ∈ ℬ_k(d₀).
• C5For any v ∈ (0, U], inf_u∈[v,U] eigmin B_k{β_0k(u)} > 0, where eigmin(·) denotes the minimum eigenvalue of a matrix.
• C6The bandwidth sequence h satisfies nh^2r → 0, nh^2(d+1) → ∞, and nh^d+1/ log n → ∞.
• C7The functions, f(z), g_Z(t), π(t, z), and p_k(t, z) are uniformly bounded away from zero, and have r continuous and bounded partial derivatives with respect to t and the continuous components of z almost surely.

Note that conditions C1–C5 are the same as those adopted by Sun et al. (2016) for justifying the use of equation (2) for estimating the GART model with fully observed event types. It is worth mentioning that condition C3 implies that the support of L must include 0 and the support of R must cover exp{X^⊤β_0k(U)} for all X ∈ 𝒳. This constraint is necessary to ensure the identifiability of {β_0k(u) : u ∈ (0, U]. Conditions C6 and C7 are common assumptions in literature (Chen et al., 2015; Qiu et al., 2017, for example) that ensure the desirable large sample properties of nonparametric kernel estimators π̂(t, z) and p̂_k(t, z). We have the following theorems:

Theorem 1

Suppose model (1) holds for u ∈ (0, U]. Under the regularity conditions C1–C7, if lim_n→∞ ||𝒮_L(n)|| = 0, then ${sup}_{u\in [v,U]}\Vert {\widehat{\mathit{\beta }}}_k^L(u)-{\mathit{\beta }}_{0k}(u)\Vert \stackrel{p}{\to }0$ for k = 1, …, K and L=IPW or EEP, where 0 < v < U.

Theorem 2

Suppose model (1) holds for u ∈ (0, U]. Under the regularity conditions C1–C7, if lim_n→∞ n^1/2||𝒮_L(n)|| = 0, then $n^{1/2}\{{\widehat{\mathit{\beta }}}_k^L(u)-{\mathit{\beta }}_{0k}(u)\}$ converges weakly to a Gaussian process for u ∈ [v,U] with covariance Σ(s, t) ≐ E[η_ik(s)η_ik(t)^⊤], where 0 < v < U, η_ik(u) = B_k{β_0k(u)}⁻¹ϕ(ξ_ik),

$${\mathit{\xi }}_{ik}(\tau )={\mathbf{X}}_i\left\{N_{ik}^{\mathit{AIPW}}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_{0k}(\tau )\}-{\int }_0^{\tau }{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_{0k}(u)\})g(u)du\right\},$$

$\mathit{\varphi }(\mathbf{w})(u)={\int }_0^u\mathcal{I}(s,u)d\mathbf{w}(s)$ is a linear operator, and

$$\mathcal{I}(s,t)=\prod _{u\in (s,t]}[{\mathbf{I}}_p+\mathbf{J}\{{\mathit{\beta }}_{0k}(u)\}{\mathbf{B}}_k{\{{\mathit{\beta }}_{0k}(u)\}}^{-1}g(u)du].$$

Note that, Theorem 2 not only establishes the weak convergence result for the proposed estimators but also indicates that the proposed IPW and EEP estimators have the same limit distributions. Detailed proofs of Theorems 1–2 are provided in the Supplementary Materials.

4. Inferences

4.1 Resampling approach

For inference on β_0k(u), we propose a simple resampling procedure by adapting the work of Jin et al. (2001). Suppose {ζ_i, i = 1, …, n} are independent and identically distributed variables from a nonnegative known distribution with mean 1 and variance 1, such as the exponential distribution with rate 1.

We first need to obtain the resampled versions of π(t, z) and p_k(t, z), which are respectively

$${\widehat{\pi }}^{\ast }(t,\mathbf{z})=\frac{{\sum }_{i=1}^n{\zeta }_i{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}-{\mathbf{z}}_2)\int K_h(s-t)A_i(s)d{N}_{i·}(s)}{{\sum }_{i=1}^n{\zeta }_i{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}={\mathbf{z}}_2)\int K_h(s-t)d{N}_{i·}(s)}$$

and

$${\widehat{p}}_k^{\ast }(t,\mathbf{z})=\frac{{\sum }_{i=1}^n{\zeta }_i{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}={\mathbf{z}}_2)\int K_h(s-t)A_i(s){\delta }_{ik}(s)d{N}_{i·}(s)}{{\sum }_{i=1}^n{\zeta }_i{\mathbf{K}}_h({\mathbf{Z}}_{1i}-{\mathbf{z}}_1)I({\mathbf{Z}}_{2i}={\mathbf{z}}_2)\int K_h(s-t)A_i(s)d{N}_{i·}(s)}.$$

Then we define ${\mathit{\beta }}_k^{\mathrm{L}\ast }(·)$ as the generalized solution to the perturbed estimating equation,

$$n^{-1/2}\sum _{i=1}^n{\zeta }_i{\mathbf{X}}_i\left\{{\widehat{N}}_{ik}^{\mathrm{L}\ast }(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(u)\})-{\int }_0^u{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }{\mathit{\beta }}_k(s)\})g(s)ds\right\}=0,$$ (10)

where ${\widehat{N}}_{ik}^{\mathrm{L}\ast }(·)$ is ${\widehat{N}}_{ik}^{\mathrm{L}}$, with π̂ or p̂_k replaced by π̂^* or ${\widehat{p}}_k^{\ast }$ respectively. We can obtain ${\mathit{\beta }}_k^{\mathrm{L}\ast }(·)$ using a similar procedure to that described in subsection 2.3. It can be shown that the conditional distribution of $n^{1/2}\{{\mathit{\beta }}_k^{\mathrm{L}\ast }(u)-{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)\}$ based on the observed data and the unconditional distribution of $n^{1/2}\{{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)-{\mathit{\beta }}_{k0}(u)\}$ have the same limiting distribution. By fixing the data at the observed values and repeatedly generating {ζ_i, i = 1, …, n}, we can obtain a large number of realizations of ${\mathit{\beta }}_k^{\mathrm{L}\ast }(u)$. The empirical distribution of ${\mathit{\beta }}_k^{\mathrm{L}\ast }(u)$ can be used to estimate the covariance of ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)$ or to construct the confidence interval of β_k0(u).

4.2 Sample-based variance and covariance estimation

We develop a sample-based approach to estimate the variance and covariance of ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(·)$, following the lines of Sun et al. (2016). Specifically, define ${\mathbf{L}}_{nk}^{\mathrm{L}}(\mathbf{b})=n^{-1/2}{\sum }_{i=1}^n{\mathbf{X}}_i{\widehat{N}}_{ik}^{\mathrm{L}}(\text{exp}\{{\mathbf{X}}_i^{\top }\mathbf{b}\}),{\mathit{\iota }}_{ik}^{\mathrm{L}}(u)={\mathbf{X}}_i{\widehat{N}}_{ik}^{\mathrm{L}}(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)\}),{\mathbf{\Omega }}_{nk}^{\mathrm{L}}(u)=n^{-1}{\sum }_{i=1}^n{\{{\mathit{\iota }}_{ik}^{\mathrm{L}}(u)\}}^{\otimes 2}$, and ${\stackrel{\sim }{\mathbf{L}}}_n(\mathbf{b})=n^{-1/2}{\sum }_{i=1}^n{\mathbf{X}}_i{Y}_i(\text{exp}\{{\mathbf{X}}_i^{\top }\mathbf{b}\})$. The following are steps to obtain consistent estimates for B_k{β_0k(τ )} and J{β_0k(τ)}, the key unknown components of the asymptotic covariance from Theorem 2:

1. Find a nonsingular and symmetric p × p matrix ${\mathbf{E}}_{nk}^{\mathrm{L}}(u)\equiv \{{\mathbf{e}}_{nk,1}^{\mathrm{L}}(u),\dots ,{\mathbf{e}}_{nk,p}^{\mathrm{L}}(u)\}$ such that ${\mathbf{\Omega }}_{nk}^{\mathrm{L}}(u)={\{{\mathbf{E}}_{nk}^{\mathrm{L}}(u)\}}^2$.

2. Find the solution ${\mathbf{b}}_{nk,j}^{\mathrm{L}}(u)$ by solving the equation

   $${\mathbf{L}}_{nk}^{\mathrm{L}}(\mathbf{b})={\mathbf{L}}_{nk}^{\mathrm{L}}({\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u))+{\mathbf{e}}_{nk,j}^{\mathrm{L}}(u)$$ (11)
   for b, j = 1, …, p. The working estimating equation (11) is monotone and can be solved by minimizing the following L₁ function:

   $$\sum _{i=1}^n\sum _{j=1}^{\infty }{\widehat{\omega }}_{i,j,k}^{\mathrm{L}}\mid log(T_i^{(j)})-{\mathbf{X}}_i^{\top }\mathbf{b}\mid +\left|R^{\ast }-{\left\{-\sum _{i=1}^n\sum _{j=1}^{\infty }{\mathbf{X}}_i^{\top }{\widehat{\omega }}_{i,j,k}+2\sum _{i=1}^n{\mathbf{X}}_i{\widehat{N}}_{ik}^{\mathrm{L}}(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)\})+2n^{1/2}{\mathbf{e}}_{nk,j}^{\mathrm{L}}(u)\right\}}^{\top }\mathbf{b}\right|.$$

   with the same strategy presented for minimizing $W_{l,k}^{\mathrm{L}\ast }(\mathbf{h})$.

3. Compute ${\mathbf{D}}_{nk}^{\mathrm{L}}(u)\doteq \{{\mathbf{b}}_{nk,1}^{\mathrm{L}}(u)-{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u),\dots ,{\mathbf{b}}_{nk,p}^{\mathrm{L}}(u)-{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)\}$, and ${\stackrel{\sim }{\mathbf{E}}}_{nk}^{\mathrm{L}}(u)\doteq \{{\stackrel{\sim }{\mathbf{L}}}_n({\mathbf{b}}_{nk,1}^{\mathrm{L}}(u))-{\stackrel{\sim }{\mathbf{L}}}_n({\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)),\dots ,{\stackrel{\sim }{\mathbf{L}}}_n({\mathbf{b}}_{nk,p}^{\mathrm{L}}(u))-{\stackrel{\sim }{\mathbf{L}}}_n({\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u))\}$.

4. Calculate $n^{-1/2}{\mathbf{E}}_{nk}^{\mathrm{L}}(u){\mathbf{D}}_{nk}^{\mathrm{L}}{(u)}^{-1}$ and $n^{-1/2}{\stackrel{\sim }{\mathbf{E}}}_{nk}^{\mathrm{L}}(u){\mathbf{D}}_{nk}^{\mathrm{L}}{(u)}^{-1}$, which are consistent estimates for B_k{β_0k(u)} and J{β_0k(u)} respectively.

Denote B̂_k(u) and Ĵ_k(u) as the estimators of B_k{β_0k(u)} and J{β_0k(u)} respectively, and denote ${\widehat{\mathit{\eta }}}_{ik}^{\mathrm{L}}(t)={\widehat{\mathbf{B}}}_k{(t)}^{-1}\widehat{\mathit{\varphi }}({\widehat{\mathit{\xi }}}_{ik}^{\mathrm{L}})$, where ϕ̂(·) is the plug-in estimate for the operator ϕ(·) (defined in Theorem 2). Let ${\widehat{N}}_{ik}^{\text{AIPW}}(t)={\sum }_{j=1}^{\infty }\left[\frac{A_i^{(j)}}{{\widehat{\pi }}_i^{(j)}}{\delta }_{ik}^{(j)}+\left(1-\frac{A_i^{(j)}}{{\widehat{\pi }}_i^{(j)}}\right){\widehat{p}}_{ik}^{(j)}\right]I(L_i<T_i^{(j)}\le R_i\wedge t)$, and ${\widehat{\mathit{\xi }}}_{ik}^{\mathrm{L}}(u)={\mathbf{X}}_i\left\{{\widehat{N}}_i^{\text{AIPW}}\left(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(u)\}\right)-{\int }_0^u{Y}_i\left(\text{exp}\{{\mathbf{X}}_i^{\top }{\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(s)\}\right)g(s)ds\right\}$, for i = 1, …, n and k = 1, …, K and L = IPW or EEP. A consistent sample-based estimate for Σ(s, t) is given by $n^{-1}{\sum }_{i=1}^n{\widehat{\mathit{\eta }}}_{ik}^{\mathrm{L}}(s){\widehat{\mathit{\eta }}}_{ik}^{\mathrm{L}}{(t)}^{\top }$.

4.3 Second-stage exploration of varying effects

Given ${\widehat{\mathit{\beta }}}_k^{\mathrm{L}}(\tau )$’s on a range of τ’s, we can employ second-stage inference to summarize and explore the underlying varying pattern of β_0k(u). The second-stage inference procedures can be carried out by adapting the lines of Sun et al. (2016).

Below we illustrate the second-stage inference procedures via a case where the interest is to assess the constancy of a covariate effect. This problem corresponds to testing the null hypothesis, $H_{k0,j}:{\mathit{\beta }}_{k0}^{(j)}(u)={\rho }_0$, u ∈ [u_L, u_U], where ρ₀ is an unspecified constant. Here and in the rest of this subsection, the superscript ^(j) indicates the jth component of a vector (j = 2, …, p), and we omit the superscript ^L that indicates IPW or EEP.

For H₀, we can use the test statistic $\mathcal{T}=n^{1/2}{\int }_{u_L}^{u_U}\mathrm{\Xi }(u)\{{\widehat{\mathit{\beta }}}_k^{(j)}(u)-{\widehat{\rho }}_k^{(j)}\}du$, where Ξ(u) is a non-constant weight function satisfying ${\int }_{u_L}^{u_U}\mathrm{\Xi }(u)du=1$, and ${\widehat{\rho }}_k={(u_U-u_L)}^{-1}{\int }_{u_L}^{u_U}{\widehat{\mathit{\beta }}}_k(u)du$. Let ${\mathcal{T}}^{\ast }=n^{1/2}{\int }_{u_L}^{u_U}\mathrm{\Xi }(u)[\{{\widehat{\mathit{\beta }}}_k^{\ast (j)}(u)-{\widehat{\mathit{\beta }}}_k^{(j)}(u)\}-({\widehat{\rho }}_k^{\ast (j)}-{\widehat{\rho }}_k^{(j)})]du$, where ${\widehat{\rho }}_k^{\ast }={(u_U-u_L)}^{-1}{\int }_{u_L}^{u_U}{\widehat{\mathit{\beta }}}_k^{\ast }(u)du$. We may reject H_k0,j if 𝒯 > d_1−α/2 or 𝒯 < d_α/2, where d_α/2 and d_1−α/2 are the (α/2)th and the (1 − α/2)th empirical quantiles of 𝒯^*. Accepting H_k0,j for all j = 2, …, p may indicate the adequacy of a AFT model when g(·) = 1. Following the arguments of Li and Peng (2014), we can show that the presented constancy test procedure has a type-I error approaching α as n → ∞. The power of the test may be influenced by the choice of the weight function Ξ(u). In practice, one may choose Ξ(u) according to the observed pattern of β̂_k(u) such that it emphasizes the differences from the null to avoid poor power. Note that, we can also show that ρ̂_k is a consistent estimate for the average covariate effect, defined as ${(u_U-u_L)}^{-1}{\int }_{u_L}^{u_U}{\mathit{\beta }}_{k0}(u)du$. The standard error of ρ̂_k can be obtained as the empirical standard deviation of ${\widehat{\rho }}_k^{\ast }$. When β_k0(u) is indeed constant over u, such a constant effect equals the average covariate effect, and hence can be estimated by ρ̂_k.

5. Simulation Studies

We conduct Monte Carlo simulations to examine the finite sample performance of the proposed method. We consider the situation where there exist two event types (i.e. K = 2). Let { $T_k^{\ast (j)}$, j = 1, 2, …} be a sequence of ordered random numbers following a standard homogeneous Poisson process; in another word, { $T_k^{\ast (j)}-T_k^{\ast (j-1)}$: j = 1, 2, …} are independent and identically exponetial(1) random variables with $T_k^{\ast (0)}=0$. The type-k recurrent event times are generated as

$$T_k^{(j)}=exp\left\{min\left(1,\frac{{\rho }_{1k}·T_k^{\ast (j)}}{1.5{\gamma }_k}\right)·X_1+{\rho }_{2k}·X_2\right\}\frac{{\rho }_{0k}·T_k^{\ast (j)}}{{\gamma }_k},k=1,2;j=1,2,\dots ,$$

where the two covariates X₁ and X₂ follow the Bernoulli distribution, Bernoulli(0.5), and the uniform distribution Uniform(−0.5, 0.5), respectively. The frailty γ_k, which determines the level of intra-individual correlation, is drawn from the following two cases:

• Case 1: γ_k = 1;

• Case 2: γ_k ~ Gamma(2, 1/2) with E(γ_k) = 1 and Var(γ_k) = 1/2.

Under these simulation setups,

$${\tau }_{\mathbf{X},k}(u)=\text{exp}\{log({\rho }_{0k}·u)+min(1,{\rho }_{1k}·u/1.5)·X_1+{\rho }_{2k}·X_2\}$$

for k = 1, 2. It is seen that X₁’s effect on time to expected frequency increases with u, while X₂’s effect is constant. In addition, we generate L_i from ω · Uniform(0, 1) and R_i from Uniform(L, 12), where ω is a Bernoulli(0.8) random variable. We set ρ₀₁ = ρ₁₁ = ρ₂₁ = 1.5 to yield the average number of observed type-1 recurrent events per subject about 2.7, and ρ₀₂ = ρ₁₂ = ρ₂₂ = 2 to let that of type-2 events approximately 2.

We simulate missing event types by drawing $A_i^{(j)}$ at each recurrent event time $T_i^{(j)}$ from a $\mathit{Bernoulli}({\pi }_i^{(j)})$, where $\pi (t,\mathbf{z})=1-\frac{1}{1+\text{exp}\{\mathbf{z}{(t)}^{\top }\mathit{\alpha }\}}$, and z(t) = (X₁, t)^⊤. In our simulations, we set α = (1, 0.15)^⊤, leading to about 30% missing event types. For each data scenario, we generate 500 datasets of sample size n = 200.

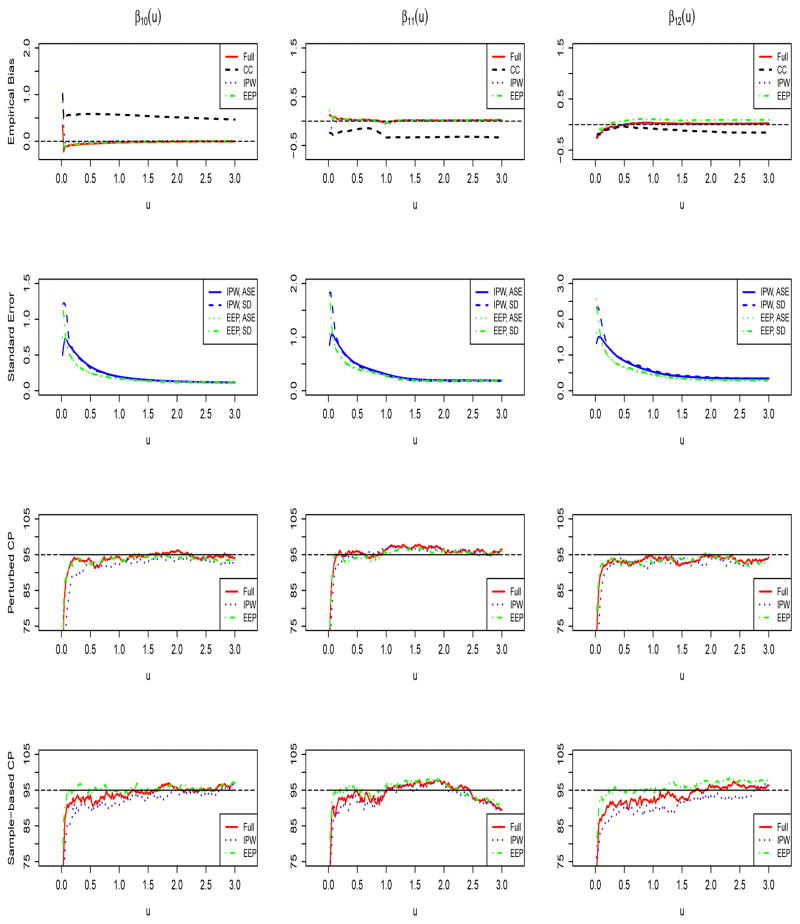
We fit the GART model (1) to each simulated dataset setting g(u) = 1. We apply the proposed IPW and EEP methods, adopting an equally spaced grid on u ∈ (0, 3] with step size 0.02, and choosing the kernel function as the Normal kernel, K(x) = (2π)^−1/2 exp(−x²/2). We compare our methods with the naive complete-case (CC) analysis which only uses the events with known event types and the hypothetical Full analysis which applies Sun et al. (2016)’s method to the underlying full data which contain the complete event type information. In Figure 1, we present the simulation results for the type-1 event coefficient estimates in Case 2. In the first row of Figure 1, we plot the empirical bias of the IPW estimator (dotted lines), the EEP estimator (dash dotted lines), the CC estimator (dashed lines), and the Full estimator (solid lines). The results show that the proposed IPW and EEP estimators exhibit very small bias except for those corresponding to small u’s. In contrast, the CC method produces very biased coefficient estimation. The second row of Figure 1 depicts the empirical standard derivation (SD) and the average standard errors (ASE) (based on the resampling method) versus expected frequency u for the proposed IPW and EEP estimators. We observe that the empirical SD and ASE agree with each other very well. The standard errors of IPW estimator are slightly larger than those of EEP estimator.

Figure 1.

The simulation results for event type 1 coefficients with Case 2. IPW, the inverse probability weighting estimator; EEP, the estimating equation projection estimator; CC, the complete-case estimator; Full, the full data estimator. SD, the empirical standard derivation. ASE, the average standard error. CP, the coverage probability.

In our simulations, we evaluate both resampling-based and sample-based inference procedures. For the resampling method, the resampling size of 100 is chosen. The coverage probabilities of 95% confidence intervals obtained from both inference approaches are depicted in the third row and fourth row of Figure 1 respectively. It shows that the resampling procedure and the sample-based strategy have quite comparable performance. The resulting coverage probabilities (CP) of the two proposed estimators are fairly close to the nominal value; the resampling procedure may perform slightly better than the sample-based method. This is consistent with the observed large bias of the CC estimator. The computation of the sample-based approach is about 2 to 3 times faster than that of the resampling procedure.

We have very similar observations on the results from fitting the GART model for type-2 events in Case 2 and results obtained in Case 1; these results are relegated to the Supplementary Materials (see Figures S1-S3). In some unreported simulations, we find that using a different kernel function, such as the Epanechnikov kernel K(x) = 0.75(1 − x²)I(|x| < 1), yields little change to the empirical performance of the proposed estimators.

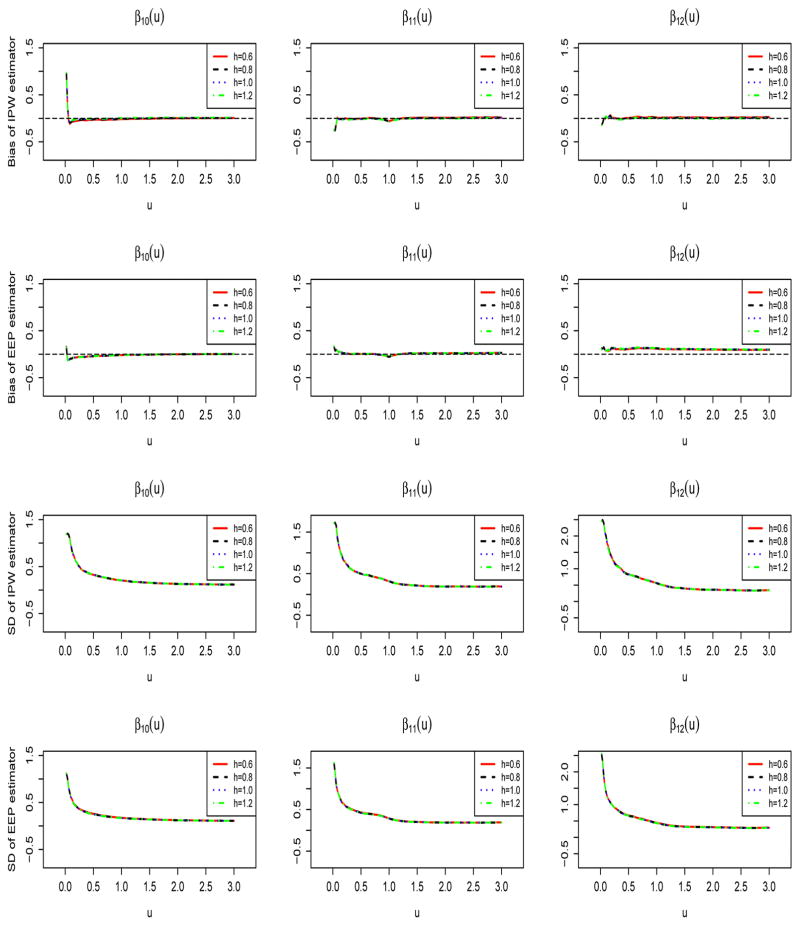
We also investigate the sensitivity of the proposed procedures to bandwidth selection. We consider Case 2 with 500 replications of sample size n = 200. Figure 2 presents the proposed coefficient estimates for type-1 event with different choices of h: h = 0.6 (solid lines), h = 0.8 (dashed lines), h = 1.0 (dotted lines) and h = 1.2 (dot dashed lines). The results for type-2 event are presented in Figure S4 of the Supplementary Materials. As seen from Figure 2, the empirical bias and empirical standard derivations corresponding to different values of h are almost the same. This indicates that the performance of the proposed IPW and EEP methods are insensitive with respect to the choice of bandwidth h.

Figure 2.

The comparison of event type 1 coefficient estimates for Case 2 under different values of h. IPW, the inverse probability weighting estimator; EEP, the estimating equation projection estimator. SD, the empirical standard derivation.

6. A Real Data Example

Cystic fibrosis (CF) is a life-limiting genetic disorder with an incidence rate in Caucasian approximately 1:3400 (Boat and Acton, 2007). Cystic Fibrosis Foundation (CFF) patient registry (CFFPR) that has documented the diagnosis, treatments and health of all known cystic fibrosis patients at more than 120 CFF-accredited care centers across the United States since 1970s (Knapp et al., 2016). Pseudomonas aeruginosa (Pa) is one of major pathogens in CF lungs that leads to chronic infections and lung function decay. Pa types, mucoid, nonmucoid, or mucoid status unknown, have been reported in CFFPR. It is of scientific interest to assess how the recurrence times of nonmucoid Pa infections and mucoid Pa infections are influenced respectively by potential risk factors in young CF children.

We consider a dataset from the 2007 CFFPR registry data, which includes 4,144 subjects who were born after 1997 and had known diagnosis factor mode before the end of year 2007. During the follow-up of these subjects, 9,615 nonmucoid Pa infections and 3,393 mucoid Pa infections were recorded, along with 1,585 Pa infections with unknown types. The percentage of nonmucoid, mucoid, and missing Pa infection types are 65.9%, 23.2%, and 10.9% respectively. The number of positive Pa infections (nonmucoid and mucoid) observed for each subject ranges from 1 to 40, with mean 3.5 and median 2.

In our data analysis, with time origin set as the birth of each subject, the recurrent event time T^(j) stands for the age of a CF child at his/her jth Pa infection, L corresponds to the age at registry entry, and R corresponds to the age at death or the last follow-up. In our dataset, 13.8% of subjects entered the study right after birth, and L = 0 in these cases. We consider risk factors including sex and diagnosis factor (meconuim ileus status; newborn screening; family history and signs/symptoms). The summary statistics of these risk factors are provided in Table 1. The covariates included in our models are coded as Sex, 1 if the subject was female and 0 otherwise; MI, 1 if the subject is diagnosed by meconuim ileus and 0 otherwise; NewScreen, 1 if the subject is done newborn screening and 0 otherwise; FamilyHis, 1 if the subject’s family has the history of CF and 0 otherwise.

Table 1.

Summary Statistics of Sex and Diagnosis Factor in the CFFPR dataset

	Sex		Diagnosis Factor
	Male	Female	MI	NewScreen	FamilyHis	Symptoms
n (%)	2031 (49%)	2113 (51%)	1090 (26%)	624 (15%)	197 (5%)	2233 (54%)

MI: meconuim ileus; NewScreen: newborn screening; FamilyHis: family history; Symptoms: signs/symptoms

We apply the proposed methods to this CFFPR dataset with the covariates described above, setting g(u) = 1. We choose the Normal kernel function and the bandwidth h = 4n^−1/3sd(T) as suggested in Qiu et al. (2017). We use the proposed resampling procedure for inference such as confidence intervals. In our analysis, we adopt the MAR assumption (4) with Z_i including covariates, Sex, MI, NewScreen, and FamilyHis, which means, these observed covariates can fully account for the missingness of the PA infection type. This is a reasonable assumption for the CFFPR dataset because, according to the investigation of Gouskova et al. (2017), the two major causes of missing PA infection types are (a) lack of technology to classify the type of PA infection as mucoid or nonmucoid; (b) data recording negligence. Since the MAR assumption is not statistically verifiable (Little and Rubin, 2002), we perform a sensitivity analysis by considering different specifications of Z_i. As shown in the Supplementary Materials (see Section S4), when Z_i only includes NewScreen and FamilyHis, the analysis results are very similar to those in Figure 4. This suggests the robustness of the proposed method to the variations of the adopted MAR model.

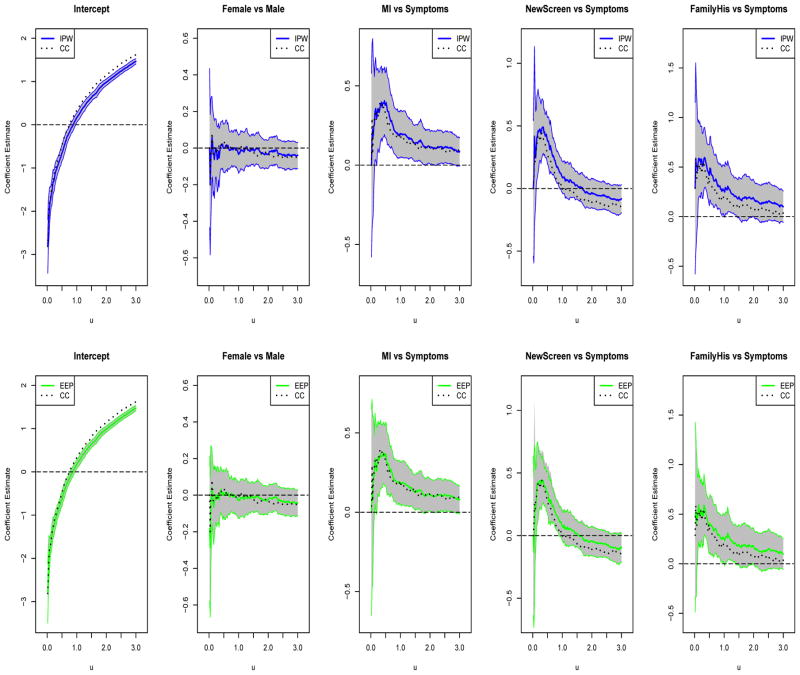
Figure 4.

CFFPR data example: the proposed IPW coefficient estimates (solid lines in the top row) and their corresponding 95% pointwise confidence intervals, the proposed EEP coefficient estimates (solid lines in the bottom row) and their corresponding 95% pointwise confidence intervals, along with the complete-case (CC) coefficient estimates (dotted lines) for mucoid PA infection

In Figures 3 and 4, we plot the estimated coefficients along with the 95% pointwise confidence intervals for the coefficients for the nonmucoid and mucoid Pa infections respectively. The inverse probability weighting (IPW) estimates are shown in the first row in solid lines, while the estimating equation projection (EEP) estimators are plotted in solid lines in the second row. It can be seen that the two proposed estimators demonstrate little difference.

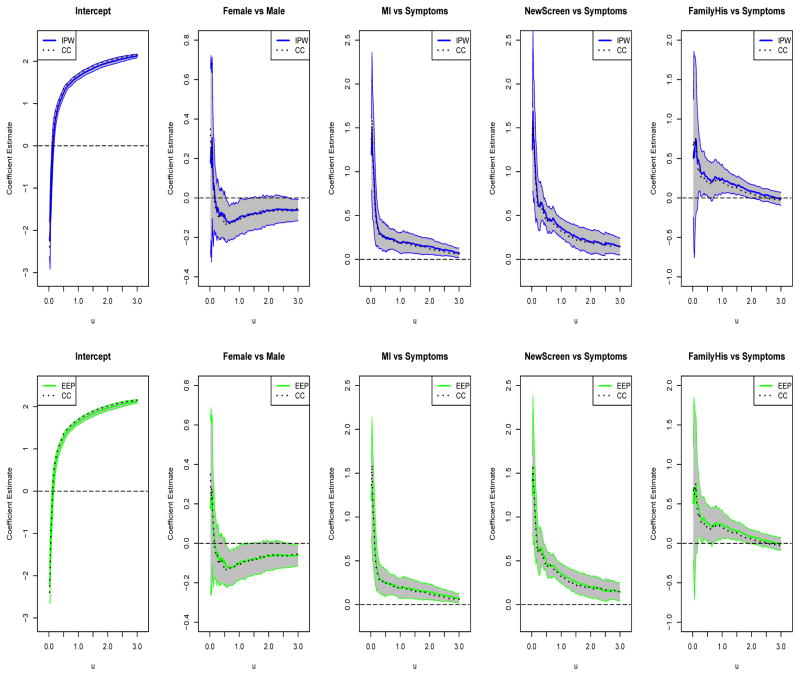
Figure 3.

CFFPR data example: the proposed IPW coefficient estimates (solid lines in the top row) and their corresponding 95% pointwise confidence intervals (shaded); the proposed EEP coefficient estimates (solid lines in the bottom row) and their corresponding 95% pointwise confidence intervals (shaded), along with the complete-case (CC) coefficient estimates (dotted lines) for nonmucoid PA infection

In Figures 3 and 4, the intercept coefficient estimates represent the estimated log time to expected frequency of nonmucoid or mucoid Pa infection for the reference group, which consists of CF boys diagnosed by signs/symptoms. For example, for this reference group, the time from birth to expected nonmucoid and mucoid Pa infection frequency of 1.0 are approximately 0.36 and 2.04 years respectively. This indicates a much later development of mucoid Pa infection compared to nonmucoid Pa infection in CF children, which is consistent with the common clinical manifestations of Pa infections.

The nonintercept coefficient estimates depict the estimated effects of covariates, where negative ones indicate more rapid progression to recurrence of nonmucoid or mucoid Pa infections. We see from Figure 3 that there is no significant difference in recurrence times of nonmucoid Pa infections between CF boys and CF girls. Newborn screening (NewScreen) shows a positive effect on the time to expected frequency of nonmucoid Pa infections with u < 0.1; however, its effect seems to diminish at larger u’s. The estimated coefficients for MI and FamilyHis are mostly significantly above zero. These results may reflect the benefits of early CF diagnosis, as CF children typically are diagnosed earlier through MI, new born screening, and family history than through signs/symptoms.

Considering mucoid Pa infections, we have some different findings regarding the covariate effects. That is, in Figure 4, the estimated coefficients for Sex are significantly negative for most u’s, suggesting that CF girls tend to develop mucoid Pa infections sooner than CF boys. The estimated coefficients for MI, NewScreen and FamilyHis are significantly positive except for those with large u’s, indicating s that CF children diagnosed by symptoms developed mucoid PA earlier than those diagnosed by the other methods. Importantly, the beneficial effect of newborn screening on mucoid Pa is stronger than that on the nonmucoid Pa. This finding is encouraging in that early diagnosis of newborn screening significantly delays the onset of mucoid Pa, as well as repeated mucoid Pa.

In Figures 3 and 4, we also plot the coefficient estimates of the complete-case (CC) analysis (dotted lines). Some major discrepancy exists between the CC analysis, which naively exclude Pa infections with unknown Pa types, and our estimates for nonmucoid Pa infections. Specifically, the intercept coefficients for nonmucoid Pa estimated by the CC method are significantly larger than those from the proposed IPW and EEP methods. This indicates that the CC analysis would significantly overestimate the time to expected frequency of nonmucoid Pa infection. One possible explanation is that the majority of missing Pa types may in fact be nonmucoid Pa but are ignored by the CC analysis, leading to over-optimistic estimates for time to expected frequency of nonmucoid Pa infections. Moreover, the proposed estimates and the naive CC estimates generally diverge as u increases. This may relate to the fact that the total number of events with missing event type cumulates over time.

We also conduct constancy tests for each covariate effect. The weight function is chosen as Ξ(u) = 2I{u ≤ (u_L + u_U)/2}/(u_U − u_L) with u_L = 0.02 and u_U = 3. Our constancy tests confirm the diminishing pattern of the estimated coefficients for NewScreen observed in Figure 3, with p < 0.01. Our tests also suggest that constant effects may be adequate for all the other covariates considered in the fitted GART models. The average covariate effect estimates provided in Table 2 may serve as the estimates for these constant effects.

Table 2.

The CFFPR example: Estimated average covariate effects (EstAvg) and the corresponding standard errors (SE)

Event Type	Method		Sex	MI	FamilyHis
Mucoid	IPW	EstAvg	−0.066	0.219	0.173
		SE	0.038	0.049	0.065
	EEP	EstAvg	−0.067	0.217	0.172
		SE	0.038	0.048	0.063
Nonmucoid	IPW	EstAvg	−0.019	0.182	0.260
		SE	0.043	0.050	0.095
	EEP	EstAvg	−0.020	0.170	0.248
		SE	0.042	0.048	0.093

7. Concluding Remarks

In this paper, we investigate the generalized accelerated recurrence time model for multivariate recurrent event data with missing event types. We employ two strategies, the inverse probability weighting and the estimating equation projection, to handle the missing event types. The two proposed estimators have desirable asymptotic properties and are shown to be asymptotically equivalent.

As discussed in Section 2, we adopt a missing at random (MAR) mechanism for the missing event types, which is weaker than the assumption of missing completely at random. Our MAR mechanism implies π_k(t, z) is the same for each event type k. This may not be realistic in practice when some types of events are more likely to be missing. In that case, the event types are not missing at random (NMAR). Some additional unverifiable modeling of the event type missing mechanism would be warranted to tackle the non-identifiability issue. When the event types are missing at random but under a mechanism changing over time, we expect the kernel estimator of π(t, z) or p_k(t, z) would take a much more complicated form and likely lack sufficient efficiency with moderate sample sizes. Developing methods for handling these situations merits future research.

Regarding the bandwidth h for the nonparametric kernel estimators of π(t, z) and p_k(t, z), the optimal bandwidths may be chosen by minimizing the mean square errors of the kernel estimators, but may be difficult to estimate. Several authors (Wang and Wang, 2001; Chen et al., 2015; Qiu et al., 2017) have studied data-driven methods for selecting bandwidths in the classical survival setting with only non-recurrent events. It is worth investigating their extensions the settings with multivariate recurrent events data.