Electrocardiogram Sampling Frequency Range Acceptable for Heart Rate Variability Analysis

Abstract

Objectives

Heart rate variability (HRV) has gained recognition as a noninvasive marker of autonomic activity. HRV is considered a promising tool in various clinical scenarios. The optimal electrocardiogram (ECG) sampling frequency required to ensure sufficient precision of R–R intervals for HRV analysis has not yet been determined. Here, we aimed to determine the acceptable ECG sampling frequency range by analyzing ECG signals from patients who visited an emergency department with the chief complaint of acute intoxication or overdose.

Methods

The study included 83 adult patients who visited an emergency department with the chief complaint of acute poisoning. The original 1,000-Hz ECG signals were down-sampled to 500-, 250-, 100-, and 50-Hz sampling frequencies with linear interpolation. R–R interval data were analyzed for time-domain, frequency-domain, and nonlinear HRV parameters. Parameters derived from the data on down-sampled frequencies were compared with those derived from the data on 1,000-Hz signals, and Lin's concordance correlation coefficients were calculated.

Results

Down-sampling to 500 or 250 Hz resulted in excellent concordance. Signals down-sampled to 100 Hz produced acceptable results for time-domain analysis and Poincaré plots, but not for frequency-domain analysis. Down-sampling to 50 Hz proved to be unacceptable for both time- and frequency-domain analyses. At 50 Hz, the root-mean-squared successive differences and the power of high frequency tended to have high values and random errors.

Conclusions

A 250-Hz sampling frequency would be acceptable for HRV analysis. When frequency-domain analysis is not required, a 100-Hz sampling frequency would also be acceptable.

I. Introduction

Heart rate variability (HRV), characterized by fluctuations in the time interval between successive heart beats, was first suggested as a marker of fetal distress in 1965, and it subsequently gained recognition as a noninvasive marker of autonomic activity [1]. HRV is considered a promising tool for predicting mortality in emergency patients transported via ambulance or trauma victims [2,3], predicting sudden cardiac arrests [4], and diagnosing poisoning or overdose [5,6]. The optimal electrocardiogram (ECG) sampling frequency required to ensure sufficient precision of R–R intervals for HRV analysis is yet to be determined. Although some previous physiological studies have recommended a minimum sampling frequency of ≥500 Hz, claiming that a smaller sampling frequency may result in stronger high-frequency components in spectral analysis [1,7], some have argued that lower sampling frequencies, such as 100 Hz or even 50 Hz, might be acceptable with interpolation [8,9]. While modern microprocessors have sufficient calculating power for signals sampled at 1,000 Hz or more, devices specifically designed for research purpose are usually required to acquire data with such high sampling frequencies [2,3,10]. To date, results from studies on sampling frequencies have been derived from healthy subjects, and few such studies have incorporated actual patient populations. Here, we aimed to determine the acceptable ECG sampling frequency range by analyzing ECG signals from patients who visited an emergency department with the chief complaint of acute intoxication or overdose.

II. Methods

The study utilized ECG signals collected for previously reported research on the utility of HRV in the diagnosis of acute cholinesterase inhibitor poisoning, which involved 83 adult patients who visited an emergency department with the chief complaint of acute poisoning in the earliest period of the patients' stay in the emergency department that provided data of appropriate quality. Emergency treatments, including tracheal intubation, intravenous access, and the first dose of an antidote such as atropine, were given prior to signal acquisition [6]. The ECG signals were acquired and digitized at a 1,000-Hz frequency using a custom-built sampling device from the analog ECG output port of a LIFEPAK 20 monitor-defibrillator (Physio-Control, Redmond, WA, USA). The Physio-Toolkit software package was used to process the ECG signals [11]. The original 1,000-Hz ECG signals were down-sampled to 500-, 250-, 100-, and 50-Hz sampling frequencies with the xform command, which applies linear interpolation when altering sampling frequencies. The timing of QRS waves was detected by the gqrs command and subsequently converted into R–R interval data with the ann2rr command. One case was excluded from further analysis because the gqrs function could not reliably detect QRS complexes from the data on 1,000-Hz signals.

The R–R interval data were analyzed for time-domain, frequency-domain, and nonlinear HRV parameters using Kubios HRV Standard version 3.0 (Kubios Oy Ltd., Kuopio, Finland) from 5-minute sections of the signal tracing [12]. The HRV parameters used for further analysis and their definitions are summarized in Table 1. Parameters derived from data on the 500-, 250-, 100-, and 50-Hz down-sampled frequencies were compared to those derived from data on 1,000-Hz signals, and Lin's concordance correlation coefficients (CCC) with respective 95% confidence intervals (CI) were calculated. The sampling frequencies were considered unacceptable when the CCCs for the respective parameters were <0.9 [13,14]. Bland-Altman analysis was performed to determine the limits of agreement between results from different frequencies. MedCalc Software version 18.2.1 (Med-Calc Software bvba, Ostend, Belgium; http://www.medcalc.org; 2018) was used for statistical analysis.

Table 1. List of heart rate variability parameters used in the analyses.

III. Results

The CCCs of HRV parameters derived from the variable sampling frequencies compared with those derived from the 1,000 Hz signals are presented in Table 2. Down-sampling to 500 or 250 Hz resulted in excellent concordance. Signals down-sampled to 100 Hz produced acceptable results for time-domain analysis and Poincaré plots, but not for frequency-domain analysis. Down-sampling to 50 Hz proved to be unacceptable for both time- and frequency-domain analyses. Further information about the error pattern is presented as Pearson's ρ and bias correction factor (C_b). Pearson's ρ represents deviations of dots from the 45° line of the scatterplot, indicating precision, and C_b represents how far the best-fit line deviates from the 45° line and can be interpreted as a measure of accuracy [13]. Table 2 shows that the decrease in C_b is insignificant down to 100 Hz, but it becomes significant with the root-mean-squared successive differences (RMSSD), power of low frequency (LF), power of high frequency (HF), and Poincaré plot width at 50 Hz.

Table 2. CCCs of heart rate variability parameters from down-sampled ECGs in comparison with parameters from 1,000-Hz original ECG.

CCC: concordance correlation coefficient, ECG: electrocardiogram, RMSSD: root-mean-squared successive differences, pNN50: proportion of NN50 to total number of R–R intervals, VLF: power of very low frequency, LF: power of low frequency, HF: power of high frequency, CI: confidence interval.

^aPearson's ρ (precision), ^bbias correction factor C_b (accuracy).

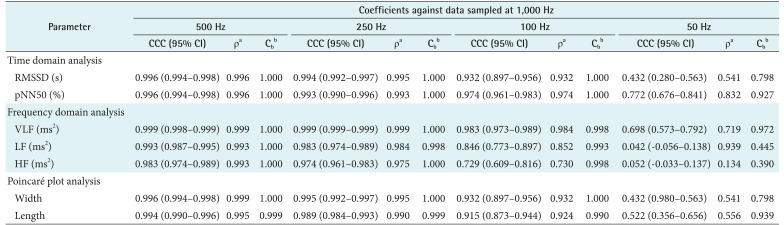
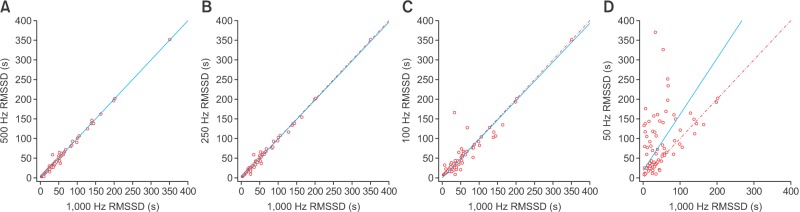
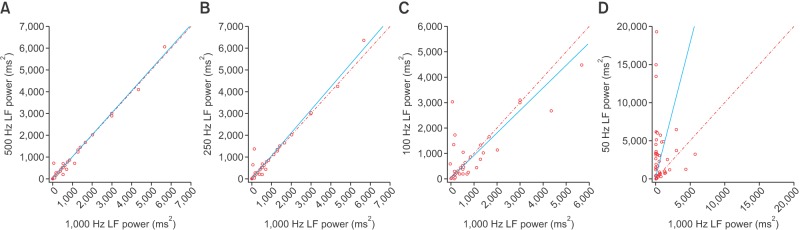
Scatterplots of the RMSSD, LF, and HF power spectral density from various frequencies in comparison with those from 1,000 Hz are presented in Figures 1, 2, and 3, respectively. At 50 Hz, the RMSSD and HF power tended to have high values and random errors. The scatterplots graphically represent the correlation as well as the precision and accuracy of the down-sampled data.

Figure 1. Scatterplot of the root-mean-squared successive differences (RMSSD) derived from down-sampled electrocardiography recordings in comparison with those from 1,000-Hz signals: (A) 500 Hz, (B) 250 Hz, (C) 100 Hz, and (D) 50 Hz. Lines of equity and regression lines are also displayed.

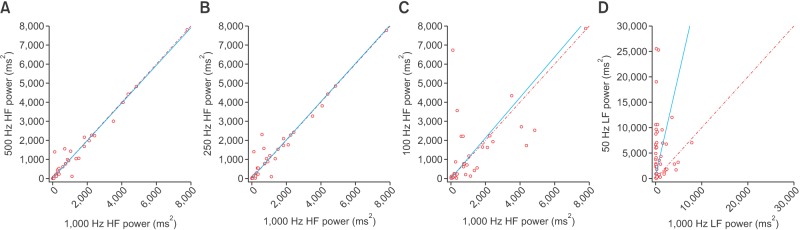
Figure 2. Scatterplot of the low-frequency (LF) power spectral density derived from down-sampled electrocardiography recordings in comparison with those from 1,000-Hz signals: (A) 500 Hz, (B) 250 Hz, (C) 100 Hz, and (D) 50 Hz. Lines of equity and regression lines are also displayed.

Figure 3. Scatterplot of the high-frequency (HF) power spectral density derived from down-sampled electrocardiography recordings in comparison with those from 1,000-Hz signals: (A) 500 Hz, (B) 250 Hz, (C) 100 Hz, and (D) 50 Hz. Lines of equity and regression lines are also displayed.

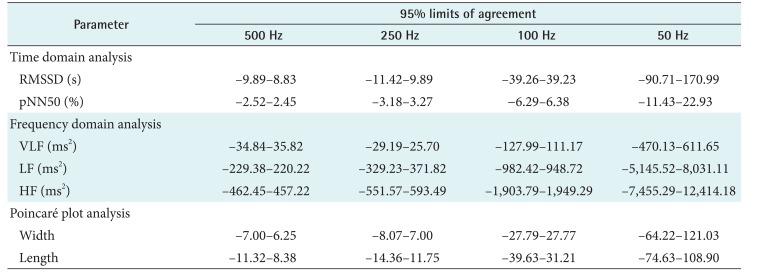
The results from the Bland-Altman plot analysis are summarized in Table 3, and plots comparing parameter values from 100-Hz down-sampled data with those from 1,000-Hz sampled data are presented in Figure 4. Although the agreement limits of the frequency-domain parameters look wide in Table 3, the dots in the Bland-Altman plot are aggregated in a rather narrow range. The larger limits of agreement are due to the larger actual values.

Table 3. Results of Bland-Altman plot analysis summarized as percentage differences from 95% limits of agreement of heart rate variability parameters from down-sampled ECGs in comparison with parameters from 1,000-Hz original ECG.

ECG: electrocardiogram, RMSSD: root-mean-squared successive differences, pNN50: proportion of NN50 to total number of R–R intervals, VLF: power of very low frequency, LF: power of low frequency, HF: power of high frequency.

Figure 4. Bland-Altman plots of agreement between heart rate variability parameters from 100-Hz down-sampled signals and those from 1,000-Hz signals: (A) root-mean-squared successive differences (RMSSD), (B) proportion of NN50 to total number of R–R intervals (pNN50), (C) power of very low frequency (VLF), (D) power of low frequency (LF), (E) power of high frequency (HF), (F) Poincaré plot width, and (G) Poincaré plot length. Lines and values indicating 95% limits of agreement are presented.

IV. Discussion

This study compared the values of HRV parameters calculated from ECG tracings with those calculated from various sampling frequencies acquired from patients from the emergency department. HRV is known to be associated with the interplay of the sympathetic and parasympathetic autonomic nervous systems [15]. As many commercial devices provide automated measurements of HRV, the meaning and significance of HRV parameters from various sources began to create confusion. To solve this problem, the European Society of Cardiology and the North American Society of Pacing and Electrophysiology published standardized methods of measurement and nomenclature [1]. Because some of the suggested parameters depend on recording length, the durations of recordings need to be standardized for analysis. Usually, short-term 5-minute recordings or 24-hour long-term recordings are used [1]. We used 5-minute recordings because the dataset was collected to evaluate the utility of HRV in the diagnosis of acute poisoning. Parameters used to quantify HRV are categorized into time-domain, frequency-domain, and nonlinear parameters. Time-domain parameters are the simplest to analyze and are derived from statistical summarization of R–R interval variations or differences in consecutive R–R intervals [6]. Frequency-domain analysis incorporates Fourier transformation of R–R time series and calculation of power spectral density [6]. Spectral power in the HF band (0.15–0.4 Hz) of the HRV signal is believed to reflect the cardiac vagal activity influenced by the respiratory cycle, whereas the LF band (0.04–0.15 Hz) is related to the baroreceptor control and is mediated by both vagal and sympathetic systems [10]. Poincaré plot analysis is a nonlinear method of HRV analysis utilizing a scatterplot of the current R–R interval plotted against the preceding R–R interval. The plot provides summary information as well as detailed beat-to-beat information on the behavior of the heart [16].

One of the many important choices faced in designing studies on HRV is the sampling frequency. Earlier recommendations were to use higher sampling frequencies, perhaps ≥500 Hz, and the most common sampling frequencies used in the studies conducted in the period from 1999 to 2002 were 500 and 1,000 Hz [1,15]. However, obtaining ECG signals with such high sampling frequencies in a clinical setting is not always practical because the signals that can be obtained are often limited by the technical capability of available medical devices. In studies analyzing the ECG signal data downloaded from defibrillator monitors [3] or Holter recorders [10], the available sampling frequencies were limited to 125 Hz. In the era of telemonitoring and wearable devices, determining lower acceptable sampling frequency ranges has become more important because of limitations imposed by smaller device sizes and lower battery capacities.

Our results indicate that a 250-Hz sampling frequency would provide excellent results for HRV analysis. If frequency-domain analysis is not required, a 100-Hz sampling frequency would be acceptable. Our results are comparable to those of Ziemssen et al. [8], who reported a good correlation of RMSSD values between ECG sampling frequencies of 500 and 100 Hz. However, the scatterplots from the present study reveal more variation than that from the study of Ziemssen et al. [8], probably because of more variation in the health conditions of the subjects. Although Mahdiani et al. [9] claimed that a 50-Hz sampling frequency could be acceptable for time-domain analysis, our results indicate that a 50-Hz sampling frequency would be unacceptable, whereas a 100-Hz sampling frequency would be acceptable for time-domain analysis. There are some differences between the methods of the present study and that of Mahdiani et al. [9]. First, the present study included acute emergency patients rather than healthy individuals; therefore, more variations in autonomic status and interference influenced the results. Second, linear interpolation was applied when the ECG signals in our study were down-sampled, whereas Mahdiani et al. [9] used bicubic interpolation. Bicubic interpolation might have produced more accurate R–R intervals and thus resulted in better correlation with signals sampled at higher frequencies. However, this study aimed to evaluate the possibility of utilizing clinically available devices, and it cannot be guaranteed that bicubic interpolation is commonly used in available devices. The simpler approach used in our study would be more suitable for the intended application.

Bland-Altman plot analysis was conducted to assess the agreement between two methods of measurement [17]. Although the Bland-Altman plot is normally a plot of differences against the mean of two measurements, we used the parameters calculated from 1,000-Hz signals as the reference method rather than the mean of values from the two sampling frequencies because sampling with frequencies higher than 500 Hz is the established standard research method in HRV analysis [18]. Table 3 summarizes how much deviation from the standard method is expected when lower sampling frequencies are used, and the limits of agreement should be considered when interpreting such data.

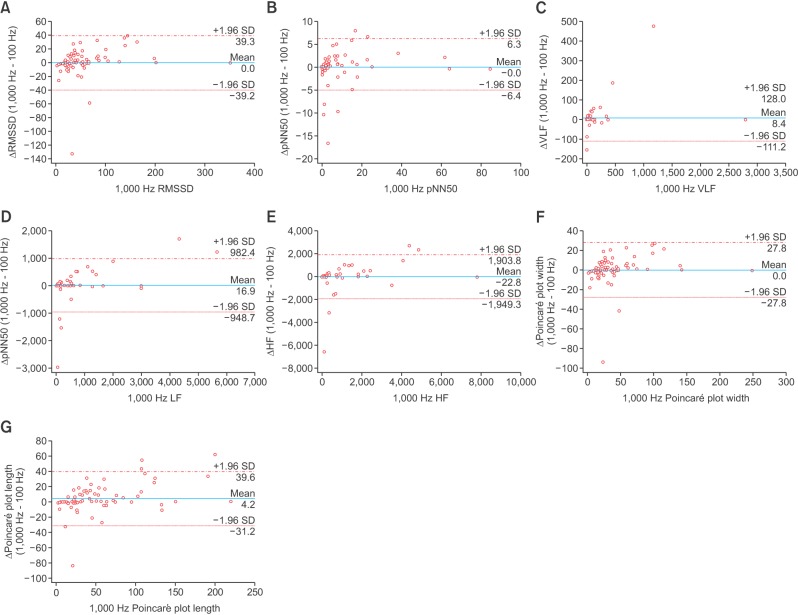
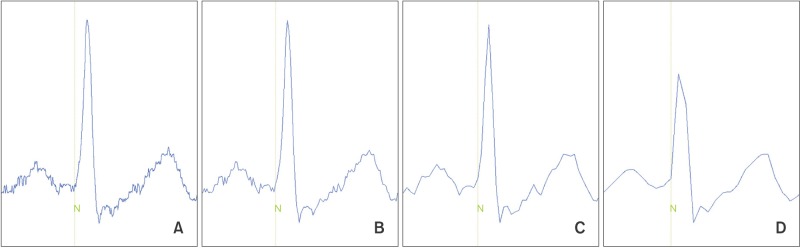
It appears that HF elements are prone to loss by down-sampling. ECG waveforms and the detected points for each corresponding QRS complex are displayed in Figure 5. The gqrs command of the Physio-Toolkit identifies the beginning points of QRS complexes instead of QRS peak points. The Physio-Toolkit is by far the most trusted and widely used HRV software [19], and the performance of the gqrs command has proved to be excellent [20]. Figure 6 presents the R–R series with 1,000- and 50-Hz sampling frequencies derived from the ECG of a patient poisoned with an organophosphate insecticide. The loss of small details of the R–R intervals is evident at the 50-Hz sampling frequency. This is thought to be attributable to the poor concordance of HF power, especially by exaggeration of the power spectral density at certain frequencies as observed in Figure 2.

Figure 5. Electrocardiograms of single cardiac cycle and onset of QRS complexes detected by the gqrs command in Physio-Toolkit from various sampling frequencies. (A) 1,000 Hz, (B) 250 Hz, (C) 100 Hz, and (D) 50 Hz.

Figure 6. R–R interval series graph from electrocardiography recordings sampled at frequencies of (A) 1,000 Hz and (B) 50 Hz. Loss of detailed information of R–R intervals is noted.

There were some limitations of this study. The study utilized an ECG signal dataset obtained from ED patient with acute poisoning. The data were collected for the purpose of validating the diagnostic utility of HRV parameters in identifying substance intoxication; in this clinical context, obtaining a reliable history is often difficult or impossible, especially in cases of acute poisoning [6,21]. The HRV results would reflect the effects of toxic substances as well as therapeutic interventions and anxiety of ED patients. The results cannot be generalized to those in different clinical situations. However, we believe that the results can provide meaningful insight to the scientific community because previous studies on sampling frequency for HRV analysis have been limited to healthy individuals, and data on patient populations have been very rarely considered. Additionally, there are several different algorithms for signal interpolation and QRS detection. Different down-sampling and processing algorithms would produce results different from those of this study.

In conclusion, a 250-Hz sampling frequency would be acceptable for HRV analysis in cases of acute poisoning. When frequency-domain analysis is not required, a 100-Hz sampling frequency would also be acceptable.