Abstract
The aim was to evaluate the kinetic parameters, total color differences (∆E*) and browning index differences (∆BI) of air flow pineapple drying. The experiments were performed on air temperatures at 60 and 70 °C, and air velocities at 1.5 and 2.0 m/s. The kinetic parameter (k) increased when air temperature was increased for all air velocity. The effective diffusivity coefficient (Deff) increased as high as the temperature of the heating medium. The variation of Deff of swirling flow was ranging from 6.72 × 10−9 to 10.23 × 10−9 m2/s, while the variation of Deff of non-swirling flow was ranging from 6.40 × 10−9 to 9.42 × 10−9 m2/s. The drying time of swirling flow was shorter than non-swirling flow in each drying condition. Moreover, the ∆E* and ∆BI of pineapple in swirling flow were lower than that obtained from non-swirling flow. Therefore, the convective drying using swirling flow can be minimized for drying time and color deterioration.
Keywords: Pineapple, Drying kinetic, Effective diffusivity coefficient, Browning index differences, Total color differences
Introduction
Pineapple (Ananas comosus) is a tropical fruit and is produced in several countries such as Thailand, Brazil, India, Philippines and China. Pineapple contains important nutrients such as carbohydrates, sugars, Vitamin A and C and beta carotene, protein, fat, ash, fiber and antioxidants introducing to flavonoids, citric and ascorbic acid. Moreover, pineapple has attractive sensorial such as texture, flavor, taste and color [28]. In 2012, Thailand produced 2,650,000 metric tons of pineapples and is the first largest producer of pineapple in the world [13]. However, pineapple is perishable fruit. So, an alternative method to preserve the quality and extend shelf life of pineapple is drying.
Convective drying, especially tray drying, has been widely used as a method for preserving the agricultural product because it is simple to operate and inexpensive. In many researches, the pineapples were dried by convective drying at various conditions. The air temperature was used in a wide range of 40–80 °C while the air velocity was performed at 0.5 to 3.8 m/s [1, 10, 28]. Nevertheless, the convective drying has the negative impact on the product qualities such as color, taste, flavor, texture and nutrient content because of high air temperature exposure and long drying time [20].
In order to improve quality dried product, the combination of a new technologies with convective drying is possible to preserve product quality e.g. hot air drying with microwave, radio-frequency, infrared radiation and power ultrasound enhancement [19]. One important characteristic of the convective drying that can affect the product quality is the flow type which is normally two kinds: swirling flow and non-swirling flow. The non-swirling flow was normally used in the convective drying. The swirling flow was ordinary found in spray and fluidized bed dryer which sample was impelled together with the air flow. So, heat and mass transfer of the swirling flow type dryer were high.
In tray dryer, swirling flow type is less well-known when compared to the non-swirling flow type, although some researchers have studied the effect of swirling flow on drying of potato, pumpkin, and apple [2, 3]. Compared to non-swirling air flow, the swirling air flow can be used for heat and mass transfer enhancement in drying process [16]. Çakmak and Yildiz [6] studied on grape seed drying in a new designed solar dryer with swirling flow. The drying processes were performed at three different air velocities (0.5, 1 and 1.5 m/s) with swirling flow and non-swirling flow. The results showed that the drying time decreased by increasing the air velocity. Moreover, the swirling flow provided the shorter drying time than the other that without swirling flow at the same air velocity. Özbey and Söylemez [23] investigated the effect of swirling flow on fluidized bed drying of wheat grains. They reported that the swirling flow enhanced the drying capability of granular wheat material in fluidized bed dryer up to 38% increase when compared to non-swirling flow. The aim of this experiment was to evaluate the effects of air flow on pineapple drying behavior which was compared between swirling flow type and non-swirling flow type in terms of kinetics including total color differences (∆E*) and browning index differences (∆BI).
Materials and methods
Sample preparation
Pineapples were purchased in a local market (Nakhon Pathom, Thailand). For the sample selection, the pineapples were measured the total soluble solid (TSS) content and firmness. The initial TSS and firmness (expressed as N) were determined by refractometer (Optika HR-130, Italy) and penetrometer (FT 327, Italy) with a 8 mm tip, respectively. The initial TSS and firmness of each sample could be 13.46 ± 0.84° Brix and 26.87 ± 5.15 N, respectively. The pineapples were washed, peeled and cut into a slab shape with sized in 1 × 2 × 1 cm (width × lengths × thickness). The initial moisture content was 711.63 ± 5.60% (dry basis) according to AOAC method [4].
Experimental setup
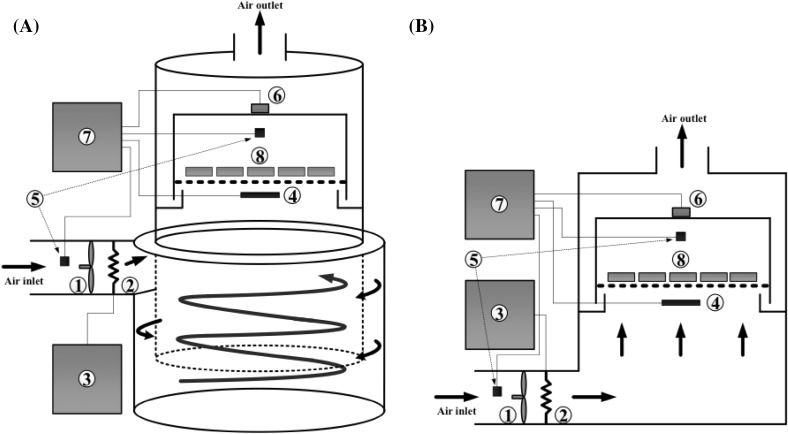
The experimental setup of swirling flow and non-swirling flow type dryer, as presented in Fig. 1, consisted of a fan, heater, temperature controller and drying chamber. However, the shape of the drying chamber for the hot air dryer was entirely different. The drying chamber of swirling flow type dryer was a cyclonic shape and the other one was a rectangular shape as shown in Fig. 1(A) and (B), respectively. The cyclonic drying chamber was constructed by stainless steel in size 0.5 cm thickness. The stainless steel was a concentric cylinder formed with two layers. The outer layer is sized in a 50 cm diameter and 30 cm height and the inner layer is sized in 40 cm diameter and 50 cm height cylinder. The space of these two layers was sealed by stainless steel sheet. The drying chamber of non-swirling flow type dryer was rectangular shape and manufactured by stainless steel with sized in 30 × 30 × 50 cm (width × length × height). This sieve of tray was manufactured with stainless steel in square shape that is sized in 25 × 25 cm.
Fig. 1.
The experimental setup of (A) swirling flow type dryer; and (B) non-swirling flow type dryer was comprised (1) fan; (2) heater; (3) temperature controller; (4) PT100; (5) temperature and humidity sensors; (6) load cell; (7) data loggers; and (8) samples
The drying air was forced through the drying chamber and sample tray. The air velocity was adjusted manually. The air velocity could be adjusted between 0 and 3 m/s. The heating system consisted of a 1000 W of electric wire heater placed at a channel of air inlet and connected with temperature controller as illustrated in Fig. 1. The air temperature was adjusted in the range of 40–90 °C.
Drying procedures
The air temperature and air velocity were set to a desired value at 60 and 70 °C, and 1.5 and 2.0 m/s, respectively. These drying conditions were mostly selected and suitable for air-dried pineapple production [1, 10, 28]. Samples were placed on the tray and then put into the drying chamber after the temperature of drying chamber reached steady state. The samples were dried until moisture content was approximately 15.00% (dry basis). The sample weight, ambient temperature, inlet and outlet relative humidity, inlet and outlet air temperatures were recorded every 1 min by the data logger (Lufft Opus 200). The sample weight was measured by load cell. The inlet and outlet air temperature and relative humidity were measured by temperature and humidity sensor. The ambient temperature was measured by PT100 sensor (Polyscience, USA) while the air velocity passing through the tray was measured by a vane type anemometer (Lutron AM-4201).
Data analysis of drying parameters
The initial moisture content, moisture content at any time and equilibrium moisture content of the sample were estimated from the weight as shown in following equation.
| 1 |
| 2 |
| 3 |
where Xi is the initial moisture content (kg water · kg dry matter−1), wi is the initial weight of the samples (kg), wd is the dry weight of the samples (kg), Xt is the moisture content at any time (kg water · kg dry matter−1), wt is the weight of the samples at any time (kg), Xeq is the equilibrium moisture content (kg water · kg dry matter−1) and weq is the weight of the samples at equilibrium (kg) in each condition. For equilibrium moisture content assessment, the samples in all conditions were dried for 24 h to achieve the constant weight.
In this work, the moisture content of the samples was converted to moisture ratio (MR) by using Eq. (4).
| 4 |
The drying curves were plotted between MR (from the experiment) and drying time. The drying models in Table 1 were considered to clarify the drying curves in our experiment. The non-linear regression analysis was carried out in Microsoft Excel 2010 to evaluate the model constants.
Table 1.
Drying models used to describe pineapple drying
| Model no. | Model | Equation | References |
|---|---|---|---|
| 1 | Lewis | MR = exp(− kt) | [21] |
| 2 | Page | MR = exp(− ktn) | [24] |
| 3 | Henderson and Pabis | MR = a exp(− kt) | [14] |
| 4 | Logarithmic | MR = a exp(− kt) + c | [34] |
where a, c, k and n are the model constants and t is the drying time (s)
The statistical parameters were used to fit the quality of the model. They were the coefficient of determination (R2), the reduced Chi-square (χ2) and the root mean square error (RMSE) which can be calculated as the Eqs. (5), (6) and (7), respectively:
| 5 |
| 6 |
| 7 |
where MRexp is the experimental moisture ratio (−), MRpre is the predicted moisture ratio (−), n is the number of observations and z is the number of constants in the drying model.
The drying rate (DR) of pineapple is defined by the changes in moisture content per each unit of time, which can be calculated by using Eq. (8).
| 8 |
where DR is the drying rate (kg water · kg dry matter−1 s−1), Xt+∆t is the moisture content at t + ∆t (kg water · kg dry matter−1), Xtis the moisture content at t (kg water · kg dry matter−1) and ∆t is the time increment (s).
The effective moisture diffusivity (Deff) was predicted by a diffusion model in Eq. (9) [11, 25]. The diffusion model based on the Fick’s second law of diffusion and used to describe the moisture transport from the sample and drying capability of the dryers. Assumptions of diffusion model are uniform initial moisture content, non-shrinking slab and constant Deff throughout the sample.
| 9 |
where X, Y and Z are the half thickness of the samples (m) in the width, length and thickness, respectively, Deff is the effective moisture diffusivity (m2/s) and n, m and k are the indexes of summations.
The drying time is anticipated to be large enough so that all other terms of the series may be regarded as in significant compared to the first. Therefore, Eq. (9) turned into:
| 10 |
where L2 = X2 + Y2 + Z2.
In the falling rate period, the slope of drying model relates to constant Deff [12]. The Deff in this study, thus, was calculated from the slope (m) of ln(MR) versus drying time [30] as the following equation:
| 11 |
Enhancement index
The Deff was assumed constant value for throughout the process. Thus, the enhancement index (EI) was defined as dimensionless enhancement ratio from Deff of the swirling flow type dryer and normalized by that of the non-swirling flow type dryer as showed in Eq. (12).
| 12 |
where EI is the enhancement index, Deff,Swirling is the effective moisture diffusivity of the swirling flow type dryer (m2/s) and Deff,Non-swirling is the effective moisture diffusivity of the non-swirling flow type dryer (m2/s).
The error of EI was calculated by uncertainties of the effective diffusion coefficient of swirling and non-swirling flow. It can be written as:
| 13 |
Color assessment
The initial and final color of the samples in drying process were measured by Hunter Lab (Miniscan XE plus). Twenty samples were measured and resulted as the mean of its. Color of the samples were reported in L* (lightness), a* (red/green) and b* (yellow/blue). In addition, total color differences (∆E*) and browning index differences (∆BI) were calculated by using Eqs. (14) and (15), respectively [26].
| 14 |
| 15 |
| 16 |
where L*0 is the initial L* value of the samples, a*0 is the initial a* value of the samples, b0 is the initial b* value of the samples and BI0 is the initial BI value of the samples.
Statistical analysis
All experiments were performed in duplicate. The experimental data was statistically analyzed by SPSS v.18. The mean differences of Deff, ∆E* and ∆BI were analyzed by one-way analysis of variance (one-way ANOVA). The Duncan’s multiple range test was used to multiple comparisons of significant treatment effect. A significance level of 0.05 (p < 0.05) was used to determination of significance.
Results and discussion
The drying curves were fitted by different drying models. The best model was selected from the highest R2 values, the lowest RMSE and χ2 values. The fitting statistics of various drying models were shown in Table 2. These models provided the high R2 values in the range of 0.9338–0.9856. The Page model obtained the highest R2 values including the lowest RMSE and χ2 values in almost all drying conditions. Hence, the Page model was used to describe the drying curves of pineapples drying in all drying conditions.
Table 2.
Fitting statistics of various drying models from swirling flow and non-swirling flow type dryer at various conditions
| Drying conditions | Model no. | Model constants | R2 | RMSE | χ 2 |
|---|---|---|---|---|---|
| Swirling flow | |||||
| 60 °C and 1.5 m/s | 1 | k = 1.1436 × 10−4 | 0.9852 | 3.0777 × 10−2 | 9.4740 × 10−4 |
| 2 | k = 1.5076 × 10−4, n = 0.9703 | 0.9856 | 3.0405 × 10−2 | 9.2485 × 10−4 | |
| 3 | a = 0.9980, k = 1.1607 × 10−4 | 0.9850 | 3.1083 × 10−2 | 9.6660 × 10−4 | |
| 4 | a = 1.0000, k = 1.1437 × 10−4, c = 2.4980 × 10−5 | 0.9852 | 3.0777 × 10−2 | 9.4781 × 10−4 | |
| 60 °C and 2.0 m/s | 1 | k = 1.2872 × 10−4 | 0.9529 | 4.6178 × 10−2 | 2.1326 × 10−3 |
| 2 | k = 1.5454 × 10−4, n = 0.9800 | 0.9594 | 4.6093 × 10−2 | 2.1250 × 10−3 | |
| 3 | a = 0.9977, k = 1.2844 × 10−4 | 0.9592 | 4.6175 × 10−2 | 2.1326 × 10−3 | |
| 4 | a = 0.9971, k = 1.2917 × 10−4, c = 1.7680 × 10−3 | 0.9592 | 4.6166 × 10−2 | 2.1319 × 10−3 | |
| 70 °C and 1.5 m/s | 1 | k = 1.4499 × 10−4 | 0.9758 | 3.6672 × 10−2 | 1.3451 × 10−3 |
| 2 | k = 1.4698 × 10−4, n = 0.9985 | 0.9758 | 3.6671 × 10−2 | 1.3454 × 10−3 | |
| 3 | a = 1.0202, k = 1.6845 × 10−4 | 0.9626 | 4.5632 × 10−2 | 2.0832 × 10−3 | |
| 4 | a = 1.0000, k = 1.4499 × 10−4, c = 2.1480 × 10−6 | 0.9758 | 3.6672 × 10−2 | 1.3457 × 10−3 | |
| 70 °C and 2.0 m/s | 1 | k = 1.7221 × 10−4 | 0.9713 | 3.7903 × 10−2 | 1.4370 × 10−3 |
| 2 | k = 1.9318 × 10−4, n = 0.9870 | 0.9713 | 3.7871 × 10−2 | 1.4349 × 10−3 | |
| 3 | a = 1.0360, k = 2.2005 × 10−4 | 0.9422 | 5.3774 × 10−2 | 2.8929 × 10−3 | |
| 4 | a = 0.9999, k = 1.7239 × 10−4, c = 2.8630 × 10−4 | 0.9713 | 3.7903 × 10−2 | 1.4377 × 10−3 | |
| Non-swirling flow | |||||
| 60 °C and 1.5 m/s | 1 | k = 1.1053 × 10−4 | 0.9522 | 5.6395 × 10−2 | 3.1810 × 10−3 |
| 2 | k = 1.3423 × 10−4, n = 0.9791 | 0.9523 | 5.6297 × 10−2 | 3.1707 × 10−3 | |
| 3 | a = 1.0009, k = 1.1531 × 10−4 | 0.9505 | 5.7377 × 10−2 | 3.2936 × 10−3 | |
| 4 | a = 1.0001, k = 1.1046 × 10−4, c = − 1.8970 × 10−4 | 0.9522 | 5.6395 × 10−2 | 3.1824 × 10−3 | |
| 60 °C and 2.0 m/s | 1 | k = 1.2186 × 10−4 | 0.9338 | 3.2431 × 10−2 | 1.0519 × 10−3 |
| 2 | k = 1.0999 × 10−4, n = 1.0111 | 0.9397 | 3.0957 × 10−2 | 9.5851 × 10−4 | |
| 3 | a = 1.0061, k = 1.2262 × 10−4 | 0.9379 | 3.1416 × 10−2 | 9.8719 × 10−4 | |
| 4 | a = 1.0061, k = 1.2255 × 10−4, c = − 1.6190 × 10−4 | 0.9381 | 3.1358 × 10−2 | 9.8365 × 10−4 | |
| 70 °C and 1.5 m/s | 1 | k = 1.3721 × 10−4 | 0.9553 | 3.3084 × 10−2 | 1.0947 × 10−3 |
| 2 | k = 1.4295 × 10−4, n = 0.9955 | 0.9570 | 3.2484 × 10−2 | 1.0554 × 10−3 | |
| 3 | a = 0.9895, k = 1.3577 × 10−4 | 0.9565 | 3.2652 × 10−2 | 1.0663 × 10−3 | |
| 4 | a = 0.9896, k = 1.3549 × 10−4, c = − 5.7130 × 10−4 | 0.9566 | 3.2609 × 10−2 | 1.0636 × 10−3 | |
| 70 °C and 2.0 m/s | 1 | k = 1.5854 × 10−4 | 0.9454 | 5.6577 × 10−2 | 3.2016 × 10−3 |
| 2 | k = 1.8097 × 10−4, n = 0.9853 | 0.9454 | 5.6543 × 10−2 | 3.1984 × 10−2 | |
| 3 | a = 0.9952, k = 1.6368 × 10−4 | 0.9444 | 5.7089 × 10−2 | 3.2604 × 10−3 | |
| 4 | a = 1.0000, k = 1.5845 × 10−4, c = − 1.5620 × 10−4 | 0.9454 | 5.6577 × 10−2 | 3.2029 × 10−3 | |
R2 is the coefficient of determination
χ2 is the reduced Chi-square
RMSE is the root mean square error
Drying curves of pineapples with different air velocity conditions are presented in Fig. 2(A) and (B). The results indicated that the drying time decreased when air temperature and air velocity were increased. Consequently, the driving force for heat transfer and mass transfer between the air and the pineapple was enhanced by the higher air temperature and air velocity [18, 35]. Similarly, previous literatures have been reported in various food products [5, 27]. Moreover, the drying time from swirling flow type dryer was much shorter than the drying time from non-swirling flow type dryer which was about 4–8% when compared with the same condition because the swirling air flow was forced through the sample tray which induced the small eddies on the samples surface. The shear stress of the small eddies disturbed the vapor density. The vapor density was reduced and, as a result, the mass transfer was enhanced [17, 31]. In addition, the air around the pineapples surface was always replaced by heated fresh air resulting from the swirling of the air [31]. Therefore, the surface temperature of the samples was increased and causing the increase of water evaporation in the samples [33]. The non-swirling flow type dryer at 60 °C and 1.5 m/s provided the highest drying time of 532 min while the shortest drying time of 338 min was obtained from the swirling flow type dryer at 70 °C and 2.0 m/s. These results complied with Çakmak and Yildiz [6] who reported the swirling flow in solar dryer led to the increase of the drying rate and the decrease of the drying time.
Fig. 2.
Drying curves and drying rate of pineapples from swirling flow and non-swirling flow type dryer with air temperature at 60 and 70 °C. (A) drying curves at 1.5 m/s air velocity; (B) drying curves at 2.0 m/s air velocity; (C) drying rate at 1.5 m/s air velocity; (D) drying rate at 2.0 m/s air velocity
In the study, the drying rate was evaluated by using Eq. (8) and was shown in Fig. 2(C) and (D) at different air velocity conditions. The results indicated that the drying rate linearly decreased with decrease of MR. In all drying experiments, constant rate period was not found. Only falling rate period was observed for drying of pineapple which complied to previously reported [2, 28]. Furthermore, the drying rate increased along with air temperature and air velocity. The highest drying rate was obtained from the swirling flow type dryer at 70 °C and 2.0 m/s. On the other hand, the non-swirling flow type dryer at 60 °C and 1.5 m/s provided the lowest drying rate. In addition, the results of m and Deff, were fitted by using Eq. (11) as illustrated in Table 3. As the results of drying rate, m and Deff increased when air temperature was increased in any air velocity values. The variation of Deff from swirling flow type dryer was in the range of (6.72–10.23) × 10−9 m2/s, while the variation of Deff from non-swirling flow type dryer was in the range of (6.40–9.42) × 10−9 m2/s.
Table 3.
Slope (m) of the ln(MR) versus drying time, effective diffusivity coefficient (Deff) and EI from swirling flow and non-swirling flow type dryer at various conditions
| Drying conditions | m (s−1) × 104 | Deff (m2/s) × 109 | EI (−) |
|---|---|---|---|
| Swirling flow | |||
| 60 °C and 1.5 m/s | 1.11 ± 0.02c | 6.72 ± 0.09c | 1.05 ± 0.04 |
| 60 °C and 2.0 m/s | 1.27 ± 0.03bc | 7.69 ± 0.16bc | 1.03 ± 0.02 |
| 70 °C and 1.5 m/s | 1.43 ± 0.03abc | 8.67 ± 0.16abc | 1.05 ± 0.02 |
| 70 °C and 2.0 m/s | 1.68 ± 0.01a | 10.23 ± 0.04a | 1.09 ± 0.01 |
| Non-swirling flow | |||
| 60 °C and 1.5 m/s | 1.05 ± 0.03c | 6.40 ± 0.16c | – |
| 60 °C and 2.0 m/s | 1.22 ± 0.02bc | 7.43 ± 0.14bc | – |
| 70 °C and 1.5 m/s | 1.36 ± 0.01abc | 8.24 ± 0.05abc | – |
| 70 °C and 2.0 m/s | 1.55 ± 0.01ab | 9.42 ± 0.04ab | – |
abcDifferent letters in the same column indicate significant differences (p < 0.05)
The EI from swirling flow type dryer at various conditions was illustrated in Table 3. The results presented that the efficiency of hot air drying was improved by using the swirling flow type dryer due to the boundary air layer of the samples surface was disturbed by circulation of the air around the sample surface. Because of this reason, the convective heat transfer coefficient and evaporation rate were enhanced which resulted on the efficiency of hot air drying process [7]. Similarly, the efficiencies of swirling flow and non-swirling flow type dryer were enhanced by increase of air temperature and air velocity. The EI from swirling flow type dryer at 60 °C and 1.5 m/s and 60 °C and 2.0 m/s were 1.05 and 1.03, respectively, whereas the EI at 70 °C and 1.5 m/s and 70 °C and 2.0 m/s were 1.05 and 1.09, respectively.
In this work, the color changes of pineapple at various conditions were estimated by ∆E* and ∆BI which were represented in Fig. 3. The color changes in the samples were resulted by Maillard reaction (non-enzymatic browning reaction) and pigment destruction. However, the enzymatic browning reaction was inattentive in the study because it was normally susceptible to high temperature at more than 50 °C [22]. When considering the ∆E* in Fig. 3(A), the highest ∆E* value was obtained by the non-swirling flow type dryer at 60 °C and 2.0 m/s while the lowest ∆E* value was achieved from the swirling flow type dryer at 70 °C and 2.0 m/s. The ∆E* values from swirling flow and non-swirling flow type dryer were only significantly different in the drying condition at 60 °C and 2.0 m/s, whereas the ∆E* values from swirling flow type dryer in the other conditions were not significantly different. Nevertheless, the color changes of the samples in the swirling flow type dryer was low, forasmuch its drying time was shorter than in non-swirling flow type dryer. Correspondingly, Rattanathanalerk et al. [29] reported that the ∆E* values of pineapple juice was significantly increased by enhancement the heating temperatures and processing times of thermal process. Moreover, the increased temperature enhanced the color changes because of carotenoid isomerization [8, 32] and non-enzymatic browning reaction [9].
Fig. 3.
Effect of different drying conditions on (A) total color differences (∆E*); and (B) browning index differences (∆BI) of pineapple. Data are shown as the mean ± SD. Means with different lower case letters are significantly different (p < 0.05)
For the ∆BI of pineapple at various conditions, they were expressed in Fig. 3(B). The ∆BI of pineapple drying from swirling flow type dryer were lower than in non-swirling flow type dryer when compared at the same condition. However, the ∆BI from swirling flow and non-swirling flow type dryer were not significantly difference in the drying condition at 70 °C and 2.0 m/s. The highest ∆BI was obtained from the non-swirling flow type dryer at 60 °C and 2.0 m/s, while the lowest ∆BI was obtained from the swirling flow type dryer at 70 °C and 2.0 m/s. The increased ∆BI caused the brown color in the samples that was produced by Maillard reaction, pigment destruction and sample shrinkage during the drying process [15]. From the Fig. 3(B), it illustrated that the ∆BI of swirling flow in mostly conditions was lower than in non-swirling flow. It displayed that the brown color occurred in swirling flow was less than in non-swirling flow. Thus, the color of the drying products produced by swirling flow system was capable to be conserved.
Acknowledgements
This project was supported by a new researcher grants from Ministry of Science and Technology of the National Science and Technology Development Agency-NSTDA (SCH-NR2014-161).
References
- 1.Agarry SE, Ajani AO, Aremu MO. Thin layer drying kinetics of pineapple: Effect of blanching temperature–time combination. Nig. J. Basic Appl. Sci. 2013;21(1):1–10. [Google Scholar]
- 2.Akpinar EK, Midilli A, Bicer Y. Single layer drying behavior of potato slices in a convective cyclone dryer and mathematical modeling. Energ. Convers. Manage. 2003;44:1689–1705. doi: 10.1016/S0196-8904(02)00171-1. [DOI] [Google Scholar]
- 3.Akpinar EK. Evaluation of convective heat transfer coefficient of various crops in cyclone type dryer. Energ. Convers. Manage. 2005;46:2439–2454. doi: 10.1016/j.enconman.2004.11.006. [DOI] [Google Scholar]
- 4.AOAC. Official methods of analysis. AOAC Official Method 935.29. Association of Official Analytical Chemists, Gaithersburg, MD (2000).
- 5.Babalis SJ, Papanicolaou E, Kyriakis N, Belessiotis VG. Evaluation of thin-layer drying model for describing drying kinetics of figs (Ficuscarica) J. Food Eng. 2006;75:205–214. doi: 10.1016/j.jfoodeng.2005.04.008. [DOI] [Google Scholar]
- 6.Çakmak G, Yildiz C. Design of a new solar dryer system with swirling flow for drying seeded grape. Int. Commun. Heat Mass. 2009;36:984–990. doi: 10.1016/j.icheatmasstransfer.2009.06.012. [DOI] [Google Scholar]
- 7.Chang F, Dhir VK. Mechanisms of heat transfer enhancement and slow decay of swirl in tubes using tangential injection. Int. J. Heat Fluid Fl. 1995;16(2):78–87. doi: 10.1016/0142-727X(94)00016-6. [DOI] [Google Scholar]
- 8.Chen HE, Peng HY, Chen BH. Changes of carotenoids, color and vitamin A contents during processing of carrot juice. J. Agr. Food Chem. 1995;43(7):1912–1918. doi: 10.1021/jf00055a029. [DOI] [Google Scholar]
- 9.Chutintrasri B, Noomhorm A. Color degradation kinetics of pineapple puree during thermal processing. LWT Food Sci. Technol. 2007;40(2):300–306. doi: 10.1016/j.lwt.2005.11.003. [DOI] [Google Scholar]
- 10.Cortellino G, Pani P, Torreggiani D. Crispy air-dried pineapple rings: optimization of processing parameters. Procedia Food Sci. 2011;1:1324–1330. doi: 10.1016/j.profoo.2011.09.196. [DOI] [Google Scholar]
- 11.Crank J. The Mathematics of diffusion. Oxford: Clarendon Press; 1975. [Google Scholar]
- 12.Dutta PP, Baruah DC. Drying modelling and experimentation of Assam black tea (Camellia sinensis) with producer gas as a fuel. Appl. Therm. Eng. 2014;63:495–502. doi: 10.1016/j.applthermaleng.2013.11.035. [DOI] [Google Scholar]
- 13.FAO. FoSTAT Database Collections, Agricultural Data, Food and Agriculture Organization of the United Nations 2012. www.faostat.fao.org. Accessed June 23, 2015.
- 14.Henderson SM, Pabis S. Grain drying theory I: temperature effect on drying coefficient. J. Agric. Eng. Res. 1961;6:169–174. [Google Scholar]
- 15.Hosseinpour S, Rafiee S, Mohtasebi SS, Aghbashlo M. Application of computer vision technique for on-line monitoring of shrimp color changes during drying. J. Food Eng. 2013;115:99–114. doi: 10.1016/j.jfoodeng.2012.10.003. [DOI] [Google Scholar]
- 16.Huntington DH. The influence of the spray drying process on product properties. Dry. Technol. 2004;22(6):1261–1287. doi: 10.1081/DRT-120038730. [DOI] [Google Scholar]
- 17.Javed KH, Mahmud T, Purba E. Enhancement of mass transfer in a spray tower using swirling gas flow. Chem. Eng. Res. Des. 2006;84(6):465–477. doi: 10.1205/cherd.05119. [DOI] [Google Scholar]
- 18.Kha TC, Nguyen MH, Roach PD, Stathopoulos CE. Microencapsulation of Gacoil: Optimization of spray drying conditions using response surface methodology. Powder technol. 2014;264:298–309. doi: 10.1016/j.powtec.2014.05.053. [DOI] [Google Scholar]
- 19.Kowalski SJ, Rajewska K. Convective drying enhanced with microwave and infrared radiation. Dry. Technol. 2009;27(7):878–887. doi: 10.1080/07373930903014837. [DOI] [Google Scholar]
- 20.Kowalski SJ, Szadzińska J, Łechtańska J. Non-stationary drying of carrot: Effect on product quality. J. Food Eng. 2013;118:393–399. doi: 10.1016/j.jfoodeng.2013.04.028. [DOI] [Google Scholar]
- 21.Lewis WK. The rate of drying solid materials. J. Ind. Eng. Chem. 1921;13(5):427–432. doi: 10.1021/ie50137a021. [DOI] [Google Scholar]
- 22.Martinez MV, Whitaker JR. The biochemistry and control of enzymatic browning. Trends Food Sci. Tech. 1995;6(6):195–200. doi: 10.1016/S0924-2244(00)89054-8. [DOI] [Google Scholar]
- 23.Özbey M, Söylemez MS. Effect of swirling flow on fluidized bed drying of wheat grains. Energ. Convers. Manage. 2005;46:1495–1512. doi: 10.1016/j.enconman.2004.08.005. [DOI] [Google Scholar]
- 24.Page GE. Factors influencing the maximum rates of air drying shelled corn in thin layers. M.S. thesis. Department of Mechanical Engineering, Purdue University, Lafayette, USA. (1949).
- 25.Pasban A, Sadrnia H, Mohebbi M, Shahidi SA. Spectral method for simulating 3D heat and mass transfer during drying of apple slices. J. Food Eng. 2017;212:201–212. doi: 10.1016/j.jfoodeng.2017.05.013. [DOI] [Google Scholar]
- 26.Pothula AK, Igathinathane C, Shen J, Nichols K, Archer D. Milled industrial beet color kinetics and total soluble solid contents by image analysis. Ind. Crop. Prod. 2015;65:159–169. doi: 10.1016/j.indcrop.2014.12.001. [DOI] [Google Scholar]
- 27.Rafiee S, Sharifi M. KeyhaniA, Omid M, Jafari A, Mohtasebi SS, Mobli H. Modeling effective moisture diffusivity of orange slices (Thompson Cv.) Int. J. Food Prop. 2010;13:32–40. doi: 10.1080/10942910802144345. [DOI] [Google Scholar]
- 28.Ramallo LA, Mascheroni RH. Quality evaluation of pineapple fruit during drying process. Food Bioprod. Process. 2012;90:275–283. doi: 10.1016/j.fbp.2011.06.001. [DOI] [Google Scholar]
- 29.Rattanathanalerk M, Chiewchan N, Srichumpoung W. Effect of thermal processing on the quality loss of pineapple juice. J. Food Eng. 2005;66:259–265. doi: 10.1016/j.jfoodeng.2004.03.016. [DOI] [Google Scholar]
- 30.Rayaguru K, Routray W. Mathematical modelling of thin layer drying kinetics of stone apple slices. Int. Food Res. J. 2012;19(4):1503–1510. [Google Scholar]
- 31.Sedahmed GH, Abdel-Aziz MH, Abdo MSE, Hassan MS, Konsowa AH. Mass and heat transfer the surface of a gas sparged pool of liquid to an immiscible liquid under swirling flow and potential applications. Chem. Eng. Res. Des. 2017;125:88–95. doi: 10.1016/j.cherd.2017.06.037. [DOI] [Google Scholar]
- 32.Singleton VL, Gortner WA, Young HY. Carotenoid pigments of pineapple fruit. I. Acid-catalyzed isomerization of the Pigments. J. Food Sci. 1961;26(1):49–52. doi: 10.1111/j.1365-2621.1961.tb00039.x. [DOI] [Google Scholar]
- 33.Tang Y, Min J, Wu X. Selection of convective moisture transfer driving potential and its impacts upon porous plate air-drying characteristics. Int. J. Heat Mass Transf. 2018;116:371–376. doi: 10.1016/j.ijheatmasstransfer.2017.09.040. [DOI] [Google Scholar]
- 34.Yagcioglu A, Degirmencioglu A, Cagatay F. Drying characteristics of laurel leaves under different conditions. In Başçetinçelik A. (Ed.), Proceedings of the 7th International Congress on Agricultural Mechanization and Energy, 26–27 May, Adana, Turkey. Faculty of Agriculture, Çukurova University. pp. 565–569 (1999).
- 35.Zhu A, Shen X. The model and mass transfer characteristics of convection drying of peach slices. Int. J. Heat Mass Tran. 2014;72:345–351. doi: 10.1016/j.ijheatmasstransfer.2014.01.001. [DOI] [Google Scholar]