Structure of the interferon-receptor complex determined by distance constraints from double-mutant cycles and flexible docking

Abstract

The pleiotropic activity of type I interferons has been attributed to the specific interaction of IFN with the cell-surface receptor components ifnar1 and ifnar2. To date, the structure of IFN has been solved, but not that of the receptor or the complex. In this study, the structure of the IFN-α2–ifnar2 complex was generated with a docking procedure, using nuclear Overhauser effect-like distance constraints obtained from double-mutant cycle experiments. The interaction free energy between 13 residues of the ligand and 11 of the receptor was measured by double-mutant cycles. Of the 100 pairwise interactions probed, five pairs of residues were found to interact. These five interactions were incorporated as distance constraints into the flexible docking program prodock by using fixed and movable energy-gradient grids attached to the receptor and ligand, respectively. Multistart minimization and Monte Carlo minimization docking of IFN-α2 onto ifnar2 converged to a well-defined average structure, with the five distance constraints being satisfied. Furthermore, no structural artifacts or intraloop energy strain were observed. The mutual binding sites on IFN-α2 and ifnar2 predicted from the model showed an almost complete superposition with the ones determined from mutagenesis studies. Based on this structure, differences in IFN-α2 versus IFN-β binding are discussed.

Type I interferons (IFNs) are a family of homologous cytokines that potently elicit an antiviral and antiproliferative state in cells. All human type I IFNs (IFN-α, -β, and -ω) bind to a cell surface receptor consisting of two transmembrane proteins, type I IFN receptor (ifnar) 1 (1) and ifnar2 (2), which associate upon binding. IFN binds with high affinity to ifnar2, probably recruiting ifnar1 subsequently. Type I IFNs belong to the class of helical cytokines and are built of five helices. The structures of human IFN-α2 (3) and IFN-β have been resolved (4). The receptor structures are unknown, but can be modeled by homology to human cytokine receptors with known structures such as tissue factor (5) and IFN-γ receptor (6). Mutational studies have revealed the mutual binding sites on IFN-α2 and ifnar2. On IFN-α2, ifnar2 binds to the A helix (residues 12–15), the AB loop (residues 26–35), and the E helix (residues 144–153) (7), whereas on ifnar2, IFN-α2 binds to three loops of the N-terminal domain of the receptor (residues 45–52, 75–82, and 102–106) with no significant binding detected toward the C-terminal domain (8–10). Determination of the receptor-ligand structure will significantly promote our understanding of IFN signaling at the molecular level.

Docking of protein complexes, and calculating the conformational changes that occur at the binding interface, is a computational challenge. Rigid protein docking software algorithms are fast and can be used to dock two proteins for which the NMR or x-ray structures have been solved independently (11, 12). However, successful docking relies on the similarity between the unbound and complex protein structures, because accurate prediction of global and local conformational changes is currently difficult (13). Without it, additional information from mutagenesis studies, genetic studies, or bioinformatics is necessary to locate the interacting surfaces. Most of these methods do not provide the relative orientation of the two proteins, but only the location of the binding sites. This problem can be solved by using a more advanced procedure for mutagenesis, in which pairs of residues (X and Y located on proteins E₁ and E₂, respectively) are mutated both singly and doubly, allowing the construction of a double-mutant cycle (DMC) (14, 15). Assuming that only neighboring residues interact, this method can be used to identify distance constraints between the two proteins. To verify that significant interaction free energies (ΔΔG_int) are found mainly between neighboring residues, the relation between the distance and interaction free energy was evaluated for 71 pairwise inter-residue interactions for which both values of ΔΔG_int and the structure at atomic resolution are known (data are from refs. 16–20). In most cases (39 of 42), values of ΔΔG_int > 2.5 kJ/mol were determined between neighboring pairs of residues (d < 5 Å). Yet, a favorable interaction free energy was not found between all neighboring residues; in nine of 38 cases in which the interaction free energy was less than 2.5 kJ/mol, the inter-residue distance was less than 5 Å. Therefore, it is correct to assume that favorable interaction energies, determined from DMCs, pertain mostly to neighboring residues. However, the absence of a significant interaction free energy does not indicate that these two residues are remote. This distance/free energy relation is the basis for the development of the distance constraint docking method, applied here to dock the IFN-α2-receptor complex.

DMC data have previously been used for rough docking of a peptide inhibitor to a K⁺ channel pore, a peptide to an antibody, and a ligand to a receptor (21–23). The innovation in the present work is to adapt the mutagenesis information into NMR-style inter-residue distance constraints and use these constraints to drive the docking computationally. DMC data are used for precise docking of a protein–protein complex. The docking simulation is based on multistart minimization or Monte Carlo minimization (MCM), with various steps to balance the optimization of the experimental constraints and the ECEPP/3 energy at the flexible interface. Docking of IFN-α2 onto ifnar2 by using both methods converged to a well-defined average structure, with the five determined distance constraints being satisfied.

Methods

Protein Expression and Purification.

IFN-α2 and ifnar2-extracellular domain (EC) were expressed in Escherichia coli and purified, and their concentrations were determined as described (7, 24).

Site-Directed Mutagenesis.

Site-directed mutagenesis was carried out by PCR amplification of the complete plasmids for expression with 18–21 nucleotide primers containing the mutated codon by using high-fidelity polymerases pwo (Roche Diagnostics) and pfu (Stratagene) as described (10).

Binding Measurements.

Ifnar2-EC–IFN-α2 interactions were monitored by a label-free optical probe (reflectometric interference spectroscopy) that detects bimolecular interaction at interfaces in real time under flow-through conditions (25). The experimental set-up has been described (25). All measurements were carried out by using 20 mM Hepes (pH 7.5), 150 mM NaCl, and 0.01% Triton X-100 as a running buffer. Ifnar2-EC was immobilized to the surface by using the non-neutralizing anti-ifnar2-EC mAb 46.10 followed by cross-linking with a second mAb (117.7) (gift from Daniela Novick, Weizmann Institute) (7, 25). The binding curves were evaluated with biaevaluation software (Biacore, Uppsala) by using a simple one-to-one kinetic model. For the determination of (equilibrium) dissociation constants K_D, the equilibrium response was plotted against the concentration and fitted by the law of mass action.

DMCs.

The free energy of interaction between two amino acid residues ΔΔG_int was determined from the change in interaction free energy upon mutation ΔΔG according to Eq. 1:

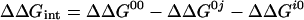1

with i and j representing the wild-type residues and 0 being the respective Ala mutant (15). Values of ΔΔG were determined from the dissociation rate constants (k_d) for mutants for which k_d < 0.3 s⁻¹. In this case, ΔΔG_kd is calculated from (12, 18):

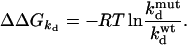2

For faster dissociating mutant ligand-receptor pairs, the dissociation kinetics could not be resolved by reflectometric interference spectroscopy. For these cases, the (equilibrium) dissociation constant K_D was used instead of k_d to calculate ΔΔG (ΔΔG_KD). The values for ΔΔG (and therefore of ΔΔG_int) determined by using either k_d or K_D were consistent (25), indicating that potential systematic errors cancel out when relative values (of ΔΔG) are calculated (16, 25). The SEM for ΔΔG is estimated to be 0.75 kJ/mol (each mutant was measured at least three times). Accordingly, a standard error of 1.0 kJ/mol is estimated for ΔΔG_int. A threshold of 2.5 kJ/mol was used to decide whether the interaction between a pair of residues is significant.

Molecular Docking.

The docking procedure based on DMC-derived distance constraints will be reported in a forthcoming paper (J.-Y.T. and H.A.S., unpublished work) and thus are outlined here only briefly.

Reference Structures.

The NMR structure of IFN-α2 [Protein Data Bank code 1ITF (3)] and a model of ifnar2-EC based on its homology with IFN-γ receptor and tissue factor (10) were used for this study. Before docking, the structural elements kept flexible during docking [IFN-α2 (D2-E42, E141-E146, M148-S160) and ifnar2-EC (L44-V57, W74-V82, C97-M107, V127-Q138, K155-N167, E188-Q193)] were regularized to standard geometry and energy-minimized independently by using the ECEPP/3 force field (26) to avoid high loop energy at the beginning of the docking.

Molecular System.

Each molecule was split into a flexible and a fixed portion. The flexible part included all residues that are in the binding interface [60 for IFN-α2 and 65 for ifnar2-EC (see above)]. The total energy of the protein complex was expressed as:

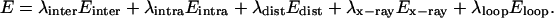3

E_inter represents the ECEPP/3 interactions between the rigid or flexible residue segments, E_intra is the intramolecular energy of the flexible segments, E_dist represents the interresidue distance constraint energy, E_x-ray are the x-ray constraints of the heavy atoms of the flexible structural elements in the energy-minimized IFN-α2 and ifnar2 starting structure (to prevent them from unfolding during docking), and E_loop is the loop closure constraint (27). The weights (λ) were used to balance the driving force, expressed here by the distance constraints and the other terms, especially the ECEPP/3 intramolecular and interatomic energy. Some were fixed during the docking procedure: (λ_inter = 1, λ_intra = 1, λ_dist = 30, λ_loop = 1,000) and some were varied during the simulation: λ_x-ray = 100, 10, 0 for the three successive energy-minimization refinements in a given docking run. The values of these weight factors were estimated a priori by assuring that none of the external constraints (in particular E_dist), exceeds the ECEPP/3 energy terms by more than 2–3 orders of magnitude.

Distance Constraints.

The distance constraint energy term is similar to the one used for nuclear Overhauser effect distance constraint optimization (28). A harmonic force was imposed when the distance violation was more than the user-defined minimal distance, i.e., 5 Å for the first minimization steps and 3 Å for the following two minimization steps. If the violation was more than 2 Å from the minimal distance, the harmonic distance was replaced by a quasi-linear branch (29).

Energy and Gradient Grids.

The ECEPP/3 van der Waals and electrostatic contributions of the frozen parts of both the receptor and ligand proteins were stored in three-dimensional grids. The receptor grid was fixed (i.e., no translation or rotation was allowed), and the ligand grid was allowed to move together with the ligand as a rigid body. A B-spline extrapolation scheme was used to ensure continuity within the grid and facilitated gradient-based minimization (30–32). These two grids speed up the docking simulations by about two orders of magnitude depending on the size of the system.

MCM.

The perturbations of the dihedral angles, and the rotation and translation of the ligand, were made along the normal modes of the system (32). The amplitude of the perturbation (step size) was such that 10% of the side-chain dihedral angles and 1% of the backbone dihedral angles could move significantly (by about 30°-60°), between 0.2 and 2 Å for the translation and between 10° and 30° for the rotation angle. A temperature of 1,000 K was chosen for MCM. The number of iterations for each minimization was 300 for the first 500 MCM steps and 600 for the last 100 MCM steps. After the MCM runs, full minimization (6,000 iterations steps) was carried out with λ_x-ray = 0.1, with all of the other weight factors as before.

Before being implemented for docking of IFN-α2 to ifnar2, the algorithm was tested on the interaction between barnase and barstar, for which DMC data and the relevant structures are available (20, 33). The influence of several parameters on the quality of the results was evaluated, in particular, the number of distance constraints used, the effect of using wrong distance constraints, the weights of the distance penalty term, and the position of the starting conformations. The results show that the simulations are relatively stable using 4–9 distance constraints, even if an erroneous constraint was deliberately introduced. The rms deviation (rmsd) value of the docked structure was ≈2 Å relative to the crystallographically determined structure (J.-Y.T. and H.A.S., unpublished work). The rmsd values throughout this work are mean rmsds of all backbone atoms. In the case of the IFN-α2 receptor complex, all ifnar2 structures were overlaid, and the mean rmsd of all backbone atoms of IFN-α2 was computed.

Results

DMC Analysis of the IFN-α2–ifnar2 Interface.

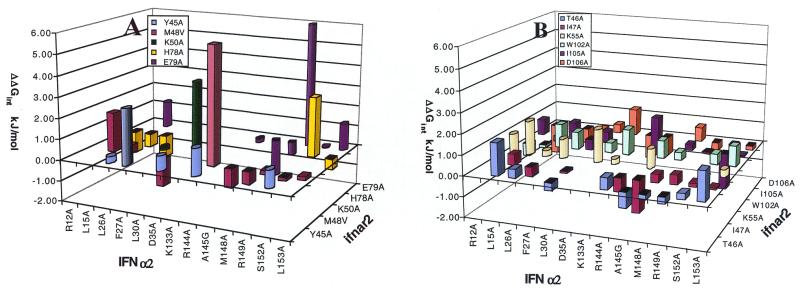
The respective binding sites of IFN-α2 and ifnar2 were previously mapped by means of site-directed mutagenesis (7, 10). Here, we extended these studies by carrying out a systematic DMC analysis of the interface. Because the structure of the complex is unknown, the potential interactions between 13 residues of IFN-α2 and 11 residues of ifnar2, which are located within the mutual binding epitopes, were systematically probed by using DMCs (Table 1 and Fig. 1; Tables 2 and 3, which are published as supporting information on the PNAS web site, www.pnas.org). Binding assays were carried out by heterogeneous phase detection with reflectometric interference spectroscopy, with ifnar2-EC being immobilized to the surface (25). Interaction free energies were calculated by using consistently either k_d or K_D for any one DMC (see Methods).

Table 1.

Interaction free energies determined from DMCs by using the respective mutations

Ifnar2/IFNα2	Y45A*	T46A†	I47A†	M48V†	K50A*	K55A*	H78A*†	E79A†	W102A*†	I105A*†	D106A*†
R12A					−0.1	0.9	−1.1*		−0.6*	0.8*	−1.5*
L15A		1.6	0.5	1.9		1.7	−0.7*|2.1†	1.3	−1.1*|1.8†	−0.3†
L26A	0.3	0.4	−0.5	0.4		0.3	−1.1*|−1.4†		1.1*	0.8*|0.6†	−2.1*|0.7†
F27A	2.7				−0.2	1.0			0.8*	−0.6*	0.1*
L30A		−0.4	−0.1	−1.3				1.0		0.5†	0.4†
D35A	0.7				3.4	1.6			0.5*		1.3*
K133A					−0.6	0.3			1.3*		−1.2*
R144A	1.3	0.6	−0.7	5.7				−0.2		1.5†	1.5*|0.6†
A145G		−0.7	−1.6	−0.9		1.0		−1.8	0.9*
M148A		−0.2	0.4	−0.6				−0.6	0.4†	0.3†	0.7†
R149A		−0.3	0.4	0.2				8.1		−0.1†	−0.4†
S152A	0.8	0.3	0.2	−0.1		−0.1	2.9*|4.8†	0.0	0.5*|−0.3†	−1.8†	−0.5*|0.3†
L153A		1.4	0.1	0.2		0.4	0.5*|−0.3†	1.3	1.0†	0.0†	−0.6*|1.0†

^*ΔΔG_int in kJ/mol, determined from changes in the dissociation rate constant (see Eqs. 1 and 2). 

^† ΔΔG_int in kJ/mol, determined from changes in K_D as guided by the law of mass action. Boldface indicates values of ΔΔG_int > 2.5 kJ. 

Figure 1.

DMC analysis of the IFN-α2–ifnar2 complex. Values of ΔΔG_int determined from changes in k_d or K_D are presented as round and square bars, respectively. Data are from Table 1. (A) The calculated ΔΔG_int values for residues where an interprotein interaction was identified (ΔΔG_int > 2.5 kJ/mol). (B) The calculated ΔΔG_int values for residues where no interprotein interaction was identified.

Values of ΔΔG_int determined from changes in k_d or K_D are presented in Fig. 1 as round and square bars, respectively. In case of doubt, both values were calculated (see Tables 1–3), giving similar results. Fig. 1A shows those residues for which at least one interprotein interaction was identified (ΔΔG_int > 2.5 kJ/mol). Fig. 1B shows the calculated ΔΔG_int values for residues for which no obvious interacting partner was identified. From the 90 DMC values presented in Fig. 1, only five are above 2.5 kJ/mol, which is defined here as being significant. On IFN-α2, three of the interacting residues are located on the E helix (R144, R149, and S152), and two are located on the AB loop (F27 and D35). Despite a major effort, no pairwise interactions were found to involve L30 or R33 (data are not shown for R33A because the very low affinity of this mutant makes the error of these measurements much larger), or R12 and L15, which are located on the A helix of IFN-α2 and were identified to bind ifnar2 (7). On ifnar2, three of the residues interacting with IFN-α2 are located on the 45–52 loop (Y45, M48, and K50) and two are on the 76–79 loop (H78 and E79). No pairwise interactions were found involving residues W102, I105, or D106, which are located on the loop connecting the first and second IgG-like domain on ifnar2. The largest interaction free energy (ΔΔG_int= 8 kJ/mol) was determined between R149 (IFN-α2) and E79 (ifnar2). These two residues are located at the center of their respective binding surfaces, and both were defined previously as hot spots for binding. A second interaction connecting the E helix of IFN-α2 with ifnar2 is between R144 (IFN-α2) and M48 (ifnar2). A third interaction (S152-H78) connects the E helix (IFN-α2) with the 76–79 loop of ifnar2, making a potential hydrogen bond. On the AB loop (IFN-α2), F27 probably forms an aromatic interaction with Y45 (ifnar2), and D35 (IFN-α2) forms a potential salt bridge with K50 (ifnar2). Although the last three pairs of residues are not hot-spot residues, their interaction free energies are still >2.5 kJ/mol and significantly larger than the measured background (of other pairwise interactions involving these residues).

Determining the Structure of the IFN-α2–ifnar2 Complex.

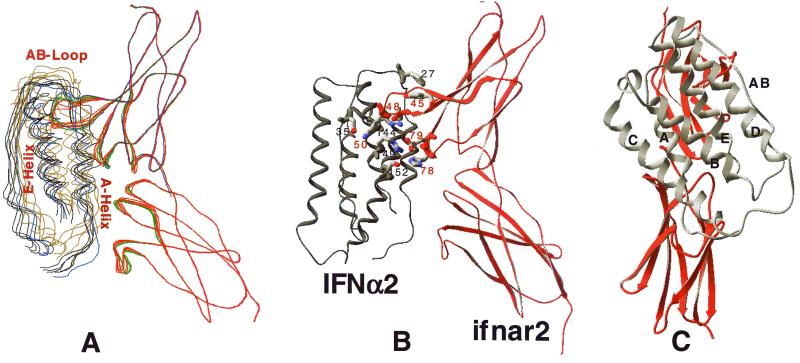
The docking of IFN-α2 (NMR structure 1ITF) to the model of ifnar2 was carried out by using two methods: a multistart four-step minimization (10 independent runs) and a multistart MCM simulation (five independent runs). The starting points were random positions and orientations of the ligand at about 15 Å above the binding region on the receptor. In the first approach, three minimization steps were used to balance the distance constraint driving force and the ECEPP/3 energy as the ligand approaches the receptor. The fourth step was carried out without distance and x-ray constraints. The 10 minimizations converged with a mean rmsd of 1.6 Å between them (Fig. 2A). Each of the five distance constraints were satisfied within less than 0.5-Å violation in all 10 complex structures (Fig. 2B).

Figure 2.

Structure of the IFN-α2–ifnar2 complex. The structure was calculated by using either multistart minimization or multistart MCM, keeping some of the backbone and side chains flexible (see Methods). (A) Ribbon structure of the complex of 10 independent docking experiments (minimization, black and red; MCM, brown and green), and using only the first domain of ifnar2 (blue). (B) Ribbon structure of the complex; shown are the 10 residues that contribute to the five distance constraints. (C) Back view of the complex, with the letters marking the helices and AB loop of IFN.

A potential problem with the minimization procedure is that it may not allow large structural rearrangements to occur. To test this, five independent multistart MCM simulations were carried out, starting from the same random structures. All of these MCM runs converged, albeit with larger fluctuations between the individual structures (mean rmsd of 2.8 Å). The structures obtained from the MCM simulations are very close to the ones obtained by the four-stage minimization procedure (Fig. 2A).

Discussion

DMCs measure the binding free energy between two amino acids. The method was developed to deconvolute the thermodynamics of a system and to relate these to available structural information (15, 28). However, it has been recognized that DMC data also can serve to indicate structural proximity (22, 23). Here, we used DMC data to provide distance constraints that are incorporated into a molecular docking program designed to model protein–protein interactions in the absence of sufficiently good structural data.

The five identified interprotein interactions were used to dock IFN-α2 on ifnar2 by using two methods of calculations. The computational faster method uses distance constraint energy minimization, relaxing the x-ray and distance constraints during the progression of the simulation. The structures obtained from 10 individual simulations converged, suggesting that the docked complex does not depend on the starting position of the ligand. Moreover, relaxing all distance constraints at the end of the simulation did not cause a large decrease in ECEPP/3 energy or movement of the structure. Therefore, the distance constraints did not bias the structure toward unrealistic binding modes. A drawback of the minimization technique is that it may optimize the distance constraints quickly, without exploring the conformational space of the flexible domains properly. To overcome this problem, five MCM simulations were carried out as well. At the end of the MCM runs, the five structures converged to a similar unique average structure as obtained previously with the four-stage minimization procedure, however, with a larger rmsd between them.

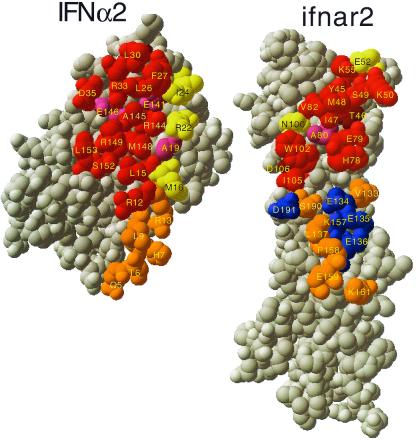
It is in fact likely that the convergence of the structures correlates directly with the quality of the selections of the residues involved in the distance constraints, and that the structures represent the best estimate of the IFN-α2–ifnar2 complex. Independent of these docking experiments, the interaction sites on IFN-α2 and ifnar2 were probed by single mutagenesis (9–12). The good agreement between the active sites as determined from single mutagenesis and the binding interface provides an experimental measure of the quality of the model (Fig. 3). Most of the residues affecting binding upon mutation are located within the suggested interface, including all of the “hot spots.” The exceptions are T46 and D106 on ifnar2. In the model of ifnar2, both of these residues are buried beneath residues involved directly in binding, suggesting an indirect contribution of these residues to binding. A number of residues located at the edge of the suggested binding interface do not contribute significantly toward binding affinity. These include M16, R22, and I24 on IFN-α2 and E52 and N100 on ifnar2. However, it is well established that residues located at the periphery of the binding site are often inert (34). Moreover, mutations of any one of these residues cause a small, but significant, change in k_d of the complex (7, 10) (but less than 2-fold, which is the threshold used in Fig. 3). Analyzing the degree of conservation of interface residues between different IFN-α subtypes reveals that the functional hot-spot residues (numbers 30, 33, 144, 145, 148, and 149) are fully conserved. Other interface residues are only partially conserved. For ifnar2, the sequence homology with other human cytokine receptors is low, thus no conservation was either expected or found.

Figure 3.

Comparison of the mutual binding sites of IFN-α2 and ifnar2, as determined from mutagenesis, with the interface of the structure of the complex. The structure of the complex was opened up, by rotating IFN-α2 by 180°. Threshold for interface residues is 5 Å. Active residues are defined as those for which a mutation to Ala causes a decrease of at least 2-fold in binding affinity. Binding site residues were divided into those that interact with the C-terminal domain of ifnar2-EC (orange and blue) and the N-terminal domain of ifnar2-EC (all other colors). Red, active residues located within the binding site. Yellow, nonactive residues located in the binding site. Magenta, residues located in the binding site for which the activity was not determined. Brown, active residues located outside the binding site. Blue, residues located within the binding site of the second domain of ifnar2, but with no binding active. Orange, residues located within the binding site and the second domain of ifnar2, but with the activity not measured.

The structure of the IFN-α2–ifnar2 complex suggests that IFN-α2 interacts with both domains of ifnar2 (Figs. 2 and 3). This mode of binding is in agreement with that found for other human cytokine receptors, such as IL4-R, human growth hormone receptor, and IFN-γ receptor (6, 35), but is not supported by mutagenesis studies of the IFN-α2–ifnar2 complex (Fig. 3) (8–10). None of the 16 single mutations introduced in the second domain of ifnar2 caused a reduction in affinity of more than 2-fold (8–10). Moreover, a truncated ifnar2, lacking the second domain, binds IFN-α2 with reasonable affinity (unpublished data). The angle between the two domains of ifnar2 was modeled by using IFN-γ receptor as a template. But because of the large variation in this angle between different human cytokine receptors (35) one cannot be sure that the model of ifnar2 is correct in this respect. A different relative orientation between the two domains of ifnar2 would shift the second domain away from the IFN binding site. To determine whether the calculated structure of the IFN-α2–ifnar2 interface would be different in the absence of the second domain, the docking simulation was repeated by using only the first domain of ifnar2 (blue line in Fig. 2A). The structure of this complex is similar to that using the whole ifnar2 protein. The buried surface area between IFN-α2 and ifnar2 in the proposed model is 2,450 Ų for interactions of both domains of ifnar2 with IFN-α2 and 1,600 Ų for interactions between only the first domain of ifnar2 with IFN-α2. Both values are within the range expected for protein–protein interactions (36). Thus, the mode of interaction of the second domain of ifnar2 with IFN-α2 remains uncertain.

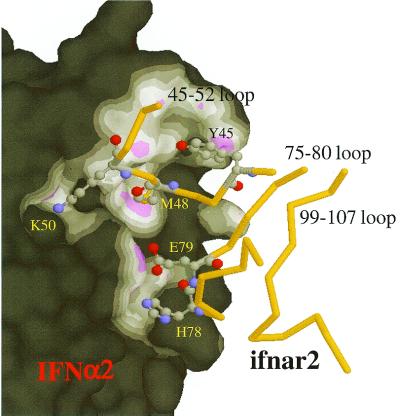
The most outstanding structural feature in the IFN-α2–ifnar2 interface is the deep insertion of the 45–52 loop of ifnar2 into the groove formed around Ala-145 on IFN-α2 (Fig. 4). Three distance constraints connect this loop to IFN-α2 (Figs. 2B and 4). Single-mutation studies have implied that this groove is at the center of the binding epitope, with four hot-spot residues of IFN-α2 being located at its rim (7). Thus, it is not surprising to find hot-spot residues (T46, I47, and M48) along the ifnar2 loop that penetrates into IFN-α2. A closer look at the interactions made by this loop reveals that the backbone oxygens of S49 and K50 (ifnar2) make two potential hydrogen bonds with the side chain of R33. This finding may explain that no interacting residues were identified for R33 despite its strong contribution to binding. A second important binding determinant is between the central part of the E helix of IFN-α2 (R149 and S152) and the 76–82 loop of ifnar2 (including E79 and H78 that bind R149 and S152). Although this ifnar2 loop binds a flat part of the IFN-α2 surface, it is of major importance for binding, as demonstrated by the large binding free energy between R149 and E79. No experimental pairwise interactions were identified on either the A helix of IFN-α2 or the 102–106 loop of ifnar2. Interestingly, these two secondary structure domains are in close proximity in the model, which could explain their contribution to binding affinity as determined by mutagenesis.

Figure 4.

Close-up view of the IFN-α2–ifnar2 binding site. The surface of IFN-α2 is colored according to the distance from ifnar2 (magenta < 3 Å, white < 4 Å). The penetration of the 45–52 loop of ifnar2 into a groove on the surface of IFN-α2 should be noted.

IFN-β interacts with ifnar2 with a similar set of residues as IFN-α2, but with very different ΔΔG values upon mutation (9, 10). It is tempting to try to explain this difference by using the model generated here, assuming that IFN-β binds to the same epitope of ifnar2 as IFN-α2. In Fig. 5, IFN-β was superimposed onto IFN-α2 in complex with ifnar2. Analysis of the differences between the two interacting epitopes shows that W22 (IFN-β), which replaces A19 (IFN-α2), potentially binds W102 of ifnar2 tightly. This could explain why W102 is a hot spot for binding IFN-β but not IFN-α2. It would be interesting to test this hypothesis experimentally. A second site in which a large deviation between IFN-β and IFN-α2 was observed is for the R35A mutation in IFN-β, which causes a reduction in binding of only 10-fold, whereas the homologous mutation in IFN-α2 (R33A) causes a 10,000-fold reduction in binding (7). This phenomenon can now be explained by the difference in the angular orientation between these two residues. Although R33 (IFN-α2) makes two main-chain hydrogen bonds with the 45–52 loop of ifnar2, R35 (IFN-β) points away from ifnar2. Another interesting difference shown in Fig. 5 relates to the depth of the groove around A145, which is a valine in IFN-β. This may explain the lesser importance of M48 (ifnar2) in binding IFN-β (12).

Figure 5.

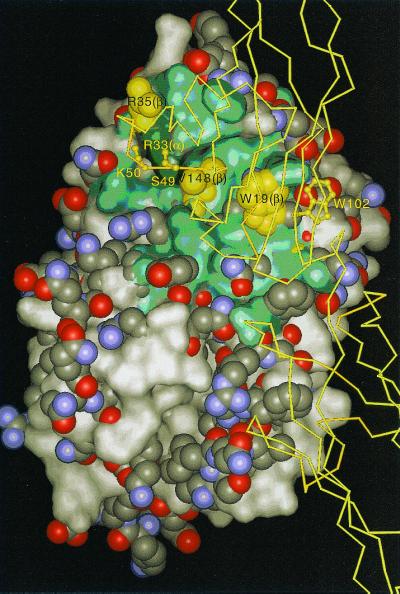
Comparison of the IFN-α2 and potential IFN-β binding sites for ifnar2. IFN-β (space-filled atoms) was overlaid onto IFN-α2 (shown as solvent accessible surface). The binding site of the N-terminal domain of ifnar2 on IFN-α2 is colored green. Locations at which IFN-α2 or IFN-β protrude are represented as surface or space-filled atoms, respectively.

The proposed structure of IFN-α2–ifnar2 is a model generated in an NMR-like fashion using experimentally determined distance constraints. For this reason, its reliability is substantially higher than that of a theoretical docking. The convergence of the docked structures shows that the determined complex is unique, i.e., the number of distance constraints was sufficient to lead to a converged average structure. However, because of the small number of constraints, its quality is not that of a structure determined by x-ray or NMR. Therefore, one should not expect atomic resolution; yet, it provides insight into the interface structure and the interprotein contacts formed. In addition to structural data, this method provides ambient useful thermodynamic data. The method presented here offers an alternative for structure determination of protein–protein interactions when structural characterization of such complexes cannot be carried out.

Abbreviations

DMC

double-mutant cycle

ifnar

type I IFN receptor

EC

extracellular domain

MCM

Monte Carlo minimization

rmsd

rms deviation