Large-scale QM/MM free energy simulations of enzyme catalysis reveal the influence of charge transfer

Abstract

Hybrid quantum mechanical-molecular mechanical (QM/MM) simulations provide key insights into enzyme structure–function relationships. Numerous studies have demonstrated that large QM regions are needed to systematically converge ground state, zero temperature properties with electrostatic embedding QM/MM. However, it is not well known if ab initio QM/MM free energy simulations have this same dependence, in part due to the hundreds of thousands of energy evaluations required for free energy estimations that in turn limit QM region size. Here, we leverage recent advances in electronic structure efficiency and accuracy to carry out range-separated hybrid density functional theory free energy simulations in a representative methyltransferase. By studying 200 ps of ab initio QM/MM dynamics for each of five QM regions from minimal (64 atoms) to one-sixth of the protein (544 atoms), we identify critical differences between large and small QM region QM/MM in charge transfer between substrates and active site residues as well as in geometric structure and dynamics that coincide with differences in predicted free energy barriers. Distinct geometric and electronic structure features in the largest QM region indicate that important aspects of enzymatic rate enhancement in methyltransferases are identified with large-scale electronic structure.

1. Introduction

Mixed quantum mechanical (QM)/molecular mechanics (MM), i.e., QM/MM modeling^1–9 remains the method of choice for simulating enzymes¹⁰ owing to its ability to balance accuracy in describing chemical rearrangements, polarization, and charge transfer at an enzyme active site with the low computational cost needed to enable sampling. Computational cost in QM/MM is typically minimized by employing small QM region sizes on the order of tens of atoms (i.e. ligands and a few direct residues)^{9, 11–12}, bringing to the fore the study and improvement of QM/MM boundary treatment^{7, 13–22} and embedding (i.e., polarizable) approach^23–29. Nevertheless, QM region size minimization is limited by the inability to describe charge transfer between MM residues and the QM active site.^30–31 At the same time, advances over the past decade^{30, 32–39} in computational efficiency now enable fully ab initio, quantum chemical simulation of polypeptides^{32, 40–46} as well as QM/MM treatments of enzymes with large (> 100 atoms) QM regions, enabling systematic studies^47–57 that have identified in static calculations a slow approach to asymptotic limits as QM regions are enlarged radially in QM/MM calculations. Such slow approach to asymptotic limit (at ca. 500–1000 atoms) has been observed for wide-ranging static properties, including: NMR shieldings,^47–48 proton transfer,⁵⁸ solvation effects,⁴⁹ barrier heights,^50–52 forces⁵³, excitation energies,^{54, 59–60} partial charges,⁵⁵ bond critical points⁶¹, and redox potentials⁵⁶. This strong sensitivity to QM region size has motivated ongoing method development for general^{50, 62–65} or system-specific⁵⁶ QM region determination, including through the response of QM active site residues to perturbation of surrounding environmental residues treated at the MM^{50, 66} or QM^{52, 67–68} level to enable atom-economical, quantitative QM/MM.

Although electronic structure calculations on over 1,000 atoms have become increasingly routine, a potential of mean force requires hundreds of thousands of energy evaluations, meaning that large-QM (i.e., > 100 atoms) QM/MM free energy calculations have overwhelmingly been carried out^{53, 69–73} with semi-empirical methods that depend strongly on the quality of parameterization⁷⁴ for adequate description of long-range charge transfer, hydrogen bonding, and electrostatic interactions. In order to assess i) whether qualitative differences emerge from large-scale QM/MM and ii) how sensitive QM/MM free energy simulations (FES) are to QM region size, we carried out the first large-scale, range-corrected, hybrid density functional theory (DFT) QM/MM free energy simulations with large (> 500 atom) QM regions. For this study, we select catechol O-methyltransferase (COMT), a representative member of a large class of S-adenosyl-L-methionine (SAM)-dependent⁷⁵ methyltransferases (MTases) responsible for gene signaling⁷⁶, protein repair^77–78, and neurotransmitter regulation⁷⁵.

The outline of the rest of this work is as follows. In section 2, we review the computational details of the QM/MM free energy simulations. In section 3, we present the reasoning for selected QM regions in QM/MM FES simulations of COMT and subsequent observations of energetic, structural, and electronic properties for differing QM regions. Finally, in section 4, we present our conclusions.

2. Computational Details

Hybrid quantum-mechanical/molecular mechanics (QM/MM) dynamics with electrostatic embedding and hydrogen link atoms, i. e.:

$$E_{\text{QM/MM}}=E_{QM}+E_{\text{QM/MM}}+E_{MM}$$ 1

employed the AMBER^79–80 interface⁵⁴ to TeraChem^{35, 81}. QM atoms were treated at the ωPBEh⁸²/6–31G*⁸³ level of theory with semi-empirical (i.e., D3⁸⁴) dispersion, and the MM atoms were treated with the ff14SB AMBER force field^85–86 or TIP3P⁸⁷ for water, as motivated by tests in previous work^{52, 67}. Specifically, for numerous snapshots, it was observed that the 6–31G* basis produced consistent results with those obtained after incorporation of diffuse functions and additional polarization functions⁶⁷. A range-separated hybrid was chosen after it was observed that some electronic properties, including spatial placement and energetic gap of the frontier orbitals, was erroneous with global hybrids^{52, 67}. These dynamics were carried out with spherical boundary conditions in a 41-Å radius sphere extracted from an NpT-equilibrated rectangular boundary conditions box from Ref. 70. The sphere was simulated with no electrostatic cutoff and a 1.5 kcal/mol^.Ų restraining potential at the boundary (see ESI). A 0.5 fs timestep was used and constant temperature (T = 300 K) was enforced by a Langevin thermostat. These 27,852-atom starting structures were obtained from prior⁷⁰ classical MD and semi-empirical QM/MM (SQM/MM) equilibration of COMT (PDB ID: 3BWM⁸⁸, protonation states given in ESI Table S1). In that prior work⁷⁰, the SQM region contained substrates, Mg²⁺ and its coordinating residues (D141, D169, N170, water), along with nearby E199 and K144 residues, whereas the remaining atoms were in the MM region. This −1 net charge, 147-atom SQM region is similar to the M2 region in the present work (see Sec. 3).

The reaction coordinate in umbrella sampling was defined as an antisymmetric linear combination of distances (LCOD) between the S-C and C-O bonds, which break and form, respectively, during methyl transfer. Variable force constants ranging from 10 to 240 kcal/mol^.Ų were employed to minimize the number of windows required, which was 14 in total, while maximizing overlap over the LCOD range (details provided in ESI Table S2). The weighted-histogram analysis method (WHAM)^89–90, as implemented in the Grossfield lab software package⁹¹, was used to reconstruct one-dimensional free energy curves with 0.02 Å bin widths from umbrella sampling⁹². Starting from the endpoint of SQM/MM dynamics (30 ps per window in Ref. 70), a 2 ps equilibration at the QM/MM level was discarded before completing 15 ps production runs for the free energy calculations in five QM/MM regions ranging from 64 atoms to 544 atoms in size for a total of 1.05 ns production QM/MM dynamics (Figure 1 and ESI Table S3). Mulliken partial charges, as computed at each time step, were analyzed by summing over each residue to minimize errors in partial charge assignment intrinsic in the Mulliken approach. The methyl partial charge is partitioned between SAM and CAT according to progress along the reaction coordinate, as in previous work⁵².

Figure 1.

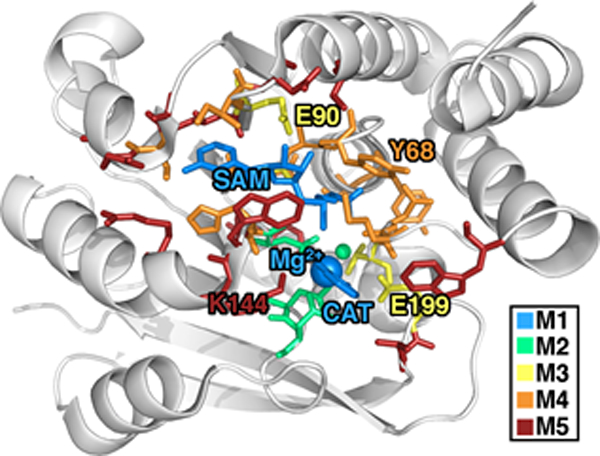
COMT structure with residues included in 5 QM region models shown as sticks, colored according to the smallest model in which they first appear: SAM, Mg²⁺, and CAT substrates-only model (64-atom, +2 net charge M1, blue), Mg²⁺ coordination sphere (109-atom, 0 net charge M2, green), critical residues (170-atom, −2 net charge M3, yellow), full systematic QM/MM region (325-atom, −3 net charge M4, orange), and a large QM model (544-atom, −1 net charge M5, red).

3. Results and Discussion

We investigate the effects of QM region size on dynamics and free energy evaluations in catechol O-methyltransferase (COMT), a representative member of a large class of methyltransferases (MTases).⁷⁵ COMT is an S-adenosyl-L-methionine (SAM)- and Mg²⁺-dependent MTase⁷⁵ that reacts with catecholamine substrates bound in a bidentate fashion to Mg²⁺ at the active site⁹³ (Figure 1). The rate-determining⁹⁴, direct S_N2 methyl transfer⁹⁵ from SAM⁹⁶ to a Lys-deprotonated catecholate^97–98 (CAT) has been the focus of kinetic studies^{93, 99–101} that estimate a free energy barrier estimate of 18.1¹⁰⁰-19.2¹⁰¹ kcal/mol for the soluble, human form of the enzyme. COMT has also been the focus of numerous DFT^{52, 102–103} and semi-empirical^{70–72, 104–105} computational studies^{71, 102–106} that have produced a wide range (i.e., 3–30 kcal/mol) of free energy barriers that can be brought into agreement with experiment through various corrections (e.g., a spline that approximates differences between semi-empirical and MP2 energies¹⁰⁷).

We previously identified that static properties⁵² of COMT (e.g., barrier heights, and structures) obtained with range-separated hybrid DFT are slow to converge to asymptotic large-QM limits (ca. 300–500 atoms) through an evaluation of these properties with 10 increasing radial cutoffs for protein water and residue inclusion in the QM region. We then developed systematic methods to identify which residues were most essential in static calculations^{52, 67–68}. Using these methods^{52, 67–68}, we obtained 0 K QM/MM activation energies and reaction energies within 1 kcal/mol of the asymptotically converged result with around half the number of atoms (around 200 vs. 500 atoms). The systematic selection methods focused on charge transfer between residues to revealed essential hydrogen bonding interactions and salt bridges as well as surprising nonpolar contributions to the enzyme active site⁶⁷. If interactions were captured across the QM/MM boundary, despite proximity (e.g., a lysine proximal to a glutamate near the active site), then those residues were not selected for the QM region. Now, we investigate if the regions that were shown to be asymptotically converged in 0 K QM/MM show similar or even reduced QM region size dependence than the prior 0 K studies.

For the largest-scale QM/MM free energy simulations in this work, we select a QM region of 544 atoms (28 protein residues) motivated by these prior^{52, 67} convergence studies and employ range separated hybrid DFT in a polarized double-ζ basis set. Both basis and method are selected as a compromise for what is presently feasible to carry out the > 400k energy evaluations on the largest QM region selected (see Computational Details and ESI Table S3). Our smaller QM regions are motivated by prior studies or our own systematic QM region construction results for convergence of static properties⁶⁷: i) M1 (64 atoms, +1 net charge): CAT, SAM, and Mg²⁺ only, ii) M2 (109 atoms, 0 net charge): added Mg²⁺ coordination sphere (D141, D169, and N170),, iii) M3 (170 atoms, −2 net charge): four additional key residues, V42, G66, E90, and E199, from static substrate-deletion analysis, iv) M4 (325 atoms, −3 net charge): nine more residues from systematically-selected QM regions for static calculations⁶⁷, and v) M5 (544 atoms, −1 net charge): a 28–residue region obtained from prior radial convergence studies⁵² (see Figure 1 and ESI Table S3). The system sizes span an order of magnitude from 64 atoms with no link atoms for M1 to 544 atoms including 26 link atoms for M5 (see Computational Details). Because each free energy simulation requires nearly half a million single point energy evaluations, we took inspiration from our prior studies to select two QM regions ranging from minimal in size (M1 or M2) to systematically converged (M4 and M5) or nearly converged (M3) at the 0 K QM/MM limit observed for several 600–1000 atom QM regions^{52, 67}. Thus, the central theme of this work is to identify if free energy simulations have similar or reduced sensitivity to QM region size as our prior 0 K QM/MM simulations.^{52, 67} In the present work, the single water within 4 Å of the reacting atoms on SAM and catecholate is included in the QM region, motivated by i) the fact that more distant (ca. 5–6 Å) water molecules were shown to have limited effect on 0 K barrier heights in prior work⁵² and ii) that our fixed QM boundary approach would not be equipped to handle water diffusion across the boundary during the dynamics of the free energy simulations.

The 544–atom model (M5) predicts a ΔG^‡ of 19.9 kcal/mol that is within 1–2 kcal/mol of best experimental estimates^100–101 (Figure 2). However, similar agreement with experimental ΔG^‡ has been achieved with a number of levels of theory and QM region sizes in prior work. Using a combination of long-time classical and semi-empirical (i.e., PM6¹⁰⁸) SQM/MM dynamics, we previously determined⁷⁰ that semi-empirical barrier heights were sensitive to inclusion of the Mg²⁺ coordination sphere and residues adjacent to the substrates. The inclusion of both types of residues produced barrier heights (ca. 21–22 kcal/mol) in nearly as good agreement with experiment as the present large-QM/MM simulations¹⁰⁹. Concurrent with our PM6 SQM/MM COMT study⁷⁰, a complementary SQM/MM study⁷² was published in which 15 PM6 SQM regions were compared to study methyl transfer between a partial model of SAM (i.e., S(CH₃)₃⁺) and catecholate in COMT. In both studies^{70, 72}, the importance of the inclusion of Mg²⁺ and its coordination sphere in the SQM region were recognized. Therefore, in 13 of the models studied in Ref. 72, Mg²⁺, sidechain-only models of the Mg²⁺ coordination sphere, and the sidechains of up to four additional protein residues were included in the SQM region. These 13 sub–100 atom SQM regions produced variations of the barrier height of approximately 5 kcal/mol⁷², with all models underestimating the experimental barrier height, as would be expected from the use of SQM/MM methods. Larger variations (~20 kcal/mol) were seen in the free energy of reaction.⁷² Both SQM/MM studies^{70, 72} highlighted that reaction free energies were in fact even more sensitive to QM region size than the free energy barrier, consistent with expectations from Brønsted-Evans-Polanyi relations. However, they also seemed to indicate that relatively small SQM regions could be chosen to achieve reasonable agreement (i.e., within 5 kcal/mol) with the experimental ΔG^‡.^{70, 72} Our present work differs from these prior studies because, despite these apparent successes, the reliability of SQM to predict essential energetic¹¹⁰ or density¹¹¹ properties governed by an appropriate balance of non-covalent interactions, long-range charge transfer, and electrostatics remains an active area of research⁷⁴. Although corrections have been developed to address potential limitations, they are achieved by fitting to higher levels of theory on small gas phase test sets¹¹². The present work directly treats a full model of SAM and a much larger portion of the protein environment with range-separated hybrid DFT, which improves treatment of long-range charge transfer over both SQM methods and DFT with global hybrids or semi-local exchange-correlation functionals.^{40, 52, 113}

Figure 2.

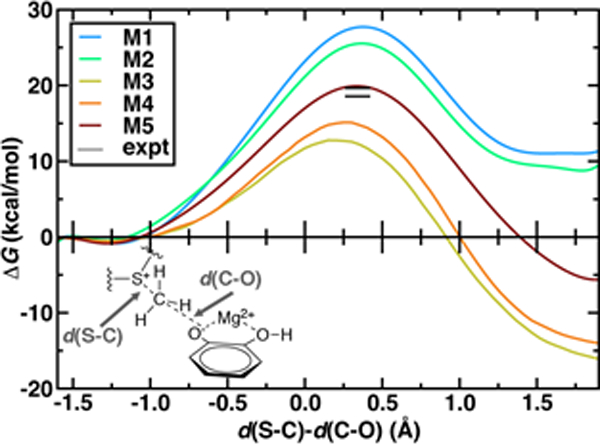
Potentials of mean force (kcal/mol) for QM regions M1 through M5 plotted against the LCOD as defined in the main text and shown in bottom left inset. The experimental range^100–101 is indicated by horizontal lines.

First, rather than aiming for agreement of the theoretical and experimental free energy barriers, which might be arrived at without a complete description of the active site chemistry, we focus on electronic structure properties and dynamics at the active site of our large-scale QM/MM simulation. We will then return to the question of understanding the degree of holistic consistency of energetic, geometric, and electronic structure properties of the five QM regions we have studied. Based on gas phase models, it has been argued¹⁰⁶ that the positively charged SAM and negatively charged CAT become neutral species at the transition state (TS), eliminating the electrostatic driving force for the reaction. The role of the greater enzyme environment in COMT has been debated^{52, 71, 101, 114}, but the unexpectedly short non-bonded SAM-CAT distance observed experimentally⁸⁸ and in QM/MM geometry optimizations^{52, 114} appears electrostatically driven. Indeed, in our dynamics, we observe charge transfer mediated prolonged electrostatic attraction across the reaction coordinate defined by the difference in bond length of the cleaving S-C and forming C-O bonds (Figure 3a). At the TS, the summed Mulliken partial charges on SAM (positive) and CAT (negative) fragments are roughly 2/3 of the magnitude they are in the Michaelis complex (d(S-C)-d(C-O), Δ ~; −1 Å, see Figure 3). Only when the product is fully formed do the SAM- and CAT-summed charges approach zero, even when taking into account dynamic fluctuations in partial charges on both substrates (shaded ranges in Figure 3a). It is also noteworthy that the SAM substrate reaches a peak positive formal charge near the shortened non-bonded distances observed in crystal structures between the substrates (ca. Δ = −0.8 Å, d(S-C)=1.82 Å d(C-O)=2.62 Å) likely due to proximity and enhanced charge transfer to N41/V42 from the SAM carboxylate (ESI Figure S2 and Tables S4–S6).

Figure 3.

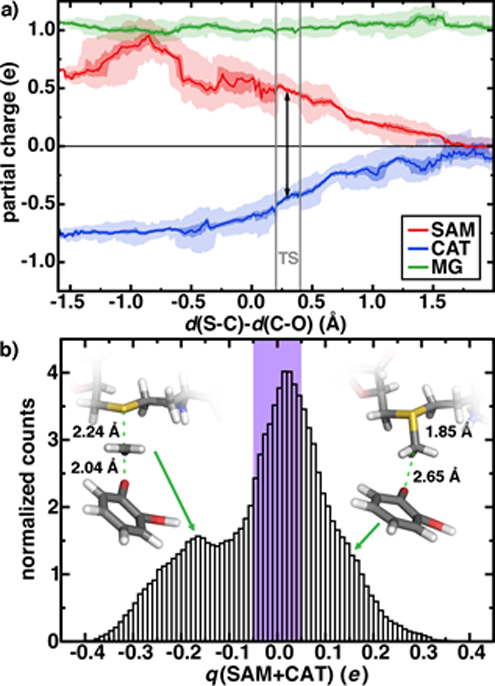
a) Sum of charges on SAM (red), CAT (blue), and Mg²⁺ (green) during methyl transfer reaction in the M5 QM/MM model. Over 0.01 Å bins of simulation data, average charges are indicated by lines, the first to third interquartile range is indicated by the darker shaded region and the full range of charges are indicated by light shading. The methyl charge is partitioned between substrates as described in the main text, and the TS region is indicated as gray vertical bars with average charge separation shown as a black arrow. b) Normalized histogram of partial charges summed over SAM and CAT (in e) across 200 ps of aggregated M5 free energy simulation. The purple bars represent ±0.05 e range and each bin is 0.01 e wide.

The net charge on the combined positive SAM and negative CAT substrates represents the degree of charge transfer between substrates and the surrounding enzyme environment. If this quantity remains close to zero in the QM/MM free energy simulations, then we can expect that increasingly accurate embedding^23–29 (i.e., polarizable) might be able to capture prolonged electrostatic attraction between residues. However, we observe a wide distribution of net charge from −0.4 to 0.4 on the substrates during our simulation, and only 1/3 of the simulation time is spent with the summed substrate charge within ± 0.05 e (Figure 3b). Decomposing the formal charge across the reaction coordinate reveals that a formal positive charge (charge transfer away from the substrates) mediates the shortened Michaelis complex structures observed earlier, whereas charge accumulates on the substrates leading up to the TS and in the product (Figure 3b and ESI Figures S3–S4).

One might expect that the charge transfer between the substrates and the surrounding environment could be localized to only a few charged residues within hydrogen bonding distance of the substrates. We computed by-residue partial charges and compared the dependence of maximum fluctuations (i.e., the difference of maximum and minimum by-residue charges observed during the simulation) to the closest heavy atom distance between the residue and SAM/CAT/Mg²⁺ substrates averaged over the reactant, TS, and product geometries (Figure 4 and ESI Table S4). We observe very large charge fluctuations (ca. 0.7 e) for some proximal and charged residues (e.g., E199) but moderate fluctuations for all residues in the QM region of this model (min. of 0.08 e) and surprisingly little closest-heavy-atom-distance dependence (ESI Figure S2 and Tables S4–S6). To test if charge fluctuations are still localized between pairs of hydrogen bonding residues, we also summed the partial charges of the substrates and the 14 residues with closest heavy atom distances within 3.0 Å of the substrates. This portion of the M5 QM region exhibits just as large fluctuations in deviations from formal charge, with at least three distinct peak features in a wide −0.5 to +0.2 e deviation range and only 26% of all frames within 0.05 e of the expected formal charge (ESI Figure S5).

Figure 4.

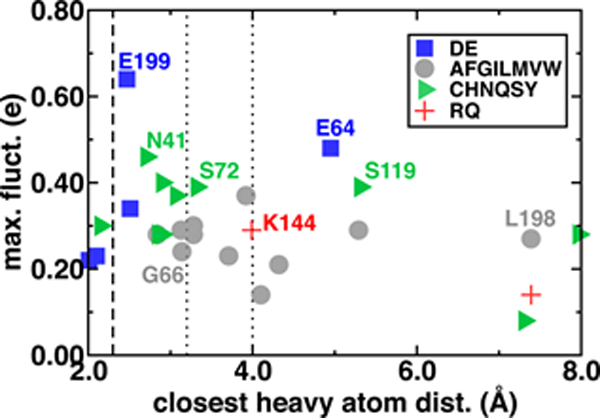
Range of by-residue summed partial charges including link atoms (max. fluct., e) sampled for each residue grouped by negatively charged (blue squares), nonpolar (gray circles), polar (green triangles), and positively charged (red crosses), with residue types indicated in legend plotted against the average closest heavy atom distance between the residue and SAM, CAT, or Mg²⁺. Vertical lines indicate approximate covalent bond (dashed), moderate hydrogen bond (dotted), and weak hydrogen bond (dotted) distance cutoffs.

As an example of weak distance dependence, D141 and D169, which form the Mg²⁺ coordination sphere, exhibit lower fluctuations than nonpolar L198, which is 7 Å from the closest substrate heavy atoms (Figure 4). Perhaps surprisingly, similar magnitude fluctuations are observed for both polar and nonpolar residues, and a comparison of charge standard deviations preserves trends (ESI Figures S6–S8). Large fluctuations in residues beyond typical hydrogen bonding distances to the substrates (i.e., ~;3.25 Å, see Figure 4) can be rationalized by proximity to substrate-neighboring residues that have large fluctuations. For example, the relatively high fluctuations for substrate-distant L198 are a consequence of its being adjacent to E199, and the somewhat distant E64 hydrogen bonds with S72, which in turn hydrogen bonds with SAM (see ESI). On the other hand, D141 and D169 have among the lowest fluctuations for charged residues, despite significant deviations from formal charges (ESI Figure S9). This highlights that fluctuations arise predominantly in mobile residues that vary in active site proximity along the reaction coordinate rather than protein residues that remain covalently coordinated to the substrates (ESI Table S4).

The delicate interplay of charge transfer between the substrate and the enzyme environment can be observed through the structure of the reacting substrates and Mg²⁺, also highlighting the crucial importance of Mg²⁺ in COMT catalysis⁷⁵. The four Mg²⁺-O bonds with the protein, i.e., D141, D169, N170, and a water molecule are relatively unchanged across the reaction coordinate but differ in length (Figure 5). Although D169 and D141 Mg²⁺-O^- bonds are shorter than the neutral N170 bond (2.02–2.10 Å vs. 2.17 Å) as expected, the Mg²⁺-water bond is substantially shorter (2.02 Å) than observed for hexa-aqua complexes¹¹⁵ (Figure 5 and ESI Text S1). Across the reaction coordinate, charge transfer mediated prolonged electrostatic attraction is evident in the Mg²⁺-O bond of the catecholate oxygen that carries out nucleophilic attack on the SAM methyl group. Initially, this bond is the shortest (ca. 2.00 Å) of all Mg²⁺-O bonds and remains in the range of the D141 and D169 Mg²⁺-carboxylate bond lengths until well past the TS (ca. Δ = 0.7 Å, d(S-C)=2.59 Å d(C-O)=1.89 Å). Thus, Mg²⁺ plays the critical role not only of positioning catechol for nucleophilic attack but in maintaining the strong nucleophilic character of the catecholate oxygen. This observation is consistent with prior work that revealed⁷⁰ the importance of a QM description to capture this interaction to reproduce experimental structural observations, which was frequently neglected in prior SQM/MM studies¹⁰⁷.

Figure 5.

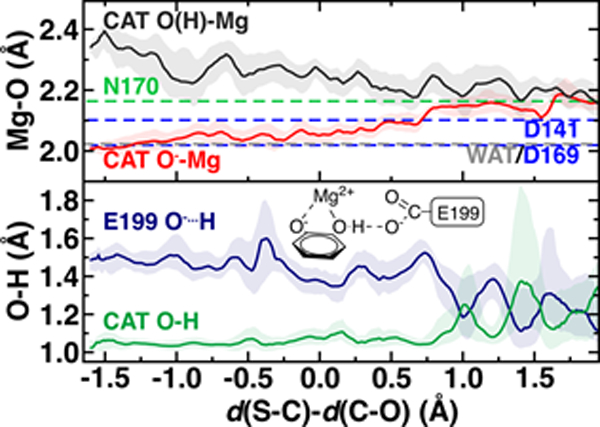
Mg²⁺ coordination sphere (top) and catecholate (bottom) structural properties in the M5 QM/MM model across the reaction coordinate. At top, the median, averaged distance is reported as dashed lines for N170 (green), D141 and D169 (blue), and water (WAT, gray) as a reference for the CAT O(H) (dark gray) and CAT O^- (red) distances to Mg²⁺ across the reaction coordinate. At bottom, catechol hydrogen atom distance to neighboring E199 (dark blue) and to the catechol oxygen atom (dark green) are plotted along the reaction coordinate. The remaining quantities are the median values obtained at 0.01 Å increments and averaged over a 0.1 Å window with the range of variations shown as a shaded region. A schematic of E199, Mg²⁺, and CAT is shown in inset at bottom.

In comparison, the catechol oxygen distance to Mg²⁺ is the longest in the octahedral coordination sphere, becoming comparable in length to the methylated oxygen-Mg²⁺ distance only in the product (Figure 5). The long catechol-Mg²⁺ bond length is likely due to competition with a strong hydrogen bond that forms with the E199 carboxylate, leading to a shared hydrogen atom between the two species in the product state (both O-H ca. 1.2 Å) typically indicative of a low-barrier hydrogen bond¹¹⁶ that would be unlikely to be suitably described across a QM/MM boundary (Figure 5). Thus, it would appear that charge transfer effects only observable with large QM regions can influence both energetics and structure/dynamics across the reaction coordinate.

The remaining question is to what extent these large-scale QM/MM observations of geometric and electronic structure trends are preserved in smaller models in spite of moderate discrepancies in energetics (Figure 2). In order to evaluate QM region dependence in dynamics, we now compare our four increasingly large QM regions (M1-M4) to our largest QM simulation (M5). Wide ranges of both ΔG^‡ and ΔG_r as well as TS character are observed across M1-M5 (Figures 2 and 6 and ESI Table S7). Consistent with prior SQM/MM^{70, 72} and trends in our static results⁵², both M1 and M2 substantially overestimate the ΔG^‡, predict an uphill ΔG_r, and underestimate the charge separation at the transition state with respect to M5 (Figure 6 and ESI Table S7). The 170-atom M3 region incorporates four proximal residues beyond those in the Mg²⁺ coordination sphere, overstabilizing the transition state and product (i.e., ΔG^‡(M3) < ΔG^‡ (M5) or expt.), despite underestimating the separation of the substrate charges in the transition state and predicting substrate neutralization in advance of the products (Figure 6 and ESI Figure S10). Analysis of partial charges reveals that the absence of N41/V42 interactions with the SAM carboxylate likely accounts for the more neutral overall SAM charge but an absence of charge transfer with a QM K144 adjacent to the catecholate overestimates the nucleophilic character of the attacking catecholate oxygen.

Figure 6.

Comparison of ΔG^‡ (in kcal/mol), ΔG_r (in kcal/mol) charge separation of SAM and CAT at the TS (ΔQ in e), and anionic catecholate-Mg²⁺ bond length progress in the TS with respect to difference between the reactant and product (in %) for five QM regions. Error bars for top and bottom left hand side panels come from bootstrapping and they correspond to standard deviations in quantities on the top and bottom right.

Finally, M4 was selected systematically^{52, 67–68} on the basis of charge/Fukui shift analysis on 20 0 K snapshots of COMT and confirmed to have a 0 K barrier height within 1 kcal/mol of 0 K converged (i.e., M5) values.⁶⁷ Agreement of QM/MM dynamics, energetics, and charge density between M4 and M5 is slightly worse than the equivalent regions in prior study⁶⁷ but by far in the best agreement of any two regions (Figure 6). Like M3, M4 overstabilizes the TS and products with respect to M5 but does so by overestimating the charge separation at the TS, suggesting enhanced electrostatic attraction as the driving force for M4 barrier underestimation (Figure 6).. The differences in characteristics between M4 and M5 can likely be attributed to the absence of K144 from the M4 QM region, which was distant from the substrate in the selected 0 K snapshots but proximal throughout the 300 K dynamics in this work (ESI Table S4). The absence of K144 in the QM region has the additional effect of producing a shorter Mg²⁺-O^- CAT bond in the TS for M5 than in the other 4 QM regions (Figure 6 and ESI Table S8). Overall, the static-QM-selected regions M3 and M4 bear the best qualitative agreement with the large-scale M5 region. Thus, we find greater disagreement (i.e., 3–5 kcal/mol free energy differences vs. 0–1 kcal/mol 0 K electronic energy differences) among QM regions that had been previously systematically converged for 0 K properties⁶⁷, emphasizing that deviations are likely due to enhanced sensitivity during dynamics. This observation over QM regions that differ by as much as 375 atoms in size is consistent with prior observations made of 5 kcal/mol free energy barrier fluctuations for varying SQM regions of much more similar (ca. 100 atoms) in size⁷². Remaining differences highlight that quantitative agreement through systematic QM region selection will require sampling¹¹⁷ a wider range of possible configurations relevant during dynamics. Furthermore, as computing power continues to increase, even larger QM regions and longer timescales in QM/MM dynamics should be employed to identify the limits of convergence beyond this study.

4. Conclusions

In conclusion, we have leveraged accelerated electronic structure approaches to carry out a large-scale study of over 1 ns of ab initio, range-separated hybrid DFT QM/MM dynamics with QM regions from 64 to 544 atoms in size. These large-scale QM/MM studies revealed QM-region-dependent differences in electronic and geometric structure. In addition to accurate prediction of the free energy barrier for methyl transfer, charge separation and neutralization only in the product structure are observed with large QM/MM free energy simulations. Differences in geometry (e.g., relative Mg²⁺-catecholate oxygen bond lengths) and > 0.4 e fluctuations of summed charge on residues 5 Å away from the substrates (i.e., E64 or S119) indicate the extent to which substrate–active site charge transfer can play a key role in enzyme mechanism. This long-range substrate-active site charge transfer is consistent with notions that the enzyme creates an electrostatic driving force for the reaction by stabilizing the transition state but highlights that in some cases large-scale QM regions may be needed to fully observe this effect. These studies also reveal that differences in electronic environments also give rise to differences in dynamics and structure in a manner that will likely enhance not decrease QM region dependence for free energy simulations and dynamics. Such observations should motivate the continued improvement of QM/MM through i) improved embedding schemes and boundary treatment, including to allow charge transfer, ii) incorporation of large, beyond-DFT QM regions (e.g., through reduced-scaling correlated wavefunction theory), and iii) development of efficient sampling techniques and free energy decomposition. We note, however, that the large number of hydrogen bonds between charged residues and substrates in the active site of COMT and homologous MTases likely show a larger QM region dependence than a number of cases where small QM-region QM/MM studies may still encapsulate essential physics.

Although the best agreement with the largest QM region was obtained from systematically constructed QM/MM regions (325 atoms vs. 544 atoms in size) obtained from analysis of two dozen 0 K snapshots, variations between the M4 and M5 QM regions in energetics and properties were still apparent. These differences were observed to be due to fluctuations in the orientations of residues during dynamics absent from the 0 K geometry optimizations and barrier evaluations in previous work that had shown smoother convergence with QM region size. As accelerated electronic structure calculations and computing power become increasingly available, it is anticipated that these calculations could be repeated with alternative QM regions of even larger size to confirm stricter property convergence (e.g., free energies within 1 kcal/mol). Overall, this work also reinforces the importance of systematic QM region construction including dynamic benchmarking of substrate electronic properties to identify minimal sufficient QM regions in future QM/MM studies. Methods that directly incorporate dynamic fluctuations of electronic properties during dynamics to construct QM regions are currently being developed in our group.