Abstract
Metopic craniosynostosis is a condition caused by the premature fusion of the metopic cranial suture. If untreated, it can result into brain growth restriction, increased intracranial pressure, visual impairment, and cognitive delay. Frontoorbital advancement is the widely accepted surgical approach to correct cranial shape abnormalities in patients with metopic craniosynostosis, but the outcome of the surgery remains very dependent on the expertise of the surgeon because of the lack of objective and personalized cranial shape metrics to target during the intervention. We propose in this paper a locally affine diffeomorphic surface registration framework to create an optimal interventional plan personalized to each patient. Our method calculates the optimal surgical plan by minimizing cranial shape abnormalities, which are quantified using objective metrics based on a normative model of cranial shapes built from 198 healthy cases. It is guided by clinical osteotomy templates for fronto-orbital advancement, and it automatically calculates how much and in which direction each bone piece needs to be translated, rotated and/or bent. Our locally affine framework models separately the transformation of each bone piece while ensuring the consistency of the global transformation. We used our method to calculate the optimal surgical plan for 23 patients, obtaining a significant reduction of malformations (p < 0.001) between 40.38% and 50.85% in the simulated outcome of the surgery using different osteotomy templates. In addition, malformation values were within healthy ranges (p > 0.01).
Index Terms: Craniosynostosis, locally affine, surgical plan, osteotomy, registration
I. Introduction
A. Craniosynostosis
Non-syndromic craniosynostosis is a condition affecting 1 in 2100–2500 live births [1] in which one or more cranial sutures fuse early, producing head malformations because of the compensatory brain growth along the direction parallel to the fused suture. If untreated, craniosynostosis can cause brain growth restriction, increased intra-cranial pressure, visual impairment and cognitive delay. Treating craniosynostosis often requires surgery to reconstruct the cranial vault and allow the brain to develop normally.
In this work, we focus on the early fusion of the metopic suture, which is the suture that separates the two frontal bones, as shown in Figure 1. Patients with metopic craniosynostosis typically develop a triangular shape of the head due to the constrained growth of the frontal cranial bones, which is called trigonocephaly. Although the clinical diagnosis of craniosynostosis is usually done by visually inspecting the head shape and the fused sutures in Computed Tomography (CT) images of the head [2], the specific diagnosis of metopic craniosynostosis is more challenging. The reason is that the metopic suture fuses early in healthy subjects too, so diagnosis of metopic craniosynostosis is mostly based on the subjective assessment of the cranial shape of the patient.
Fig. 1.
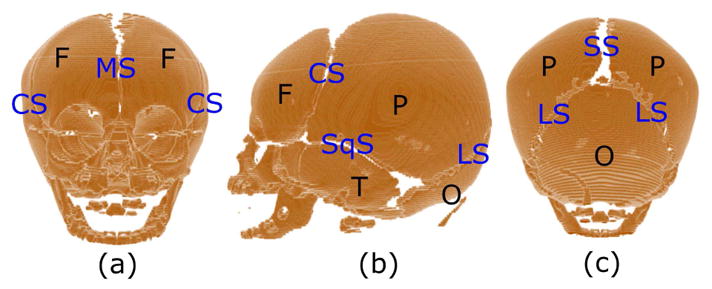
Cranial bones: (a) frontal, (b) lateral and (c) posterior views of the cranium of a healthy control subject (age 1 month). The main cranial bones are labeled in black as F (frontal), P (parietal), T (temporal), and O (occipital) and are separated by open sutures. The main sutures are labeled in blue as MS (metopic), CS (coronal), SqS (squamous), SS (sagittal), and LS (lambdoid).
An automatic and quantitative framework for an objective assessment of craniosynostosis was proposed in [3], where a multi-atlas of healthy cranial shapes was used to quantify cranial shape abnormalities using two different descriptors: (1) the malformations, which are the local Euclidean distances between the surface representation of the patient’s cranial shape and its closest normal shape in the multi-atlas space, and (2) the curvature discrepancies, defined as their local curvature differences. These descriptors, together with the suture fusion information obtained from the patient’s CT image, were shown to provide an accurate automatic diagnosis of craniosynostosis [4]–[6].
After diagnosis of metopic craniosynostosis, fronto-orbital advancement is the most widely accepted surgical approach to create a normal cranial shape. During the intervention, the supra-orbital bar and the frontal bones are separated from the rest of the cranium and reshaped to correct the trigonocephaly and allow for a normal brain development [7]. Depending on the degree of malformations, it may be necessary to divide the frontal bones and/or the supra-orbital bar in smaller bone pieces to create a normal shape. Although the work presented in [3] proposed a solution for an objective diagnosis of metopic craniosynostosis, it did not address the problem of how to create a normal shape during surgical treatment. Currently, there are no reproducible and objective methods to create the optimal cranial shape during the intervention, and the outcome of the intervention is very dependent on the expertise of the surgeons.
Computer aided planning software [8] has improved significantly cranio-maxillofacial interventions. Several groups have explored the use of these systems to plan craniosynostosis surgical treatment [9] and, as shown in [10], they generally provide a better and faster cranial vault reconstruction. However, these tools need substantial manual interaction to create a plan for surgery and the results are very dependent on the expertise of the specialists. In addition, the reference models used for visual guidance were either population averages or age-matched templates [11], which do not adapt to the specific cranial shape of the patient.
In the current work, we focus on the surgical treatment for the reconstruction of the cranial shape of patients with metopic craniosynostosis. We aim at defining a patient-specific, automatic, and reproducible method to plan fronto-orbital advancement based on quantitative and objective metrics. We model the solution as a locally affine diffeomorphic surface registration problem in which the goal is to deform the patient’s cranial shape (i.e. reposition and reshape cranial bone pieces) to create a cranial shape as close as possible to its closest shape from a normative statistical shape multi-atlas. Our automatic framework is designed around the clinical osteotomy templates for fronto-orbital advancement.
B. Surface-Based Registration
Methods for surface registration in medical imaging have been proposed to quantify surface dissimilarities and/or to model surface matching transformations [12], [13]. Surface registration is often addressed as a problem of finding point correspondences, which presents two main problems. First, no structural information is considered by only using point coordinates, so this approach can result into surfaces with similar point distribution but different geometry. Second, these methods assume that there is a one-to-one point correspondence but, in most cases, it is necessary to register surfaces with different point distributions. A surface matching method where surfaces were represented as currents was presented in [14]. Using this kind of representation, it is possible to compare two surfaces with different number of points. Moreover, surface comparison in the space of currents is sensitive both to point location and surface geometry.
To solve the problem of creating a normal cranial shape during surgery that we address in this paper, the surgeon repositions and remodels a set of bone pieces to create a global cranial shape that is as close as possible to a healthy shape. Therefore, our solution needs to account both for the individual transformation of each bone piece and for their interactions. The concept of a global deformable transformation model that incorporates different regions with specific properties was introduced in [15] for image registration. In that work, a set of local rigid transformations was estimated, one for each rigid object present in the images. These local transformations were combined with a global deformable transformation based on radial basis functions using a weighting scheme. Although, that framework ensured rigidity at specific regions of the image, invertibility of the transformation was not guaranteed and the accuracy of the results was constrained by the resolution of the grid of control points and the properties of the radial functions.
An image registration method to combine different rigid/affine transformations was proposed in [16], using Gaussian weighting functions centered at predefined anchor points to obtain a diffeomorphic deformable transformation. An improved mathematical framework for poly-affine registration was also presented in [17]. Those frameworks enabled non-rigid registration of medical images using a small number of parameters in comparison to other state-of-the-art non-rigid registration methods. However, although different local rigid/affine transformations were combined, rigidity/affinity was not ensured at any specific region of the image.
In our previous work [18], we proposed a method to incorporate rigid regions in an image-based registration framework based on the transformation model proposed in [16], by incorporating a new weighting scheme controlling the contribution of each local rigid transformation at each region of the image. We then created a preliminary surface-based registration framework in [19] where local regions (i.e. bone pieces) were modeled using affine transformations instead of only rigid. In the current paper, we present our new surface registration framework that allows not only for bone repositioning, but also bone bending. We calculate the dissimilarity between the source and target surfaces in the space of currents and we improve the weighting scheme to adjust dynamically to the changes introduced by the transformation at each discretization point during the temporal integration of the velocity field estimated. Compared to [17], our transformation model is region-wise affine and unlike in [19], we model the transformation of each bone piece with reference to its center of mass, which facilitates implementing the transformation of each bone piece to the operating room. We also extend our framework to evaluate different osteotomy plans for the same patient, and we compare the surgical outcome simulated using each osteotomy plan in terms of three different metrics: reduction of malformations, reduction of curvature discrepancies, and minimum bone stress to implement the optimal plan. We estimated the optimal surgical plan for 8 more patients with respect to our preliminary work presented in [19], evaluating a total of 23 patients with metopic craniosynostosis. Finally, we built a new normative statistical shape multi-atlas with 198 healthy subjects used as a reference to quantify cranial shape abnormalities, thus incorporating 98 healthy cases with respect our previous work [19].
II. Methods
In this section, we first summarize our methods to obtain the surface representing the patient’s cranial shape, segment the cranial bones, and quantify cranial shape abnormalities. Then, we describe in detail the components of the proposed surface-based registration framework (dissimilarity measure and transformation model) to calculate the optimal transformation of the patient’s cranium that creates a cranial shape as close as possible to its closest normal shape from a normative multi-atlas. In addition, we present the approach that we followed to design different clinical osteotomy templates for the surgical intervention. A summary of the framework proposed is presented in Figure 2.
Fig. 2.
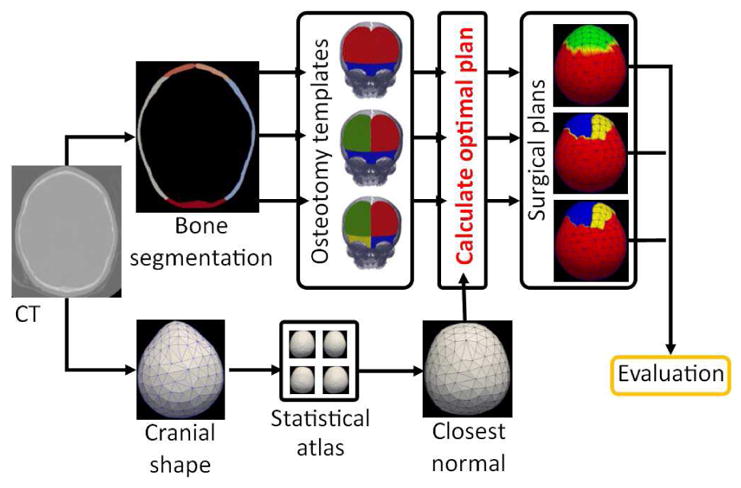
Pipeline of the proposed framework. We segment the cranial bones from the CT image of a patient, and we evaluate different subdivisions of the cranial bones following a set of predefined osteotomy templates. For each osteotomy template evaluated, we calculate the optimal surgical plan using the registration framework proposed, which minimizes the difference between the patient’s cranial shape and its closest normal from a normative statistical shape multi-atlas. Finally, we evaluate the surgical outcome from the optimal plan calculated with each osteotomy template based on different criteria: minimization of malformations, minimization of curvature discrepancies, or minimum bone stress.
A. Cranial Shape Extraction, Bone Segmentation and Quantification of Malformations
Given the CT image of a patient’s head, we obtain the mesh representing its cranial surface as presented in [3]. First, we extract the bones from the CT image using thresholding based on the Hounsfield units of bone tissue, thus creating a binary image of the bones. Then, we obtain the surface representing the patient’s cranial shape from the binary image by the constrained relaxation of an embedding sphere, as presented in [20]. The result is a single-layered continuous mesh.
From the binary image created previously, we segment the different cranial bones using a method based on graph-cuts [21]. First, we label manually the cranial bones on the binary image of a healthy subject used as reference. Then, given the binary image of a new patient’s cranium, we register it to the reference template as explained in [3]. This registration estimates the pose and scale to align the patient’s cranial shape to the reference subject only considering the base of the cranium, thus minimizing the impact of the malformation in the cranial vault area caused by craniosynostosis. Then, we minimize the following cost function to label the cranial bones:
| (1) |
where α is a weighting parameter, l is a labeling scheme assigning label lx to voxel at coordinates x, and dl is the distance to the cranial bone with label l in the reference template. K is the set of all pairs of neighboring voxels in the image, and Vx, y(lx, ly) is a term that penalizes if neighboring voxels have different labels assigned, with value 1 if lx ≠ ly, and 0 otherwise. Note that the first term in the equation guides the segmentation based on the reference template, while the second penalizes for neighboring voxels having different labels.
Quantification of cranial shape abnormalities is done by comparing the patient’s cranial shape with its closest normal shape from a normative multi-atlas, as explained in [3]. Once the closest normal shape to the patient’s cranial shape is identified, two different descriptors are used to quantify cranial shape abnormalities: (1) the malformations, which are the local Euclidean distances between the mesh representation of the patient’s cranial shape and its closest normal shape in the multi-atlas space, and (2) the curvature discrepancies, which are their local curvature differences.
B. Surface Dissimilarity
The goal of our registration framework is to repair the patient’s cranial shape (source mesh) by deforming it to best fit its closest normal shape (target mesh) from the normative statistical shape multi-atlas. To compare these two surfaces, we propose to use a global dissimilarity measure based on a representation of the surfaces in the space of currents [14]. We chose this kind of representation because it allows us to quantify shape differences by taking into account both point distances and geometric structure (curvature), which are the two descriptors of cranial shape abnormalities presented in [3]. The transformed source mesh and the target mesh can then be compared using the following dissimilarity measure:
| (2) |
where S is the discrete current associated to the source triangulated mesh, U is the discrete current associated to the target mesh, ϕ# is the push-forward of the transformation ϕ in the current S, and W* is the dual space associated to a reproducible kernel Hilbert Space [14].
A Dirac current applied to a given vector field in a reproducible kernel Hilbert space W can be seen as the realization of that vector field with respect to the oriented segment n at point c. Thus, the discrete current associated to the surface S can be written as , where each f is a triangle of the surface S, nf represents the normal vector to the triangle, and cf represents the coordinates at the triangle center [14]. Then, the dissimilarity between two triangulated surfaces S and U can be expressed as:
| (3) |
which translates to:
| (4) |
where f and g represent triangles of S, q and r represent triangles of U, and kW is the kernel associated to W. In our implementation, we used an isotropic Gaussian kernel. Since our goal is to compare the patient’s cranial shape transformed during surgery and its closest normal shape from a normative multi-atlas, their dissimilarity based on Equation (4) is
| (5) |
where S is the patient’s cranial surface, U is its closest normal surface, φ represents the transformation applied to S during surgery, φ(cf ) is the transformed coordinates of the center cf of triangle f, and φ(nf ) is the transformed normal vector of triangle f.
C. Locally Affine Transformation Model
Having established a metric to compare the source and target surfaces globally, here we define a way to transform the source mesh to best fit the target mesh. As discussed in the Introduction section, our transformation model must preserve specific properties (i.e. affine) in local regions of the mesh (i.e. bone pieces).
Let T = (R, t) be an affine transformation with linear part R (including rotation and scaling) and translation t in homogeneous coordinates, in which the first 3×3 components are represented by R, the last column by t, and the bottom-right element is 1. The affine transformation of a point at coordinates x expressed in homogeneous coordinates is calculated as φ(x) = Tx. In [17], image registration was modeled as a temporal process transforming point coordinates from time s = 0 to time s = 1, and the matrix logarithm of T was proposed to define a family of velocity vector fields associated to T. Hence, the logarithm of T is defined as:
| (6) |
where LR is the principal logarithm of R, but Lt is not necessarily equal to t [17]. As shown in [17], if the eigenvalues of T are not negative, which is subject to only allowing rotations lower than 180 degrees, there is only one solution to Equation (6) called principal logarithm. This is not a problem in the current application because during the surgical approach of fronto-orbital advancement the cranial bone pieces are mostly advanced and bent and, therefore, we do not expect large rotations. Using this notation, the family of velocity vector fields associated to the transformation T is
| (7) |
where s ∈ [0, 1] represents the time. It is important to remark that in this scheme, the velocity of a point at coordinates x is constant in time. The transformed coordinates of a point at coordinates x and time s can then be calculated as:
| (8) |
In the poly-rigid/affine framework described in [16], the authors showed that, given N rigid/affine transformations, they can be composed in an invertible way by combining the velocity associated to them using the following equation:
| (9) |
where wi (x) is the weight of the transformation associated with region i at coordinates x, and υi (x) is the velocity of the local transformation with index i.
As it was shown in [17], based on the Scaling and Squaring method [22], the transformation of a point at coordinates x from time s = 0 to time with velocity defined as in Equation (9) can be approximated as
| (10) |
where Ti is the affine transformation with index i, is the 2M root of Ti, and the weights wi (x) are normalized. Among the available solutions to estimate the squared root of a matrix, we followed the iterative approximation presented in [23]. Then, the final point coordinates at time s = 1 is obtained by composing 2M times that transformation:
| (11) |
where the input to the transformation represented as. indicates that it comes from the output of the previously composed function. Equation (11) can also be expressed recursively as:
| (12) |
where 2M is the number of discretization subintervals used to approximate the transformation when integrating temporally the velocity field, and φm (x) is the transformation at inter-mediate subinterval m = 0..2M. Note that Equations (11) and (12) show that the transformation of a point can be calculated as the composition of smaller transformation.
In the original work on poly-affine transformations [16], all local transformations were defined as centered on the origin of coordinates, which worked well because the objective was not to preserve local properties at specific regions. In our work, we associate each local transformation to one region in the source surface defined by a cranial bone piece. To facilitate implementing the transformation of each bone piece in the operating room, we model the transformation of each bone piece i with reference to its center of mass. Therefore, we re-write Equation (12) as
| (13) |
where ai is the center of mass of the bone piece with index i.
D. Locally Affine Regions
In the poly-rigid and poly-affine transformation frameworks on image registration [16], [17], the authors proposed a global transformation model calculated by combining different rigid/affine transformations using Gaussian functions centered at predefined anchor points. With such approach, no single region of the image was constrained to present a specific rigid/affine behavior. On the contrary, every region presented a weighted combination of rigid/affine transformations with the weights defined by the initial coordinates of the point transformed.
In [18], we introduced a mathematical image registration framework to constrain specific image regions to be purely rigid. To achieve that, we proposed to calculate Signed Distance Functions (SDF) [24] for each region (i.e. bone piece) on the source image. These SDFs provide the distance of each point in the Euclidean space to the boundary of each region (bone piece), with a positive sign if the point is outside the region, and a negative sign otherwise. Then, we calculated the weights wi associated to each local transformation i using a logistic function as a smooth and differentiable approximation to a Heaviside step function, thus preserving smoothness and invertibility of the global transformation:
| (14) |
where c is a positive constant controlling the slope of the weight function at the transition point (i.e., region boundaries), and SDFi (x) is the SDF of region (bone piece) with index i calculated at coordinates x. Note that wi approximates to 1 inside the region associated to the local transformation i, while it approximates to 0 as the distance from that region increases. The result of using this weighting scheme was a global transformation that at each region was defined by the local transformation associated to it. Note that, although the weights of the transformations associated to other regions are not exactly zero with this scheme, their value is very close to zero and the contribution of their local transformation is negligible.
However, by using previous approach, the weights were estimated statically based on the source image, and they were not updated as the rigid regions were modified at each temporal integration step in Equation (12). This means that the area where an object (bone piece) with specific properties (e.g. rigid or affine) could be transformed without modifying those properties were predefined and did not change during optimization (see Figure 3(a)). To overcome this problem, we propose to define a weighting scheme that dynamically adapts to changes at each temporal integration step. Hence, we define the weight function as
Fig. 3.
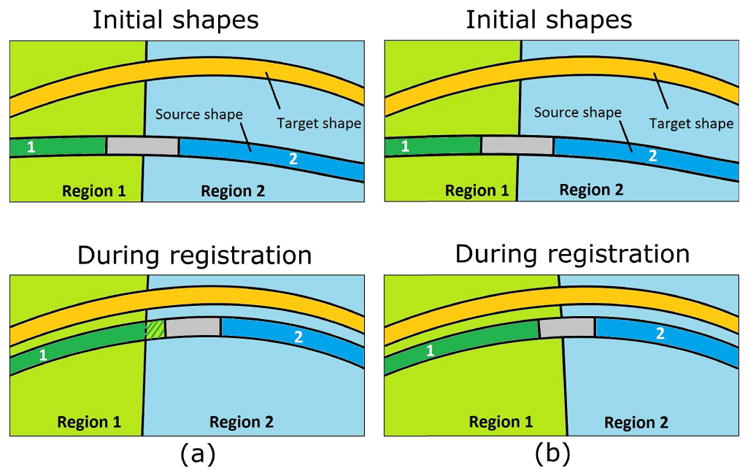
Dynamic weighting scheme proposed. (a) illustrates the problem of the weighting scheme proposed in [18] with an example of which the source surface includes two affine areas (labeled as 1 and 2). The affine regions were predefined before registration so, if a part of the surface was transformed to another region during registration, it would lose its affine properties (as represented with stripes); (b) shows how the proposed scheme updates the regions at each temporal integration step, thus preserving the local properties in the source mesh (e.g. affine). Note how the moving surface becomes more similar to the target surface during registration in terms of distance and curvature.
| (15) |
and we rewrite the transformation from Equation (13) as
| (16) |
where is the signed distance between the point at coordinates x and the region (bone piece) associated with transformation i at the temporal integration step m, and is the weight of transformation i at the temporal integration step m. Importantly, this equation is only valid under the assumption that the velocity field associated to each local transformation is constant. The improved optimization scheme proposed is illustrated in Figure 3(b) and compared to previous scheme represented in Figure 3(a).
E. Osteotomy Plan for Metopic Craniosynostosis Treatment
Surgery for the treatment of metopic craniosynostosis consists in advancing and reshaping the frontal cranial bones of the patient to create a normal cranial shape, which is known as fronto-orbital advancement surgery [7]. In practice, the supra-orbital bar and the frontal bones (show in Figure 1) are separated from the rest of the cranium and advanced and/or reshaped. This allows creating a healthy cranial shape that allows for a normal brain development. However, depending on the degree of cranial shape abnormalities, it is necessary to divide the frontal bones and/or the supra-orbital bar in smaller pieces to increase the flexibility of reshaping the bones to obtain a normal shape. We propose to create different digital osteotomy templates defined by surgical practice, including subdivisions of the frontal bones and supra-orbital bar, and to use them to evaluate different osteotomy plans for each patient. These osteotomy templates define how many subdivisions of each frontal bone will be considered in the calculation of the optimal plan and, therefore, how many local affine transformations Ti need to be combined using Equation (16). Then, given the simulated outcome from each surgical plan, we can automatically choose the optimal template based on objective criteria (e.g. malformations, bone stress…), or other criteria considered by the surgeon.
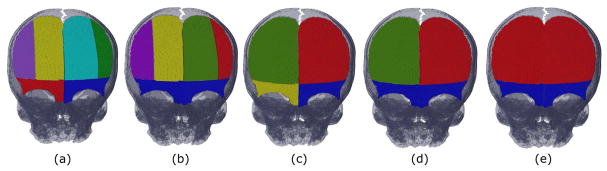
To create each digital osteotomy template, we follow a similar approach to the one we used to segment the cranial bones. First, the subdivisions of each bone piece were manually delineated in a reference image template from a healthy control, as shown in Figure 4(a). Then, we used Eq. (1) to label these subdivisions on the patient’s cranium, but setting the second term to zero. The effect of this is that the subdivision of each cranial bone is solely guided by the template, since there are no anatomical references in the images to use for guidance. In the templates shown in Figure 4, frontal bones are considered together, separated into left and right bones, or by subdivision of each frontal bone into two vertical sections. Similarly, the supra-orbital bar is considered as a unique piece or by subdivision into left and right sections. These templates are defined by common clinical practice to perform fronto-orbital advancement [7], [25]. Next, to estimate the optimal surgical plan using one osteotomy template, we define one local affine transformation for each bone piece in the osteotomy template, and we combine them using Eq. (16).
Fig. 4.
Frontal view of the digital osteotomy templates used to calculate the optimal surgical plan, together with the cranium of the reference control case used for segmentation. Each osteotomy template considered the subdivision of the frontal bones and supra-orbital bar in (a) 6, (b) 5, (c) 4, (d) 3, and (e) 2 bone pieces. Each color represents a bone piece remodeled and repositioned during surgery using a local affine transformation.
F. Bone Surface Preservation and Optimization
In the proposed framework, bone bending is modeled using affine transformations. However, affine transformations may also scale the bone surface, which is undesired in the current application. To constrain bone surface change, we include the following surface preservation term in our metric:
| (17) |
where l are the labels of each cranial bone piece in the patient’s cranial surface S, Sl are the triangles of the bone piece with label l in S, nf is the normal vector to triangle f εSl, and φ(nf ) represents its transformation. Finally, a global smoothing regularization term was included:
| (18) |
where pεP represents all the triangles at the cranial sutures in S (areas between bones, see Figure 1), and qεQp represents the neighboring triangles of p. If M (S,U, φ) is the surface dissimilarity term defined in Equation (5) between the patient’s cranial surface after applying transformation φ and its closest normal cranial shape U, the final cost function to calculate the optimal surgical plan is then:
| (19) |
where β and γ are positive weighting constants balancing the contribution of the surface preservation and smoothing terms to the cost function. To minimize the cost function, we used a regular gradient descent optimizer, which updated iteratively the value of all the transformation parameters together using the gradient of the cost function with respect to them. The parameters of transformation φ are the elements of all the local affine transformations Ti : 9 parameters of its linear part R, and 3 of is translation t. Therefore, the total number of parameters is 12 times the number of local affine transformations. The derivation details are provided in the supplementary material, section B.
III. Experiments and Results
A. Data Description
We constructed a normative statistical shape multi-atlas as proposed in [3]. We collected head CT images (average in plane resolution of 0.36±0.05 mm, and average slice separation of 1.49±1.26 mm) from 198 control subjects (99 females, 99 males, age 5.28±3.65 months), who were selected from the subjects reported to the emergency room for trauma at Children’s National Health System. The control cases were manually screened to exclude any pathology that may affect the cranial shape: hydrocephalus, intra-cranial tumor, intra-cranial hemorrhage, hardware (e.g. shunts), and prior craniofacial surgery. We evaluated the optimal surgical planning framework proposed on a total of 23 patients with metopic craniosynostosis (7 females, 16 males, age 3.52±4.48 months). The in-plane resolution of the patients’ CT images was 0.40±0.04 mm, with a slice separation of 2.35±1.75 mm.
B. Experiments
Table 1 shows the malformations and curvature discrepancies calculated in the frontal bones both for the healthy controls in the normative statistical shape multi-atlas and for the patients with metopic craniosynostosis.
TABLE I.
Comparison of malformations and curvature discrepancies between healthy controls and patients with metopic craniosynostosis. Differences indicate the reduction of malformations and curvature discrepancies in the controls compared to the patients. The p-values are estimated using a Wilcoxon rank sum test between patients and controls.
| Patients | Controls | Difference | p-value | |
|---|---|---|---|---|
| Mean malformations (mm) | 2.90±1.34 | 1.32±0.58 | −54.63% | <0.001 |
| Maximum malformations (mm) | 5.32±0.43 | 2.63±1.06 | −50.61% | <0.001 |
| Mean curvature discrepancies (mm−1) | 1.10±0.22 | 0.60±0.17 | −45.76% | <0.001 |
| Maximum curvature discrepancies (mm−1) | 2.68±0.12 | 1.57±0.52 | −41.40% | <0.001 |
For each patient, we calculated the optimal surgical plan using the different osteotomy templates represented in Figure 4, creating plans involving 2, 3, 4, 5 and 6 bone pieces. Thus, using each osteotomy template, we estimated one global transformation, which includes a local affine matrix for each bone piece delineated in the patient’s cranial shape following that osteotomy template. The average time of computation to calculate each interventional plan was 4.0 ± 2.4 hours in an Intel i7 Core desktop computer with 32GB of memory. Note that this is offline computational time that does not require human supervision. The value for the weighting term γ in Eq. (19) was set empirically to 10 times the initial value of M (S,U). The weighting term β was estimated based on the cranial shape abnormalities differences between the healthy controls and the patients with metopic craniosynostosis presented in Table 1. Targeting an approximate reduction of cranial shape abnormalities of 50%, we estimated β using the following formula:
| (20) |
where δ is the maximum allowed surface change in the frontal bones. Based on the agreement of our expert surgeons, we set this change to 0.5%, thus allowing very small surface changes as a consequence of bone cutting and bending.
We applied the different transformations calculated with different osteotomy templates to the patient’s cranial shape to obtain the simulated outcome of the surgical plan (post-operative). Then, we quantified the cranial shape abnormalities in the frontal bones of the post-operative shape of each patient, and we compared them with the pre-operative values. In addition, we calculated the von Mises stress in the bones to show the feasibility of implementing the surgical plan. Table 2 shows the average results obtained from the optimal plan calculated for each osteotomy template. The mean malformation reductions ranged between 40.38% and 50.85%, while the average reduction on curvature discrepancies ranged between 19.77% and 26.73%. We used a Wilcoxon rank sum test to compare the pre-operative and post-operative cranial shape abnormalities using the different osteotomy plans and we obtained p-values lower than 0.01 both for the malformations and for the curvature discrepancies for all osteotomy templates. On the other hand, we estimated the average von Mises stress in the bones, which ranged between 33.21 MPa and 43.47 MPa for the different osteotomy templates. The maximum allowable stress in the cranial bones is 87MPa [26].
TABLE II.
Cranial shape abnormalities and von Mises stress in the frontal bones from the simulated outcome of the surgical plan calculated using different osteotomy templates. We also present the percentage of change from the pre-operative value.
| Osteotomy template | 2 bone pieces | 3 bone pieces | 4 bone pieces | 5 bone pieces | 6 bone pieces | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | Change (%) | Value | Change (%) | Value | Change (%) | Value | Change (%) | Value | Change (%) | |
| Mean malformations (mm) | 1.72±0.80 | −40.38±12.05 | 1.53±0.78 | −41.23±12.97 | 1.50±0.76 | −47.59±16.04 | 1.43±0.73 | −50.47±10.79 | 1.43±0.70 | −50.85±12.52 |
| Max. malformations (mm) | 3.59±019 | −28.06±21.01 | 3.22±0.29 | −36.58±19.51 | 3.23±0.37 | −36.45±23.23 | 3.12±0.33 | −37.17±20.45 | 3.06±0.30 | −37.18±24.03 |
| Mean curvature discrepancies (mm−1) | 0.87±0.18 | −19.77±16.01 | 0.84±0.19 | −22.56±16.41 | 0.84±0.19 | −22.87±14.36 | 0.80±0.18 | −25.50±20.44 | 0.78±0.17 | −26.73±23.83 |
| Max. curvature discrepancies (mm−1) | 2.16±0.09 | −16.66±21.95 | 1.93±0.11 | −22.21±22.34 | 1.95±0.11 | −22.15±26.15 | 1.87±0.09 | −24.08±21.44 | 1.80±0.08 | −29.77±23.20 |
| Stress (MPa) | 33.21±16.52 | 38.29±22.17 | 43.47±23.35 | 35.91±21.39 | 38.08±24.11 | |||||
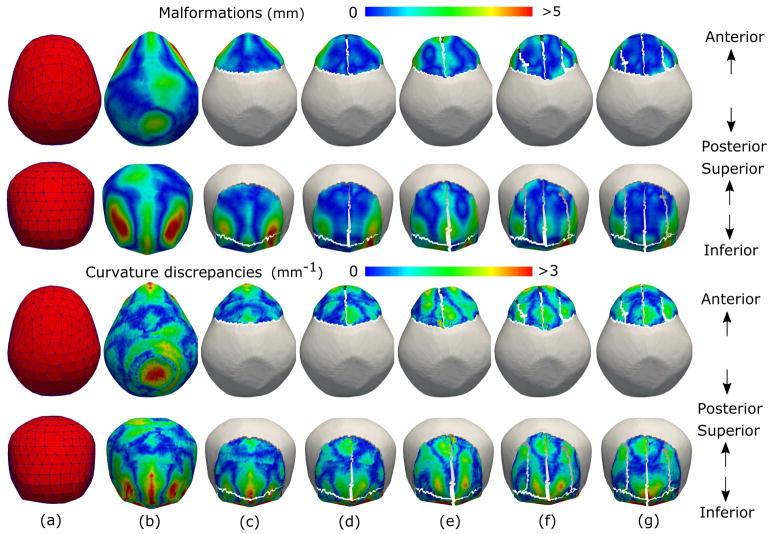
We also checked if the malformations in the post-operative cranial shapes were on healthy ranges by comparing them with the healthy controls, obtaining p-values for the distance malformations of 0.01, 0.35, 0.40, 0.76 and 0.84 for the osteotomy plans involving 2, 3, 4, 5 and 6 pieces, respectively. As expected, using a more flexible osteotomy template with more bone pieces resulted in better shape correction in average. However, malformations were correctly reduced within the healthy ranges using templates with 3 or more bone pieces. On the other hand, the p-values obtained for the curvature discrepancies were lower than 0.01 for all osteotomy plans considered. A discussion of these results is provided later in the manuscript. As a visual example, Figure 5 shows the pre-operative and simulated outcome of the surgical plan using different osteotomy templates for one patient with metopic craniosynostosis. Note that cranial shape abnormalities are often also present in other cranial bones in patients with metopic craniosynostosis due to compensatory cranial growth, but they are not targeted in a typical surgical procedure of fronto-orbital advancement.
Fig. 5.
Simulated correction of cranial shape abnormalities using our automatic osteotomy plan for a patient with metopic craniosynostosis. Superior (first row) and frontal (second row) views of the malformations and curvature discrepancies on the cranial shape on (b) the pre-operative mesh, and the simulated outcome of the surgical planning calculated for osteotomy plans with (c) 2, (d) 3, (e) 4, (f) 5, and (g) 6 bone pieces. For an improved visualization, Figures (c)–(g) only show the malformations and curvature discrepancies in the transformed bone pieces. As it can be observed, Figures (c)–(g) are more similar to (a) than (b).
Since the interventional plan calculated for one patient may not obtain the minimum of both malformations, curvature discrepancies and stress using the same osteotomy template (same number of bone subdivisions), we evaluated which osteotomy template achieved the optimal interventional plan for each patient according to three criteria: (1) minimization of malformations, (2) minimization of curvature discrepancies, and (3) minimization of bone stress. The mean malformation values, curvature discrepancies and stress estimated on the outcome of the optimal interventional plan chosen according to each of those criteria are shown in Table 3. The p-values obtained when comparing the post-operative malformations with the healthy controls were 0.74, 0.53, and 0.34 for the three criteria, respectively. The p-value obtained for the curvature discrepancies when using the minimization of curvature discrepancies as a criterion was 0.002. The p-values were lower than 0.001 for the other 2 criteria. The average stress had its maximum of 54.97±26.00 MPa when the minimum malformations were used as a criterion, and its minimum of 31.54±7.98 MPa when the minimum stress was used. Finally, we show in Figure 6 on how many patients we should use each osteotomy template to obtain the optimal surgical plan according to the three criteria considered.
TABLE III.
Cranial shape abnormalities reductions in the frontal bones for the optimal osteotomy plan using criteria for minimum malformations, minimum curvature discrepancies, and minimum stress. Values after simulated correction are presented with the percentage of change from pre-operative values.
| Malformations (mm) | Curvature discrepancies (mm−1) | Stress (MPa) | |||
|---|---|---|---|---|---|
| Criteria | Value | Change (%) | Value | Change (%) | Value |
| Minimum malformations | 1.35±0.70 | −53.15±11.41 | 0.77±0.16 | −28.08±15.33 | 54.97±26.00 |
| Minimum curvature discrepancies | 1.48±0.75 | −48.88±11.78 | 0.73±0.15 | −32.45±14.21 | 44.32±19.25 |
| Minimum stress | 1.53±0.81 | −47.62±11.37 | 0.84±0.18 | −21.20±23.92 | 31.54±7.98 |
Fig. 6.
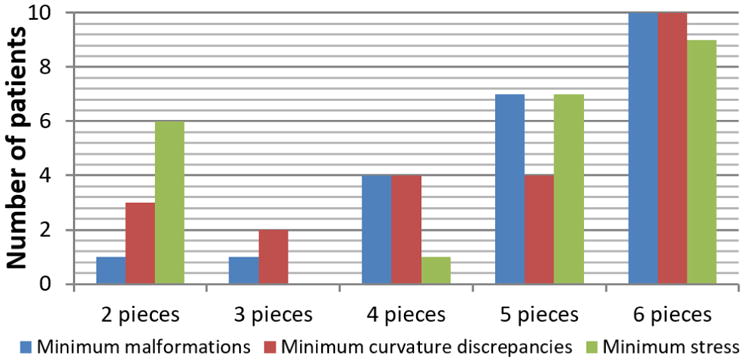
Bar diagram showing on how many patients we should use each osteotomy template to obtain the optimal surgical plan according to the three criteria considered: (1) minimization of malformations, (2) minimization of curvature discrepancies, and (3) minimization of bone stress.
IV. Discussion
We presented a new surface registration framework that allowed estimating a global transformation that preserved local properties (i.e. affine properties) on different regions. Our framework integrated the concepts of local rigid regions introduced in [15], and the poly-rigid/affine transformations presented in [27] for image registration, in a single mathematical framework using a dynamic local weighting scheme. In addition, we adapted the new framework to surface registration, using a dissimilarity measure based on currents that takes into account both the point distribution and the geometry of the surfaces. The registration framework presented in this paper is dependent on the invertibility of the local transformations Ti and the existence of its logarithm. This is guaranteed if all the eigenvalues of Ti are positive. This was discussed in [17], where the authors showed that this does not present a problem as long as the rotation angles of the affine transformations are lower than 180 degrees. We do not expect large rotations for the clinical application presented in this paper, since fronto-orbital advancement surgery consists in advancing and bending the frontal cranial bones.
We used our surface registration framework to estimate and simulate the optimal post-surgical cranial shape to target during fronto-orbital advancement surgery for the correction of metopic craniosynostosis. We evaluated different numbers of cranial bone subdivisions using different osteotomy templates. Our automatic framework achieved simulated post-operative cranial shapes with significant reductions of malformations and curvature discrepancies (p<0.01). In addition, the average stress calculated with all osteotomy templates considered were under the maximum allowable stress in the cranial bones of 87MPa [26], showing their feasibility. Importantly, the malformations in the cranial frontal bones were corrected to match normative healthy standards. Moreover, our expert surgeons, who have guided the development of the technology, agree on the potential of the results obtained with the proposed framework and the significance of these results.
Although all the osteotomy templates evaluated achieved a significant reduction of malformations and curvature discrepancies, the same template did not necessarily obtain the minimum of malformations, curvature discrepancies, and stress. The results in Table 3 and Figure 6 show that the number of bone subdivisions needed to obtain the optimal plan for each patient depends on its specific cranial shape and the severity of its cranial shape abnormalities. Since both cranial bone segmentation and the subsequent bone subdivision into smaller pieces are guided by reference templates, the quality of the reference images has a direct impact on the accuracy of delineating each bone piece and, therefore, on the results of the optimal plan calculated with them. In this work, we chose the reference template as a healthy subject for which all the cranial bones and sutures were clearly visible from the CT image.
A noted potential shortcoming of our approach is that the simulated post-surgical curvature discrepancies were different than the normative values from control cases (p<0.01). This may be due to the inclusion in the dataset of 3 patients with severe metopic craniosynostosis for which the osteotomy templates considered in this paper did not achieve curvature discrepancies within health ranges (their optimal post-operative curvature discrepancies were 1.01, 1.03, and 1.06 mm−1, respectively). The solution for these specific cases could be the evaluation of other osteotomy templates that included more complex bone subdivisions to achieve a higher reduction of curvature discrepancies. On the other hand, helmet therapy may be an option to consider in severe cases to keep guiding cranial shape correction after the surgery [28].
As it may be expected intuitively, Figure 6 shows that the osteotomy template including the highest number of bone pieces was more likely to be optimal for the three criteria considered. Although more and smaller bone pieces would most likely achieve a better cranial shape reconstruction, the optimal approach depends on the cranial shape of the patient, which indicates the need of a personalized approach as the one we present in this work. Given the personalized simulated outcome of the surgery calculated for each osteotomy plan, the surgeon can choose the optimal solution based on different criteria: reduction of malformations, reduction of curvature discrepancies, and minimum stress. In addition, if several osteotomy templates achieve similar outcomes, the surgeon can choose the one requiring the least number of bone cuts, thus minimizing the time of surgery and potential risk and morbidity for the patient.
Comparing this framework with our preliminary work presented in [18], we achieved an optimal reduction of malformations of 53.15% in average, compared to the 49% reported in [18]. In addition, the current approach operates in the surface domain, as compared to previous approach [18] on image registration. This allows accounting for both global and local structural information of the cranial shapes, which we achieved using a surface-based dissimilarity metric based on currents [14]. In addition, the current approach models the transformation of each cranial bone piece using affine transformations, allowing for bone bending and increasing the degrees of freedom to calculate the optimal surgical plan. By modeling bone bending, we have achieved an optimal reduction of curvature discrepancies of 32.45%, which could not be achieved with the rigid framework proposed in [18]. Importantly, operating in the surface domain also facilitates promoting smooth post-surgical cranial shapes and controlling bone piece surface preservation, which would be very complex and inefficient in the image domain.
Our surface registration approach builds on the poly-affine transformation model presented in [17] and the surface matching method presented in [14]. Compared to the former, we adapted its transformation model to constrain each bone piece to have one translation, rotation and bending, which is essential for the clinical translation of this framework to the operating room. In addition, we adapted it to the surface domain to compare the cranial geometry of the patient with its closest normal shape, which allows us to control bone surface and transitions between bone pieces. While the method presented in [17] and the one presented in this paper have the same number of degrees of freedom, the method in [17] provides an elastic behavior for each cranial bone through a combination of multiple affine transformations. Although that elastic behavior would likely allow obtaining simulated post-surgical cranial shapes more similar to the closest normal shape, we chose a unique affine transformation for each bone piece, which is clinically intuitive and can be translated to clinical practice. Similarly, the large deformation framework used combined in [14] with their novel surface matching method would also provide precise results, but it would not constrain bone pieces to present a specific translation, rotation, and bending, and it would also model each bone piece as an elastic object, which is not clinically feasible.
The framework presented in this paper constitutes the first fully automatic, quantitative, and objective framework for the surgical planning of fronto-orbital advancement. This automatic and objective approach is essential for the standardization and reproducibility of cranial vault reconstruction surgery, and has the potential to enhance the implementation of surgical techniques in centers with low patient volume where specialized clinical expertise is not available. Our framework, together with our previous works on quantification of cranial shape abnormalities, and automatic and quantitative diagnosis of craniosynostosis [3], [5], [6], constitutes the first quantitative framework for the pre-to-intra-operative management of metopic craniosynostosis.
Future work includes the creation of more complex osteotomy templates to evaluate more surgical approaches, and their extension to plan the surgery for the correction of other types of craniosynostosis. Although current intracranial volume increase is implicitly guided by the closest normal shape from a normative statistical atlas of cranial shapes, this framework could be extended to include an explicit normative brain growth volume model, as the one presented in [29]. Novel technological developments during the last few years (e.g. 3D printing, virtual/augmented reality…) have provided different options to translate this technology to the operating room. Among the different options available, printing in 3D the personalized optimal solution calculated for each patient would provide an intuitive and simple way to show the surgeon how to reposition optimally each bone piece. Finally, a prospective clinical validation will be necessary to translate this framework to clinical practice, in which we propose the acquisition of radiation-free 3D photography [30] to compare the surgical outcome of the proposed optimal plan and current subjective approaches. This prospective work will include the comparison of other parameters such as time of surgery, bleeding, duration of hospitalization, and complication rate.
V. Conclusions
We presented a diffeomorphic surface registration method that allows for the preservation of local affine properties in different surface regions by introducing a dynamic weighting scheme. Our framework calculates surface dissimilarities in the space of currents, which is sensitive to both the spatial location and the geometry of the surfaces. We applied our registration method to the development of the first automatic, quantitative, and objective framework to design the optimal interventional plan for the surgical treatment of metopic craniosynostosis. Our framework estimates the bone piece repositioning and bending necessary to achieve the optimal post-surgical cranial shapes, obtaining a significant reduction of malformations to healthy ranges.
Supplementary Material
Acknowledgments
This work was partly funded by the National Institutes of Health, Eunice Kennedy Shriver National Institute of Child Health and Human Development under grant NIH5R42HD080712.
Contributor Information
Antonio R. Porras, Sheikh Zayed Institute for Pediatric Surgical Innovation, Children’s National Health System, Washington, DC, USA
Beatriz Paniagua, Kitware Inc., Carrboro, NC, USA.
Scott Ensel, Sheikh Zayed Institute for Pediatric Surgical Innovation, Children’s National Health System, Washington, DC, USA.
Robert Keating, Division of Neurosurgery, Children’s National Health System, Washington, DC, USA.
Gary F. Rogers, Division of Plastic Surgery, Children’s National Health system, Washington, DC, USA
Andinet Enquobahrie, Kitware Inc., Carrboro, NC, USA.
Marius George Linguraru, Sheikh Zayed Institute for Pediatric Surgical Innovation, Children’s National Health System, Washington, DC, USA.
References
- 1.Lajeunie E, Le Merrer M, Bonaïti-Pellie C, Marchac D, Renier D. Genetic study of nonsyndromic coronal craniosynostosis. Am J Med Genet. 1995 Feb;55(4):500–504. doi: 10.1002/ajmg.1320550422. [DOI] [PubMed] [Google Scholar]
- 2.Branson HM, Shroff MM. Craniosynostosis and 3-Dimensional Computed Tomography. Semin Ultrasound, CT MRI. 2011;32(6):569–577. doi: 10.1053/j.sult.2011.07.002. [DOI] [PubMed] [Google Scholar]
- 3.Mendoza CS, Safdar N, Okada K, Myers E, Rogers GF, Linguraru MG. Personalized assessment of craniosynostosis via statistical shape modeling. Med Image Anal. 2014 May;18(4):635–646. doi: 10.1016/j.media.2014.02.008. [DOI] [PubMed] [Google Scholar]
- 4.Qi J, Zuki D, Wood B, Rogers G, Meyer C, Ortiz R, Mendoza CS, Enquobahrie A, Linguraru MG. Postoperative Evaluation of Craniosynostosis based on 3D Statistical Shape Model. Int J Comput Assist Radiol Surg. 2015;10(S1):S105–6. [Google Scholar]
- 5.Wood BC, Mendoza CS, Oh AK, Myers E, Safdar N, Linguraru MG, Rogers GF. What’s in a Name? Accurately Diagnosing Metopic Craniosynostosis Using a Computational Approach. Plast Reconstr Surg. 2016;137(1):205–213. doi: 10.1097/PRS.0000000000001938. [DOI] [PubMed] [Google Scholar]
- 6.Mendoza CS, Safdar N, Myers E, Kittisarapong T, Rogers GF, Linguraru MG. An optimal set of landmarks for metopic craniosynostosis diagnosis from shape analysis of pediatric CT scans of the head. SPIE Medical Imaging. 2013;8670:86702T. [Google Scholar]
- 7.Mendonca D, Gejje S, Kaladagi N. Fronto-orbital advancement: Revisited. J Cleft Lip Palate Craniofacial Anomalies. 2015 Jan;2(1):20–26. doi: 10.4103/2348-2125.150746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schramm A, Gellrich NC, Schmelzeisen R. Navigational Surgery of the Facial Skeleton. Springer; Berlin Heidelberg: 2007. [Google Scholar]
- 9.Chim H, Wetjen N, Mardini S. Virtual Surgical Planning in Craniofacial Surgery. Semin Plast Surg. 2014 Sep;28(3):150–158. doi: 10.1055/s-0034-1384811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mardini S, Alsubaie S, Cayci C, Chim H, Wetjen N, Cam CAD. Three-dimensional preoperative virtual planning and template use for surgical correction of craniosynostosis. J Plast Reconstr Aesthetic Surg. 2014;67(3):336–343. doi: 10.1016/j.bjps.2013.11.004. [DOI] [PubMed] [Google Scholar]
- 11.Saber NR, Phillips J, Looi T, Usmani Z, Burge J, Drake J, Kim PCW. Generation of normative pediatric skull models for use in cranial vault remodeling procedures. Child’s Nerv Syst. 2012;28(3):405–410. doi: 10.1007/s00381-011-1630-7. [DOI] [PubMed] [Google Scholar]
- 12.Audette MA, Ferrie FP, Peters TM. An algorithmic overview of surface registration techniques for medical imaging. Med Image Anal. 2000;4(3):201–217. doi: 10.1016/s1361-8415(00)00014-1. [DOI] [PubMed] [Google Scholar]
- 13.Tam GKL, Cheng ZQ, Lai YK, Langbein FC, Liu Y, Marshall D, Martin RR, Sun XF, Rosin PL. Registration of 3d point clouds and meshes: A survey from rigid to Nonrigid. IEEE Trans Vis Comput Graph. 2013;19(7):1199–1217. doi: 10.1109/TVCG.2012.310. [DOI] [PubMed] [Google Scholar]
- 14.Vaillant M, Glaunès J. Information processing in medical imaging. Vol. 19. Springer; Berlin Heidelberg: 2005. Surface Matching via Currents; pp. 381–392. [DOI] [PubMed] [Google Scholar]
- 15.Little JA, Hill DLG, Hawkes DJ. Deformations incorporating rigid structures [medical imaging]. Proceedings of the Workshop on Mathematical Methods in Biomedical Image Analysis; 1996. pp. 104–113. [Google Scholar]
- 16.Arsigny V, Pennec X, Ayache N. Polyrigid and polyaffine transformations: A novel geometrical tool to deal with non-rigid deformations – Application to the registration of histological slices. Med Image Anal. 2005 Dec;9(6):507–523. doi: 10.1016/j.media.2005.04.001. [DOI] [PubMed] [Google Scholar]
- 17.Arsigny V, Commowick O, Ayache N, Pennec X. A fast and log-euclidean polyaffine framework for locally linear registration. J Math Imaging Vis. 2009;33(2):222–238. [Google Scholar]
- 18.Porras AR, Zukic D, Equobahrie A, Rogers GF, Linguraru MG. Personalized Optimal Planning for the Surgical Correction of Metopic Craniosynostosis. 5th International Workshop on Clinical Image-Based Procedures. Translational Research in Medical Imaging; Cham: Springer; 2016. pp. 60–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Porras AR, Paniagua B, Enquobahrie A, Ensel S, Shah H, Keating R, Rogers GF, Linguraru MG. Medical Image Computing and Computer-Assisted Intervention (MICCAI) Springer; Cham: 2017. Locally Affine Diffeomorphic Surface Registration for Planning of Metopic Craniosynostosis Surgery; pp. 479–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pope P. Shrinkwrap?: 3D Model Abstraction for Remote Sensing. 2009 ASPRS Annual Meeting; 2009. pp. 9–13. [Google Scholar]
- 21.Liu L, Raber D, Nopachai D, Commean P, Sinacore D, Prior F, Pless R, Ju T. Interactive separation of segmented bones in CT volumes using graph cut. Med Image Comput Comput Interv. 2008;11(1):296–304. doi: 10.1007/978-3-540-85988-8_36. [DOI] [PubMed] [Google Scholar]
- 22.Higham NJ. The Scaling and Squaring Method for the Matrix Exponential Revisited. SIAM J Matrix Anal Appl. 2005;26(4):1179–1193. [Google Scholar]
- 23.Cheng SH, Higham NJ, Kenney CS, Laub AJ. Approximating the Logarithm of a Matrix to Specified Accuracy. SIAM J Matrix Anal Appl. 2001;22(4):1112–1125. [Google Scholar]
- 24.Danielsson PE. Euclidean distance mapping. Comput Graph Image Process. 1980;14(3):227–248. [Google Scholar]
- 25.Soleman J, Thieringer F, Beinemann J, Kunz C, Guzman R. Computer-assisted virtual planning and surgical template fabrication for frontoorbital advancement. Neurosurg Focus. 2015 May;38(5):E5. doi: 10.3171/2015.3.FOCUS14852. [DOI] [PubMed] [Google Scholar]
- 26.Ortiz R, Zukic D, Qi J, Wood B, Rogers GF, Enquobahrie A, Linguraru MG. Stress analysis of cranial bones for craniosynostosis surgical correction. Int J Comput Radiol Surg. 2015;10(S1):S107–8. [Google Scholar]
- 27.Arsigny V, Pennec X, Ayache N. Polyrigid and polyaffine transformations: A new class of diffeomorphisms for locally rigid or affine registration. Medical Image Computing and Computer-Assisted Intervention (MICCAI); Berlin Heidelberg: Springer; 2003. pp. 829–837. [Google Scholar]
- 28.Berry-Candelario J, Ridgway EB, Grondin RT, Rogers GF, Proctor MR. Endoscope-assisted strip craniectomy and postoperative helmet therapy for treatment of craniosynostosis. Neurosurg Focus. 2011 Aug;31(2):E5. doi: 10.3171/2011.6.FOCUS1198. [DOI] [PubMed] [Google Scholar]
- 29.Paniagua B, Emodi O, Hill J, Fishbaugh J, Pimenta La, Aylward SR, Andinet E, Gerig G, Gilmore J, van Aalst Ja, Styner M. 3D of Brain Shape and Volume After Cranial Vault Remodeling Surgery for Craniosynostosis Correction in Infants. Proc Soc Photo Opt Instrum Eng. 2013;8672:86720V. doi: 10.1117/12.2006524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tu L, Porras AR, Ensel S, Tsering D, Paniagua B, Enquobahrie A, Oh A, Keating R, Rogers GF, Linguraru MG. Intracranial Volume Quantification from 3D Photography. Computer Assisted and Robotic Endoscopy and Clinical Image-Based Procedures. CARE 2017, CLIP 2017; Cham: Springer; 2017. pp. 116–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.