STATIC AND ROVING SENSOR DATA FUSION FOR SPATIO-TEMPORAL HAZARD MAPPING WITH APPLICATION TO OCCUPATIONAL EXPOSURE ASSESSMENT

Abstract

Rapid technological advances have drastically improved the data collection capacity in occupational exposure assessment. However, advanced statistical methods for analyzing such data and drawing proper inference remain limited. The objectives of this paper are (1) to provide new spatio-temporal methodology that combines data from both roving and static sensors for data processing and hazard mapping across space and over time in an indoor environment, and (2) to compare the new method with the current industry practice, demonstrating the distinct advantages of the new method and the impact on occupational hazard assessment and future policy making in environmental health as well as occupational health. A novel spatio-temporal model with a continuous index in both space and time is proposed, and a profile likelihood-based model fitting procedure is developed that allows fusion of the two types of data. To account for potential differences between the static and roving sensors, we extend the model to have nonhomogenous measurement error variances. Our methodology is applied to a case study conducted in an engine test facility, and dynamic hazard maps are drawn to show features in the data that would have been missed by existing approaches, but are captured by the new method.

1. Introduction.

Occupational exposure assessment refers to assessment of the level of contaminants an employee is exposed to during their work shift. The traditional method for occupational exposure assessment is personal monitoring using lightweight devices that can be worn by the workers. Personal exposure estimates are typically sought because they can be compared against regulatory standards to ensure compliance with existing laws. However, personal monitoring is generally expensive and requires workers to carry equipment with them during their work. As such, it is common for a small number of measurements, on asmall number of employees, to be collected [Tornero-Velez et al. (1997), Cherrie (2003)], resulting in small sample sizes that cannot accurately capture true levels of contamination. Additionally, without the ability to track worker location, there is little ability to apportion exposures to different areas or tasks.

Occupational hazard maps, contour plots of contaminant concentration over the two-dimensional floor plan of the workplace, have gained popularity as a method to overcome some of the limitations of the traditional personal sampling that is generally expensive with small sample sizes [Koehler and Peters (2013), Peters et al. (2006, 2012), Evans et al. (2008), Ologe, Akande and Olajide (2006)]. Hazard maps are commonly produced by industrial hygienists or researchers using direct-reading instruments (DRIs) to capture contaminant concentrations at high spatial resolution following a predetermined grid throughout the facility of interest (hereafter, roving sensors). Such maps are powerful tools to communicate risk in an easily understood format and to guide decisions on control strategies aimed at reducing worker exposures [O’Brien (2003)].

Hazard maps that rely on roving monitor data alone, while cost-effective to produce and conceptually simple, likely fail to represent the temporal variability in concentrations present in many occupational settings [Koehler and Volckens (2011), Lake et al. (2015)]. Augmenting the data with static sensors that collect time series data, but at a few locations, can allow practitioners to expand the temporal and spatial coverage of data collection [Lake et al. (2015)]. As DRIs become more affordable and accessible, these types of exposure data (from static and roving sensors with known spatial information) are expected to become more abundant, but rigorous statistical methods for analyzing data and drawing proper inference remain limited. The current hazard mapping approach to occupational exposure assessment, although novel, represents several challenges. Maps that are created from roving sensor data alone are often either collected over a short temporal interval or aggregated over time and neglect the temporal variability in the dataset. As such, temporal variability can be mistakenly displayed as spatial variability. In our previous work, we compared maps created using the roving sensor data and static sensor data separately [Lake et al. (2015)]. The method employed was somewhat ad hoc because a comprehensive statistical methodology was lacking to combine the datasets (static and roving) to provide a representation of exposures across space and time. The maps should give not only the most representative indication of the mean value, accounting for both data types, but also an indication of the variability in concentrations, as a function of both time and space.

Statistical methods for integrating different sources of data in space and/or time have been researched in the past. For example, Isaacson and Zimmerman (2000) developed methodology for combining environmental data that are temporally correlated and from two measurement systems. Their autoregressive moving-average models allowed a common time trend, system-specific measurement errors and missing data, for which the inference was conducted by both frequentist and Bayesian approaches. Cowles et al. (2002) extended Isaacson and Zimmerman (2000) to temporally correlated data from multiple measurement systems that are measured at distinct sites in space. A Bayesian approach was taken to estimate the long-term trend and evaluate differences among the measurement systems. Further, Smith and Cowles (2007) considered an integrated model for correlating point-referenced radon and areal uranium data for quantifying a common spatial process using also a Bayesian approach, whereas Sahu, Gelfand and Holland (2010) fused point-referenced and areal wet deposition data in space and time. Such prior research is illuminating, but none considered the possibility of roving sensors, and thus is not directly applicable for the hazard mapping under consideration. The objectives of this paper are (1) to develop new spatio-temporal methodology that combines data from both roving and static sensors for data processing and hazard mapping across space and over time in an indoor environment and (2) to compare the new method with the current industry practice, demonstrating the distinct advantages of the new method and the impact on occupational hazard assessment and future policy making in environmental health as well as occupational health.

Combining data from static and roving sensors in a statistically sound way is challenging. First of all, while the roving sensors expand the spatial coverage of data, the observations are sparse in time at any given location. This is in contrast to the static sensors that are at a smaller number of sampling locations, but observations are denser in time at each sampling location. An ad hoc approach would be to analyze the two types of data separately, but there is potential benefit to be gained by developing statistical methodology that pools the two data sources and takes full advantage of their respective strengths. In addition, inaccurate and missing data can be a thorny issue in such data analysis due to different measurement systems, instrumentation failures, and uneven or asynchronous monitoring times, etc. To address these challenges, we propose a novel spatio-temporal process that has a continuous index in both space and time; that is, in the spatial domain of interest, the sampling locations can occur anywhere, in which sense the modeling is geostatistical [see, e.g., Cressie (1993)], whereas within the temporal window of interest, the sampling can occur at any time and thus the modeling may be viewed as functional [see, e.g., Ramsay and Silverman (2005)]. We then develop a model fitting procedure that allows the fusion of the two types of data based on profile likelihood accompanied by a fast computational algorithm. Further, to account for potential differences between the static and roving sensors, we extend the spatio-temporal model to allow for inhomogenous measurement error variances. Finally, we compare our new methodology with the current industrial standard/practice which does not model temporal variability and generates hazard maps from data averaged in time.

As we will demonstrate in a case study conducted in an engine test facility, the dynamic hazard maps that interpolate across space and over time are far more informative and representative of the evolution of hazard levels in space and time. This finding can impact the way occupational hazards are to be mapped in the future and move the industry and regulation forward to more accurate assessment of environmental hazards.

2. Application and data.

2.1. Case study.

A study was conducted in the spring of 2013 in an engine test facility located in Colorado to evaluate occupational exposure [Lake et al. (2015)]. The facility has two rooms, both rectangular in shape (14.8 m by 6.5 m and 14.8 m by 33.7 m, respectively), separated by a sliding door and encompassing a combined area of about 595 m². A floor plan is shown in Figure 1(a). In one experiment, for example, an active engine, located in the upper left corner of the facility [black square in Figure 1(a)], was operating between 10:00:00 am and 11:10:00 am, while the sliding door was open. Measurements of noise intensity were collected by 18 static sensors and 2 roving sensors. The locations of the static sensors are given in Figure 1(a), whereas the pathways of the roving sensors are shown in Figure 1(b). The static sensors started collecting data at 9:45:00 am and ended at 11:23:20 am when they were turned off. The operation of the first roving sensor started at 10:28:45 am and that of the second roving sensor started at 10:52:45 am. Both roving sensors were in operation until the end of the experiment, but not continuously. Static sensor measurements were collected at every minute, while roving sensors measured hazard levels with a resolution of 20 seconds. There are thus 100 sampled points for each of the 18 static sensors, 105 sampled points for the first roving sensor and 72 sampled points for the second roving sensor, for a total of 1977 observations.

Fig. 1.

(a) The floor plan of the engine test facility. The black rectangle in the upper left corner is the source of noise, white rectangles are offices, gray rectangles are inactive engines, and dark gray rectangles are floor openings. The locations of static sensors are numbered from 1 to 18. (b) The pathway of the first roving sensor is drawn in open circles. The pathway of the second roving sensor is similar, and thus omitted.

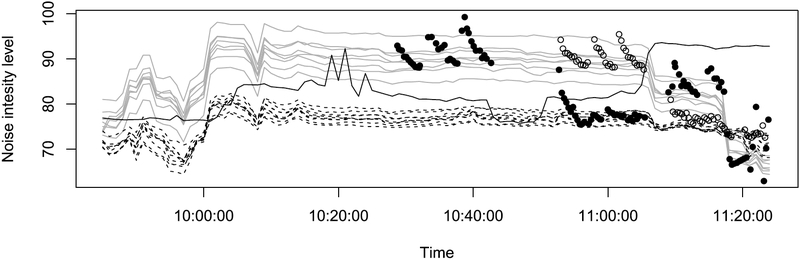
The measurements sampled over time are plotted in Figure 2. For each static sensor, a time series of noise intensity is plotted. The static sensors near the active engine in the upper left corner of the facility had higher intensity (gray solid lines) than those further away (dashed lines). One static sensor (#18) was far away from the active engine but had high noise intensity due to an unexpected noise source outside the facility (black solid line). The roving sensors are also displayed as filled circles (sensor 1) or open circles (sensor 2).

Fig. 2.

Observed noise intensity over time from 9:45:00 am to 11:23:20 am. Gray solid lines are time series for static sensors near one noise source (#1 through 7, and 17). The black solid line is near the secondary noise source (#18). Dashed lines are for the remainder static sensors. Filled and open circles are samples taken by the first roving sensor that started at 10:28:45 am and the second roving sensor that started at 10:52:20 am, respectively.

The static sensors all have dense sampling points in time, and thus relatively complete profiles of the temporal processes at the sampling locations (Figure 2). However, the spatial coverage by the static sensors is limited to the 18 sampling locations where they were installed [Figure 1(a)]. In contrast, each roving sensor has a wider spatial coverage [Figure 1(b)], but the information at any given location is sparse in time (Figure 2). The sampling time points for the roving sensors are also irregularly spaced, with occasional breaks that vary from about 20 seconds to about 5 minutes.

2.2. Current practice of hazard mapping.

In a recent review of hazard mapping approaches, Koehler and Peters (2013) noted that relatively simple methods have been used to construct maps, often averaging the sensors in time before employing a spatial interpolation technique, or interpolating across space for a fixed time and averaging the maps. We show static maps commonly obtained by industrial hygienists for the case study in Figure 3, after averaging over all data in time at each unique sampling location. The map labeled “Roving” is based on kriging estimates and uses the roving sensors exclusively. It corresponds to early practice with DRIs and still is the most common approach. The map labeled “Roving and Static” incorporates both sources of data. The aggregated map gives equal weights to observations available in the roving path (only one or two data points) and the ones from the static sensors (a hundred observations over the data collection period). Both maps tend to show local features that are not necessarily informative. In addition, the map labeled “Static” uses only static sensor data. It loses the local features provided by roving sensors due to a fairly limited spatial coverage. All these static maps naturally fail to capture the evolution of the hazard level in time and, as we will demonstrate, misrepresent the intensity of a secondary noise source in the southeastern part of the facility. Health effects of short duration but high-level exposures are unclear, and the static maps in current practice have limited capacity for studying these events.

Fig. 3.

Static maps of the noise intensity obtained by kriging using the roving sensor data only (left), the roving and static sensor data (center) and the static sensor data only (right), averaging data at the same location in time.

3. Data and model specification.

3.1. Data specification.

We now specify the notation for the spatio-temporal process of a generic hazard. Let $D\subset {ℝ}^2$ denote a two-dimensional spatial domain of interest, and let [0, T] denote a temporal window of interest where T > 0. Let s₁, … , s_nS denote the locations of the static sensors, where s_{i =} (s_i,x, s_i,y)′ is the location of the ith static sensor and n_S is the number of static sensors. For the ith static sensor, let there be p_i sampling time points, denoted as t_k,i, for k = 1, … , p_i, i = 1, … , n_S. In contrast, let n_R denote the number of roving sensors. For the jth roving sensor, let there be q_j sampling time points. A roving sensor generally has different sampling locations at different sampling time points and, therefore, the sampling locations are denoted by r_1,j, … , r_qj,j , where r_,j = (r_l,j,x, rl,j,y)′ is associated with sampling time t_l,j , for l = 1, … , q_j, j = 1, … , n_R. Let y_s(t) denote the intensity of a hazard at a given point in time t in [0, T] and a given spatial location s = (s_x, s_y)′ ∈ D. We will denote the samples collected by the static sensors as y_si(t_k,i), for k = 1, … , p_i, i = 1, … , n_S, and the samples collected by the roving sensors as y_rl,j (t_l,j), for l = 1, … , q_j , j = 1, … , n_R.

3.2. Model specification.

To model the static sensor data {y_si(t_k,i)} and roving sensor data {y_rl,j (t_l,j)}, we consider a spatio-temporal model

$$y_s(t)={\mu }_s(t)+{\eta }_s(t)+{\epsilon }_s(t),$$ (1)

where μ_s(t) is a deterministic mean function, η_s(t) is a random spatio-temporal process with $\mathbb{E}\left({\eta }_s(t)\right)=0$ and covariance function γ (t, s, t′, s′) = Cov(η_s(t), η_s′(t′)), and ε_s(t) is a measurement error process with $\mathbb{E}\left({\epsilon }_s(t)\right)=0$, constant variance σ² = Var(ε_s(t)) and zero correlation [Cressie and Wikle (2011)]. Further, we assume that the spatio-temporal process η_s(t) is square integrable and the spatio-temporal covariance function of η_s(t) at location s ∈ D satisfies

$$\gamma \left(t,s,t^{\prime },s\right)={\gamma }_0\left(t,t^{\prime }\right),$$ (2)

where γ₀(t, t′) γ (t, s₀, t′, s₀) is a temporal covariance function at any spatial location s₀ ∈ D; that is, the temporal correlation function η_s(t) and η_s(t′) is invariant in space.

The spatio-temporal process η_s(t) has a type of Karhunen–Loève decomposition [see, e.g., Gromenko and Kokoszka (2013)]:

$${\eta }_s\left(t\right)={\displaystyle \sum _{\mathcal{l}=1}^{\infty }{\xi }_{\mathcal{l}}}\left(s\right){\phi }_{\mathcal{l}}\left(t\right),$$ (3)

where ${\left\{{\phi }_{\mathcal{l}}\left(t\right)\right\}}_{\mathcal{l}=1}^{\infty }$ is a sequence of deterministic orthogonal temporal functions and ${\left\{{\xi }_{\mathcal{l}}\left(s\right)\right\}}_{\mathcal{l}=1}^{\infty }$ is a sequence of zero-mean random spatial processes that are uncorre lated with each other. The decomposition (3) represents the spatio-temporal process as a linear combination of the temporal basis functions φ_ℓ(t) (based on the temporal covariance function) with the random spatial processes ξ_ℓ(s) as coefficients.

We assume that the spatial covariance function of ξ_ℓ(s) takes on the form

$$\text{Cov}\left({\xi }_{\mathcal{l}}\left(s\right),{\xi }_{\mathcal{l}}\left(s^{\prime }\right)\right)={\lambda }_{\mathcal{l}}{\rho }_{\mathcal{l}}\left(\Vert s-s^{\prime }\Vert ;{\theta }_{\mathcal{l}}\right),$$

where λ_ℓ = Var(ξ_ℓ(s)) is the variance of ξ_ℓ(s), ρ_ℓ(⋅; θ_ℓ) is a correlation function parameterized by θ_ℓ and ∥ · ∥ denotes the Euclidean distance. From (3), we can write the spatio-temporal covariance function γ (t, s, t′, s′) of η_s(t) as

$$\gamma \left(t,s,t^{\prime },s^{\prime }\right)={\displaystyle \sum _{\mathcal{l}=1}^{\infty }\text{Cov}\left({\xi }_{\mathcal{l}}\left(s\right),{\xi }_{\mathcal{l}}\left(s^{\prime }\right)\right){\phi }_{\mathcal{l}}(t){\phi }_{\mathcal{l}}(t^{\prime })}.$$ (4)

In the case s = s′, (4) is reduced to the temporal covariance function ${\gamma }_0=\left(t,t^{\prime }\right)={\displaystyle {\sum }_{\mathcal{l}=1}^{\infty }{\lambda }_{\mathcal{l}}}{\phi }_{\mathcal{l}}\left(t\right){\phi }_{\mathcal{l}}\left(t^{\prime }\right)$ This makes clear that ${\left\{{\phi }_{\mathcal{l}}\left(t\right)\right\}}_{\mathcal{l}=1}^{\infty }$ are analogous to the eigenfunctions of γ₀(t, t′) with the corresponding eigenvalues ${\left\{{\lambda }_{\mathcal{l}}\right\}}_{\mathcal{l}=1}^{\infty }$ It is based on (4) that we will devise a semiparametric likelihood approach to fitting the spatio-temporal model (1) to the static and roving sensor data, as well as mapping the true spatio-temporal process of the hazard μ_s(t) + η_s(t), while taking into account the spatial and temporal variability.

Our modeling approach is tailored toward the distinct features of static and roving sensor data. The spatial index is continuous in the spatial domain, and the temporal index is continuous within the time window. Thus, the sensors can be placed anywhere in the study area and do not need to be on a regular grid. Further, sampling can occur at any point in time and no regular time intervals are required. In addition, our modeling framework is semiparametric and flexible. The specification of the deterministic mean function μ_s(t) is nonparametric, while the specification of the spatio-temporal process is semiparametric in the sense that the spatial covariance function Cov(ξ_ℓ(s), ξ_ℓ(s′)) in (4) is parametric but the temporal covariance function γ₀(t, t′) in (2) is nonparametric. The nonparametric specification allows for capturing different sources for a hazard, some of which are unexpected to be present or are present at unexpected time intervals, such as the outside noise near sensor #18 in the case study.

The class of spatio-temporal covariance functions (4) is broad, encompassing processes that are nonstationary and nonseparable in space and time with the separable case corresponding to λ_ℓ = 0 for ℓ ≥ 2 These properties can be contrasted to spatio-temporal kriging [Cressie and Wikle (2011), page 321], which in many practical scenarios requires the specification of the spatio-temporal covariance function, and the time series of the spatial process approach [Cressie and Wikle (2011), page 336], which requires the temporal coordinates to be sampled at regular intervals.

4. Statistical inference.

4.1. Profile likelihood estimation.

Parameter estimation by maximum likelihood can be challenging due the large number of parameters in the model (1). Thus, we use the idea of functional principal components and develop a profile likelihood approach to estimating the model parameters [Ramsay and Silverman (2005)]. Further, only finitely many eigenvalues are estimable from a sample covariance matrix in the nonparametric specification of the covariance function and, therefore, it is necessary that, for some L ≤ min_i{p_i} [see Wahba (1990), page 5],

$${\eta }_s\left(t\right)\approx {\displaystyle \sum _{\mathcal{l}=1}^L{\xi }_{\mathcal{l}}}\left(s\right){\phi }_{\mathcal{l}}\left(t\right).$$ (5)

Let y_si = (y_si(t₁), … , y_si(t_pi))′ and μ_si = (μ_si(t₁),…, μ_si(t_pi))′ denote the vector of the data from the ith static sensor at time points t_k for k = 1, . . . , p_i and the corresponding mean vector for i = 1, . . . , n_S. Let $y_{r_j}={\left(y_{r_{1,j}}\left(t_1,j\right),\dots ,y_{r_{q_j}{,}_j}\left(t_{q_j,j}\right)\right)}^{\prime }$ and ${\mu }_{r_j}={\left({\mu }_{r_{\text{1},j}}\left(t_{1,j}\right),\dots ,{\mu }_{r_{q_j},j}\left(t_{q_j,j}\right)\right)}^{\prime }$ denote the vector of the data from the jth roving sensor at spatial locations r_l,j and time points t_l,j for l = 1, . . . , q_j and the corresponding mean vector for j = 1, … , n_R. Also, let $y=\left(y_{s_1}^{\text{'}},\dots ,y_{s_{n_{\text{S}}}}^{\text{'}},y_{r_1}^{\text{'}},\dots ,y_{r_{n_{\text{R}}}}^{\text{'}}\right)\text{'}$ and $\mu =\left({\mu }_{s_1}^{\text{'}},\dots ,{\mu }_{s_{n_{\text{S}}}}^{\text{'}},{\mu }_{r_1}^{\text{'}},\dots ,{\mu }_{r_{n_{\text{R}}}}^{\text{'}}\right)\text{'}$ denote the vector of all the observations and the corresponding mean vector.

Let $\Phi =\text{diag}\left\{\text{diag}{\left\{A_i\right\}}_{i=1}^{n_{\text{S}}},\text{\hspace{0.17em}diag}{\left\{\text{diag}{\left\{b_{l,j}\right\}}_{l=1}^{q_j}\right\}}_{j=1}^{n_{\text{R}}}\right\}$ denote a block diagonal matrix, where

$$A_i=\left(\begin{array}{ccc}{\phi }_1(t_{1,i})& \cdots & {\phi }_1(t_{p_i,i})\\ ⋮& \ddots & ⋮\\ {\phi }_L(t_{1,i})& \cdots & {\phi }_L(t_{p_i,i})\end{array}\right)\begin{array}{l}\text{and}\hfill \end{array}{b}_{l,j}\left(\begin{array}{c}{\phi }_1(t_{l,j})\\ ⋮\\ {\phi }_L(t_{l,j})\end{array}\right).$$

Let

$$\Lambda =\left(\begin{array}{l}{\Lambda }_{\text{S},\text{S}}\hfill \\ {\Lambda }_{\text{R},\text{S}}\hfill \end{array}\begin{array}{l}{\Lambda }_{\text{S},\text{R}}\hfill \\ {\Lambda }_{\text{R},\text{R}}\hfill \end{array}\right)$$

with ${\Lambda }_{\text{S},\text{S}}={(\text{diag}{\left\{{\lambda }_{\mathcal{l}}{\rho }_{\mathcal{l}}\left(\Vert s_i-s_{i^{\prime }}\Vert ;{\theta }_{\mathcal{l}}\right)\right\}}_{\mathcal{l}=1}^L)}_{i,i^{\prime }=1}^{n_{\text{S}}}$, where λ_ℓρ_ℓ(∥s − s′∥) = Cov(ξ_ℓ(s), ξ_ℓ(s′)), λ_ℓ = Var (ξ_ℓ(s)) and ρ_ℓ(⋅) is a spatial correlation function that may be modeled by the Matérn class [Stein (1999)]. Note Λ_S,S is a block matrix with blocks corresponding to distinct spatial locations. The submatrices Λ_S,R and Λ_R,R are defined analogously; however, for a given roving sensor, each distinct spatial location corresponds to its own block. This illustrates that the covariance structure is more complex than a sampling scheme that involves only static sensors, showing that roving sensors play a role in both spatial and temporal dependence. The rank of Λ can be as large as $L(n_S+{\displaystyle {\sum }_{j=1}^{n_R}{q}_j})$.

Suppose η_s(t) and ε_s(t) are Gaussian processes. Then ξ_ℓ(s) are Gaussian processes, and y follows a multivariate Gaussian distribution with mean μ and covariance

$$\sum ={\Phi }^{\prime }\Lambda \Phi +{\sigma }^2{I}_N,$$ (6)

where $N={\displaystyle {\sum }_{i=1}^{n_{\text{S}}}{p}_i+}{\displaystyle {\sum }_{j=1}^{n_{\text{R}}}{q}_j}$ is the total sample size combining static and roving sensor data and I_N is the N-dimensional identity matrix.

Estimation of all the components is not always possible depending on the choices made for the parameters θ_ℓ in the spatial correlation function ρ_ℓ(⋅) and those made for the shape of the temporal process φ_ℓ(⋅) We now develop a profile likelihood approach to parameter estimation. At initialization, we estimate the mean function μ_s(t) by ordinary least squares (OLS) and denote the estimated mean function as ${\widehat{\mu }}_s(t)$. For example, a fitted mean function could comprise both a linear model spatially and a nonparametric model temporally,

$${\widehat{\mu }}_s(t)={\widehat{\beta }}_0+{\widehat{\beta }}_x{s}_x+{\widehat{\beta }}_y{s}_y+{\displaystyle \sum _{k=1}^K{\widehat{\beta }}_k{B}_k(t)}$$ (7)

where s = (s_x, s_y)′, B_k(·) are cubic spline basis functions, K is the number of basis functions that controls the smoothness of $\widehat{\mu }$ and $\widehat{\beta }$ are the OLS estimates of the coefficients. Let ${\widehat{\mu }}_{\text{OLS}}$ denote the vector of ${\widehat{\mu }}_s(t)$ at all sampling locations and time points. Let $\widehat{y}=y-{\widehat{\mu }}_{\text{OLS}}$ denote the detrended data comprising ${\widehat{y}}_{s_i}=\left({\widehat{y}}_{s_i}\left(t_i,k\right):k=1,\dots ,p_i\right)\text{'}$ for i =1, … ,n_S ${\widehat{y}}_{r_j}\left({\widehat{y}}_{r_{j,l}}\left(t_{j,l}\right):l=1,\dots ,q_j\right)\text{'}$ for j = 1, … , n_R.

Next, we estimate λ_ℓ and φ_ℓ(t) by applying a functional principal component analysis to the data from the static sensors [Ramsay and Silverman (2005), pages 178–182]. In this step, we estimate the temporal covariance function ${\widehat{\gamma }}_0(t,t\text{'})$ from vectors ${\widehat{y}}_{s_i}$ expanded in B-spline basis functions, obtaining a functional estimate of $y_{s_i}(t)-{\mu }_{s_i}(t)$ denoted by ${\widehat{y}}_{s_i}(t)$. Thus,

$${\widehat{\gamma }}_0(t,t\text{'})=n_{\text{S}}^{-1}{\displaystyle \sum _{i=1}^{n_{\text{S}}}{\widehat{y}}_{s_i}}(t){\widehat{y}}_{s_i}(t)\text{'}.$$ (8)

The estimate of the first temporal function ${\widehat{\phi }}_1(\cdot )$ is the maximizer of

$$\underset{{\Vert f(t)\Vert }_{\zeta }=1}{\text{max}}{\displaystyle {\int }_0^T{\displaystyle {\int }_0^{T}f(t)}}{\widehat{\gamma }}_0(t,t\text{'})f(t\text{'})\text{\hspace{0.17em}d}t\text{\hspace{0.17em}d}t\text{'},$$ (9)

where ∥f(t)∥_ζ = 1 in the L^ζ norm ${\langle f,g\rangle }_{\zeta }={\displaystyle {\int }_0^{T}f(t)g(t)}\text{d}t+\zeta {\displaystyle {\int }_0^{T}f"(t)g"(t)\text{\hspace{0.17em}d}t}$ is an inner product, and ζ is a tunning parameter that controls the smoothness of the estimates. The estimates of the subsequent temporal functions ${\widehat{\phi }}_{\mathcal{l}}(\cdot )$ for ℓ ≥ 2 are the maximizer of (9) under the constraint of orthogonality of ${\widehat{\phi }}_{\mathcal{l}}(\cdot )$ and ${\widehat{\phi }}_{\mathcal{l}\text{'}}(\cdot )$ (in the 〈·,·〉_ζ sense) for all ℓ′ < ℓ. Finally, λ_ℓ is estimated by

$${\widehat{\lambda }}_{\mathcal{l}}={\displaystyle {\int }_0^T{\displaystyle {\int }_0^T{\widehat{\phi }}_{\mathcal{l}}(t)}}{\widehat{\gamma }}_0(t,t\text{'}){\widehat{\phi }}_{\mathcal{l}}(t\text{'})\text{\hspace{0.17em}d}t\text{\hspace{0.17em}d}t\text{'}$$

for ℓ = 1, …, L.

Unlike static sensors, it is not possible to obtain a full time series of data at a fixed location r_j,l for the roving sensor. Therefore, estimates of φ_ℓ(t) are based on static sensors only, and the values of ${\widehat{\phi }}_{\mathcal{l}}(t)$ for the roving sensors are interpolated by evaluating the estimates ${\widehat{\phi }}_{\mathcal{l}}(t)$ at time points t_l,j for l = 1, … , q_j , j = 1, . . . , n_R. The smoothness of φ_ℓ(t) estimates is influenced by the number of basis functions K, the tuning parameter ζ and the number of functional principal components L.

Given $\widehat{\mu }$, ${\widehat{\lambda }}_{\mathcal{l}}$ and ${\widehat{\phi }}_{\mathcal{l}}(t)$, we minimize the negative profile log-likelihood of θ and σ² defined as

$$\begin{gathered} f\left(\theta ,{\sigma }^2\right)=-2\mathcal{l}\left(\theta ,{\sigma }^2\right) \\ \propto \widehat{y}\text{'}{\sum }_1{\left(\theta ,{\sigma }^2\right)}^{-1}\widehat{y}+\text{log}\left[\text{det}\left\{{\sum }_1{\left(\theta ,{\sigma }^2\right)}^{-1}\right\}\right], \end{gathered}$$ (10)

where $\widehat{y}=y-\widehat{\mu }$ is the detrended data vector and ${\sum }_1\left(\theta ,{\sigma }^2\right)=\sum \left(\theta ,{\sigma }^2;{\widehat{\lambda }}_{\mathcal{l}},{\widehat{\phi }}_{\mathcal{l}}(t)\right)$ is the covariance (6) parameterized by θ and σ² and evaluated at ${\widehat{\lambda }}_{\mathcal{l}}$ and ${\widehat{\phi }}_{\mathcal{l}}(t)$ The solutions to (10) can be obtained by using box-constrained optimization to ensure that all estimated parameters are positive. Further, the coefficients in the mean function (7) are updated by

$$\widehat{\beta }={(X^{\prime }{\widehat{\Sigma }}^{-1}X)}^{-1}X{\widehat{\Sigma }}^{-1}y,$$

where $\widehat{\Sigma }=\Sigma (\widehat{\theta },{\widehat{\sigma }}^2;{\widehat{\lambda }}_{\mathcal{l}}{\widehat{\phi }}_{\mathcal{l}}(t))$ is the covariance (6) evaluated at the parameter estimates and X is the design matrix for the covariates in (7).

4.2. Spatio-temporal kriging and prediction of spatial loadings.

To predict y_s0(t) at an unsampled location s₀ and time t₀, we use

$${\widehat{y}}_{s_0}(t_0)={\widehat{\mu }}_{s_0}(t_0)+{\widehat{\eta }}_{s_0}(t_0)={\widehat{\mu }}_{s_0}(t_0)+{\widehat{\Sigma }}_{s_0,t_0}{\widehat{\Sigma }}^{-1}(y-\widehat{\mu }),$$ (11)

where ${\widehat{\Sigma }}_{s_0,t_0}=\widehat{\Phi }{\left(t_0\right)}^{\prime }\widehat{\Lambda }(s_0)\widehat{\Phi }(t_0)$, $\widehat{\Phi }(t_0)$ is Φ evaluated at t₀, and $\widehat{\Lambda }(s_0)=({\widehat{\Lambda }}_{s_0,\text{S}}{\widehat{\Lambda }}_{s_0,\text{R}})$, with ${\Lambda }_{s_0,\text{S}}=\{{\text{diag{λ}}_{\mathcal{l}}{\rho }_{\mathcal{l}}{\text{(}\Vert s_0-s_i\Vert \text{;\hspace{0.17em}}{\theta }_{\mathcal{l}}\text{}}}_{\mathcal{l}=1}^L{\}}_{i=1}^{n_{\text{S}}}$, and ${\Lambda }_{s_0,\text{R}}={\left\{\text{diag{}{\lambda }_{\mathcal{l}}{\rho }_{\mathcal{l}}{\text{(}\Vert s_0-r_{l,j}\Vert \text{;\hspace{0.17em}}{\theta }_{\mathcal{l}}\text{}}}_{\mathcal{l}=1}^L\right\}}_{l=1}^{q_{\text{j}}}{,}_{j=1}^{n_{\text{R}}}$. Equation (11) is used over a fine spatial grid to generate the hazard maps over time. The prediction standard error is given by ${\widehat{\sigma }}_{s_0}(t_0)$, where

$${\widehat{\sigma }}_{s_0}^2(t_0)={\widehat{\sigma }}^2+{\displaystyle \sum _{\mathcal{l}=1}^L{\widehat{\lambda }}_{\mathcal{l}}{\widehat{\phi }}_{\mathcal{l}}^2(t_0)-}{{\widehat{\Sigma }}^{\prime }}_{s_0,t_0}{\widehat{\Sigma }}^{-1}{\widehat{\Sigma }}_{s_0,t_0}+(x-X^{\prime }{\widehat{\Sigma }}^{-1}{\widehat{\Sigma }}_{s_0,t_0}{)}^{\prime }{(X^{\prime }{\widehat{\Sigma }}^{-1}X)}^{-1}(x-X^{\prime }{\widehat{\Sigma }}^{-1}{\widehat{\Sigma }}_{s_0,t_0}),$$ (12)

and x are the covariates in (7) evaluated at s₀ and t_0.

We can also predict the spatial loadings ξ (s) using conditional expectations in an approach similar to Yao, Müller and Wang (2005) for nonspatial data. Let $s_1^{*},\dots ,s_m^{*}\in D$ be the unsampled locations of interest. The ℓth loading evaluated at locations $s_1^{*},\dots ,s_m^{*}$ is a linear predictor of $({\xi }_{\mathcal{l}}(s_1^{*}),\dots ,{\xi }_{\mathcal{l}}(s_m^{*}))$. Assuming ${\{{\xi }_{\mathcal{l}}(s_1^{*}),\dots ,{\xi }_{\mathcal{l}}(s_m^{*})\}}_{\mathcal{l}=1}^{\infty }$ and ε_s(t) are jointly Gaussian, we have

$$\begin{gathered} ({\widehat{\xi }}_{\mathcal{l}}(s_1^{*}),\dots ,{\widehat{\xi }}_{\mathcal{l}}(s_m^{*}){)}^{\prime }=\widehat{\mathbb{E}}(({\xi }_{\mathcal{l}}(s_1^{*}),\dots ,{\xi }_{\mathcal{l}}(s_m^{*}){)}^{\prime }|y) \\ ={\widehat{\Sigma }}_{{\xi }_{\mathcal{l}},y}{\widehat{\Sigma }}^{-1}(y-\widehat{\mu }), \end{gathered}$$

where ${\widehat{\Sigma }}_{{\xi }_{\mathcal{l}},y}$ is the plug-in estimate of ${\Sigma }_{{\xi }_{\mathcal{l}},y}$ and ${\Sigma }_{{\xi }_{\mathcal{l}},y}$ is the sample covariance of $({\xi }_{\mathcal{l}}(s_1^{*}),\dots ,{\xi }_{\mathcal{l}}(s_m^{*}){)}^{\prime }$ and y, given by

$${\Sigma }_{{\xi }_{\mathcal{l}},y}={\text{λ}}_{\mathcal{l}}\left(\begin{array}{ccc}{\phi }_{\mathcal{l}}(t_{1,1}){\rho }_{\mathcal{l}}(\Vert s_1^{*}-s_1\Vert ;{\theta }_{\mathcal{l}})& \cdots & {\phi }_{\mathcal{l}}(t_{q_{n_{\text{R}}},n_{\text{R}}}){\rho }_{\mathcal{l}}(\Vert s_1^{*}-r_{q_{n_{\text{R}}},n_{\text{R}}}\Vert ;{\theta }_{\mathcal{l}})\\ ⋮& \ddots & ⋮\\ {\phi }_{\mathcal{l}}(t_{1,1}){\rho }_{\mathcal{l}}(\Vert s_m^{*}-s_1\Vert ;{\theta }_{\mathcal{l}})& \cdots & {\phi }_{\mathcal{l}}(t_{q_{n_{\text{R}}},n_{\text{R}}}){\rho }_{\mathcal{l}}(\Vert s_m^{*}-r_{q_{n_{\text{R}}},n_{\text{R}}}\Vert ;{\theta }_{\mathcal{l}})\end{array}\right),$$

and $\widehat{\Sigma }$, y and $\widehat{\mu }$ are as defined in Section 4.1.

4.3. Inhomogeneous variances.

The model given in (1) assumes that the measurement error variance is the same for the static and roving sensors. In practice, however, this assumption does not always hold. In the following we extend the data model to accommodate the situation that the measurement error variance for the static sensors is different from the roving sensors.

Consider model (1) again,

$$y_s(t)={\mu }_s(t)+{\eta }_s(t)+{\epsilon }_s(t),$$ (13)

but with measurement error variances $\text{Var(}{\epsilon }_s\text{(}t\text{))\hspace{0.17em}=\hspace{0.17em}}{\sigma }_{\text{S}}^2$ for static sensors and $\text{Var(}{\epsilon }_s\text{(}t\text{))\hspace{0.17em}=\hspace{0.17em}}{\sigma }_{\text{R}}^2$ for roving sensors. The model (13) will be referred to as the inhomogeneous variance case. The model (1) is a special case where ${\sigma }_{\text{S}}^2={\sigma }_{\text{R}}^2$ and will be referred to as the homogeneous variance case. In the inhomogeneous variance case, the covariance is a general case of (6), and the estimation algorithm is modified by using

$$\Sigma ={\Phi }^{\prime }\Lambda \Phi +{\sigma }_{\text{S}}^2{D}_{\text{S}}+{\sigma }_{\text{R}}^2{D}_{\text{R}},$$ (14)

where D_S, D_R are diagonal matrices with diagonal entries equal to 1 for static and roving sensors, respectively, and 0 otherwise. The model (13) allows the fusion of the two sources of data with varying degrees of spatio-temporal resolutions and drawing inference about the true underlying process μ_s(t) + η_s(t). The profile-likelihood approach to parameter estimation is modified as follows. The data are detrended with initial estimates of μ using (7), and the λ_ℓ and φ_ℓ(t) terms are estimated using functional principal component analysis over the static sensors as before. Given $\widehat{\mu }$, ${\widehat{\lambda }}_{\mathcal{l}}$ and $\widehat{\phi }(t)$, we minimize the negative profile log-likelihood of θ, ${\sigma }_{\text{S}}^2$ and ${\sigma }_{\text{R}}^2$ defined as

$$f(\theta ,{\sigma }_{\text{S}}^2,{\sigma }_{\text{R}}^2)=-2\mathcal{l}(\theta ,{\sigma }_{\text{S}}^2,{\sigma }_{\text{R}}^2)={\widehat{y}}^{\prime }{\Sigma }_2{(\theta ,{\sigma }_{\text{S}}^2,{\sigma }_{\text{R}}^2)}^{-1}\widehat{y}+\text{\hspace{0.17em}log[det{}{\Sigma }_2(\theta ,{\sigma }_{\text{S}}^2,{\sigma }_{\text{R}}^2)\text{}]\hspace{0.17em}+\hspace{0.17em}}N\text{\hspace{0.17em}log(2}\pi \text{),}$$ (15)

Where $\widehat{y}=y-\widehat{\mu }$ and ${\Sigma }_2(\theta ,{\sigma }_{\text{S}}^2,{\sigma }_{\text{R}}^2)=\Sigma (\theta ,{\sigma }_{\text{S}}^2,{\sigma }_{\text{R}}^2;{\widehat{\lambda }}_{\mathcal{l}},{\widehat{\phi }}_{\mathcal{l}}(t))$ given in (14) is parameterized by θ, ${\sigma }_{\text{S}}^2$ and ${\sigma }_{\text{R}}^2$ evaluated at ${\widehat{\lambda }}_{\mathcal{l}}$ and ${\widehat{\phi }}_{\mathcal{l}}(t)$. The coefficients in the mean function are updated by

$$\widehat{\beta }={(X^{\prime }{\widehat{\Sigma }}^{-1}X)}^{-1}X{\widehat{\Sigma }}^{-1}y,$$

where $\widehat{\Sigma }=\Sigma (\widehat{\theta },{\widehat{\sigma }}_{\text{S}}^2,{\widehat{\sigma }}_{\text{R}}^2;{\widehat{\lambda }}_{\mathcal{l}},{\widehat{\phi }}_{\mathcal{l}}(t))$ and X is the design matrix for the covariates in (7).

5. Case study: Spatio-temporal occupational hazard mapping.

5.1. Model fitting.

Before fitting an inhomogeneous variance model for the noise data, we selected the tuning parameters by a leave-one-sensor-out cross-validation approach. More specifically, we considered a grid of values for the number of deterministic spline basis functions K, the number of temporal principal components L and the principal components smoothing parameters ζ , and searched for a minimizer of the estimated mean squared prediction error (MSPE); see Appendix A.2 of the Supplemental Materials. The selected parameters are L = 3, K = 12 and ζ = 0. The estimated deterministic component is

$${\widehat{\mu }}_s(t)=83.64-0.40s_x+0.31s_y+\widehat{S}(t),$$

where the spline term $\widehat{S}(t)$ is shown in Figure 7(a). The estimates of the spatial process variances are ${\widehat{\lambda }}_1=13.20$, ${\widehat{\lambda }}_2=8.07$ and ${\widehat{\lambda }}_3=0.13$. The estimates for spatial range parameters, assuming an exponential spatial covariance model ${\rho }_{\mathcal{l}}(\Vert s_i-s_{i^{\prime }}\Vert ;{\theta }_{\mathcal{l}})=\text{exp{}-\Vert s_i-s_{i^{\prime }}\Vert /{\theta }_{\mathcal{l}}\text{}}$, for ℓ = 1, 2, 3, are ${\widehat{\theta }}_1=22.34$, ${\widehat{\theta }}_2=10.831$ and ${\widehat{\theta }}_3=40.34$. The nonparametric estimates of the temporal functions φ_ℓ(⋅) are shown in Figure 7(b). The estimated measurement error variances are ${\widehat{\sigma }}_{\text{S}}^2=1.49$ and ${\widehat{\sigma }}_{\text{R}}^2=1.05$. The parameter estimates for the homogeneous variance case and for the case in which only the static sensor data are used are given in Table 1. The inhomogeneous variance case is denoted by STDF (which stands for spatio-temporal data fusion), the homogeneous variance case by STDFh, and the scenario with static sensors only by STDF*.

Fig. 7.

(a) Deterministic effect for the temporal component estimated with a spline function; (b)${\widehat{\phi }}_{\mathcal{l}}(t)$, ℓ = 1, 2, 3 components, corresponding to a random effect in the temporal component.

Table 1.

Parameter estimates and cross-validated standard errors (in parenthesis). STDF denotes spatio-temporal data fusion for the inhomogeneous variance case, STDFh for the homogeneous variance case, and STDF* for only the static sensors

Coefficient	STDF	STDFh	STDF*
β0	83.64 (4.52)	83.53 (4.49)	82.23 (3.59)
βx	−0.40 (0.08)	−0.40 (0.08)	−0.38 (0.11)
βy	0.31 (0.04)	0.31 (0.04)	0.31 (0.04)
θ1	22.34 (2.93)	22.20 (2.95)	13.17 (1.83)
θ2	10.93 (2.13)	12.08 (1.88)	30.99 (2.57)
θ3	40.34 (11.15)	40.34 (11.10)	32.56 (8.42)
${\sigma }_{\text{S}}^2$	1.49 (0.16)	1.48 (0.15)	1.46 (0.12)
${\sigma }_{\text{R}}^2$	1.05 (0.29)	–	–

A series of dynamic hazard maps for the predicted noise intensity using our STDF model in Figure 4 show overall low intensity levels at the beginning and near the end of the study (panels 09:50 am and 11:20 am). They identify peaks in most time transects around the spatial coordinates S_x = 2.5 and s_y = 35, the noise source located. The noise intensity decreases as the readings are made further away from the noise source. In addition, a secondary noise source located near sensor #18 is captured [see also Figure 1(a)]. The standard errors of the predicted noise intensity across time and space are plotted in Figure 5. As expected, lower standard errors are found near the static sensors and along the trajectories of the roving sensors, as shown in Figure 1. The prediction standard error is larger at sites further apart from the static sensors location. The locations visited by the roving sensors display smaller standard errors than unsampled sites but higher standard errors than the static sensors’ sites. The prediction standard error levels at roving sensor locations are carried over time and do not change as a function of the roving sensor position. The prediction standard errors are also larger in general at the end of the experiment (starting at around 11:20 am). This corresponds to the time period in which the main source of noise was turned off, and the secondary noise source increased in intensity, as shown in Figure 2. Such an increase in the standard error levels is due to ${\widehat{\phi }}_2(t)$ in (12), which captures the temporally short, but high local noise intensity change around sensor 18 and the temporally short, abrupt decrease in noise intensity in the northernmost room.

Fig. 4.

Dynamic hazard maps with contour lines obtained from the spatio-temporal data fusion (STDF) method; each panel corresponds to a point in time from 9:50 am to 11:20 am at 10-minute intervals.

Fig. 5.

Prediction standard error maps for the dynamic hazard maps given in Figure 4; each panel corresponds to a point in time from 9:50 am to 11:20 am at 10-minute intervals.

Figure 6 maps the estimated $({\widehat{\xi }}_{\mathcal{l}}(s_1^{*}),\dots ,{\widehat{\xi }}_{\mathcal{l}}(s_m^{*}){)}^{\prime }$, ℓ = 1, 2, 3 over a fine grid of spatial locations $s_1^{*},\dots ,s_m^{*}$, with each ℓ loading standardized to have zero mean and standard deviation one. The temporal components ${\widehat{\phi }}_{\mathcal{l}}(t)$, ℓ = 1, 2, 3 are shown in Figure 7(b). The interpretation of the the temporal functions φ_ℓ(⋅) can be made in light of Figure 2, as well as the Karhunen–Loève expansion based on (5). The first temporal component ${\widehat{\phi }}_1$ is nearly constant around 1 (Figure 7). The corresponding ${\widehat{\xi }}_1(s)$ shown in Figure 6 shows higher noise intensity values in the northern room and near the secondary source around sensor #18. For the second temporal component, since ${\widehat{\phi }}_2$ is negative until approximately 11:10 am, it subtracts the ${\widehat{\xi }}_2(s)$ effect from ${\widehat{\xi }}_1(s)$, but after 11:10 am it adds the effect of the secondary noise source. Thus, in the dynamic hazard maps (Figure 4), the noise intensity is higher in the northern room before 11:10 am, and afterward the noise intensity is higher near sensor #18. The third temporal component ${\widehat{\phi }}_3$ is associated with a much variance (${\widehat{\lambda }}_3=0.13$), and does not impact the hazard map as much as the first two components. The roles of ${\widehat{\phi }}_3$ and ${\widehat{\xi }}_3(s)$ seem to be compensating ${\widehat{\xi }}_1(s)$ and ${\widehat{\xi }}_2(s)$ at the very beginning and the very end of the experiment in order for the hazard map to be closer to background noise.

Fig. 6.

Estimated $({\widehat{\xi }}_{\mathcal{l}}(s_1^{*}),\dots ,{\widehat{\xi }}_{\mathcal{l}}(s_m^{*}){)}^{\prime }$, ℓ = 1, 2, 3. Each ℓ loading is standardized to have zero mean and standard deviation one. The associated variability coefficients are ${\widehat{\lambda }}_1=13.20$, ${\widehat{\lambda }}_2=8.07$ and ${\widehat{\lambda }}_3=0.13$.

The standard errors for the parameter estimates are obtained via cross-validation by leaving one sensor out at each time, as detailed in Appendix A.1, and are shown in Table 1. While the main objective of Table 1 is to quantify the uncertainty regarding the parameter estimates, we note that the large range parameter estimate ${\widehat{\theta }}_3$ reflects a relatively weak spatial dependence. Consequently, the standard error for ${\widehat{\theta }}_3$ also might be inflated by static sensors within a certain radius of each other being removed during the cross-validation step. Table 1 also displays how the roving sensors affect the estimates of the spatial dependence coefficients. When only the static sensors are used, the range parameter estimates ${\widehat{\theta }}_2$ and ${\widehat{\theta }}_3$ are similar. However, when the roving sensors are included, the estimate ${\widehat{\theta }}_2$ becomes quite a bit smaller than ${\widehat{\theta }}_3$ and is more informative, in the sense that the spatial effect of the secondary noise source becomes more prominent owing to the roving sensors near this secondary source toward the end of the experiment. This illustrates that the inclusion of roving sensors adds information about the spatial dependence at finer scales.

5.2. Scientific implications.

Both static (Figure 3) and dynamic (Figure 4) hazard maps capture the high noise intensity in the northern room near the working engine. However, the dynamic hazard maps also show that the average intensity of hazard exposure in the southern room increases during the period between 10:00 am and 11:00 am when the engine in the northern room is turned on. Further, the outside noise source is detected in the southeastern corner after 11:10 am. In particular, the intensity levels exceed 85 dB, which is generally viewed as a harmful level for exposures longer than 8 hours. While the static maps do detect a small noise peak near the same location, the predicted intensity levels are understated.

The problem of interpolating hazard maps in time and space from discrete sampled observations was discussed in Koehler and Peters (2013). While kriging is well accepted for spatial interpolation in the occupational hygiene literature, often the observations or the hazard maps are averaged in time to produce estimates, and thus the temporal aspect of the data is ignored. To compare our method with the existing approaches, we consider kriging using the roving data only and kriging while incorporating roving and static sensor data, both averaging the observations in time. We also consider fixed-time universal kriging (UK), fixed-time thin-plate spline (TPS) and fixed-time simple linear regression on the spatial coordinates (LM). By fixed-time we mean that a time point is fixed and the spatial map is constructed for the data corresponding to the time transect selected, thus preserving some of the temporal structure from the data.

To compare the methods globally, the MSPE values for our spatio-temporal data fusion method are obtained using the leave-one-sensor-out cross-validation described in Appendix A.1. We generate prediction maps at every time point in which the static sensors were sampled, and averaged the values across space and over time. When including the roving sensors, the inhomogeneous variance case (STDF) has an MSPE of 11.82, and the homogeneous version (STDFh) has an MSPE of 11.66. When using only the static sensors (STDF*), the MSPE is 14.56. The MSPE for the static map using roving sensors only is 37.42, and the MSPE for the static map incorporating roving and static sensor data is 38.33. This shows a clear advantage of our method over the current practice of using static maps. For the other alternative approaches, the MSPE for fixed-time universal kriging (UK) is 24.4, thin-plate spline regression (TPS) is 14.99, and simple linear regression model (LM) is 25.14, all of which are outperformed by our method. We observe that the homogeneous variance case gives similar predictions to the inhomogeneous variance case.

In Figure 8 we focus on a small-scale example from the dataset to illustrate the possibility of detecting short duration hazard intensity peaks. The static sensors are sampled every minute (Section 2.1), and thus the measurements are available between 11:04 am and 11:05 am. For the UK and TPS generated maps, we use data from 11:04 am and 11:05 am, and interpolate linearly the values from the maps at times 11:04:20 and 11:04:40. We can see in Figure 8 that UK maps do not capture the secondary noise source in the southeastern part of the facility. This is because the method underestimates the range of spatial dependence, and produces predictions that resemble a plane except where the static sensors are located. On the other hand, the TPS method oversmooths the data, losing local features such as the sharper distinction between the northern and southern rooms in the facility. We omit the linear model estimates, which are planes only. In addition, Figure 9 shows the corresponding standard error maps for each method in Figure 8. We observe that the STDF maps generally have lower standard errors than those of UK. The TPS only has comparable standard errors when very near the static sensors, but otherwise much higher standard errors than either STDF or UK.

Fig. 8.

Comparison of STDF hazard map with maps created by universal kriging (UK) and thin–plate splines (TPS) methods. For the UK and TPS, data are from 11:04:00 and 11:05:00, and interpolated linearly between 11:04:20 and 11:04:40. Black points mark the static sensor locations, while white points mark the roving sensor locations at the corresponding time.

Fig. 9.

Comparison of standard errors of STDF hazard maps with the standard error of universal kriging (UK) and thin-plate splines (TPS) methods. For UK and TPS, data are from 11:04:00 and 11:05:00, and interpolated linearly between 11:04:20 and 11:04:40. Black points mark the static sensor locations, while white points mark the roving sensor locations at the corresponding time.

A final remark is that we can consider cases in which the spatial covariance function is not exponential. For example, we repeated the analysis using the Matérn class of covariance functions, with known smoothness parameter ν = 2.5. The resulting hazard maps (not shown) are similar except for slightly smoother contour lines. We anticipate that our method is robust to the choice of a covariance function in the Matérn class.

6. Discussion.

In this paper, we have developed a spatio-temporal static and roving data fusion model, with each data sensor having potentially different instrument variances. The approach to model fitting and statistical inference has been applied to produce hazard maps that capture dependence across space and over time in indoor environments. Modeling the spatio-temporal dependence structure allows the hazard maps to capture features that are missed by the current practice in occupational hazard assessment. Furthermore, our approach enables continuous-time prediction of hazard, which the existing approaches are unable to produce.

With the semiparametric model specification, our method is able to detect unexpected hazard sources that occur sporadically during a study. A sudden fluctuation of intensity, such as the secondary noise source in the southeastern corner of the facility, are undetected or underestimated when using current practices, but can be detected by our method. Moreover, health effects of short duration but high-level exposures are unclear, and our method provides a way to better capture such transient exposures.

Cross-validation shows that our methodology outperforms the traditional methods in the scientific application, a conclusion that is corroborated by the simulation study given in Appendix B of the Supplemental Materials. The simulations have also demonstrated that our method is robust to different instrument variances, while the traditional approaches tend to provide less accurate prediction.

While the height of the sensors is not accounted for directly, the model with heterogeneous measurement error variances may accommodate possibly different heights for different sensors. It would be interesting, however, to examine this third dimension more closely, as well as to consider three-dimensional hazard maps when data are collected at different heights [see, e.g., Tracey et al. (2014)].

Other covariance modeling allows for nonseparability, although stationarity in time is generally assumed [Gneiting (2002), Ma (2003), Quick, Banerjee and Carlin (2015)]. Stein (2005) proposed models that are asymmetric in time, allowing for different smoothness degrees in space over time. It may be of interest to extend such models and develop estimation methods for fusion of static and roving sensor data. Moreover, while the methodology developed here is geared toward spatio-temporal hazard mapping, we believe that other scientific disciplines might benefit from our approach for fusing data with very different spatial and/or temporal scales. For example, for data collected by individuals with personal devices versus data collected at stationary monitoring stations used to study exposure and averse health effects in environmental epidemiology [see, e.g., Hall and McMullen (2004)]. The applicability of our approach to other scientific studies is currently under investigation, such as integration of animal movement data with static field cameras in ecological monitoring. At this point, our preliminary studies show that when the sample size increases, the increase in the computational cost is higher for more roving sensor data than static sensor data. For datasets of much larger sample size with more sampling locations and/or time points, the proposed profile likelihood approach would need to be improved for it to be more computationally feasible by utilizing some form of approximation, such as blocking [Caragea and Smith (2007), Chu, Wang and Zhu (2014)] or tapering [Furrer, Genton and Nychka (2006), Kaufman, Schervish and Nychka (2008), Du, Zhang and Mandrekar (2009), Chu, Zhu and Wang (2011)], in the covariance matrix inversion. We leave this for future research as well.