Abstract
Background
Recent years have witnessed an upsurge in the development of methods for estimating current source densities (CSDs) in the neocortical tissue from their recorded local field potential (LFP) reflections using microelectrode arrays. Among these, methods utilizing linear arrays work under the assumption that CSDs vary as a function of cortical depth; whereas they are constant in the tangential direction, infinitely or in a confined cylinder. This assumption is violated in the analysis of neuronal activity propagating along the neocortical sheet, e.g. propagation of alpha waves or cortical spreading depression.
New method
Here, we developed a novel mathematical method (waveCSD) for CSD analysis of LFPs associated with a planar wave of neocortical neuronal activity propagating at a constant velocity towards a linear probe.
Results
Results show that the algorithm is robust to the presence of noise in LFP data and uncertainties in knowledge of propagation velocity. Also, results show high level of accuracy of the method in a wide range of electrode resolutions. Using in vivo experimental recordings from the rat neocortex, we employed waveCSD to characterize transmembrane currents associated with cortical spreading depressions.
Comparison with existing method(s)
Simulation results indicate that waveCSD has a significantly higher reconstruction accuracy compared to the widely-used inverse CSD method (iCSD), and the regularized kernel CSD method (kCSD), in the analysis of CSDs originating from propagating neuronal activity.
Conclusions
The waveCSD method provides a theoretical platform for estimation of transmembrane currents from their LFPs in experimental paradigms involving wave propagation.
Keywords: Current source density analysis, Local field potential, Cortical spreading depression, Wave propagation
1. Introduction
Development of high-resolution, multi-contact microelectrode arrays (MEA), have revolutionized methods for estimation of transmembrane currents from their extracellular local field potential (LFP) reflections. This estimation procedure is known as current source density (CSD) analysis. CSD analysis methods have recently been expanded to multidimensional domains(2D - (Łęski et al., 2011; Potworowski et al., 2012), 3D - (Łęski et al., 2007; Potworowski et al., 2012; Riera et al., 2014; Riera et al., 2012); however, the most widely used application is to determine CSDs associated with neocortical columns using linear arrays (Freeman and Nicholson, 1975; Mitzdorf, 1985; Nicholson and Freeman, 1975; Nicholson and Llinas, 1975; Pettersen et al., 2006; Potworowski et al., 2012). For a detailed review of CSD analysis methods and their applications, refer to (Einevoll et al., 2013).
Methods developed for neocortical CSD analysis using linear arrays assume that CSDs vary only as a function of cortical depth (z-axis) and that their tangential (x-y) extension can be either infinite (Nicholson and Freeman, 1975) or confined to a circular disk of a predefined radius around the electrodes–the inverse CSD method (iCSD (Pettersen et al., 2006)) and the kernel CSD (kCSD) method (Potworowski et al., 2012). The layer-based and columnar organization of the mammalian neocortex is the physiological foundation for the tangential (laminar) symmetry in the aforementioned methods for CSD analysis. This assumption is suitable for most experimental paradigms where neuronal activations are expected to localize in specific functional structures of neocortex, and CSD analysis results have significantly aided in the determination of neuronal circuit organization in sensorial (Riera et al., 2014; Schroeder et al., 1998), motor (Aroniadou and Keller, 1993; Barth et al., 1990) and cognitive (Godlove et al., 2014) cortical regions.
However, in several experimental conditions, neuronal activity propagates continuously along large areas of the neocortical sheet. Alpha rhythm waves are reported to originate in the occipital regions and propagate progressively to frontal regions at a velocity of ~30 cm/s (Lopes da Silva and Storm van Leeuwen, 1978; Nunez, 1974; Nunez and Cutillo, 1995). Global traveling waves are also reported in studies using scalp EEG (Burkitt et al., 2000; Hughes et al., 1995; Hughes et al., 1992; Massimini et al., 2004), as well as in studies with direction measurements using optical imaging techniques (Wu et al., 2008). Cortical spreading depression, a well-studied phenomenon associated with migraine aura, is another example where an electro-diffusional wave propagates along the cortical mantle at a reported velocity of 3–5 mm/min (Lauritzen, 1994; Leo, 1944). These examples along with recent discoveries of traveling waves in visual perception (Wilson et al., 2001) and sensorimotor integration (Zanos et al., 2015), call for the development of novel CSD analysis methods accounting for the propagating nature of neuronal activity. For more information about cortical travelling waves refer to (Muller et al., 2018).
In this study, we used two mathematical constructs to develop a new method (waveCSD) for CSD analysis of experimental applications where a planar CSD wave is propagating along the neocortex with a constant velocity. Similar to the iCSD method, our waveCSD method works based on the inversion of the electrostatic forward model of LFP generation. First, we expand the planar wave in cubic spline bases and assume compact support in the direction of propagation. Second, to account for the ill-conditioning of the forward problem discrete kernel, we use Tikhonov regularization scheme. The use of regularization techniques has been shown to significantly improve the reconstruction accuracy, especially in the presence of noise in the voltage data (Potworowski et al., 2012). Using simulations, we evaluate the sensitivity of waveCSD to the observation noise, the electrode spatial resolution, and the uncertainties in the knowledge of the planar wave velocity. We also compare the reconstruction accuracy of waveCSD with spline-iCSD (Pettersen et al., 2006), and kCSD (Potworowski et al., 2012) methods adapted to the reconstruction of CSDs emerging from the propagation of neuronal activity. Finally, we apply the waveCSD method to determine neocortical transmembrane ionic currents associated with cortical spreading depression in rats.
2. Materials and Methods
2.1. CSD analysis of a planar wave of neocortical neuronal activity (waveCSD method)
Assuming constant and isotropic tissue conductivity, the relationship between the current source density in the brain, denoted by C, and the generated LFPs, denoted by V, is determined by the Poisson equation (Goto et al., 2010; Nicholson and Freeman, 1975):
| (1) |
Assuming an infinite medium, the solution to Eq. (1) at an electrode position is provided by:
| (2) |
Here, we propose a method for simulating an experimental setup in which a wave of neuronal activity, originated in a location ( ), is moving tangentially along the cortex with a constant velocity v, and a linear probe is perpendicularly inserted into the neocortex along the z direction to record the resultant LFP. We assume that is far enough from the electrode array to render the propagating wave planar. In this model, the propagation direction is along the x-axis, thereby allowing us to drop the y -dependency of C in Eq. (2):
| (3) |
| (4) |
where yf = −ys = α are the limits of the cortex in the y direction assuming y0 = 0. Since the propagation velocity is assumed constant, the CSD profile at any x location can be written using the d’Alembert’s formula:
| (5) |
Note that we only study propagation of the wave towards the electrodes. Assuming that the CSD has a spatial compact support in the x direction at any given time instance t, the x integration in Eq. (3) can be simplified to:
| (6) |
where
| (7) |
x0 is the x location of the wave at time t0 = 0 (here we set x0 = 0), and L is the assumed length of the wave in the x direction, whose shape will be defined using cubic splines. Using a change of variables (i.e. τ = x − vt), Eq. (6) can be reorganized into:
| (8) |
Upon discretizing C(τ, z) in a two-dimensional rectangular grid for τ and z via bicubic splines, the linearized version of Eq. (8), for each time instance t, is written as follows:
| (9) |
where and c is a column vector of the CSD values to be determined at the grid points (here we assume nτ and nz points in the τ and z directions, respectively). The derivation of Eq. (10) and elements of Q is outlined in Appendices A and B. We have added Gaussian noise , where ne is the number of electrodes, to Eq. (9) to account for uncorrelated instrumental noise in the recordings with standard deviation σn. In the simulations of this paper, we quantify σn as percentages of the maximum absolute value of the LFP.
The inverse problem associated with Eq. (9), i.e. estimating c given v, is both ill-posed and ill-conditioned. Thus, we use the Tikhonov regularization scheme (Tikhonov et al., 1977) for estimation of current sources ĉ:
| (11) |
where Γ = Ine is the Tikhonov matrix and λ is the optimal regularization parameter, determined via generalized cross-validation (GCV) method (Wahba, 1990) through minimization of the following evaluation function (E(λ)):
| (12) |
Where P(λ) is the projection matrix defined as:
| (13) |
The estimation of other model parameters, i.e. v and α, from the LFP data is also done using Eq. (12). More specifically, a wide range of v and α values will be chosen for a given LFP recording. For any pair of v and α values, i.e., (vi, αj), the corresponding Q matrix will be calculated and the regularization parameter λij will be estimated. The pair which has the lowest GCV score, i.e., (Eij(λij), will be chosen as the optimal model parameters. In this paper, we denote the CSD profile reconstructed using the waveCSD method as cwaveCSD.
2.2. CSD analysis of a propagating wave using iCSD and kCSD methods
iCSD (Pettersen et al., 2006) is the pioneering method which utilized the inverse problem of Eq. (2) for the CSD analysis of LFP recordings using multielectrode arrays with various configurations. In the original article by Pettersen et al. (2006), three model-based iCSD methods (i.e., step-, delta-, and spline-iCSD) were proposed and applied to the LFP data from linear (laminar) probes. The authors also developed iCSD methods for off-center electrode placements. In this paper, all comparisons will be made with the spline-iCSD method centered at the electrodes. The assumption in this method is that the CSD is constant in the tangential direction and is confined to a cylinder of a predefined diameter—usually the size of a cortical column—around the electrodes. Potworowski and coworkers (2012) further generalized the iCSD method to kCSD method, a non-parametric CSD analysis methodology which utilizes reproducing kernel Hilbert spaces for the reconstruction of current source densities which can be applied to various configuration of recording electrodes. Major improvements in the kCSD method compared to iCSD are: I) incorporation of regularization algorithms to improve the reconstruction accuracy in the presence of observation noise in voltage data, and II) estimation of model parameters using k-fold cross-validation algorithm from the LFP recordings. The kCSD method also assumes that current sources are confined in a cylinder, and that the tangential extension of the sources are either defined using a step function, or a Gaussian profile. In this paper, we use the Gaussian profile of current sources in the 1D kCSD method for all comparative simulations.
Throughout this paper, we refer to spline-iCSD and 1D kCSD as iCSD and kCSD, respectively. Application of either iCSD or kCSD method to LFP gives a temporal distribution of the variation of CSDs along the z direction, here denoted as and , respectively. Neither method is intended to account for propagating CSD waves originating far from the electrodes and covering large-scale neocortical distances. Hence, to be able to interpret the solution of iCSD and kCSD methods as a wave of length L propagating towards the electrode with a constant velocity v, these temporal maps should be converted to spatial propagating profiles, denoted as and , respectively. This conversion, which allows for the comparison of accuracy of reconstruction of iCSD and kCSD with waveCSD, is done using a linear transformation of the profile as follows:
| (14) |
The up and running version of the iCSD method (CSDPlotter) can be downloaded from (http://web.eng.fiu.edu/jrieradi/CSDPlotter/).
2.3. Reconstruction accuracy measures
Using simulations, we compare the reconstruction accuracy between waveCSD, iCSD and kCSD methods. A known CSD profile (cground–truth) of length L, propagating towards the electrodes at a constant velocity v, was used to generate simulated LFP data using the forward model of Eq. (8). At any desired Gaussian noise level, 50 distributions of the noisy simulated LFP were constructed (random number generator seeding was shuffled to assure different noise distributions in each trial), and source reconstruction was performed using all three methods for all trials. It should be noted that noise filtering in the iCSD method is achieved by applying a Gaussian spatial filter on the estimated CSD from unfiltered LFP recordings (Pettersen et al., 2006). The model parameters for iCSD (the diameter of the cylinder (d)), and kCSD (the cylinder radius (R) and thickness (h) of the Gaussians) methods were selected using the following approach: Firstly, k-fold cross-validation algorithm implemented in the kCSD method is applied to the LFP data to choose optimal R and h. Secondly, since both iCSD and kCSD methods work under the same assumption that current sources are confined in a cylinder, and that parameter estimation is not included in the original iCSD method, d in the iCSD method was chosen same as that of kCSD method, i.e., d = 2R. The effect of changing d in the reconstruction using iCSD method was also separately studied. We calculate the accuracy of a given method by comparing its reconstructed profile, , with cground–truth, using the Relative Difference Measure (RDM) and the Magnitude (MAG) ratio. The RDM primarily quantifies differences in shape between the profiles, while MAG quantifies their relative magnitude (Gramfort et al., 2010).
| (15) |
| (16) |
The condition where RDM = 0 and MAG= 1 indicates identical profiles and optimal accuracy.
2.4. Recording LFP data during Cortical Spreading Depression
A total of five rats were used in this study to record LFPs using an A1x32 linear probe during cortical spreading depression. All procedures were conducted in agreement with the Institutional Animal Care and Use Committee at Florida International University (IACUC 15-014).
2.4.1. Animal preparation and cortical spreading depression induction
A mixture of 5% isoflurane and pure oxygen was supplied to a hermetically sealed box (1 L/min, 14.7 psi) to induce anesthesia in rats. For each rat, the scalp was shaved, and the rat was fixed to a stereotaxy (Narishige, Japan). The isoflurane level was reduced to 1.75–2.50% to stabilize the breathing rate to 50–55 breaths per minute. The scalp and the underlying connective tissue were removed to set the positions for the burr holes (for reference and ground electrodes), and the craniotomies (for cortical spreading depression induction and probe insertion). Burr holes were made approximately 1 mm posterior to lambda and the reference and ground electrodes were placed in direct contact with the intracranial spinal fluid. The two craniotomies, one 2mm anterior and the other 4 mm posterior to Bregma, were positioned on the right hemisphere approximately 2 mm lateral from the midline. The posterior craniotomy was used for induction of cortical spreading depression, and the anterior craniotomy was used for LFP recording using the linear (A1x32) probe. The probe was perpendicularly inserted approximately 1.7 mm into the neocortex using a micromanipulator control system (MPC-200/ROE 200/MPC-385/MPC-325 Sutter Instruments). The accurate positioning and depth of probe penetration was histologically verified postmortem. The cortical spreading depression events were induced via topical application of ~20–40 μl of 1M solution of potassium acetate (CH3CO2K) in distilled water (Milli-Q, Millipore Corp.). The leakage of CH3CO2K to the recording craniotomy was prevented using a dental cement barrier between the two craniotomies. The concentration of isoflurane anesthesia was reduced (0.25–0.5%, 1 L/min pure O2, 14.7 psi), and was supplemented with intraperitoneally-administered Dexmedetomidine hydrochloride (Dexdomitor, 0.25 mg/kg), to ensure that the spontaneous cortical brain activity was minimally compromised The efficacy of this approach was previously tested and verified by our group (Song et al., 2016). Throughout the recording, rat physiology (i.e. body temperature (~37 °C) and respiration rate (~28 breaths per minute) was constantly monitored using the PowerLab 8/35 data acquisition device and the LabChart software (ADInstruments). The rat’s body temperature was kept at the desired range using a heating pad (TPZ-0510EA, Texas Scientific Instruments, LLC) with a water-circulating pump (TP700, Texas Scientific Instruments, LLC).
2.4.2. Intracranial recordings
Two recordings, 30 minutes each, were performed for each rat. At the end of the first recording, the posterior craniotomy was washed with saline and dried before the start of the second recording. The spontaneous brain activity was recorded for 5 minutes before the CH3CO2K solution was administered to the posterior craniotomy. The LFPs were recorded with a PZ5 AC amplifier at 25 kHz (Tucker & Davis Technologies, TDT). The amplifier was connected to a signal processing unit (RZ2, TDT) by an optical fiber, and to a preamplifier by a coaxial cable. The OpenEx software (TDT) was used for recordings. The raw data was notch-filtered in MATLAB to remove the 60Hz artifacts, and a low-frequency (1–170 Hz) Butterworth IIR bandpass filter was used to extract the LFPs from the raw data.
2.5. cwaveCSD associated with cortical spreading depression
CSD analysis was performed on LFPs obtained from rats during cortical spreading depression using the waveCSD method. In order to check if individual CSD reconstructions exhibit a consistent and reproducible pattern across rats, the grand average CSD profile was obtained after nonlinear coregistration of the reconstructed CSDs. This was done through warping the reconstruction using a landmark-based nonlinear registration method based on the Approximate Thin Plate Splines (TPS) transformation outlined in (Rohr et al., 2001). For each individual, each landmark was chosen to represent a particular feature of visible contrast of the CSD reconstruction common to all individuals. Besides, their topological order was preserved across individuals to avoid folding of the transformations, i.e. negative values of their Jacobian. Since the TPS transformations are infinitely differentiable and no folding occurs, we ensure they capture the inter-individual diffeomorphic variability of rat neocortex expected in a group of normal rats.
2.6. Statistical analysis
Results are shown as mean±std, unless stated otherwise. The normality of the distribution of the accuracy measures (RDM and MAG) across methods (i.e. waveCSD, iCSD, and kCSD) at different noise levels is tested using the Kolmogorov-Smirnov (KS) test. Since all distributions failed the KS test (data not shown here), a BoxCox transformation (Box and Cox, 1964) is applied to the difference of the RDM and MAG measures across methods and a paired t-test is used to analyze if the difference is significant.
3. Results
3.1. Application of waveCSD, iCSD, and kCSD methods to neocortical planar waves of neuronal activity
To study the accuracy of waveCSD method in the reconstruction of propagating current sources compared to iCSD and kCSD methods, an arbitrary ground-truth profile waveform of CSDs (Fig. 1, top left panel) was assumed to propagate towards a 16-electrode laminar probe, positioned 6 mm away, with a constant velocity of 4 mm/min. This waveform, containing non-compensated, oblique sink and source current densities, was used in all simulations performed in this paper, unless stated otherwise. Comparative simulations for two other ground-truth profile examples are also provided in Appendix C.
Figure 1. Comparison of the accuracy of waveCSD, iCSD, and kCSD methods in the reconstruction of LFPs generated from a ground-truth waveform.
A) A ground-truth waveform (the CSD profile, top left) is assumed to be generated 6 mm away from an A1x16 probe, inserted perpendicularly in the cortex with an inter-electrode spacing of 100 μm. The first electrode is assumed to be 100 μm deep in the brain tissue. Here, the waveform propagates towards the electrodes at a constant velocity of 4 mm/min. The resultant LFPs are shown in the top right panel (black → most superficial electrode, and red → deepest electrode in the probe). B) Model parameter estimation for kCSD method using k-fold cross-validation technique as described in (Potworowski et al., 2012). The left panel shows cross-validation error for a wide range of R and h values, and the inset confirms that the selected parameters (the red dot) coincide with the global minimum of cross-validation error values. The estimated diameter (2R) for the kCSD method is used for source reconstruction in the iCSD method shown in panel C. C) Source reconstruction using iCSD, kCSD and waveCSD methods without the presence of noise in the LFP data. (iCSD- RDM: 0.47, MAG: 0.67; kCSD- 0.47, MAG: 0.88, waveCSD- RDM: 0.01, MAG: 0.99). Both RDM and MAG measures confirm that the waveCSD method provides more accurate CSD reconstruction among all methods (i.e. RDM closer to zero and MAG closer to 1 in the waveCSD method). For comparison purposes, colorbar ranges and labels are the same as in 1 A left panel. Parameters: waveCSD method- The temporal resolution of the Q matrix is 1 [s]. nτ = 40; nz = 30; L = 3 [mm]; σ = 0.3 [S/mm]; α = 3.5 [mm]. kCSD method- R = 2.2 [mm]; h = 0.44 [mm]; number of sources (nSrc) = 320. iCSD method- d = 4.4 [mm].
The resultant forward solution to Eq. (6) (i.e. the LFP distributions in the electrodes) is depicted in Fig. 1A top right panel. As described in section 2.3 and illustrated in Fig. 1B, optimal model parameters of the kCSD method were estimated from the LFP data via k-fold cross-validation technique and are used for the source reconstruction using both kCSD and iCSD models. All methods were utilized to reconstruct the waveform from the LFP data without the presence of noise (Fig. 1C). The RDM and MAG measures indicate that waveCSD was more accurate than iCSD, and kCSD. Additionally, results indicate that while RDM measure of both kCSD and iCSD were identical for the given waveform (RDM – 0.47), kCSD performed better in terms of MAG measure in comparison with iCSD (iCSD- MAG: 0.67; kCSD – MAG: 0.88).
Fig 2. shows that waveCSD outperforms iCSD and kCSD for a wide range of observation noise in the LFP data (Fig. 2). As illustrated in Fig. 2A, although increasing for all methods, the RDM measure is lower for waveCSD than for iCSD and kCSD. We tested if this difference was statistically significant. Since the normality of the distribution of the RDM measure across trials failed the Kolmogorov-Smirnov (KS) test, we applied the BoxCox transformation to the difference between the RDM values of the waveCSD method with iCSD and kCSD methods. A paired t-test rejected the null hypothesis of zero difference for all noise levels with p≈0. With this negligible p-value we decided there was no need for any further statistical analysis in the following simulations. On the other hand, Fig. 2B depicts the MAG measures for waveCSD decreases with increasing noise levels, while it increases for both iCSD and kCSD. For the given CSD example waveform at levels of noise below 10%, waveCSD is more accurate (i.e., MAG~1) than iCSD and kCSD. In the interval ~10–20%, MAG values intersect, being close to 1 for all methods. In this interval, the MAG values for iCSD and kCSD are closer to 1 around the 20% noise level, compared to waveCSD. At higher noise levels, all methods diverge from the optimal MAG value. Two examples of source reconstruction using all three methods are provided in Fig. 2C and and Fig. 2D for 10% and 30% noise levels, respectively. These examples further confirm that the inclusion of regularization techniques in both kCSD and waveCSD methods improves the quality of source reconstruction compared to iCSD method, particularly at higher percentages of noise in the data. For all the simulations in Fig. 2, the wave velocity was fixed to 4 mm/min.
Figure 2. Effect of observation noise on reconstruction accuracy of waveCSD compared to iCSD and kCSD.
Accuracy of reconstruction of all methods are compared for different values of Gaussian observation noise (as percent of the maximum LFP signal) added to the LFP data shown in Fig. 1, top right panel. A) RDM values for all three methods across 50 realizations of the observations are shown as mean±std for each noise level. Noise reduction in the iCSD method was performed by applying a Gaussian spatial filter on the reconstructed CSD from unfiltered LFP recordings (Gaussian filter sigma: σgf = 0.1 [mm]) Results indicate that at all noise levels waveCSD method outperforms iCSD and kCSD methods (RDM values closer to zero in waveCSD). B) MAG values for all three methods across 50 realizations of the observations are shown as mean±std for each noise level. Results show a decreasing trend in the MAG measure for waveCSD method as the noise level increases, while both iCSD and kCSD methods show the opposite trend. Two examples of the average reconstructed CSD profile using all three methods are provided in panels C and D for 10 and 30% noise levels, respectively. Parameters are as stated in Fig. 1.
Fig. 3 shows the comparison of the accuracy of the methods in CSD reconstruction at a range of known velocity values (between 3 to 8 mm/min) at 10% noise level. For the waveCSD method, the Q matrix corresponding to each known velocity was computed and the CSD was reconstructed. For each velocity value, optimal parameters for kCSD and iCSD models were selected as described in section 2.3. The MAG measure remains almost unchanged with wave velocity in all methods (Fig. 3A). The RDM measure exhibits a similar behavior in kCSD and iCSD methods, while it slightly increases with velocity in the waveCSD method (Fig. 3B). For the given waveform, waveCSD shows better performance in both RDM and MAG measures compared to kCSD and iCSD. Examples provided in panels C and D show source reconstruction for each method at 4 and 7 mm/min, respectively.
Figure 3. Effect of waveform velocity on the reconstruction accuracy of waveCSD, kCSD and iCSD methods.
The accuracy of methods, as measured by RDM and MAG, are compared as a function of the known velocity of the ground-truth waveform presented in Figure 1A, top left panel. 10% Gaussian noise was added to the LFP data, and optimal parameters of kCSD and iCSD methods were selected for each velocity value as explained in section 2.3. RDM and MAG values are shown as mean±std across 50 realizations of the observation noise. Noise reduction in the iCSD method was performed by applying a Gaussian spatial filter on the reconstructed CSD from unfiltered LFP recordings (Gaussian filter sigma: σgf = 0.1 [mm]). A) kCSD and iCSD show no change in the RDM value at different velocities, while waveCSD RDM increases slightly with the increase in wave velocity. B) All MAG traces remain almost unchanged across different velocity values. Two examples of the average reconstructed CSD profile using all three methods are provided in panels C and D for 3 and 7 mm/min wave velocity, respectively. Parameters are as stated in Fig. 1.
As mentioned earlier, in simulations shown in Figs. 1–3, the parameter d in iCSD method was selected based on the optimal radius (R) of kCSD, obtained from k-fold cross-validation technique. Since model parameter selection algorithms are not implemented for iCSD, in Fig. 4 we demonstrate the changes in RDM and MAG of iCSD method as a function of different values of d. For comparison purposes, we also show the constant traces of these measures for waveCSD—by definition independent from d. For iCSD both measures decrease with the diameter increase, relatively faster for MAG than for RDM (RDM from ~0.85 to ~0.8, MAG from ~4.5 to ~1.4, for d values from 300 to 700 μm), a trend that persisted for even extremely large values of d (as RDM→0.77 and MAG→0.70 for d → +∞). In this limit, in spite of MAG measure indicating a similar performance of both methods, waveCSD still outperforms iCSD with regards to RDM.
Figure 4. Dependency of CSD reconstruction accuracy to the diameter of the designated cylinder used in the iCSD method.

The top panel shows that both RDM and MAG values in the iCSD method decrease as a function of d. However, the changes are more drastic for the MAG measure (MAG: ~4.5 → ~1.5; RDM: ~0.85 → ~0.75, for d: 300 →700 μm). A limit case of d → ∞ is also provided in the bottom panel. Noise reduction in the iCSD method was performed by applying a Gaussian spatial filter on the reconstructed CSD from unfiltered LFP recordings (Gaussian filter sigma: σgf = 0.1 [mm]). waveCSD method is independent of d, thereby both measures are constant throughout. v = 4 mm/min, and 10% noise is added to the LFP data. The rest of the parameters are as stated in Fig. 1.
3.2. Robustness of the waveCSD method to noise and MEA resolution
Fig. 5 shows the robustness of the reconstructed CSD profile using the waveCSD method to the presence of noise and to the number of electrodes used in the probe. For each noise level, electrode number and velocity value, the average of MAG and RDM across 50 CSD reconstruction trials is shown. Fig. 5A and 5B show the accuracy of reconstruction at different ranges of propagation velocity and varying noise levels. Fig. 5A and Fig. 5B show that at any known velocity value, increasing the noise level reduces the accuracy of the source reconstruction (RDM away from 0, and MAG away from 1). Similarly, at any given noise level, increasing the velocity of the waveform decreases the reconstruction accuracy. Fig. 5C and 5D demonstrate a case in which a constant velocity of 4 mm/min is used for all simulations, and the source reconstruction accuracy is analyzed with respect to the number of electrodes in the probe. As can be observed in both panels, at any electrode resolution, increasing the noise level increases the error of reconstruction. Meanwhile, at any given noise percentage, increasing the resolution of the recording results in increased reconstruction accuracy.
Figure 5. Robustness of the CSD analysis using waveCSD method to noise and electrode resolution.
A–B) RDM and MAG measures are shown for cwaveCSD from the LFP data in Fig. 1A right panel, for a range of known velocities and different noise levels. The colorbar for the MAG measure is inverted compared to RDM (blue colored regions indicate desirable RDM and MAG values; red regions indicate areas with high error in reconstruction). At any given velocity, increase in the noise level decreases the accuracy of the reconstruction (RDM away from zero, and MAG away from one) and vice versa. C–D) RDM and MAG measures are shown as a function of electrode resolution at different noise levels for the average reconstructed CSD profile (cwaveCSD) of the LFP data of the ground-truth waveform. At any electrode resolution, increase in the noise level decreases the accuracy of reconstruction, whereas at any given noise, increasing the number of recording electrodes, increases the reconstruction accuracy. Parameters are as described in Fig. 1 except nτ = 30 and nz = 10.
3.3. Errors associated with uncertainties in the knowledge of wave velocity in waveCSD method
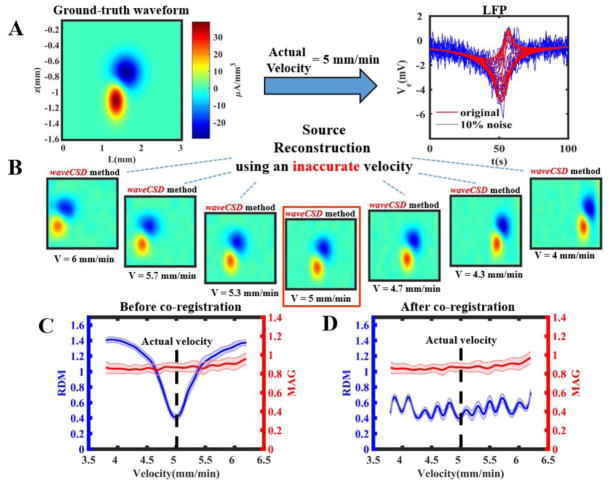
So far, we have assumed that one has an accurate knowledge of the velocity of the propagating wave. However, the velocity measurement might not be highly accurate. We performed the following procedure to evaluate the effect of assuming incorrect values of the velocities in the waveCSD reconstruction. The ground-truth CSD waveform (as shown in Fig. 6A, left panel) was assumed to propagate with a velocity of 5 mm/min. The resultant LFPs (shown in Fig. 6A, right panel) was calculated using Eq. (6) with 10% noise. Then, a set of CSDs (Fig. 6B) were estimated using Q matrices corresponding to inaccurate velocities ranging from 4 to 6 mm/min. As observed in panel B, the most noticeable difference in the reconstructed profiles is the change in the location of the CSDs predominantly in the x direction. This observation is verified when RDM and MAG measures are compared before and after a linear co-registration of the reconstructed profiles through translation along the x axis (Fig. 6C and 6D, respectively). Results in both Fig. 6C and 6D show that if reconstruction is performed using the Q matrix with an assumed accurate velocity (Fig. 6B, middle box), the reconstruction error is minimal (Notice the RDM in Fig. 6C). Fig. 6C also shows that while the RDM measure is significantly affected by estimations assuming inaccurate velocities; the MAG measure does not significantly change. These results indicate that in spite of lack of precise knowledge of the velocity of the propagating wave, the waveCSD method can still provide CSD reconstruction with high accuracy, given the consideration that the location of the CSDs might be shifted mainly in the x direction.
Figure 6. Reconstruction accuracy under uncertainties in the knowledge of velocity of the waveform in the waveCSD method.
A) Under 10% noise, LFPs (right panel, red traces: unnoisy, blue traces: noisy) from an A1x16 probe were simulated assuming a ground-truth CSD waveform (left panel) propagating with at v = 5 mm/min towards the electrodes. B) The noisy simulated LFPs were used to estimate the CSD using the waveCSD method assuming a range of wave velocities from 4 to 6 mm/min. Profiles show a monotonic shift in the position of CSDs relative to the error in the assumed velocity. C) RDM and MAG measures for the reconstructed profiles using velocity values are shown as mean±std. If the actual velocity is used for the reconstruction (highlighted box in panel B), the accuracy is maximal. Note that the RDM measure is significantly dependent on the velocity error, while the MAG measure does not significantly change. D) Both RDM and MAG are almost unchanged after linear coregistration of reconstructed profiles in panel B along the x axis. Parameters used in simulations: temporal resolution of the Q matrices: 1 [s]; nτ = 20; nz = 10. Rest of the parameters are as described in Fig. 1.
3.4. Parameter estimation in waveCSD method using GCV from the LFP data
As explained in section 2.1, the main parameters of the waveCSD method, i.e., α and v, are estimated from the LFP data using generalized cross-validation technique. To test the accuracy of parameter estimation, a ground-truth CSD waveform shown in Fig. 7A left panel is assumed to be generated 6 mm away from an A1x16 probe and propagate towards the electrodes at 5 mm/min. The actual α used for the generation of LFPs (Fig. 7A right panel) was set to 3 mm. The waveform is generated by superposition of 10 Gaussian profiles with random amplitude, spread, and angle using the methodology described in (Potworowski et al., 2012). A wide range of α and v values were selected (α ∈ [1,5]; v ∈ [3,7]), and for each pair of parameter values, the corresponding Q matrix was calculated. Using these matrices, source reconstruction was performed on the LFP data without observation noise, and the pair which minimized the GCV score was selected as the optimal parameter set (red dot in Fig. 7B panels). As can be observed in the figure, the method successfully found actual parameter values in the absence of noise. Moreover, the optimal parameter set also coincided with optimal RDM and MAG measures. The same procedure was repeated for a wide range of noise levels in the LFP data (Fig. 7C). For each percentage of noise and for each parameter pair, 50 realizations of the noisy LFP were reconstructed. Fig. 7C confirms the successful parameter estimation even at high levels of observation noise in the LFP data.
Figure 7. waveCSD model parameter estimation from the LFP data using GCV technique.
A) A ground-truth profile was generated via superposition of 10 Gaussian profiles with random amplitude, spread, and angle (left panel). The resultant LFP profile (right panel) were generated from a A1x16 electrode assuming the waveform was generated 6 mm away from the electrodes and propagated towards the probe with a velocity of 5 mm/min (black → most superficial electrode, and red → deepest electrode in the probe). The limits of the cortex in the y direction (i.e. Yf =−ys = α) was set to be from [-3, 3] [mm]. B) For a wide range of velocity and α values the corresponding Q matrices were calculated (blue dots) and the parameter pair which minimized the GCV score was selected as the optimal set (the red dot). RDM and MAG measures are also shown for each parameter pair. In all simulations in the panel no noise was added to the LFP data. C) Parameter estimation was performed in the presence of varying percentages of the observation noise in the LFP data. For each noise level and each parameter set, 50 realizations of the noisy data were reconstructed. Data is shown is mean±std, and the actual values of velocity and α are shown in red dashed lines.
3.5. Transmembrane current sources during cortical spreading depression
LFP recordings from five rats were used to reconstruct the transmembrane CSDs during cortical spreading depression. Fig. 8A shows the LFP data from one rat recorded using an A1x32 probe. To solely account for the distribution of CSDs during a cortical spreading depression event, CSD analysis was performed after removing the natural resting-state brain activity and the silencing period (i.e. regions before and after the highlighted box in Fig. 8A). LFP data was down-sampled to the temporal resolution of the Q matrix used for the reconstruction (Fig. 8A inset). The reconstructed CSD profile of Fig. 8A inset is shown in Fig. 8B. The corresponding Q matrix for the reconstruction was computed based on an assumed velocity of 3 mm/min, a value commonly reported in literature for the velocity of the moving wave during cortical spreading depression (Gorji, 2001; Grafstein, 1956; Lauritzen, 1994). Note that we have already addressed the potential errors that are introduced in the reconstruction if this choice of velocity is not accurate (see Fig. 6).
Figure 8. CSD analysis of LFPs recorded during cortical spreading depression in rats using the waveCSD method.
A) The LFP recordings of one rat using an A1x32 probe during cortical spreading depression is shown in the left panel. The resting brain activity and silencing period after the event were excluded in the source reconstruction using the waveCSD method (right panel). LFP data was resampled to the temporal resolution of the Q matrix used for the CSD analysis (i.e., 0.2 [s]). The resampled data is shown using a color gradient from black to red (black → most superficial electrode, and red → deepest electrode in the probe). B) Reconstructed CSD profile of the resampled LFP data in panel A inset using the waveCSD method. C) Heat maps of the resampled LFP and the simulated LFP (resulting from forward modeling of the profile in the panel B using Eq. (8)) are demonstrated. Please note that panels B and C have different x-axes. For the reconstructed waveCSD model (panel B), the x-axis represents space, along the propagating direction. For the LFP heat maps (panel C), the x-axis represents time. D) Simulated LFP is superimposed onto the original resampled LFP. The insets demonstrate the electrodes with the best and the worst reconstruction determined based on the sum of square of the errors between the original and the reconstructed trace. Parameters used for the computation of the Q matrix for CSD analysis of the data: nτ = 30; nz = 20; L = 1 [mm]; temporal resolutions: 0.2 [s]. The rest of parameters are as described in Fig. 1.
Fig. 8D shows the extent to which the data (Fig. 8A inset) can be fitted by the forward model in Eq. (8) using the estimated CSD obtained in Fig. 8B. To that end, the “simulated” LFP was computed from the estimated CSD and was superimposed onto the original LFP. Fig. 8D insets show the electrodes with best and worst LFP reconstruction, as determined by the sum of square of errors between the original LFP trace and the reconstructed trace. The LFP heat maps, i.e., the temporal voltage profile, of the resampled LFP in Fig. 8A inset and the simulated LFP are compared in Fig. 8C.
Fig. 9A demonstrates the grand average CSD profile across rats after nonlinear diffeomorphic coregistration of the reconstructed CSDs (data from five rats; see section 2.4). The average CSD profile suggests a complex, multipolar configuration of current sources in different layers of the cortex during cortical spreading depression. The accurate probe positioning and penetration depth were verified via histology, postmortem (Fig. 9B). The schematic in Fig. 9C illustrates major layer-specific cellular populations in the neocortex.
Figure 9. Average profile of transmembrane current sources during cortical spreading depression in rats after nonlinear coregistration of the reconstructed profiles.
A) The grand average transmembrane CSD profile across five rats during cortical spreading depression using the waveCSD method is depicted. The averaging was performed after application of a landmark-based nonlinear diffeomorphic coregistration to individual reconstructed current sources. B) The histology image showing the accurate positioning and the desired penetration depth of the probe in the rat neocortex. C) The schematic representing major cellular substrates across different layers (i.e., Supra-Granular, Granular, and Infra-Granular) of the rat neocortex, e.g. excitatory pyramidal cells (layer II/III – black, layer V – brown and layer VI – blue), excitatory spiny stellate cells (yellow), inhibitory interneurons (basket cells – blue/black and Martinotti cells – red/blue), and layer II/III glia cells (green).
4. Discussion
CSD analysis of electrical signals in the brain has been revolutionized owing to the progress in development of high resolution MEAs for the spatiotemporal signal acquisition in different experimental settings. To date, CSD analysis methods utilizing LFP recordings from linear probes do not take the propagation of neuronal activity along the cortical sheet into account. In this paper, we provide a theoretical framework for the reconstruction of propagating CSDs with the assumption that these waves are planar and have a constant velocity. An immediate application of the waveCSD method is the CSD analysis of transmembrane currents during a cortical spreading depression event.
4.1. Comparison of waveCSD, kCSD, and iCSD methods in the CSD analysis of propagating neuronal activity
The iCSD method developed by Pettersen et al. (2006) has shown high level of accuracy in a variety of applications and has been one of the most widely-used CSD analysis techniques in the past decade (Einevoll et al., 2013; Łęski et al., 2011; Pettersen et al., 2006). The development of kCSD method, which provided a kernel-based methodology, further overcame main deficiencies of the iCSD method through incorporation of regularizing techniques to improve reconstruction quality, as well as inclusion of cross-validation algorithms to estimate optimal parameters given a data set. However, the assumptions in these methods do not account for propagation of neuronal activity along the neocortex in CSD reconstruction. Thus, if these methods are used for CSD analysis of conditions where such propagations are involved, the interpretations have to be drawn with care and results might not necessarily be highly accurate. It should be noted that in this paper, iCSD is synonymously referred to spline-iCSD method for laminar probes described in (Pettersen et al., 2006), and not the inverse current source density analysis method in general. In the case of CSD analysis of a propagating neocortical wave, the following key assumptions of the iCSD and kCSD methods are violated:
Firstly, when the wave of neuronal activity approaches the probe, current sources far from the electrodes contribute to the LFP data. Hence, the assumption that only current sources near the electrodes, i.e. inside the designated cylinder, contribute to the LFP data is not valid. Consequently, the choice of d in the analysis of CSDs emerging from the propagation of neuronal activity using the iCSD or kCSD methods can significantly affect the accuracy of the reconstruction. In particular, the lower the value of d, the higher the magnitude of reconstructed CSDs to account for the contribution of far current sources (see Fig. 4 for the iCSD method). As shown in Figs. 1, C1 and C2, the cross-validation algorithm in kCSD method selected significantly higher diameter of current sources around the probe compared to the typical value of a cortical column in the barrel cortex (~500 [μm]), primarily used in the iCSD method for reconstruction of the sources. Even though these choices of parameters improved the reconstruction accuracy (compare Fig. 1 and Fig. 4); still, the reconstructed CSD profiles are far from the ground-truth waveforms (Figs. 1, C1 and C2). This indicates that if model assumptions are not in line with the physiology of the phenomenon, e.g., a planer wave in this paper, the reconstruction error can be significant.
It is also noteworthy that several studies (Berens et al., 2008; Kajikawa and Schroeder, 2011; Kreiman et al., 2006; Lindén et al., 2011; Nauhaus et al., 2009; Wang et al., 2005) cast doubt on the traditional assumption that LFPs are generated within hundreds of micrometers from the recording electrode (Kajikawa and Schroeder, 2011; Katzner et al., 2009; Xing et al., 2009), by providing evidence on the spatial reach of the LFPs in the order of several millimeters. Additionally, the contribution of current sources to the LFP data is highly dependent on correlation. Thus, in physiological phenomena where the spatial activity is highly correlated, distant sources do indeed contribute to the LFP data (Lindén et al., 2011), which is surely the case for cortical spreading depression.
Secondly, in the case of a propagating neocortical wave of neuronal activity towards the linear probe, CSDs cannot be assumed constant in the tangential direction, i.e. there is no tangential symmetry of the current sources around the electrodes. Both iCSD and kCSD methods provide the distribution of CSDs as though they were tangentially symmetric around the probe within the designated cylinder, which does not describe the actual phenomenon.
Since the assumptions in the derivation of waveCSD method are particular to phenomena involving a planar wave of neuronal activity, the accuracy of the reconstruction is higher than those of kCSD and iCSD methods in simulations performed in this paper (see Figs. 1–4, C1 and C2). Hence, even though the application of kCSD or iCSD methods provides valuable information about the distribution of CSDs in a variety of experimental paradigms, they must be cautiously used and interpreted if they are used to analyze currents originating from propagating neuronal activity. It should be noted that the same reasoning is applied to waveCSD method, where one should expect lower accuracy compared to kCSD or iCSD methods if waveCSD is applied for experimental paradigms where neuronal activity is static and of cylindrical symmetry. Similarly, waveCSD method is expected to have high reconstruction errors if the propagating wave does not have the same characteristics (e.g., constant velocity and planar symmetry) as ones assumed in model derivation. Hence, the applicability of waveCSD has to be evaluated for each particular experimental situation. The waveCSD method, as it stands, is expected to yield higher reconstruction accuracy when applied to global brain traveling waves, e.g., those related to brain rhythms (Burkitt et al., 2000; Hughes et al., 1995; Lopes da Silva and Storm van Leeuwen, 1978; Massimini et al., 2004; Nunez and Cutillo, 1995), sensory-evoked activity or spreading depression waves, as compared to more local spiral waves in the brain (Huang et al., 2010).
4.2. CSD analysis of cortical spreading depression
In an early study, Wadman et al. (1992) performed a CSD analysis of the sustained DC shifts attributed to spreading depression in CA1 and dentate gyrus of the rat hippocampus using the traditional CSD analysis method (Nicholson and Freeman, 1975). The spreading depression was induced by repetitive electric stimulation of different afferent pathways. The results of the study indicated a large current sink in the proximal regions of the apical dendrites and major current sources in the deep layers where the cell soma resides. Authors reported changes in the polarity of CSDs both with time and along the depth of hippocampus. Another study by (Makarova et al., 2008) also used the traditional CSD analysis method to obtain current source densities in CA1 of rats during spreading depression induced by electrical stimulation of hippocampal ipsilateral CA3 region. The temporal CSD profile of spreading depression showed a rapid (>0.5 s), high intensity, current source and sink sequence at the front of the wave. More recently, using the same CSD analysis methodology, (Nasretdinov et al., 2017) observed similar intense, rapid outward-inward current sequences at the wavefront, followed by more spread current sources and sinks, in KCl-evoked spreading depression in the barrel cortex of rats.
The temporal and spatial changes in the polarity of CSDs were also observed in our study despite differences in the brain region of interest, spreading depression induction method, and the CSD analysis methodology (see Figs. 8A and 9A). The average profile of the transmembrane currents during cortical spreading depression (Fig. 9A) indicates that the overall shape of the reconstructed CSD is consistent across all the rats used in this experiment. The magnitude of currents appears to be significantly larger at deeper layers (Infra-Granular). Additionally, the change in the polarity of CSDs is more drastic in deeper layers (Infra-Granular) in comparison with superficial (Supra-Granular) and middle layers (Granular).
Under the set of assumptions used in the derivation of the waveCSD method (see section 2.1), the first current sources which emerge during a cortical spreading depression event appear to be at the Supra-Granular layer. Subsequently, the transmembrane currents seem to originate in the Granular region and propagate towards the Supra-Granular and Infra-Granular layers. This can be viewed as the noticeable shift in the relative position of the CSDs across the depth of the cortex in Fig. 9A. The knowledge of distribution of the transmembrane currents during a cortical spreading depression event can provide important insights into understanding mechanisms underlying this complex phenomenon. Detailed analysis of such mechanisms, however, is beyond the scope of the present study.
4.3. Improvement in the waveCSD method and future directions
The waveCSD method assumes that the propagation velocity of the wave of neuronal activity is constant across all layers of the neocortex. This assumption is not valid in all experimental paradigms. In cortical spreading depression, for instance, Basarsky et al. (Basarsky et al., 1998) reported that the propagation of the depolarization wave is significantly faster in the outmost layers of rat cortical slices. In another study, Richter and Lehmenkuhler (Richter and Lehmenkühler, 1993) provided evidence for the existence of a barrier for the genesis and propagation of spreading depression along the depth of the cortex. These results were in agreement with early studies by Leão and Morison (Leao and Morison, 1945) and Leão (Leão, 1951) indicating that cortical spreading depression genesis and duration is layer sensitive. A recent study by our group (unpublished data) also revealed that the propagation velocity of cortical spreading depression in rats changes along the depth of the cortex.
All these evidence, along with the variability in the reported propagation velocity of the cortical spreading depression in previous studies (Lauritzen, 1994), indicate that an avenue for improvement in the waveCSD method is the incorporation of depth-dependency in the tangential propagation velocity (i.e. v as a function of z).
The observations presented in Fig. 6 corroborate the idea that the mismatch in the actual versus accounted velocity value in the waveCSD method results in a shift in the position of the reconstructed CSDs, predominantly in the x direction. Thus, the use of a constant velocity for CSD analysis of a cortical spreading depression event might explain relative positioning of CSDs across cortical layers as shown in Figs. 8–9.
The waveCSD method assumes the propagation of a single wave of neuronal activity towards the electrodes. Evidence in literature point to the co-existence of multiple distinct waves during spreading depression (e.g., calcium waves propagating along and across layers in hippocampal organ cultures (Kunkler and Kraig, 1998), as well as in mouse neocortical slices (Peters et al., 2003)). Thus, a more general and realistic approach for the CSD analysis of such multi-mechanistic phenomena using the waveCSD method is to incorporate multiple waves approaching the electrodes along different cortical lamina. However, it is important to note that the waveCSD method is a general investigative tool which encompasses a variety of applications and is not restricted to cortical spreading depression. Hence, incorporation of the above-mentioned modifications was not the focus of the current study.
Similar to other methods for CSD analysis, waveCSD only takes the Ohmic currents into account in the reconstruction of CSDs from their respective LFP reflections. However, there has been a growing controversy in recent years on the potential role of diffusive currents and the extent of their importance on the recorded extracellular potentials (Cabo and Riera, 2014; Destexhe and Bedard, 2012; Einevoll et al., 2013; Gratiy et al., 2013; Riera and Cabo, 2013; Riera et al., 2012). A recent theoretical study by Halnes and colleagues (Halnes et al., 2016) suggests that diffusive currents can indeed have comparable influences on the extracellular potentials in the vicinity of a small population of active neurons in the cortex in the range of frequencies up to 10 Hz. Additionally, theoretical research groups have also demonstrated that the magnitude of diffusive currents in both intra- and extra-cellular space can be comparable to Ohmic currents in the presence of steep concentration gradients in the ionic substrates (Halnes et al., 2016; Qian and Sejnowski, 1989). Cortical spreading depression is a clear-cut example of a neurological condition where such steep changes in the ionic concentrations is observed (Feuerstein et al., 2010; Kramer et al., 2016; Obrenovitch et al., 2002; Sword et al., 2017). Hence, another future direction of the current research is to incorporate the diffusive currents in the derivation of the waveCSD method.
Conclusions
To our knowledge, the method outlined in this paper is the first to account for the propagation of neocortical neuronal activity in the reconstruction of CSDs from their LFP reflections. Robustness of the method to the presence of observation noise, and the uncertainties in the knowledge of propagation velocity, was verified in different sets of simulations. Using simulations, the waveCSD method showed higher reconstruction accuracy compared to the iCSD method in the CSD analysis of transmembrane currents originating from propagating neuronal activity. In this study, we utilized the waveCSD method to provide a novel profile of the distribution of transmembrane CSDs during a cortical spreading depression event. As discussed earlier, the waveCSD method is far from ideal and several factors can enhance the reliability of the method in the analysis of CSDs in different experimental settings. However, since the waveCSD method is specifically designed for the CSD analysis of propagating neuronal waves in the cortex, we believe that the combination of this method with theoretical models as ones developed in (Mori, 2015), has the potential to provide a theoretical platform to unravel the underlying mechanisms of several neurological phenomena involving the propagation of neuronal activity.
Highlights.
Novel current source density analysis method accounting for neocortical wave propagation
Application for transmembrane current estimation in cortical spreading depression
Acknowledgments
Funding
This study was supported by the National Institutes of Health (1 R56NS094784-01A1), the National Science Foundation (DMS-1516176 and DMS-1516978), Ronald E McNair Post-baccalaureate Achievement Program (Daniel E. Rivera-Espada), and Coulter Undergraduate Research Excellence (CURE) Program at Florida International University (Daniel E. Rivera-Espada).
We would like to thank Amirali Nilchian for technical support, Lakshmini Balachandar, Ricardo Siu, and Andres Pena for insightful discussions.
Appendix A. Discretization of the waveCSD forward problem
Throughout this Appendix, with some modifications, we base our derivations on the methodology outlined in (Łęski et al., 2011) and (Łęski et al., 2007). Before providing the detailed derivation of the discretized version of Eq. (8) in the main document, we provide an introduction on bicubic spline in two dimensions.
Assume a rectangular grid shown in Fig. A1, where i ranges from 1 to nx, and j ranges from 1 to ny (nx and ny are the number of nodes in the x and y directions, respectively). To interpolate f(x, y) using bicubic splines in the rectangular grid shown in Fig. A1, we first recap the derivation of cubic splines in a single direction:
Assume a set of n data points (xi, f(xi)) at regularly spaced grid points: x1 < x2 < ··· < xn. The cubic spline S(x) is defined as:
| (A.1) |
where S(x) ∈ C2 in [x1, xn] satisfying S(xi) = f(xi), and each Si(x) is a cubic polynomial. For xi ≤ x ≤ xi+1, from (Press et al., 1996) one can write:
| (A.2) |
where
; P2(x) = 1 − P1(x); and .
Gx is a square matrix of length n, whose matrix product with the vectorized function values at the nodes, will provide the second derivative estimation of f(x) at the grid points. This matrix can be computed assuming different types of boundary conditions, including “natural”, “not-a-knot”, and “clamped”. Details of the derivation of the G matrix is provided in Appendix B. hx is the increment size in the x direction (for simplicity, here we assume equi-spaced grid points).
The interpolating bicubic spline function Sb(x, y) of a two-dimensional function f(x, y) in a box of the grid, defined as the domain xi ≤ x ≤ xi+1 ∩ yj ≤ y ≤ yj+1 (the highlighted box in Fig. A1) is obtained by applying the above method in both dimensions. We first apply the cubic spline in the x direction:
| (A.3) |
where . fxx is the partial second derivative of function f in the x direction.
Now, for yj ≤ y ≤ yj+1, we apply the cubic spline in the y direction:
| (A.4) |
where . Definitions of Gy, P(y), and hy are the same as those described for x, but in the y direction. Hence, Sb(x, y) can be written as:
| (A.5) |
Where Aαβb are the elements of the following matrix:
| (A.6) |
Noting that each element of Ab is a linear combination of the values of the function in all the np points in the grid, {fp}p=1,…,np, Eq. (A.6) takes the form:
| (A.7) |
where Eαβbp is the coefficient standing by the base {Pα,b(x)Pβ,b(y)} in the box b, assuming that only a unit current source is placed at the point p in the rectangular grid and the rest of the grid points take the value of zero. The interpolation of the function f(x, y) over the entire domain is therefore achieved from Sb(x, y) for different boxes in the domain:
| (A.8) |
where nb = (nx − 1)(ny − 1) is the total number of boxes in the grid. Now, using this introduction, we derive the discretized form of Eq. (8) in the main text, rewritten below:
| (8) |
To do so, we discretize the (τ, z) space into a set of nτ and nz grid points in the τ and z directions, respectively. Here, we use “clamped” boundary condition for bicubic splines in both dimensions (i.e. zero derivatives for the boundaries of the domain), since this choice of boundary condition provided the best fit among the other choices including “natural” and “not-a-knot” (data not shown). The final discretized equation can be represented as:
| (A.9) |
Where
np = nτnz is the total number of points in the grid; v and c are as described in the main text. The Q matrix is as defined as follows:
| (A.10) |
| (A.11) |
| (A.12) |
where the integration is over box b (total (nτ − 1)(nz − 1) boxes in the grid), nt is the total number of time points in the simulation, and ne is the number of electrodes in the probe. The rest of the parameters and functions are as described earlier, but for τ and z.
Appendix B. Derivation of the G matrix for different boundary conditions
The formula stated in Eq. (A.2) guarantees S(x) ∈ C2 in [x1, xn]. The only downside to this formula is that one does not have the knowledge of the second derivative values of the function at grid points. However, since S(x) ∈ C2 in [x1, xn], the following system provides (n − 2) equations relating the second order derivatives at the interior grid points to the function values at the nodes.
| (B.1) |
Which yields:
| (B.2) |
To complete the system of n equations and n unknowns, two additional equations for the second derivatives on the first and last grid points are required. Derivation of these two equations depend on the choice the boundary condition for the domain. Popular choices of boundary conditions are “natural”, “clamped”, and “not-a-knot”. Here we provide the G matrix for each of these types of splines. For simplicity, here we have assumed uniform distribution of the grid points in the domain, however, the methodology can easily be expanded for non-uniform distributions.
Natural spline
In “natural” spline, the second derivative of the function at first and last nodes are assumed to be zero. Hence, the following system of n equations and n unknowns can find second derivative values of the function based on the values of the function at the nodes.
| (B.3) |
The system of equations in (B.3) can be written in the matrix format:
| (B.4) |
where f″ = [f″(x1), f″(x2), …, f″(xn)]T; f = [f(x1), f(x2), …, f(xn)]T; and T and D are sparse square matrices of length n as follows:
The G matrix for “natural” spline (Gnat) can then be simply computed from Tnat and Dnat matrices:
| (B.5) |
Clamped spline
In “clamped” spline, the derivative of the function at the ends of the domain is assumed to be clamped to specified values (i.e. f′(x1) = a; f′(x1) = b). Without loss of generality, here we assume a = b = 0. The system of equations can thus be written as follows:
| (B.6) |
Hence, Tclamp and Dclamp matrices can be derived as follows:
And similarly,
| (B.7) |
Not-a-knot spline
In “not-a-knot” spline, the third derivate of the function is assumed to continuous at x2 and xn−1. The system of equations can thus be written as follows:
| (B.8) |
Hence, Tnknot and Dnknot matrices can be derived as follows:
And similarly,
| (B.9) |
Appendix C. Comparison of waveCSD with iCSD and kCSD methods in example Gaussian ground-truth waveforms
Figure A1.

Discretization of a rectangular grid of size nx×ny
Figure C1. Comparison of the accuracy of waveCSD, iCSD, and kCSD methods in the reconstruction of LFPs generated from a ground-truth waveform.
A) A ground-truth waveform (the CSD profile, top left) is assumed to be generated 6 mm away from an A1x16 probe, inserted perpendicularly in the cortex with an inter-electrode spacing of 100 μm. The first electrode is assumed to be 100 μm deep in the brain tissue. Here, the waveform propagates towards the electrodes at a constant velocity of 4 mm/min. The resultant LFPs are shown in the top right panel (black → most superficial electrode, and red → deepest electrode in the probe). B) Model parameter estimation for kCSD method using k-fold cross-validation technique as described in (Potworowski et al., 2012). The left panel shows cross-validation error for a wide range of R and h values, and the inset confirms that the selected parameters (the red dot) coincide with the global minimum of cross-validation error values. The estimated diameter (2R) for the kCSD method is used for source reconstruction in the iCSD method shown in panel C. C) Source reconstruction using iCSD, kCSD and waveCSD methods without the presence of noise in the LFP data. (iCSD- RDM: 0.62, MAG: 0.18; kCSD- 0.62, MAG: 0.33, waveCSD- RDM: 0.01, MAG: 0.99). Both RDM and MAG measures confirm that the waveCSD method provides more accurate CSD reconstruction among all methods (i.e. RDM closer to zero and MAG closer to 1 in the waveCSD method). For better visualization, colorbar ranges are different in figures. Parameters: waveCSD method- same as Fig. 1. kCSD method- R = 1.6 [mm]; h = 0.14. D) mean±std for RDM and MAG of 50 realization of the noisy LFP data at each noise level for all three methods. Noise reduction in the iCSD method was performed by applying a Gaussian spatial filter on the reconstructed CSD from unfiltered LFP recordings (Gaussian filter sigma: σgf = 0.1 [mm]).
Figure C2. Comparison of the accuracy of waveCSD, iCSD, and kCSD methods in the reconstruction of LFPs generated from a ground-truth waveform.
A) A ground-truth waveform (the CSD profile, top left) is assumed to be generated 6 mm away from an A1x16 probe, inserted perpendicularly in the cortex with an inter-electrode spacing of 100 μm. The first electrode is assumed to be 100 μm deep in the brain tissue. Here, the waveform propagates towards the electrodes at a constant velocity of 4 mm/min. The waveform is generated by superposition of 10 random Gaussian sources with random amplitude, spread, and angles. The resultant LFPs are shown in the top right panel (black → most superficial electrode, and red → deepest electrode in the probe). B) Model parameter estimation for kCSD method using k-fold cross-validation technique as described in (Potworowski et al., 2012). The left panel shows cross-validation error for a wide range of R and h values, and the inset confirms that the selected parameters (the red dot) coincide with the global minimum of cross-validation error values. The estimated diameter (2R) for the kCSD method is used for source reconstruction in the iCSD method shown in panel C. C) Source reconstruction using iCSD, kCSD and waveCSD methods without the presence of noise in the LFP data. For comparison purposes, colorbar ranges and labels are the same as in C1 A left panel. (iCSD- RDM: 0.64, MAG: 0.54; kCSD- 0.66, MAG: 0.72, waveCSD-RDM: 0.05, MAG: 0.99). Both RDM and MAG measures confirm that the waveCSD method provides more accurate CSD reconstruction among all methods (i.e. RDM closer to zero and MAG closer to 1 in the waveCSD method). Parameters: waveCSD method- same as Fig. 1. kCSD method- R = 2.2 [mm]; h = 0.35. D) mean±std for RDM and MAG of 50 realization of the noisy LFP data at each noise level for all three methods. Noise reduction in the iCSD method was performed by applying a Gaussian spatial filter on the reconstructed CSD from unfiltered LFP recordings (Gaussian filter sigma: σgf = 0.1 [mm]).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aroniadou VA, Keller A. The patterns and synaptic properties of horizontal intracortical connections in the rat motor cortex. Journal of neurophysiology. 1993;70:1553–69. doi: 10.1152/jn.1993.70.4.1553. [DOI] [PubMed] [Google Scholar]
- Barth DS, Baumgartner C, Di S. Laminar interactions in rat motor cortex during cyclical excitability changes of the penicillin focus. Brain research. 1990;508:105–17. doi: 10.1016/0006-8993(90)91123-x. [DOI] [PubMed] [Google Scholar]
- Basarsky TA, Duffy SN, Andrew RD, MacVicar BA. Imaging spreading depression and associated intracellular calcium waves in brain slices. Journal of Neuroscience. 1998;18:7189–99. doi: 10.1523/JNEUROSCI.18-18-07189.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P, Keliris GA, Ecker AS, Logothetis NK, Tolias AS. Feature selectivity of the gamma-band of the local field potential in primate primary visual cortex. Frontiers in neuroscience. 2008;2:199. doi: 10.3389/neuro.01.037.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Box GE, Cox DR. An analysis of transformations. Journal of the Royal Statistical Society. Series B (Methodological) 1964:211–52. [Google Scholar]
- Brennan KC, Beltrán-Parrazal L, López-Valdés HE, Theriot J, Toga AW, Charles AC. Distinct vascular conduction with cortical spreading depression. Journal of neurophysiology. 2007;97:4143–51. doi: 10.1152/jn.00028.2007. [DOI] [PubMed] [Google Scholar]
- Burkitt GR, Silberstein RB, Cadusch PJ, Wood AW. Steady-state visual evoked potentials and travelling waves. Clinical Neurophysiology. 2000;111:246–58. doi: 10.1016/s1388-2457(99)00194-7. [DOI] [PubMed] [Google Scholar]
- Cabo A, Riera JJ. How the active and diffusional nature of brain tissues can generate monopole signals at micrometer sized measures. 2014 arXiv preprint arXiv:1410.0274. [Google Scholar]
- Charles AC, Baca SM. Cortical spreading depression and migraine. Nature Reviews Neurology. 2013;9:637. doi: 10.1038/nrneurol.2013.192. [DOI] [PubMed] [Google Scholar]
- Chen S, Li P, Luo W, Gong H, Zeng S, Luo Q. Time-varying spreading depression waves in rat cortex revealed by optical intrinsic signal imaging. Neuroscience letters. 2006;396:132–6. doi: 10.1016/j.neulet.2005.11.025. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Bedard C. Do neurons generate monopolar current sources? Journal of neurophysiology. 2012;108:953–5. doi: 10.1152/jn.00357.2012. [DOI] [PubMed] [Google Scholar]
- Einevoll GT, Kayser C, Logothetis NK, Panzeri S. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nature Reviews Neuroscience. 2013;14:770–85. doi: 10.1038/nrn3599. [DOI] [PubMed] [Google Scholar]
- Feuerstein D, Manning A, Hashemi P, Bhatia R, Fabricius M, Tolias C, Pahl C, Ervine M, Strong AJ, Boutelle MG. Dynamic metabolic response to multiple spreading depolarizations in patients with acute brain injury: an online microdialysis study. Journal of Cerebral Blood Flow & Metabolism. 2010;30:1343–55. doi: 10.1038/jcbfm.2010.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman J, Nicholson C. Experimental optimization of current source-density technique for anuran cerebellum. Journal of Neurophysiology. 1975;38:369–82. doi: 10.1152/jn.1975.38.2.369. [DOI] [PubMed] [Google Scholar]
- Godlove DC, Maier A, Woodman GF, Schall JD. Microcircuitry of agranular frontal cortex: testing the generality of the canonical cortical microcircuit. Journal of Neuroscience. 2014;34:5355–69. doi: 10.1523/JNEUROSCI.5127-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorji A. Spreading depression: a review of the clinical relevance. Brain Research Reviews. 2001;38:33–60. doi: 10.1016/s0165-0173(01)00081-9. [DOI] [PubMed] [Google Scholar]
- Goto T, Hatanaka R, Ogawa T, Sumiyoshi A, Riera J, Kawashima R. An evaluation of the conductivity profile in the somatosensory barrel cortex of Wistar rats. Journal of neurophysiology. 2010;104:3388–412. doi: 10.1152/jn.00122.2010. [DOI] [PubMed] [Google Scholar]
- Grafstein B. Mechanism of spreading cortical depression. Journal of neurophysiology. 1956;19:154–71. doi: 10.1152/jn.1956.19.2.154. [DOI] [PubMed] [Google Scholar]
- Gramfort A, Papadopoulo T, Olivi E, Clerc M. OpenMEEG: opensource software for quasistatic bioelectromagnetics. Biomedical engineering online. 2010;9:45. doi: 10.1186/1475-925X-9-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratiy SL, Pettersen KH, Einevoll GT, Dale AM. Pitfalls in the interpretation of multielectrode data: on the infeasibility of the neuronal current-source monopoles. Journal of neurophysiology. 2013;109:1681–2. doi: 10.1152/jn.01047.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halnes G, Mäki-Marttunen T, Keller D, Pettersen KH, Andreassen OA, Einevoll GT. Effect of ionic diffusion on extracellular potentials in neural tissue. PLoS computational biology. 2016;12:e1005193. doi: 10.1371/journal.pcbi.1005193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X, Xu W, Liang J, Takagaki K, Gao X, Wu J-y. Spiral wave dynamics in neocortex. Neuron. 2010;68:978–90. doi: 10.1016/j.neuron.2010.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes JR, Ikram A, Fino JJ. Characteristics of travelling waves under various conditions. Clinical Electroencephalography. 1995;26:7–22. doi: 10.1177/155005949502600104. [DOI] [PubMed] [Google Scholar]
- Hughes JR, Kuruvilla A, Fino JJ. Topographic analysis of visual evoked potentials from flash and pattern reversal stimuli: evidence for “travelling waves”. Brain topography. 1992;4:215–28. doi: 10.1007/BF01131153. [DOI] [PubMed] [Google Scholar]
- Kajikawa Y, Schroeder CE. How local is the local field potential? Neuron. 2011;72:847–58. doi: 10.1016/j.neuron.2011.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzner S, Nauhaus I, Benucci A, Bonin V, Ringach DL, Carandini M. Local origin of field potentials in visual cortex. Neuron. 2009;61:35–41. doi: 10.1016/j.neuron.2008.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasretdinov A, Lotfullina N, Burkhanova G, Chernova K, Zakharov A, Khazipov R. Direct Current Coupled Recordings of Cortical Spreading Depression Using Silicone Probes. Frontiers in cellular neuroscience. 2017;11:408. doi: 10.3389/fncel.2017.00408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer DR, Fujii T, Ohiorhenuan I, Liu CY. Cortical spreading depolarization: pathophysiology, implications, and future directions. Journal of Clinical Neuroscience. 2016;24:22–7. doi: 10.1016/j.jocn.2015.08.004. [DOI] [PubMed] [Google Scholar]
- Kreiman G, Hung CP, Kraskov A, Quiroga RQ, Poggio T, DiCarlo JJ. Object selectivity of local field potentials and spikes in the macaque inferior temporal cortex. Neuron. 2006;49:433–45. doi: 10.1016/j.neuron.2005.12.019. [DOI] [PubMed] [Google Scholar]
- Kunkler PE, Kraig RP. Calcium waves precede electrophysiological changes of spreading depression in hippocampal organ cultures. Journal of Neuroscience. 1998;18:3416–25. doi: 10.1523/JNEUROSCI.18-09-03416.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauritzen M. Pathophysiology of the migraine aura: the spreading depression theory. Brain. 1994;117:199–210. doi: 10.1093/brain/117.1.199. [DOI] [PubMed] [Google Scholar]
- Leao A, Morison R. Propagation of spreading cortical depression. The Journal of Nervous and Mental Disease. 1945;102:512. [Google Scholar]
- Leão AA. The slow voltage variation of cortical spreading depression of activity. Electroencephalography and clinical neurophysiology. 1951;3:315–21. doi: 10.1016/0013-4694(51)90079-x. [DOI] [PubMed] [Google Scholar]
- Leo AA. Spreading depression of activity in the cerebral cortex. Journal of neurophysiology. 1944;7:359–90. doi: 10.1152/jn.1947.10.6.409. [DOI] [PubMed] [Google Scholar]
- Łęski S, Pettersen KH, Tunstall B, Einevoll GT, Gigg J, Wójcik DK. Inverse current source density method in two dimensions: inferring neural activation from multielectrode recordings. Neuroinformatics. 2011;9:401–25. doi: 10.1007/s12021-011-9111-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Łęski S, Wójcik DK, Tereszczuk J, Œwiejkowski DA, Kublik E, Wróbel A. Inverse current-source density method in 3D: reconstruction fidelity, boundary effects, and influence of distant sources. Neuroinformatics. 2007;5:207–22. doi: 10.1007/s12021-007-9000-z. [DOI] [PubMed] [Google Scholar]
- Lindén H, Tetzlaff T, Potjans TC, Pettersen KH, Grün S, Diesmann M, Einevoll GT. Modeling the spatial reach of the LFP. Neuron. 2011;72:859–72. doi: 10.1016/j.neuron.2011.11.006. [DOI] [PubMed] [Google Scholar]
- Lopes da Silva F, Storm van Leeuwen W. The cortical alpha rhythm in dog: the depth and surface profile of phase. Raven Press; New York: 1978. [Google Scholar]
- Makarova J, Gómez-Galán M, Herreras O. Variations in tissue resistivity and in the extension of activated neuron domains shape the voltage signal during spreading depression in the CA1 in vivo. European Journal of Neuroscience. 2008;27:444–56. doi: 10.1111/j.1460-9568.2008.06022.x. [DOI] [PubMed] [Google Scholar]
- Massimini M, Huber R, Ferrarelli F, Hill S, Tononi G. The sleep slow oscillation as a traveling wave. Journal of Neuroscience. 2004;24:6862–70. doi: 10.1523/JNEUROSCI.1318-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. 1985 doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- Mori Y. A multidomain model for ionic electrodiffusion and osmosis with an application to cortical spreading depression. Physica D: Nonlinear Phenomena. 2015;308:94–108. [Google Scholar]
- Muller L, Chavane F, Reynolds J, Sejnowski TJ. Cortical travelling waves: mechanisms and computational principles. Nature Reviews Neuroscience. 2018 doi: 10.1038/nrn.2018.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nauhaus I, Busse L, Carandini M, Ringach DL. Stimulus contrast modulates functional connectivity in visual cortex. Nature neuroscience. 2009;12:70–6. doi: 10.1038/nn.2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson C, Freeman JA. Theory of current source-density analysis and determination of conductivity tensor for anuran cerebellum. Journal of neurophysiology. 1975;38:356–68. doi: 10.1152/jn.1975.38.2.356. [DOI] [PubMed] [Google Scholar]
- Nicholson C, Llinas R. Real time current source-density analysis using multi-electrode array in cat cerebellum. Brain research. 1975;100:418–24. doi: 10.1016/0006-8993(75)90494-1. [DOI] [PubMed] [Google Scholar]
- Nunez PL. Wavelike properties of the alpha rhythm. IEEE Transactions on Biomedical Engineering. 1974:473–82. [Google Scholar]
- Nunez PL, Cutillo BA. Neocortical dynamics and human EEG rhythms. Oxford University Press; USA: 1995. [Google Scholar]
- Obrenovitch TP, Urenjak J, Wang M. Nitric oxide formation during cortical spreading depression is critical for rapid subsequent recovery of ionic homeostasis. Journal of Cerebral Blood Flow & Metabolism. 2002;22:680–8. doi: 10.1097/00004647-200206000-00006. [DOI] [PubMed] [Google Scholar]
- Peters O, Schipke CG, Hashimoto Y, Kettenmann H. Different mechanisms promote astrocyte Ca2+ waves and spreading depression in the mouse neocortex. Journal of Neuroscience. 2003;23:9888–96. doi: 10.1523/JNEUROSCI.23-30-09888.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen KH, Devor A, Ulbert I, Dale AM, Einevoll GT. Current-source density estimation based on inversion of electrostatic forward solution: effects of finite extent of neuronal activity and conductivity discontinuities. Journal of neuroscience methods. 2006;154:116–33. doi: 10.1016/j.jneumeth.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Potworowski J, Jakuczun W, Łȩski S, Wójcik D. Kernel current source density method. Neural computation. 2012;24:541–75. doi: 10.1162/NECO_a_00236. [DOI] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in C. Cambridge university press; Cambridge: 1996. [Google Scholar]
- Qian N, Sejnowski T. An electro-diffusion model for computing membrane potentials and ionic concentrations in branching dendrites, spines and axons. Biological Cybernetics. 1989;62:1–15. [Google Scholar]
- Richter F, Lehmenkühler A. Spreading depression can be restricted to distinct depths of the rat cerebral cortex. Neuroscience letters. 1993;152:65–8. doi: 10.1016/0304-3940(93)90484-3. [DOI] [PubMed] [Google Scholar]
- Riera J, Cabo A. Reply to Gratiy et al. Journal of neurophysiology. 2013;109:1684–5. doi: 10.1152/jn.00014.2013. [DOI] [PubMed] [Google Scholar]
- Riera JJ, Goto T, Kawashima R. A methodology for fast assessments to the electrical activity of barrel fields in vivo: from population inputs to single unit outputs. Frontiers in neural circuits. 2014:8. doi: 10.3389/fncir.2014.00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riera JJ, Ogawa T, Goto T, Sumiyoshi A, Nonaka H, Evans A, Miyakawa H, Kawashima R. Pitfalls in the dipolar model for the neocortical EEG sources. Journal of neurophysiology. 2012;108:956–75. doi: 10.1152/jn.00098.2011. [DOI] [PubMed] [Google Scholar]
- Rohr K, Stiehl HS, Sprengel R, Buzug TM, Weese J, Kuhn M. Landmark-based elastic registration using approximating thin-plate splines. IEEE Transactions on medical imaging. 2001;20:526–34. doi: 10.1109/42.929618. [DOI] [PubMed] [Google Scholar]
- Schroeder CE, Mehta AD, Givre SJ. A spatiotemporal profile of visual system activation revealed by current source density analysis in the awake macaque. Cerebral cortex (New York, NY: 1991) 1998;8:575–92. doi: 10.1093/cercor/8.7.575. [DOI] [PubMed] [Google Scholar]
- Song Y, Torres RA, Garcia S, Frometa Y, Bae J, Deshmukh A, Lin W-C, Zheng Y, Riera JJ. Dysfunction of Neurovascular/Metabolic Coupling in Chronic Focal Epilepsy. IEEE Transactions on Biomedical Engineering. 2016;63:97–110. doi: 10.1109/TBME.2015.2461496. [DOI] [PubMed] [Google Scholar]
- Sword J, Croom D, Wang PL, Thompson RJ, Kirov SA. Neuronal pannexin-1 channels are not molecular routes of water influx during spreading depolarization-induced dendritic beading. Journal of Cerebral Blood Flow & Metabolism. 2017;37:1626–33. doi: 10.1177/0271678X16639328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tikhonov AN, Arsenin VIAk, John F. Solutions of ill-posed problems. Winston; Washington, DC: 1977. [Google Scholar]
- Wadman W, Juta A, Kamphuis W, Somjen G. Current source density of sustained potential shifts associated with electrographic seizures and with spreading depression in rat hippocampus. Brain research. 1992;570:85–91. doi: 10.1016/0006-8993(92)90567-s. [DOI] [PubMed] [Google Scholar]
- Wahba G. Spline models for observational data. Siam; 1990. [Google Scholar]
- Wang C, Ulbert I, Schomer DL, Marinkovic K, Halgren E. Responses of human anterior cingulate cortex microdomains to error detection, conflict monitoring, stimulus-response mapping, familiarity, and orienting. Journal of Neuroscience. 2005;25:604–13. doi: 10.1523/JNEUROSCI.4151-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HR, Blake R, Lee S-H. Dynamics of travelling waves in visual perception. Nature. 2001;412:907–10. doi: 10.1038/35091066. [DOI] [PubMed] [Google Scholar]
- Wu J-Y, Huang X, Zhang C. Propagating waves of activity in the neocortex: what they are, what they do. The Neuroscientist. 2008;14:487–502. doi: 10.1177/1073858408317066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xing D, Yeh C-I, Shapley RM. Spatial spread of the local field potential and its laminar variation in visual cortex. Journal of neuroscience. 2009;29:11540–9. doi: 10.1523/JNEUROSCI.2573-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanos TP, Mineault PJ, Nasiotis KT, Guitton D, Pack CC. A sensorimotor role for traveling waves in primate visual cortex. Neuron. 2015;85:615–27. doi: 10.1016/j.neuron.2014.12.043. [DOI] [PubMed] [Google Scholar]