In situ manipulation and switching of dislocations in bilayer graphene

A materials scientist’s dream come true: manipulating and controlling individual dislocations in situ.

Abstract

Topological defects in crystalline solids are of fundamental interest in physics and materials science because they can radically alter the properties of virtually any material. Of particular importance are line defects, known as dislocations, which are the main carriers of plasticity and have a tremendous effect on electronic and optical properties. Understanding and controlling the occurrence and behavior of those defects have been of major and ongoing interest since their discovery in the 1930s. This interest was renewed with the advent of two-dimensional materials in which a single topological defect can alter the functionality of the whole system and even create new physical phenomena. We present an experimental approach to directly manipulate dislocations in situ on the nanometer scale by using a dedicated scanning electron microscope setup. With this approach, key fundamental characteristics such as line tension, defect interaction, and node formation have been studied. A novel switching reaction, based on the recombination of dislocation lines, was found, which paves the way for the concept of switches made of a bimodal topological defect configuration.

INTRODUCTION

Topological line defects in crystalline solids, known as dislocations, are one of the most fundamental and fascinating phenomena studied in materials science. They not only are the main carriers of plasticity (1–3) but also can heavily influence the electrical (4–7) and optical properties (8, 9) of materials. This ability of dislocations to determine physical properties becomes even more important in the age of two-dimensional materials, where a single defect may change the behavior of the whole material. For instance, in bilayer graphene, the thinnest material that can contain in-plane dislocations (10, 11), these defects can act as valley-polarized transport channels (12), reflect plasmons (13), and induce a linear magnetoresistance (14). Here, we report the direct manipulation of individual dislocations in free-standing bilayer graphene by in situ scanning electron microscopy (SEM). Fundamental dislocation phenomena such as line tension, dislocation reaction, and node formation are demonstrated. In addition, out-of-plane dislocations are found to offer the unique ability to serve as anchor points and switching sites for in-plane dislocations. We show how these fundamental properties of dislocations can be used to build switches made of topological defects.

RESULTS

The interest in bilayer graphene, a stack of two layers of purely sp²-hybridized carbon, has surged in recent years due to its fascinating optical (15) and electronic properties (16, 17). But also from a structural point of view, bilayer graphene is very intriguing, because it is the thinnest material to host extended in-plane dislocations (10), also described in literature as solitons (11) or domain walls (18), as well as stacking faults (10, 11), two of the most fundamental defects in crystalline solids. In bilayer graphene, there are two energetically degenerate stacking orders of AB and AC in addition to a third unfavorable AA stacking in which all atoms of both layers lie on top of each other. In one bilayer graphene sheet, the stacking order can be changed by the introduction of in-plane partial dislocations (or short: partials) with a Burgers vector of $\frac{\mathit{a}}{3}\langle 1\overline{1}00\rangle$ (see fig. S1 for a detailed description of stacking orders). Usually, only the stacking orders of AB and AC are observed, with AA only occurring at graphene layer edges (19) or in dislocation nodes (11). Perfect in-plane dislocations with a Burgers vector of $\frac{\mathit{a}}{3}\langle 11\overline{2}0\rangle$ dissociate into two partials connected by a stacking fault, which is especially favorable energetically in bilayer graphene because the stacking fault energy for a change from AB to AC is zero (10). Dislocations with a Burgers vector component perpendicular to the line direction (edge-type dislocations) can reduce their energy by relaxing into an extended topographic ripple in the membrane (10, 20). Using a tip, controlled by a micromanipulator, those ripples can be moved around akin to a carpet fold, as schematically shown in Fig. 1A. In addition, out-of-plane dislocations are considered in this study, which cannot be moved around mechanically (see Fig. 1B for an overview of the here-considered defects). Dislocations in bilayer graphene have been characterized using transmission electron microscopy (TEM) (10, 11) in the free-standing case and near-field infrared nanoscopy (13, 18) in the non–free-standing (supported) case, where dislocation manipulations have been recently demonstrated by Jiang et al. (21). Here, we present an alternative way to visualize defects in free-standing bilayer graphene by using SEM in the transmission mode (tSEM). This allows the simultaneous imaging and usage of micromanipulators due to the large chamber. Figure 1C shows the general setup inside the chamber of the SEM: A low-energy (500 V to 30 kV) electron probe is scanned over a sample, and the interaction with the graphene leads to the emission of secondary electrons containing topographic information, while transmitted electrons carry crystallographic and, through this, also topographic information (see fig. S2 for details on contrast formation in tSEM). The comparatively low energy of the electrons increases the interaction of the probe with the sample while maintaining a spatial resolution of <1 nm. Figure 1D shows a typical dark-field (DF) tSEM image of bilayer graphene containing three dislocations at the upper end of a hole in the support film. In addition, the graphene membrane shows features attributed to topography running diagonally from left to right through the membrane. Using a piezo-controlled micromanipulator with a fine tip, we can manipulate individual dislocations directly in situ, enabling the characterization and exploitation of fundamental properties of those defects. Among the fundamental properties are line tension (associated with dislocation line energy), mutual interaction of dislocations, and the possibility of dislocation reactions and node formation (22).

Fig. 1. Overview of the dislocation manipulation.

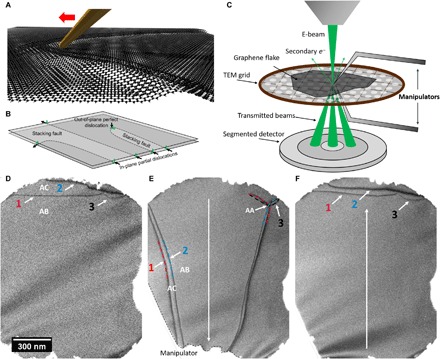
(A) Artistic representation of the manipulation process. Dislocations in bilayer graphene, which relax into atomic-scale topographic ripples, can be controlled using a fine tip mounted on a piezo-driven micromanipulator. (B) Overview of the types of dislocations to be considered for this work: In-plane dislocations are mobile contrary to the sessile out-of-plane dislocations. In-plane dislocations are of the partial type and necessitate a stacking fault between them. (C) Schematic representation of the in situ setup in the SEM. A low-energy electron probe is scanned over a graphene flake on a TEM grid. The transmitted electrons carrying the crystallographic information are detected with a segmented detector, allowing bright-field and different DF imaging modes (see fig. S2 for details on contrast formation). Micromanipulators can be placed below and above the sample to allow access from both sides for manipulations and mechanical cleaning. (D to F) Exemplary in situ dislocation manipulation process: Three dislocations are visible at the upper part of the hole in the support film. Dislocations 1 and 2 (as well as 3 and 2) enclose a different stacking order of AC stacking, compared to the AB stacking elsewhere. (E) Using a micromanipulator, the dislocations can be extended to about three times their length, in turn also changing their character from dominantly screw type to edge type and vice versa. The interaction of the dislocations also results in a dislocation reaction, creating an intersection that includes the energetically unfavorable AA stacking [see fig. S6 for high-resolution TEM (HRTEM) of such an intersection]. (F) Releasing the micromanipulator leads to an almost complete reversal of the dislocation structure due to line tension.

In our setup, several manipulators can be used at the same time, enabling the combined usage of different tip sizes and allowing mechanical cleaning. Graphene is unavoidably contaminated by organic residuals. These residuals alter the mechanical behavior of dislocations (see fig. S3 for a manipulation on an uncleaned sample) and have a detrimental effect on the image quality due to the increase in diffuse scattering. Usual cleaning methods for graphene include thermal annealing (23), plasma treatment (24), and chemical activation (25), all of which lack the ability to thoroughly and site-specifically clean bilayer graphene. Instead, in this study, we use two micromanipulators to mechanically clean bilayer graphene from both sides. During the process, we moved tungsten tips over the top and bottom graphene surface in a sweeping motion, removing adsorbed contaminants (see movie S1). This process can be repeated if electron beam–induced contamination accumulates on the membrane. We can then control the dislocations either by using the same tips also used for cleaning or by using a third tip. Figure 1 (D to F) shows an exemplary manipulation of a triplet of in-plane dislocations (see movie S2 for the whole manipulation). Although it appears that only two dislocations are present, during the manipulation, it becomes apparent that the lower line consists of two separate dislocations (1, 3), which are pinned at an out-of-plane dislocation (see below). Using a micromanipulator, dislocations 1 and 2 are elongated to about three times their original length. In the process, the majority of dislocation 1 is changed from a more screw type (see fig. S4 for the correlation of Burgers vector and contrast width) to a more edge type, and for dislocation 2, the same process happens vice versa. Edge- and screw-type dislocations are expected to have a different line energy associated with them (see also fig. S5) (20). Dislocation 3 is not directly controlled by the manipulator tip but is influenced by the other dislocations and forced to undergo a reaction. This kind of reaction [which is similar to what was already described in pioneering work on graphite in the 1960s (26)] results in the formation of a node containing AA stacking, necessitating three distinct partial dislocations with different Burgers vectors (see fig. S6 for a detailed look at dislocation nodes). After release of the manipulator (Fig. 1F), the dislocations return to their initial configuration, with only dislocation 2 being a bit further inside the window compared to the initial state. This can be attributed to contamination on the window edges that hinder the complete relaxation. The reversal of the dislocations to their original locations illustrates the fundamental effect of line tension, which shortens the dislocations and drives the system back to a state of low energy. Looking further into the movement of the dislocations, it becomes apparent that dislocations 1 and 3 are pinned at a point inside of the membrane. At this point, a third out-of-plane dislocation must be attached to fulfill a basic rule of dislocations, namely, that the sum of Burgers vectors must add up to zero at any dislocation node (22). By carefully evaluating the direction and sign of Burgers vectors of the attached in-plane dislocations using DF-TEM (see fig. S7 for a complete analysis), we can deduce that all out-of-plane dislocations are perfect dislocations with Burgers vectors of type $\frac{\mathit{a}}{3}\langle 11\overline{2}0\rangle$. This is in agreement with the fact that from a structural point of view, these out-of-plane dislocations are nothing but dislocations in monolayer graphene, which are known to have this type of Burgers vector (27–29). Because an out-of-plane dislocation has a line direction perpendicular to the basal plane, there must be an abrupt 90° change in the line direction associated with the continuation as in-plane dislocations. Out-of-plane dislocations are sessile at room temperature, making them ideal anchor points for in-plane dislocations that are otherwise free to move owing to weak Peierls potential in the basal plane.

Looking further into dislocation configurations with arrays of out-of-plane dislocations (see Fig. 2A), we found a switching mechanism. The out-of-plane dislocations are arranged along a line, indicating a small-angle grain boundary (ca. 0.2°). At each out-of-plane dislocation, two in-plane partial dislocations are attached, with one being predominantly screw type and the other being predominantly edge type. Figure 2B shows the alternating character of the dislocations signified by the line thickness (see also fig. S4). We believe the dislocations to be grown-in during the synthesis, as shown in Fig. 2C. An out-of-plane dislocation of the perfect type is present in the first layer of the bilayer graphene. Upon growth of the second layer, the dislocation must either continued or kink and follow the growth direction. Because of the weak van der Waals–type binding between the layers, the latter option seems to be preferred. To minimize the defect energy, the dislocation then splits into two partials. Note that because of the absence of stacking fault energy in bilayer graphene, there is no attractive force between the two partials, meaning that the splitting width is solely determined by line tension and interaction with surrounding dislocations. Figure 2 (D to G) shows frames from an in situ manipulation experiment (see movies S3 and S4 for the whole manipulation), in which a switching reaction was observed. The switching is based on the recombination of dislocation lines at out-of-plane dislocations, enabling the connection and separation of spatially confined areas of different stacking. Looking at out-of-plane dislocation II shows the different steps of this process in more detail. First, in-plane dislocations C and D are attached to II. Upon starting the manipulation, a first switching reaction is induced, resulting in A and D being attached to II, whereas C is now attached to I (see Fig. 2E). By moving the manipulator further (Fig. 2F), additional switching reactions are induced: Now, A and B are attached to II, whereas C and D are attached to I. E is locally attracted to II, as seen by the bending of the dislocation line close to the out-of-plane dislocation, forming an energetically favorable, metastable intersection. Moving the manipulator further induces the rearrangement of dislocation lines involved in this intersection: The part of E spanning between II and III recombines with the whole length of A to form a new dislocation line attached to III. The rest of E is now only fixed on II. In total, I, II, and III have undergone switching reactions and are now connected to partial dislocations different from those before. IV did not show any switching behavior because the manipulator only slightly influences the in-plane dislocations (G and H) attached to it, also showing how locally controlled these reactions can take place. However, not only the dislocation connections are rearranged, but also areas of different stacking orders are combined or divided using this process. Each in-plane partial dislocation changes the stacking order of the graphene sheets from AB to AC or vice versa (signified in Fig. 2, E to G, by light gray shading). By moving partial dislocations, we can increase the areas of a specific stacking order without necessarily changing the energy of the system due to the stacking fault energy being zero. In the example, two formerly separated areas of AC stacking are combined to form a pathway of AC stacking (shaded green in Fig. 2, D and G). A and B, as well as E and F, enclose areas of AC stacking. By attaching B and E at II and A and F at III, the separated areas can join up to form a larger area of that stacking order, in turn dividing the large area of AB stacking into two independent segments.

Fig. 2. Switching reactions at a dislocation array pinned at out-of-plane dislocations.

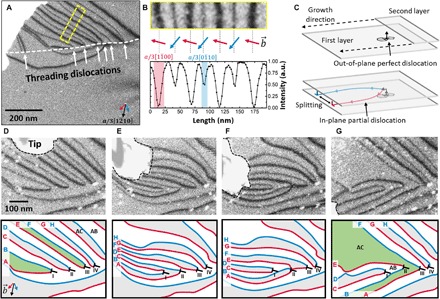
(A) Overview of the membrane containing an array: Pairs of in-plane partial dislocations are pinned at out-of-plane dislocations. Because those dislocations all lie on a line, there is a small-angle tilt grain boundary (ca. 0.2°) in the first layer. (B) The magnification of several dislocation lines shows the alternating screw and edge character of the defects. The contrast width in the tSEM images fits very well to the relation between Burgers vector and line direction (see also fig. S4). a.u., arbitrary units. (C) Proposed growth mechanism of the in-plane dislocations: A perfect out-of-plane dislocation is present in the first layer. Upon growth of the second layer, the dislocation line turns perpendicular to the original direction and follows the growth of the second layer. To minimize the energy of the system, the dislocation splits into two partial dislocations. (D to G) Frames from an in situ experiment with a fine tip (see movies S3 and S4), in which dislocation switching reactions were observed. For each image, a schematic representation including information about Burgers vectors, stacking orders, and dislocation labeling is shown. Because of the influence of the manipulator, the dislocations are forced to move, and different line segments and areas with the same stacking order recombine. Dislocation A, for instance, is attached to out-of-plane dislocation I at the beginning of the manipulation but changes its attachment step by step to be finally linked to out-of-plane dislocation III. During this process, the two green AC stacked areas also combine to form a larger area of this stacking, in turn dividing the area of AB stacking, meaning that it is possible to travel from one area to the other without crossing a topological defect.

DISCUSSION

Dislocation reactions are governed by the intrinsic defect properties (for example, line tension), the mutual interaction of dislocations, and the application of external forces. Without an external stimulus, the dislocations will return to a state of lowest energy, where mobile dislocation segments shorten as a result of line tension. On the basis of these fundamental properties and the unique possibility of initiating dislocation reactions, it is conceivable to build “topological switches” with two distinct stable states. Here, we use the word topological to signify that we can alternate between two states, which are, in principle, invariant to other properties such as total energy or mass except for the arrangement of topological defects. By switching between appropriate arrangements, it is possible to traverse a sample without encountering a topological defect in one state while always encountering such a defect in the other state. Such a dislocation-based topological switch is laid out in Fig. 3. Taking into account the ability of dislocations to alter materials properties, which recent findings showed for bilayer graphene (30, 31), it is conceivable that such a switch could be used to control functional properties. The switch consists of a ribbon of bilayer graphene with a defined dislocation arrangement contained in it. Metallic pads on either end of the ribbon can be used to contact the structure electrically. There are two distinct states that can be reversibly achieved by mechanical manipulation of the dislocation arrangement. The basis of the switch is two out-of-plane dislocations acting as anchor points for two in-plane dislocations each. In what we call the On state, the two partial dislocations point outward the ribbon edge, leaving a connected path of AB stacking open (see Fig. 3A). The switching can now be initiated by connecting one partial to the other out-of-plane dislocation (similar to the process demonstrated in Fig. 2), using the manipulation approach described in this work (see Fig. 3B). Dislocations can freely move along the ribbon edges (see fig. S8 for an example of dislocations interacting with a free edge). In the resulting Off state, two parallel lines of partial dislocations stretch through the ribbon, enclosing a segment of AC stacking (see Fig. 3C). The distance of the lines is solely determined by the distance of the out-of-plane dislocations. In this case, traveling from one contact to the other, two topological defects have to be passed. This can lead to an insulating transport state if they are spaced out correctly (30). In the presence of a transverse magnetic field, the influence of the dislocations on the transport is expected to be accentuated. For the practical realization of such a switch, a defined dislocation configuration is needed. By screening several samples, we have found structures that could be exploited for further investigations using patterning techniques, as shown in Fig. 3D. The detailed description of the switching processes (Fig. 3, E and F) highlights the fundamental characteristic of line tension that can be used to complete the switching process once a reconnection of the dislocation lines is achieved. Because both stacking orders are energetically equivalent, the energy of the two different states only depends on the length of the dislocation lines and can therefore be equivalent in both states. Although difficult to realize, we firmly believe that such a switch could help confirm experimentally the influence of topological defects and their intrinsic properties on the transport in bilayer graphene. It further shows the fundamental possibility of using topological defects as building blocks for functional elements. Recent work by Jiang et al. (21), in principle, enables similar devices also on supported bilayer graphene, where the intrinsic properties of dislocations are altered by strong substrate interactions.

Fig. 3. Schematic representation of a topological switch with potential functional properties and the switching process.

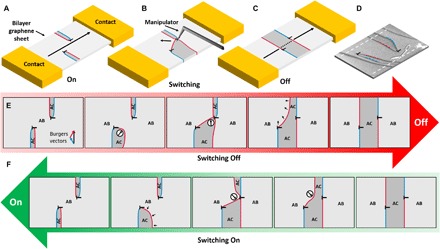
(A) Perspective view of the switch in the “On” position. A defined dislocation configuration is contained in a ribbon of bilayer graphene contacted at two sides. Mechanical switching (B) can change the dislocation state from an open to a closed configuration (C), meaning that, traversing the membrane, a topological defect is encountered in one state, while none is encountered in the other state (30). (D) Graphene membrane with a real dislocation configuration similar to the proposed switch, which could be transformed into the element by lithographic means. (E) The detailed process of the switching reaction from On to Off: Extension of a partial dislocation in the direction of the second out-of-plane dislocation leads to a recombination of dislocation lines. Line tension then straightens the dislocations to a defined state of minimal energy, with two dislocation lines running parallel through the ribbon. The configuration can be switched back (F) by connecting the other partial to the second out-of-plane dislocation.

In summary, using a new approach to image dislocations in free-standing bilayer graphene and simultaneously manipulate them mechanically on the nanoscale, fundamental properties of these topological defects, such as line tension, dislocation interaction, and node formation, could be directly revealed in situ. Moreover, a reaction between mobile in-plane dislocations anchored to sessile out-of-plane dislocations has been found, which alters the interconnectivity of bilayer graphene areas with identical stacking order (AB or AC). On the basis of these findings, the layout of a reversible “topological switch” with expected functional properties has been proposed.

MATERIALS AND METHODS

Sample preparation

Chemical vapor deposition–grown nominally bilayer graphene (Trivial Transfer Graphene) was purchased from ACS Material. The graphene films were delivered on a substrate and covered by a poly(methyl methacrylate) (PMMA) transfer layer. The graphene film was floated on deionized (DI) water, fished onto a piece of filter paper, and cut in rectangles with a size of approximately 2 mm × 2 mm. The rectangular pieces were then floated on DI water and picked up with Quantifoil TEM support films. To dissolve the PMMA layer, the TEM grid was immersed in acetone for 20 s and put into a saturated acetone vapor atmosphere under reflux for 2 hours afterward.

Microscopy

Scanning electron microscopy

A FEI Helios NanoLab 660 instrument equipped with a STEM III detector and the capacity to fit up to four micromanipulators (Kleindiek MM3A) inside the chamber was used for SEM imaging and in situ manipulation of dislocations. For manipulation experiments 2 or 3, MM3A manipulators were attached to the door of the microscope. The manipulators were equipped with commercial W tips (apex size of ca. 100 nm) or with focused ion beam–milled fine tips with apex sizes of ca. 25 nm. The microscope was operated at 20 kV in immersion mode. For tSEM imaging, the segmented STEM detector was read out according to the optimized contrast, as shown in fig. S2.

Transmission electron microscopy

A double-corrected FEI Titan Themis³ 300 electron microscope was used for DF-TEM and aberration-corrected HRTEM. The microscope was operated at 80 kV to reduce knock-on damage. For HRTEM, the monochromator was excited to reduce chromatic aberration and thus enhance resolution. Micrographs were recorded on a FEI Ceta camera.

Burgers vector analysis

$\{11\overline{2}0\}$ DF-TEM was used for Burgers vector evaluation. The $\vec{\mathit{g}}.\vec{\mathit{b}}=0$ invisibility criterion was applied to extract the direction of the Burgers vector for the respective dislocation (10). While the invisibility criterion can be used to identify the direction of the Burgers vector, its absolute sign cannot be derived. To determine the sign of the Burgers vector, we studied the change in DF-TEM contrast of the dislocation upon tilting the bilayer graphene membrane. The tilting axis was chosen perpendicular to the $\{11\overline{2}0\}$ diffraction vector so that the excitation error continuously changes during tilting (rocking curve scan). By tilting a few degrees away from the [0001] zone axis, the strain and (in the presence of an edge component) buckling of the membrane led to an asymmetric bright-dark contrast of the dislocation, as revealed in fig. S7. From the orientation of the bright-dark contrast, the absolute sign of the Burgers vector can be unambiguously derived. In the case of an edge dislocation, the sign of the Burgers vector determined whether an additional row of atoms was “inserted” in the top or bottom graphene layer. To interpret the sign of the Burgers vector, in this manner, the convention for the definition of the Burgers vector was fixed throughout the analysis. Here (in figs. S4 and S7), the so-called finish-to-start/right-hand convention (32) for the definition of the Burgers vector was used.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/8/eaat4712/DC1

Fig. S1. Stacking orders in bilayer graphene.

Fig. S2. Imaging modes in tSEM.

Fig. S3. Manipulation of a dislocation without mechanical cleaning.

Fig. S4. The relationship between dislocation type and line width.

Fig. S5. Example demonstrating the interplay of membrane topography and dislocation line direction.

Fig. S6. AA stacking in dislocation nodes.

Fig. S7. Complete analysis of the Burgers vector of dislocations.

Fig. S8. Dislocation interaction with free edges.

Movie S1. Exemplary cleaning of bilayer graphene.

Movie S2. Manipulation of three individual dislocations showing fundamental properties of dislocations.

Movie S3. Manipulation of an array of dislocations pinned to threading dislocations.

Movie S4. The whole, unabridged manipulation from movie S3.